ವ್ಯಾಖ್ಯಾನಗಳು. ನಾವು ಹಲವಾರು ಕೋನಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ (ಚಿತ್ರ 37): ASB, BSC, CSD, ಇದು ಅನುಕ್ರಮವಾಗಿ ಒಂದಕ್ಕೊಂದು ಪಕ್ಕದಲ್ಲಿದೆ, ಸಾಮಾನ್ಯ ಶೃಂಗದ ಸುತ್ತಲೂ ಒಂದೇ ಸಮತಲದಲ್ಲಿದೆ.

ASB ಕೋನದ ಸಮತಲವನ್ನು ಸಾಮಾನ್ಯ ಬದಿಯ SB ಸುತ್ತಲೂ ತಿರುಗಿಸೋಣ ಇದರಿಂದ ಈ ಸಮತಲವು ಕೆಲವನ್ನು ಮಾಡುತ್ತದೆ ದ್ವಿಮುಖ ಕೋನ BSC ವಿಮಾನದೊಂದಿಗೆ. ನಂತರ, ಫಲಿತಾಂಶದ ಡೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಬದಲಾಯಿಸದೆ, ನಾವು ಅದನ್ನು ಸರಳ ರೇಖೆಯ ಎಸ್‌ಸಿ ಸುತ್ತಲೂ ತಿರುಗಿಸುತ್ತೇವೆ ಇದರಿಂದ ಬಿಎಸ್‌ಸಿ ಪ್ಲೇನ್ ಸಿಎಸ್‌ಡಿ ಪ್ಲೇನ್‌ನೊಂದಿಗೆ ನಿರ್ದಿಷ್ಟ ಡೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಮಾಡುತ್ತದೆ. ಪ್ರತಿಯೊಂದು ಸಾಮಾನ್ಯ ಬದಿಯ ಸುತ್ತ ಈ ಅನುಕ್ರಮ ತಿರುಗುವಿಕೆಯನ್ನು ಮುಂದುವರಿಸೋಣ. ಕೊನೆಯ ಬದಿಯ SF ಮೊದಲ ಭಾಗ SA ಯೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾದರೆ, ನಂತರ ಒಂದು ಫಿಗರ್ ರಚನೆಯಾಗುತ್ತದೆ (ಚಿತ್ರ 38), ಇದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಬಹುಮುಖ ಕೋನ. ಕೋನಗಳನ್ನು ASB, BSC,... ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಫ್ಲಾಟ್ ಕೋನಗಳುಅಥವಾ ಅಂಚುಗಳು, ಅವರ ಕಡೆ SA, SB, ... ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಪಕ್ಕೆಲುಬುಗಳು, ಮತ್ತು ಸಾಮಾನ್ಯ ಶೃಂಗ S- ಮೇಲ್ಭಾಗಬಹುಮುಖ ಕೋನ.

ಪ್ರತಿಯೊಂದು ಅಂಚು ಕೂಡ ಒಂದು ನಿರ್ದಿಷ್ಟ ದ್ವಿಮುಖ ಕೋನದ ತುದಿಯಾಗಿದೆ; ಆದ್ದರಿಂದ, ಒಂದು ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದಲ್ಲಿ ಅನೇಕ ದ್ವಿಮುಖ ಕೋನಗಳು ಮತ್ತು ಅದರಲ್ಲಿ ಎಲ್ಲಾ ಅಂಚುಗಳಿರುವಷ್ಟು ಸಮತಲ ಕೋನಗಳಿವೆ. ಚಿಕ್ಕ ಸಂಖ್ಯೆಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದಲ್ಲಿ ಮೂರು ಮುಖಗಳಿವೆ; ಈ ಕೋನವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ತ್ರಿಕೋನಾಕಾರದ. ಚತುರ್ಭುಜ, ಪಂಚಭುಜಾಕೃತಿ ಇತ್ಯಾದಿ ಕೋನಗಳಿರಬಹುದು.

ಬಹುಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಶೃಂಗದಲ್ಲಿ ಇರಿಸಲಾಗಿರುವ S ಅಕ್ಷರದಿಂದ ಅಥವಾ SABCDE ಅಕ್ಷರಗಳ ಸರಣಿಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಅದರಲ್ಲಿ ಮೊದಲನೆಯದು ಶೃಂಗವನ್ನು ಸೂಚಿಸುತ್ತದೆ, ಮತ್ತು ಇತರವುಗಳು - ಅವುಗಳ ಸ್ಥಳದ ಕ್ರಮದಲ್ಲಿ ಅಂಚುಗಳು.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನವು ಅದರ ಪ್ರತಿಯೊಂದು ಮುಖದ ಸಮತಲದ ಒಂದು ಬದಿಯಲ್ಲಿ ಸಂಪೂರ್ಣವಾಗಿ ನೆಲೆಗೊಂಡಿದ್ದರೆ ಅದನ್ನು ಪೀನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದು ಅನಿರ್ದಿಷ್ಟವಾಗಿ ವಿಸ್ತರಿಸಲ್ಪಡುತ್ತದೆ. ಇದು, ಉದಾಹರಣೆಗೆ, ರೇಖಾಚಿತ್ರ 38 ರಲ್ಲಿ ತೋರಿಸಿರುವ ಕೋನ. ಇದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ, ಡ್ರಾಯಿಂಗ್ 39 ರಲ್ಲಿ ಕೋನವನ್ನು ಪೀನ ಎಂದು ಕರೆಯಲಾಗುವುದಿಲ್ಲ, ಏಕೆಂದರೆ ಇದು ASB ಅಂಚಿನ ಅಥವಾ BCC ಅಂಚಿನ ಎರಡೂ ಬದಿಗಳಲ್ಲಿದೆ.

ನಾವು ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದ ಎಲ್ಲಾ ಮುಖಗಳನ್ನು ಸಮತಲದೊಂದಿಗೆ ಛೇದಿಸಿದರೆ, ವಿಭಾಗದಲ್ಲಿ ಬಹುಭುಜಾಕೃತಿ ರೂಪುಗೊಳ್ಳುತ್ತದೆ ( abcde ) ಪೀನ ಬಹುಭುಜಾಕೃತಿಯ ಕೋನದಲ್ಲಿ, ಈ ಬಹುಭುಜಾಕೃತಿ ಕೂಡ ಪೀನವಾಗಿರುತ್ತದೆ.

ನಾವು ಪೀನವನ್ನು ಮಾತ್ರ ಪರಿಗಣಿಸುತ್ತೇವೆ ಬಹುಮುಖ ಕೋನಗಳು.

ಪ್ರಮೇಯ. ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದಲ್ಲಿ, ಪ್ರತಿ ಪ್ಲೇನ್ ಕೋನವು ಇತರ ಎರಡು ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ.

ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನ SABC (ಚಿತ್ರ 40) ನಲ್ಲಿರುವ ಸಮತಲ ಕೋನಗಳಲ್ಲಿ ದೊಡ್ಡದು ಕೋನ ASC ಆಗಿರಲಿ.

ನಾವು ಈ ಕೋನದಲ್ಲಿ ASD ಕೋನವನ್ನು ರೂಪಿಸೋಣ, ASB ಕೋನಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ಕೆಲವು ಸರಳ ರೇಖೆಯ AC ಅನ್ನು ಛೇದಿಸುವ SD ಅನ್ನು ಕೆಲವು ಹಂತದಲ್ಲಿ D. ನಾವು SB = SD ಅನ್ನು ಯೋಜಿಸೋಣ. A ಮತ್ತು C ನೊಂದಿಗೆ B ಅನ್ನು ಸಂಪರ್ಕಿಸುವ ಮೂಲಕ, ನಾವು \(\Delta\)ABC ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಇದರಲ್ಲಿ

AD+DC< АВ + ВС.

ASD ಮತ್ತು ASB ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮಾನವಾಗಿರುತ್ತವೆ ಏಕೆಂದರೆ ಅವುಗಳು ಪ್ರತಿಯೊಂದೂ ನಡುವೆ ಸಮಾನ ಕೋನವನ್ನು ಹೊಂದಿರುತ್ತವೆ ಸಮಾನ ಬದಿಗಳು: ಆದ್ದರಿಂದ AD = AB. ಆದ್ದರಿಂದ, ಪಡೆದ ಅಸಮಾನತೆಯಲ್ಲಿ ನಾವು AD ಮತ್ತು AB ಸಮಾನ ಪದಗಳನ್ನು ತ್ಯಜಿಸಿದರೆ, ನಾವು DC ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ< ВС.

ಈಗ ನಾವು SCD ಮತ್ತು SCB ತ್ರಿಕೋನಗಳಲ್ಲಿ, ಒಂದರ ಎರಡು ಬದಿಗಳು ಇನ್ನೊಂದರ ಎರಡು ಬದಿಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಆದರೆ ಮೂರನೇ ಬದಿಗಳು ಸಮಾನವಾಗಿರುವುದಿಲ್ಲ; ಈ ಸಂದರ್ಭದಲ್ಲಿ, ದೊಡ್ಡ ಕೋನವು ಈ ಬದಿಗಳಲ್ಲಿ ದೊಡ್ಡದಕ್ಕೆ ವಿರುದ್ಧವಾಗಿರುತ್ತದೆ; ಅಂದರೆ,

∠CSD< ∠ CSВ.

ಈ ಅಸಮಾನತೆಯ ಎಡಭಾಗಕ್ಕೆ ASD ಕೋನವನ್ನು ಸೇರಿಸುವ ಮೂಲಕ ಮತ್ತು ಅದಕ್ಕೆ ಸಮಾನವಾದ ಕೋನ ASB ಅನ್ನು ಬಲಕ್ಕೆ ಸೇರಿಸುವ ಮೂಲಕ, ನಾವು ಸಾಬೀತುಪಡಿಸಬೇಕಾದ ಅಸಮಾನತೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ:

∠ASC< ∠ CSB + ∠ ASB.

ಅತಿದೊಡ್ಡ ಸಮತಲ ಕೋನವು ಇತರ ಎರಡು ಕೋನಗಳ ಮೊತ್ತಕ್ಕಿಂತ ಕಡಿಮೆ ಎಂದು ನಾವು ಸಾಬೀತುಪಡಿಸಿದ್ದೇವೆ. ಇದರರ್ಥ ಪ್ರಮೇಯವು ಸಾಬೀತಾಗಿದೆ.

ಪರಿಣಾಮ. ಕೋನ ASB ಅಥವಾ ಕೋನ CSB ಮೂಲಕ ಕೊನೆಯ ಅಸಮಾನತೆಯ ಎರಡೂ ಬದಿಗಳಿಂದ ಕಳೆಯಿರಿ; ನಾವು ಪಡೆಯುತ್ತೇವೆ:

∠ASC - ∠ASB< ∠ CSB;

∠ASC - ∠CSB< ∠ ASB.

ಬಲದಿಂದ ಎಡಕ್ಕೆ ಈ ಅಸಮಾನತೆಗಳನ್ನು ಪರಿಗಣಿಸಿ ಮತ್ತು ಆ ಕೋನ ASC ಅನ್ನು ದೊಡ್ಡದಾಗಿದೆ ಎಂದು ಪರಿಗಣಿಸಿ ಮೂರು ಮೂಲೆಗಳುಇತರ ಎರಡು ಕೋನಗಳ ವ್ಯತ್ಯಾಸಕ್ಕಿಂತ ಹೆಚ್ಚು, ನಾವು ತೀರ್ಮಾನಕ್ಕೆ ಬರುತ್ತೇವೆ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದಲ್ಲಿ, ಪ್ರತಿ ಪ್ಲೇನ್ ಕೋನವು ಇತರ ಎರಡು ಕೋನಗಳ ವ್ಯತ್ಯಾಸಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.

ಪ್ರಮೇಯ. ಪೀನ ಬಹುಮುಖ ಕೋನದಲ್ಲಿ, ಎಲ್ಲಾ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು 4d (360°) ಗಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ. .

SABCDE ಪೀನ ಕೋನದ ಮುಖಗಳನ್ನು (ಚಿತ್ರ 41) ಕೆಲವು ಸಮತಲದೊಂದಿಗೆ ಛೇದಿಸೋಣ; ಇದರಿಂದ ನಾವು ಪೀನ ಅಡ್ಡ-ವಿಭಾಗವನ್ನು ಪಡೆಯುತ್ತೇವೆ ಎನ್-ಗೊನ್ ಎಬಿಸಿಡಿಇ.

ಎ, ಬಿ, ಸಿ, ಡಿ ಮತ್ತು ಇ ಬಿಂದುಗಳಲ್ಲಿ ಶೃಂಗಗಳನ್ನು ಹೊಂದಿರುವ ಪ್ರತಿಯೊಂದು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳಿಗೆ ಮೊದಲು ಸಾಬೀತಾಗಿರುವ ಪ್ರಮೇಯವನ್ನು ಅನ್ವಯಿಸುವುದರಿಂದ, ನಾವು ಪ್ಯಾಚೋಲಿಮ್:

∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

ಈ ಎಲ್ಲಾ ಅಸಮಾನತೆಗಳನ್ನು ನಾವು ಪದದಿಂದ ಪದವನ್ನು ಸೇರಿಸೋಣ. ನಂತರ ಎಡಭಾಗದಲ್ಲಿ ನಾವು ಬಹುಭುಜಾಕೃತಿಯ ABCDE ಯ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತವನ್ನು ಪಡೆಯುತ್ತೇವೆ, ಅದು 2 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. dn - 4ಡಿ , ಮತ್ತು ಬಲಭಾಗದಲ್ಲಿ - ABS, SBC, ಇತ್ಯಾದಿ ತ್ರಿಕೋನಗಳ ಕೋನಗಳ ಮೊತ್ತ, ಶೃಂಗದಲ್ಲಿ ಇರುವ ಕೋನಗಳನ್ನು ಹೊರತುಪಡಿಸಿ S. ಅಕ್ಷರದೊಂದಿಗೆ ಈ ಕೊನೆಯ ಕೋನಗಳ ಮೊತ್ತವನ್ನು ಸೂಚಿಸುತ್ತದೆ X , ನಾವು ಸೇರ್ಪಡೆಯ ನಂತರ ಪಡೆಯುತ್ತೇವೆ:

2dn - 4ಡಿ < 2dn - x .

ವ್ಯತ್ಯಾಸಗಳಿಂದ 2 dn - 4ಡಿ ಮತ್ತು 2 dn - x ಮೈನುಯೆಂಡ್‌ಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ, ನಂತರ ಮೊದಲ ವ್ಯತ್ಯಾಸವು ಎರಡನೆಯದಕ್ಕಿಂತ ಕಡಿಮೆಯಿರಬೇಕಾದರೆ, ಸಬ್‌ಟ್ರಾಹೆಂಡ್ 4 ಡಿ ಕಳೆಯುವುದಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿತ್ತು X ; ಅಂದರೆ 4 ಡಿ > X , ಅಂದರೆ X < 4ಡಿ .

ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳ ಸಮಾನತೆಯ ಸರಳ ಪ್ರಕರಣಗಳು

ಪ್ರಮೇಯಗಳು. ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ:

1) ಎರಡು ಸಮಾನವಾದ ಮತ್ತು ಒಂದೇ ಅಂತರದ ಸಮತಲ ಕೋನಗಳ ನಡುವೆ ಸುತ್ತುವರಿದ ಸಮಾನ ದ್ವಿಮುಖ ಕೋನದ ಉದ್ದಕ್ಕೂ, ಅಥವಾ

2) ಸಮಾನ ಸಮತಲ ಕೋನದ ಉದ್ದಕ್ಕೂ ಎರಡು ಸಮಾನ ಮತ್ತು ಒಂದೇ ಅಂತರದ ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳ ನಡುವೆ ಸುತ್ತುವರಿದಿದೆ.

1) S ಮತ್ತು S 1 ಎರಡು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳಾಗಿರಲಿ (ಚಿತ್ರ 42), ಇದಕ್ಕಾಗಿ ∠ASB = ∠A 1 S 1 B 1, ∠ASC = ∠A 1 S 1 C 1 (ಮತ್ತು ಇವುಗಳು ಸಮಾನ ಕೋನಗಳುಒಂದೇ ರೀತಿಯಲ್ಲಿ ಇದೆ) ಮತ್ತು ಡೈಹೆಡ್ರಲ್ ಕೋನ AS ಡೈಹೆಡ್ರಲ್ ಕೋನ A 1 S 1 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ನಾವು S 1 ಕೋನವನ್ನು S ಕೋನಕ್ಕೆ ಸೇರಿಸೋಣ ಇದರಿಂದ ಅವರ ಅಂಕಗಳು S 1 ಮತ್ತು S, ಸರಳ ರೇಖೆಗಳು S 1 A 1 ಮತ್ತು SA ಮತ್ತು ವಿಮಾನಗಳು A 1 S 1 B 1 ಮತ್ತು ASB ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ. ನಂತರ S 1 B 1 ಅಂಚು SB ಉದ್ದಕ್ಕೂ ಹೋಗುತ್ತದೆ (A 1 S 1 B 1 ಮತ್ತು ASB ಕೋನಗಳ ಸಮಾನತೆಯಿಂದಾಗಿ), A 1 S 1 C 1 ವಿಮಾನವು ASC ಉದ್ದಕ್ಕೂ ಹೋಗುತ್ತದೆ (ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳ ಸಮಾನತೆಯ ಕಾರಣದಿಂದಾಗಿ ) ಮತ್ತು S 1 C 1 ಅಂಚು SC ಅಂಚಿನಲ್ಲಿ ಹೋಗುತ್ತದೆ (A 1 S 1 C 1 ಮತ್ತು ASC ಕೋನಗಳ ಸಮಾನತೆಯ ಕಾರಣದಿಂದಾಗಿ). ಹೀಗಾಗಿ, ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳು ಅವುಗಳ ಎಲ್ಲಾ ಅಂಚುಗಳೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ, ಅಂದರೆ. ಅವರು ಸಮಾನರಾಗಿರುತ್ತಾರೆ.

2) ಎರಡನೆಯ ಚಿಹ್ನೆ, ಮೊದಲನೆಯಂತೆಯೇ, ಎಂಬೆಡಿಂಗ್ ಮೂಲಕ ಸಾಬೀತಾಗಿದೆ.

ಸಮ್ಮಿತೀಯ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳು

ತಿಳಿದಿರುವಂತೆ, ಲಂಬ ಕೋನಗಳುನಾವು ಸರಳ ರೇಖೆಗಳು ಅಥವಾ ಸಮತಲಗಳಿಂದ ರೂಪುಗೊಂಡ ಕೋನಗಳ ಬಗ್ಗೆ ಮಾತನಾಡುವಾಗ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಈ ಹೇಳಿಕೆಯು ನಿಜವಾಗಿದೆಯೇ ಎಂದು ನೋಡೋಣ.

ನಾವು ಮುಂದುವರಿಸೋಣ (ಚಿತ್ರ 43) SABCDE ಕೋನದ ಎಲ್ಲಾ ಅಂಚುಗಳು ಶೃಂಗ S ಅನ್ನು ಮೀರಿ, ನಂತರ ಮತ್ತೊಂದು ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ SA 1 B 1 C 1 D 1 E 1 ರಚನೆಯಾಗುತ್ತದೆ, ಇದನ್ನು ಕರೆಯಬಹುದು ಲಂಬವಾದಮೊದಲ ಕೋನಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ. ಎರಡೂ ಕೋನಗಳು ಕ್ರಮವಾಗಿ ಸಮಾನ ಸಮತಲ ಮತ್ತು ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳನ್ನು ಹೊಂದಿವೆ ಎಂದು ನೋಡುವುದು ಸುಲಭ, ಆದರೆ ಎರಡೂ ನೆಲೆಗೊಂಡಿವೆ ಹಿಮ್ಮುಖ ಕ್ರಮ. ವಾಸ್ತವವಾಗಿ, ವೀಕ್ಷಕನು ಅದರ ಶೃಂಗದಲ್ಲಿ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದ ಹೊರಗಿನಿಂದ ನೋಡುತ್ತಿರುವುದನ್ನು ನಾವು ಕಲ್ಪಿಸಿಕೊಂಡರೆ, SA, SB, SC, SD, SE ಅಂಚುಗಳು ಅವನಿಗೆ ಅಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ಇದೆ ಎಂದು ತೋರುತ್ತದೆ, ಆದರೆ SA 1 B ಕೋನವನ್ನು ನೋಡಿದರೆ 1 C 1 D 1 E 1, ಅವನು ಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ಇರುವ ಅಂಚುಗಳನ್ನು SA 1, SB 1, ... ನೋಡುತ್ತಾನೆ.

ಅನುಗುಣವಾದ ಸಮತಲ ಮತ್ತು ದ್ವಿಮುಖ ಕೋನಗಳೊಂದಿಗೆ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳು, ಆದರೆ ವಿರುದ್ಧ ಕ್ರಮದಲ್ಲಿ ನೆಲೆಗೊಂಡಿವೆ, ಸಾಮಾನ್ಯವಾಗಿ ಗೂಡುಕಟ್ಟಿದಾಗ ಸಂಯೋಜಿಸಲಾಗುವುದಿಲ್ಲ; ಅಂದರೆ ಅವರು ಸಮಾನರಲ್ಲ. ಅಂತಹ ಕೋನಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಮ್ಮಿತೀಯ(ಶೃಂಗ S ಗೆ ಸಂಬಂಧಿಸಿದಂತೆ). ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಅಂಕಿಗಳ ಸಮ್ಮಿತಿಯನ್ನು ಕೆಳಗೆ ಹೆಚ್ಚು ವಿವರವಾಗಿ ಚರ್ಚಿಸಲಾಗುವುದು.

ಇತರ ವಸ್ತುಗಳು

ಒಂದೇ ಬಿಂದುವಿನಿಂದ ಹೊರಹೊಮ್ಮುವ ಮತ್ತು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಮಲಗದೇ ಇರುವ ಮೂರು ಕಿರಣಗಳನ್ನು ಎ, ಬಿ, ಸಿ ಎಂದು ಪರಿಗಣಿಸೋಣ. ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನ (abc) ಮೂರು ಫ್ಲಾಟ್ ಕೋನಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟಿದೆ (ab), (bc) ಮತ್ತು (Fig. 2) ಈ ಕೋನಗಳನ್ನು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಮುಖಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಅವುಗಳ ಬದಿಗಳನ್ನು ಅಂಚುಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ; ಸಮತಟ್ಟಾದ ಕೋನಗಳ ಸಾಮಾನ್ಯ ಶೃಂಗವನ್ನು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಶೃಂಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದ ಪರಿಕಲ್ಪನೆಯನ್ನು ಇದೇ ರೀತಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ (ಚಿತ್ರ 3).

ಪಾಲಿಹೆಡ್ರಾನ್

ಸ್ಟೀರಿಯೊಮೆಟ್ರಿಯಲ್ಲಿ, ದೇಹಗಳೆಂದು ಕರೆಯಲ್ಪಡುವ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಅಂಕಿಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ. ದೃಶ್ಯ (ಜ್ಯಾಮಿತೀಯ) ದೇಹವನ್ನು ಆಕ್ರಮಿಸಿಕೊಂಡಿರುವ ಜಾಗದ ಭಾಗವಾಗಿ ಕಲ್ಪಿಸಬೇಕು ಭೌತಿಕ ದೇಹಮತ್ತು ಮೇಲ್ಮೈಯಿಂದ ಸೀಮಿತವಾಗಿದೆ.

ಪಾಲಿಹೆಡ್ರಾನ್ ಒಂದು ದೇಹವಾಗಿದ್ದು, ಅದರ ಮೇಲ್ಮೈ ಒಳಗೊಂಡಿರುತ್ತದೆ ಸೀಮಿತ ಸಂಖ್ಯೆಫ್ಲಾಟ್ ಬಹುಭುಜಾಕೃತಿಗಳು (ಚಿತ್ರ 4). ಬಹುಭುಜಾಕೃತಿಯು ಅದರ ಮೇಲ್ಮೈಯಲ್ಲಿರುವ ಪ್ರತಿಯೊಂದು ಸಮತಲ ಬಹುಭುಜಾಕೃತಿಯ ಸಮತಲದ ಒಂದು ಬದಿಯಲ್ಲಿದ್ದರೆ ಅದನ್ನು ಪೀನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಒಂದು ಸಾಮಾನ್ಯ ಭಾಗಅಂತಹ ಸಮತಲ ಮತ್ತು ಪೀನ ಪಾಲಿಹೆಡ್ರನ್ನ ಮೇಲ್ಮೈಯನ್ನು ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಪೀನ ಪಾಲಿಹೆಡ್ರನ್ನ ಮುಖಗಳು ಚಪ್ಪಟೆಯಾಗಿರುತ್ತವೆ ಪೀನ ಬಹುಭುಜಾಕೃತಿಗಳು. ಮುಖಗಳ ಬದಿಗಳನ್ನು ಪಾಲಿಹೆಡ್ರನ್ನ ಅಂಚುಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ಶೃಂಗಗಳನ್ನು ಪಾಲಿಹೆಡ್ರನ್ನ ಶೃಂಗಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಪರಿಚಿತ ಘನದ ಉದಾಹರಣೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಇದನ್ನು ವಿವರಿಸೋಣ (ಚಿತ್ರ 5). ಒಂದು ಘನವಿದೆ ಪೀನ ಬಹುಮುಖಿ. ಇದರ ಮೇಲ್ಮೈ ಆರು ಚೌಕಗಳನ್ನು ಒಳಗೊಂಡಿದೆ: ABCD, BEFC, .... ಇವು ಅದರ ಮುಖಗಳಾಗಿವೆ. ಘನದ ಅಂಚುಗಳು ಈ ಚೌಕಗಳ ಬದಿಗಳಾಗಿವೆ: AB, BC, BE,.... ಘನಾಕೃತಿಯ ಶೃಂಗಗಳು ಚೌಕಗಳ ಶೃಂಗಗಳಾಗಿವೆ: A, B, C, D, E, .... ಘನವು ಆರು ಮುಖಗಳು, ಹನ್ನೆರಡು ಅಂಚುಗಳು ಮತ್ತು ಎಂಟು ಶೃಂಗಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.

ಸರಳವಾದ ಪಾಲಿಹೆಡ್ರಾ - ಪ್ರಿಸ್ಮ್‌ಗಳು ಮತ್ತು ಪಿರಮಿಡ್‌ಗಳು, ಇದು ನಮ್ಮ ಅಧ್ಯಯನದ ಮುಖ್ಯ ವಸ್ತುವಾಗಿದೆ - ನಾವು ಮೂಲಭೂತವಾಗಿ ದೇಹದ ಪರಿಕಲ್ಪನೆಯನ್ನು ಬಳಸದ ವ್ಯಾಖ್ಯಾನಗಳನ್ನು ನೀಡುತ್ತೇವೆ. ಅವುಗಳಿಗೆ ಸೇರಿದ ಜಾಗದಲ್ಲಿನ ಎಲ್ಲಾ ಬಿಂದುಗಳನ್ನು ಸೂಚಿಸುವ ಜ್ಯಾಮಿತೀಯ ಅಂಕಿಗಳೆಂದು ಅವುಗಳನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ. ಪರಿಕಲ್ಪನೆ ಜ್ಯಾಮಿತೀಯ ದೇಹಮತ್ತು ಅದರ ಮೇಲ್ಮೈ ಒಳಗೆ ಸಾಮಾನ್ಯ ಪ್ರಕರಣನಂತರ ನೀಡಲಾಗುವುದು.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ

ಒಂದು ಪಾಲಿಹೆಡ್ರಲ್ ಕುಹರದಿಂದ ಸೀಮಿತವಾದ ಜಾಗದ ಭಾಗ ಶಂಕುವಿನಾಕಾರದ ಮೇಲ್ಮೈ, ಇದರ ದಿಕ್ಕು ಸ್ವಯಂ-ಛೇದಕಗಳಿಲ್ಲದ ಸಮತಟ್ಟಾದ ಬಹುಭುಜಾಕೃತಿಯಾಗಿದೆ. ಈ ಮೇಲ್ಮೈಯ ಮುಖಗಳನ್ನು ಮೊಸಾಯಿಕ್ನ ಮುಖಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ಮೇಲ್ಭಾಗವನ್ನು ಮೊಸಾಯಿಕ್ನ ಮೇಲ್ಭಾಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಎಂ.ಯು. ಅದರ ಎಲ್ಲಾ ರೇಖೀಯ ಕೋನಗಳು ಮತ್ತು ಅದರ ಎಲ್ಲಾ ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳು ಸಮಾನವಾಗಿದ್ದರೆ ಇದನ್ನು ನಿಯಮಿತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಮೆರೊಯ್ ಎಂ. ಯು. ಬಹುಭುಜಾಕೃತಿಯ ಮುಖಗಳ ಛೇದನದಿಂದ ಪಡೆದ ಗೋಳಾಕಾರದ ಬಹುಭುಜಾಕೃತಿಯಿಂದ ಸೀಮಿತವಾದ ಪ್ರದೇಶವಾಗಿದೆ, ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ಗೋಳ ಒಂದಕ್ಕೆ ಸಮಾನ, ಮತ್ತು M. y ನ ಶೃಂಗದಲ್ಲಿ ಕೇಂದ್ರದೊಂದಿಗೆ. ಘನ ಕೋನವನ್ನೂ ನೋಡಿ.

ದೊಡ್ಡದು ಸೋವಿಯತ್ ವಿಶ್ವಕೋಶ. - ಎಂ.: ಸೋವಿಯತ್ ಎನ್ಸೈಕ್ಲೋಪೀಡಿಯಾ. 1969-1978 .

ಇತರ ನಿಘಂಟುಗಳಲ್ಲಿ "ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ" ಏನೆಂದು ನೋಡಿ:

ಘನ ಕೋನವನ್ನು ನೋಡಿ... ದೊಡ್ಡದು ವಿಶ್ವಕೋಶ ನಿಘಂಟು

ಘನ ಕೋನವನ್ನು ನೋಡಿ. * * * ಪಾಲಿಹೆಡಲ್ ಆಂಗಲ್ ಪಾಲಿಹೆಡಲ್ ಆಂಗಲ್, ಘನ ಕೋನವನ್ನು ನೋಡಿ (ಘನ ಕೋನವನ್ನು ನೋಡಿ) ... ವಿಶ್ವಕೋಶ ನಿಘಂಟು

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಿಕ್ನ ಒಂದು ಕುಹರದಿಂದ ಸೀಮಿತವಾದ ಜಾಗದ ಭಾಗ. ಸ್ವಯಂ-ಛೇದಕಗಳಿಲ್ಲದ ಸಮತಟ್ಟಾದ ಬಹುಭುಜಾಕೃತಿಯ ಸಮೂಹಕ್ಕೆ ಮೇಲ್ಮೈ ನಿರ್ದೇಶಿಸುತ್ತದೆ. ಈ ಮೇಲ್ಮೈಯ ಮುಖಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ. M. u. ನ ಅಂಚುಗಳು, M. u ನ ತುದಿಯ ಮೇಲ್ಭಾಗ. ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸರಿಯಾದ... ಗಣಿತದ ವಿಶ್ವಕೋಶ

ಘನ ಕೋನ ನೋಡಿ... ನೈಸರ್ಗಿಕ ವಿಜ್ಞಾನ. ವಿಶ್ವಕೋಶ ನಿಘಂಟು

ಬಹುಮುಖ ಕೋನ- ಗಣಿತ. ಒಂದು ಬಿಂದು (ಕೋನದ ಶೃಂಗ) ಮೂಲಕ ಹಾದುಹೋಗುವ ಹಲವಾರು ವಿಮಾನಗಳಿಂದ ಸುತ್ತುವರಿದ ಜಾಗದ ಒಂದು ಭಾಗ ... ಅನೇಕ ಅಭಿವ್ಯಕ್ತಿಗಳ ನಿಘಂಟು

ಬಹುಮುಖಿ, ಬಹುಮುಖಿ, ಬಹುಮುಖಿ (ಪುಸ್ತಕ). 1. ಹಲವಾರು ಮುಖಗಳು ಅಥವಾ ಬದಿಗಳನ್ನು ಹೊಂದಿರುವುದು. ಬಹುಮುಖಿ ಕಲ್ಲು. ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ (ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುವ ಹಲವಾರು ವಿಮಾನಗಳಿಂದ ಸೀಮಿತವಾದ ಜಾಗದ ಭಾಗ; ಮ್ಯಾಟ್.). 2. ವರ್ಗಾವಣೆ...... ನಿಘಂಟುಉಷಕೋವಾ

- (ಮ್ಯಾಟ್.). ನಿರ್ದಿಷ್ಟ ಸಮತಲದಲ್ಲಿ O ಬಿಂದುವಿನಿಂದ OA ಮತ್ತು 0B ನೇರ ರೇಖೆಗಳನ್ನು ನಾವು ಎಳೆದರೆ, ನಾವು AOB ಕೋನವನ್ನು ಪಡೆಯುತ್ತೇವೆ (ಚಿತ್ರ 1). ಅಮೇಧ್ಯ. 1. ಪಾಯಿಂಟ್ 0 ಎಂದು ಕರೆಯಲಾಗಿದೆ ಕೋನದ ಶೃಂಗ, ಮತ್ತು ನೇರ ರೇಖೆಗಳು OA ಮತ್ತು 0B ಕೋನದ ಬದಿಗಳಾಗಿ. ಎರಡು ಕೋನಗಳನ್ನು ΒΟΑ ಮತ್ತು Β 1 Ο 1 Α 1 ನೀಡಲಾಗಿದೆ ಎಂದು ಭಾವಿಸೋಣ ಆದ್ದರಿಂದ ನಾವು ಅವುಗಳನ್ನು ವಿಧಿಸೋಣ.

- (ಮ್ಯಾಟ್.). ನಿರ್ದಿಷ್ಟ ಸಮತಲದಲ್ಲಿ O ಬಿಂದುವಿನಿಂದ OA ಮತ್ತು 0B ನೇರ ರೇಖೆಗಳನ್ನು ನಾವು ಎಳೆದರೆ, ನಾವು AOB ಕೋನವನ್ನು ಪಡೆಯುತ್ತೇವೆ (Fig. 1). ಅಮೇಧ್ಯ. 1. ಪಾಯಿಂಟ್ 0 ಎಂದು ಕರೆಯಲಾಗಿದೆ ಕೋನದ ಶೃಂಗ, ಮತ್ತು ನೇರ ರೇಖೆಗಳು OA ಮತ್ತು 0B ಕೋನದ ಬದಿಗಳಾಗಿ. ΒΟΑ ಮತ್ತು Β1Ο1Α1 ಎಂಬ ಎರಡು ಕೋನಗಳನ್ನು ನೀಡಲಾಗಿದೆ ಎಂದು ಭಾವಿಸೋಣ. ಶೃಂಗಗಳು O... ವಿಶ್ವಕೋಶ ನಿಘಂಟು F.A. ಬ್ರೋಕ್ಹೌಸ್ ಮತ್ತು I.A. ಎಫ್ರಾನ್

ಈ ಪದವು ಇತರ ಅರ್ಥಗಳನ್ನು ಹೊಂದಿದೆ, ಕೋನ (ಅರ್ಥಗಳು) ನೋಡಿ. ಕೋನ ∠ ಆಯಾಮ ° SI ಘಟಕಗಳು ರೇಡಿಯನ್ ... ವಿಕಿಪೀಡಿಯಾ

ಫ್ಲಾಟ್, ಜ್ಯಾಮಿತೀಯ ಚಿತ್ರ, ಒಂದು ಬಿಂದುವಿನಿಂದ (ಮೇಲ್ಮೈಯ ಶೃಂಗ) ಹೊರಹೊಮ್ಮುವ ಎರಡು ಕಿರಣಗಳಿಂದ (ಮೇಲ್ಮೈಯ ಬದಿಗಳು) ರೂಪುಗೊಂಡಿದೆ. ಪ್ರತಿಯೊಂದು U., ಕೆಲವು ವೃತ್ತದ O ಕೇಂದ್ರದಲ್ಲಿ ಶೃಂಗವನ್ನು ಹೊಂದಿರುವ (ಕೇಂದ್ರ U.), ವೃತ್ತದ ಮೇಲೆ ಒಂದು ಆರ್ಕ್ AB ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತದೆ, ಇದು ಸುತ್ತುವರೆದಿದೆ... ... ಗ್ರೇಟ್ ಸೋವಿಯತ್ ಎನ್ಸೈಕ್ಲೋಪೀಡಿಯಾ

ಪಾಲಿಹೆಡಲ್ ಕೋನಗಳು

ಬಹುಭುಜಾಕೃತಿಯ ಕೋನವು ಬಹುಭುಜಾಕೃತಿಯ ಪ್ರಾದೇಶಿಕ ಅನಲಾಗ್ ಆಗಿದೆ. ಸಮತಲದಲ್ಲಿರುವ ಬಹುಭುಜಾಕೃತಿಯು ಸರಳವಾದ ಮುಚ್ಚಿದ ಮುರಿದ ರೇಖೆಯಿಂದ ರೂಪುಗೊಂಡ ಆಕೃತಿ ಮತ್ತು ಅದರ ಮೂಲಕ ಸೀಮಿತವಾದ ಆಂತರಿಕ ಪ್ರದೇಶವಾಗಿದೆ ಎಂದು ನೆನಪಿಸಿಕೊಳ್ಳಿ. ನಾವು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿನ ಕಿರಣವನ್ನು ಸಮತಲದಲ್ಲಿರುವ ಬಿಂದುವಿನ ಅನಲಾಗ್ ಎಂದು ಪರಿಗಣಿಸುತ್ತೇವೆ ಮತ್ತು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಸಮತಲ ಕೋನವು ಸಮತಲದಲ್ಲಿನ ವಿಭಾಗದ ಅನಲಾಗ್ ಎಂದು ಪರಿಗಣಿಸುತ್ತೇವೆ. ನಂತರ ಸಮತಲದ ಮೇಲೆ ಸರಳ ಮುಚ್ಚಿದ ಮುರಿದ ರೇಖೆಯ ಅನಲಾಗ್ ಸಮತಲ ಕೋನಗಳ ಸೀಮಿತ ಗುಂಪಿನಿಂದ ರೂಪುಗೊಂಡ ಮೇಲ್ಮೈಯಾಗಿದೆ.ಎ 1 ಎಸ್.ಎ. 2 , ಎ 2 ಎಸ್.ಎ. 3 , …, ಎ ಎನ್ -1 ಎಸ್ಎ ಎನ್, ಎ ಎನ್ ಎಸ್ಎ 1 ಸಾಮಾನ್ಯ ಶೃಂಗದೊಂದಿಗೆಎಸ್ (ಚಿತ್ರ 1), ಇದರಲ್ಲಿ ಸಾಮಾನ್ಯ ಕಿರಣದ ಬಿಂದುಗಳನ್ನು ಹೊರತುಪಡಿಸಿ ನೆರೆಯ ಮೂಲೆಗಳು ಸಾಮಾನ್ಯ ಬಿಂದುಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ ಮತ್ತು ಪಕ್ಕದ ಮೂಲೆಗಳು ಹೊಂದಿರುವುದಿಲ್ಲ ಸಾಮಾನ್ಯ ಅಂಕಗಳು, ಸಾಮಾನ್ಯ ಶೃಂಗವನ್ನು ಹೊರತುಪಡಿಸಿ. ಸೂಚಿಸಿದ ಮೇಲ್ಮೈಯಿಂದ ರೂಪುಗೊಂಡ ಆಕೃತಿ ಮತ್ತು ಅದರ ಮೂಲಕ ಸೀಮಿತವಾದ ಜಾಗದ ಎರಡು ಭಾಗಗಳಲ್ಲಿ ಒಂದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಬಹುಮುಖ ಕೋನ. ಸಾಮಾನ್ಯ ಮೇಲ್ಭಾಗಎಸ್ಎಂದು ಕರೆದರು ಮೇಲ್ಭಾಗಬಹುಮುಖ ಕೋನ. ಕಿರಣಗಳುಎಸ್.ಎ. 1 , …, ಎಸ್ಎ ಎನ್ಎಂದು ಕರೆಯುತ್ತಾರೆ ಪಕ್ಕೆಲುಬುಗಳುಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ, ಮತ್ತು ಸಮತಲವು ಸ್ವತಃ ಕೋನಗಳುಎ 1 ಎಸ್.ಎ. 2 , ಎ 2 ಎಸ್.ಎ. 3 , …, ಎ ಎನ್ -1 ಎಸ್ಎ ಎನ್, ಎ ಎನ್ ಎಸ್ಎ 1 – ಅಂಚುಗಳುಬಹುಮುಖ ಕೋನ. ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಅಕ್ಷರಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆಎಸ್.ಎ. 1 … ಎ ಎನ್, ಅದರ ಅಂಚುಗಳ ಮೇಲೆ ಶೃಂಗ ಮತ್ತು ಬಿಂದುಗಳನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಮುಖಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅವಲಂಬಿಸಿ, ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳನ್ನು ಟ್ರೈಹೆಡ್ರಲ್, ಟೆಟ್ರಾಹೆಡ್ರಲ್, ಪೆಂಟಾಹೆಡ್ರಲ್ (ಚಿತ್ರ 2) ಇತ್ಯಾದಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಪೀನ, ಇದು ಪೀನದ ಆಕೃತಿಯಾಗಿದ್ದರೆ, ಅಂದರೆ. ಅದರ ಯಾವುದೇ ಎರಡು ಬಿಂದುಗಳೊಂದಿಗೆ ಅವುಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ಒಂದನ್ನು ಸಹ ಒಳಗೊಂಡಿದೆಸಾಲಿನ ವಿಭಾಗ. ಚಿತ್ರ 2 ರಲ್ಲಿ, ಟ್ರೈಹೆಡ್ರಲ್ ಮತ್ತು ಟೆಟ್ರಾಹೆಡ್ರಲ್ ಕೋನಗಳು ಪೀನವಾಗಿರುತ್ತವೆ, ಆದರೆ ಪೆಂಟಗೋನಲ್ ಕೋನವು ಅಲ್ಲ.
ತ್ರಿಕೋನಗಳ ಕೆಲವು ಗುಣಲಕ್ಷಣಗಳನ್ನು ಮತ್ತು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳ ಸಮಾನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪರಿಗಣಿಸೋಣ.
ಆಸ್ತಿ 1(ತ್ರಿಕೋನ ಅಸಮಾನತೆ). ತ್ರಿಕೋನದ ಪ್ರತಿಯೊಂದು ಬದಿಯು ಅದರ ಇತರ ಎರಡು ಬದಿಗಳ ಮೊತ್ತಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ.
ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳಿಗೆ ಇದೇ ರೀತಿಯ ಆಸ್ತಿ ಈ ಕೆಳಗಿನ ಆಸ್ತಿಯಾಗಿದೆ.
ಆಸ್ತಿ 1". ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಪ್ರತಿಯೊಂದು ಸಮತಲ ಕೋನವು ಅದರ ಇತರ ಎರಡು ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ.
ಪುರಾವೆ. ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಪರಿಗಣಿಸಿ SABC . ಅದರ ಸಮತಲ ಕೋನಗಳಲ್ಲಿ ದೊಡ್ಡದು ಕೋನವಾಗಿರಲಿ ಎ.ಎಸ್.ಸಿ.. ಆಗ ಅಸಮಾನತೆಗಳು ನಿಲ್ಲುತ್ತವೆ

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

ಹೀಗಾಗಿ, ಅಸಮಾನತೆಯನ್ನು ಸಾಬೀತುಪಡಿಸಲು ಇದು ಉಳಿದಿದೆ ASC< ಎ.ಎಸ್.ಬಿ.+ BSC.
ಅದನ್ನು ಅಂಚಿನಲ್ಲಿ ಇಡೋಣ ಎ.ಎಸ್.ಸಿ.ಮೂಲೆಯಲ್ಲಿ ಎ.ಎಸ್.ಡಿ., ಸಮಾನ ಎ.ಎಸ್.ಬಿ. , ಮತ್ತು ಅವಧಿ ಬಿಅದನ್ನು ಆರಿಸಿಕೊಳ್ಳೋಣ SB = SD(ಚಿತ್ರ 3). ನಂತರ ತ್ರಿಕೋನಗಳು ಎ.ಎಸ್.ಬಿ.ಮತ್ತು ಎ.ಎಸ್.ಡಿ.ಸಮಾನ (ಎರಡು ಬದಿಗಳಲ್ಲಿ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನ) ಮತ್ತು, ಆದ್ದರಿಂದ, AB = AD. ತ್ರಿಕೋನ ಅಸಮಾನತೆಯನ್ನು ಬಳಸೋಣ ಎ.ಸಿ.< AB + BC . ಎರಡೂ ಬದಿಗಳಿಂದ ಕಳೆಯುವುದು AD = AB, ನಾವು ಅಸಮಾನತೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ ಡಿಸಿ< BC. ತ್ರಿಕೋನಗಳಲ್ಲಿ DSCಮತ್ತು BSCಒಂದು ಕಡೆ ಸಾಮಾನ್ಯವಾಗಿದೆ ( ಎಸ್.ಸಿ.), SD = SBಮತ್ತು ಡಿಸಿ< BC. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ವಿರುದ್ಧ ದೊಡ್ಡ ಭಾಗಒಂದು ದೊಡ್ಡ ಕೋನವನ್ನು ಹೊಂದಿದೆ ಮತ್ತು ಆದ್ದರಿಂದ, DSC< BSC . ಈ ಅಸಮಾನತೆಯ ಎರಡೂ ಬದಿಗಳಿಗೆ ಕೋನವನ್ನು ಸೇರಿಸುವುದು ಎ.ಎಸ್.ಡಿ. , ಸಮಾನ ಎ.ಎಸ್.ಬಿ., ನಾವು ಅಗತ್ಯವಾದ ಅಸಮಾನತೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ ASC< ಎ.ಎಸ್.ಬಿ.+ BSC.

ಫಲಿತಾಂಶ 1.ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು 360 ಕ್ಕಿಂತ ಕಡಿಮೆಯಿದೆ° .
ಪುರಾವೆ. ಅವಕಾಶ SABC- ಕೊಟ್ಟಿರುವ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನ. ಶೃಂಗದೊಂದಿಗೆ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಪರಿಗಣಿಸಿ ಎ, ಅಂಚುಗಳಿಂದ ರೂಪುಗೊಂಡಿದೆ ಎಬಿಎಸ್, ಎಸಿಎಸ್ಮತ್ತು ಕೋನ BAC. ಸಾಬೀತಾದ ಆಸ್ತಿಯ ಕಾರಣ, ಅಸಮಾನತೆ ಹೊಂದಿದೆ BAC< BAS+ CAS. ಅಂತೆಯೇ, ಶೃಂಗಗಳನ್ನು ಹೊಂದಿರುವ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳಿಗೆ ಬಿಮತ್ತು ಇದರೊಂದಿಗೆಅಸಮಾನತೆಗಳಿವೆ: ಎಬಿಸಿ< ಎಬಿಎಸ್+ ಸಿಬಿಎಸ್, ಎಸಿಬಿ< ಎಸಿಎಸ್+ BCS. ಈ ಅಸಮಾನತೆಗಳನ್ನು ಸೇರಿಸುವುದು ಮತ್ತು ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದು ಎಬಿಸಿ 180 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ° , ನಾವು 180 ° ಪಡೆಯುತ್ತೇವೆ < BAS+CAS+ ABS+CBS+BCS+ ACS = 180 ° - ASB+ 180° - BSC+ 180° - ಎ.ಎಸ್.ಸಿ.. ಆದ್ದರಿಂದ, ASB+BSC+ASC< 360 ° .
ಫಲಿತಾಂಶ 2.ಪೀನ ಬಹುಮುಖ ಕೋನದ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು 360 ಕ್ಕಿಂತ ಕಡಿಮೆಯಿದೆ.
ಪುರಾವೆಯು ಹಿಂದಿನದಕ್ಕೆ ಹೋಲುತ್ತದೆ.
ಫಲಿತಾಂಶ 3.ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳ ಮೊತ್ತವು 180 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ° .
ಪುರಾವೆ. ಅವಕಾಶ SABC- ತ್ರಿಕೋನ ಕೋನ. ಕೆಲವು ಪಾಯಿಂಟ್ ಆಯ್ಕೆ ಮಾಡೋಣ ಪಅದರ ಒಳಗೆ ಮತ್ತು ಅದರಿಂದ ಲಂಬಗಳನ್ನು ಬಿಡಿ PA 1 , ಪಿ.ಬಿ. 1 , ಪಿಸಿ 1 ಅಂಚಿನಲ್ಲಿ (ಚಿತ್ರ 4).

ಫ್ಲಾಟ್ ಮೂಲೆಗಳು ಬಿ 1 ಪಿಸಿ 1 , ಎ 1 ಪಿಸಿ 1 , ಎ 1 ಪಿ.ಬಿ. 1 ಅಂಚುಗಳೊಂದಿಗೆ ಅನುಗುಣವಾದ ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳನ್ನು ಪೂರಕಗೊಳಿಸಿ SA, SB, SC 180 ವರೆಗೆ° . ಆದ್ದರಿಂದ, ಈ ದ್ವಿಮುಖ ಕೋನಗಳ ಮೊತ್ತವು 540 ಆಗಿದೆ° - ( ಬಿ 1 ಪಿಸಿ 1 +A 1 ಪಿಸಿ 1 + ಎ 1 ಪಿ.ಬಿ. 1 ) ಶೃಂಗದೊಂದಿಗೆ ಟ್ರೈಹೆಡ್ರಲ್‌ನ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತ ಎಂದು ಪರಿಗಣಿಸಿ ಪಕೋನ 360 ಕ್ಕಿಂತ ಕಡಿಮೆ° , ಮೂಲ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ದ್ವಿಮುಖ ಕೋನಗಳ ಮೊತ್ತವು 180 ಕ್ಕಿಂತ ಹೆಚ್ಚಿದೆ ಎಂದು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ° .
ಆಸ್ತಿ 2.ತ್ರಿಕೋನದ ದ್ವಿಭಾಜಕಗಳು ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆಸ್ತಿ 2".ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ದ್ವಿಮುಖ ಕೋನಗಳ ದ್ವಿಭಾಜಕ ವಿಮಾನಗಳು ಒಂದು ಸರಳ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಛೇದಿಸುತ್ತವೆ.
ಪುರಾವೆಯು ವಿಮಾನ ಪ್ರಕರಣಕ್ಕೆ ಹೋಲುತ್ತದೆ. ಅವುಗಳೆಂದರೆ, ಅವಕಾಶ SABC- ತ್ರಿಕೋನ ಕೋನ. ಡೈಹೆಡ್ರಲ್ ಕೋನದ ಬೈಸೆಕ್ಟಲ್ ಪ್ಲೇನ್ ಎಸ್.ಎ.ಅದರ ಮುಖಗಳಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿರುವ ಕೋನದ GMT ಆಗಿದೆ ಎ.ಎಸ್.ಸಿ.ಮತ್ತು ಎ.ಎಸ್.ಬಿ.. ಅಂತೆಯೇ, ದ್ವಿಮುಖ ಕೋನದ ದ್ವಿಭಾಜಕ ಸಮತಲ ಎಸ್.ಬಿ.ಅದರ ಮುಖಗಳಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿರುವ ಕೋನದ GMT ಆಗಿದೆ ಬಿ.ಎಸ್.ಎ.ಮತ್ತು BSC . ಅವರ ಛೇದನದ ಸಾಲು ಆದ್ದರಿಂದಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಎಲ್ಲಾ ಮುಖಗಳಿಂದ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ, ಡೈಹೆಡ್ರಲ್ ಕೋನದ ದ್ವಿಭಾಜಕ ಸಮತಲವು ಅದರ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ ಎಸ್.ಸಿ. .
ಆಸ್ತಿ 3.ತ್ರಿಕೋನದ ಬದಿಗಳಿಗೆ ಲಂಬ ದ್ವಿಭಾಜಕಗಳು ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆಸ್ತಿ 3".ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಮುಖಗಳ ದ್ವಿಭಾಜಕಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು ಮತ್ತು ಈ ಮುಖಗಳಿಗೆ ಲಂಬವಾಗಿ ಒಂದು ಸರಳ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಛೇದಿಸುತ್ತವೆ.
ಪುರಾವೆಯು ಹಿಂದಿನ ಆಸ್ತಿಯ ಪುರಾವೆಗೆ ಹೋಲುತ್ತದೆ.
ಆಸ್ತಿ 4.ತ್ರಿಕೋನದ ಮಧ್ಯಭಾಗಗಳು ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆಸ್ತಿ 4".ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಅಂಚುಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು ಮತ್ತು ವಿರುದ್ಧ ಮುಖಗಳ ದ್ವಿಭಾಜಕಗಳು ಒಂದು ಸರಳ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಛೇದಿಸುತ್ತವೆ.
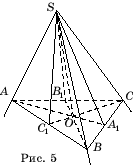
ಪುರಾವೆ. ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಪರಿಗಣಿಸಿ SABC,SA=SB=SC(ಚಿತ್ರ 5). ನಂತರ ದ್ವಿಭಾಜಕಗಳು ಎಸ್.ಎ. 1 , ಎಸ್.ಬಿ. 1 , ಎಸ್.ಸಿ. 1 ಮೂಲೆಗಳು BSC, ASC, ASB ಅನುಗುಣವಾದ ತ್ರಿಕೋನಗಳ ಮಧ್ಯಭಾಗಗಳಾಗಿವೆ. ಅದಕ್ಕೇ ಎ.ಎ. 1 , ಬಿಬಿ 1 , CC 1 - ತ್ರಿಕೋನದ ಮಧ್ಯಭಾಗಗಳು ಎಬಿಸಿ. ಅವಕಾಶ ಓ- ಅವರ ಛೇದನದ ಬಿಂದು. ನೇರ ಆದ್ದರಿಂದಪರಿಗಣನೆಯಲ್ಲಿರುವ ಎಲ್ಲಾ ಮೂರು ವಿಮಾನಗಳಲ್ಲಿ ಒಳಗೊಂಡಿರುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ, ಅವುಗಳ ಛೇದನದ ರೇಖೆಯಾಗಿದೆ.

ಆಸ್ತಿ 5.ತ್ರಿಕೋನದ ಎತ್ತರಗಳು ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆಸ್ತಿ 5". ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಅಂಚುಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ಮತ್ತು ವಿರುದ್ಧ ಮುಖಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ವಿಮಾನಗಳು ಒಂದು ಸರಳ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ಛೇದಿಸುತ್ತವೆ.
ಪುರಾವೆ. ಶೃಂಗದೊಂದಿಗೆ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಪರಿಗಣಿಸಿ ಎಸ್ಮತ್ತು ಪಕ್ಕೆಲುಬುಗಳು a, b, cಸೂಚಿಸೋಣ ಎ 1 , ಬಿ 1 , ಸಿ 1 - ಅನುಗುಣವಾದ ಅಂಚುಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ಮತ್ತು ಈ ಮುಖಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ವಿಮಾನಗಳೊಂದಿಗೆ ಮುಖಗಳ ಛೇದನದ ಸಾಲುಗಳು (ಚಿತ್ರ 6). ಪಾಯಿಂಟ್ ಅನ್ನು ಸರಿಪಡಿಸೋಣ ಸಿಅಂಚಿನಲ್ಲಿ ಸಿಮತ್ತು ಅದರಿಂದ ಲಂಬಗಳನ್ನು ಬಿಡಿ ಸಿ.ಎ. 1 ಮತ್ತು ಸಿ.ಬಿ. 1 ನೇರ ರೇಖೆಗಳಲ್ಲಿ ಎ 1 ಮತ್ತು ಬಿ 1 . ಸೂಚಿಸೋಣ ಎಮತ್ತು ಬಿಸಾಲು ಛೇದಕಗಳು ಸಿ.ಎ. 1 ಮತ್ತು ಸಿ.ಬಿ. 1 ನೇರ ರೇಖೆಗಳೊಂದಿಗೆ ಎಮತ್ತು ಬಿ. ನಂತರ ಎಸ್.ಎ. 1 ಪ್ರೊಜೆಕ್ಷನ್ ಆಗಿದೆ ಎ.ಎ. 1 ಅಂಚಿಗೆ BSC. ಏಕೆಂದರೆ ಬಿ.ಸಿ.ಲಂಬವಾಗಿರುವ ಎಸ್.ಎ. 1 , ನಂತರ ಅದು ಲಂಬವಾಗಿರುತ್ತದೆ ಮತ್ತು ಎ.ಎ. 1 . ಅಂತೆಯೇ, ಎ.ಸಿ.ಲಂಬವಾಗಿರುವ ಬಿಬಿ 1 . ಹೀಗಾಗಿ, ಎ.ಎ. 1 ಮತ್ತು ಬಿಬಿ 1 ತ್ರಿಕೋನದ ಎತ್ತರಗಳಾಗಿವೆ ಎಬಿಸಿ. ಅವಕಾಶ ಓ- ಅವರ ಛೇದನದ ಬಿಂದು. ರೇಖೆಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವಿಮಾನಗಳು ಎಮತ್ತು ಎ 1 , ಬಿಮತ್ತು ಬಿ 1 ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿ ಎಬಿಸಿಮತ್ತು, ಆದ್ದರಿಂದ, ಅವರ ಛೇದನದ ಸಾಲು ಆದ್ದರಿಂದಲಂಬವಾಗಿರುವ ಎಬಿಸಿ. ಅಂದರೆ, ಆದ್ದರಿಂದಲಂಬವಾಗಿರುವ ಎಬಿ. ಇನ್ನೊಂದು ಕಡೆ, COಲಂಬವಾಗಿರುವ ಎಬಿ. ಆದ್ದರಿಂದ, ವಿಮಾನವು ಅಂಚಿನ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ ಸಿಮತ್ತು ಆದ್ದರಿಂದವಿರುದ್ಧ ಮುಖಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ.
ಆಸ್ತಿ 6 (ಸೈನ್ ಪ್ರಮೇಯ). ತ್ರಿಕೋನದಲ್ಲಿ ಎಬಿಸಿಪಕ್ಷಗಳೊಂದಿಗೆ a, b, cಅದರಂತೆ, ಸಮಾನತೆಗಳು ನಡೆಯುತ್ತವೆ ಎ : ಪಾಪ ಎ = ಬಿ: ಪಾಪ ಬಿ=ಸಿ: ಪಾಪ ಸಿ.
ಆಸ್ತಿ 6".ಎ, ಬಿ, ಜಿ - ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಫ್ಲಾಟ್ ಕೋನಗಳು, a, b, c- ಅವುಗಳ ವಿರುದ್ಧ ದ್ವಿಮುಖ ಕೋನಗಳು. ನಂತರಪಾಪ ಎ: ಪಾಪ ಎ= ಪಾಪ ಬೌ: ಪಾಪ ಬಿ= ಪಾಪ ಜಿ: ಪಾಪ ಸಿ.
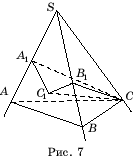
ಪುರಾವೆ.ಅವಕಾಶ SABC- ತ್ರಿಕೋನ ಕೋನ. ಹಂತದಿಂದ ಬಿಡೋಣ ಸಿಲಂಬವಾಗಿರುವ CC 1 ವಿಮಾನಕ್ಕೆ ಎ.ಎಸ್.ಬಿ.ಮತ್ತು ಲಂಬವಾಗಿ ಸಿ.ಎ. 1 ಅಂಚಿನಲ್ಲಿ ಎಸ್.ಎ.(ಚಿತ್ರ 7). ನಂತರ ಕೋನ ಸಿ.ಎ. 1 ಸಿ 1 ತಿನ್ನುವೆ ರೇಖೀಯ ಕೋನದ್ವಿಮುಖ ಕೋನ ಎ. ಅದಕ್ಕೇ CC 1 = ಸಿ.ಎ. 1 ಪಾಪ ಎ = ಎಸ್.ಸಿ.ಪಾಪ ಬಿ ಪಾಪ ಎ. ಅಂತೆಯೇ ಅದನ್ನು ತೋರಿಸಲಾಗಿದೆ CC 1 = CB 1 ಪಾಪ b = SCಪಾಪ ಒಂದು ಪಾಪ ಬಿ. ಪರಿಣಾಮವಾಗಿ, ಸಮಾನತೆ ಪಾಪಬಿ ಪಾಪ a =ಪಾಪ ಎ ಪಾಪ ಬಿಮತ್ತು, ಆದ್ದರಿಂದ, ಸಮಾನತೆ ಪಾಪಎ: ಪಾಪ ಎ= ಪಾಪ : ಪಾಪ ಬಿ. ಇದೇ ರೀತಿಯಲ್ಲಿ ಸಮಾನತೆ ಪಾಪ ಎಂಬುದು ಸಾಬೀತಾಗಿದೆಬೌ: ಪಾಪ ಬಿ= ಪಾಪ ಜಿ: ಪಾಪ ಸಿ.

ಆಸ್ತಿ 7.ಒಳಗೆ ಇದ್ದರೆ ಪೀನ ಚತುರ್ಭುಜನೀವು ವೃತ್ತವನ್ನು ಕೆತ್ತಲು ಸಾಧ್ಯವಾದರೆ, ಎದುರು ಬದಿಗಳ ಮೊತ್ತವು ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಆಸ್ತಿ 7".ಒಂದು ಗೋಳವನ್ನು ಪೀನ ಚತುರ್ಭುಜ ಕೋನಕ್ಕೆ ಕೆತ್ತಿದರೆ, ವಿರುದ್ಧ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಸಾಹಿತ್ಯ
1. ಹದಮರ್ಡ್ ಜೆ. ಎಲಿಮೆಂಟರಿ ಜ್ಯಾಮಿತಿ. ಭಾಗ II. ಸ್ಟೀರಿಯೊಮೆಟ್ರಿ. - ಎಂ.: ಉಚ್ಪೆಡ್ಗಿಜ್, 1938.
2. ಪೆರೆಪೆಲ್ಕಿನ್ ಡಿ.ಐ. ಸರಿ ಪ್ರಾಥಮಿಕ ಜ್ಯಾಮಿತಿ. ಭಾಗ II. ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಜ್ಯಾಮಿತಿ. - M.-L.: ಗೊಸ್ಟೆಖಿಜ್ಡಾಟ್, 1949.
3. ಎನ್ಸೈಕ್ಲೋಪೀಡಿಯಾ ಪ್ರಾಥಮಿಕ ಗಣಿತ. ಪುಸ್ತಕ IV. ರೇಖಾಗಣಿತ. - ಎಂ.; 1963.
4. ಸ್ಮಿರ್ನೋವಾ I.M. ಪಾಲಿಹೆಡ್ರಾ ಜಗತ್ತಿನಲ್ಲಿ. - ಎಂ.: ಶಿಕ್ಷಣ, 1995.

ಪಾಠದ ಪಠ್ಯ ಪ್ರತಿಲೇಖನ:

ಪ್ಲಾನಿಮೆಟ್ರಿಯಲ್ಲಿ, ಅಧ್ಯಯನದ ವಸ್ತುಗಳಲ್ಲಿ ಒಂದು ಕೋನವಾಗಿದೆ.

ಕೋನವು ಒಂದು ಬಿಂದುವನ್ನು ಒಳಗೊಂಡಿರುವ ಜ್ಯಾಮಿತೀಯ ಆಕೃತಿಯಾಗಿದೆ - ಕೋನದ ಶೃಂಗ ಮತ್ತು ಈ ಬಿಂದುವಿನಿಂದ ಹೊರಹೊಮ್ಮುವ ಎರಡು ಕಿರಣಗಳು.

ಎರಡು ಕೋನಗಳು, ಒಂದು ಬದಿಯು ಸಾಮಾನ್ಯವಾಗಿದೆ ಮತ್ತು ಇತರ ಎರಡು ಒಂದರ ಮುಂದುವರಿಕೆಯಾಗಿದೆ, ಪ್ಲಾನಿಮೆಟ್ರಿಯಲ್ಲಿ ಪಕ್ಕದ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ದಿಕ್ಸೂಚಿಯನ್ನು ಸಮತಲ ಕೋನದ ಮಾದರಿ ಎಂದು ಪರಿಗಣಿಸಬಹುದು.

ಡೈಹೆಡ್ರಲ್ ಕೋನದ ಪರಿಕಲ್ಪನೆಯನ್ನು ನಾವು ನೆನಪಿಸಿಕೊಳ್ಳೋಣ.

ಇದು ನೇರ ರೇಖೆ a ಮತ್ತು ಎರಡು ಅರ್ಧ-ವಿಮಾನಗಳು c ನಿಂದ ರೂಪುಗೊಂಡ ಆಕೃತಿಯಾಗಿದೆ ಸಾಮಾನ್ಯ ಗಡಿಮತ್ತು, ಜ್ಯಾಮಿತಿಯಲ್ಲಿ ಒಂದೇ ಸಮತಲಕ್ಕೆ ಸೇರದಿರುವುದನ್ನು ಡೈಹೆಡ್ರಲ್ ಕೋನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅರ್ಧ-ವಿಮಾನಗಳು ದ್ವಿಮುಖ ಕೋನದ ಮುಖಗಳಾಗಿವೆ. ನೇರ ರೇಖೆ a ಡೈಹೆಡ್ರಲ್ ಕೋನದ ಅಂಚು.

ಮನೆಯ ಮೇಲ್ಛಾವಣಿಯು ಡೈಹೆಡ್ರಲ್ ಕೋನವನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ತೋರಿಸುತ್ತದೆ.

ಆದರೆ ಚಿತ್ರ ಎರಡರಲ್ಲಿರುವ ಮನೆಯ ಮೇಲ್ಛಾವಣಿಯು ಸಾಮಾನ್ಯ ಶೃಂಗದೊಂದಿಗೆ ಆರು ಚಪ್ಪಟೆ ಕೋನಗಳಿಂದ ರೂಪುಗೊಂಡ ಆಕೃತಿಯ ರೂಪದಲ್ಲಿ ಮಾಡಲ್ಪಟ್ಟಿದೆ ಆದ್ದರಿಂದ ಕೋನಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಕ್ರಮದಲ್ಲಿಮತ್ತು ಮೊದಲ ಮತ್ತು ಕೊನೆಯದು ಸೇರಿದಂತೆ ಪಕ್ಕದ ಕೋನಗಳ ಪ್ರತಿಯೊಂದು ಜೋಡಿಯು ಹೊಂದಿದೆ ಸಾಮಾನ್ಯ ಭಾಗ. ಈ ಛಾವಣಿಯ ಆಕಾರವನ್ನು ಏನೆಂದು ಕರೆಯುತ್ತಾರೆ?

ರೇಖಾಗಣಿತದಲ್ಲಿ, ಕೋನಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟ ಆಕೃತಿ

ಮತ್ತು ಈ ಕೋನವನ್ನು ಮಾಡಿದ ಕೋನಗಳನ್ನು ಪ್ಲೇನ್ ಕೋನಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಸಮತಲ ಕೋನಗಳ ಬದಿಗಳನ್ನು ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದ ಅಂಚುಗಳು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಪಾಯಿಂಟ್ O ಅನ್ನು ಕೋನದ ಶೃಂಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳ ಉದಾಹರಣೆಗಳನ್ನು ಟೆಟ್ರಾಹೆಡ್ರನ್ ಮತ್ತು ಪ್ಯಾರಲೆಲೆಪಿಪ್ಡ್‌ನಲ್ಲಿ ಕಾಣಬಹುದು.

ಟೆಟ್ರಾಹೆಡ್ರನ್ ಡಿಬಿಎ, ಎಬಿಸಿ, ಡಿಬಿಸಿಯ ಮುಖಗಳು ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ BADC ಅನ್ನು ರೂಪಿಸುತ್ತವೆ. ಹೆಚ್ಚಾಗಿ ಇದನ್ನು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಸಮಾನಾಂತರವಾಗಿ, AA1D1D, ABCD, AA1B1B ಮುಖಗಳು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನ AA1DB ಅನ್ನು ರೂಪಿಸುತ್ತವೆ.

ಸರಿ, ಮನೆಯ ಮೇಲ್ಛಾವಣಿಯು ಷಡ್ಭುಜೀಯ ಕೋನದ ಆಕಾರದಲ್ಲಿ ಮಾಡಲ್ಪಟ್ಟಿದೆ. ಇದು ಆರು ಫ್ಲಾಟ್ ಕೋನಗಳನ್ನು ಒಳಗೊಂಡಿದೆ.

ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಕ್ಕೆ ಹಲವಾರು ಗುಣಲಕ್ಷಣಗಳು ನಿಜ. ನಾವು ಅವುಗಳನ್ನು ರೂಪಿಸೋಣ ಮತ್ತು ಸಾಬೀತುಪಡಿಸೋಣ. ಎಂಬ ಹೇಳಿಕೆಯನ್ನು ಇಲ್ಲಿ ಹೇಳುತ್ತದೆ

ಮೊದಲನೆಯದಾಗಿ, ಯಾವುದೇ ಪೀನದ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಕ್ಕೆ ಅದರ ಎಲ್ಲಾ ಅಂಚುಗಳನ್ನು ಛೇದಿಸುವ ಸಮತಲವಿದೆ.

ಪುರಾವೆಗಾಗಿ, ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನ OA1A2 A3...An ಅನ್ನು ಪರಿಗಣಿಸಿ.

ಷರತ್ತಿನ ಪ್ರಕಾರ, ಇದು ಪೀನವಾಗಿರುತ್ತದೆ. ಕೋನವು ಅದರ ಪ್ರತಿಯೊಂದು ಸಮತಲ ಕೋನಗಳ ಸಮತಲದ ಒಂದು ಬದಿಯಲ್ಲಿದ್ದರೆ ಅದನ್ನು ಪೀನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಷರತ್ತಿನ ಪ್ರಕಾರ, ಈ ಕೋನವು ಪೀನವಾಗಿರುತ್ತದೆ, ನಂತರ ಅಂಕಗಳು O, A1, A2, A3, OA1A2 ಸಮತಲದ ಒಂದು ಬದಿಯಲ್ಲಿ ಇರುತ್ತದೆ

ಕೈಗೊಳ್ಳೋಣ ಮಧ್ಯರೇಖೆತ್ರಿಕೋನ OA1A2 ನ KM ಮತ್ತು OA3, OA4, OA ಅಂಚುಗಳಿಂದ ಆಯ್ಕೆಮಾಡಿ OKM ಸಮತಲದೊಂದಿಗೆ ಚಿಕ್ಕದಾದ ದ್ವಿಮುಖ ಕೋನವನ್ನು ರೂಪಿಸುವ ಅಂಚನ್ನು. ಇದು ಅಂಚಿನ OAi ಆಗಿರಲಿ.(ಓಎ ಒಟ್ಟು)

ನಾವು ಅರ್ಧ-ಪ್ಲೇನ್ α ಅನ್ನು ಬೌಂಡರಿ CM ನೊಂದಿಗೆ ಪರಿಗಣಿಸೋಣ, ಡೈಹೆಡ್ರಲ್ ಕೋನ OKMAi ಅನ್ನು ಎರಡು ಡೈಹೆಡ್ರಲ್ ಕೋನಗಳಾಗಿ ವಿಭಜಿಸೋಣ. A ನಿಂದ An ವರೆಗಿನ ಎಲ್ಲಾ ಶೃಂಗಗಳು ಸಮತಲದ ಒಂದು ಬದಿಯಲ್ಲಿ α ಮತ್ತು ಇನ್ನೊಂದು ಬದಿಯಲ್ಲಿ O ಬಿಂದು. ಪರಿಣಾಮವಾಗಿ, ಸಮತಲ α ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನದ ಎಲ್ಲಾ ಅಂಚುಗಳನ್ನು ಛೇದಿಸುತ್ತದೆ. ಹೇಳಿಕೆ ಸಾಬೀತಾಗಿದೆ.

ಪೀನ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನಗಳು ಮತ್ತೊಂದು ಪ್ರಮುಖ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿವೆ.

ಪೀನದ ಬಹುಮುಖ ಕೋನದ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು 360 ° ಗಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ.

O ಬಿಂದುವಿನಲ್ಲಿ ಶೃಂಗದೊಂದಿಗೆ ಪೀನದ ಬಹುಮುಖ ಕೋನವನ್ನು ಪರಿಗಣಿಸಿ. ಸಾಬೀತಾದ ಹೇಳಿಕೆಯ ಕಾರಣದಿಂದಾಗಿ, ಅದರ ಎಲ್ಲಾ ಅಂಚುಗಳನ್ನು ಛೇದಿಸುವ ಸಮತಲವಿದೆ.

ನಾವು ಅಂತಹ ಸಮತಲವನ್ನು ಸೆಳೆಯೋಣ α, ಇದು ಕೋನದ ಅಂಚುಗಳನ್ನು A1, A2, A3 ಮತ್ತು An ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸೋಣ.

ಸಮತಲ ಕೋನದ ಹೊರ ಪ್ರದೇಶದಿಂದ ಸಮತಲ α ತ್ರಿಕೋನವನ್ನು ಕತ್ತರಿಸುತ್ತದೆ. ಕೋನಗಳ ಮೊತ್ತವು 180° ಆಗಿದೆ. A1OA2 ನಿಂದ AnOA1 ವರೆಗಿನ ಎಲ್ಲಾ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು ಅಭಿವ್ಯಕ್ತಿಗೆ ಸಮಾನವಾಗಿದೆ ಎಂದು ನಾವು ಪಡೆಯುತ್ತೇವೆ, ನಾವು ಈ ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಪರಿವರ್ತಿಸುತ್ತೇವೆ, ನಾವು ನಿಯಮಗಳನ್ನು ಮರುಹೊಂದಿಸುತ್ತೇವೆ, ನಾವು ಪಡೆಯುತ್ತೇವೆ

IN ಈ ಅಭಿವ್ಯಕ್ತಿಬ್ರಾಕೆಟ್‌ಗಳಲ್ಲಿ ಸೂಚಿಸಲಾದ ಮೊತ್ತಗಳು ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನದ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತಗಳಾಗಿವೆ, ಮತ್ತು ತಿಳಿದಿರುವಂತೆ ಅವು ಮೂರನೇ ಸಮತಲ ಕೋನಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿದೆ.

ಕೊಟ್ಟಿರುವ ಪಾಲಿಹೆಡ್ರಲ್ ಕೋನವನ್ನು ರೂಪಿಸುವ ಎಲ್ಲಾ ಟ್ರೈಹೆಡ್ರಲ್ ಕೋನಗಳಿಗೆ ಈ ಅಸಮಾನತೆಯನ್ನು ಬರೆಯಬಹುದು.

ಪರಿಣಾಮವಾಗಿ, ನಾವು ಸಮಾನತೆಯ ಕೆಳಗಿನ ಮುಂದುವರಿಕೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ

ಪೀನ ಬಹುಮುಖ ಕೋನದ ಸಮತಲ ಕೋನಗಳ ಮೊತ್ತವು 360 ಡಿಗ್ರಿಗಳಿಗಿಂತ ಕಡಿಮೆಯಿದೆ ಎಂದು ಉತ್ತರವು ಸಾಬೀತುಪಡಿಸುತ್ತದೆ.