ហេតុអ្វីបានជាផលិតផលឆ្លងកាត់ស្មើនឹងសូន្យ? ផលិតផលឆ្លងកាត់ - និយមន័យ លក្ខណៈសម្បត្តិ រូបមន្ត ឧទាហរណ៍ និងដំណោះស្រាយ

៧.១. និយមន័យនៃផលិតផលឆ្លងកាត់

វ៉ិចទ័រ​បី​ដែល​មិន​មែន​ coplanar a, b និង c ដែល​បាន​យក​តាម​លំដាប់​ដែល​បាន​ចង្អុល​បង្ហាញ បង្កើត​ជា​វ៉ិចទ័រ​បី​ខាង​ស្ដាំ ប្រសិនបើ​ចាប់ពី​ចុង​វ៉ិចទ័រ​ទី​បី c នោះ​វេន​ខ្លី​បំផុត​ពី​វ៉ិចទ័រ​ទីមួយ a ទៅ​វ៉ិចទ័រ​ទីពីរ b ត្រូវ​បាន​គេ​មើល​ឃើញ។ ត្រូវច្រាសទ្រនិចនាឡិកា ហើយដៃឆ្វេងបីដង បើទ្រនិចនាឡិកា (សូមមើលរូប .16)។

ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ a និងវ៉ិចទ័រ b ត្រូវបានគេហៅថាវ៉ិចទ័រ c ដែល៖

1. កាត់កែងទៅនឹងវ៉ិចទ័រ a និង b, i.e. c ^ a និង c ^ ខ ;

2. មាន​ប្រវែង​ជា​លេខ​ស្មើ​នឹង​ផ្ទៃ​នៃ​ប្រលេឡូក្រាម​ដែល​សង់​លើ​វ៉ិចទ័រ a និងខដូចនៅសងខាង (សូមមើលរូបទី 17) i.e.

3. វ៉ិចទ័រ a, b និង c បង្កើតបានជាដៃស្តាំបីដង។

ផលិតផលឈើឆ្កាងត្រូវបានតំណាង a x b ឬ [a,b] ។ ទំនាក់ទំនងខាងក្រោមរវាងវ៉ិចទ័រឯកតា ខ្ញុំធ្វើតាមដោយផ្ទាល់ពីនិយមន័យនៃផលិតផលវ៉ិចទ័រ j និង k

(សូមមើលរូបទី 18)៖
i x j = k, j x k = i, k x i = j ។ជាឧទាហរណ៍ ចូរយើងបញ្ជាក់

ខ្ញុំ xj = k ។ ^ 1) k^i, k

j; 2) |k |=1 ប៉ុន្តែ |ខ្ញុំ x j

| = |i | និង|J | sin(90°)=1;

3) វ៉ិចទ័រ i, j និង

បង្កើតជាបីដងខាងស្តាំ (សូមមើលរូបទី 16)។

៧.២. លក្ខណៈសម្បត្តិនៃផលិតផលឆ្លងកាត់ = -(1. នៅពេលរៀបចំកត្តាឡើងវិញ ផលិតផលវ៉ិចទ័រផ្លាស់ប្តូរសញ្ញា i.e.).

និង xb =(b xa) (សូមមើលរូប 19)។

វ៉ិចទ័រ a xb និង b xa គឺ collinear មានម៉ូឌុលដូចគ្នា (ផ្ទៃនៃប្រលេឡូក្រាមនៅតែមិនផ្លាស់ប្តូរ) ប៉ុន្តែត្រូវបានតម្រង់ទិសផ្ទុយគ្នា (បីដង a, b, a xb និង a, b, b x a នៃទិសផ្ទុយគ្នា) ។ ដូច្នេះ axb b xa ខ 2. ផលិតផលវ៉ិចទ័រមានទ្រព្យសម្បត្តិរួមបញ្ចូលគ្នាដោយគោរពតាមកត្តាមាត្រដ្ឋានពោលគឺ l (a xb) = (l a) x b = a x (l b) ។ ខអនុញ្ញាតឱ្យ l > 0 ។ វ៉ិចទ័រ l (a xb) កាត់កែងទៅនឹងវ៉ិចទ័រ a និង b ។ វ៉ិចទ័រ ( axbលីត្រ axbក) x axb b xa ខក៏កាត់កែងទៅនឹងវ៉ិចទ័រ a និង

(វ៉ិចទ័រ a, axbប៉ុន្តែដេកនៅលើយន្តហោះដូចគ្នា) ។ នេះមានន័យថាវ៉ិចទ័រ axb(a xb) និង ( axb<0.

collinear ។ វាច្បាស់ណាស់ថាទិសដៅរបស់ពួកគេស្របគ្នា។ ពួកគេមានប្រវែងដូចគ្នា៖ ខនោះហើយជាមូលហេតុ<=>(a xb)=

xb ។ វាត្រូវបានបញ្ជាក់តាមរបៀបស្រដៀងគ្នាសម្រាប់

3. វ៉ិចទ័រមិនសូន្យពីរ a និង

(គឺ collinear ប្រសិនបើ និងលុះត្រាតែផលិតផលវ៉ិចទ័ររបស់ពួកគេស្មើនឹងសូន្យវ៉ិចទ័រ ពោលគឺ a ||bនិង xb = 0 ។ ខជាពិសេស i * i = j * j = k * k = 0 ។

4. ផលិតផលវ៉ិចទ័រមានទ្រព្យសម្បត្តិចែកចាយ៖

៧.៣. ការបង្ហាញផលិតផលឆ្លងកាត់នៅក្នុងលក្ខខណ្ឌនៃកូអរដោនេ

យើងនឹងប្រើតារាងផលិតផលឆ្លងកាត់នៃវ៉ិចទ័រ i, ទំនាក់ទំនងខាងក្រោមរវាងវ៉ិចទ័រឯកតា ខ្ញុំធ្វើតាមដោយផ្ទាល់ពីនិយមន័យនៃផលិតផលវ៉ិចទ័រនិង k:

ប្រសិនបើទិសដៅនៃផ្លូវខ្លីបំផុតពីវ៉ិចទ័រទីមួយទៅទីពីរស្របគ្នានឹងទិសដៅនៃព្រួញនោះផលិតផលគឺស្មើនឹងវ៉ិចទ័រទីបីប្រសិនបើវាមិនស្របគ្នានោះវ៉ិចទ័រទីបីត្រូវបានថតដោយសញ្ញាដក។

សូមអោយវ៉ិចទ័រពីរ a = a x i + a y ត្រូវបានផ្តល់ឱ្យ ទំនាក់ទំនងខាងក្រោមរវាងវ៉ិចទ័រឯកតា ខ្ញុំធ្វើតាមដោយផ្ទាល់ពីនិយមន័យនៃផលិតផលវ៉ិចទ័រ+a z និងនិង b = b x ខ្ញុំ+ ខ y ទំនាក់ទំនងខាងក្រោមរវាងវ៉ិចទ័រឯកតា ខ្ញុំធ្វើតាមដោយផ្ទាល់ពីនិយមន័យនៃផលិតផលវ៉ិចទ័រ+b z និង. ចូរយើងស្វែងរកផលគុណវ៉ិចទ័រនៃវ៉ិចទ័រទាំងនេះដោយគុណពួកវាជាពហុធា (យោងតាមលក្ខណៈសម្បត្តិនៃផលិតផលវ៉ិចទ័រ)៖

រូបមន្តលទ្ធផលអាចត្រូវបានសរសេរកាន់តែខ្លី៖

ចាប់តាំងពីផ្នែកខាងស្តាំនៃសមភាព (7.1) ទាក់ទងទៅនឹងការពង្រីកនៃកត្តាកំណត់លំដាប់ទីបីនៅក្នុងលក្ខខណ្ឌនៃធាតុនៃសមភាពជួរទីមួយ (7.2) គឺងាយស្រួលចងចាំ។

៧.៤. កម្មវិធីមួយចំនួននៃផលិតផលឆ្លងកាត់

ការបង្កើតភាពជាប់គ្នានៃវ៉ិចទ័រ

ការស្វែងរកផ្ទៃនៃប្រលេឡូក្រាម និងត្រីកោណ

យោងទៅតាមនិយមន័យនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ កនិង ខ |a xb | =|a | *|b|sin g, i.e. S គូ = |a x b|. ដូច្នេះហើយ D S = 1/2|a x b| ។

ការកំណត់ពេលនៃកម្លាំងអំពីចំណុចមួយ។

អនុញ្ញាតឱ្យកម្លាំងត្រូវបានអនុវត្តនៅចំណុច A F = ABនិងអនុញ្ញាតឱ្យ អំពី- ចំណុចមួយចំនួននៅក្នុងលំហ (សូមមើលរូបទី 20)។

វាត្រូវបានគេស្គាល់ពីរូបវិទ្យាថា ពេលនៃកម្លាំង ច ទាក់ទងទៅនឹងចំណុច អំពីហៅថាវ៉ិចទ័រ មដែលឆ្លងកាត់ចំណុច អំពីនិង៖

1) កាត់កែងទៅនឹងយន្តហោះឆ្លងកាត់ចំនុច O, A, B;

2) លេខស្មើនឹងផលិតផលនៃកម្លាំងក្នុងមួយដៃ

3) បង្កើតជាបីខាងស្តាំជាមួយវ៉ិចទ័រ OA និង A B ។

ដូច្នេះ M = OA x F ។

ស្វែងរកល្បឿនបង្វិលលីនេអ៊ែរ

ល្បឿន vចំណុច M នៃតួរឹងបង្វិលជាមួយល្បឿនមុំ វជុំវិញអ័ក្សថេរត្រូវបានកំណត់ដោយរូបមន្តរបស់អយល័រ v =w xr ដែល r = OM ដែល O គឺជាចំណុចថេរមួយចំនួននៃអ័ក្ស (សូមមើលរូបភាពទី 21) ។

មុននឹងផ្តល់គំនិតនៃផលិតផលវ៉ិចទ័រ ចូរយើងងាកទៅរកសំណួរនៃការតំរង់ទិសនៃវ៉ិចទ័របីវិមាត្រ a →, b →, c → ក្នុងចន្លោះបីវិមាត្រ។

ដើម្បីចាប់ផ្តើម យើងដាក់វ៉ិចទ័រ a → , b → , c → ពីចំនុចមួយ។ ការតំរង់ទិសនៃបី a → , b → , c → អាចជាស្តាំឬឆ្វេងអាស្រ័យលើទិសដៅនៃវ៉ិចទ័រ c →ខ្លួនវាផ្ទាល់។ ប្រភេទនៃបីបី a → , b → , c → នឹងត្រូវបានកំណត់ពីទិសដៅដែលវេនខ្លីបំផុតត្រូវបានធ្វើឡើងពីវ៉ិចទ័រ a → ទៅ b → ពីចុងបញ្ចប់នៃវ៉ិចទ័រ c → .

ប្រសិនបើវេនខ្លីបំផុតត្រូវបានអនុវត្តច្រាសទ្រនិចនាឡិកានោះបីដងនៃវ៉ិចទ័រ a → , b → , c → ត្រូវបានគេហៅថា ត្រឹមត្រូវ។ប្រសិនបើទ្រនិចនាឡិកា - ឆ្វេង.

បន្ទាប់​មក​យក​វ៉ិចទ័រ​មិន​ជាប់​ជួរ​គ្នា​ពីរ a → និង b → ។ ចូរយើងគូររូបវ៉ិចទ័រ A B → = a → និង A C → = b → ពីចំនុច A ។ ចូរយើងសង់វ៉ិចទ័រ A D → = c → ដែលកាត់កែងគ្នាទាំង A B → និង A C → ។ ដូច្នេះនៅពេលសាងសង់វ៉ិចទ័រដោយខ្លួនឯង A D → = c → យើងអាចធ្វើវាតាមពីរវិធីដោយផ្តល់ឱ្យវានូវទិសដៅមួយឬផ្ទុយ (សូមមើលរូបភាព) ។

លំដាប់បីនៃវ៉ិចទ័រ a → , b → , c → អាចជា ដូចដែលយើងបានរកឃើញ ស្តាំ ឬឆ្វេង អាស្រ័យលើទិសដៅនៃវ៉ិចទ័រ។

ពីខាងលើយើងអាចណែនាំនិយមន័យនៃផលិតផលវ៉ិចទ័រ។ និយមន័យនេះត្រូវបានផ្តល់ឱ្យសម្រាប់វ៉ិចទ័រពីរដែលបានកំណត់នៅក្នុងប្រព័ន្ធកូអរដោនេចតុកោណនៃលំហបីវិមាត្រ។

និយមន័យ ១

ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រពីរ a → និង b → យើង​នឹង​ហៅ​វ៉ិចទ័រ​ដែល​បាន​កំណត់​ក្នុង​ប្រព័ន្ធ​កូអរដោណេ​ចតុកោណ​នៃ​លំហ​បី​វិមាត្រ​ដូច​ជា៖

• ប្រសិនបើវ៉ិចទ័រ a → និង b → ជាប់គ្នា វានឹងក្លាយជាសូន្យ។
• វានឹងកាត់កែងទៅនឹងវ៉ិចទ័រ a → ​​ និងវ៉ិចទ័រ b → i.e. ∠ a → c → = ∠ b → c → = π 2 ;
• ប្រវែងរបស់វាត្រូវបានកំណត់ដោយរូបមន្ត៖ c → = a → · b → · sin ∠ a → , b → ;
• បីដងនៃវ៉ិចទ័រ a → , b → , c → មានទិសដៅដូចគ្នាទៅនឹងប្រព័ន្ធកូអរដោនេដែលបានផ្តល់ឱ្យ។

ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ a → និង b → មានសញ្ញាណដូចខាងក្រោមៈ a → × b → ។

សំរបសំរួលនៃផលិតផលវ៉ិចទ័រ

ដោយសារវ៉ិចទ័រណាមួយមានកូអរដោនេជាក់លាក់នៅក្នុងប្រព័ន្ធកូអរដោនេ យើងអាចណែនាំនិយមន័យទីពីរនៃផលិតផលវ៉ិចទ័រ ដែលនឹងអនុញ្ញាតឱ្យយើងស្វែងរកកូអរដោនេរបស់វាដោយប្រើកូអរដោនេនៃវ៉ិចទ័រដែលបានផ្តល់ឱ្យ។

និយមន័យ ២

នៅក្នុងប្រព័ន្ធសំរបសំរួលរាងចតុកោណនៃលំហបីវិមាត្រ ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រពីរ a → = (a x ; a y ; a z) និង b → = ( ​​b x ; b y ; b z ) ត្រូវបានគេហៅថា វ៉ិចទ័រ c → = a → × b → = (a y b z − a z b y) i → + (a z b x − a x b z) j → + (a x b y − a y b x) k → , ដែល i → , j → , k → គឺជាវ៉ិចទ័រកូអរដោណេ។

ផលិតផលវ៉ិចទ័រអាចត្រូវបានតំណាងថាជាកត្តាកំណត់នៃម៉ាទ្រីសការ៉េលំដាប់ទីបី ដែលជួរទីមួយមានវ៉ិចទ័រ i → , j → , k → ជួរទីពីរមានកូអរដោនេនៃវ៉ិចទ័រ a → និងជួរទីបី មាន​កូអរដោណេ​នៃ​វ៉ិចទ័រ b → ក្នុង​ប្រព័ន្ធ​កូអរដោណេ​រាង​ចតុកោណ​ដែល​បាន​ផ្តល់​ឱ្យ នេះ​ជា​កត្តា​កំណត់​នៃ​ម៉ាទ្រីស​មើល​ទៅ​ដូច​នេះ៖ c → = a → × b → = i → j → k → a x a y a z b x b y b z

ការពង្រីកកត្តាកំណត់នេះទៅក្នុងធាតុនៃជួរទីមួយ យើងទទួលបានសមភាព៖ c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j y → a x · a → × b → = (a y b z − a z b y) i → + (a z b x − a x b z) j → + (a x b y − a y b x) k →

លក្ខណៈសម្បត្តិនៃផលិតផលឆ្លងកាត់

វាត្រូវបានគេដឹងថាផលិតផលវ៉ិចទ័រនៅក្នុងកូអរដោនេត្រូវបានតំណាងថាជាកត្តាកំណត់នៃម៉ាទ្រីស c → = a → × b → = i → j → k → a x a y a z b x b y b z បន្ទាប់មកនៅលើមូលដ្ឋាន លក្ខណៈសម្បត្តិនៃកត្តាកំណត់ម៉ាទ្រីសខាងក្រោមត្រូវបានបង្ហាញ លក្ខណៈសម្បត្តិនៃផលិតផលវ៉ិចទ័រ៖

1. អង់ទីករ a → × b → = − b → × a → ;
2. ការចែកចាយ a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → ឬ a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. associativity λ a → × b → = λ a → × b → ឬ a → × (λ b →) = λ a → × b → ដែល λ ជាចំនួនពិតតាមអំពើចិត្ត។

ទ្រព្យសម្បត្តិទាំងនេះមានភស្តុតាងសាមញ្ញ។

ជាឧទាហរណ៍ យើងអាចបញ្ជាក់អំពីទ្រព្យសម្បត្តិប្រឆាំងការកុម្មុយនិស្តនៃផលិតផលវ៉ិចទ័រ។

ភស្តុតាងនៃការប្រឆាំងនឹងការផ្លាស់ប្តូរ

តាមនិយមន័យ a → × b → = i → j → k → a x a y a z b x b y b z និង b → × a → = i → j → k → b x b y b z a x a y a z ។ ហើយប្រសិនបើជួរពីរនៃម៉ាទ្រីសត្រូវបានប្តូរ នោះតម្លៃនៃកត្តាកំណត់នៃម៉ាទ្រីសគួរតែផ្លាស់ប្តូរទៅផ្ទុយគ្នា ដូច្នេះ a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a - b → × a → , ដែលនិងបង្ហាញថាផលិតផលវ៉ិចទ័រគឺប្រឆាំង។

ផលិតផលវ៉ិចទ័រ - ឧទាហរណ៍និងដំណោះស្រាយ

ក្នុងករណីភាគច្រើនមានបញ្ហាបីប្រភេទ។

នៅក្នុងបញ្ហានៃប្រភេទទីមួយ ប្រវែងនៃវ៉ិចទ័រពីរ និងមុំរវាងពួកវាជាធម្មតាត្រូវបានផ្តល់ឱ្យ ហើយអ្នកត្រូវស្វែងរកប្រវែងនៃផលិតផលវ៉ិចទ័រ។ ក្នុងករណីនេះ សូមប្រើរូបមន្តខាងក្រោម c → = a → · b → · sin ∠ a → , b → ។

ឧទាហរណ៍ ១

រកប្រវែងនៃផលគុណវ៉ិចទ័រនៃវ៉ិចទ័រ a → និង b → បើអ្នកដឹង a → = 3, b → = 5, ∠ a →, b → = π 4 ។

ដំណោះស្រាយ

ដោយកំណត់ប្រវែងនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ a → និង b → យើងដោះស្រាយបញ្ហានេះ: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 ២ ២.

ចម្លើយ៖ 15 2 2 .

បញ្ហានៃប្រភេទទីពីរមានទំនាក់ទំនងជាមួយកូអរដោណេវ៉ិចទ័រ ដែលនៅក្នុងពួកវា ផលិតផលវ៉ិចទ័រ ប្រវែងរបស់វា ។ល។ ត្រូវបានស្វែងរកតាមរយៈកូអរដោនេដែលគេស្គាល់នៃវ៉ិចទ័រដែលបានផ្តល់ឱ្យ a → = (a x; a y; a z) និង b → = (b x; b y; b z) .

ចំពោះ​បញ្ហា​ប្រភេទ​នេះ អ្នក​អាច​ដោះស្រាយ​ជម្រើស​ការងារ​បាន​ច្រើន។ ឧទាហរណ៍ មិនមែនកូអរដោនេនៃវ៉ិចទ័រ a → និង b → អាចត្រូវបានបញ្ជាក់ទេ ប៉ុន្តែការពង្រីករបស់វាទៅជាវ៉ិចទ័រសំរបសំរួលនៃទម្រង់ b → = b x · i → + b y · j → + b z · k → និង c → = a → × b → = (a y b z − a z b y) i → + (a z b x − a x b z) j → + (a x b y - a y b x) k → ឬវ៉ិចទ័រ a → និង b → អាចត្រូវបានបញ្ជាក់ដោយកូអរដោនេនៃការចាប់ផ្តើមរបស់ពួកគេ និងចំណុចបញ្ចប់។

សូមពិចារណាឧទាហរណ៍ខាងក្រោម។

ឧទាហរណ៍ ២

នៅក្នុងប្រព័ន្ធសំរបសំរួលរាងចតុកោណ វ៉ិចទ័រពីរត្រូវបានផ្តល់ឱ្យ: a → = (2; 1; - 3), b → = (0; - 1; 1) ។ ស្វែងរកផលិតផលឆ្លងកាត់របស់ពួកគេ។

ដំណោះស្រាយ

តាមនិយមន័យទីពីរ យើងរកឃើញផលគុណវ៉ិចទ័រនៃវ៉ិចទ័រពីរក្នុងកូអរដោណេដែលបានផ្តល់ឱ្យ៖ a → × b → = (a y · b z − a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y − a y · b x) · k → = = (1 · 1 - ( 3) · ( − 1)) · i → + (((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) − 1 · 0) · k → = = − 2 i → − 2 j → − 2 k → .

ប្រសិនបើយើងសរសេរផលិតផលវ៉ិចទ័រតាមរយៈកត្តាកំណត់នៃម៉ាទ្រីស នោះដំណោះស្រាយចំពោះឧទាហរណ៍នេះមើលទៅដូចនេះ៖ a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = − 2 i → − 2 j → − 2 k → .

ចម្លើយ៖ a → × b → = − 2 i → − 2 j → − 2 k → .

ឧទាហរណ៍ ៣

រកប្រវែងនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ i → - j → និង i → + j → + k → ដែល i →, j →, k → គឺជាវ៉ិចទ័រឯកតានៃប្រព័ន្ធកូអរដោណេចតុកោណ។

ដំណោះស្រាយ

ដំបូង ចូរយើងស្វែងរកកូអរដោនេនៃផលិតផលវ៉ិចទ័រដែលបានផ្តល់ឱ្យ i → - j → × i → + j → + k → នៅក្នុងប្រព័ន្ធកូអរដោនេចតុកោណដែលបានផ្តល់ឱ្យ។

គេដឹងថាវ៉ិចទ័រ i → - j → និង i → + j → + k → មានកូអរដោនេ (1; - 1; 0) និង (1; 1; 1) រៀងគ្នា។ ចូរយើងរកប្រវែងនៃផលិតផលវ៉ិចទ័រដោយប្រើកត្តាកំណត់នៃម៉ាទ្រីស បន្ទាប់មកយើងមាន i → - j → × i → + j → + k → = i → j → k → 1 − 1 0 1 1 1 = - i → - j → + 2 k → .

ដូច្នេះផលិតផលវ៉ិចទ័រ i → - j → × i → + j → + k → មានកូអរដោនេ (- 1 ; - 1 ; 2) នៅក្នុងប្រព័ន្ធកូអរដោនេដែលបានផ្តល់ឱ្យ។

យើងរកឃើញប្រវែងនៃផលិតផលវ៉ិចទ័រដោយប្រើរូបមន្ត (មើលផ្នែកលើការស្វែងរកប្រវែងវ៉ិចទ័រ)៖ i → - j → × i → + j → + k → = − 1 2 + − 1 2 + 2 2 = ៦.

ចម្លើយ៖ i → − j → × i → + j → + k → = 6 ។ .

ឧទាហរណ៍ 4

នៅក្នុងប្រព័ន្ធកូអរដោនេ Cartesian រាងចតុកោណ កូអរដោនេនៃបីពិន្ទុ A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) ត្រូវបានផ្តល់ឱ្យ។ ស្វែងរកវ៉ិចទ័រកាត់កែងទៅ A B → និង A C → នៅពេលតែមួយ។

ដំណោះស្រាយ

វ៉ិចទ័រ A B → និង A C → មានកូអរដោនេដូចខាងក្រោម (- 1 ; 2 ; 2) និង (0 ; 4 ; 1) រៀងគ្នា។ ដោយបានរកឃើញផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ A B → និង A C → វាច្បាស់ណាស់ថាវាជាវ៉ិចទ័រកាត់កែងតាមនិយមន័យទាំង A B → និង A C → នោះគឺជាដំណោះស្រាយចំពោះបញ្ហារបស់យើង។ ចូររកវា A B → × A C → = i → j → k → − 1 2 2 0 4 1 = − 6 i → + j → − 4 k → ។

ចម្លើយ៖ - 6 i → + j → − 4 k → . - មួយនៃវ៉ិចទ័រកាត់កែង។

បញ្ហានៃប្រភេទទីបីគឺផ្តោតលើការប្រើប្រាស់លក្ខណៈសម្បត្តិនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ។ បន្ទាប់​ពី​អនុវត្ត​ការ​ដែល​យើង​នឹង​ទទួល​បាន​ដំណោះ​ស្រាយ​ចំពោះ​បញ្ហា​ដែល​បាន​ផ្តល់​ឱ្យ​។

ឧទាហរណ៍ 5

វ៉ិចទ័រ a → និង b → កាត់កែង ហើយប្រវែងរបស់វាគឺ 3 និង 4 រៀងគ្នា។ រកប្រវែងនៃផលិតផលវ៉ិចទ័រ 3 a → − b → × a → − 2 b → = 3 a → × a → − 2 b → + − b → × a → − 2 b → = = 3 a → × a → + 3 · a → × − 2 · b → + − b → × a → + − b → × − 2 · ខ → .

ដំណោះស្រាយ

ដោយទ្រព្យសម្បត្តិចែកចាយនៃផលិតផលវ៉ិចទ័រ យើងអាចសរសេរ 3 a → − b → × a → − 2 b → = 3 a → × a → − 2 b → + − b → × a → − 2 b → = = 3 a → × a → + 3 a → × − 2 ខ → + − b → × a → + − b → × − 2 ខ →

ដោយទ្រព្យសម្បត្តិនៃសមាគម យើងយកមេគុណលេខចេញពីសញ្ញានៃផលិតផលវ៉ិចទ័រក្នុងកន្សោមចុងក្រោយ៖ 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + − b → × − 2 · b → = = 3 · a → × a → + 3 · (− 2) · a → × b → + (− 1) · b → × a → + (− 1) · (− 2) · b → × b → = = 3 a → × a → − 6 a → × b → − b → × a → + 2 b → × b →

ផលិតផលវ៉ិចទ័រ a → × a → និង b → × b → ស្មើនឹង 0 ដោយហេតុថា a → × a → = a → · a → · sin 0 = 0 និង b → × b → = b → · b → · sin . .

ពី anticommutativity នៃផលិតផលវ៉ិចទ័រវាដូចខាងក្រោម - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ខ → ។ .

ដោយប្រើលក្ខណសម្បត្តិរបស់ផលិតផលវ៉ិចទ័រ យើងទទួលបានសមភាព 3 · a → - b → × a → - 2 · b → = = − 5 · a → × b → ។

តាមលក្ខខណ្ឌ វ៉ិចទ័រ a → និង b → កាត់កែង ពោលគឺ មុំរវាងពួកវាស្មើនឹង π 2 ។ ឥឡូវនេះអ្វីៗដែលនៅសល់គឺត្រូវជំនួសតម្លៃដែលបានរកឃើញទៅក្នុងរូបមន្តសមស្រប៖ 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 ។

ចម្លើយ៖ 3 a → − b → × a → − 2 b → = 60 ។

ប្រវែងនៃផលិតផលវ៉ិចទ័រតាមនិយមន័យគឺស្មើនឹង a → × b → = a → · b → · sin ∠ a → , b → ។ ចាប់តាំងពីវាត្រូវបានគេស្គាល់រួចហើយ (ពីវគ្គសិក្សា) ថាតំបន់នៃត្រីកោណគឺស្មើនឹងពាក់កណ្តាលនៃផលិតផលនៃប្រវែងនៃភាគីទាំងពីររបស់វាគុណនឹងស៊ីនុសនៃមុំរវាងភាគីទាំងនេះ។ ដូច្នេះប្រវែងនៃផលិតផលវ៉ិចទ័រគឺស្មើនឹងផ្ទៃនៃប្រលេឡូក្រាម - ត្រីកោណទ្វេដែលជាផលិតផលនៃជ្រុងក្នុងទម្រង់ជាវ៉ិចទ័រ a → និង b → ដែលដាក់ចេញពីចំណុចមួយដោយស៊ីនុសនៃ មុំរវាងពួកវា sin ∠ a →, b → ។

នេះគឺជាអត្ថន័យធរណីមាត្រនៃផលិតផលវ៉ិចទ័រ។

អត្ថន័យរូបវន្តនៃផលិតផលវ៉ិចទ័រ

នៅក្នុងមេកានិច សាខាមួយនៃរូបវិទ្យា អរគុណចំពោះផលិតផលវ៉ិចទ័រ អ្នកអាចកំណត់ពេលនៃកម្លាំងដែលទាក់ទងទៅនឹងចំណុចមួយក្នុងលំហ។

និយមន័យ ៣

នៅពេលកម្លាំង F → អនុវត្តទៅចំណុច B ទាក់ទងទៅនឹងចំណុច A យើងនឹងយល់ពីផលិតផលវ៉ិចទ័រខាងក្រោម A B → × F → ។

ប្រសិនបើអ្នកសម្គាល់ឃើញកំហុសនៅក្នុងអត្ថបទ សូមរំលេចវា ហើយចុច Ctrl+Enter

មុំរវាងវ៉ិចទ័រ

ដើម្បីអោយយើងណែនាំពីគោលគំនិតនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រពីរ យើងត្រូវយល់អំពីគោលគំនិតបែបនេះជាមុនសិន ដូចជាមុំរវាងវ៉ិចទ័រទាំងនេះ។

ចូរយើងផ្តល់វ៉ិចទ័រពីរ $\overline(α)$ និង $\overline(β)$ ។ ចូរយើងយកចំនុច $O$ ក្នុងលំហ ហើយគូសវ៉ិចទ័រ $\overline(α)=\overline(OA)$ និង $\overline(β)=\overline(OB)$ ពីវា បន្ទាប់មកមុំ $AOB$ នឹងត្រូវបានគេហៅថាមុំរវាងវ៉ិចទ័រទាំងនេះ (រូបភាពទី 1) ។

កំណត់សម្គាល់៖ $∠(\overline(α),\overline(β))$

គោលគំនិតនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ និងរូបមន្តសម្រាប់ស្វែងរក

និយមន័យ ១

ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រពីរគឺជាវ៉ិចទ័រកាត់កែងទៅនឹងវ៉ិចទ័រទាំងពីរនេះ ហើយប្រវែងរបស់វានឹងស្មើនឹងផលគុណនៃប្រវែងនៃវ៉ិចទ័រទាំងនេះជាមួយនឹងស៊ីនុសនៃមុំរវាងវ៉ិចទ័រទាំងនេះ ហើយវ៉ិចទ័រនេះមានពីរដំបូងមាន ទិសដៅដូចគ្នានឹងប្រព័ន្ធកូអរដោណេ Cartesian ។

កំណត់សម្គាល់៖ $\overline(α)х\overline(β)$ ។

តាមគណិតវិទ្យាវាមើលទៅដូចនេះ៖

1. $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
3. $(\overline(α)х\overline(β),\overline(α),\overline(β))$ និង $(\overline(i),\overline(j),\overline(k))$ គឺ ទិសដៅដូចគ្នា (រូបភាពទី 2)

ជាក់ស្តែង ផលិតផលខាងក្រៅនៃវ៉ិចទ័រនឹងស្មើនឹងសូន្យវ៉ិចទ័រក្នុងករណីពីរ៖

1. ប្រសិនបើប្រវែងនៃវ៉ិចទ័រមួយ ឬទាំងពីរគឺសូន្យ។
2. ប្រសិនបើមុំរវាងវ៉ិចទ័រទាំងនេះស្មើនឹង $180^\circ$ ឬ $0^\circ$ (ចាប់តាំងពីក្នុងករណីនេះ ស៊ីនុសគឺសូន្យ)។

ដើម្បីមើលយ៉ាងច្បាស់ពីរបៀបដែលផលិតផលឆ្លងកាត់នៃវ៉ិចទ័រត្រូវបានរកឃើញ សូមពិចារណាឧទាហរណ៍ខាងក្រោមនៃដំណោះស្រាយ។

ឧទាហរណ៍ ១

ស្វែងរកប្រវែងនៃវ៉ិចទ័រ $\overline(δ)$ ដែលនឹងក្លាយជាលទ្ធផលនៃផលគុណវ៉ិចទ័រនៃវ៉ិចទ័រ ជាមួយនឹងកូអរដោនេ $\overline(α)=(0,4,0)$ និង $\overline(β) =(3,0,0)$។

ដំណោះស្រាយ.

ចូរពណ៌នាវ៉ិចទ័រទាំងនេះនៅក្នុងលំហកូអរដោនេ Cartesian (រូបភាពទី 3)៖

រូបភាពទី 3. វ៉ិចទ័រនៅក្នុងលំហសំរបសំរួល Cartesian ។ Author24 - ការផ្លាស់ប្តូរការងារសិស្សតាមអ៊ីនធឺណិត

យើងឃើញថាវ៉ិចទ័រទាំងនេះស្ថិតនៅលើអ័ក្ស $Ox$ និង $Oy$ រៀងគ្នា។ ដូច្នេះ មុំរវាងពួកវានឹងមានតម្លៃ $90^\circ$។ ចូរយើងស្វែងរកប្រវែងនៃវ៉ិចទ័រទាំងនេះ៖

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

បន្ទាប់មក តាមនិយមន័យ 1 យើងទទួលបានម៉ូឌុល $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

ចម្លើយ៖ ១២ ដុល្លារ។

ការគណនាផលិតផលឆ្លងកាត់ពីកូអរដោណេវ៉ិចទ័រ

និយមន័យ 1 បង្កប់ន័យភ្លាមៗនូវវិធីសាស្រ្តមួយសម្រាប់ការស្វែងរកផលិតផលវ៉ិចទ័រសម្រាប់វ៉ិចទ័រពីរ។ ដោយសារវ៉ិចទ័រ បន្ថែមពីលើតម្លៃរបស់វាក៏មានទិសដៅដែរ វាមិនអាចទៅរួចទេក្នុងការស្វែងរកវាដោយប្រើតែបរិមាណមាត្រដ្ឋាន។ ប៉ុន្តែក្រៅពីនេះ វាក៏មានវិធីមួយដើម្បីស្វែងរកវ៉ិចទ័រដែលផ្តល់ឱ្យយើងដោយប្រើកូអរដោនេ។

អនុញ្ញាតឱ្យយើងផ្តល់វ៉ិចទ័រ $\overline(α)$ និង $\overline(β)$ ដែលនឹងមានកូអរដោនេ $(α_1,α_2,α_3)$ និង $(β_1,β_2,β_3)$ រៀងគ្នា។ បន្ទាប់មកវ៉ិចទ័រនៃផលិតផលឈើឆ្កាង (ដូចជាកូអរដោនេរបស់វា) អាចត្រូវបានរកឃើញដោយប្រើរូបមន្តខាងក្រោម៖

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

បើមិនដូច្នោះទេ ការពង្រីកកត្តាកំណត់ យើងទទួលបានកូអរដោនេដូចខាងក្រោម

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

ឧទាហរណ៍ ២

ស្វែងរកវ៉ិចទ័រនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័ររួម $\overline(α)$ និង $\overline(β)$ ជាមួយកូអរដោនេ $(0,3,3)$ និង $(-1,2,6)$ ។

ដំណោះស្រាយ.

ចូរយើងប្រើរូបមន្តដែលបានផ្តល់ឱ្យខាងលើ។ យើងទទួលបាន

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k )=(12,-3,3)$

ចម្លើយ៖ $(12,-3,3)$។

លក្ខណសម្បត្តិនៃផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ

សម្រាប់វ៉ិចទ័រចំនួនបីដែលលាយគ្នាដោយបំពាន $\overline(α)$, $\overline(β)$ និង $\overline(γ)$ ក៏ដូចជា $r∈R$ លក្ខណៈសម្បត្តិខាងក្រោមមាន៖

ឧទាហរណ៍ ៣

ស្វែងរកតំបន់នៃប្រលេឡូក្រាមដែលចំនុចកំពូលមានកូអរដោនេ $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ និង $(3,8,0) $

ដំណោះស្រាយ.

ជាដំបូង ចូរយើងពណ៌នាប៉ារ៉ាឡែលនេះក្នុងលំហកូអរដោនេ (រូបភាពទី ៥)៖

រូបភាពទី 5. ប៉ារ៉ាឡែលក្នុងលំហកូអរដោនេ។ Author24 - ការផ្លាស់ប្តូរការងារសិស្សតាមអ៊ីនធឺណិត

យើងឃើញថាភាគីទាំងពីរនៃប្រលេឡូក្រាមនេះត្រូវបានសាងសង់ដោយប្រើវ៉ិចទ័ររួមជាមួយនឹងកូអរដោនេ $\overline(α)=(3,0,0)$ និង $\overline(β)=(0,8,0)$ ។ ដោយប្រើទ្រព្យសម្បត្តិទីបួនយើងទទួលបាន:

$S=|\overline(α)х\overline(β)|$

ចូរយើងស្វែងរកវ៉ិចទ័រ $\overline(α)х\overline(β)$:

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

ដូច្នេះ

$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$

ជាក់ស្តែងនៅក្នុងករណីនៃផលិតផលវ៉ិចទ័រ លំដាប់ដែលវ៉ិចទ័រត្រូវបានគេយកជាបញ្ហា លើសពីនេះទៅទៀត

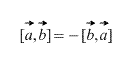
ដូចគ្នានេះផងដែរដោយផ្ទាល់ពីនិយមន័យវាដូចខាងក្រោមថាសម្រាប់កត្តាមាត្រដ្ឋាន k (លេខ) ខាងក្រោមគឺពិត:

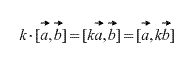
ផលិតផលឆ្លងកាត់នៃវ៉ិចទ័រ collinear គឺស្មើនឹងវ៉ិចទ័រសូន្យ។ ជាងនេះទៅទៀត ផលិតផលឆ្លងកាត់នៃវ៉ិចទ័រពីរគឺសូន្យប្រសិនបើ និងលុះត្រាតែពួកវាជាប់គ្នា។ (ក្នុងករណីមួយក្នុងចំណោមពួកវាជាវ៉ិចទ័រសូន្យ វាចាំបាច់ត្រូវចាំថាវ៉ិចទ័រសូន្យគឺស្របទៅនឹងវ៉ិចទ័រណាមួយតាមនិយមន័យ)។

ផលិតផលវ៉ិចទ័រមាន ទ្រព្យសម្បត្តិចែកចាយនោះគឺ

បង្ហាញផលិតផលវ៉ិចទ័រតាមរយៈកូអរដោនេនៃវ៉ិចទ័រ។

សូមឱ្យវ៉ិចទ័រពីរត្រូវបានផ្តល់ឱ្យ

(របៀបស្វែងរកកូអរដោនេនៃវ៉ិចទ័រពីកូអរដោនេនៃចំណុចចាប់ផ្តើមនិងចុងបញ្ចប់របស់វា - សូមមើលអត្ថបទចំនុចផលិតផលនៃវ៉ិចទ័រ ធាតុ និយមន័យជំនួសនៃផលិតផលចំនុច ឬការគណនាផលិតផលចំនុចនៃវ៉ិចទ័រពីរដែលបញ្ជាក់ដោយកូអរដោនេរបស់វា។)

ហេតុអ្វីបានជាអ្នកត្រូវការផលិតផលវ៉ិចទ័រ?

មានវិធីជាច្រើនដើម្បីប្រើផលិតផលឈើឆ្កាង ឧទាហរណ៍ដូចដែលបានសរសេរខាងលើ ដោយការគណនាផលិតផលឈើឆ្កាងនៃវ៉ិចទ័រពីរ អ្នកអាចដឹងថាតើពួកវាជាគូលីនេអ៊ែរ។

ឬ​វា​អាច​ត្រូវ​បាន​ប្រើ​ជា​វិធី​មួយ​ដើម្បី​គណនា​ផ្ទៃ​នៃ​ប្រលេឡូក្រាម​ដែល​បាន​សាងសង់​ពី​វ៉ិចទ័រ​ទាំងនេះ។ ដោយផ្អែកលើនិយមន័យប្រវែងនៃវ៉ិចទ័រលទ្ធផលគឺជាផ្ទៃនៃប្រលេឡូក្រាមដែលបានផ្តល់ឱ្យ។

វាក៏មានកម្មវិធីមួយចំនួនធំនៅក្នុងអគ្គិសនី និងម៉ាញេទិចផងដែរ។

ការគណនាផលិតផលវ៉ិចទ័រតាមអ៊ីនធឺណិត។

ដើម្បីស្វែងរកផលិតផលមាត្រដ្ឋាននៃវ៉ិចទ័រពីរដោយប្រើម៉ាស៊ីនគិតលេខនេះ អ្នកត្រូវបញ្ចូលកូអរដោនេនៃវ៉ិចទ័រទីមួយក្នុងជួរទីមួយតាមលំដាប់លំដោយ និងទីពីរក្នុងជួរទីពីរ។ កូអរដោនេនៃវ៉ិចទ័រអាចត្រូវបានគណនាពីកូអរដោនេនៃការចាប់ផ្តើមនិងចុងបញ្ចប់របស់វា (សូមមើលអត្ថបទ ផលិតផលចំនុចនៃវ៉ិចទ័រ ធាតុ និយមន័យជំនួសនៃផលិតផលចំនុច ឬការគណនាផលិតផលចំនុចនៃវ៉ិចទ័រពីរដែលផ្តល់ដោយកូអរដោនេរបស់វា។)

សិល្បៈវ៉ិចទ័រគឺជា pseudovector កាត់កែងទៅនឹងយន្តហោះដែលបង្កើតឡើងដោយកត្តាពីរ ដែលជាលទ្ធផលនៃប្រតិបត្តិការគោលពីរ "ការគុណវ៉ិចទ័រ" លើវ៉ិចទ័រនៅក្នុងលំហអឺគ្លីឌាបីវិមាត្រ។ ផលិតផលវ៉ិចទ័រមិនមានលក្ខណៈសម្បត្តិនៃការផ្លាស់ប្តូរ និងការផ្សារភ្ជាប់គ្នាទេ (វាគឺជាការប្រឆាំងគ្នា) ហើយមិនដូចផលិតផលមាត្រដ្ឋាននៃវ៉ិចទ័រទេ គឺជាវ៉ិចទ័រ។ ប្រើយ៉ាងទូលំទូលាយនៅក្នុងកម្មវិធីវិស្វកម្ម និងរូបវិទ្យាជាច្រើន។ ឧទាហរណ៍ សន្ទុះមុំ និងកម្លាំង Lorentz ត្រូវបានសរសេរតាមគណិតវិទ្យាជាផលិតផលវ៉ិចទ័រ។ ផលិតផលឈើឆ្កាងមានប្រយោជន៍សម្រាប់ "វាស់" កាត់កែងនៃវ៉ិចទ័រ - ម៉ូឌុលនៃផលិតផលឈើឆ្កាងនៃវ៉ិចទ័រពីរគឺស្មើនឹងផលិតផលនៃម៉ូឌូលីរបស់ពួកគេ ប្រសិនបើពួកវាកាត់កែង ហើយថយចុះដល់សូន្យ ប្រសិនបើវ៉ិចទ័រស្រប ឬប្រឆាំងប៉ារ៉ាឡែល។

ផលិតផលវ៉ិចទ័រអាចត្រូវបានកំណត់តាមវិធីផ្សេងៗគ្នា ហើយតាមទ្រឹស្តី ក្នុងចន្លោះនៃវិមាត្រណាមួយ n មួយអាចគណនាផលិតផលនៃវ៉ិចទ័រ n-1 ដោយហេតុនេះទទួលបានវ៉ិចទ័រតែមួយកាត់កែងទៅនឹងពួកវាទាំងអស់។ ប៉ុន្តែប្រសិនបើផលិតផលត្រូវបានកំណត់ចំពោះផលិតផលគោលពីរដែលមិនសំខាន់ជាមួយនឹងលទ្ធផលវ៉ិចទ័រ នោះផលិតផលវ៉ិចទ័រប្រពៃណីត្រូវបានកំណត់តែក្នុងចន្លោះបីវិមាត្រ និងប្រាំពីរវិមាត្រប៉ុណ្ណោះ។ លទ្ធផល​នៃ​ផលិតផល​វ៉ិចទ័រ ដូចជា​ផលិតផល​មាត្រដ្ឋាន អាស្រ័យ​លើ​ម៉ែត្រ​នៃ​លំហ Euclidean។

មិនដូចរូបមន្តសម្រាប់គណនាវ៉ិចទ័រផលិតផលមាត្រដ្ឋានពីកូអរដោណេក្នុងប្រព័ន្ធកូអរដោណេចតុកោណកែងទេ រូបមន្តសម្រាប់ផលិតផលឈើឆ្កាងអាស្រ័យលើការតំរង់ទិសនៃប្រព័ន្ធកូអរដោណេចតុកោណ ឬនិយាយម្យ៉ាងទៀត "ភាពរីករាយ" របស់វា។

និយមន័យ៖
ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រ a និងវ៉ិចទ័រ b ក្នុងលំហ R3 គឺជាវ៉ិចទ័រ c ដែលបំពេញតម្រូវការដូចខាងក្រោមៈ
ប្រវែងវ៉ិចទ័រ c គឺស្មើនឹងផលគុណនៃប្រវែងវ៉ិចទ័រ a និង b និងស៊ីនុសនៃមុំφរវាងពួកវា៖
|c|=|a||b|sin φ;
វ៉ិចទ័រ c គឺជាអ័រតូហ្គោនទៅនឹងវ៉ិចទ័រនីមួយៗ a និង b;
វ៉ិចទ័រ c ត្រូវបានដឹកនាំដូច្នេះបីដងនៃវ៉ិចទ័រ abc គឺស្តាំដៃ;
ក្នុងករណីលំហ R7 ការផ្សារភ្ជាប់នៃវ៉ិចទ័របីដង a, b, c ត្រូវបានទាមទារ។
ការកំណត់៖
c===a × ខ

អង្ករ។ 1. ផ្ទៃនៃប្រលេឡូក្រាមស្មើនឹងម៉ូឌុលនៃផលិតផលវ៉ិចទ័រ

លក្ខណៈសម្បត្តិធរណីមាត្រនៃផលិតផលឈើឆ្កាង:
លក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់សម្រាប់ភាពជាប់គ្នានៃវ៉ិចទ័រមិនសូន្យពីរ គឺផលិតផលវ៉ិចទ័ររបស់ពួកគេស្មើនឹងសូន្យ។

ម៉ូឌុលផលិតផលឆ្លងកាត់ ស្មើតំបន់ សប្រលេឡូក្រាមសាងសង់លើវ៉ិចទ័រកាត់បន្ថយទៅជាប្រភពដើមទូទៅ កនិង ខ(សូមមើលរូបទី 1) ។

ប្រសិនបើ អ៊ី- ឯកតាវ៉ិចទ័រ orthogonal ទៅវ៉ិចទ័រ កនិង ខហើយបានជ្រើសរើសបី a,b,e- ត្រូវហើយ សគឺជាតំបន់នៃប្រលេឡូក្រាមដែលបានសាងសង់នៅលើពួកវា (កាត់បន្ថយទៅជាប្រភពដើមទូទៅ) បន្ទាប់មករូបមន្តសម្រាប់ផលិតផលវ៉ិចទ័រមានសុពលភាព៖
=S អ៊ី

រូប ២. បរិមាណនៃ parallelepiped ដោយប្រើវ៉ិចទ័រនិងផលិតផលមាត្រដ្ឋាននៃវ៉ិចទ័រ; បន្ទាត់ចំនុចបង្ហាញការព្យាករនៃវ៉ិចទ័រ c លើ a × b និងវ៉ិចទ័រ a ទៅ b × c ជំហានដំបូងគឺស្វែងរកផលិតផលមាត្រដ្ឋាន

ប្រសិនបើ គ- វ៉ិចទ័រមួយចំនួន π - យន្តហោះណាមួយដែលមានវ៉ិចទ័រនេះ អ៊ី- វ៉ិចទ័រឯកតាដេកនៅក្នុងយន្តហោះ π និង orthogonal ទៅ c,g- ឯកតាវ៉ិចទ័រ orthogonal ទៅយន្តហោះ π និងដឹកនាំដូច្នេះបីដងនៃវ៉ិចទ័រ ឧជាការត្រឹមត្រូវ បន្ទាប់មកសម្រាប់ការកុហកណាមួយនៅក្នុងយន្តហោះ π វ៉ិចទ័រ ករូបមន្តគឺត្រឹមត្រូវ៖
=Pr e a |c|g
ដែល Pr e a គឺជាការព្យាករនៃវ៉ិចទ័រ e ទៅលើ a
|c|- ម៉ូឌុលនៃវ៉ិចទ័រ គ

នៅពេលប្រើផលិតផលវ៉ិចទ័រ និងមាត្រដ្ឋាន អ្នកអាចគណនាបរិមាណនៃប៉ារ៉ាឡែលភីបដែលបង្កើតនៅលើវ៉ិចទ័រដែលកាត់បន្ថយទៅជាប្រភពដើមទូទៅ ក, ខនិង គ. ផលិតផលបែបនេះនៃវ៉ិចទ័របីត្រូវបានគេហៅថាចម្រុះ។
V=|a(b×c)|
តួលេខនេះបង្ហាញថាបរិមាណនេះអាចត្រូវបានរកឃើញតាមពីរវិធី៖ លទ្ធផលធរណីមាត្រត្រូវបានរក្សាទុកសូម្បីតែនៅពេលដែលផលិតផល "មាត្រដ្ឋាន" និង "វ៉ិចទ័រ" ត្រូវបានផ្លាស់ប្តូរ៖
V=a×b c=a b×c

ទំហំនៃផលិតផលឈើឆ្កាងអាស្រ័យទៅលើស៊ីនុសនៃមុំរវាងវ៉ិចទ័រដើម ដូច្នេះផលិតផលឈើឆ្កាងអាចត្រូវបានគេដឹងថាជាកម្រិតនៃ "ការកាត់កែង" នៃវ៉ិចទ័រ ដូចជាផលិតផលមាត្រដ្ឋានអាចត្រូវបានគេមើលឃើញថាជាកម្រិតនៃ "ភាពស្របគ្នា ”។ ផលិតផលវ៉ិចទ័រនៃវ៉ិចទ័រឯកតាពីរគឺស្មើនឹង 1 (វ៉ិចទ័រឯកតា) ប្រសិនបើវ៉ិចទ័រដើមកាត់កែង ហើយស្មើនឹង 0 (វ៉ិចទ័រសូន្យ) ប្រសិនបើវ៉ិចទ័រស្របគ្នា ឬប្រឆាំងប៉ារ៉ាឡែល។

កន្សោមសម្រាប់ផលិតផលឈើឆ្កាងនៅក្នុងកូអរដោនេ Cartesian
ប្រសិនបើវ៉ិចទ័រពីរ កនិង ខកំណត់ដោយសំរបសំរួល Cartesian រាងចតុកោណរបស់ពួកគេ ឬច្បាស់ជាងនេះ តំណាងនៅក្នុងមូលដ្ឋាន orthonormal
a=(a x,a y,a z)
b=(b x,b y,b z)
ហើយ​ប្រព័ន្ធ​កូអរដោណេ​គឺ​ជា​ដៃស្តាំ បន្ទាប់មក​ផលិតផល​វ៉ិចទ័រ​របស់​ពួកគេ​មាន​ទម្រង់
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
ដើម្បីចងចាំរូបមន្តនេះ៖
i =∑ε ijk a j b k
កន្លែងណា ε ijk- និមិត្តសញ្ញា Levi-Civita ។