Systems of equations are widely used in the economic sector for mathematical modeling of various processes. For example, when solving problems of production management and planning, logistics routes (transport problem) or equipment placement.
Systems of equations are used not only in mathematics, but also in physics, chemistry and biology, when solving problems of finding population size.
A system of linear equations is two or more equations with several variables for which it is necessary to find a common solution. Such a sequence of numbers for which all equations become true equalities or prove that the sequence does not exist.
Linear equation
Equations of the form ax+by=c are called linear. The designations x, y are the unknowns whose value must be found, b, a are the coefficients of the variables, c is the free term of the equation.
Solving an equation by plotting it will look like a straight line, all points of which are solutions to the polynomial.
Types of systems of linear equations
The simplest examples are considered to be systems of linear equations with two variables X and Y.
F1(x, y) = 0 and F2(x, y) = 0, where F1,2 are functions and (x, y) are function variables.
Solve system of equations - this means finding values (x, y) at which the system turns into a true equality or establishing that suitable values of x and y do not exist.
A pair of values (x, y), written as the coordinates of a point, is called a solution to a system of linear equations.
If systems have one common solution or no solution exists, they are called equivalent.
Homogeneous systems of linear equations are systems whose right-hand side is equal to zero. If the right part after the equal sign has a value or is expressed by a function, such a system is heterogeneous.
The number of variables can be much more than two, then we should talk about an example of a system of linear equations with three or more variables.
When faced with systems, schoolchildren assume that the number of equations must necessarily coincide with the number of unknowns, but this is not the case. The number of equations in the system does not depend on the variables; there can be as many of them as desired.
Simple and complex methods for solving systems of equations
There is no general analytical method for solving such systems; all methods are based on numerical solutions. The school mathematics course describes in detail such methods as permutation, algebraic addition, substitution, as well as graphical and matrix methods, solution by the Gaussian method.
The main task when teaching solution methods is to teach how to correctly analyze the system and find the optimal solution algorithm for each example. The main thing is not to memorize a system of rules and actions for each method, but to understand the principles of using a particular method
Solving examples of systems of linear equations in the 7th grade general education curriculum is quite simple and explained in great detail. In any mathematics textbook, this section is given enough attention. Solving examples of systems of linear equations using the Gauss and Cramer method is studied in more detail in the first years of higher education.
Solving systems using the substitution method
The actions of the substitution method are aimed at expressing the value of one variable in terms of the second. The expression is substituted into the remaining equation, then it is reduced to a form with one variable. The action is repeated depending on the number of unknowns in the system
Let us give a solution to an example of a system of linear equations of class 7 using the substitution method:
As can be seen from the example, the variable x was expressed through F(X) = 7 + Y. The resulting expression, substituted into the 2nd equation of the system in place of X, helped to obtain one variable Y in the 2nd equation. Solving this example is easy and allows you to get the Y value. The last step is to check the obtained values.
It is not always possible to solve an example of a system of linear equations by substitution. The equations can be complex and expressing the variable in terms of the second unknown will be too cumbersome for further calculations. When there are more than 3 unknowns in the system, solving by substitution is also inappropriate.
Solution of an example of a system of linear inhomogeneous equations:
Solution using algebraic addition
When searching for solutions to systems using the addition method, equations are added term by term and multiplied by various numbers. The ultimate goal of mathematical operations is an equation in one variable.
Application of this method requires practice and observation. Solving a system of linear equations using the addition method when there are 3 or more variables is not easy. Algebraic addition is convenient to use when equations contain fractions and decimals.
Solution algorithm:
- Multiply both sides of the equation by a certain number. As a result of the arithmetic operation, one of the coefficients of the variable should become equal to 1.
- Add the resulting expression term by term and find one of the unknowns.
- Substitute the resulting value into the 2nd equation of the system to find the remaining variable.
Method of solution by introducing a new variable
A new variable can be introduced if the system requires finding a solution for no more than two equations; the number of unknowns should also be no more than two.
The method is used to simplify one of the equations by introducing a new variable. The new equation is solved for the introduced unknown, and the resulting value is used to determine the original variable.
The example shows that by introducing a new variable t, it was possible to reduce the 1st equation of the system to a standard quadratic trinomial. You can solve a polynomial by finding the discriminant.
It is necessary to find the value of the discriminant using the well-known formula: D = b2 - 4*a*c, where D is the desired discriminant, b, a, c are the factors of the polynomial. In the given example, a=1, b=16, c=39, therefore D=100. If the discriminant is greater than zero, then there are two solutions: t = -b±√D / 2*a, if the discriminant is less than zero, then there is one solution: x = -b / 2*a.
The solution for the resulting systems is found by the addition method.
Visual method for solving systems
Suitable for 3 equation systems. The method consists in constructing graphs of each equation included in the system on the coordinate axis. The coordinates of the intersection points of the curves will be the general solution of the system.
The graphical method has a number of nuances. Let's look at several examples of solving systems of linear equations in a visual way.
As can be seen from the example, for each line two points were constructed, the values of the variable x were chosen arbitrarily: 0 and 3. Based on the values of x, the values for y were found: 3 and 0. Points with coordinates (0, 3) and (3, 0) were marked on the graph and connected by a line.
The steps must be repeated for the second equation. The point of intersection of the lines is the solution of the system.
The following example requires finding a graphical solution to a system of linear equations: 0.5x-y+2=0 and 0.5x-y-1=0.
As can be seen from the example, the system has no solution, because the graphs are parallel and do not intersect along their entire length.
The systems from examples 2 and 3 are similar, but when constructed it becomes obvious that their solutions are different. It should be remembered that it is not always possible to say whether a system has a solution or not; it is always necessary to construct a graph.
The matrix and its varieties
Matrices are used to concisely write a system of linear equations. A matrix is a special type of table filled with numbers. n*m has n - rows and m - columns.
A matrix is square when the number of columns and rows are equal. A matrix-vector is a matrix of one column with an infinitely possible number of rows. A matrix with ones along one of the diagonals and other zero elements is called identity.
An inverse matrix is a matrix when multiplied by which the original one turns into a unit matrix; such a matrix exists only for the original square one.
Rules for converting a system of equations into a matrix
In relation to systems of equations, the coefficients and free terms of the equations are written as matrix numbers; one equation is one row of the matrix.
A matrix row is said to be nonzero if at least one element of the row is not zero. Therefore, if in any of the equations the number of variables differs, then it is necessary to enter zero in place of the missing unknown.
The matrix columns must strictly correspond to the variables. This means that the coefficients of the variable x can be written only in one column, for example the first, the coefficient of the unknown y - only in the second.
When multiplying a matrix, all elements of the matrix are sequentially multiplied by a number.
Options for finding the inverse matrix
The formula for finding the inverse matrix is quite simple: K -1 = 1 / |K|, where K -1 is the inverse matrix, and |K| is the determinant of the matrix. |K| must not be equal to zero, then the system has a solution.
The determinant is easily calculated for a two-by-two matrix; you just need to multiply the diagonal elements by each other. For the “three by three” option, there is a formula |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . You can use the formula, or you can remember that you need to take one element from each row and each column so that the numbers of columns and rows of elements are not repeated in the work.
Solving examples of systems of linear equations using the matrix method
The matrix method of finding a solution allows you to reduce cumbersome entries when solving systems with a large number of variables and equations.
In the example, a nm are the coefficients of the equations, the matrix is a vector x n are variables, and b n are free terms.
Solving systems using the Gaussian method
In higher mathematics, the Gaussian method is studied together with the Cramer method, and the process of finding solutions to systems is called the Gauss-Cramer solution method. These methods are used to find variables of systems with a large number of linear equations.
The Gauss method is very similar to solutions by substitution and algebraic addition, but is more systematic. In the school course, the solution by the Gaussian method is used for systems of 3 and 4 equations. The purpose of the method is to reduce the system to the form of an inverted trapezoid. By means of algebraic transformations and substitutions, the value of one variable is found in one of the equations of the system. The second equation is an expression with 2 unknowns, while 3 and 4 are, respectively, with 3 and 4 variables.
After bringing the system to the described form, the further solution is reduced to the sequential substitution of known variables into the equations of the system.
In school textbooks for grade 7, an example of a solution by the Gauss method is described as follows:
As can be seen from the example, at step (3) two equations were obtained: 3x 3 -2x 4 =11 and 3x 3 +2x 4 =7. Solving any of the equations will allow you to find out one of the variables x n.
Theorem 5, which is mentioned in the text, states that if one of the equations of the system is replaced by an equivalent one, then the resulting system will also be equivalent to the original one.
The Gaussian method is difficult for middle school students to understand, but it is one of the most interesting ways to develop the ingenuity of children enrolled in advanced learning programs in math and physics classes.
For ease of recording, calculations are usually done as follows:
The coefficients of the equations and free terms are written in the form of a matrix, where each row of the matrix corresponds to one of the equations of the system. separates the left side of the equation from the right. Roman numerals indicate the numbers of equations in the system.
First, write down the matrix to be worked with, then all the actions carried out with one of the rows. The resulting matrix is written after the "arrow" sign and the necessary algebraic operations are continued until the result is achieved.
The result should be a matrix in which one of the diagonals is equal to 1, and all other coefficients are equal to zero, that is, the matrix is reduced to a unit form. We must not forget to perform calculations with numbers on both sides of the equation.
This recording method is less cumbersome and allows you not to be distracted by listing numerous unknowns.
The free use of any solution method will require care and some experience. Not all methods are of an applied nature. Some methods of finding solutions are more preferable in a particular area of human activity, while others exist for educational purposes.
The Gaussian method for solving systems of linear algebraic equations consists of sequentially eliminating unknowns using elementary transformations and reducing them to an upper triangular equation (step or trapezoidal). Then they solve the system from end to beginning by substituting the solutions found.
Let's consider examples of solving systems of linear equations using the Gauss method, using as a reference the collection of problems by V.P. Dubovik, I.I. Yurik. "Higher Mathematics".
-------------
Solve a system of linear algebraic equations.
1) Let's transform the original system to a stepwise form. To do this, from the second equation we subtract the first, multiplied by 3, and from the fourth, subtract the first, multiplied by 4.
As a result, from the third equation we have. We substitute the resulting value into the original equation to find
We substitute the obtained values into the first equation
The solution to the system of three linear equations will be the following values of the variables
2) We have a system of three equations with four unknowns. In such cases, one variable can be free, and the rest will be expressed through it. Let us reduce the system to a stepwise form. To do this, subtract the first from the second and third equations
From the last two equations we obtain identical solutions
After substitution into the first equation we get
This equation relates three variables. Thus, any of the variables can be expressed in terms of the other two
So we get the following solution
3) We have a sparse system of fifth-order linear equations with five unknowns. Let's reduce it to a step form. From the second equation we subtract the first and write it in a form convenient for analysis
From the second equation we find that . We substitute the values into all the lower equations and transfer them beyond the equal sign. Let’s also swap the second and third equations
The fourth and fifth equations are equivalent. Let's express one of the variables through another
We substitute the resulting value into the second equation and find
From the first equation we determine
The solution to the system of equations is as follows
When calculating systems of linear algebraic equations using the Gauss method, it is necessary to reduce the system of linear equations to a stepwise form. To do this, it is convenient to write variables under variables, as in the last example, this will speed up the solution. The rest all depends on the matrix that needs to be solved and your skills.
A system of m linear equations with n unknowns called a system of the form
Where a ij And b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n– unknown. In the designation of coefficients a ij first index i denotes the equation number, and the second j– the number of the unknown at which this coefficient stands.
We will write the coefficients for the unknowns in the form of a matrix 
, which we'll call matrix of the system.
The numbers on the right side of the equations are b 1 ,…,b m are called free members.
Totality n numbers c 1 ,…,c n called decision of a given system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.
Our task will be to find solutions to the system. In this case, three situations may arise:
A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called non-joint.
Let's consider ways to find solutions to the system.
MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS
Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:
Consider the system matrix 
and matrices columns of unknown and free terms 
Let's find the work
those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then, using the definition of matrix equality, this system can be written in the form
or shorter A∙X=B.
Here are the matrices A And B are known, and the matrix X unknown. It is necessary to find it, because... its elements are the solution to this system. This equation is called matrix equation.
Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, inverse of the matrix A: . Because the A -1 A = E And E∙X = X, then we obtain a solution to the matrix equation in the form X = A -1 B .
Note that since the inverse matrix can only be found for square matrices, the matrix method can only solve those systems in which the number of equations coincides with the number of unknowns. However, matrix recording of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A will not be square and therefore it is impossible to find a solution to the system in the form X = A -1 B.
Examples. Solve systems of equations.
CRAMER'S RULE
Consider a system of 3 linear equations with three unknowns:
Third-order determinant corresponding to the system matrix, i.e. composed of coefficients for unknowns,
called determinant of the system.
Let's compose three more determinants as follows: replace sequentially 1, 2 and 3 columns in the determinant D with a column of free terms
Then we can prove the following result.
Theorem (Cramer's rule). If the determinant of the system Δ ≠ 0, then the system under consideration has one and only one solution, and
Proof. So, let's consider a system of 3 equations with three unknowns. Let's multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation – on A 21 and 3rd – on A 31:
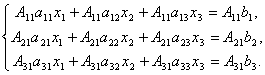
Let's add these equations:
Let's look at each of the brackets and the right side of this equation. By the theorem on the expansion of the determinant in elements of the 1st column
Similarly, it can be shown that and .
Finally, it is easy to notice that 
Thus, we obtain the equality: .
Hence, .
The equalities and are derived similarly, from which the statement of the theorem follows.
Thus, we note that if the determinant of the system Δ ≠ 0, then the system has a unique solution and vice versa. If the determinant of the system is equal to zero, then the system either has an infinite number of solutions or has no solutions, i.e. incompatible.
Examples. Solve system of equations
GAUSS METHOD
The previously discussed methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gauss method is more universal and suitable for systems with any number of equations. It consists in the consistent elimination of unknowns from the equations of the system.
Consider again a system of three equations with three unknowns:
.
We will leave the first equation unchanged, and from the 2nd and 3rd we will exclude the terms containing x 1. To do this, divide the second equation by A 21 and multiply by – A 11, and then add it to the 1st equation. Similarly, we divide the third equation by A 31 and multiply by – A 11, and then add it with the first one. As a result, the original system will take the form:
Now from the last equation we eliminate the term containing x 2. To do this, divide the third equation by, multiply by and add with the second. Then we will have a system of equations:
From here, from the last equation it is easy to find x 3, then from the 2nd equation x 2 and finally, from 1st - x 1.
When using the Gaussian method, the equations can be swapped if necessary.
Often, instead of writing a new system of equations, they limit themselves to writing out the extended matrix of the system:
and then bring it to a triangular or diagonal form using elementary transformations.
TO elementary transformations matrices include the following transformations:
- rearranging rows or columns;
- multiplying a string by a number other than zero;
- adding other lines to one line.
Examples: Solve systems of equations using the Gauss method.
Thus, the system has an infinite number of solutions.
5.1. Cramer's RuleHaving established the basic properties and methods of calculating the determinants of matrices of any order, let us return to the main task - solving and studying systems of 1st order equations. Let's begin our study of this issue by analyzing the main case when the number of equations coincides with the number of unknowns.
Let us multiply all terms of the 1st equation of system (1) by A 11 - the algebraic complement of the element A 11 of matrix A, all terms of the 2nd equation of system (1) on A 21 - algebraic complement of the element A 21 matrices A, finally, all terms of the nth equation of system (1) on A n1 - algebraic complement of the element A n1 of matrix A. Then we obtain the system
(1")
Let's add all the equations of the system term by term, we get
(
a i1 A i1)x 1 +( a i2 A i1)x 2 +...+( a in A i1)x n =b i A i1
According to the theorem about algebraic complements, we have
a i1 A i1 =det A a i2 A i1 =0, ........., a in A i1 =0
Therefore, the resulting equation can be rewritten in the form 
Consider the matrix
,
Obtained from matrix A by replacing the elements of the 1st column with a column of free terms of the system equations. Expanding det B1 over the elements of the 1st column, we obtain det B 1 =b i A i1 , and therefore 
Similarly, multiplying the equations of system (1) by Аі2 (u=1, 2, ... n) and adding them, we obtain 
,
By doing this in the future, we obtain a system of equations
(2),
Where matrix Bk is obtained from A by replacing the kth column with a column of free terms. Obviously, any solution to system (1) is also a solution to system (2).
(3)
Recall that formulas (3) were obtained with the assumption that system (1) has a solution. By directly substituting the found values of X i into system (1), one can verify that they are a solution to system (1) and, therefore, under the assumption that 
, system (1) has a solution and, moreover, a unique one.
^ Theorem (Cramer's theorem): if the determinant of the main matrix of a system of n first-order equations with n unknowns is nonzero, then the system has a unique solution. In this case, the value of each of the unknowns is equal to the part of the division of the determinants of the two matrices: the denominator contains the determinant of the main matrix of the system, and the numerator contains the determinant of the matrix obtained from the main matrix of the system by replacing the column that corresponds to the selected unknown with a column of free terms.
From this theorem it follows that if the system of equations is homogeneous, that is, the free terms in all equations of the system are equal to zero, and if the determinant of the main matrix of the system is different from zero, then the system has only a zero solution. Indeed, in this case, the matrices whose determinants are in the numerator of formulas (3) contain a column that includes only zeros, and, therefore, all numbers X i are equal to zero. The following theorem follows from what has been proved:
^ If a system of n homogeneous equations of the 1st order with n unknowns has at least one non-zero solution, then the determinant of the main matrix of the system is equal to zero. Indeed, if this determinant were not equal to zero, then the system would have only a zero solution, which contradicts the condition.
In the future, we will prove that the equality of the determinant of the system to zero is not only a mandatory, necessary condition for the existence of a non-zero solution, but also a sufficient condition for the existence of such a solution. In other words, if the determinant of a system of homogeneous equations is equal to zero, then the system has a nonzero solution (and an infinite number of such solutions).
^ 5.2. Solving and studying systems of first-order equations by the method of complete elimination (Gauss Method).
Cramer's formulas make it possible, using the method of calculating determinants, to find the numerical values of the solution to a system of equations in the case when the determinant of the main matrix of the system is different from zero. But the practical application of these formulas is complicated in many cases. First of all, it should be noted that to find solutions using formulas (3), it is necessary to calculate n+1 determinants of the nth order, which is quite labor-intensive work, even when using the techniques that were indicated in §4. But the most important thing is that in the case when the coefficients of the equation are given approximately (in real problems this almost always happens), the error in the solution can be quite large. This is explained by the fact that the terms that are included in each of the determinants through which the solution of the system is determined can be quite large (remember, they are the product of n factors - various coefficients of the extended matrix of the system), and the determinant itself, which is an algebraic sum such terms may be small. Even in the case when the coefficients in the system of initial equations are known exactly, but the calculations themselves are carried out taking into account only a given number of significant figures, for the same reasons we can get quite large errors in the result. Therefore, in the practical solution of systems of equations, in most cases they use not Cramer’s formulas, but other calculation methods.
In this course we will consider the method of complete elimination regarding the solution of systems of 1st order equations also in the case when the number of equations does not coincide with the number of unknowns. But we will begin the presentation of this method with the main case: when the number of equations coincides with the number of unknowns.
Thus, let again be given a system of n equations with n unknowns:
(1)
Since at least one of the coefficients a i1 is different from zero (otherwise x1 would not be included in the system at all), and the equations in the system can be swapped, then without any restriction of generality we can assume that 
Let's divide the 1st equation of the system by a11 and bring it to the form,
Multiplying all terms of the resulting equation by ai1 and subtracting from і th equation of system (1), we obtain a new system
(2),
i=1, 2, ..., n; k=1, 2, ... , n
Since the equations of system (2) are obtained as linear combinations of the equations of system (1), then any solution to system (1) is also a solution to system (2). At the same time, since
Then the equations of system (1) can be obtained as a linear combination of the equations of system (2). Consequently, any solution to system (2) is also a solution to system (1). Thus, systems (1) and (2) are equivalent. (The linear combination of two equations with 11 x 1 +c 12 x 2 +...+c 1n x n =d 1 i, with 21 x 1 +c 22 x 2 +...+c 2n x n =d 2 will be call the equation 1 (c 11 x 1 +c 12 x 2 +...+c 1n x n) + 2 (c 21 x 1 +c 22 x 2 +...+c 2n x n)= 1 d 1 + 2 d 2, where 1 and 2 are numbers)
Let us now compare the determinants D1 and D2 of the main matrices of systems (1) and (2). The first row of the main matrix of the system (2) is obtained from the first row of the main matrix of the system (1) by dividing by A eleven . This operation corresponds to dividing D1 by a11. Other rows are obtained by subtracting from the corresponding rows of the main matrix of system (1) values proportional to the first row. This operation does not change the value of the determinant. It follows that the determinant D2 of the main matrix of system (2) is equal to 
. And therefore 
, If 
and D2=0 if D1=0. Finally, we note that we carried out calculations only with the coefficients of the equations of system (1), so there is no need to write the equations themselves. It is enough to write only the extended matrix of the system and transform only the elements of this matrix.
We will denote the transition from one extended matrix to another, that is, in fact, the transition from one system of equations to a system equivalent to it, by the symbol 
or 
.
Then the operations performed can be written as follows:
We will first assume that the determinant D1 of the main matrix of system (1) is nonzero. Then, as stated above, 
, and therefore, in extreme cases, one of the numbers 
(u=1, 2, ... , n) is different from zero, since if all were equal to zero, the determinant D2 of the main matrix of system (2) would also be equal to zero.
Since the equations in system (2) can be swapped, therefore, without limitation, we can assume that 
. Let us divide the 2nd equation of system (2) by 
,
multiply the resulting line by (i=1, 3, 4, ... , n) and subtract it from the i-th line.
Then we will have
The system of equations that corresponds to the matrix B 3 is equivalent to system (2), and therefore to the original system (1). The determinant D3 of the main matrix of this system is non-zero, since the determinant D2 is non-zero. Hence, in extreme cases, one of the numbers 
(u=3, ... , n) is different from zero and you can again carry out the same operations as before. Continuing similar thoughts, after n operations we obtain the matrix
The corresponding system of equations has the form
(3),
Its only solution is (4)
Since system (3) is equivalent to system (1) and has a unique solution, then the original system (1) also has a unique solution, which is determined by formulas (4).
Example 1 . Solve the system
Solution
x1=1; x2=-1; x3=0; x4=2
Note that if the system is homogeneous, that is, all numbers bi (u=1, 2, ... , n) are equal to zero, then all numbers are equal to zero 
Therefore, system (1) in this case has only a zero solution.
Let now the determinant D1 of the main matrix of system (1) be equal to zero. Then it is no longer possible to say that among the numbers 
(u=m, m+1, ... , n) obtained after the (m-1)th stage of transformations, there will be at least one that is different from zero. Moreover, at some stage all these numbers will definitely become equal to zero (otherwise we would have a different case). Thus, let the matrix be obtained
Let us rearrange the m-th column of the matrix to the place of the n-th one, and all those following the m-th column, except for the column of free terms 
let's move one place to the left (such an operation obviously means rearranging the unknowns in the equations of the system or renumbering them, which, of course, does not change the solution of the system). As a result, we get the matrix
,
I=1, 2, ... , n;
k=m, m+1, ... , n.
Continuing the same transformations as before, we ultimately obtain the matrix
(5)
Matrix (5) corresponds to the system of equations
(6),
in which the unknown 
different from unknown X і
in system (1) only by numbering. Since system (6) is equivalent to system (1), then the conclusion about the solution of system (1) is equivalent to the conclusion about the solution to system (6).
Obviously, if at least one of the numbers 
(u=k+1, ... , n) is not equal to zero, then the equation of system (6), and therefore the equation of system (1), are incompatible. If all (i=k+1, ... , n) are equal to zero, then the equations are consistent. At the same time unknown 
Any values can be given, and the system has the following solutions:
,
where t1, t2, ... , te ( 
=n-k) arbitrary
In order to make it convenient to return to the original system of unknowns, it is useful to write the designations of the corresponding unknowns over the columns of the matrices that are obtained during the transformations. We also point out that if the original system (1) is homogeneous, then all numbers (u=1, 2, ... , n) are equal to zero. Therefore, the following two statements hold.
1. A system of homogeneous equations of the 1st order is always consistent.
2. If the determinant of a system of homogeneous equations of the 1st order is equal to zero, then the system has an infinite number of solutions.
Example 2
Solution
The system of equations that corresponds to the resulting matrix has the form:
The system is consistent, x4=t is arbitrary. The system has an infinite number of solutions
where t is an arbitrary number.
Note that if the free terms in the equations were different than those specified in the condition, the system could be incompatible. Let, for example, b4=1. Then the transformed matrix of the system will be
and the last equation of the system will take the form 0x1+0x2+0x3+0x4=1, which makes no sense.
Example 3.
Solution.
The system is compatible, x2=t is arbitrary; x1=1-t, x2=t, x3=-2, x4=1.
The analyzed method can be transferred without any changes to the case when the number of unknowns does not coincide with the number of equations.
II. Examples of problem solving
1.20. Solve the system
Let's calculate the determinant of the system
Since the determinant of the system is nonzero, we apply Cramer's rule. To calculate the determinant of detB1, we replace the column 
determinant of the system by a column of free terms 
. We have
The determinant detB2 is obtained by replacing the column 
determinant of the system by a column of free terms:
According to Cramer's rule, we find 
; 
The set of numbers (5;-4) is the only solution to this system.
1.21. Find system solutions
Determinant of system coefficients other than zero:
detA= 
=2·3·(-5)+5·(-9) ·2+(-8) ·4·3-(-8) ·3·2-5·4·(-5)-2·3· (-9)=-140
Therefore, we can apply Cramer's rule
from here we find 
; 
; 
The set of numbers (3, 2, 1) is the only solution to the system.
1.22. Solve the system
/IVp+II-I-III/ ~
It is easy to see that the determinant of the system coefficients is equal to zero, since its 4th row consists of zeros. The last row of the extended matrix indicates that the system is not compatible.
1.23. Solve the system
Let us write down the extended matrix of the system
/IIp. -2· I, IIIp. -I, IVp. -II-III/ ~
~
/divide ІІІр. at (-3), IVp. by (-3)/
~
/ІІІр. +2· ІІ/ ~
As a result of all the transformations, this system of linear equations was reduced to a triangular form.
It has only one solution.
x3=1 x4=-1 x2=-2 x1=2 ▲
The equations are compatible, x4=t is arbitrary,
1.25. Find system solutions
The system is consistent, x4=t is arbitrary,
1.26. Solve the system
The system is compatible, x4=t arbitrary, x1=t, x2=-2t, x3=0, x4=t. ▲
^
§6 Matrix rank, theorem on the compatibility of systems of first-order equations
To study many issues related to solving systems of 1st order equations, the concept is often introduced matrix rank.
Definition. The rank of a matrix is the highest order of the nonzero determinant of a square submatrix obtained from a given matrix by deleting some rows and columns.
Consider, for example, the matrix
By deleting any number of rows and columns, it is impossible to obtain a square matrix of order higher than 3 from a given matrix. Hence, its rank cannot be more than three. But by crossing out one of the columns, we will get square matrices that have two identical rows, and therefore their determinants are equal to zero. Hence, the rank of the original matrix is less than 3. By crossing out, for example, the 3rd and 4th columns and the 3rd row, we get a square matrix 
, whose determinant is not equal to zero. Thus, all determinants of a 3rd order submatrix are equal to zero, but among the determinants of 2nd order matrices there is a nonzero one. Thus, the rank of the original matrix is equal to two.
Let's prove the theorem: the rank of a matrix does not change during linear operations on its rows.
Indeed, linear operations with rows of any matrix lead to the same linear operations with rows of any submatrix. But, as stated above, during linear operations with rows of square matrices, the determinants of these matrices are obtained from one another by multiplying by a number different from zero. Hence, the zero determinant remains zero, and the non-zero determinant remains non-zero, that is, the highest order of the non-zero determinant of the submatrices cannot change. Obviously, rearranging the columns does not affect the rank of the matrix, since such a rearrangement can only affect the sign of the corresponding determinants.
From the proven theorem it follows that the transformed matrices considered in the previous section have the same rank as the original ones. Therefore, the rank of the main matrix of a system of first-order equations is equal to the number of ones on the main diagonal of the transformed matrix.
Let us now prove the theorem about the compatibility of systems of 1st order equations (the Kronecker-Capelli theorem): In order for a system of first-order equations to be compatible, it is necessary and sufficient that the rank of the extended matrix coincides with the rank of the main matrix.
Let the rank of the main matrix of the system be equal to k. If the rank of the system's extended matrix is also k, then this means that either the system contains only k equations, or all numbers 
(i= k+1, ... , k) in the transformed matrix are equal to zero (otherwise the rank of the extended matrix of the transformed, and therefore the original system, would be k +1)
Let the rank of the transformed (and therefore the original) extended matrix of the system be greater than k, that is, greater than the number of ones on the main diagonal of the transformed matrix. Then there is at least one submatrix of (k+1) order whose determinant is not equal to zero. Such a submatrix can only be obtained by adding to the identity matrix of order k (which is in the upper left corner of the transformed matrix) some one row and column, which consists of the first k free terms of the equations of the transformed system and any one free term from the next n-k equations. For the determinant of the specified submatrix to be non-zero, this last added element, that is, the number (i=k+1, ... , k), must also be non-zero. But, as was proven earlier, in this case 
the system is incompatible. Therefore, the system is compatible if and only if the rank of the main matrix matches the rank of the extended matrix.
II. Examples of problem solving
1.39. Calculate the rank of a matrix using elementary transformations
Where is the sign 
indicates that the matrices connected by it are obtained from one another by elementary transformations, and therefore have the same rank.
The rank of matrix A is 2, that is, r=2. ^
1.40. Using elementary transformations, calculate the rank of the matrix
r=3 , because the determinant of a triangular matrix from the first three columns is not equal to zero. ▲
Calculating the rank of a matrix using the framing method
We choose a second-order minor in this matrix that is different from zero. Then we calculate the third-order minors that frame (include) the chosen one until we find among them a non-zero one. Next, we calculate the fourth-order minors that frame the third-order nonzero minor until we find a nonzero one among them, etc. If you find a non-zero minor of the rth order, and all minors of the (r+1)th order framing it are equal to zero or they no longer exist, then the rank of the matrix is equal to r.
1.41. Calculate matrix rank
∆ 
Crossed out III. , since 2·ІІр. +I isІІІр.
Let's choose, for example, 
Let's calculate the third-order minors that frame it
minor of the third order different from zero.
It is contained in the fourth order determinant of a given matrix, which is equal to zero. Therefore, r=3. ▲
1.42. Solve systems of equations
a) Here r(A)=3, r(B)=3; system compatible, defined.
Because the 
,
then from the first three systems, for example, according to Cramer’s formulas, we find
x1=-1, x2=0, x3=1
b) Here r(A)=2, r(B)=2; the system is compatible but not defined.
Determinant 
and from the first two equations of the system
where the unknowns x3 and x4 can be given any values.
c) in this case r(A)=2, r(B)=3; and the system is incompatible.
1.43. Using the Gaussian method (sequential elimination of unknowns), solve a homogeneous system of equations:
and find its fundamental system of solutions.
Let's write out the extended matrix of the system (in this case, the zero column can, of course, not be written). After clear transformations we will have
that is, the given system is equivalent to the following:
Here r=3, and the three unknowns can be expressed in terms of the latter, for example, like this:
x 2 = -2x 3 -3x 4 -9x 5 = -2x 3 -12x 5
x 1 = -2x 2 -3x 3 -4x 4 -5x 5 =x 3 +15x 5
The fundamental system can be obtained if the free unknowns x3, x5 are given the value x3=1, x5=0 (then x1=1, x2=-2, x4=0) and the value x3=0, x5=1 (then x1=15, x2=-12, x4=1). This gives a fundamental system of solutions:
e 1 =(1, -2, 1, 0, 0), e 2 =(15, -12, 0, 1, 1)
Using the fundamental system, the general solution is often written as a linear combination of solutions e 1 ta e 2, that is:
1.44. Find the fundamental system of solutions to the system of linear equations and write down its general solution
Let's discard the third line. The system has been reduced to a stepwise one with the main unknowns x1, x2 and free unknowns x3, x4:
From the last equation 
. From the first 
There are 2 free unknowns. Therefore, we take a second-order determinant with unit elements of the main diagonal and zero elements of the secondary diagonal: 
.
Let's get a vector e 1 =
(
)
Vectors e 1 and e represent a fundamental system of solutions.
Now the general solution can be written as
Assigning coefficients 
,
any (arbitrary) numerical values we will obtain various partial solutions.
/subtract IV from all lines/ 
Lines II, III, V, which are proportional to the first line, will be crossed out. In the resulting matrix we rearrange columns I and II:
The rank of the matrix is 2.
Main unknowns x2 and x1. Free - x3, x4, x5. The system now looks like:
Assigning sequentially values to the free unknowns that are equal to the elements of the columns of the determinant
1) x3=1, x4=0, x5=0; 2) x3=0, x4=1, x5=0; 3) x3=0, x4=0, x5=1
1) x2=1, x1=1; 2) x2=1, x1=-2; 3) x2=-2, x1=1
that is, vectors C 1 = (1, 2, 1, 0, 0)
C 2 =(-2, 1, 0, 1, 0)
C 3 =(1, -2, 0, 0, 1)
constitute a fundamental system of solutions. The general solution of the system will now remain.
Coefficient matrix
has rank r=2 (check).
Let's choose for the basic minor 
Then the reduced system has the form:
Where, counting x3=c1, x4=c2, x5=c3, we find
General solution of the system
From the general solution we find the fundamental system of solutions
Using the fundamental system, the general solution can be written
e=с1e1+с2e2+с3e3
^
§7 Basic operations with matrices
In the previous paragraph, linear operations with rows and columns of various matrices were widely used. But in some questions of linear algebra it is necessary to consider operations with matrices as with a single object.
The study of operations with matrices is based on the concept of matrix equality. We will proceed from this definitions: Two matrices of the same dimension are said to be equal if all their corresponding elements are equal.
Consequently, matrices A and B of the same dimension nxm are equal if and only if Aik=Bik i=1, 2,... , n; k=1, 2,... , m. At the same time, we emphasize once again that only matrices of the same dimension can be compared.
The sum of two matrices A and B of the same dimension nxm is a matrix C of the same dimension such that
(C) ik =(A) ik +(B) ik (1)
Therefore, when adding matrices (you can only add matrices of the same dimension), you must add all their corresponding elements.
Since adding matrices reduces to adding numbers - elements of these matrices, obviously, there is a commutative and associative property.
A+B=B+A; (A+B)+C=A+(B+C) (2)
The product of matrix A and number (or number and matrix A) is matrix B such that
(B) ik =(A) ik (3),
that is, when multiplying a matrix by a number (or numbers by a matrix), all elements of the matrix must be multiplied by this number. Recall that when multiplying by the number of the determinant of the matrix, it was enough to multiply only the elements of any row (or column) by this number.
It is easy to check that when a matrix is multiplied by a number, the distribution property holds:
(A+B)=A+B; (+)=A+B (4)
Let us now define the product of two matrices. Let matrix A of dimension nxm and matrix B of dimension mxp be given.
Definition. The product of matrix A of dimension nxm by matrix B of dimension mxp is a matrix C of dimension nxp such that
(5),
in other words, to obtain an element that is in the i-th row and in the k-th column of the product matrix, you need to calculate the sum of the products of the elements of the i-th row of the first factor and the corresponding elements of the k-th column of the second factor. Therefore, in order to be able to add the specified sum, the number of columns in the first matrix (that is, the number of elements in each row) must be equal to the number of rows in the other (that is, the number of elements in each column).
Example 1.
Find AB
Solution. Matrix A has a dimension of 3x2, matrix B has a dimension of 2x2; the product exists - it is a 3x2 matrix.
The product of matrices does not have the commutable property: AB, generally speaking, is not equal to BA.
Firstly, from the fact that AB can be calculated, it does not at all follow that BA makes sense. For example, in the example just discussed, rearranging factors, that is, multiplying B by A, is impossible, since it is impossible to multiply a 2x2 matrix by a 3x2 matrix - the number of columns of the first matrix here is not equal to the number of rows of the other. But even if the product BA exists, then often 
. Let's look at an example.
Let 
. Then
At the same time, it can be proven (we recommend that the reader perform such a proof) that
(AB)C=A(BC) (6)
A(B+C)=AB+AC
(it is usually assumed that all these works have meaning).
According to the definition of a matrix product, it is always possible to multiply square matrices of the same order, and the product will be a matrix of the same order. Let us note without proof one of the properties of the product of square matrices of the same order: the determinant of the product of two matrices of the same order is equal to the product of the determinants of the matrices that are multiplied.
Very often we have to consider the product of a matrix of dimension nxm by a matrix of dimension mx1, that is, a matrix with one column. Obviously, we should get a matrix of dimension nx1 as a result, that is, also a matrix with one column. Let, for example, you need to multiply the matrix
to the matrix 
As a result, we get the matrix 
, the elements of which are calculated using the formulas:
But this means that the system of 1st order equations discussed in the previous paragraph can be written in a very convenient matrix form: AX=B.
An essential role in various applications of matrix algebra is played by a square matrix in which all diagonal elements (that is, elements that are on the main diagonal) are equal to 1, and all other elements are equal to zero. Such a matrix is called the identity matrix. Obviously, the determinant of the identity matrix
= 1
The following properties of the identity matrix are characteristic: let a square matrix A of order n and an E-unit matrix of the same order be given. Then AE=EA=A.
Really 
, But 
Therefore in total 
only those components for which e=k are different from zero. Consequently, (AE) ік =(A) ік, and hence AE=A. We obtain similarly for the product EA.
Examples of problem solving
1.61. Find the product AB and BA of two matrices
∆ The product AB does not exist, since the number of columns of matrix A is not equal to the number of rows of matrix B. The number of columns of matrix B is equal to the number of rows of matrix A. Therefore, the product BA exists:
1.62. Find the 2A+5B matrix if
1. Substitution method: from any equation of the system we express one unknown through another and substitute it into the second equation of the system.
Task. Solve the system of equations:
Solution. From the first equation of the system we express at through X and substitute it into the second equation of the system. Let's get the system 
equivalent to the original one.
After bringing similar terms, the system will take the form:
From the second equation we find: . Substituting this value into the equation at = 2 - 2X, we get at= 3. Therefore, the solution to this system is a pair of numbers.
2. Algebraic addition method: By adding two equations, you get an equation with one variable.
Task. Solve the system equation:
Solution. Multiplying both sides of the second equation by 2, we get the system 
equivalent to the original one. Adding the two equations of this system, we arrive at the system 
After bringing similar terms, this system will take the form: 
From the second equation we find . Substituting this value into equation 3 X + 4at= 5, we get 
, where . Therefore, the solution to this system is a pair of numbers.
3. Method for introducing new variables: we are looking for some repeating expressions in the system, which we will denote by new variables, thereby simplifying the appearance of the system.
Task. Solve the system of equations:
Solution. Let's write this system differently: 
Let x + y = u, xy = v. Then we get the system
Let's solve it using the substitution method. From the first equation of the system we express u through v and substitute it into the second equation of the system. Let's get the system 
those. 
From the second equation of the system we find v 1 = 2, v 2 = 3.
Substituting these values into the equation u = 5 - v, we get u 1 = 3,
u 2 = 2. Then we have two systems
Solving the first system, we get two pairs of numbers (1; 2), (2; 1). The second system has no solutions.
Exercises for independent work
1. Solve systems of equations using the substitution method.