Among functional series, the most important place is occupied by power series.
A power series is a series
whose terms are power functions arranged in increasing non-negative integer powers x, A c 0 , c 1 , c 2 , c n - constant values. Numbers c 1 , c 2 , c n - coefficients of series terms, c 0 - free member. The terms of the power series are defined on the entire number line.
Let's get acquainted with the concept areas of convergence of the power series. This is a set of variable values x, for which the series converges. Power series have a fairly simple convergence region. For real variable values x the convergence region consists either of one point, or is a certain interval (convergence interval), or coincides with the entire axis Ox .
When substituting the values into the power series x= 0 will result in a number series
c 0 +0+0+...+0+... ,
which converges.
Therefore, when x= 0 any power series converges and, therefore, its area of convergence cannot be the empty set. The structure of the region of convergence of all power series is the same. It can be established using the following theorem.
Theorem 1 (Abel's theorem). If a power series converges at some value x = x 0, different from zero, then it converges, and, moreover, absolutely, for all values of | x| < |x 0 | . Please note: both the starting value “X is zero” and any value of “X” that is compared with the starting value are taken modulo - without taking into account the sign.
Consequence. If power series diverges at some value x = x 1, then it diverges for all values of | x| > |x 1 | .
As we have already found out earlier, any power series converges at the value x= 0. There are power series that converge only when x= 0 and diverge for other values X. Excluding this case from consideration, we assume that the power series converges at some value x = x 0, different from zero. Then, according to Abel's theorem, it converges at all points of the interval ]-| x 0 |, |x 0 |[ (an interval whose left and right boundaries are the x values at which the power series converges, taken with a minus sign and a plus sign, respectively), symmetrical about the origin.
If the power series diverges at a certain value x = x 1, then, based on the corollary of Abel’s theorem, it diverges at all points outside the segment [-| x 1 |, |x 1 |] . It follows that for any power series there is an interval symmetric with respect to the origin, called convergence interval, at each point of which the series converges, at the boundaries it can converge, or it can diverge, and not necessarily at the same time, and outside the segment the series diverges. Number R is called the radius of convergence of the power series.
In special cases convergence interval of power series can degenerate to a point (then the series converges only when x= 0 and it is considered that R= 0) or represent the entire number line (then the series converges at all points of the number line and it is assumed that ).
Thus, determining the region of convergence of a power series consists in determining its convergence radius R and studying the convergence of the series at the boundaries of the convergence interval (at ).
Theorem 2. If all the coefficients of a power series, starting from a certain one, are different from zero, then its radius of convergence is equal to the limit at the ratio of the absolute values of the coefficients of the common terms of the series that follow it, i.e.
Example 1. Find the region of convergence of the power series
Solution. Here
Using formula (28), we find the radius of convergence of this series:
Let us study the convergence of the series at the ends of the convergence interval. Example 13 shows that this series converges at x= 1 and diverges at x= -1. Consequently, the region of convergence is the half-interval.
Example 2. Find the region of convergence of the power series
Solution. The coefficients of the series are positive, and
Let us find the limit of this ratio, i.e. radius of convergence of the power series:
Let us study the convergence of the series at the ends of the interval. Substitution of values x= -1/5 and x= 1/5 in this row gives:
The first of these series converges (see Example 5). But then, by virtue of the theorem in the “Absolute convergence” section, the second series also converges, and the region of its convergence is the segment
Example 3. Find the region of convergence of the power series
Solution. Here
Using formula (28) we find the radius of convergence of the series:
Let us study the convergence of the series for values of . Substituting them in this series, we respectively obtain
Both series diverge because the necessary condition for convergence is not satisfied (their common terms do not tend to zero at ). So, at both ends of the convergence interval, this series diverges, and the region of its convergence is the interval.
Example 5. Find the region of convergence of the power series
Solution. We find the relation where , and 
:
According to formula (28), the radius of convergence of this series
,
that is, the series converges only when x= 0 and diverges for other values X.
Examples show that at the ends of the convergence interval the series behave differently. In example 1, at one end of the convergence interval the series converges, and at the other, it diverges; in example 2, it converges at both ends; in example 3, it diverges at both ends.
The formula for the radius of convergence of a power series is obtained under the assumption that all coefficients of the series terms, starting from a certain point, are different from zero. Therefore, the use of formula (28) is permissible only in these cases. If this condition is violated, then the radius of convergence of the power series should be sought using d'Alembert's test, or, by replacing the variable, transforming the series to a form in which the specified condition is satisfied.
Example 6. Find the interval of convergence of the power series
Solution. This series does not contain terms with odd degrees X. Therefore, we transform the series, setting . Then we get the series
to find the radius of convergence of which we can apply formula (28). Since , a , then the radius of convergence of this series
From the equality we obtain , therefore, this series converges on the interval .
Sum of power series. Differentiation and integration of power seriesLet for the power series
radius of convergence R> 0, i.e. this series converges on the interval .
Then each value X from the convergence interval corresponds to a certain sum of the series. Therefore, the sum of the power series is a function of X on the convergence interval. Denoting it by f(x), we can write the equality
understanding it in the sense that the sum of the series at each point X from the convergence interval is equal to the value of the function f(x) at this point. In the same sense, we will say that the power series (29) converges to the function f(x) on the convergence interval.
Outside the convergence interval, equality (30) makes no sense.
Example 7. Find the sum of the power series
Solution. This is a geometric series for which a= 1, a q= x. Therefore, its sum is a function 
. A series converges if , and is its convergence interval. Therefore equality
is valid only for values, although the function 
defined for all values X, except X= 1.
It can be proven that the sum of the power series f(x) is continuous and differentiable on any interval within the convergence interval, in particular at any point in the convergence interval of the series.
Let us present theorems on term-by-term differentiation and integration of power series.
Theorem 1. Power series (30) in the interval of its convergence can be differentiated term by term an unlimited number of times, and the resulting power series have the same radius of convergence as the original series, and their sums are respectively equal to .
Theorem 2. Power series (30) can be integrated term by term an unlimited number of times in the range from 0 to X, if , and the resulting power series have the same radius of convergence as the original series, and their sums are correspondingly equal
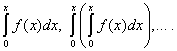
Let the function be given f(x), which needs to be expanded into a power series, i.e. represent in the form (30):
The task is to determine the coefficients 
row (30). To do this, differentiating equality (30) term by term, we consistently find:
……………………………………………….. (31)
Assuming in equalities (30) and (31) X= 0, we find
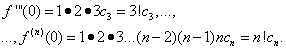
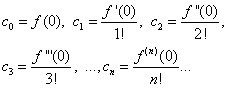
Substituting the found expressions into equality (30), we obtain
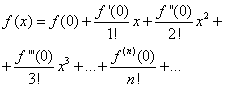(32)
Let us find the Maclaurin series expansion of some elementary functions.
Example 8. Expand the function in a Maclaurin series
Solution. The derivatives of this function coincide with the function itself:
Therefore, when X= 0 we have
Substituting these values into formula (32), we obtain the desired expansion:
(33)
This series converges on the entire number line (its radius of convergence).
In the theory of functional series, the central place is occupied by the section devoted to the expansion of a function into a series.
Thus, the task is set: for a given function we need to find such a power series
which converged on a certain interval and its sum was equal to 
,
those.
=
..
This task is called the problem of expanding a function into a power series.
A necessary condition for the decomposability of a function in a power series is its differentiability an infinite number of times - this follows from the properties of convergent power series. This condition is satisfied, as a rule, for elementary functions in their domain of definition.
So let's assume that the function 
has derivatives of any order. Is it possible to expand it into a power series? If so, how can we find this series? The second part of the problem is easier to solve, so let’s start with it.
Let us assume that the function 
can be represented as the sum of a power series converging in the interval containing the point X 0 :
=
..
(*)
Where A 0 ,A 1 ,A 2 ,...,A P ,... – unknown (yet) coefficients.
Let us put in equality (*) the value x = x 0 , then we get
.
Let us differentiate the power series (*) term by term
=
..
and believing here x = x 0 , we get
.
With the next differentiation we obtain the series
=
..
believing x = x 0 ,
we get 
, where 
.
After P-multiple differentiation we get
Assuming in the last equality x = x 0 ,
we get 
, where
So, the coefficients are found
,
,
,
…,
,….,
substituting which into the series (*), we get
The resulting series is called next to Taylorfor function
.
Thus, we have established that if the function can be expanded into a power series in powers (x - x 0 ), then this expansion is unique and the resulting series is necessarily a Taylor series.
Note that the Taylor series can be obtained for any function that has derivatives of any order at the point x = x 0 . But this does not mean that an equal sign can be placed between the function and the resulting series, i.e. that the sum of the series is equal to the original function. Firstly, such an equality can only make sense in the region of convergence, and the Taylor series obtained for the function may diverge, and secondly, if the Taylor series converges, then its sum may not coincide with the original function.
3.2. Sufficient conditions for the decomposability of a function in a Taylor seriesLet us formulate a statement with the help of which the task will be solved.
If the function
in some neighborhood of point x 0 has derivatives up to (n+
1) of order inclusive, then in this neighborhood we haveformulaTaylor
WhereR n (X)-the remainder term of the Taylor formula – has the form (Lagrange form)
Where dotξ lies between x and x 0 .
Note that there is a difference between the Taylor series and the Taylor formula: the Taylor formula is a finite sum, i.e. P - fixed number.
Recall that the sum of the series S(x) can be defined as the limit of a functional sequence of partial sums S P (x) at some interval X:
.
According to this, to expand a function into a Taylor series means to find a series such that for any XX
Let us write Taylor's formula in the form where
notice, that 
defines the error we get, replace the function f(x)
polynomial S n (x).
If 
, That 
,those. the function is expanded into a Taylor series. Vice versa, if 
, That 
.
Thus we proved criterion for the decomposability of a function in a Taylor series.
In order for the functionf(x) expands into a Taylor series, it is necessary and sufficient that on this interval
, WhereR n (x) is the remainder term of the Taylor series.
Using the formulated criterion, one can obtain sufficientconditions for the decomposability of a function in a Taylor series.
If insome neighborhood of point x 0 the absolute values of all derivatives of the function are limited to the same number M≥ 0, i.e.
, To in this neighborhood the function expands into a Taylor series.
From the above it follows algorithmfunction expansionf(x) in the Taylor series in the vicinity of a point X 0 :
1. Finding derivatives of functions f(x):
f(x), f’(x), f”(x), f’”(x), f (n) (x),…
2. Calculate the value of the function and the values of its derivatives at the point X 0
f(x 0 ), f’(x 0 ), f”(x 0 ), f’”(x 0 ), f (n) (x 0 ),…
3. We formally write the Taylor series and find the region of convergence of the resulting power series.
4. We check the fulfillment of sufficient conditions, i.e. we establish for which X from the convergence region, remainder term R n (x)
tends to zero as 
or
.
The expansion of functions into a Taylor series using this algorithm is called expansion of a function into a Taylor series by definition or direct decomposition.
How to insert mathematical formulas on a website?
If you ever need to add one or two mathematical formulas to a web page, then the easiest way to do this is as described in the article: mathematical formulas are easily inserted onto the site in the form of pictures that are automatically generated by Wolfram Alpha. In addition to simplicity, this universal method will help improve the visibility of the site in search engines. It has been working for a long time (and, I think, will work forever), but is already morally outdated.
If you regularly use mathematical formulas on your site, then I recommend you use MathJax - a special JavaScript library that displays mathematical notation in web browsers using MathML, LaTeX or ASCIIMathML markup.
There are two ways to start using MathJax: (1) using a simple code, you can quickly connect a MathJax script to your website, which will be automatically loaded from a remote server at the right time (list of servers); (2) download the MathJax script from a remote server to your server and connect it to all pages of your site. The second method - more complex and time-consuming - will speed up the loading of your site's pages, and if the parent MathJax server becomes temporarily unavailable for some reason, this will not affect your own site in any way. Despite these advantages, I chose the first method as it is simpler, faster and does not require technical skills. Follow my example, and in just 5 minutes you will be able to use all the features of MathJax on your site.
You can connect the MathJax library script from a remote server using two code options taken from the main MathJax website or on the documentation page:
One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically monitors and loads the latest versions of MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.
The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's all. Now learn the markup syntax of MathML, LaTeX, and ASCIIMathML, and you are ready to insert mathematical formulas into your site's web pages.
Any fractal is constructed according to a certain rule, which is consistently applied an unlimited number of times. Each such time is called an iteration.
The iterative algorithm for constructing a Menger sponge is quite simple: the original cube with side 1 is divided by planes parallel to its faces into 27 equal cubes. One central cube and 6 cubes adjacent to it along the faces are removed from it. The result is a set consisting of the remaining 20 smaller cubes. Doing the same with each of these cubes, we get a set consisting of 400 smaller cubes. Continuing this process endlessly, we get a Menger sponge.
If the function f(x) has derivatives of all orders on a certain interval containing point a, then the Taylor formula can be applied to it:
,
Where r n– the so-called remainder term or remainder of the series, it can be estimated using the Lagrange formula:
, where the number x is between x and a.
f(x)=
at point x 0 = Number of row elements 3 4 5 6 7
Use the expansion of elementary functions e x , cos(x), sin(x), ln(1+x), (1+x) m
Rules for entering functions:
If for some value X r n→0 at n→∞, then in the limit the Taylor formula becomes convergent for this value Taylor series:
,
Thus, the function f(x) can be expanded into a Taylor series at the point x under consideration if:
1) it has derivatives of all orders;
2) the constructed series converges at this point.
When a = 0 we obtain a series called the Maclaurin series:
,
Expansion of the simplest (elementary) functions in the Maclaurin series:
Exponential functions
, R=∞
Trigonometric functions 
, R=∞ 
, R=∞
, (-π/2< x < π/2), R=π/2
The function actgx does not expand in powers of x, because ctg0=∞
Hyperbolic functions
Logarithmic functions
, -1