The solution to the impasse was found by the Danish scientist Niels Bohr in 1913, who received the Nobel Prize in 1922.
Bohr made assumptions that were called Bohr's postulates.
· First postulate (stationary state postulate):electrons move only along certain(stationary)orbits. Wherein, even when moving at speed,they do not emit energy.
· Second postulate (frequency rule):emission and absorption of energy in the form of a quantum of light (hn) occurs only when an electron transitions from one stationary state to another. The magnitude of the light quantum is equal to the difference in energies of those stationary states,between which the electron jumps: .
It follows that the change in atomic energy associated with radiation when a photon is absorbed is proportional to frequency ν:
Orbit quantization rule : Of all the electron orbits, only those are possible,for which the angular momentum is equal to an integer multiple of Planck’s constant:
| , | (6.3.2) |
Where n= 1, 2, 3,... – the main quantum number.
Let us obtain an expression for the energy of an electron in an atom.
Consider an electron (Fig. 6.6a) moving at speed in the field of an atomic nucleus with a charge Ze(at Z= 1 – hydrogen atom).
 | |||
| A | b |
The equation of electron motion has the form:
 .
|
(6.3.3) |
From formula (6.3.3) it is clear that the centrifugal force is equal to the Coulomb force, where .
Let us substitute the value υ from (6.3.2) into (6.3.3) and obtain an expression for the radii of stationary orbits (Fig. 6.6, b):
| . | (6.3.4) |
The radius of the first orbit of a hydrogen atom is called Bohr radius . At n =1, Z= 1 for hydrogen we have:
Å = 0.529·10 –10 m.
The internal energy of an atom is composed of the kinetic energy of the electron (the nucleus is motionless) and the potential energy of interaction of the electron with the nucleus:
.
From the equation of electron motion it follows that, i.e. kinetic energy is equal to potential energy. Then we can write:
.
Let us substitute here the expression for the radius of the first orbit and get:
 .
|
(6.3.5) |
It is taken into account here that Planck’s constant, i.e. .
For a hydrogen atom at Z= 1 we have:
 .
|
(6.3.6) |
From formula (6.3.6) it is clear that it takes only discrete energy values, because n = 1, 2, 3….
The diagram of energy levels determined by equation (6.3.6) is shown in Fig. 6.1 and 6.7.
When an electron in a hydrogen atom passes from the state n in a state k a photon with energy is emitted:
.
Emission frequency:
.
A generalized Balmer formula has been obtained, which agrees well with experiment. The expression before the brackets, as already mentioned, is called Rydberg constant :
.
A major success of Bohr's theory was the calculation of the Rydberg constant for hydrogen-like systems and the explanation of the structure of their line spectra. Bohr was able to explain the lines of the spectrum ionized helium He theoretically calculated the ratio of the mass of the proton to the mass of the electron, which was in accordance with experiment, an important confirmation of the main ideas contained in his theory. Bohr's theory played a huge role in the creation of atomic physics. During the period of its development (1913–1925), important discoveries were made that were forever included in the treasury of world science.
However, along with the successes, significant shortcomings were discovered in Bohr's theory from the very beginning. The most important of them was internal inconsistency theories: mechanical connection of classical physics with quantum postulates. The theory could not explain the question of intensities spectral lines. A serious failure was the absolute impossibility of applying the theory to explain the spectra of a helium atom containing two electrons in its orbit, and even more so for multi-electron atoms (Fig. 6.8).
It became clear that Bohr's theory was only a transitional stage on the path to creating a more general and correct theory. Quantum mechanics was such a theory.
To view demos, click on the appropriate hyperlink:
Atom (from ancient Greek ἄτομος - indivisible) is the smallest chemically indivisible part of a chemical element, which is the bearer of its properties. An atom consists of an atomic nucleus and electrons. The nucleus of an atom consists of positively charged protons and uncharged neutrons. If the number of protons in the nucleus coincides with the number of electrons, then the atom as a whole turns out to be electrically neutral. Otherwise, it has some positive or negative charge and is called an ion. Atoms are classified according to the number of protons and neutrons in the nucleus: the number of protons determines whether the atom belongs to a certain chemical element, and the number of neutrons determines the isotope of this element.
Although the word atom originally meant a particle that is not divided into smaller parts, according to scientific concepts it is composed of smaller particles called subatomic particles. An atom consists of electrons, protons, all atoms except hydrogen-1 also contain neutrons.
The electron is the lightest particle that makes up an atom, with a mass of 9.11·10−31 kg, a negative charge and a size too small to be measured by modern methods. Protons have a positive charge and are 1836 times heavier than an electron (1.6726·10−27 kg). Neutrons have no electrical charge and are 1839 times heavier than an electron (1.6929·10−27 kg). In this case, the mass of the nucleus is less than the sum of the masses of its constituent protons and neutrons due to the mass defect effect. Neutrons and protons have a comparable size, about 2.5 × 10−15 m, although the sizes of these particles are poorly defined.
Bohr's postulates are the basic assumptions formulated by Niels Bohr in 1913 to explain the pattern of the line spectrum of the hydrogen atom and hydrogen-like ions (Balmer-Rydberg formula) and the quantum nature of the emission and absorption of light. Bohr proceeded from Rutherford's planetary model of the atom.
An atom can only be in special stationary, or quantum, states, each of which has a specific energy. In a stationary state, an atom does not emit electromagnetic waves.
An electron in an atom, without losing energy, moves along certain discrete circular orbits, for which the angular momentum is quantized: , where are natural numbers, and is Planck’s constant. The presence of an electron in the orbit determines the energy of these stationary states.
When an electron moves from an orbit (energy level) to an orbit, a quantum of energy is emitted or absorbed, where are the energy levels between which the transition occurs. When moving from an upper level to a lower one, energy is emitted; when moving from a lower to an upper level, it is absorbed.
Using these postulates and the laws of classical mechanics, Bohr proposed a model of the atom, now called the Bohr model of the atom. Subsequently, Sommerfeld expanded Bohr's theory to the case of elliptical orbits. It is called the Bohr-Sommerfeld model.
A hydrogen atom is a physical system consisting of an atomic nucleus carrying an elementary positive electrical charge and an electron carrying an elementary negative electrical charge. The atomic nucleus may contain a proton or a proton with one or more neutrons, forming isotopes of hydrogen. The electron is predominantly located in a thin concentric spherical layer around the atomic nucleus, forming the electron shell of the atom. The most probable radius of the electron shell of a hydrogen atom in a stable state is equal to the Bohr radius a0 = 0.529 Å.
The hydrogen atom has a special significance in quantum mechanics and relativistic quantum mechanics because for it the two-body problem has an exact or approximate analytical solution. These solutions are applicable for different hydrogen isotopes, with appropriate corrections.
In quantum mechanics, a hydrogen atom is described by a two-particle density matrix or two-particle wave function. It is also simplistically considered as an electron in the electrostatic field of an infinitely heavy atomic nucleus that does not participate in motion (or simply in the Coulomb electrostatic potential of the form 1/r). In this case, the hydrogen atom is described by a reduced single-particle density matrix or wave function.
In 1913, Niels Bohr proposed a model of the hydrogen atom, which had many assumptions and simplifications, and derived from it the emission spectrum of hydrogen. The model's assumptions were not completely correct, but nevertheless led to the correct values for the energy levels of the atom.
The results of Bohr's calculations were confirmed in 1925-1926 by rigorous quantum mechanical analysis based on the Schrödinger equation. The solution to the Schrödinger equation for an electron in the electrostatic field of an atomic nucleus is derived in analytical form. It describes not only electron energy levels and emission spectrum,
Quantization of electron energy in an atom Some physical quantities related to microobjects change not continuously, but abruptly. Quantities that can only take on well-defined, that is, discrete values (the Latin “discretus” means divided, discontinuous) are said to be quantized.
In 1900, the German physicist M. Planck, who studied the thermal radiation of solids, came to the conclusion that electromagnetic radiation is emitted in the form of separate portions - quanta - of energy. The value of one energy quantum is ΔE = hν,
where ΔE is the quantum energy, J; ν - frequency, s-1; h is Planck's constant (one of the fundamental constants of nature), equal to 6.626·10−34 J·s.
Energy quanta were later called photons.
The idea of energy quantization made it possible to explain the origin of line atomic spectra, consisting of a set of lines combined in a series.
Let's go back to 1911. By this time, the discreteness of the microcosm was most clearly manifested in atomic spectra. It turned out that atoms absorb and emit light only of a certain wavelength, and the spectral lines are grouped into so-called series (Fig. 3.1).
Rice. 3.1. Wavelengths emitted by a hydrogen atom: the spectrum consists of series (the first three are shown)-
sequences of lines condensing to a certain (different for each series) limiting minimum
value; only four lines of the Balmer series lie in the visible range
Rice. 3.2. (a) Line emission spectra of hydrogen, mercury and helium gases: (b) absorption spectrum of hydrogen
Rice. 3.3. Continuous emission spectra provide heated solid and liquid substances, highly compressed gases, high-temperature plasma
For the spectrum of hydrogen, the simplest of atoms, a simple formula was established (not derived, but guessed!)
|
|
Here -
wavelength of hydrogen atom radiation, n And k > n -
whole numbers, R -
so-called Rydberg constant (
, Where -
off-system unit of energy "Rydberg", equal to half an atomic energy unit) .
It turned out that the Lyman series is described by this formula for the values ,
Balmer series -
at , Paschen series -
at, etc. Limit (minimum) values for wavelengths are obtained from (3.1) at:
Rice. 3.4. Johannes Robert Rydberg (1854–1919)
Rice. 3.5. Theodore Lyman (1874–1954)
Rice. 3.6. Lyman Spectral Series
Rice. 3.7. Johann Jacob Balmer (1825–1898)
Rice. 3.8. Visible hydrogen emission lines in the Balmer series. Hα is the red line on the right, having a wavelength of 656.3 nm. The leftmost line - Hε, corresponds to radiation already in the ultraviolet region of the spectrum at a wavelength of 397.0 nm
Rice. 3.9. Louis Karl Heinrich Friedrich Paschen (1865–1947)
Rice. 3.10. All lines of the Paschen series are located in the infrared range
In addition, as a result of studying the properties of gases, it was known by that time that the sizes of atoms are approximately
equal Therefore, the theory explaining the spectrum and sizes of atoms had to include some parameter that would allow constructing a quantity with the dimension of length (constant e And m -
electron charge and mass -
not enough for this). There was no such parameter in the classical theory. It could have been the Rydberg constant, but its origins were dark and mysterious.
In 1911, E. Rutherford published a theoretical work ( Rutherford E., Philosophical Magazine, v. 21, p. 669–688 , 1911), in which, based on the analysis of experiments performed in 1908–1909 years by his students - intern Hans Geiger and graduate student Ernst Marsden - ( Geiger H., Marsden T., Proceedings of the Royal Society of London, Series A, v. 82, p. 495–499 , 1909) asserted the presence inside an atom of a positively charged nucleus, in which almost the entire mass of the atom is concentrated.
Rice. 3.11. Ernest Rutherford (1871–1937)
Video 3.2. A little history. Black hat and scattering model.Subsequently, in one of his lectures, E. Rutherford himself recalled those times as follows (quoted from the book by J. Trigg, Crucial Experiments in Modern Physics, Moscow, MIR, 1974, p. 77): “...I remember... A very excited Geiger came to me and said: “We seem to have received several cases of scattering - particles back...”. This is the most incredible event that has happened in my life. It's almost as incredible as if you fired a 15-inch shell at tissue paper and it bounced off it and hit you. In analyzing this, I realized that such backward scattering must be the result of a single collision and, after doing calculations, I saw that this was in no way possible unless it was assumed that the overwhelming majority of the mass of the atom was concentrated in a tiny nucleus. That’s when I came up with the idea of an atom with a tiny, massive center where the charge is concentrated.” Let us add on our own that the words “backward scattering” actually meant scattering by 150 degrees; scattering at large angles did not allow observation by the design of the installation used at that moment.
The schematic diagram of Rutherford's experiments is shown in Fig. 3.12. A diagram of the actual installation can be found in the book by J. Trigg cited above.
Rice. 3.12. Schematic of Rutherford's scattering experiment - particles
Video 3.3. Rutherford's full-scale experiment in a laboratory setup. Video 3.4. Rutherford's experience "from the inside" (laboratory setup). Video 3.5. Computer model of Rutherford's experience.From a radioactive source enclosed in a lead container, particles were directed onto thin foil F from the metal being tested. Scattered particles fell on a screen covered with a layer of zinc sulfide crystals, capable of glowing when hit by fast charged particles. Scintillations (flashes) on the screen were observed by eye using a microscope. Observations of scattered particles in Rutherford's experiment could be carried out at different angles to the original direction of the beam. It was found that most particles passed through a thin layer of metal with little or no deflection. However, a small part of the particles are deflected at significant angles exceeding 30°. Very rare particles (approximately one in ten thousand) experienced deflections at angles close to . Obviously, a particle can only be thrown back if the positive charge of the atom and its mass are concentrated in a very small volume inside the atom. Thus it was opened atomic nucleus- a body of small dimensions compared to an atom, in which all the positive charge and almost all of its mass are concentrated. The dimensions of the nucleus were estimated by E. Rutherford in 1911, the estimate was less than or on the order of .
Video 3.6. Impact parameter and trajectory shape. Video 3.7. The charge of the scattered particle and the shape of the trajectory. Video 3.8. The energy of the scattered particle and the shape of the trajectory. Video 3.9. Nuclear charge and trajectory shape.
Rice. 3.13. Diagram of alpha particle scattering on the nucleus of a gold atom
Rice. 3.14. Scheme of alpha particle flux scattering in thin gold foil
A planetary model of the hydrogen atom emerged: a proton with an electron in orbit. Physicists love unified models, but here the big was repeated so beautifully in the small, in the atom - the Solar System.
Rice. 3.15. Diagram of Rutherford's nuclear (planetary) model of the atom
The problem was that an electron performing finite, and therefore accelerated, motion near the nucleus must fall onto the nucleus. The fact is that the electron is charged and, with accelerated movement, must emit electromagnetic radiation, that is, stationary movement is impossible. Classical electrodynamics predicts that, having rapidly lost its energy and angular momentum, the electron should fall onto the nucleus in approximately . During this time the light travels about 1.5 cm(it turns out that we see only “dead” atoms, but this is not so!). Rutherford understood the problem, but deliberately concentrated on the fact of the existence of the nucleus, believing that the question of the stability of the atom would be resolved by studying the behavior of atomic electrons. This was destined to be done in 1913 by N. Bohr, who proposed a new theory of the atom.
Rice. 3.16. Instability of the Rutherford model of the atom
Bohr's postulates
Bohr's first postulate
Here we can see the “forced” introduction of discreteness (not all orbits are allowed), as well as the typical physics “sweeping of the problem under the rug”: if there is no explanation for something, they take it for granted and study the consequences in the hope that someday they will understand and reason.
Rice. 3.17. Illustration of Bohr's first postulate
Bohr's second postulate
This postulate reflects the conservation of energy and the Planck–Einstein relation.
Rice. 3.18. Illustration for Bohr's second postulate
Bohr's third postulate
An inevitable consequence: since the remaining orbits for the electron are forbidden, the transition occurs abruptly; it makes no sense to talk about the path and energy of the electron between orbits: the laws of mechanics do not apply there.
Bohr's fourth postulate
Planck's constant ħ has the dimension of angular momentum and together with the charge of the electron e and its mass m allows you to create a length dimension parameter. This leads to the ability to calculate the size of an atom.
Rice. 3.19. Niels Henrik David Bohr (1885–1962)
Application of Bohr's postulates
Classical mechanics for an electron rotating in a circular orbit of radius R with speed v around a nucleus with a charge Ze, gives the equation of motion
Therefore energy E and angular momentum L electrons are expressed in terms of the orbital radius R:
If Bohr's quantization condition is applied to the last expression L=nħ (n=1, 2, 3, …), then the following results will be obtained.
Rice. 3.20. Bohr atom model
Characteristics of a hydrogen-like atom
Radii of allowed orbits
|
|
Energy of an electron in a stationary orbit
Constant AIN,
having the dimension of length is called Bohr radius: 
. The meaning of the number -
number of allowed orbit. Bohr radius -
radius of the lowest orbit in a hydrogen atom.
Formula (3.3) determines discrete the energy values that an electron can have in a hydrogen atom, or, as they say, energy levels. Negative values correspond to bound states of an electron in an atom, that is, movements in a limited region of space (analogue in classical physics - the movement of planets in ellipses, as opposed to hyperbolic and parabolic trajectories that go to infinity).
When solving problems about the behavior of an electron in an atom, expressions usually arise that include the square of the electron's electric charge in combination with the electric constant. It is very useful to introduce a dimensionless combination of fundamental world constants - the so-called fine structure constant:
|
|
which, together with the atomic number and orbital number, determines the scale of relativistic effects in the atom. To make this clearer, let us rewrite formula (3.3) so that its right-hand side includes the fine structure constant:
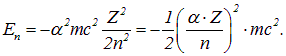
Because of the multiplier, the energies characteristic of an atom turn out to be four orders of magnitude less than the rest energy of the electron. This is a manifestation of the nonrelativism of fairly light atomic systems. As can be seen from the last expression in the above formula, relativistic effects cease to be small corrections for electrons closest to the nucleus in heavy atoms.
Example 1. Let us determine the speed of the electron by n th orbit of the Bohr atom. Radius nth orbit is determined by the formula
Where a B- Bohr radius. Electron speed v can be expressed in terms of angular momentum L=nħ:
Let us simplify the expression for the Bohr radius using the introduced fine structure constant:
|
|
Substituting this expression into the above formula for the electron speed, we obtain for n th orbits
Rice. 3.21. Diagram of energy levels and transitions in the hydrogen atom according to Bohr's theory:
solid lines (transitions from top to bottom) - emission, dotted lines (transitions from bottom to top) - absorption.
Boundaries (limits) of series are shown 
, which correspond to transitions from level c
- boundaries between continuum and discrete spectrum
Bohr's statement about the discreteness of the energy spectrum of atoms was experimentally confirmed in the Frank-Hertz experiments, which consisted of bombarding mercury vapor with electrons in a vacuum tube and measuring the dependence of the anode current on the accelerating potential difference. The experimental diagram is shown in Fig. 3.22.
Rice. 3.22. Frank's experiment scheme - Hertz
In a tube filled with mercury vapor under low pressure (about 1 mm Hg), there are three electrodes: an anode, a cathode and a grid. Electrons escaping from the surface of a heated cathode due to thermionic emission are accelerated by voltage U, applied between the cathode and the grid. This voltage can be changed using a potentiometer P. A weak reverse field with a potential difference of the order of 0.5BB, inhibiting the movement of electrons to the anode. The dependence of the current was determined I in the anode circuit from the applied voltage U. The results obtained are shown in Fig. 3.23.
Rice. 3.23. Dependence of current I in the anode circuit on the applied voltage U in the Frank-Hertz experiment
The current strength first increases monotonically and reaches a maximum at voltage 4.9 V, after which with growth U falls sharply, reaches a minimum and begins to rise again. Current maxima are repeated at voltages 9.8 V, 14.7 V etc. The alternation of maxima at equal distances from each other proved the discrete nature of the change in the energy of the atom.
Video 3.10. Experience of Frank and Hertz. Demonstration installation. Video 3.11. Experience of Frank and Hertz. Comparison of current-voltage characteristics for neon and helium. Video 3.12. Experience of Frank and Hertz. Laboratory setup 1. Video 3.12. Experience of Frank and Hertz. Laboratory setup 2.
The atomic number of an element is an integer, so after rounding we get Z=2, which corresponds to helium.
As noted above, even before the advent of Bohr's theory, the spectrum of the hydrogen atom was studied and formula (3.1) was empirically established. But when observing the spectrum of the Sun, lines were noticed that seemed to violate this formula, since they corresponded to half-integer values n And k. After the appearance of Bohr's theory, it became clear that quantum numbers n And k still must be integers, and the apparent half-integer values can be explained differently. Indeed, from formula (3.6) for the frequencies emitted by a hydrogen-like atom, it follows that
that is, the observed lines belong to the ion of the element with Z=2. As you know, this element has a “solar” name - helium.
The existence of discrete energy levels is a fundamental property of atoms (as well as molecules and atomic nuclei).
Let's try to apply the laws of physics known to us to imagine the structure of the atom, which explains the discreteness of its energy levels.
Let's consider the simplest of atoms - the hydrogen atom. The atomic number of hydrogen in the periodic table of elements is equal to one, therefore, a hydrogen atom consists of a positive nucleus, the charge of which is equal to , and one electron. Between the nucleus and the electron there is a force of attraction between charges. The presence of this force provides radial (centripetal) acceleration, due to which a light electron rotates around a heavy nucleus in a circular or elliptical orbit in the same way as a planet rotates around the Sun under the influence of gravity. Thus, the different possible states of the atom correspond to the difference in the size (and shape) of the orbit of the electron rotating around the nucleus.
The energy of an electron in an atom is composed of the kinetic energy of motion along the orbit and the potential energy in the electric field of the nucleus. It can be shown (see at the end of the paragraph) that the energy of an electron in a circular orbit, and therefore the energy of the atom as a whole, depends on the radius of the orbit: a smaller radius of the orbit corresponds to a smaller energy of the atom. But, as we saw in § 204, the energy of an atom can take not any, but only certain selected values. Since energy is determined by the radius of the orbit, each energy level of the atom corresponds to an orbit of a certain selected radius.
The picture of possible circular orbits of an electron in a hydrogen atom is shown in Fig. 367. The main energy level of an atom corresponds to an orbit of the smallest radius.
Rice. 367. Possible orbits of an electron in a hydrogen atom: the radius of orbits increases in proportion to , i.e. in relation, etc.
Normally the electron is in this orbit. When a sufficiently large portion of energy is imparted, the electron moves to another energy level, i.e., “jumps” to one of the outer orbits. As indicated, in such an excited state the atom is unstable. After some time, the electron moves to a lower level, i.e., “jumps” to an orbit of smaller radius. The transition of an electron from a distant orbit to a near one is accompanied by the emission of a light quantum.
So, from the nuclear model of the atom and the discreteness of its energy levels, the existence of selected, “allowed” electron orbits in the atom follows. The question arises why an electron cannot rotate around a nucleus in an orbit of an arbitrary radius. What is the physical difference between permitted and unauthorized orbits?
The laws of mechanics and electricity, familiar to us from previous sections of the textbook (see volumes I, II), do not give any answer to these questions. From the point of view of these laws, all orbits are completely equal. The existence of dedicated orbits contradicts these laws.
An equally striking contradiction to the laws of physics known to us is the stability of the atom (in the ground state). We know that any charge moving with acceleration emits electromagnetic waves. Electromagnetic radiation carries away energy. In an atom, an electron moves at high speed in an orbit of small radius and, therefore, has a huge centripetal acceleration. According to the laws we know, an electron must lose energy by emitting it in the form of electromagnetic waves. But, as stated above, if an electron loses energy, the radius of its orbit decreases. Consequently, the electron cannot rotate in an orbit of constant radius. Calculations show that as a result of a decrease in the radius of the orbit due to radiation, the electron would have to fall onto the nucleus in a hundred-millionth of a second. This conclusion sharply contradicts our daily experience, which indicates the stability of atoms.
So, there is a contradiction between the data on the structure of the atom obtained from experiment, and between the basic laws of mechanics and electricity, also found experimentally.
But we should not forget that the laws mentioned were found and tested in experiments with bodies containing a very large number of electrons and a large number of atoms. We have no reason to believe that these laws apply to the movement of an individual electron in an atom. Moreover, the discrepancy between the behavior of an electron in an atom and the laws of classical physics indicates the inapplicability of these laws to atomic phenomena (see also § 210).
Above we outlined the so-called planetary model of the atom, i.e. the idea of electrons rotating in allowed orbits around an atomic nucleus. When justifying the planetary model, we used the laws of classical physics. But, as already noted and as we will see in more detail in § 210, the motion of an electron in an atom belongs to a field of phenomena in which classical mechanics is inapplicable. It is not surprising, therefore, that a deeper study of the “microworld” showed the incompleteness and rough approximation of the planetary model; the actual picture of the atom is more complex. Nevertheless, this model correctly reflects many of the basic properties of the atom, and therefore, despite its approximation, it is sometimes used.
Let us consider the dependence of the energy of a hydrogen atom on the radius of the electron orbit. We determine the kinetic energy of electron motion along an orbit of radius from the condition that centripetal acceleration is provided by the force of coulomb attraction of charges (in the SI system). Equating the acceleration created by this force to the centripetal acceleration, we find that the kinetic energy of the electron is inversely proportional to the radius of the orbit, i.e. 
.
Let us select two orbits of radius and . The kinetic energy of electron rotation in the second orbit is greater than in the first by an amount 
.
If the orbits are not far apart from each other, then . Therefore, the quantity in the denominator can be neglected, and the difference in kinetic energies will be approximately equal.
The potential energy of the electron, on the contrary, is greater in the first, distant orbit, because to remove the electron from the series, work must be done against the forces of electrical attraction acting between the electron and the nucleus; this work goes towards increasing potential energy.
Let an electron be transferred from a near orbit to a distant one along a radial path. The path length is 
. The electric force along this path is not constant in magnitude. But since the orbits are close to one another, for an approximate calculation of the work it is possible to use the value of the force at the average distance of the electron from the nucleus, equal to 
.
According to Coulomb's law, the force is , and the work on the path, equal to the increase in potential energy, will be equal to .
Thus, when an electron moves from a distant orbit to a near one, the decrease in its potential energy is equal to twice the increase in kinetic energy. We proved this theorem for close orbits, the distance between which satisfies the condition . By summing up the changes in electron energy during transitions between successive pairs of close orbits, we are convinced that the theorem is also valid for arbitrarily distant orbits.
Let us now consider an infinitely distant orbit, i.e. Let us take the potential energy of the electron on it as the origin of potential energy, i.e., let us set 
. Kinetic energy goes to zero at; when moving from an orbit to a final orbit of radius, it will increase by an amount. The potential energy will decrease by twice the amount, i.e.
.(206.1)
The total energy of the electron is therefore equal to 
; the smaller the orbital radius, the smaller it is (minus sign!).
13.7. Hydrogen atom (hydrogen-like atom) according to Bohr's theory
13.7.3. Electron orbits in an atom
According to orbit quantization rule ( Sommerfeld's principle) the relationship between the energy of stationary states of an electron in an atom, the radius of its orbit and the speed in this orbit is given by the formula
mvr = nℏ,
where m is the electron mass, m = 9.11 ⋅ 10 −31 kg; v - electron speed; r is the radius of the electron orbit; ℏ - reduced Planck constant, ℏ = h /2π ≈ 1.055 ⋅ 10 −34 J ⋅ s; h is Planck’s constant, h = 6.626 ⋅ 10 −34 J ⋅ s; n is the principal quantum number.
From the rule of quantization of orbits it follows that the stationary states of an electron in an atom correspond only to such electron orbits for which the condition is satisfied
mv n r n = n ℏ,
where r n is the radius of the electron in the orbit with number n; v n - electron speed in orbit with number n; m is the electron mass, m = 9.11 ⋅ 10 −31 kg; ℏ - reduced Planck constant, ℏ = h /2π ≈ 1.055 ⋅ 10 −34 J ⋅ s; h is Planck’s constant, h = 6.626 ⋅ 10 −34 J ⋅ s; n is the principal quantum number.
Radius of stationary electron orbit
r n = ℏ 2 n 2 k Z e 2 m ,
where k = 1/4πε 0 ≈ 9 ⋅ 10 9 N ⋅ m 2 /Cl 2; ε 0 - electrical constant, ε 0 = 8.85 ⋅ 10 −12 F/m; Z - serial number of the element; e is the electron charge, e = −1.6 ⋅ 10 −19 C; m is the electron mass, m = 9.11 ⋅ 10 −31 kg; ℏ - reduced Planck constant, ℏ = h /2π ≈ 1.055 ⋅ 10 −34 J ⋅ s; h is Planck’s constant, h = 6.626 ⋅ 10 −34 J ⋅ s; n is the principal quantum number.
First orbit radius electron in a hydrogen atom (Z = 1 and n = 1) is equal to
r 1 = ℏ 2 k e 2 m = 0.53 ⋅ 10 − 10 m
and is called first Bohr radius.
To simplify calculations radius of the nth orbit electron in a hydrogen-like atom, use the formula
r (Å) = 0.53 ⋅ n 2 Z,
where r (Å) is the radius in angstroms (1 Å = 1.0 ⋅ 10 −10 m); Z is the serial number of a chemical element in the Periodic Table of Elements D.I. Mendeleev; n = 1, 2, 3, … is the main quantum number.
Speed of an electron in a stationary orbit in a hydrogen-like atom is determined by the formula
v n = k Z e 2 n ℏ ,
where k = 1/4πε 0 ≈ 9 ⋅ 10 9 N ⋅ m 2 /Cl 2; ε 0 - electrical constant, ε 0 = 8.85 ⋅ 10 −12 F/m; Z - serial number of the element; e is the electron charge, e = −1.6 ⋅ 10 −19 C; ℏ - reduced Planck constant, ℏ = = h /2π ≈ 1.055 ⋅ 10 −34 J ⋅ s; h is Planck’s constant, h = 6.626 ⋅ 10 −34 J ⋅ s; n is the principal quantum number.
Electron speed in the first orbit in a hydrogen atom (Z = 1 and n = 1) is equal to
v n = k e 2 ℏ = 2.2 ⋅ 10 6 m/s.
To simplify calculations of the value electron speed in the nth orbit in a hydrogen-like atom, the formula is used
v (m/s) = 2.2 ⋅ 10 6 ⋅ Z n ,
where v (m/s) - velocity module in m/s; Z is the serial number of a chemical element in the Periodic Table of Elements D.I. Mendeleev; n = 1, 2, 3, … is the main quantum number.
Example 21. An electron in a helium atom moves from the first orbit to an orbit whose radius is 9 times larger. Find the energy absorbed by the atom.
Solution . The energy absorbed by a helium atom is equal to the energy difference:
∆E = E 2 − E 1 ,
where E 1 is the electron energy corresponding to the orbital radius r 1 ; E 2 is the electron energy corresponding to the orbital radius r 2 .
The electron energies in a helium atom (Z = 2) are determined by the following formulas:
- in a state with the principal quantum number n 1 = 1 -
E 1 (eV) = − 13.6 Z 2 n 1 2 = − 54.4 eV;
- state with principal quantum number n 2 -
E 2 (eV) = − 54.4 n 2 2 .
To determine the energy E 2 we use the expression for the radii of the corresponding orbits:
- for an orbit with a principal quantum number n 1 = 1 -
r 1 (Å) ≈ 0.53 n 1 2 Z = 0.265 Å;
- orbits with principal quantum number n 2 -
r 2 (Å) ≈ 0.265 n 2 2.
Radius ratio
r 2 (Å) r 1 (Å) = 0.265 n 2 2 0.265 = n 2 2
allows us to determine the principal quantum number of the second state:
n 2 = r 2 (Å) r 1 (Å) = 9 = 3,
where r 2 /r 1 is the ratio of orbital radii specified in the condition, r 2 /r 1 = 9.
From the energy ratio
E 2 E 1 = 1 n 2 2
it follows that the energy of an electron in a helium atom in the second state is
E 2 = E 1 n 2 2 = − 54.4 eV 3 2 = − 6.04 eV.
The energy absorbed by the atom during the indicated transition is the difference
∆E = E 2 − E 1 = −6.04 − (−54.4) = 48.4 eV.
Consequently, during the indicated transition, the atom absorbed an energy equal to 48.4 eV.