“Domain of definition of a function” - The domain of definition of a quadratic function is any real number. A function is called logarithmic if the variable value is under the logarithm sign. Logarithmic function. A function whose variable is in the exponent is called exponential. Quadratic function.
“General properties of functions” - General properties of functions. Find the domain of definition of the function. Even function. Whether this function is even or odd. Using the graph, determine the set of values of the function. Using the graph, determine the values of X. Using the graph, determine the intervals of decrease in the function. Function f(x) is increasing. The function y=f(x) is given.
“Increasing and decreasing function” - Increasing and decreasing sine function. Let's look at another example. The intervals of decreasing cosine are segments, n is an integer. Let, for example, the function f be even and increasing on the interval where b>a?0. Increasing and decreasing functions. Increasing and decreasing cosine function. The figure below shows a graph of a function defined on the interval [-1;10].
"Application of Continuity" - Meaning of Expression. Geometric meaning of derivative. Interval method. Write an equation for the tangent to the graph of the function. Tangent to the graph of a function. The graph is close to a tangent. Formula. Let's calculate using the formula. The tangent to the curve at a given point M is the limiting position of the secant NM. Hyperbola.
“Extremum of function” - Dependence of gas pressure on temperature. Lesson topic: “Signs of increasing and decreasing functions. Test. Change in current strength when the circuit is opened. Investigation of a function to an extremum". Change of alternating current. Plan: Dependence of current on voltage. Dependence of gas pressure on volume. Topic: “Signs of increasing and decreasing functions.
“Functions and their properties” - The independent variable is called an argument. Increasing function. Definition of a function. Even and odd functions. Monotonicity of the function. The values of the dependent variable are called the values of the function. All values of the independent variable form the domain of definition of the function -D (f). 1. The function values are positive.
There are a total of 23 presentations in the topic
Topic: Methods for using limited functions.
Life is good because of what's in it
you can do math.
(Leonard Euler)Goals: development of new unconventional thinking, which can be successfully applied in other areas of human activity (cybernetics, computer technology, economics, radiophysics, chemistry, etc.).
Tasks: - training in assessing the objective and subjective difficulty of tasks and the reasonable choice of these tasks in the exam;
Creating a “piggy bank” of unconventional and unusual reasoning.
During the classes:
Org. moment. Students formulate the topic of the lesson by completing the Unified State Exam assignments parts A and B and deciphering the topic in descending order of the answers received. (Encrypt 12 cards numbered from -2 to 10 as supposed words) (Appendix 1 and 2)
limitations
2. Divide students into 2 groups, give them the set “Theory + 10 tasks” (Appendix 3 and 4), ask them to choose those tasks that can be completed for this theoretical part, and justify their choice.3. Show the progress of these tasks on the board by students: Noskova K., Dedevshin I., Veselov I.4. Divide the tasks from the card into 2 groups to solve them, followed by self-test using a sheet of ready-made solutions. (Appendix 5)5. Distribute to the groups sheets describing new non-standard methods for solving equations and inequalities for choosing the next topic (as a homework assignment, find problems in the Unified State Exam collections that can be solved using this method) (Appendix 6)6. Student reflection (filling out the table) F.I. studentAnnex 1.
Solve these tasks and arrange the answers in descending order, collect the topic of our lesson based on the answers.
Find the abscissa of the point in the graph of the function y=3x 2 -7x+7, in which the tangent of the tangent angle is equal to -1.
Appendix 2.
9 2 0 7Study of functions using derivatives. 10 5 1 -1Method of using limited functions. 4 -2 8 12Solving inequalities graphically.
3 11 6Solutions of functional equations.
Study
Appendix 3.
One of the effective methods for solving equations or inequalities is the method based on the use of bounded functions. The most well-known limited functions include, for example, some trigonometric functions; inverse trigonometric functions; functions containing modulus, degree, root with even degree and others.
The most common inequalities are the following:
│f(x) │≥
0, -1
≤
sinx ≤
1, -1
≤
cosx ≤
1, -
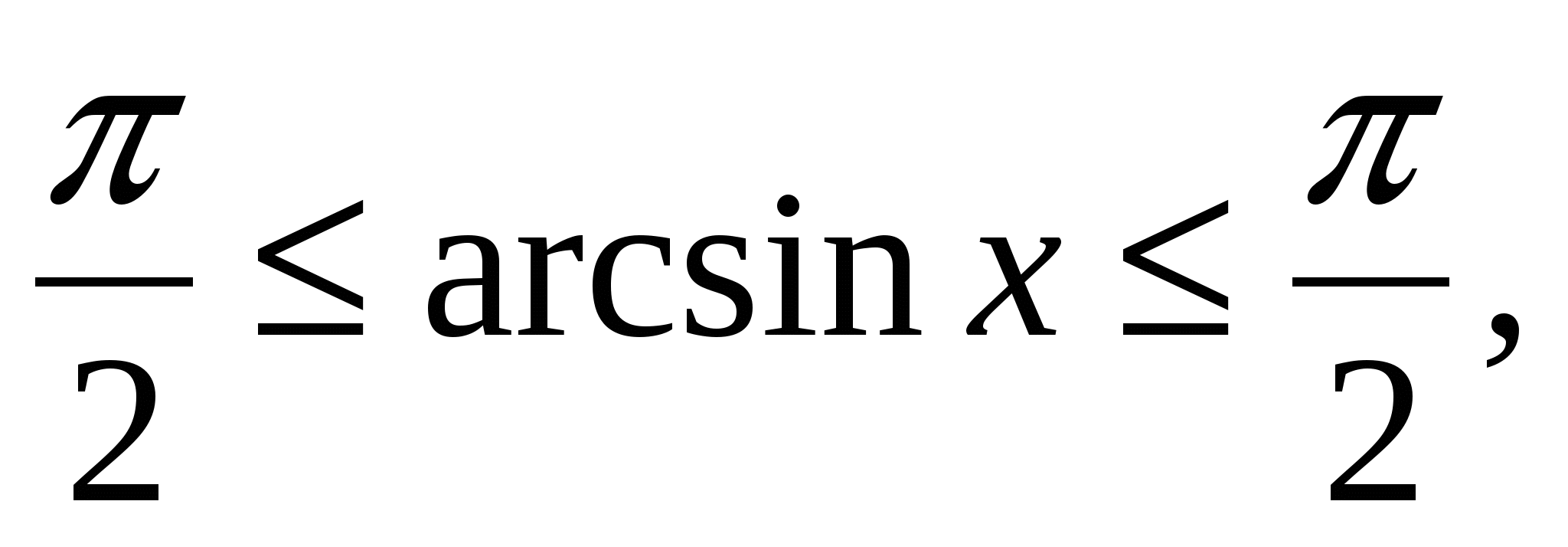
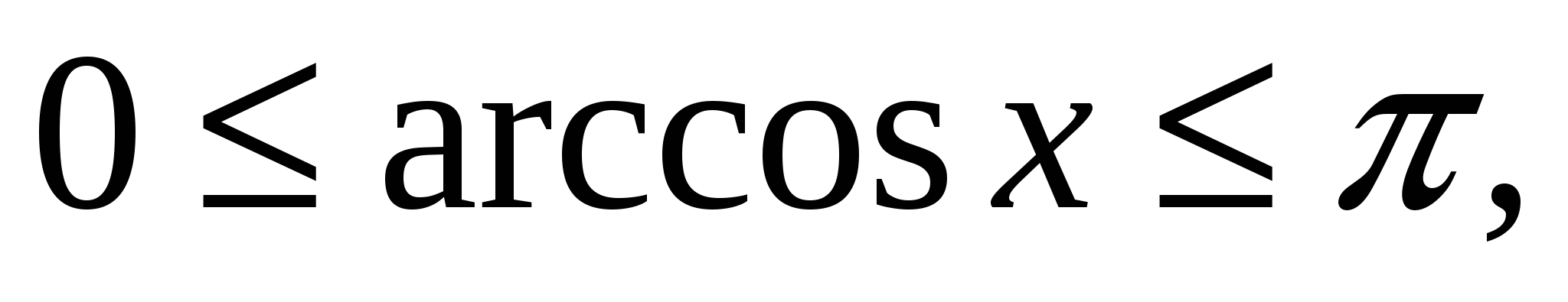 -
-

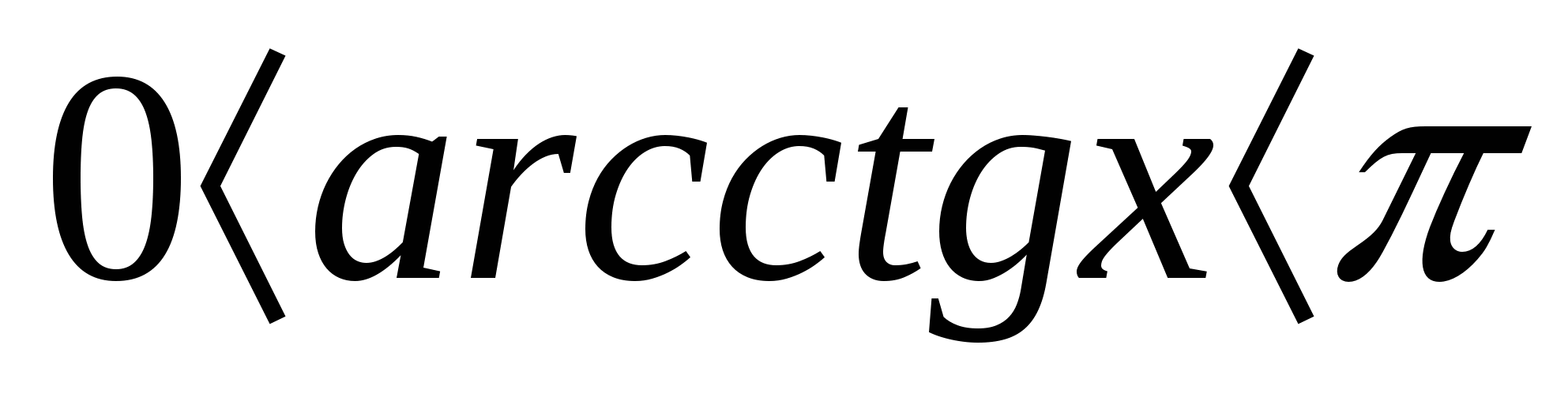 ,
a f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
,
a f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
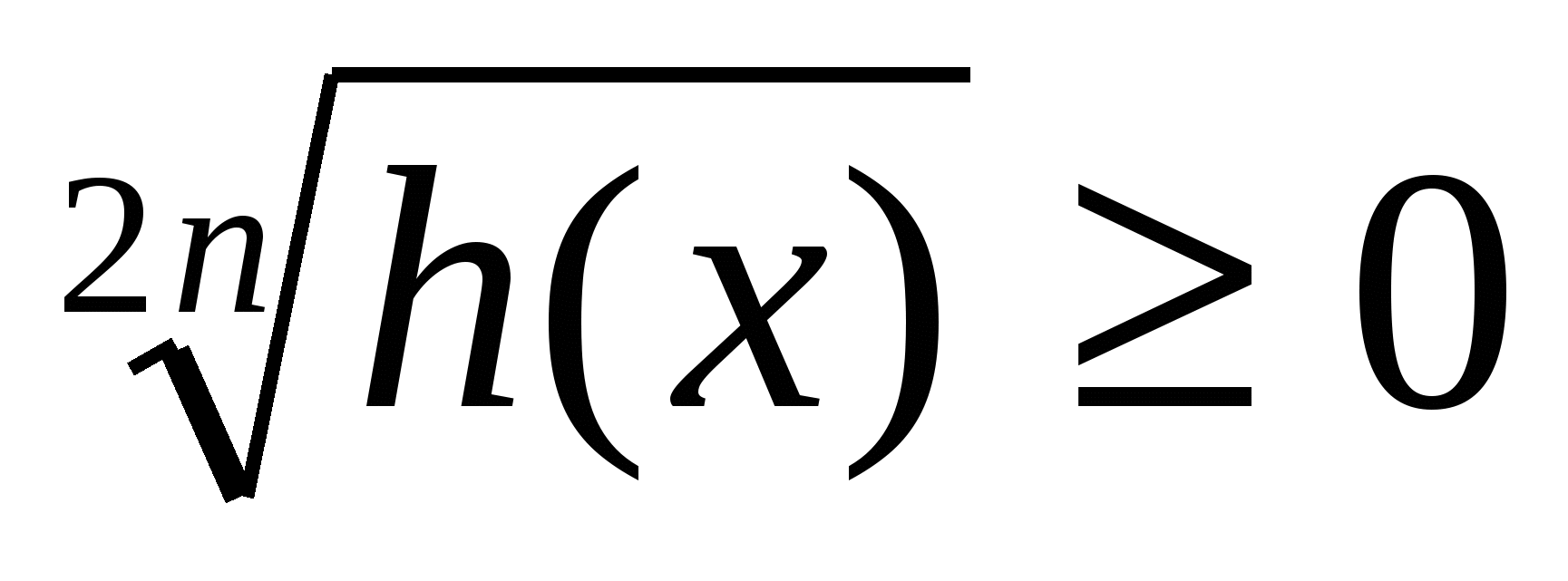 ,
a+
≥
2,
b+
≤
-2
and many others. Here n -natural number, h(x) ≥
0,
a>0,
b
0.
,
a+
≥
2,
b+
≤
-2
and many others. Here n -natural number, h(x) ≥
0,
a>0,
b
0.
In addition to the simplest inequalities given above, there are also more complex ones, in particular, trigonometric inequalities -,
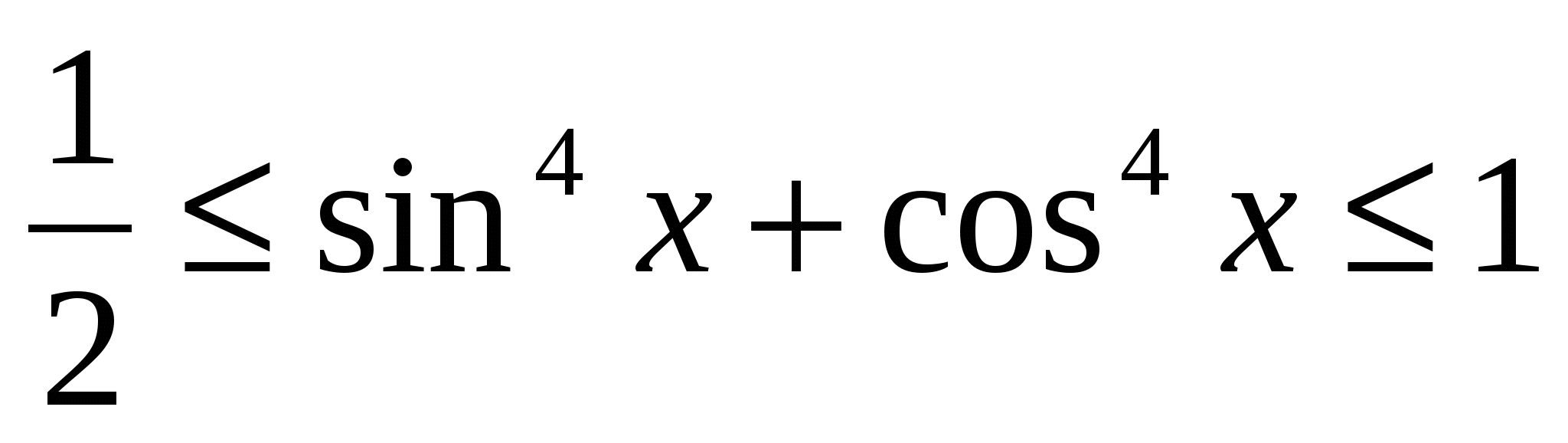 ,
,
and inequalities with modules of the form 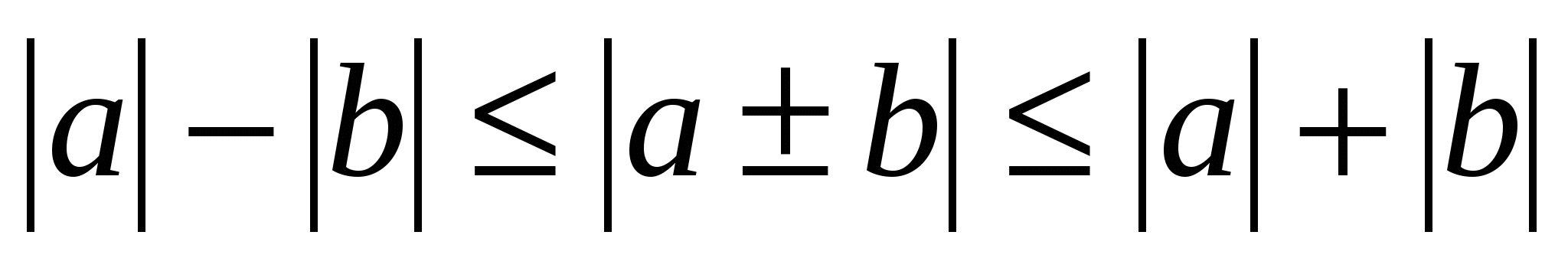 .
.
Example 1.Solve the equation: 
Solution:
Let's select a complete square on the right side of the equation, i.e. . It follows that 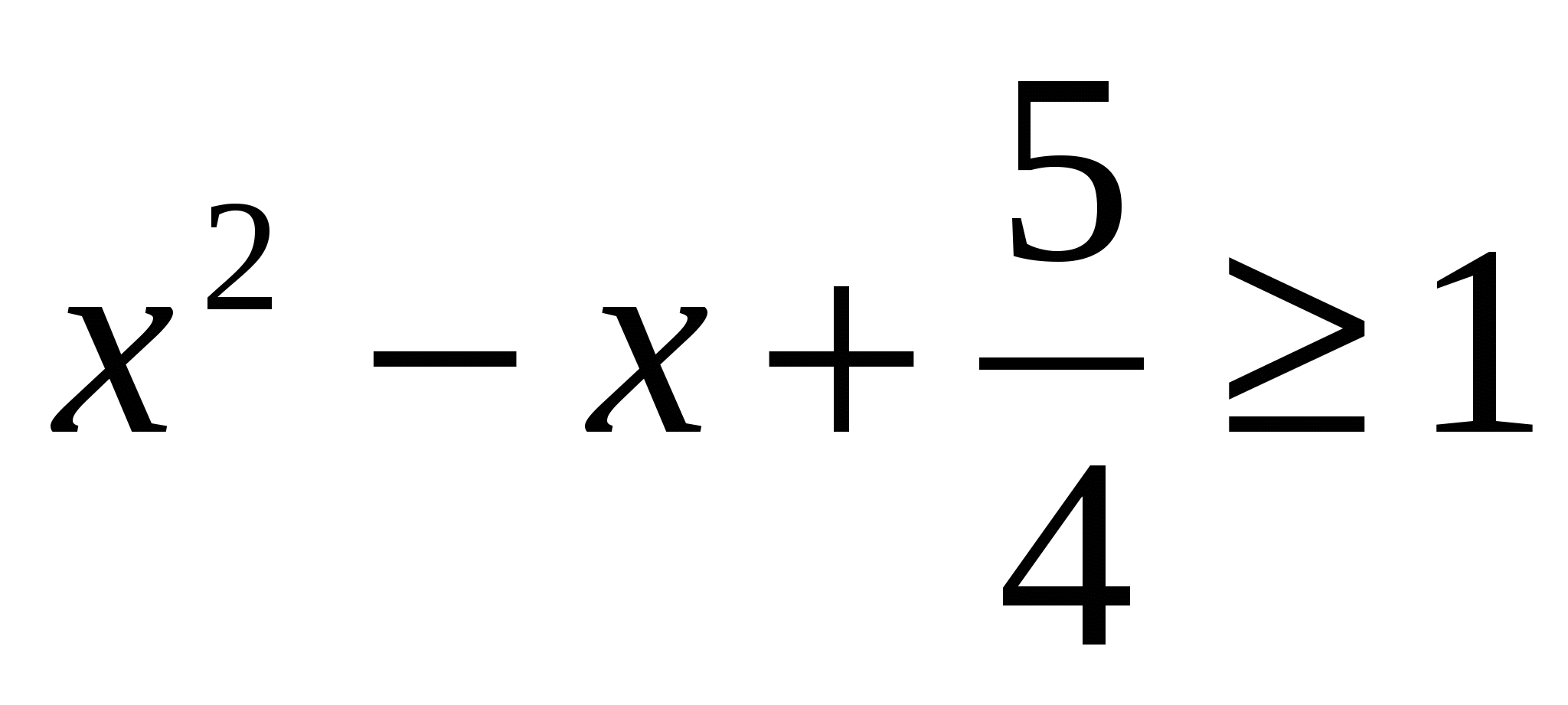 . Since in this case sinπ x ≤
1, then we obtain a system of equations
. Since in this case sinπ x ≤
1, then we obtain a system of equations 
Solving the second equation of the system, we get that x=. By substituting into the first equation we make sure that the found value of x is a solution to the system, and therefore is a solution to the original equation.
Answer: x=.
Example 2.Solve the equation: 

Solution: since However sin2 π x ≤
1. Therefore, 5+4 sin2 π x ≤
9. Thus, we obtain a system of equations: 
From here we obtain a system of equations  , from the first equation we find x=. Let's substitute it into the second equation of the system and make sure that x = is a solution to the system, and therefore is a solution to the original equation.
, from the first equation we find x=. Let's substitute it into the second equation of the system and make sure that x = is a solution to the system, and therefore is a solution to the original equation.
Answer: x=
Appendix 4.
From the proposed list of tasks, select those that can be solved using the limited function method.
1. Solve the equation x 2 -4 x=(2-cos  2. Find the number of integer solutions to the inequality x 2ctg 2
2. Find the number of integer solutions to the inequality x 2ctg 2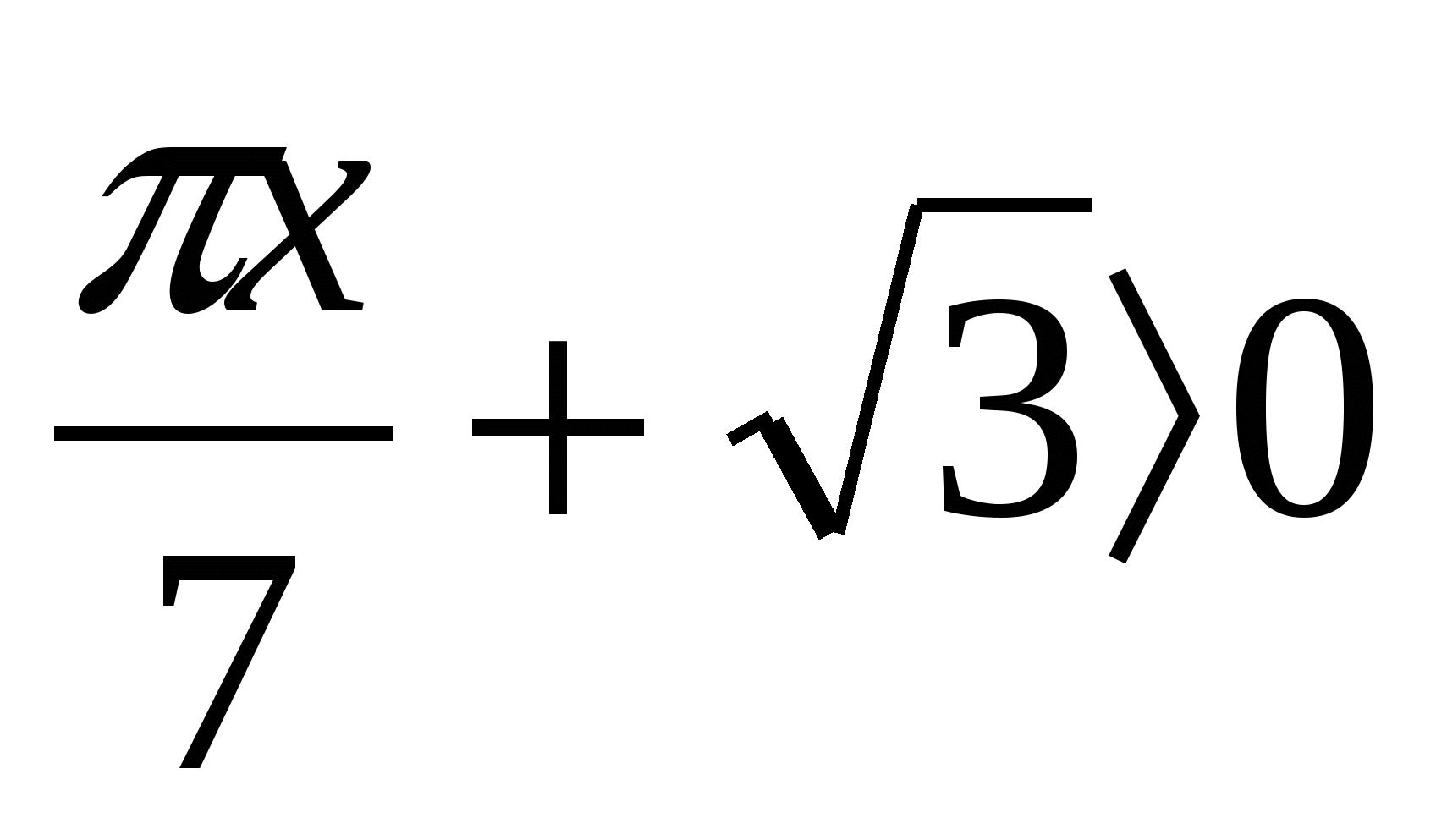 3. Solve the equation
3. Solve the equation 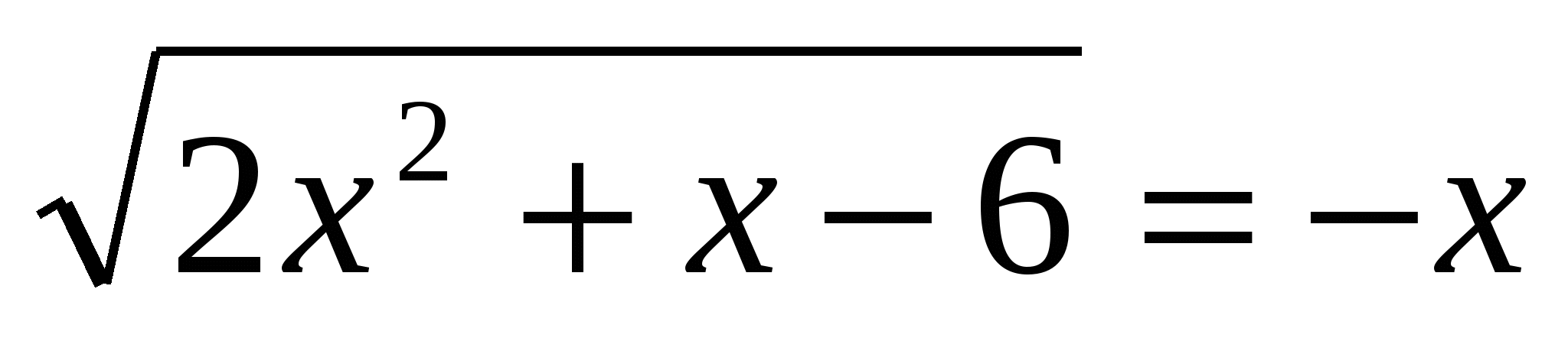 4. Solve equation 3-(5. Find the number of integer solutions to the inequality 16's 2 ≥0 that satisfy condition 3 tg 2
4. Solve equation 3-(5. Find the number of integer solutions to the inequality 16's 2 ≥0 that satisfy condition 3 tg 2  6. Solve the equation
6. Solve the equation  7. Solve the equation -25x 2 +40x-23=( cos
7. Solve the equation -25x 2 +40x-23=( cos 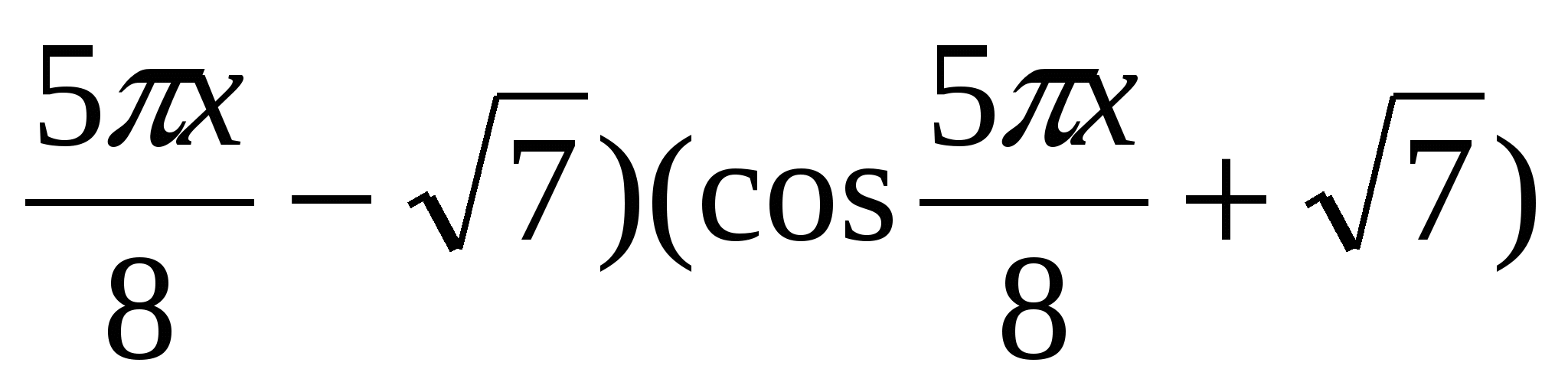 8. Find the product of the roots of the equation x
8. Find the product of the roots of the equation x  9. Solve the equation
9. Solve the equation  10. Solve equation 3- cos 2
10. Solve equation 3- cos 2 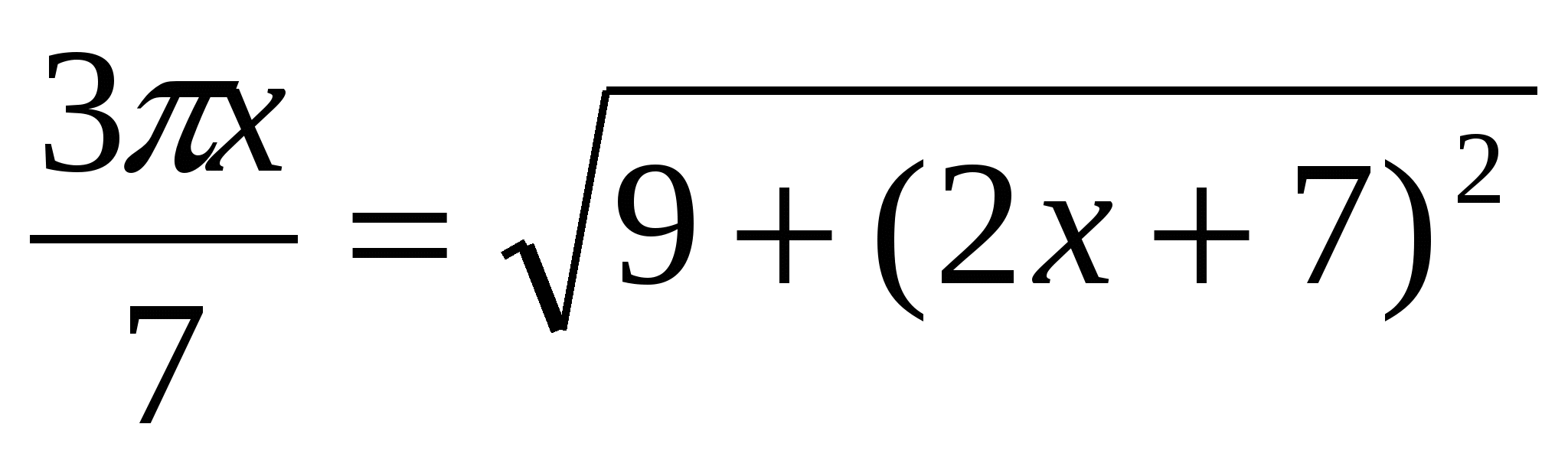
Self-test sheet.
Appendix 5.
1. Solve the equation
Solution: because , then because and then
we get a system of equations
solve the first equation, get x=, substitute this value into the second equation
2 . Solve the equation 3-
cos 2 Solution: because , then because and then
we get a system of equations
solve the second equation, get x=, substitute this value into the first equation
this means x= is a solution to the original equation. Answer: x=
3. Find the number of integer solutions to the inequality x 2
+7х-8≤0, satisfying the condition ctg 2 Solution: because and then for any admissible values of x we will find the zeros of the quadratic trinomial, using Vieta’s theorem we will solve the inequality by the method of intervals
That. we know that
integer values of x are numbers eliminated Answer: 8 integer solutions 4 . Find the number of integer solutions to the inequality 16's 2 ≥0 that satisfy condition 3 tg 2 Solution: because and then for any permissible values of x, we find the zeros of the expression, x = and x = Solve the inequality using the method of intervals
That. we know that
integer values of x are numbers eliminated Answer: 7 integer solutions
Appendix 6.
Method of using monotonicity of functions. When solving an equation like f(x)=g(x) in some cases, an effective method is that uses the monotonicity of the functions y= f(x) and y= g(x). If the function y= f(x) is continuous and increases (decreases) on the segment a≤ x ≤ b, and the function у= g(x) is continuous and decreases (increases) on the same segment, then the equation f(x)=g(x) on the segment a≤ x ≤ b can have no more than one root, which means it is necessary to either try to find the only root of the equation by selection, or show that such a root does not exist. This method is especially effective in the case when both sides of the equation f(x) = g(x) are “inconvenient” functions for joint study. Comment: If function y= f(x) increases, and the function y= g(x) decreases for a≤ x ≤ b And wherein f(a)>g(A), then the roots of the equation are among a≤ x ≤ b No.
Example: Solve the equationSolution: The range of acceptable values of the equation is x 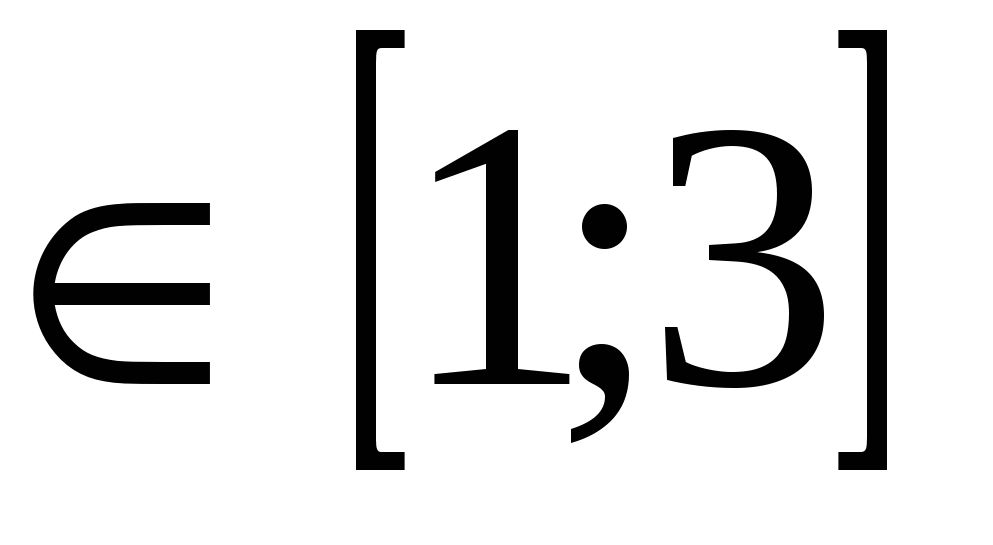 . It is easy to see that in this region the left side of the equation increases, and the right side decreases, i.e. functionf(x)=
. It is easy to see that in this region the left side of the equation increases, and the right side decreases, i.e. functionf(x)= is increasing, and the functiong(x)=
is increasing, and the functiong(x)= - decreasing. In this regard, the original equation can only have one root (if any). By selection we find this root of the equation x = 2.Answer: x=2
- decreasing. In this regard, the original equation can only have one root (if any). By selection we find this root of the equation x = 2.Answer: x=2
Method for solving functional equations.
Among the most difficult problems on the Unified State Examination are problems whose solution boils down to the consideration of functional equations of the form f(f(….f(x)…))=x or f(g(x))=f(h(x)), where f(x),g(x),h(x) are some functions and n≥ 2
Methods for solving these functional equations are based on the application of many theorems, let's consider one of them.
Theorem 1. Roots of the equation
f(x)=0 are the roots of the equation f(f(….f(x)…))=x
Example: Solve the equation x= 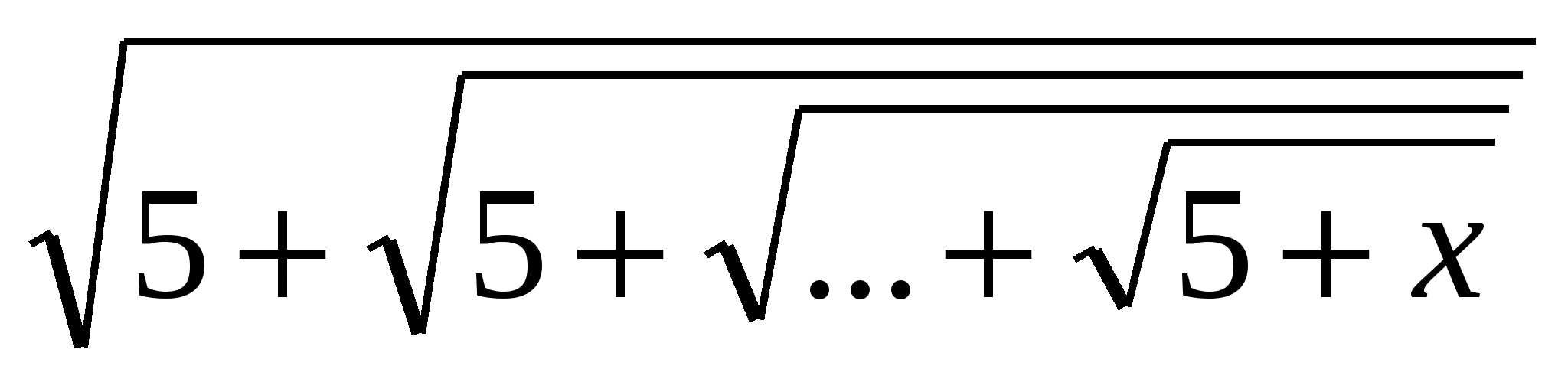 ,
where is the square root taken?nonce andn≥
1
Solution: From the problem conditions it follows that x>
0. Letf(x)=
,
where is the square root taken?nonce andn≥
1
Solution: From the problem conditions it follows that x>
0. Letf(x)=
 , then our equation can be represented as a functional
f(
f(….
f(
x)…))=
x.
Since at x>
0 functionf(x)=
increases andf(x)
>
0, then the equation x= is equivalent to the equationf(x)=
x, i.e.
=x, the positive solution of which is x=
, then our equation can be represented as a functional
f(
f(….
f(
x)…))=
x.
Since at x>
0 functionf(x)=
increases andf(x)
>
0, then the equation x= is equivalent to the equationf(x)=
x, i.e.
=x, the positive solution of which is x=  Answer: x=
Answer: x=
Galaeva Ekaterina, 11th grade student of MAOU Secondary School No. 149 in Nizhny Novgorod
The work is both applied and research in nature. For the sake of completeness of the study, the following questions were considered:
– How are the properties of a function reflected when solving equations and inequalities?
– What equations and inequalities are solved by determining the properties of the domain of definition, set of values, invariance?
– What is the solution algorithm?
– Considered tasks with parameters proposed in KIM materials in preparation for the Unified State Exam.
In her work, Ekaterina examined a wide range of tasks and systematized them according to their appearance.
Download:
Preview:
https://accounts.google.com
Slide captions:
Solve inequality Solution. The function f (x) = monotonically increases on the entire number line, and the function g (x) = monotonically decreases on the entire domain of definition. Therefore, the inequality f (x) > g (x) is satisfied if x >
Thank you for your attention!
Preview:
To use presentation previews, create a Google account and log in to it: https://accounts.google.com
Slide captions:
Application of the properties of a function when solving equations and inequalities Completed the work: Galaeva Ekaterina MBOU Secondary School No. 149 of the Moskovsky District Pupils of class 11 “A” Scientific supervisor: Fadeeva I. A. Mathematics teacher
Main directions: Studying the properties of a function: monotonicity, boundedness, domain of definition and invariance Learn the basic statements that are most often used when solving equations, inequalities and systems Solving problems from CMM materials to prepare for the Unified State Exam
Monotonicity A function increases if a larger value of the argument corresponds to a larger value of the function. A function decreases if a larger value of the argument corresponds to a smaller value of the function. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Statement 1. If the function y = f (x) is monotonic, then the equation f (x) = c has at most one root. x =2 f(x) = - monotonically decreasing, which means there are no other solutions. Answer: x =2
Statement 2. If the function y = f (x) increases monotonically, and the function y = g (x) decreases monotonically, then the equation f (x) = g (x) has at most one root. 2 - x = log (x +11) + 1 g (x) = 2 - x is monotonically decreasing, and the function f (x) = log (x + 11) + 1 is monotonically increasing on the domain of definition, which means the equation f (x ) = g (x) has at most one root. By selection we determine that x = -1. The above statement justifies the uniqueness of the solution.
a) f (x) ≤ g (x) if and only if x ϵ (- ∞ ; x 0 ]; b) f (x) ≥ g (x) if and only if x ϵ [x 0 ; +∞). The visual meaning of this statement is obvious Statement 3. If the function y = f (x) monotonically increases on the entire number line, the function y = g (x) monotonically decreases on the entire number line and f (x 0) = g (x 0), then the following statements are true:
Solve inequality Solution. The function f (x) = monotonically increases on the entire number line, and the function g (x) = monotonically decreases on the entire domain of definition. Therefore, the inequality f (x) > g (x) is satisfied if x > 2. Let us add the domain of definition of the inequality. Thus, we obtain the system Answer: (2; 5).
Statement 4. If the function y = f (x) increases monotonically, then the equations f (x) = x and f (f (x)) = x have the same set of roots, regardless of the number of embeddings. Consequence. If n is a natural number, and the function y = f (x) increases monotonically, then the equations f (x) = x and n times have the same set of roots.
Solve the equation. Answer: Solution. For x ≥1, the right side of the equation is not less than 1, and the left side is less than 1. Therefore, if the equation has roots, then any of them is less than 1. For x ≤0, the right side of the equation is non-positive, and the left side is positive, due to the fact that . Thus, any root of this equation belongs to the interval (0; 1). Multiplying both sides of this equation by x and dividing the numerator and denominator of the left side by x, we get
From = . Denoting by t, where t 0, we obtain the equation = t. Let us consider a function f (t)= 1+ that increases on its domain of definition. The resulting equation can be written in the form f (f (f (f (t))))= t, and by the corollary of Statement 4, it has the same set of solutions as the equation f (t)= t, i.e. equation 1 + = t, whence. The only positive root of this square relative equation is. This means where, i.e. , or. Answer:
Statement 1. If max f (x) = с and min g (x) = с, then the equation f (x) = g (x) has the same set of solutions as the system Boundedness The maximum value of the left side is 1 and the minimum value the right side of 1, which means that the solution to the equation is reduced to the system of equations: , from the second equation we find a possible candidate x=0, and we are convinced that it is a solution to the first equation. Answer: x=1 .
Solve the equation Solution. Since sin3x≤1 and cos4x≤1, the left side of this equation does not exceed 7. It can be equal to 7 if and only if where k , n ϵ Z . It remains to establish whether there are integers k and n for which the latter system has solutions. Answer: Z
In problems with unknowns x and parameter a, the domain of definition is understood as the set of all ordered pairs of numbers (x; a), each of which is such that after substituting the corresponding values of x and a into all relations included in the problem, they will be determined. Example 1. For each value of parameter a, solve the inequality Solution. Let us find the domain of definition of this inequality. From which it is clear that the system has no solutions. This means that the domain of definition of the inequality does not contain any pairs of numbers x and a, and therefore the inequality has no solutions. Scope Answer:
Invariance, i.e. the invariance of an equation or inequality with respect to the replacement of a variable by some algebraic expression for this variable. The simplest example of invariance is parity: if is an even function, then the equation is invariant under the change of x and – x, since = 0. Invariance
Find the roots of the equation. Solution. Note that the pair is invariant under substitution. Substituting in the equality, we get. By multiplying both sides of this equality by 2 and subtracting the equality term by term from the resulting equality, we find 3, whence. Now it remains to solve the equation, from where the roots of the equation are numbers. Answer: .
Find all values of a for each of which the equation has more than three different solutions. Solving problems with the parameter Monotonicity property
|x|= positive X= |x|= For two roots to exist, the numerator must be positive. Therefore, When the roots of the first and second equations coincide, which does not meet the requirement of the condition: the presence of more than three roots. Answer: .
Find all values of a for each of which the equation has two roots. Let's transform the equation to the form And consider the function f(x) = defined and continuous on the entire number line. The graph of this function is a broken line consisting of straight and ray segments, each link of which is part of a straight line of the form y= kt+l. f(x)= For any value, the disclosure of the modulus of the first expression k does not exceed 8, therefore the increase and decrease of the function f(x) will depend on the disclosure of the second module. At x f(x) will decrease, and at x it will increase. That is, at x=3 the function will take on the greatest value. In order for an equation to have two roots, it is necessary that f(3) Monotonicity property
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Answer: a
Find all values of the parameter a, for each of which the inequality holds for any real value of x. Let us rewrite the inequality in the form, introduce a new variable t = and consider the function f (t) =, defined and continuous on the entire number line. The graph of this function is a broken line consisting of line segments and rays, each link of which is part of a line of the form, where
Since, then t ϵ [-1; 1]. Due to the monotonic decrease of the function y = f (t), it is enough to check the left edge of this segment. Z. A is true. This means that it is possible only if the numbers u and v are of the same sign or one of them is equal to zero. , = () () 0. Having factorized the quadratic trinomials, we obtain the inequality (, from which we find that a ϵ (-∞; -1] U (2) U [ 4; +∞). Answer: (-∞; - 1] U (2) U )
