7.1. Definition of cross product
Three non-coplanar vectors a, b and c, taken in the indicated order, form a right-handed triplet if, from the end of the third vector c, the shortest turn from the first vector a to the second vector b is seen to be counterclockwise, and a left-handed triplet if clockwise (see Fig. . 16).
The vector product of vector a and vector b is called vector c, which:
1. Perpendicular to vectors a and b, i.e. c ^ a and c ^ b ;
2. Has a length numerically equal to the area of a parallelogram constructed on vectors a andb as on the sides (see Fig. 17), i.e.
3. Vectors a, b and c form a right-handed triple.


The cross product is denoted a x b or [a,b]. The following relations between the unit vectors i directly follow from the definition of the vector product, j And k(see Fig. 18):
i x j = k, j x k = i, k x i = j.
Let us prove, for example, that i xj =k.
1) k ^ i, k ^ j ;
2) |k |=1, but | i x j| = |i | |J | sin(90°)=1;
3) vectors i, j and k form a right triple (see Fig. 16).
7.2. Properties of a cross product
1. When rearranging the factors, the vector product changes sign, i.e. and xb =(b xa) (see Fig. 19).
Vectors a xb and b xa are collinear, have the same modules (the area of the parallelogram remains unchanged), but are oppositely directed (triples a, b, a xb and a, b, b x a of opposite orientation). That is axb = -(b xa).
2. The vector product has a combining property with respect to the scalar factor, i.e. l (a xb) = (l a) x b = a x (l b).

Let l >0. Vector l (a xb) is perpendicular to vectors a and b. Vector ( l a)x b is also perpendicular to vectors a and b(vectors a, l but lie in the same plane). This means that the vectors l(a xb) and ( l a)x b collinear. It is obvious that their directions coincide. They have the same length:
That's why l(a xb)= l a xb. It is proved in a similar way for l<0.
3. Two non-zero vectors a and b are collinear if and only if their vector product is equal to the zero vector, i.e. a ||b<=>and xb =0.

In particular, i *i =j *j =k *k =0 .
4. The vector product has the distribution property:
(a+b) xc = a xc + b xs.
We will accept without proof.
7.3. Expressing the cross product in terms of coordinates
We will use the cross product table of vectors i, j and k:

if the direction of the shortest path from the first vector to the second coincides with the direction of the arrow, then the product is equal to the third vector; if it does not coincide, the third vector is taken with a minus sign.
Let two vectors a =a x i +a y be given j+a z k and b =b x i+b y j+b z k. Let's find the vector product of these vectors by multiplying them as polynomials (according to the properties of the vector product):

![]()
The resulting formula can be written even more briefly:

since the right side of equality (7.1) corresponds to the expansion of the third-order determinant in terms of the elements of the first row. Equality (7.2) is easy to remember.
7.4. Some applications of cross product
Establishing collinearity of vectors

Finding the area of a parallelogram and a triangle
According to the definition of the vector product of vectors A and b |a xb | =|a | * |b |sin g, i.e. S pairs = |a x b |. And, therefore, D S =1/2|a x b |.
Determination of the moment of force about a point
Let a force be applied at point A F =AB let it go ABOUT- some point in space (see Fig. 20).

It is known from physics that moment of force F relative to the point ABOUT called a vector M, which passes through the point ABOUT And:
1) perpendicular to the plane passing through the points O, A, B;
2) numerically equal to the product of force per arm
3) forms a right triple with vectors OA and A B.
Therefore, M = OA x F.
Finding linear rotation speed
Speed v point M of a rigid body rotating with angular velocity w around a fixed axis, is determined by Euler’s formula v =w xr, where r =OM, where O is some fixed point of the axis (see Fig. 21).

Before giving the concept of a vector product, let us turn to the question of the orientation of an ordered triple of vectors a →, b →, c → in three-dimensional space.
To begin with, let’s set aside the vectors a → , b → , c → from one point. The orientation of the triple a → , b → , c → can be right or left, depending on the direction of the vector c → itself. The type of triple a → , b → , c → will be determined from the direction in which the shortest turn is made from vector a → to b → from the end of vector c → .
If the shortest turn is carried out counterclockwise, then the triple of vectors a → , b → , c → is called right, if clockwise – left.
Next, take two non-collinear vectors a → and b →. Let us then plot the vectors A B → = a → and A C → = b → from point A. Let's construct a vector A D → = c →, which is simultaneously perpendicular to both A B → and A C →. Thus, when constructing the vector itself A D → = c →, we can do two things, giving it either one direction or the opposite (see illustration).

An ordered triple of vectors a → , b → , c → can be, as we found out, right or left depending on the direction of the vector.
From the above we can introduce the definition of a vector product. This definition is given for two vectors defined in a rectangular coordinate system of three-dimensional space.
Definition 1
The vector product of two vectors a → and b → we will call such a vector defined in a rectangular coordinate system of three-dimensional space such that:
- if the vectors a → and b → are collinear, it will be zero;
- it will be perpendicular to both vector a → and vector b → i.e. ∠ a → c → = ∠ b → c → = π 2 ;
- its length is determined by the formula: c → = a → · b → · sin ∠ a → , b → ;
- the triple of vectors a → , b → , c → has the same orientation as the given coordinate system.
The vector product of vectors a → and b → has the following notation: a → × b →.
Coordinates of the vector product
Since any vector has certain coordinates in the coordinate system, we can introduce a second definition of a vector product, which will allow us to find its coordinates using the given coordinates of the vectors.
Definition 2
In a rectangular coordinate system of three-dimensional space vector product of two vectors a → = (a x ; a y ; a z) and b → = (b x ; b y ; b z) is called a vector c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , where i → , j → , k → are coordinate vectors.
The vector product can be represented as the determinant of a third-order square matrix, where the first row contains the vector vectors i → , j → , k → , the second row contains the coordinates of the vector a → , and the third row contains the coordinates of the vector b → in a given rectangular coordinate system, this is the determinant of the matrix looks like this: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Expanding this determinant into the elements of the first row, we obtain the equality: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Properties of a cross product
It is known that the vector product in coordinates is represented as the determinant of the matrix c → = a → × b → = i → j → k → a x a y a z b x b y b z , then on the basis properties of the matrix determinant the following are displayed properties of a vector product:
- anticommutativity a → × b → = - b → × a → ;
- distributivity a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → or a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- associativity λ a → × b → = λ a → × b → or a → × (λ b →) = λ a → × b →, where λ is an arbitrary real number.
These properties have simple proofs.
As an example, we can prove the anticommutative property of a vector product.
Proof of anticommutativity
By definition, a → × b → = i → j → k → a x a y a z b x b y b z and b → × a → = i → j → k → b x b y b z a x a y a z . And if two rows of the matrix are swapped, then the value of the determinant of the matrix should change to the opposite, therefore, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , which and proves that the vector product is anticommutative.
Vector product - examples and solutions
In most cases, there are three types of problems.
In problems of the first type, the lengths of two vectors and the angle between them are usually given, and you need to find the length of the vector product. In this case, use the following formula c → = a → · b → · sin ∠ a → , b → .
Example 1
Find the length of the vector product of vectors a → and b → if you know a → = 3, b → = 5, ∠ a →, b → = π 4.
Solution
By determining the length of the vector product of vectors a → and b →, we solve this problem: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Answer: 15 2 2 .
Problems of the second type have a connection with the coordinates of vectors, in them the vector product, its length, etc. are searched through the known coordinates of given vectors a → = (a x; a y; a z) And b → = (b x ; b y ; b z) .
For this type of problem, you can solve a lot of task options. For example, not the coordinates of the vectors a → and b → can be specified, but their expansions into coordinate vectors of the form b → = b x · i → + b y · j → + b z · k → and c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, or vectors a → and b → can be specified by the coordinates of their start and end points.
Consider the following examples.
Example 2
In a rectangular coordinate system, two vectors are given: a → = (2; 1; - 3), b → = (0; - 1; 1). Find their cross product.
Solution
By the second definition, we find the vector product of two vectors in given coordinates: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + (a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .
If we write the vector product through the determinant of the matrix, then the solution to this example looks like this: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .
Answer: a → × b → = - 2 i → - 2 j → - 2 k → .
Example 3
Find the length of the vector product of vectors i → - j → and i → + j → + k →, where i →, j →, k → are the unit vectors of the rectangular Cartesian coordinate system.
Solution
First, let's find the coordinates of a given vector product i → - j → × i → + j → + k → in a given rectangular coordinate system.
It is known that the vectors i → - j → and i → + j → + k → have coordinates (1; - 1; 0) and (1; 1; 1), respectively. Let's find the length of the vector product using the determinant of the matrix, then we have i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Therefore, the vector product i → - j → × i → + j → + k → has coordinates (- 1 ; - 1 ; 2) in the given coordinate system.
We find the length of the vector product using the formula (see the section on finding the length of a vector): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Answer: i → - j → × i → + j → + k → = 6 . .
Example 4
In a rectangular Cartesian coordinate system, the coordinates of three points A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) are given. Find some vector perpendicular to A B → and A C → at the same time.
Solution
Vectors A B → and A C → have the following coordinates (- 1 ; 2 ; 2) and (0 ; 4 ; 1) respectively. Having found the vector product of the vectors A B → and A C →, it is obvious that it is a perpendicular vector by definition to both A B → and A C →, that is, it is a solution to our problem. Let's find it A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Answer: - 6 i → + j → - 4 k → . - one of the perpendicular vectors.
Problems of the third type are focused on using the properties of the vector product of vectors. After applying which, we will obtain a solution to the given problem.
Example 5
Vectors a → and b → are perpendicular and their lengths are 3 and 4, respectively. Find the length of the vector product 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Solution
By the distributive property of a vector product, we can write 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
By the property of associativity, we take the numerical coefficients out of the sign of the vector products in the last expression: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
The vector products a → × a → and b → × b → are equal to 0, since a → × a → = a → · a → · sin 0 = 0 and b → × b → = b → · b → · sin 0 = 0, then 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
From the anticommutativity of the vector product it follows - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Using the properties of the vector product, we obtain the equality 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .
By condition, the vectors a → and b → are perpendicular, that is, the angle between them is equal to π 2. Now all that remains is to substitute the found values into the appropriate formulas: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Answer: 3 a → - b → × a → - 2 b → = 60.
The length of the vector product of vectors by definition is equal to a → × b → = a → · b → · sin ∠ a → , b → . Since it is already known (from the school course) that the area of a triangle is equal to half the product of the lengths of its two sides multiplied by the sine of the angle between these sides. Consequently, the length of the vector product is equal to the area of the parallelogram - a doubled triangle, namely the product of the sides in the form of vectors a → and b →, laid down from one point, by the sine of the angle between them sin ∠ a →, b →.
This is the geometric meaning of a vector product.

Physical meaning of the vector product
In mechanics, one of the branches of physics, thanks to the vector product, you can determine the moment of a force relative to a point in space.
Definition 3
By the moment of force F → applied to point B, relative to point A, we will understand the following vector product A B → × F →.
If you notice an error in the text, please highlight it and press Ctrl+Enter
Angle between vectors
In order for us to introduce the concept of the vector product of two vectors, we must first understand such a concept as the angle between these vectors.
Let us be given two vectors $\overline(α)$ and $\overline(β)$. Let us take some point $O$ in space and plot the vectors $\overline(α)=\overline(OA)$ and $\overline(β)=\overline(OB)$ from it, then the angle $AOB$ will be called the angle between these vectors (Fig. 1).
Notation: $∠(\overline(α),\overline(β))$
The concept of a vector product of vectors and the formula for finding
Definition 1
The vector product of two vectors is a vector perpendicular to both given vectors, and its length will be equal to the product of the lengths of these vectors with the sine of the angle between these vectors, and also this vector with two initial ones has the same orientation as the Cartesian coordinate system.
Notation: $\overline(α)х\overline(β)$.
Mathematically it looks like this:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ and $(\overline(i),\overline(j),\overline(k))$ are the same oriented (Fig. 2)
Obviously, the outer product of vectors will equal the zero vector in two cases:
- If the length of one or both vectors is zero.
- If the angle between these vectors is equal to $180^\circ$ or $0^\circ$ (since in this case the sine is zero).
To clearly see how the vector product of vectors is found, consider the following examples of solutions.
Example 1
Find the length of the vector $\overline(δ)$, which will be the result of the vector product of vectors, with coordinates $\overline(α)=(0,4,0)$ and $\overline(β)=(3,0,0 )$.
Solution.
Let's depict these vectors in Cartesian coordinate space (Fig. 3):
Figure 3. Vectors in Cartesian coordinate space. Author24 - online exchange of student work
We see that these vectors lie on the $Ox$ and $Oy$ axes, respectively. Therefore, the angle between them will be $90^\circ$. Let's find the lengths of these vectors:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Then, by Definition 1, we obtain the module $|\overline(δ)|$
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Answer: $12$.
Calculating the cross product from vector coordinates
Definition 1 immediately implies a method for finding the vector product for two vectors. Since a vector, in addition to its value, also has a direction, it is impossible to find it only using a scalar quantity. But besides this, there is also a way to find the vectors given to us using the coordinates.
Let us be given vectors $\overline(α)$ and $\overline(β)$, which will have coordinates $(α_1,α_2,α_3)$ and $(β_1,β_2,β_3)$, respectively. Then the vector of the cross product (namely its coordinates) can be found using the following formula:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
Otherwise, expanding the determinant, we obtain the following coordinates
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Example 2
Find the vector of the vector product of collinear vectors $\overline(α)$ and $\overline(β)$ with coordinates $(0,3,3)$ and $(-1,2,6)$.
Solution.
Let's use the formula given above. We get
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k )=(12,-3,3)$
Answer: $(12,-3,3)$.
Properties of the vector product of vectors
For arbitrary mixed three vectors $\overline(α)$, $\overline(β)$ and $\overline(γ)$, as well as $r∈R$, the following properties hold:
Example 3
Find the area of a parallelogram whose vertices have coordinates $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ and $(3,8,0)$.
Solution.
First, let's depict this parallelogram in coordinate space (Fig. 5):
Figure 5. Parallelogram in coordinate space. Author24 - online exchange of student work
We see that the two sides of this parallelogram are constructed using collinear vectors with coordinates $\overline(α)=(3,0,0)$ and $\overline(β)=(0,8,0)$. Using the fourth property, we get:
$S=|\overline(α)х\overline(β)|$
Let's find the vector $\overline(α)х\overline(β)$:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Hence
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
Obviously, in the case of a vector product, the order in which the vectors are taken matters, moreover,
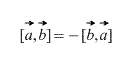
Also, directly from the definition it follows that for any scalar factor k (number) the following is true:
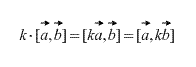
The cross product of collinear vectors is equal to the zero vector. Moreover, the cross product of two vectors is zero if and only if they are collinear. (In case one of them is a zero vector, it is necessary to remember that a zero vector is collinear to any vector by definition).

The vector product has distributive property, that is

Expressing the vector product through the coordinates of vectors.
Let two vectors be given

(how to find the coordinates of a vector from the coordinates of its beginning and end - see the article Dot product of vectors, item Alternative definition of the dot product, or calculating the dot product of two vectors specified by their coordinates.)

Why do you need a vector product?
There are many ways to use the cross product, for example, as written above, by calculating the cross product of two vectors you can find out whether they are collinear.

Or it can be used as a way to calculate the area of a parallelogram constructed from these vectors. Based on the definition, the length of the resulting vector is the area of the given parallelogram.
There are also a huge number of applications in electricity and magnetism.Online vector product calculator.
To find the scalar product of two vectors using this calculator, you need to enter the coordinates of the first vector in the first line in order, and the second in the second line. The coordinates of vectors can be calculated from the coordinates of their beginning and end (see article Dot product of vectors, item An alternative definition of the dot product, or calculating the dot product of two vectors given by their coordinates.)
Vector artwork is a pseudovector perpendicular to a plane constructed from two factors, which is the result of the binary operation “vector multiplication” over vectors in three-dimensional Euclidean space. The vector product does not have the properties of commutativity and associativity (it is anticommutative) and, unlike the scalar product of vectors, is a vector. Widely used in many engineering and physics applications. For example, angular momentum and Lorentz force are written mathematically as a vector product. The cross product is useful for "measuring" the perpendicularity of vectors - the modulus of the cross product of two vectors is equal to the product of their moduli if they are perpendicular, and decreases to zero if the vectors are parallel or antiparallel.
The vector product can be defined in different ways, and theoretically, in a space of any dimension n, one can calculate the product of n-1 vectors, thereby obtaining a single vector perpendicular to them all. But if the product is limited to non-trivial binary products with vector results, then the traditional vector product is defined only in three-dimensional and seven-dimensional spaces. The result of a vector product, like a scalar product, depends on the metric of Euclidean space.
Unlike the formula for calculating the scalar product vectors from coordinates in a three-dimensional rectangular coordinate system, the formula for the cross product depends on the orientation of the rectangular coordinate system, or, in other words, its “chirality”.
Definition:
The vector product of vector a and vector b in space R3 is a vector c that satisfies the following requirements:
the length of vector c is equal to the product of the lengths of vectors a and b and the sine of the angle φ between them:
|c|=|a||b|sin φ;
vector c is orthogonal to each of vectors a and b;
vector c is directed so that the triple of vectors abc is right-handed;
in the case of the space R7, the associativity of the triple of vectors a, b, c is required.
Designation:
c===a × b

Rice. 1. The area of a parallelogram is equal to the modulus of the vector product
Geometric properties of a cross product:
A necessary and sufficient condition for the collinearity of two nonzero vectors is that their vector product is equal to zero.
Cross Product Module equals area S parallelogram constructed on vectors reduced to a common origin a And b(see Fig. 1).
If e- unit vector orthogonal to the vectors a And b and chosen so that three a,b,e- right, and S is the area of the parallelogram constructed on them (reduced to a common origin), then the formula for the vector product is valid:
=S e
Fig.2. Volume of a parallelepiped using the vector and scalar product of vectors; the dotted lines show the projections of vector c onto a × b and vector a onto b × c, the first step is to find the scalar products
If c- some vector, π
- any plane containing this vector, e- unit vector lying in the plane π
and orthogonal to c,g- unit vector orthogonal to the plane π
and directed so that the triple of vectors ecg is right, then for any lying in the plane π
vector a the formula is correct:
=Pr e a |c|g
where Pr e a is the projection of vector e onto a
|c|-modulus of vector c
When using vector and scalar products, you can calculate the volume of a parallelepiped built on vectors reduced to a common origin a, b And c. Such a product of three vectors is called mixed.
V=|a (b×c)|
The figure shows that this volume can be found in two ways: the geometric result is preserved even when the “scalar” and “vector” products are swapped:
V=a×b c=a b×c
The magnitude of the cross product depends on the sine of the angle between the original vectors, so the cross product can be perceived as the degree of “perpendicularity” of the vectors, just as the scalar product can be seen as the degree of “parallelism”. The vector product of two unit vectors is equal to 1 (unit vector) if the original vectors are perpendicular, and equal to 0 (zero vector) if the vectors are parallel or antiparallel.
Expression for the cross product in Cartesian coordinates
If two vectors a And b defined by their rectangular Cartesian coordinates, or more precisely, represented in an orthonormal basis
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
and the coordinate system is right-handed, then their vector product has the form
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
To remember this formula:
i =∑ε ijk a j b k
Where ε ijk- symbol of Levi-Civita.
