Online method of uncertain coefficients with detailed solution. Uncertain coefficient method

The method is applicable for minimizing logical algebra functions of any number of variables.

Let's consider the case of three variables. A Boolean function in DNF can be represented in the form of all kinds of conjunctive terms that can be included in DNF:

where kО(0,1) are coefficients. The method consists in selecting coefficients in such a way that the resulting DNF is minimal.

If we now set all possible values of the variables from 000 to 111, we get 2 n (2 3 =8) equations for determining the coefficients k:

Considering the sets for which the function takes a zero value, determine the coefficients that are equal to 0 and cross them out from the equations whose right side contains 1. Of the remaining coefficients in each equation, one coefficient is equated to one, which determines the conjunction of the lowest rank. The remaining coefficients are equal to 0. So, the unit coefficients k determine the appropriate minimum form.

Example. Minimize a given function

if the values are known: ; ; ; ; ; ; ; .

Solution.

After crossing out the zero coefficients we get:

=1;

=1.

Let us equate to one the coefficient corresponding to the conjunction of the lowest rank and turning the last four equations to 1, and in the first equation it is advisable to equate the coefficient to 1. The remaining coefficients are set to 0.

Answer: type of minimized function.

It should be noted that the method of indefinite coefficients is effective when the number of variables is small and does not exceed 5-6.

Multidimensional cube

Let's consider a graphical representation of a function in the form of a multidimensional cube. Every peak n-dimensional cube can be put in correspondence with the constituent of the unit.

The subset of marked vertices is a mapping onto n-dimensional cube of a Boolean function from n variables in SDNF.

To display the function from n variables presented in any DNF, it is necessary to establish a correspondence between its miniterms and elements n-dimensional cube.

A miniterm of (n-1) rank can be considered as the result of gluing together two miniterms n-th rank, i.e.

On n-dimensional cube this corresponds to replacing two vertices that differ only in coordinate values x i, connecting these vertices with an edge (an edge is said to cover the vertices incident to it).

Thus, miniterms ( n The -1)th order corresponds to the edges of an n-dimensional cube.

Similarly, the correspondence of miniterms ( n-2)th order faces n-dimensional cube, each of which covers four vertices (and four edges).

Elements n-dimensional cube, characterized by S measurements are called S-cubes

So vertices are 0-cubes, edges are 1-cubes, faces are 2-cubes, etc.

To summarize, we can say that the miniterm ( n-S) rank in DNF for the function n variables displayed S-a cube, each S-cube covers all those cubes of lower dimension that are connected only to its vertices.

Example. In Fig. given the mapping

Here the miniterms and correspond to 1-cubes ( S=3-2=1), and miniterm x 3 displayed to 2-cubes ( S=3-1=2).

So, any DNF is mapped to n-dimensional cube in totality S-cubes that cover all vertices corresponding to the constituent units (0-cube).

Constituents. For variables x 1,x 2,…x n expression is called the constituent of the unit, and - a constituent of zero (means either or).

This constituent of one (zero) turns into one (zero) only with one corresponding set of variable values, which is obtained if all variables are taken equal to one (zero), and their negations equal to zero (one).

For example: the constituent one corresponds to the set (1011), and the constituent zero - set (1001).

Since SD(K)NF is a disjunction (conjunction) of the constituents of one (zero), it can be argued that the Boolean function it represents f(x 1 ,x 2 ,…,x n) turns to one (zero) only for sets of variable values x 1 ,x 2 ,…,x n, corresponding to these copstitutes. On other sets this function turns to 0 (one).

The opposite statement is also true, on which it is based way of representing any Boolean function specified by the table.

To do this, it is necessary to write disjunctions (conjunctions) of the constituents of one (zero), corresponding to sets of values of variables on which the function takes a value equal to one (zero).

For example, a function given by a table

correspond

The resulting expressions can be converted to another form based on the properties of the algebra of logic.

The converse statement is also true: if some collection S-cubes covers the set of all vertices corresponding to unit values of the function, then the disjunction corresponding to these S-cubes of miniterms is the expression of this function in DNF.

They say that such a collection S-cubes (or their corresponding miniterms) forms a covering of the function. The desire for a minimal form is intuitively understood as the search for such a covering, the number S-of which there would be fewer cubes, and their dimensions S- more. The coverage corresponding to the minimum form is called the minimum coverage.

For example, for the function at= the coating conforms to a non-minimal shape.

Greetings to all, dear friends!

Well, congratulations! We have safely reached the main material in the integration of rational fractions - method of uncertain coefficients. Great and mighty.) What is his majesty and power? And it lies in its versatility. It makes sense to check it out, right? I warn you that there will be several lessons on this topic. Because the topic is very long, and the material is extremely important.)

I’ll say right away that in today’s lesson (and subsequent ones too) we will deal not so much with integration, but... solving systems of linear equations! Yes Yes! So those who have problems with systems, repeat the matrices, determinants and Cramer's method. And for those comrades who are having trouble with matrices, I urge you, at worst, to refresh your memory of at least the “school” methods of solving systems - the substitution method and the term-by-term addition/subtraction method.

To begin our acquaintance, let's rewind the film a little back. Let's briefly return to previous lessons and analyze all those fractions that we integrated before. Directly, without any method of indefinite coefficients! Here they are, these fractions. I sorted them into three groups.

Group 1

In the denominator - linear function either on its own or to a degree. In a word, the denominator is the product identical brackets of the form (Ha).

For example:

(x+4) 1 = (x+4)

(x-10) 2 = (x-10)(x-10)

(2x+5) 3 = (2x+5)(2x+5)(2x+5)

And so on. By the way, don't let the parentheses confuse you (4x+5) or (2x+5) 3 with coefficient k inside. These are still, at their core, brackets of the form (Ha). Because this is the most k from such brackets you can always take it outside.

Like this:

That's all.) And it doesn't matter what exactly is in the numerator - just dx or some kind of polynomial. We always expanded the numerator in powers of the bracket (x-a), turned the large fraction into the sum of small ones, placed (where necessary) a parenthesis under the differential and integrated.

Group 2

What do these fractions have in common?

And the common thing is that in all denominators there is quadratic trinomialax 2 + bx+ c. But not just, namely in a single copy. And it doesn’t matter here whether his discriminant is positive or negative.

Such fractions were always integrated in one of two ways - either by expanding the numerator into powers of the denominator, or by isolating the perfect square in the denominator and then replacing the variable. It all depends on the specific integrand.

Group 3

These were the worst fractions to integrate. The denominator contains an indecomposable quadratic trinomial, and even to the degree n. But, again, in a single copy. Because, besides the trinomial, there are no other factors in the denominator. Such fractions were integrated over . Either directly, or reduced to it after isolating the perfect square in the denominator and subsequent replacement of the variable.

However, unfortunately, the entire rich variety of rational fractions is not limited to just these three groups considered.

But what if the denominator is different brackets? For example, something like:

(x-1)(x+1)(x+2)

Or at the same time a parenthesis (Ha) and a quadratic trinomial, something like (x-10)(x 2 -2x+17)? And in other similar cases? It is precisely in such cases that it comes to the rescue method of uncertain coefficients!

I’ll say right away: for now we will only work with correct in fractions. Those whose numerator degree is strictly less than the denominator degree. How to deal with improper fractions is described in detail in Fractions. It is necessary to select the whole part (polynomial). By dividing the numerator by the denominator with a corner or by decomposing the numerator - as you wish. And even the example is analyzed. And you will somehow integrate the polynomial. Not small already.) But we’ll also solve examples for improper fractions!

And now we begin to get acquainted. Unlike most textbooks on higher mathematics, we will not begin our acquaintance with a dry and heavy theory about the fundamental theorem of algebra, Bezout’s theorem, about the decomposition of a rational fraction into the sum of the simplest (more on these fractions later) and other tediousness, but we will start with a simple example .

For example, we need to find the following indefinite integral:

First look at the integrand. The denominator is the product of three brackets:

(x-1)(x+3)(x+5)

And all the brackets different. Therefore, our old technology with the expansion of the numerator by powers of the denominator no longer works this time: which parenthesis should be highlighted in the numerator? (x-1)? (x+3)? It’s not clear... Selecting a complete square in the denominator is also not a good idea: there’s a polynomial there third degrees (if you multiply all the brackets). What to do?

When looking at our fraction, a completely natural desire arises... Downright irresistible! From our large fraction, which uncomfortable integrate, somehow make three small ones. At least like this:

Why should you look for this particular species? And all because in this form our initial fraction is already convenient for integration! Let's sum up the denominator of each small fraction and - forward.)

Is it even possible to obtain such a decomposition? Good news! The corresponding theorem in mathematics states – yes, you can! Such a decomposition exists and is unique.

But there is one problem: the coefficients A, IN And WITH We Bye we don't know. And now our main task will be precisely identify them. Find out what our letters are equal to A, IN And WITH. Hence the name - method uncertain coefficients Let's begin our fabulous journey!

So, we have an equality that makes us dance:

Let's bring all three fractions on the right to a common denominator and add:

Now we can safely discard the denominators (since they are the same) and simply equate the numerators. Everything is as usual

Next step open all brackets(coefficients A, IN And WITH Bye better to leave it outside):

And now (important!) we line up our entire structure on the right by seniority of degrees: first we collect all the terms with x 2 into a pile, then just with x and, finally, we collect the free terms. In fact, we simply present similar ones and group the terms by powers of x.

Like this:

Now let’s comprehend the result. On the left is our original polynomial. Second degree. The numerator of our integrand. On the right too some polynomial of the second degree. Nose unknown coefficients. This equality must be valid when all valid values of x. The fractions on the left and right were the same (according to our condition)! This means that they numerator and (i.e. our polynomials) are also the same. Therefore, the coefficients at the same powers of x these polynomials must have be equal!

We start with the highest degree. From the square. Let's see what kind of coefficients we have at X 2 left and right. On the right we have the sum of the coefficients A+B+C, and on the left is a deuce. This is how our first equation is born.

We write down:

A+B+C = 2

Eat. The first equation is ready.)

Next, we follow a decreasing trajectory - we look at terms with X to the first power. On the right at X we have 8A+4B+2C. Fine. And what do we have with the X on the left? Hm... On the left there is no term with an X at all! There are only 2x 2 - 3. What to do? Very simple! This means that the coefficient of x on the left is equal to zero! We can write our left side like this:

And what? We have every right.) Hence the second equation looks like this:

8 A+4 B+2 C = 0

Well, that’s practically all. It remains to equate the free terms:

15A-5B-3C = -3

In a word, equating coefficients for the same powers of x occurs according to the following scheme:

All three of our equalities must be satisfied simultaneously. Therefore, we assemble a system from our written equations:

The system is not the most difficult for a diligent student - three equations and three unknowns. Decide as you wish. You can use the Cramer method through matrices with determinants, you can use the Gauss method, you can even use the usual school substitution.

To begin with, I will solve this system the way cultural students usually solve such systems. Namely, the Cramer method.

We begin the solution by drawing up a system matrix. Let me remind you that this matrix is just a plate made up of coefficients for unknowns.

Here she is:

First of all, let's calculate determinant of the system matrix. Or, in short, system determinant. It is usually denoted by the Greek letter ∆ (“delta”):

Great, the system determinant is not zero (-48≠0) . From the theory of systems of linear equations, this fact means that our system is consistent and has a unique solution.

The next step is to calculate determinants of unknowns ∆A, ∆B, ∆C. Let me remind you that each of these three determinants is obtained from the main determinant of the system by replacing the columns with coefficients for the corresponding unknowns with a column of free terms.

So we make up the determinants and calculate:

I will not explain in detail the technique for calculating third-order determinants here. And don't ask. This will be a complete deviation from the topic.) Those who are on topic understand what we are talking about. And, perhaps, you have already guessed exactly how I calculated these three determinants.)

That's it, everything is ready.)

This is how cultured students usually solve systems. But... Not all students are friends with and qualifiers. Unfortunately. For some, these simple concepts of higher mathematics remain forever like Chinese literacy and a mysterious monster in the fog...

Well, especially for such uncultured students, I propose a more familiar solution - method of sequential elimination of unknowns. In fact, this is an advanced "school" substitution method. There will only be more steps.) But the essence is the same. First thing I'll do is eliminate the variable WITH. To do this I will express WITH from the first equation and substitute it into the second and third:

We simplify, bring similar ones and get a new system, already with two unknown:

Now, in this new system, it is also possible to express one of the variables in terms of another. But the most attentive students will probably notice that the coefficients in front of the variable B – opposite. Two and minus two. Therefore, it will be very convenient to add both equations together in order to eliminate the variable IN and leave only the letter A.

We add the left and right parts, mentally shorten 2B And -2B and solve the equation only relative A:

Eat. The first coefficient was found: A = -1/24.

Determine the second coefficient IN. For example, from the top equation:

From here we get:

Great. The second coefficient was also found: B = -15/8 . There's still a letter left WITH. To determine it, we use the uppermost equation, where we express it through A And IN:

So:

OK it's all over Now. Unknown odds found! It doesn't matter whether through Cramer or through substitution. Main, Right found.)

Therefore, our decomposition of a large fraction into the sum of small ones will look like this:

And don’t be confused by the resulting fractional coefficients: in this procedure (the method of undetermined coefficients) this is the most common phenomenon. :)

Now it’s highly advisable to check whether we found our coefficients correctly A, B And WITH. Therefore, now we take the draft and remember the eighth grade - we add back all three of our small fractions.

If we get the original large fraction, then everything is fine. No - that means hit me and look for a mistake.

The common denominator will obviously be 24(x-1)(x+3)(x+5).

Go:

Yes!!! We got the original fraction. Which is what needed to be checked. Everything is good. So please don't hit me.)

Now let's return to our original integral. He hasn’t gotten any easier during this time, yes. But now that our fraction has been decomposed into a sum of small ones, integrating it has become a real pleasure!

See for yourself! We insert our expansion into the original integral.

We get:

We use the properties of linearity and split our large integral into a sum of small ones, placing all constants outside the integral signs.

We get:

And the resulting three small integrals are already easy to take .

We continue the integration:

That's all.) And in this lesson, don't ask me where the logarithms in the answer came from! Anyone who remembers is in the know and will understand everything. And for those who don’t remember, we follow the links. I don't just put them there.

Final answer:

Here is such a beautiful trinity: three logarithms - a coward, a seasoned one and a dunce. :) And try, guess such a tricky answer right away! Only the method of indefinite coefficients helps, yes.) Actually, we are looking into this for this purpose. What, how and where.

As a training exercise, I suggest you practice the method and integrate the following fraction:

Practice, find the integral, don’t find it difficult! The answer should be something like this:

The method of indefinite coefficients is a powerful thing. It saves even in the most hopeless situation, when you convert a fraction anyway. And here some attentive and interested readers may have a number of questions:

- What to do if the polynomial in the denominator is not factorized at all?

- HOW should one look for the decomposition of any large rational fraction into the sum of small ones? In any form? Why exactly this and not that?

- What to do if there are multiple factors in the expansion of the denominator? Or brackets in powers like (x-1) 2? In what form should we look for decomposition?

- What to do if, in addition to simple brackets of the form (x-a), the denominator simultaneously contains an indecomposable quadratic trinomial? Let's say x 2 +4x+5? In what form should we look for decomposition?

Well, the time has come to thoroughly understand where the legs grow from. In the next lessons.)

The method is applicable for minimizing logical algebra functions of any number of variables.

Let's consider the case of three variables. A Boolean function in DNF can be represented in the form of all kinds of conjunctive terms that can be included in DNF:

where kО(0,1) are coefficients. The method consists in selecting coefficients in such a way that the resulting DNF is minimal.

If we now set all possible values of the variables from 000 to 111, we get 2 n (2 3 =8) equations for determining the coefficients k:

Example. Minimize a given function

if the values are known:
;
;
;
;
;
;
;
.

Solution.

After crossing out the zero coefficients we get:

=1;

=1.

Let us equate the coefficient to unity , corresponding to the conjunction of the lowest rank and turning the last four equations to 1, and in the first equation it is advisable to equate the coefficient to 1 . The remaining coefficients are set to 0.

Answer: type of minimized function.

It should be noted that the method of indefinite coefficients is effective when the number of variables is small and does not exceed 5-6.

Multidimensional cube

Let's consider a graphical representation of a function in the form of a multidimensional cube. Every peak n-dimensional cube can be put in correspondence with the constituent of the unit.

The subset of marked vertices is a mapping onto n-dimensional cube of a Boolean function from n variables in SDNF.

To display the function from n variables presented in any DNF, it is necessary to establish a correspondence between its miniterms and elements n-dimensional cube.

Miniterm of (n-1)th rank
can be considered as the result of gluing two miniterms n-th rank, i.e.

On n-dimensional cube this corresponds to replacing two vertices that differ only in coordinate values X i, connecting these vertices with an edge (an edge is said to cover the vertices incident to it).

Thus, miniterms ( n The -1)th order corresponds to the edges of an n-dimensional cube.

Similarly, the correspondence of miniterms ( n-2)th order faces n-dimensional cube, each of which covers four vertices (and four edges).

Elements n-dimensional cube, characterized by S measurements are called S-cubes

So vertices are 0-cubes, edges are 1-cubes, faces are 2-cubes, etc.

Example. In Fig. given the mapping

Here are miniterms
And
correspond to 1-cubes ( S=3-2=1), and miniterm X 3 displayed to 2-cubes ( S=3-1=2).

So, any DNF is mapped to n-dimensional cube in totality S-cubes that cover all vertices corresponding to the constituent units (0-cube).

Constituents. For variables X 1 ,X 2 ,…X n expression
is called the constituent of the unit, and
- constituent of zero ( means either , or ).

For example: constituent unit
corresponds to the set (1011), and the constituent is zero
- set (1001).

Since SD(K)NF is a disjunction (conjunction) of the constituents of one (zero), it can be argued that the Boolean function it represents f(x 1 , x 2 ,…, x n) turns to one (zero) only for sets of variable values x 1 , x 2 ,…, x n, corresponding to these copstitutes. On other sets this function turns to 0 (one).

The opposite statement is also true, on which it is based way of representing any Boolean function specified by the table.

For example, a function given by a table

correspond

The resulting expressions can be converted to another form based on the properties of the algebra of logic.

For example, for the function at=
the coating corresponds to a non-minimum shape:

rice a) at=,

a coating on rice b) at=
, rice c) at=
minimal.

Rice. Function coverage at=:

a) non-minimal; b), c) minimum.

Displaying a function on n-measured clearly and simply with n3. A four-dimensional cube can be depicted as shown in Fig., which shows the function of four variables and its minimum coverage corresponding to the expression at=

Using this method when n>4 requires such complex formations that it loses all its advantages.

A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.

Example 1. Step 2.

We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:

We open the brackets and equate the numerator of the original integrand to the resulting expression:

In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:

We cancel all the x’s and get an equivalent system of equations:

Thus, the final expansion of the integrand into a sum of simple fractions is:

Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:

We solve the resulting system:

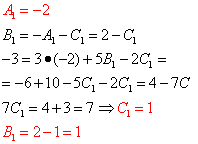
So, from here

Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

As in previous examples, we compose a system of equations:

We reduce the x's and get an equivalent system of equations:

Solving the system, we obtain the following values of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We already know from previous examples how to equate the numerator of the original fraction with the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:

Solving the system, we obtain the following values of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be the following system of equations:

Solving the system, we obtain the following values of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:

Solving the system, we obtain the following values of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

After certain actions with the resulting amount, the following system of equations should be obtained:

Solving the system, we obtain the following values of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.

Equality (I) is identity. Reducing it to integer form, we obtain the equality of 2 polynomials. But such equality is always satisfied only under the condition of term-by-term equality of these polynomials.

Equating the coefficients for the same powers of x on the left and right sides of the equality, we obtain a system of linear equations for unknown coefficients that must be solved.

Since expansion (I) always exists for any proper rational fraction, the resulting system is always consistent.

This method of finding coefficients is called the method of uncertain coefficients (a method of comparing coefficients).

Let us give an example of decomposition of a rational function into elementary fractions.

Example 6.6.27. Break down fractions into elementary fractions.

substitute the last equation into the second

Thus,
.

x=2 ;

x=3 .

Should; .

The partial value method requires less labor and therefore deserves special attention when integrating rational fractions.

If the roots of the denominator are only real, then it is advisable to use this method to determine unknown coefficients.

In other cases, both methods can be combined to determine unknown coefficients.

Comment. The method of partial values is also used in other cases, but here the identity must be differentiated.

Thus, to integrate proper rational fractions it is enough to be able to:

1) integrate elementary fractions;

2) decompose rational fractions into elementary ones.

3. Integration of rational fractions

Scheme for integrating rational fractions:

To integrate rational fractions ;

Where P(x) and Q(x) are polynomials with real coefficients, three steps are performed sequentially.

First step. If the fraction is improper, that is, the degree of the numerator P(x) is greater than or equal to the degree of the denominator Q(x), isolate the whole part of the rational fraction by dividing the numerator by the denominator according to the rule for dividing a polynomial by a polynomial. After this, the rational fraction can be written as a sum:

1) the selected integer part – the polynomial M(x);

2) proper remainder fraction :

Second step.

Proper remainder fraction decomposed into subsequent fractions.

To do this, find the roots of the equation Q(x)=0 and decompose the denominator Q(x) into factors of the first and second degrees with real coefficients:

In this expansion of the denominator, the factors of the 1st degree correspond to real roots, and the factors of the 2nd degree correspond to parallel conjugate roots.

The coefficient for a larger degree of x in the denominator Q(x) can be considered equal to 1, since this can always be achieved by dividing P(x) and Q(x) by it.

After this, the proper residual fraction is decomposed into simplest (elementary) fractions.

Third step. Find the integrals of the selected integer part and all elementary fractions (using the methods discussed above), which are then added.

Example6.6.28.

Under the integral sign there is an improper rational fraction, since the degree of the numerator is equal to the degree of the denominator, so we select the integer part.