Let's work with quadratic equations. These are very popular equations! In its most general form, a quadratic equation looks like this:
For example:
![]()
Here A =1; b = 3; c = -4
![]()
Here A =2; b = -0,5; c = 2,2
![]()
Here A =-3; b = 6; c = -18
Well, you understand...
How to solve quadratic equations? If you have a quadratic equation in front of you in this form, then everything is simple. Remember the magic word discriminant . Rarely a high school student has not heard this word! The phrase “we solve through a discriminant” inspires confidence and reassurance. Because there is no need to expect tricks from the discriminant! It is simple and trouble-free to use. So, the formula for finding the roots of a quadratic equation looks like this:

The expression under the sign of the root is the one discriminant. As you can see, to find X, we use only a, b and c. Those. coefficients from a quadratic equation. Just carefully substitute the values a, b and c This is the formula we calculate. Let's substitute with your own signs! For example, for the first equation A =1; b = 3; c= -4. Here we write it down:
The example is almost solved:


That's all.
What cases are possible when using this formula? There are only three cases.
1. The discriminant is positive. This means the root can be extracted from it. Whether the root is extracted well or poorly is another question. What is important is what is extracted in principle. Then your quadratic equation has two roots. Two different solutions.
2. The discriminant is zero. Then you have one solution. Strictly speaking, this is not one root, but two identical. But this plays a role in inequalities, where we will study the issue in more detail.
3. The discriminant is negative. The square root of a negative number cannot be taken. Well, okay. This means there are no solutions.
Everything is very simple. And what, you think it’s impossible to make a mistake? Well, yes, how...
The most common mistakes are confusion with sign values a, b and c. Or rather, not with their signs (where to get confused?), but with the substitution of negative values into the formula for calculating the roots. What helps here is a detailed recording of the formula with specific numbers. If there are problems with calculations, do that!
Suppose we need to solve the following example:
![]()
Here a = -6; b = -5; c = -1
Let's say you know that you rarely get answers the first time.
Well, don't be lazy. It will take about 30 seconds to write an extra line. And the number of errors will decrease sharply. So we write in detail, with all the brackets and signs:


It seems incredibly difficult to write out so carefully. But it only seems so. Give it a try. Well, or choose. What's better, fast or right? Besides, I will make you happy. After a while, there will be no need to write everything down so carefully. It will work out right on its own. Especially if you use practical techniques that are described below. This evil example with a bunch of minuses can be solved easily and without errors!
So, how to solve quadratic equations through the discriminant we remembered. Or they learned, which is also good. You know how to correctly determine a, b and c. Do you know how? attentively substitute them into the root formula and attentively count the result. You understand that the key word here is attentively?
However, quadratic equations often look slightly different. For example, like this:
![]()
This incomplete quadratic equations . They can also be solved through a discriminant. You just need to understand correctly what they are equal to here. a, b and c.
Have you figured it out? In the first example a = 1; b = -4; A c? It's not there at all! Well yes, that's right. In mathematics this means that c = 0 ! That's all. Substitute zero into the formula instead c, and we will succeed. Same with the second example. Only we don’t have zero here With, A b !
But incomplete quadratic equations can be solved much more simply. Without any discrimination. Let's consider the first incomplete equation. What can you do on the left side? You can take X out of brackets! Let's take it out.
![]()
And what from this? And the fact that the product equals zero if and only if any of the factors equals zero! Don't believe me? Okay, then come up with two non-zero numbers that, when multiplied, will give zero!
Does not work? That's it...
Therefore, we can confidently write: x = 0, or x = 4
All. These will be the roots of our equation. Both are suitable. When substituting any of them into the original equation, we get the correct identity 0 = 0. As you can see, the solution is much simpler than using a discriminant.
The second equation can also be solved simply. Move 9 to the right side. We get:
All that remains is to extract the root from 9, and that’s it. It will turn out:
![]()
Also two roots . x = +3 and x = -3.
This is how all incomplete quadratic equations are solved. Either by placing X out of brackets, or by simply moving the number to the right and then extracting the root.
It is extremely difficult to confuse these techniques. Simply because in the first case you will have to extract the root of X, which is somehow incomprehensible, and in the second case there is nothing to take out of brackets...
Now take note of practical techniques that dramatically reduce the number of errors. The same ones that are due to inattention... For which it later becomes painful and offensive...
First appointment. Don’t be lazy before solving a quadratic equation and bring it to standard form. What does this mean?
Let's say that after all the transformations you get the following equation:
![]()
Don't rush to write the root formula! You'll almost certainly get the odds mixed up a, b and c. Construct the example correctly. First, X squared, then without square, then the free term. Like this:
![]()
And again, don’t rush! A minus in front of an X squared can really upset you. It's easy to forget... Get rid of the minus. How? Yes, as taught in the previous topic! We need to multiply the entire equation by -1. We get:
![]()
But now you can safely write down the formula for the roots, calculate the discriminant and finish solving the example. Decide for yourself. You should now have roots 2 and -1.
Reception second. Check the roots! According to Vieta's theorem. Don't be scared, I'll explain everything! Checking last thing the equation. Those. the one we used to write down the root formula. If (as in this example) the coefficient a = 1, checking the roots is easy. It is enough to multiply them. The result should be a free member, i.e. in our case -2. Please note, not 2, but -2! Free member with your sign
. If it doesn’t work out, it means they’ve already screwed up somewhere. Look for the error. If it works, you need to add the roots. Last and final check. The coefficient should be b With opposite
familiar. In our case -1+2 = +1. A coefficient b, which is before the X, is equal to -1. So, everything is correct!
It’s a pity that this is so simple only for examples where x squared is pure, with a coefficient a = 1. But at least check in such equations! There will be fewer and fewer errors.
Reception third. If your equation has fractional coefficients, get rid of the fractions! Multiply the equation by a common denominator as described in the previous section. When working with fractions, errors keep creeping in for some reason...
By the way, I promised to simplify the evil example with a bunch of minuses. Please! Here he is.
![]()
In order not to get confused by the minuses, we multiply the equation by -1. We get:
![]()
That's all! Solving is a pleasure!
So, let's summarize the topic.
Practical tips:
1. Before solving, we bring the quadratic equation to standard form and build it Right.
2. If there is a negative coefficient in front of the X squared, we eliminate it by multiplying the entire equation by -1.
3. If the coefficients are fractional, we eliminate the fractions by multiplying the entire equation by the corresponding factor.
4. If x squared is pure, its coefficient is equal to one, the solution can be easily verified using Vieta’s theorem. Do it!
Fractional equations. ODZ.
We continue to master the equations. We already know how to work with linear and quadratic equations. The last view left - fractional equations. Or they are also called much more respectably - fractional rational equations. It is the same.
Fractional equations.
As the name implies, these equations necessarily contain fractions. But not just fractions, but fractions that have unknown in denominator. At least in one. For example:

Let me remind you that if the denominators are only numbers, these are linear equations.
How to decide fractional equations? First of all, get rid of fractions! After this, the equation most often turns into linear or quadratic. And then we know what to do... In some cases it can turn into an identity, such as 5=5 or an incorrect expression, such as 7=2. But this rarely happens. I will mention this below.
But how to get rid of fractions!? Very simple. Applying the same identical transformations.
We need to multiply the entire equation by the same expression. So that all denominators are reduced! Everything will immediately become easier. Let me explain with an example. Let us need to solve the equation:
How were you taught in elementary school? We move everything to one side, bring it to a common denominator, etc. Forget it like a bad dream! This is what you need to do when you add or subtract fractions. Or you work with inequalities. And in equations, we immediately multiply both sides by an expression that will give us the opportunity to reduce all the denominators (i.e., in essence, by a common denominator). And what is this expression?
On the left side, reducing the denominator requires multiplying by x+2. And on the right, multiplication by 2 is required. This means that the equation must be multiplied by 2(x+2). Multiply:

This is a common multiplication of fractions, but I’ll describe it in detail:

Please note that I am not opening the bracket yet (x + 2)! So, in its entirety, I write it:

On the left side it contracts entirely (x+2), and on the right 2. Which is what was required! After reduction we get linear the equation:
And everyone can solve this equation! x = 2.
Let's solve another example, a little more complicated:

If we remember that 3 = 3/1, and 2x = 2x/ 1, we can write:

And again we get rid of what we don’t really like - fractions.
We see that to reduce the denominator with X, we need to multiply the fraction by (x – 2). And a few are not a hindrance to us. Well, let's multiply. All left side and all right side:

Parentheses again (x – 2) I'm not revealing. I work with the bracket as a whole as if it were one number! This must always be done, otherwise nothing will be reduced.

With a feeling of deep satisfaction we reduce (x – 2) and we get an equation without any fractions, with a ruler!
Now let’s open the brackets:
We bring similar ones, move everything to the left side and get:
![]()
Classic quadratic equation. But the minus ahead is not good. You can always get rid of it by multiplying or dividing by -1. But if you look closely at the example, you will notice that it is best to divide this equation by -2! In one fell swoop, the minus will disappear, and the odds will become more attractive! Divide by -2. On the left side - term by term, and on the right - simply divide zero by -2, zero and we get:
![]()
We solve through the discriminant and check using Vieta’s theorem. We get x = 1 and x = 3. Two roots.
As you can see, in the first case the equation after the transformation became linear, but here it becomes quadratic. It happens that after getting rid of fractions, all the X's are reduced. Something remains, like 5=5. It means that x can be anything. Whatever it is, it will still be reduced. And it turns out to be pure truth, 5=5. But, after getting rid of fractions, it may turn out to be completely untrue, like 2=7. And this means that no solutions! Any X turns out to be untrue.
Realized the main solution fractional equations? It is simple and logical. We change the original expression so that everything we don’t like disappears. Or it interferes. In this case these are fractions. We will do the same with all sorts of complex examples with logarithms, sines and other horrors. We Always Let's get rid of all this.
However, we need to change the original expression in the direction we need according to the rules, yes... The mastery of which is preparation for the Unified State Exam in mathematics. So we are mastering it.
Now we will learn how to bypass one of main ambushes on the Unified State Exam! But first, let's see whether you fall into it or not?
Let's look at a simple example:

The matter is already familiar, we multiply both sides by (x – 2), we get:

I remind you, with brackets (x – 2) We work as if with one, integral expression!

Here I no longer wrote one in the denominators, it’s undignified... And I didn’t draw brackets in the denominators, except for x – 2 there is nothing, you don’t have to draw. Let's shorten:
![]()
Open the parentheses, move everything to the left, and give similar ones:
![]()
We solve, check, we get two roots. x = 2 And x = 3. Great.
Suppose the assignment says to write down the root, or their sum if there is more than one root. What are we going to write?
If you decide the answer is 5, you were ambushed. And the task will not be credited to you. They worked in vain... Correct answer is 3.
What's the matter?! And you try to do a check. Substitute the values of the unknown into original example. And if at x = 3 everything will grow together wonderfully, we get 9 = 9, then when x = 2 It will be division by zero! What you absolutely cannot do. Means x = 2 is not a solution, and is not taken into account in the answer. This is the so-called extraneous or extra root. We simply discard it. The final root is one. x = 3.
How so?! – I hear indignant exclamations. We were taught that an equation can be multiplied by an expression! This is an identical transformation!
Yes, identical. Under a small condition - the expression by which we multiply (divide) - different from zero. A x – 2 at x = 2 equals zero! So everything is fair.
And now what i can do?! Don't multiply by expression? Should I check every time? Again it’s unclear!
Calmly! Don't panic!
In this difficult situation, three magic letters will save us. I know what you're thinking. Right! This ODZ . Area of Acceptable Values.
In modern society, the ability to perform operations with equations containing a squared variable can be useful in many areas of activity and is widely used in practice in scientific and technical developments. Evidence of this can be found in the design of sea and river vessels, aircraft and missiles. Using such calculations, the trajectories of movement of a wide variety of bodies, including space objects, are determined. Examples with the solution of quadratic equations are used not only in economic forecasting, in the design and construction of buildings, but also in the most ordinary everyday circumstances. They may be needed on hiking trips, at sporting events, in stores when making purchases and in other very common situations.
Let's break the expression into its component factors
The degree of an equation is determined by the maximum value of the degree of the variable that the expression contains. If it is equal to 2, then such an equation is called quadratic.
If we speak in the language of formulas, then the indicated expressions, no matter how they look, can always be brought to the form when the left side of the expression consists of three terms. Among them: ax 2 (that is, a variable squared with its coefficient), bx (an unknown without a square with its coefficient) and c (a free component, that is, an ordinary number). All this on the right side is equal to 0. In the case when such a polynomial lacks one of its constituent terms, with the exception of ax 2, it is called an incomplete quadratic equation. Examples with the solution of such problems, the values of the variables in which are easy to find, should be considered first.
If the expression looks like it has two terms on the right side, more precisely ax 2 and bx, the easiest way to find x is by putting the variable out of brackets. Now our equation will look like this: x(ax+b). Next, it becomes obvious that either x=0, or the problem comes down to finding a variable from the following expression: ax+b=0. This is dictated by one of the properties of multiplication. The rule states that the product of two factors results in 0 only if one of them is zero.
Example
x=0 or 8x - 3 = 0
As a result, we get two roots of the equation: 0 and 0.375.
Equations of this kind can describe the movement of bodies under the influence of gravity, which began to move from a certain point taken as the origin of coordinates. Here the mathematical notation takes the following form: y = v 0 t + gt 2 /2. By substituting the necessary values, equating the right side to 0 and finding possible unknowns, you can find out the time that passes from the moment the body rises to the moment it falls, as well as many other quantities. But we'll talk about this later.

Factoring an Expression
The rule described above makes it possible to solve these problems in more complex cases. Let's look at examples of solving quadratic equations of this type.
X 2 - 33x + 200 = 0
This quadratic trinomial is complete. First, let's transform the expression and factor it. There are two of them: (x-8) and (x-25) = 0. As a result, we have two roots 8 and 25.
Examples with solving quadratic equations in grade 9 allow this method to find a variable in expressions not only of the second, but even of the third and fourth orders.
For example: 2x 3 + 2x 2 - 18x - 18 = 0. When factoring the right side into factors with a variable, there are three of them, that is, (x+1), (x-3) and (x+3).
As a result, it becomes obvious that this equation has three roots: -3; -1; 3.
Square Root
Another case of an incomplete second-order equation is an expression represented in the language of letters in such a way that the right-hand side is constructed from the components ax 2 and c. Here, to obtain the value of the variable, the free term is transferred to the right side, and after that the square root is extracted from both sides of the equality. It should be noted that in this case there are usually two roots of the equation. The only exceptions can be equalities that do not contain a term with at all, where the variable is equal to zero, as well as variants of expressions when the right side turns out to be negative. In the latter case, there are no solutions at all, since the above actions cannot be performed with roots. Examples of solutions to quadratic equations of this type should be considered.
In this case, the roots of the equation will be the numbers -4 and 4.
Calculation of land area
The need for this kind of calculations appeared in ancient times, because the development of mathematics in those distant times was largely determined by the need to determine with the greatest accuracy the areas and perimeters of land plots.

We should also consider examples of solving quadratic equations based on problems of this kind.
So, let's say there is a rectangular plot of land, the length of which is 16 meters greater than the width. You should find the length, width and perimeter of the site if you know that its area is 612 m2.
To get started, let's first create the necessary equation. Let us denote by x the width of the area, then its length will be (x+16). From what has been written it follows that the area is determined by the expression x(x+16), which, according to the conditions of our problem, is 612. This means that x(x+16) = 612.
Solving complete quadratic equations, and this expression is exactly that, cannot be done in the same way. Why? Although the left side still contains two factors, their product does not equal 0 at all, so different methods are used here.
Discriminant
First of all, we will make the necessary transformations, then the appearance of this expression will look like this: x 2 + 16x - 612 = 0. This means that we have received the expression in a form corresponding to the previously specified standard, where a=1, b=16, c= -612.
This could be an example of solving quadratic equations using a discriminant. Here the necessary calculations are made according to the scheme: D = b 2 - 4ac. This auxiliary quantity not only makes it possible to find the required quantities in a second-order equation, it determines the number of possible options. If D>0, there are two of them; for D=0 there is one root. In case D<0, никаких шансов для решения у уравнения вообще не имеется.
About roots and their formula
In our case, the discriminant is equal to: 256 - 4(-612) = 2704. This suggests that our problem has an answer. If you know k, the solution of quadratic equations must be continued using the formula below. It allows you to calculate the roots.

This means that in the presented case: x 1 =18, x 2 =-34. The second option in this dilemma cannot be a solution, because the dimensions of the land plot cannot be measured in negative quantities, which means x (that is, the width of the plot) is 18 m. From here we calculate the length: 18+16=34, and the perimeter 2(34+ 18)=104(m2).
Examples and tasks
We continue our study of quadratic equations. Examples and detailed solutions of several of them will be given below.
1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1
Let’s move everything to the left side of the equality, make a transformation, that is, we’ll get the type of equation that is usually called standard, and equate it to zero.
15x 2 + 20x + 5 - 12x 2 - 27x - 1 = 0
Adding similar ones, we determine the discriminant: D = 49 - 48 = 1. This means our equation will have two roots. Let's calculate them according to the above formula, which means that the first of them will be equal to 4/3, and the second to 1.
2) Now let's solve mysteries of a different kind.
Let's find out if there are any roots here x 2 - 4x + 5 = 1? To obtain a comprehensive answer, let’s reduce the polynomial to the corresponding usual form and calculate the discriminant. In the above example, it is not necessary to solve the quadratic equation, because this is not the essence of the problem at all. In this case, D = 16 - 20 = -4, which means there really are no roots.
Vieta's theorem
It is convenient to solve quadratic equations using the above formulas and the discriminant, when the square root is taken from the value of the latter. But this does not always happen. However, there are many ways to obtain the values of variables in this case. Example: solving quadratic equations using Vieta's theorem. She is named after who lived in the 16th century in France and made a brilliant career thanks to his mathematical talent and connections at court. His portrait can be seen in the article.

The pattern that the famous Frenchman noticed was as follows. He proved that the roots of the equation add up numerically to -p=b/a, and their product corresponds to q=c/a.
Now let's look at specific tasks.
3x 2 + 21x - 54 = 0
For simplicity, let's transform the expression:
x 2 + 7x - 18 = 0
Let's use Vieta's theorem, this will give us the following: the sum of the roots is -7, and their product is -18. From here we get that the roots of the equation are the numbers -9 and 2. After checking, we will make sure that these variable values really fit into the expression.
Parabola graph and equation
The concepts of quadratic function and quadratic equations are closely related. Examples of this have already been given earlier. Now let's look at some mathematical riddles in a little more detail. Any equation of the described type can be represented visually. Such a relationship, drawn as a graph, is called a parabola. Its various types are presented in the figure below.

Any parabola has a vertex, that is, a point from which its branches emerge. If a>0, they go high to infinity, and when a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x 2 . В данном случае в уравнении x 2 =0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a.
Visual representations of functions help solve any equations, including quadratic ones. This method is called graphical. And the value of the x variable is the abscissa coordinate at the points where the graph line intersects with 0x. The coordinates of the vertex can be found using the formula just given x 0 = -b/2a. And by substituting the resulting value into the original equation of the function, you can find out y 0, that is, the second coordinate of the vertex of the parabola, which belongs to the ordinate axis.
The intersection of the branches of a parabola with the abscissa axis
There are a lot of examples of solving quadratic equations, but there are also general patterns. Let's look at them. It is clear that the intersection of the graph with the 0x axis for a>0 is possible only if 0 takes negative values. And for a<0 координата у 0 должна быть положительна. Для указанных вариантов D>0. Otherwise D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х.
From the graph of the parabola you can also determine the roots. The opposite is also true. That is, if it is not easy to obtain a visual representation of a quadratic function, you can equate the right side of the expression to 0 and solve the resulting equation. And knowing the points of intersection with the 0x axis, it is easier to construct a graph.
From the history
Using equations containing a squared variable, in the old days they not only made mathematical calculations and determined the areas of geometric figures. The ancients needed such calculations for grand discoveries in the fields of physics and astronomy, as well as for making astrological forecasts.

As modern scientists suggest, the inhabitants of Babylon were among the first to solve quadratic equations. This happened four centuries before our era. Of course, their calculations were radically different from those currently accepted and turned out to be much more primitive. For example, Mesopotamian mathematicians had no idea about the existence of negative numbers. They were also unfamiliar with other subtleties that any modern schoolchild knows.
Perhaps even earlier than the scientists of Babylon, the sage from India Baudhayama began solving quadratic equations. This happened about eight centuries before the era of Christ. True, the second-order equations, the methods for solving which he gave, were the simplest. Besides him, Chinese mathematicians were also interested in similar questions in the old days. In Europe, quadratic equations began to be solved only at the beginning of the 13th century, but later they were used in their works by such great scientists as Newton, Descartes and many others.
Quadratic equation - easy to solve! *Hereinafter referred to as “KU”. Friends, it would seem that there could be nothing simpler in mathematics than solving such an equation. But something told me that many people have problems with him. I decided to see how many on-demand impressions Yandex gives out per month. Here's what happened, look:

What does it mean? This means that about 70,000 people a month are looking for this information, and this is summer, and what will happen during the school year - there will be twice as many requests. This is not surprising, because those guys and girls who graduated from school a long time ago and are preparing for the Unified State Exam are looking for this information, and schoolchildren also strive to refresh their memory.
Despite the fact that there are a lot of sites that tell you how to solve this equation, I decided to also contribute and publish the material. Firstly, I want visitors to come to my site based on this request; secondly, in other articles, when the topic of “KU” comes up, I will provide a link to this article; thirdly, I’ll tell you a little more about his solution than is usually stated on other sites. Let's get started! The content of the article:
A quadratic equation is an equation of the form:

where coefficients a,band c are arbitrary numbers, with a≠0.
In the school course, the material is given in the following form - the equations are divided into three classes:
1. They have two roots.
2. *Have only one root.
3. They have no roots. It is worth especially noting here that they do not have real roots
How are roots calculated? Just!
We calculate the discriminant. Underneath this “terrible” word lies a very simple formula:
![]()
The root formulas are as follows:

*You need to know these formulas by heart.
You can immediately write down and solve:
Example:

1. If D > 0, then the equation has two roots.
2. If D = 0, then the equation has one root.
3. If D< 0, то уравнение не имеет действительных корней.
Let's look at the equation:

In this regard, when the discriminant is equal to zero, the school course says that one root is obtained, here it is equal to nine. Everything is correct, it is so, but...
This idea is somewhat incorrect. In fact, there are two roots. Yes, yes, don’t be surprised, you get two equal roots, and to be mathematically precise, then the answer should write two roots:
x 1 = 3 x 2 = 3
But this is so - a small digression. At school you can write it down and say that there is one root.
Now the next example:

As we know, the root of a negative number cannot be taken, so there is no solution in this case.
That's the whole decision process.
Quadratic function.
This shows what the solution looks like geometrically. This is extremely important to understand (in the future, in one of the articles we will analyze in detail the solution to the quadratic inequality).
This is a function of the form:
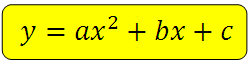
where x and y are variables
a, b, c – given numbers, with a ≠ 0
The graph is a parabola:
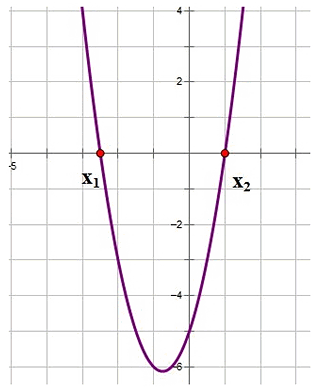
That is, it turns out that by solving a quadratic equation with “y” equal to zero, we find the points of intersection of the parabola with the x axis. There can be two of these points (the discriminant is positive), one (the discriminant is zero) and none (the discriminant is negative). Details about the quadratic function You can view article by Inna Feldman.
Let's look at examples:
Example 1: Solve 2x 2 +8 x–192=0
a=2 b=8 c= –192
D=b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Answer: x 1 = 8 x 2 = –12
*It was possible to immediately divide the left and right sides of the equation by 2, that is, simplify it. The calculations will be easier.
Example 2: Decide x 2–22 x+121 = 0
a=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

We found that x 1 = 11 and x 2 = 11
It is permissible to write x = 11 in the answer.
Answer: x = 11
Example 3: Decide x 2 –8x+72 = 0
a=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
The discriminant is negative, there is no solution in real numbers.
Answer: no solution
The discriminant is negative. There is a solution!
Here we will talk about solving the equation in the case when a negative discriminant is obtained. Do you know anything about complex numbers? I will not go into detail here about why and where they arose and what their specific role and necessity in mathematics is; this is a topic for a large separate article.
The concept of a complex number.
A little theory.
A complex number z is a number of the form
z = a + bi
where a and b are real numbers, i is the so-called imaginary unit.
a+bi – this is a SINGLE NUMBER, not an addition.
The imaginary unit is equal to the root of minus one:

Now consider the equation:

We get two conjugate roots.
Incomplete quadratic equation.
Let's consider special cases, this is when the coefficient “b” or “c” is equal to zero (or both are equal to zero). They can be solved easily without any discriminants.
Case 1. Coefficient b = 0.
The equation becomes:

Let's transform:
Example:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Case 2. Coefficient c = 0.
The equation becomes:

Let's transform and factorize:

*The product is equal to zero when at least one of the factors is equal to zero.
Example:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 or x–5 =0
x 1 = 0 x 2 = 5
Case 3. Coefficients b = 0 and c = 0.
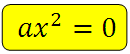
Here it is clear that the solution to the equation will always be x = 0.
Useful properties and patterns of coefficients.
There are properties that allow you to solve equations with large coefficients.
Ax 2 + bx+ c=0 equality holds
a + b+ c = 0, That
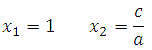
- if for the coefficients of the equation Ax 2 + bx+ c=0 equality holds
a+ c =b, That
![]()
These properties help solve a certain type of equation.
Example 1: 5001 x 2 –4995 x – 6=0
The sum of the odds is 5001+( – 4995)+(– 6) = 0, which means

Example 2: 2501 x 2 +2507 x+6=0
Equality holds a+ c =b, Means

Regularities of coefficients.
1. If in the equation ax 2 + bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 +1)∙x+ a= 0 = > x 1 = –a x 2 = –1/a.
Example. Consider the equation 6x 2 + 37x + 6 = 0.
x 1 = –6 x 2 = –1/6.
2. If in the equation ax 2 – bx + c = 0 the coefficient “b” is equal to (a 2 +1), and the coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal
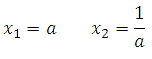
ax 2 – (a 2 +1)∙x+ a= 0 = > x 1 = a x 2 = 1/a.
Example. Consider the equation 15x 2 –226x +15 = 0.
x 1 = 15 x 2 = 1/15.
3. If in Eq. ax 2 + bx – c = 0 coefficient “b” is equal to (a 2 – 1), and coefficient “c” is numerically equal to the coefficient “a”, then its roots are equal

ax 2 + (a 2 –1)∙x – a= 0 = > x 1 = – a x 2 = 1/a.
Example. Consider the equation 17x 2 +288x – 17 = 0.
x 1 = – 17 x 2 = 1/17.
4. If in the equation ax 2 – bx – c = 0 the coefficient “b” is equal to (a 2 – 1), and the coefficient c is numerically equal to the coefficient “a”, then its roots are equal

ax 2 – (a 2 –1)∙x – a= 0 = > x 1 = a x 2 = – 1/a.
Example. Consider the equation 10x 2 – 99x –10 = 0.
x 1 = 10 x 2 = – 1/10
Vieta's theorem.
Vieta's theorem is named after the famous French mathematician Francois Vieta. Using Vieta's theorem, we can express the sum and product of the roots of an arbitrary KU in terms of its coefficients.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
In total, the number 14 gives only 5 and 9. These are roots. With a certain skill, using the presented theorem, you can solve many quadratic equations orally immediately.
Vieta's theorem, in addition. It is convenient in that after solving a quadratic equation in the usual way (through a discriminant), the resulting roots can be checked. I recommend doing this always.
TRANSPORTATION METHOD
With this method, the coefficient “a” is multiplied by the free term, as if “thrown” to it, which is why it is called "transfer" method. This method is used when the roots of the equation can be easily found using Vieta's theorem and, most importantly, when the discriminant is an exact square.
If A± b+c≠ 0, then the transfer technique is used, for example:
2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)
Using Vieta's theorem in equation (2), it is easy to determine that x 1 = 10 x 2 = 1
The resulting roots of the equation must be divided by 2 (since the two were “thrown” from x 2), we get
x 1 = 5 x 2 = 0.5.
What is the rationale? Look what's happening.
The discriminants of equations (1) and (2) are equal:
If you look at the roots of the equations, you only get different denominators, and the result depends precisely on the coefficient of x 2:

The second (modified) one has roots that are 2 times larger.
Therefore, we divide the result by 2.
*If we reroll the three, we will divide the result by 3, etc.
Answer: x 1 = 5 x 2 = 0.5
Sq. ur-ie and Unified State Examination.
I’ll tell you briefly about its importance - YOU MUST BE ABLE TO DECIDE quickly and without thinking, you need to know the formulas of roots and discriminants by heart. Many of the problems included in the Unified State Examination tasks boil down to solving a quadratic equation (geometric ones included).
Something worth noting!
1. The form of writing an equation can be “implicit”. For example, the following entry is possible:
15+ 9x 2 - 45x = 0 or 15x+42+9x 2 - 45x=0 or 15 -5x+10x 2 = 0.
You need to bring it to a standard form (so as not to get confused when solving).
2. Remember that x is an unknown quantity and it can be denoted by any other letter - t, q, p, h and others.
We continue to study the topic " solving equations" We have already become acquainted with linear equations and are moving on to getting acquainted with quadratic equations.
First, we will look at what a quadratic equation is, how it is written in general form, and give related definitions. After this, we will use examples to examine in detail how incomplete quadratic equations are solved. Next, we will move on to solving complete equations, obtain the root formula, get acquainted with the discriminant of a quadratic equation, and consider solutions to typical examples. Finally, let's trace the connections between the roots and coefficients.
Page navigation.
What is a quadratic equation? Their types
First you need to clearly understand what a quadratic equation is. Therefore, it is logical to start a conversation about quadratic equations with the definition of a quadratic equation, as well as related definitions. After this, you can consider the main types of quadratic equations: reduced and unreduced, as well as complete and incomplete equations.
Definition and examples of quadratic equations
Definition.
Quadratic equation is an equation of the form a x 2 +b x+c=0, where x is a variable, a, b and c are some numbers, and a is non-zero.
Let's say right away that quadratic equations are often called equations of the second degree. This is due to the fact that the quadratic equation is algebraic equation second degree.
The stated definition allows us to give examples of quadratic equations. So 2 x 2 +6 x+1=0, 0.2 x 2 +2.5 x+0.03=0, etc. These are quadratic equations.
Definition.
Numbers a, b and c are called coefficients of the quadratic equation a·x 2 +b·x+c=0, and coefficient a is called the first, or the highest, or the coefficient of x 2, b is the second coefficient, or the coefficient of x, and c is the free term.
For example, let's take a quadratic equation of the form 5 x 2 −2 x −3=0, here the leading coefficient is 5, the second coefficient is equal to −2, and the free term is equal to −3. Please note that when the coefficients b and/or c are negative, as in the example just given, the short form of the quadratic equation is 5 x 2 −2 x−3=0 , rather than 5 x 2 +(−2 )·x+(−3)=0 .
It is worth noting that when the coefficients a and/or b are equal to 1 or −1, then they are usually not explicitly present in the quadratic equation, which is due to the peculiarities of writing such. For example, in the quadratic equation y 2 −y+3=0 the leading coefficient is one, and the coefficient of y is equal to −1.
Reduced and unreduced quadratic equations
Depending on the value of the leading coefficient, reduced and unreduced quadratic equations are distinguished. Let us give the corresponding definitions.
Definition.
A quadratic equation in which the leading coefficient is 1 is called given quadratic equation. Otherwise the quadratic equation is untouched.
According to this definition, quadratic equations x 2 −3·x+1=0, x 2 −x−2/3=0, etc. – given, in each of them the first coefficient is equal to one. A 5 x 2 −x−1=0, etc. - unreduced quadratic equations, their leading coefficients are different from 1.
From any unreduced quadratic equation, by dividing both sides by the leading coefficient, you can go to the reduced one. This action is an equivalent transformation, that is, the reduced quadratic equation obtained in this way has the same roots as the original unreduced quadratic equation, or, like it, has no roots.
Let us look at an example of how the transition from an unreduced quadratic equation to a reduced one is performed.
Example.
From the equation 3 x 2 +12 x−7=0, go to the corresponding reduced quadratic equation.
Solution.
We just need to divide both sides of the original equation by the leading coefficient 3, it is non-zero, so we can perform this action. We have (3 x 2 +12 x−7):3=0:3, which is the same, (3 x 2):3+(12 x):3−7:3=0, and then (3:3) x 2 +(12:3) x−7:3=0, from where . This is how we obtained the reduced quadratic equation, which is equivalent to the original one.
Answer:
Complete and incomplete quadratic equations
The definition of a quadratic equation contains the condition a≠0. This condition is necessary so that the equation a x 2 + b x + c = 0 is quadratic, since when a = 0 it actually becomes a linear equation of the form b x + c = 0.
As for the coefficients b and c, they can be equal to zero, both individually and together. In these cases, the quadratic equation is called incomplete.
Definition.
The quadratic equation a x 2 +b x+c=0 is called incomplete, if at least one of the coefficients b, c is equal to zero.
In its turn
Definition.
Complete quadratic equation is an equation in which all coefficients are different from zero.
Such names were not given by chance. This will become clear from the following discussions.
If the coefficient b is zero, then the quadratic equation takes the form a·x 2 +0·x+c=0, and it is equivalent to the equation a·x 2 +c=0. If c=0, that is, the quadratic equation has the form a·x 2 +b·x+0=0, then it can be rewritten as a·x 2 +b·x=0. And with b=0 and c=0 we get the quadratic equation a·x 2 =0. The resulting equations differ from the complete quadratic equation in that their left-hand sides do not contain either a term with the variable x, or a free term, or both. Hence their name - incomplete quadratic equations.
So the equations x 2 +x+1=0 and −2 x 2 −5 x+0.2=0 are examples of complete quadratic equations, and x 2 =0, −2 x 2 =0, 5 x 2 +3=0 , −x 2 −5 x=0 are incomplete quadratic equations.
Solving incomplete quadratic equations
From the information in the previous paragraph it follows that there is three types of incomplete quadratic equations:
- a·x 2 =0, the coefficients b=0 and c=0 correspond to it;
- a x 2 +c=0 when b=0 ;
- and a·x 2 +b·x=0 when c=0.
Let us examine in order how incomplete quadratic equations of each of these types are solved.
a x 2 =0
Let's start with solving incomplete quadratic equations in which the coefficients b and c are equal to zero, that is, with equations of the form a x 2 =0. The equation a·x 2 =0 is equivalent to the equation x 2 =0, which is obtained from the original by dividing both parts by a non-zero number a. Obviously, the root of the equation x 2 =0 is zero, since 0 2 =0. This equation has no other roots, which is explained by the fact that for any non-zero number p the inequality p 2 >0 holds, which means that for p≠0 the equality p 2 =0 is never achieved.
So, the incomplete quadratic equation a·x 2 =0 has a single root x=0.
As an example, we give the solution to the incomplete quadratic equation −4 x 2 =0. It is equivalent to the equation x 2 =0, its only root is x=0, therefore, the original equation has a single root zero.
A short solution in this case can be written as follows:
−4 x 2 =0 ,
x 2 =0,
x=0 .
a x 2 +c=0
Now let's look at how incomplete quadratic equations are solved in which the coefficient b is zero and c≠0, that is, equations of the form a x 2 +c=0. We know that moving a term from one side of the equation to the other with the opposite sign, as well as dividing both sides of the equation by a non-zero number, gives an equivalent equation. Therefore, we can carry out the following equivalent transformations of the incomplete quadratic equation a x 2 +c=0:
- move c to the right side, which gives the equation a x 2 =−c,
- and divide both sides by a, we get .
The resulting equation allows us to draw conclusions about its roots. Depending on the values of a and c, the value of the expression can be negative (for example, if a=1 and c=2, then ) or positive (for example, if a=−2 and c=6, then ), it is not equal to zero , since by condition c≠0. Let's look at the cases separately.
If , then the equation has no roots. This statement follows from the fact that the square of any number is a non-negative number. It follows from this that when , then for any number p the equality cannot be true.
If , then the situation with the roots of the equation is different. In this case, if we remember about , then the root of the equation immediately becomes obvious; it is the number, since . It’s easy to guess that the number is also the root of the equation, indeed, . This equation has no other roots, which can be shown, for example, by contradiction. Let's do it.
Let us denote the roots of the equation just announced as x 1 and −x 1 . Suppose that the equation has one more root x 2, different from the indicated roots x 1 and −x 1. It is known that substituting its roots into an equation instead of x turns the equation into a correct numerical equality. For x 1 and −x 1 we have , and for x 2 we have . The properties of numerical equalities allow us to perform term-by-term subtraction of correct numerical equalities, so subtracting the corresponding parts of the equalities gives x 1 2 −x 2 2 =0. The properties of operations with numbers allow us to rewrite the resulting equality as (x 1 −x 2)·(x 1 +x 2)=0. We know that the product of two numbers is equal to zero if and only if at least one of them is equal to zero. Therefore, from the resulting equality it follows that x 1 −x 2 =0 and/or x 1 +x 2 =0, which is the same, x 2 =x 1 and/or x 2 =−x 1. So we came to a contradiction, since at the beginning we said that the root of the equation x 2 is different from x 1 and −x 1. This proves that the equation has no roots other than and .
Let us summarize the information in this paragraph. The incomplete quadratic equation a x 2 +c=0 is equivalent to the equation that
- has no roots if ,
- has two roots and , if .
Let's consider examples of solving incomplete quadratic equations of the form a·x 2 +c=0.
Let's start with the quadratic equation 9 x 2 +7=0. After moving the free term to the right side of the equation, it will take the form 9 x 2 =−7. Dividing both sides of the resulting equation by 9, we arrive at . Since the right side has a negative number, this equation has no roots, therefore, the original incomplete quadratic equation 9 x 2 +7 = 0 has no roots.
Let's solve another incomplete quadratic equation −x 2 +9=0. We move the nine to the right side: −x 2 =−9. Now we divide both sides by −1, we get x 2 =9. On the right side there is a positive number, from which we conclude that or . Then we write down the final answer: the incomplete quadratic equation −x 2 +9=0 has two roots x=3 or x=−3.
a x 2 +b x=0
It remains to deal with the solution of the last type of incomplete quadratic equations for c=0. Incomplete quadratic equations of the form a x 2 + b x = 0 allow you to solve factorization method. Obviously, we can, located on the left side of the equation, for which it is enough to take the common factor x out of brackets. This allows us to move from the original incomplete quadratic equation to an equivalent equation of the form x·(a·x+b)=0. And this equation is equivalent to a set of two equations x=0 and a·x+b=0, the latter of which is linear and has a root x=−b/a.
So, the incomplete quadratic equation a·x 2 +b·x=0 has two roots x=0 and x=−b/a.
To consolidate the material, we will analyze the solution to a specific example.
Example.
Solve the equation.
Solution.
Taking x out of brackets gives the equation . It is equivalent to two equations x=0 and . We solve the resulting linear equation: , and by dividing the mixed number by an ordinary fraction, we find . Therefore, the roots of the original equation are x=0 and .
After gaining the necessary practice, solutions to such equations can be written briefly:
Answer:
x=0 , .
Discriminant, formula for the roots of a quadratic equation
To solve quadratic equations, there is a root formula. Let's write it down formula for the roots of a quadratic equation: , Where D=b 2 −4 a c- so-called discriminant of a quadratic equation. The entry essentially means that .
It is useful to know how the root formula was derived and how it is used in finding the roots of quadratic equations. Let's figure this out.
Derivation of the formula for the roots of a quadratic equation
Let us need to solve the quadratic equation a·x 2 +b·x+c=0. Let's perform some equivalent transformations:
- We can divide both sides of this equation by a non-zero number a, resulting in the following quadratic equation.
- Now select a complete square on its left side: . After this, the equation will take the form .
- At this stage, it is possible to transfer the last two terms to the right side with the opposite sign, we have .
- And let’s also transform the expression on the right side: .
As a result, we arrive at an equation that is equivalent to the original quadratic equation a·x 2 +b·x+c=0.
We have already solved equations similar in form in the previous paragraphs, when we examined. This allows us to draw the following conclusions regarding the roots of the equation:
- if , then the equation has no real solutions;
- if , then the equation has the form , therefore, , from which its only root is visible;
- if , then or , which is the same as or , that is, the equation has two roots.
Thus, the presence or absence of roots of the equation, and therefore the original quadratic equation, depends on the sign of the expression on the right side. In turn, the sign of this expression is determined by the sign of the numerator, since the denominator 4·a 2 is always positive, that is, by the sign of the expression b 2 −4·a·c. This expression b 2 −4 a c was called discriminant of a quadratic equation and designated by the letter D. From here the essence of the discriminant is clear - based on its value and sign, they conclude whether the quadratic equation has real roots, and if so, what is their number - one or two.
Let's return to the equation and rewrite it using the discriminant notation: . And we draw conclusions:
- if D<0 , то это уравнение не имеет действительных корней;
- if D=0, then this equation has a single root;
- finally, if D>0, then the equation has two roots or, which can be rewritten in the form or, and after expanding and bringing the fractions to a common denominator we obtain.
So we derived the formulas for the roots of the quadratic equation, they look like , where the discriminant D is calculated by the formula D=b 2 −4·a·c.
With their help, with a positive discriminant, you can calculate both real roots of a quadratic equation. When the discriminant is equal to zero, both formulas give the same value of the root, corresponding to a unique solution to the quadratic equation. And with a negative discriminant, when trying to use the formula for the roots of a quadratic equation, we are faced with extracting the square root of a negative number, which takes us beyond the scope of the school curriculum. With a negative discriminant, the quadratic equation has no real roots, but has a pair complex conjugate roots, which can be found using the same root formulas we obtained.
Algorithm for solving quadratic equations using root formulas
In practice, when solving quadratic equations, you can immediately use the root formula to calculate their values. But this is more related to finding complex roots.
However, in a school algebra course we usually talk not about complex, but about real roots of a quadratic equation. In this case, it is advisable, before using the formulas for the roots of a quadratic equation, to first find the discriminant, make sure that it is non-negative (otherwise, we can conclude that the equation does not have real roots), and only then calculate the values of the roots.
The above reasoning allows us to write algorithm for solving a quadratic equation. To solve the quadratic equation a x 2 +b x+c=0, you need to:
- using the discriminant formula D=b 2 −4·a·c, calculate its value;
- conclude that a quadratic equation has no real roots if the discriminant is negative;
- calculate the only root of the equation using the formula if D=0;
- find two real roots of a quadratic equation using the root formula if the discriminant is positive.
Here we just note that if the discriminant is equal to zero, you can also use the formula; it will give the same value as .
You can move on to examples of using the algorithm for solving quadratic equations.
Examples of solving quadratic equations
Let's consider solutions to three quadratic equations with a positive, negative and zero discriminant. Having dealt with their solution, by analogy it will be possible to solve any other quadratic equation. Let's begin.
Example.
Find the roots of the equation x 2 +2·x−6=0.
Solution.
In this case, we have the following coefficients of the quadratic equation: a=1, b=2 and c=−6. According to the algorithm, you first need to calculate the discriminant; to do this, we substitute the indicated a, b and c into the discriminant formula, we have D=b 2 −4·a·c=2 2 −4·1·(−6)=4+24=28. Since 28>0, that is, the discriminant is greater than zero, the quadratic equation has two real roots. Let's find them using the root formula, we get , here you can simplify the resulting expressions by doing moving the multiplier beyond the root sign followed by reduction of the fraction:
Answer:
Let's move on to the next typical example.
Example.
Solve the quadratic equation −4 x 2 +28 x−49=0 .
Solution.
We start by finding the discriminant: D=28 2 −4·(−4)·(−49)=784−784=0. Therefore, this quadratic equation has a single root, which we find as , that is,
Answer:
x=3.5.
It remains to consider solving quadratic equations with a negative discriminant.
Example.
Solve the equation 5·y 2 +6·y+2=0.
Solution.
Here are the coefficients of the quadratic equation: a=5, b=6 and c=2. We substitute these values into the discriminant formula, we have D=b 2 −4·a·c=6 2 −4·5·2=36−40=−4. The discriminant is negative, therefore, this quadratic equation has no real roots.
If you need to indicate complex roots, then we apply the well-known formula for the roots of a quadratic equation, and perform operations with complex numbers:
Answer:
there are no real roots, complex roots are: .
Let us note once again that if the discriminant of a quadratic equation is negative, then in school they usually immediately write down an answer in which they indicate that there are no real roots, and complex roots are not found.
Root formula for even second coefficients
The formula for the roots of a quadratic equation, where D=b 2 −4·a·c allows you to obtain a formula of a more compact form, allowing you to solve quadratic equations with an even coefficient for x (or simply with a coefficient having the form 2·n, for example, or 14· ln5=2·7·ln5 ). Let's get her out.
Let's say we need to solve a quadratic equation of the form a x 2 +2 n x+c=0. Let's find its roots using the formula we know. To do this, we calculate the discriminant D=(2 n) 2 −4 a c=4 n 2 −4 a c=4 (n 2 −a c), and then we use the root formula:
Let us denote the expression n 2 −a c as D 1 (sometimes it is denoted D "). Then the formula for the roots of the quadratic equation under consideration with the second coefficient 2 n will take the form  , where D 1 =n 2 −a·c.
, where D 1 =n 2 −a·c.
It is easy to see that D=4·D 1, or D 1 =D/4. In other words, D 1 is the fourth part of the discriminant. It is clear that the sign of D 1 is the same as the sign of D . That is, the sign D 1 is also an indicator of the presence or absence of roots of a quadratic equation.
So, to solve a quadratic equation with a second coefficient 2·n, you need
- Calculate D 1 =n 2 −a·c ;
- If D 1<0 , то сделать вывод, что действительных корней нет;
- If D 1 =0, then calculate the only root of the equation using the formula;
- If D 1 >0, then find two real roots using the formula.
Let's consider solving the example using the root formula obtained in this paragraph.
Example.
Solve the quadratic equation 5 x 2 −6 x −32=0 .
Solution.
The second coefficient of this equation can be represented as 2·(−3) . That is, you can rewrite the original quadratic equation in the form 5 x 2 +2 (−3) x−32=0, here a=5, n=−3 and c=−32, and calculate the fourth part of the discriminant: D 1 =n 2 −a·c=(−3) 2 −5·(−32)=9+160=169. Since its value is positive, the equation has two real roots. Let's find them using the appropriate root formula:
Note that it was possible to use the usual formula for the roots of a quadratic equation, but in this case more computational work would have to be performed.
Answer:
Simplifying the form of quadratic equations
Sometimes, before starting to calculate the roots of a quadratic equation using formulas, it doesn’t hurt to ask the question: “Is it possible to simplify the form of this equation?” Agree that in terms of calculations it will be easier to solve the quadratic equation 11 x 2 −4 x−6=0 than 1100 x 2 −400 x−600=0.
Typically, simplifying the form of a quadratic equation is achieved by multiplying or dividing both sides by a certain number. For example, in the previous paragraph it was possible to simplify the equation 1100 x 2 −400 x −600=0 by dividing both sides by 100.
A similar transformation is carried out with quadratic equations, the coefficients of which are not . In this case, both sides of the equation are usually divided by the absolute values of its coefficients. For example, let's take the quadratic equation 12 x 2 −42 x+48=0. absolute values of its coefficients: GCD(12, 42, 48)= GCD(GCD(12, 42), 48)= GCD(6, 48)=6. Dividing both sides of the original quadratic equation by 6, we arrive at the equivalent quadratic equation 2 x 2 −7 x+8=0.
And multiplying both sides of a quadratic equation is usually done to get rid of fractional coefficients. In this case, multiplication is carried out by the denominators of its coefficients. For example, if both sides of the quadratic equation are multiplied by LCM(6, 3, 1)=6, then it will take the simpler form x 2 +4·x−18=0.
In conclusion of this point, we note that they almost always get rid of the minus at the highest coefficient of a quadratic equation by changing the signs of all terms, which corresponds to multiplying (or dividing) both sides by −1. For example, usually one moves from the quadratic equation −2 x 2 −3 x+7=0 to the solution 2 x 2 +3 x−7=0 .
Relationship between roots and coefficients of a quadratic equation
The formula for the roots of a quadratic equation expresses the roots of the equation through its coefficients. Based on the root formula, you can obtain other relationships between roots and coefficients.
The most well-known and applicable formulas from Vieta’s theorem are of the form and . In particular, for the given quadratic equation, the sum of the roots is equal to the second coefficient with the opposite sign, and the product of the roots is equal to the free term. For example, by looking at the form of the quadratic equation 3 x 2 −7 x + 22 = 0, we can immediately say that the sum of its roots is equal to 7/3, and the product of the roots is equal to 22/3.
Using the already written formulas, you can obtain a number of other connections between the roots and coefficients of the quadratic equation. For example, you can express the sum of the squares of the roots of a quadratic equation through its coefficients: .
Bibliography.
- Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Mordkovich A. G. Algebra. 8th grade. In 2 hours. Part 1. Textbook for students of general education institutions / A. G. Mordkovich. - 11th ed., erased. - M.: Mnemosyne, 2009. - 215 p.: ill. ISBN 978-5-346-01155-2.
