Instruktioner. For at løse online skal du vælge ligningstypen og indstille dimensionen af de tilsvarende matricer.
hvor A, B, C er de specificerede matricer, X er den ønskede matrix. Matrixligninger på formen (1), (2) og (3) løses gennem den inverse matrix A -1. Hvis udtrykket A·X - B = C er givet, så er det nødvendigt først at tilføje matricerne C + B og finde en løsning for udtrykket A·X = D, hvor D = C + B (). Hvis udtrykket A*X = B 2 er givet, skal matrixen B først kvadreres. Det anbefales også at sætte dig ind i de grundlæggende operationer på matricer.Eksempel nr. 1. Dyrke motion. Find løsningen til matrixligningen
Løsning. Lad os betegne:
Så vil matrixligningen blive skrevet på formen: A·X·B = C.
Determinanten af matrix A er lig med detA=-1
Da A er en ikke-singular matrix, er der en invers matrix A-1. Multiplicer begge sider af ligningen til venstre med A -1: Gang begge sider af denne ligning til venstre med A -1 og til højre med B -1: A -1 ·A·X·B·B -1 = A-1·C·B-1. Da A A -1 = B B -1 = E og E X = X E = X, så er X = A -1 C B -1
Invers matrix A -1: ![]()
Lad os finde den inverse matrix B -1.
Transponeret matrix B T:
Invers matrix B -1: ![]()
Vi leder efter matrix X ved hjælp af formlen: X = A -1 ·C·B -1 ![]()
Svar:
Eksempel nr. 2. Dyrke motion. Løs matrixligning ![]()
Løsning. Lad os betegne:
Så vil matrixligningen blive skrevet på formen: A·X = B.
Determinanten af matrix A er detA=0
Da A er en singulær matrix (determinanten er 0), har ligningen derfor ingen løsning.
Eksempel nr. 3. Dyrke motion. Find løsningen til matrixligningen
Løsning. Lad os betegne:
Så vil matrixligningen blive skrevet på formen: X A = B.
Determinanten af matrix A er detA=-60
Da A er en ikke-singular matrix, er der en invers matrix A-1. Lad os gange begge sider af ligningen til højre med A -1: X A A -1 = B A -1, hvorfra vi finder, at X = B A -1
Lad os finde den inverse matrix A -1 .
Transponeret matrix A T: 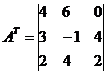
Invers matrix A -1: 
Vi leder efter matrix X ved hjælp af formlen: X = B A -1 
Svar: > 
Ved hjælp af online matrixberegneren kan du folde, trække fra, formere sig, omsætte matricer, beregne baglæns matrix, pseudo-omvendt matrix, rang matricer, determinant matrix, m-norm og l-norm af matricen, hæve matrix til magten, gange matrix med tal, gør skeletnedbrydning matricer, fjerne lineært afhængige rækker fra en matrix eller lineært afhængige kolonner, adfærd Gaussisk udelukkelse, løs matrixligning AX=B, lave LU-nedbrydning af en matrix,beregn kernen (nullrum) af en matrix, gør Gram-Schmidt ortogonalisering og Gram-Schmidt ortonormalisering.
Online matrixberegneren fungerer ikke kun med decimaltal, men også med brøker. For at indtaste brøker skal du indtaste de oprindelige matricer og indtaste tal i formularen -en eller -en/b, Hvor -en Og b heltal eller decimaler ( b positivt tal). For eksempel 12/67, -67,78/7,54, 327,6, -565.
Knappen i øverste venstre hjørne af matricen åbner en menu (fig. 1) til transformation af den originale matrix (oprettelse af en identitetsmatrix, en nulmatrix eller sletning af indholdet af celler).

Under beregninger behandles en tom celle som nul.
For enkeltmatrixoperationer (dvs. transponering, invers, pseudo-invers, skeletnedbrydning osv.), skal du først vælge en specifik matrix ved hjælp af alternativknappen.
Knapperne Fn1, Fn2 og Fn3 skifter forskellige grupper af funktioner.
Ved at klikke på de beregnede matricer åbnes en menu (fig. 2), som giver dig mulighed for at skrive denne matrix ind i de oprindelige matricer og , samt konvertere elementerne i matricen på plads til en fælles brøk, en blandet brøk eller en decimaltal.
Beregn summen, forskellen, produktet af matricer online
sum, forskel eller produkt af matricer. For at beregne summen eller forskellen af matricer er det nødvendigt, at de har samme dimension, og for at beregne produktet af matricer skal antallet af kolonner i den første matrix være lig med antallet af rækker i den anden matrix.
For at beregne summen, forskellen eller produktet af matricer:
Online matrix omvendt beregning
En online matrixberegner kan bruges til at beregne den inverse matrix. For at en invers matrix kan eksistere, skal den oprindelige matrix være en ikke-singular kvadratisk matrix.
For at beregne den inverse matrix:
For detaljeret invers matrixberegning trin for trin, brug denne matrix inverse lommeregner. Se teorien om beregning af den inverse matrix.
Beregn determinanten for en matrix online
Du kan bruge en online matrixberegner til at beregne determinanten for en matrix. For at en matrixdeterminant kan eksistere, skal den oprindelige matrix være en ikke-singular kvadratisk matrix.
For at beregne determinanten af en matrix:
For en detaljeret beregning af determinanten for en matrix trin for trin, skal du bruge denne lommeregner til at beregne determinanten for en matrix. Se teorien om beregning af determinanten for en matrix.
Beregn matrix rangering online
En online matrixberegner kan bruges til at beregne rangeringen af en matrix.
For at beregne rangeringen af en matrix:
For at beregne matrixrangeringen trin for trin i detaljer, skal du bruge denne matrixrangberegner. Se teorien om beregning af rangeringen af en matrix.
Online pseudoinvers matrixberegning
En online matrixberegner kan bruges til at beregne den pseudoinverse matrix. En pseudo-invers til en given matrix eksisterer altid.
For at beregne den pseudoinverse matrix:
Fjernelse af lineært afhængige matrixrækker eller kolonner online
Online matrixberegneren giver dig mulighed for at fjerne lineært afhængige rækker eller kolonner fra en matrix, dvs. oprette en fuld rang matrix.
Sådan fjerner du lineært afhængige matrixrækker eller kolonner:
Skeletmatrixnedbrydning online
For at udføre skeletmatrixnedbrydning online
Løsning af en matrixligning eller system af lineære ligninger AX=B online
Ved hjælp af en online matrixberegner kan du løse matrixligningen AX=B i forhold til matrixen X. I det specielle tilfælde, hvis matricen B er en kolonnevektor, vil X være en løsning til systemet af lineære ligninger AX= B.
For at løse matrixligningen:
Bemærk venligst, at matricer og skal have lige mange rækker.
Gaussisk eliminering eller reduktion af en matrix til trekantet (trin) form online
Online matrixberegneren udfører Gaussisk eliminering for både kvadratiske matricer og rektangulære matricer af enhver rang. Først udføres den sædvanlige Gauss-metode. Hvis det førende element på et tidspunkt er lig med nul, så vælges en anden mulighed for Gauss-eliminering ved at vælge det største førende element i kolonnen.
For at eliminere Gaussisk eller reducere matrixen til trekantet form
LU-nedbrydning eller LUP-nedbrydning af en matrix online
Denne matrixberegner giver dig mulighed for at udføre LU-dekomponering af en matrix (A=LU) eller LUP-dekomponering af en matrix (PA=LU), hvor L er en nedre trekantet matrix, U er en øvre trekantet (trapezformet) matrix, P er en permutationsmatrix. Først udfører programmet LU-nedbrydning, dvs. en sådan dekomponering, hvor P=E, hvor E er identitetsmatrixen (dvs. PA=EA=A). Hvis dette ikke er muligt, udføres LUP-nedbrydning. Matrix A kan enten være en kvadratisk eller en rektangulær matrix af enhver rang.
For LU(LUP)-nedbrydning:
Konstruktion af kernen (nullrum) af en matrix online
Ved hjælp af en matrixberegner kan du konstruere nulrummet (kernen) af en matrix.
At konstruere nulrummet (kernen) af matrixen.
> Hej alle sammen!!! Er der en formel, hvormed du kan fjerne skalering fra en matrix uden at kende skaleringsfaktorerne???
Vi huskede straks polær nedbrydning. Nå, matrixen M er repræsenteret som O * P. Hvor O er ortogonal, og P er positiv bestemt, symmetrisk - det vil sige en kompressions- eller ekspansionsmatrix. Her tager vi matrixen O.
Spørgsmålet opstår. Og hvis vi udvider M på den anden side, får vi P' * O'. Dekomponering i en anden rækkefølge, med forskellige a priori-matricer. Hvorfor ikke tage O'? Jeg kæmpede med spørgsmålet i cirka fem minutter, indtil jeg huskede, hvordan jeg havde givet eleverne en fejl i denne sag. Matrix O’ falder faktisk sammen med matrix O. Hvis du for nylig er færdiguddannet fra universitetet eller stadig studerer, kan du endda prøve at bevise dette faktum.
Så polær ekspansion:
For at finde den positive kvadratrod af en matrix foreslår positiv videnskab at beregne egenværdierne. For hver egenværdi skal du finde sit eget underrum og derefter omhyggeligt lave den faktiske kvadratrod af operatoren.
Da jeg forestillede mig, hvad der ville ske for en matrix tæt på identitetsmatrixen, rystede jeg. Alt vil dø på grund af flyderens unøjagtigheder, rækken af matricerne vil gå ned - et fuldstændigt kollaps lover at ske.
Hvorfor prøver ædle dons ikke gentagelser, der er kendt for at være guddommelige?
Her findes roden af et tal ved hjælp af Newtons metode. Sekvens a_(i+1) = 0,5 * (a_i + x/a_i); konvergerer stolt til kvadratroden af x. Som en test tog jeg en andens bibliotek om mat3x3 og nittede en matrixanalog.
En direkte analog af Newtons metode konvergerer hurtigt i 3-4 iterationer, test passerer som en leg. Resultatet er en polær dekomponering for matricer; effektiviteten af algoritmen er indlysende fra den elementære spektrale teori om operatorer. Tydeligt efter en halv times knirke i min hjerne.
Så vi har fundet den polære nedbrydning. Spørgsmålet er - hvorfor? Og her er jeg tvunget til at gå videre til hovedpunktet i min betænkning. Undervisning er ond. Den tid, du brugte på at huske spektraloperatorteori, er spildt med succes.
Scale Shear Rotate-nedbrydningen søges efter én gang. Vi anvender processen med ortogonalisering og ortonormalisering på matrixen. Efter kolonner. Vi får en fremragende matrix. Og hvorfor bliver resultatet værre? Ikke noget!
Jeg så et indlæg med kode i Pascal, der beregner den samme Scale Shear Rotate-nedbrydning, og pludselig indså jeg, at jeg ikke har nogen argumenter for polær dekomponering. Hvilket kræver hvem der ved hvilken slags computerteknologi.
Selvfølgelig er der mindre indvendinger, nærmest skænderier. For eksempel er tangentrum lettere at betragte som ortonormalt. Beregningsmæssigt enklere. Normalt betragter vi dPosition/du, normalen, og den tredje vektor tages vinkelret på dette par. Det er klart, at metoden er asymmetrisk med hensyn til teksturkoordinater; hvilken af dem der er først og hvilken der er anden er fuldstændig uklart. Det ser ud til at være korrekt at anvende den polære nedbrydning på den lokale transformationsmatrix.
Du kan måske bemærke forskellen mellem den "korrekte" polære nedbrydning og den "forkerte" kolonne-ortogonaliseringsproces. Du vil sandsynligvis ikke bemærke det. Og billedet bliver bestemt ikke bedre.
P.S. Det er også meget fedt at gemme animationer i Scale Shear Rotate. Tre vektorer, en quaternion. Forskydning er næsten altid 0, skala er næsten altid 1, konstante spor kan blive smidt ud. Og hvor der er ikke-konstante spor, er der en måde at presse det ud ved at specialisere skabelonen. Eller noget andet.
1)
Lad os først overveje rigtige matricer. Antag, at roden er udtrukket fra matrixen $%A$%, dvs. der er en matrix $%B$% sådan, at $%B \cdot B=A$%. Lad os også antage, at matrixen $%B$% kan reduceres til diagonal form, dvs. der er en matrix $%S$% sådan, at $%S^(-1)BS=B"$%, hvor $%B"$% er en diagonal matrix. Af lighederne $%B"B"=S^(-1)BSS^(-1)BS=S^(-1)BBS=S^(-1)AS$% følger det, at $%A"=S ^ (-1)AS$% er også en diagonal matrix, dvs. matricerne $%A$% og $%B$% reduceres til diagonal form ved den samme transformation, da elementerne i primede matricer er egenværdierne af unprimed , så følger følgende konklusioner af ovenstående betragtninger.
1.1)Hvis matrixen $%A$% er en symmetrisk positiv bestemt matrix, så udvindes roden fra den i form af en reel matrix.
1.2) Algoritmen til at beregne roden af en sådan matrix er som følger: løs egenværdiproblemet, udtræk rødderne fra egenværdierne, komponer en diagonal matrix ud fra dem, påfør den en transformation invers til transformationen, der konverterer matricen $%A$% til en diagonal form.
1.3) Antallet af forskellige matricer $%B$% er lig med $%2^n$%, fordi For hver egenværdi er der 2 rodværdier - positive og negative.
2) For en kompleks matrix vil ræsonnementet forblive gyldigt, hvis vi erstatter symmetri med enhed. Kravet om positiv bestemthed vil naturligvis blive fjernet.
3)
Løsning til den generelle sag. Lad os antage, at transformationen $%S$% bringer matrixen $%B$% ikke til diagonal, men til øvre trekantet form, dvs. matricen $%B"$% er øvre trekantet. En sådan transformation findes for enhver kvadratisk matrix. Det er let at verificere, at matrixen $%A"$% også vil vise sig at være øvre trekantet, og de diagonale elementer i matrix $%A"$% vil være kvadrater, der svarer til diagonale elementer i matrixen $%B"$%. Dette giver dig mulighed for at finde alle de diagonale elementer i matricen $%B"$% ved at tage roden af de diagonale elementer i matrixen $%A"$%, og derefter langs kæden finde alle de andre elementer i matrixen matrix $%B"$%. Herfra opnås følgende konklusioner.
3.1) En rod udvindes fra en hvilken som helst kompleks matrix; i det generelle tilfælde er sådanne rødder $%2^n$%, men der kan være sammenfaldende (flere) blandt dem.
3.2) Algoritmen til at beregne rødderne er som følger: transformer matricen $%A$% til øvre trekantet form, find matricen $%B"$% ved hjælp af den formulerede algoritme og lav den inverse transformation.
3.3) En nødvendig og tilstrækkelig betingelse for virkeligheden af rødderne af en reel matrix er, at de diagonale elementer ikke er negative efter transformation af matrixen til en trekantet form. Determinantens ikke-negativitet er en nødvendig, men ikke tilstrækkelig betingelse.
Tillæg 1 (svar på kommentar). Du mente "til en trekantet udsigt". Generelt i stk. 1, 2, alt er helt klart, men punkt 3 skal tilsyneladende tænkes mere. Pointen er, at den Gaussiske metode ikke må reduceres til transformationen $%S^(-1)AS$%, og beviset er baseret på dette. De der. beviset gælder kun for de matricer, der kan reduceres til trekantet form ved transformationen $%S^(-1)AS$%.
Tillæg 2. Det ser ud til, at i afsnit 3 generelt er alt korrekt, du skal bare bruge transformationen af matricen $%A$% til Jordan-formen - for denne transformation er der altid en matrix opnået fra løsning af egenværdiproblemet. Problemet er, at kvadratet af en Jordan-matrix ikke er en Jordan-matrix (selvom den er trekantet og endda bidiagonal). En streng begrundelse for algoritmen kræver bevis for følgende sætning: "Hvis $%A"=B"^2$% og $%A"$% er en Jordan-matrix, så er $%B"$% en trekantet matrix. " Udsagnet virker sandt, men jeg ved ikke, hvordan jeg skal bevise det endnu.
