og et skæreplan, der er parallelt med dets basis.
Eller med andre ord: afkortet pyramide- dette er et polyeder, der er dannet af en pyramide og dets tværsnit parallelt med bunden.
Et afsnit, der er parallelt med bunden af pyramiden, deler pyramiden i 2 dele. Den del af pyramiden mellem dens base og tværsnit er afkortet pyramide.
Denne sektion for en afkortet pyramide viser sig at være en af baserne i denne pyramide.
Afstanden mellem baserne i en afkortet pyramide er højden af en afkortet pyramide.
Den afkortede pyramide vil være korrekt, når pyramiden, hvorfra den var afledt, også var korrekt.
Højden af trapezsiden af sidefladen af en regulær afkortet pyramide er apotem regulær afkortet pyramide.
Egenskaber ved en afkortet pyramide.
1. Hver sideflade af en regulær afkortet pyramide er ligesidede trapezoider en størrelse.
2. Baserne i en afkortet pyramide er lignende polygoner.
3. Sidekanterne af en regulær afkortet pyramide har lige værdi og man hælder i forhold til bunden af pyramiden.
4. Sideflader afkortede pyramider er trapezformer.
5. De dihedrale vinkler ved sidekanterne af en regulær afkortet pyramide er af samme størrelse.
6. Forholdet mellem basisarealer: S2/S1 = k2.
Formler til en afkortet pyramide.
For en vilkårlig pyramide:
Rumfanget af en afkortet pyramide er lig med 1/3 af produktet af højden h (OS) med summen af arealerne af den øvre base S 1 (abcde), den nedre base af den afkortede pyramide S 2 (ABCDE) og gennemsnittet proportionalt mellem dem.
Pyramidevolumen:
Hvor S 1, S 2 — basisareal,
h— højden af den afkortede pyramide.
Sidefladeareal ![]() er lig med summen af arealerne af sidefladerne af den afkortede pyramide.
er lig med summen af arealerne af sidefladerne af den afkortede pyramide.
For en almindelig afkortet pyramide:
Regelmæssig afkortet pyramide- et polyeder, der er dannet af en regulær pyramide og dens sektion, som er parallel med basen.
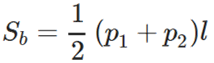
Arealet af den laterale overflade af en regulær afkortet pyramide er lig med ½ produktet af summen af omkredsen af dens baser og apotem.
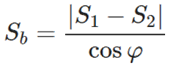
Hvor S 1, S 2- basisareal,
φ — dihedral vinkel ved bunden af pyramiden.
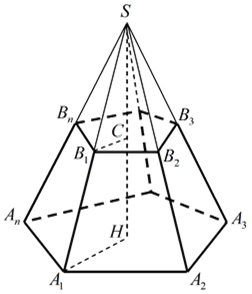
CH er højden af den afkortede pyramide, P 1 Og P2- omkredsen af baserne, S 1 Og S 2- basisarealer, S side- lateral overfladeareal, S fuld- areal fuld overflade:
Udsnit af en pyramide af et plan parallelt med bunden.
En sektion af en pyramide ved et plan, som er parallel med dens base (vinkelret på højden) og deler pyramidens højde og sidekanter i proportionale segmenter.
En sektion af en pyramide ved et plan, der er parallel med dens base (vinkelret på dens højde) er en polygon, der ligner bunden af pyramiden, og lighedskoefficienten for disse polygoner svarer til forholdet mellem deres afstande fra toppen af pyramiden.
Tværsnitsarealerne, der er parallelle med bunden af pyramiden, divideres med kvadratet af deres afstande fra toppen af pyramiden.
Følgende unikke lommeregner bruges til at konvertere eksotiske længdeenheder til...
Næste online lommeregner omkring pund. Tidligere var det meget populært...
Følgende online-beregner kan beregne væskeniveauet i en cylindrisk beholder...
Følgende online lommeregner konverterer temperaturer mellem forskellige skalaer. Husk lommeregneren...
Den næste lommeregner er interessant, fordi den konverterer gamle russiske monetære...
Følgende lommeregner vil være meget nyttig for dem, der beslutter sig for at købe eller...
Følgende lommeregner fungerer meget enkelt, du skal kun indtaste en...
Følgende online-beregner beregner en persons højde ved hjælp af det russiske målesystem...
Følgende online-beregner kan beregne skærmdimensionerne på tv'er, computere, projektorer,...
Der er 2 lommeregnere foran dig: den ene hjælper dig med at vælge fotoformat...
Følgende 2 lommeregnere oversætter givet nummer fliser i kvadratmeter…
Her er 2 online lommeregnere. De konverterer mål for areal fra metriske...
Følgende usædvanlige lommeregner konverterer længdemål fra det russiske system til...
Her er 2 lommeregnere, der er designet til at konvertere længdemål...
Den følgende simple lommeregner konverterer din indtastede toC fra Kelvin til...
Følgende lommeregner er til at konvertere kg til pund. Der er også…
Et polyeder, hvor en af dets flader er en polygon, og alle andre flader er trekanter med et fælles toppunkt, kaldes en pyramide.
Disse trekanter, der udgør pyramiden, kaldes sideflader, og den resterende polygon er basis pyramider.
I bunden af pyramiden ligger en geometrisk figur - en n-gon. I dette tilfælde kaldes pyramiden også n-carbon.
En trekantet pyramide, hvis kanter alle er lige, kaldes tetraeder.
Pyramidens kanter, der ikke hører til basen, kaldes tværgående, og deres fælles punkt- Det her vertex pyramider. De andre kanter af pyramiden kaldes normalt parter i grundlaget.
Pyramiden kaldes korrekt, hvis den har en regulær polygon ved sin basis, og alle sidekanter er ens med hinanden.
Afstanden fra toppen af pyramiden til bundens plan kaldes højde pyramider. Vi kan sige, at pyramidens højde er et segment vinkelret på basen, hvis ender er i toppen af pyramiden og på basens plan.
For enhver pyramide gælder følgende formler:
1) S fuld = S side + S hoved, Hvor
S total - pyramidens samlede overfladeareal;
S side – areal af sidefladen, dvs. summen af arealerne af alle laterale flader af pyramiden;
S hoved - område af bunden af pyramiden.
2) V = 1/3 S base N, Hvor
V er pyramidens rumfang;
H – pyramidens højde.
Til almindelig pyramide opstår:
S-siden = 1/2 P hovedh, Hvor
P hoved - omkredsen af bunden af pyramiden;
h er længden af apotemet, det vil sige længden af højden af sidefladen sænket fra toppen af pyramiden.
Den del af pyramiden, der er indesluttet mellem to planer - bundens plan og skæreplanet parallelt med bunden kaldes afkortet pyramide.
Basen af pyramiden og tværsnit af pyramiden parallelt plan hedder grunde afkortet pyramide. De resterende ansigter kaldes tværgående. Afstanden mellem basernes planer kaldes højde afkortet pyramide. Kanter, der ikke hører til baserne, kaldes tværgående.
Derudover bunden af den afkortede pyramide lignende n-gons. Hvis baserne i en afkortet pyramide er regulære polygoner, og alle sidekanter er lig med hinanden, så kaldes en sådan afkortet pyramide korrekt.
Til vilkårlig afkortet pyramide følgende formler gælder:
1) S fuld = S side + S 1 + S 2, Hvor
S total – samlet overfladeareal;
S side – areal af sidefladen, dvs. summen af arealerne af alle laterale flader af en afkortet pyramide, som er trapezoider;
S 1, S 2 - basisarealer;
2) V = 1/3(S 1 + S 2 + √(S 1 · S 2)) H, Hvor
V er volumenet af den afkortede pyramide;
H – højden af den afkortede pyramide.
Til regulær afkortet pyramide vi har også:
S-side = 1/2(P 1 + P 2) h, Hvor
P 1, P 2 - omkredse af baserne;
h – apotem (højden af sidefladen, som er en trapez).
Lad os overveje flere problemer, der involverer en afkortet pyramide.
Opgave 1.
I en trekantet afkortet pyramide med en højde lig med 10 er siderne af en af baserne 27, 29 og 52. Bestem rumfanget af den afkortede pyramide, hvis omkredsen af den anden base er 72.
Løsning.
Overvej den afkortede pyramide ABCA 1 B 1 C 1 vist i Figur 1.
1. Volumenet af en afkortet pyramide kan findes ved hjælp af formlen
V = 1/3H · (S 1 + S 2 + √(S 1 · S 2)), hvor S 1 er arealet af en af baserne, kan findes ved hjælp af Herons formel
S = √(p(p – a)(p – b)(p – c)),
fordi Opgaven angiver længderne af de tre sider af en trekant.
Vi har: p 1 = (27 + 29 + 52)/2 = 54.
S 1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 27 25 2) = 270.
2. Pyramiden er afkortet, hvilket betyder, at baserne ligger lignende polygoner. I vores tilfælde trekant ABC ligner trekant A 1 B 1 C 1. Derudover kan lighedskoefficienten findes som forholdet mellem omkredsen af de undersøgte trekanter, og forholdet mellem deres arealer vil være lig med kvadratet af lighedskoefficienten. Vi har således:
S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Derfor er S 2 = 4S 1 /9 = 4 270/9 = 120.
Så V = 1/3 10(270 + 120 + √(270 120)) = 1900.
Svar: 1900.
Opgave 2.
I en trekantet afkortet pyramide trækkes et plan gennem siden af den øverste base parallelt med den modsatte lateral ribben. I hvilket forhold opdeles rumfanget af en afkortet pyramide, hvis de tilsvarende sider af baserne er i forholdet 1:2?
Løsning.
Overvej ABCA 1 B 1 C 1 - en afkortet pyramide vist i ris. 2.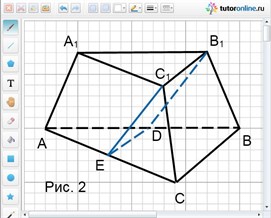
Da siderne i baserne er i forholdet 1:2, er basernes areal i forholdet 1:4 (trekant ABC svarer til trekant A 1 B 1 C 1).
Så er volumenet af den afkortede pyramide:
V = 1/3h · (S 1 + S 2 + √(S 1 · S 2)) = 1/3h · (4S 2 + S 2 + 2S 2) = 7/3 · h · S 2, hvor S 2 – areal af den øverste base, h – højde.
Men rumfanget af prismet ADEA 1 B 1 C 1 er V 1 = S 2 h og derfor,
V 2 = V – V 1 = 7/3 · h · S 2 - h · S 2 = 4/3 · h · S 2.
Så V 2: V 1 = 3: 4.
Svar: 3:4.
Opgave 3.
Siderne af baserne i en regulær firkantet afkortet pyramide er lig med 2 og 1, og højden er 3. Et plan trækkes gennem skæringspunktet for pyramidens diagonaler, parallelt med pyramidens baser, der deler pyramiden i to dele. Find volumen af hver af dem.
Løsning.
Overvej den afkortede pyramide ABCDA 1 B 1 C 1 D 1 vist i ris. 3.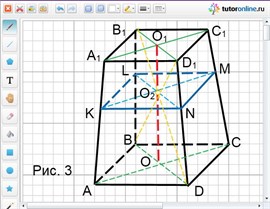
Lad os betegne O 1 O 2 = x, så OO₂ = O 1 O – O 1 O 2 = 3 – x.
Betragt trekanten B 1 O 2 D 1 og trekanten BO 2 D:
vinkel B 1 O 2 D 1 lig med vinkel VO 2 D som lodret;
vinkel BDO 2 er lig med vinkel D 1 B 1 O 2 og vinkel O 2 ВD er lig med vinkel B 1 D 1 O 2, der ligger på tværs ved B 1 D 1 || BD og sekanterne B1D og BD1, henholdsvis.
Derfor ligner trekanten B 1 O 2 D 1 trekanten BO 2 D og sideforholdet er:
В1D 1 /ВD = О 1 О 2 /ОО 2 eller 1/2 = x/(x – 3), hvorfra x = 1.
Betragt trekanten B 1 D 1 B og trekanten LO 2 B: vinkel B er fælles, og der er også et par ensidede vinkler ved B 1 D 1 || LM, hvilket betyder, at trekant B 1 D 1 B ligner trekant LO 2 B, hvorfra B 1 D: LO 2 = OO 1: OO 2 = 3: 2, dvs.
LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.
Så S KLMN = 16/9 · S A 1 B 1 C 1 D 1 = 16/9.
Så V 1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Svar: 152/27; 37/27.
www.site, ved kopiering af materiale helt eller delvist kræves et link til den originale kilde.
