Дефиниции.

Да вземем няколко ъгъла (фиг. 37): ASB, BSC, CSD, които, прилежащи последователно един към друг, са разположени в една равнина около общия връх S. Нека завъртим равнината на ъгъла ASB около общата страна SB, така че тази равнина да образува някоидвустенен ъгъл със самолет BSC. След това, без да променяме получения двустенен ъгъл, го завъртаме около правата линия SC, така че равнината BSC да образува определен двустенен ъгъл с равнината CSD. Нека продължим това последователно въртене около всяка обща страна. Ако последната страна SF съвпадне с първата страна SA, тогава се образува фигура (фиг. 38), която се наричамногостенен ъгъл . Ъгли ASB, BSC,... се наричатплоски ъгли илиръбове , техните страни SA, SB, ... се наричатребра , а общият връх S-отгоре

многостенен ъгъл. Всеки ръб също е ръб на определен двустенен ъгъл; следователно в полиедърния ъгъл има толкова много двустенни ъгли и толкова равнинни ъгли, колкото са всички ръбове в него.Най-малкото число има три лица в полиедърен ъгъл; този ъгъл се наричатриъгълна

. Може да има тетраедрични, петоъгълни и т.н. ъгли.

Многостенният ъгъл се обозначава или с една буква S, поставена на върха, или с поредица от букви SABCDE, от които първата означава върха, а останалите - ръбовете в реда на тяхното разположение.

Многостенният ъгъл се нарича изпъкнал, ако е изцяло разположен от едната страна на равнината на всяко от лицата му, което е удължено за неопределено време. Това е например ъгълът, показан на чертеж 38. Напротив, ъгълът на чертеж 39 не може да се нарече изпъкнал, тъй като е разположен от двете страни на ръба ASB или ръба BCC. Ако пресечем всички лица на многостенен ъгъл с равнина, тогава в сечението се образува многоъгълник ( abcde

). В изпъкнал многостенен ъгъл този многоъгълник също е изпъкнал. Ще разгледаме само изпъкнали.

многостенни ъгли Теорема.

В тристенния ъгъл всеки равнинен ъгъл е по-малък от сумата на другите два равнинни ъгъла.

Нека начертаем върху този ъгъл ъгъла ASD, равен на ъгъла ASB, и начертаем права AC, пресичаща SD в точка D. Нека начертаем SB = SD. Като свържем B с A и C, получаваме \(\Delta\)ABC, в което

AD+DC< АВ + ВС.

Триъгълниците ASD и ASB са еднакви, тъй като всеки от тях има равен ъгъл между тях равни страни: следователно AD = AB. Следователно, ако в полученото неравенство изхвърлим равните членове AD и AB, получаваме това DC< ВС.

Сега забелязваме, че в триъгълниците SCD и SCB две страни на единия са равни на две страни на другия, но третите страни не са равни; в този случай по-големият ъгъл лежи срещу по-голямата от тези страни; означава,

∠CSD< ∠ CSВ.

Като добавим ъгъла ASD към лявата страна на това неравенство и ъгъла, равен на него, към дясната, получаваме неравенството, което трябваше да се докаже:

∠ASC< ∠ CSB + ∠ ASB.

Доказахме, че дори най-големият равнинен ъгъл е по-малък от сбора на другите два ъгъла. Това означава, че теоремата е доказана.

Последица.

Извадете от двете страни на последното неравенство ъгъл ASB или ъгъл CSB; получаваме:< ∠ CSB;

∠ASC - ∠ASB< ∠ ASB.

∠ASC - ∠CSB Разглеждайки тези неравенства отдясно наляво и като вземем предвид този ъгъл ASC като най-голям оттри ъгъла по-голяма от разликата на другите два ъгъла, стигаме до заключението, че.

многостенни ъгли в тристенен ъгъл всеки равнинен ъгъл е по-голям от разликата на другите два ъгъла .

В изпъкнал полиедърен ъгъл сумата от всички равнинни ъгли е по-малка от 4d (360°) Нека пресечем лицата (фиг. 41) на изпъкналия ъгъл SABCDE с някаква равнина; от това получаваме изпъкнало напречно сечениеп

-gon ABCDE.

Прилагайки доказаната по-рано теорема към всеки от тристенните ъгли, чиито върхове са в точки A, B, C, D и E, ние pacholym:< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.

∠ABC Нека съберем всички тези неравенства член по член. Тогава от лявата страна получаваме сбора от всички ъгли на многоъгълника ABCDE, който е равен на 2 - 4дн d , а отдясно - сумата от ъглите на триъгълници ABS, SBC и т.н., с изключение на тези ъгли, които лежат на върха S. Означавайки сумата от тези последни ъгли с буквата X

2Нека съберем всички тези неравенства член по член. Тогава от лявата страна получаваме сбора от всички ъгли на многоъгълника ABCDE, който е равен на 2 - 4дн < 2, получаваме след добавяне: .

dn - x Нека съберем всички тези неравенства член по член. Тогава от лявата страна получаваме сбора от всички ъгли на многоъгълника ABCDE, който е равен на 2 - 4дн Тъй като в разликите 2 , получаваме след добавяне: и 2 дн умалените са еднакви, тогава за да бъде първата разлика по-малка от втората, е необходимо изваждаемото 4 , а отдясно - сумата от ъглите на триъгълници ABS, SBC и т.н., с изключение на тези ъгли, които лежат на върха S. Означавайки сумата от тези последни ъгли с буквата беше повече от самоучастието дн > , а отдясно - сумата от ъглите на триъгълници ABS, SBC и т.н., с изключение на тези ъгли, които лежат на върха S. Означавайки сумата от тези последни ъгли с буквата ; това означава 4 , а отдясно - сумата от ъглите на триъгълници ABS, SBC и т.н., с изключение на тези ъгли, които лежат на върха S. Означавайки сумата от тези последни ъгли с буквата < 4дн .

, т.е.

Най-простите случаи на равенство на тристенни ъгли Теореми.

1) Тристенните ъгли са равни, ако имат:по равен двустенен ъгъл, затворен между два съответно равни и еднакво разположени равнинни ъгъла

2) , или.

1) Нека S и S 1 са два тристенни ъгъла (фиг. 42), за които ∠ASB = ∠A 1 S 1 B 1, ∠ASC = ∠A 1 S 1 C 1 (и тези равни ъглиразположени еднакво) и двустенният ъгъл AS е равен на двустенния ъгъл A 1 S 1 .

Нека вмъкнем ъгъла S 1 в ъгъла S така, че техните точки S 1 и S, прави линии S 1 A 1 и SA и равнини A 1 S 1 B 1 и ASB съвпадат. Тогава ръбът S 1 B 1 ще минава по SB (поради равенството на ъглите A 1 S 1 B 1 и ASB), равнината A 1 S 1 C 1 ще минава по ASC (поради равенството на двустенните ъгли ) и ръбът S 1 C 1 ще минава по ръба SC (поради равенството на ъглите A 1 S 1 C 1 и ASC). Така тристенните ъгли ще съвпадат с всичките им ръбове, т.е. ще бъдат равни.

2) Вторият знак, както и първият, се доказва чрез влагане.

Симетрични многостенни ъгли

Както е известно, вертикални ъглиса равни, когато говорим за ъгли, образувани от прави или равнини. Нека видим дали това твърдение е вярно по отношение на многостенните ъгли.

Нека продължим (фиг. 43) всички ръбове на ъгъла SABCDE извън върха S, тогава се образува друг многостенен ъгъл SA 1 B 1 C 1 D 1 E 1, който може да се нарече вертикаленспрямо първия ъгъл. Лесно се вижда, че и двата ъгъла имат равни равнинни и съответно двустенни ъгли, но и двата са разположени в обратен ред. Наистина, ако си представим наблюдател, който гледа отвън многостенен ъгъл към неговия връх, тогава ръбовете SA, SB, SC, SD, SE ще му изглеждат разположени в посока, обратна на часовниковата стрелка, докато, гледайки ъгъла SA 1 B 1 C 1 D 1 E 1, той вижда ръбовете SA 1, SB 1, ..., разположени по посока на часовниковата стрелка.

Многостенните ъгли със съответно равни равнинни и двустенни ъгли, но разположени в обратен ред, обикновено не могат да се комбинират, когато са вложени; това означава, че не са равни. Такива ъгли се наричат симетричен(спрямо върха S). Симетрията на фигурите в пространството ще бъде разгледана по-подробно по-долу.

Други материали

Нека разгледаме три лъча a, b, c, излизащи от една и съща точка и не лежащи в една и съща равнина. Тристенният ъгъл (abc) е фигура, съставена от три плоски ъгъла (ab), (bc) и (ac) (фиг. 2) се наричат ​​лица на тристенен ъгъл, а техните страни се наричат ​​ръбове; общият връх на плоските ъгли се нарича връх на тристенния ъгъл. Ъглите, образувани от лицата на тристенния ъгъл, се наричат ​​двустенни ъгли.

Концепцията за многостенен ъгъл се дефинира по подобен начин (фиг. 3).

Многостен

В стереометрията се изучават фигури в пространството, наречени тела. Визуално (геометрично) тяло трябва да си представим като част от заеманото пространство физическо тялои ограничен от повърхността.

Полиедърът е тяло, чиято повърхност се състои от крайно числоплоски многоъгълници (фиг. 4). Полиедърът се нарича изпъкнал, ако е разположен от едната страна на равнината на всеки плосък многоъгълник на повърхността му. Обща часттакава равнина и повърхността на изпъкнал многостен се нарича лице. Лицата на изпъкнал многостен са плоски изпъкнали многоъгълници. Страните на лицата се наричат ​​ръбове на многостена, а върховете се наричат ​​върхове на многостена.

Нека обясним това на примера на познат куб (фиг. 5). Има куб изпъкнал многостен. Повърхнината му се състои от шест квадрата: ABCD, BEFC, .... Това са лицата му. Ръбовете на куба са страните на тези квадрати: AB, BC, BE,.... Върховете на куба са върховете на квадратите: A, B, C, D, E, .... Кубът има шест лица, дванадесет ръба и осем върха.

Ще дадем най-простите полиедри - призми и пирамиди, които ще бъдат основният обект на нашето изследване - определения, които по същество не използват понятието тяло. Те ще бъдат определени като геометрични фигури, указващи всички точки в пространството, които им принадлежат. Концепция геометрично тялои повърхността му в общ случайще бъдат дадени по-късно.

Многостенен ъгъл

част от пространството, ограничено от една многостенна кухина конична повърхност, чиято посока е плосък многоъгълник без самопресечения. Лицата на тази повърхност се наричат ​​лица на мозайката, а горната част се нарича горна част на мозайката. М. у. се нарича правилен, ако всички негови линейни ъгли и всички негови двустенни ъгли са равни. Мерой М. у. е площта, ограничена от сферичния многоъгълник, получен от пресичането на лицата на многоъгълника, сфера с радиус равно на едно, и с център във върха на M. y. Вижте също Телесен ъгъл.

Голям Съветска енциклопедия. - М.: Съветска енциклопедия. 1969-1978 .

Вижте какво е "многостенен ъгъл" в други речници:

Вижте плътен ъгъл... Голям Енциклопедичен речник

Вижте плътен ъгъл. * * * МНОГОСТЪЛЕН ЪГЪЛ МНОГОСТЪЛЕН ЪГЪЛ, вижте Телесен ъгъл (вижте ТВЪРДЕН ЪГЪЛ) ... Енциклопедичен речник

Част от пространството, ограничено от една кухина на многостенна коника. повърхност, насочваща към рояк плосък многоъгълник без самопресичане. Лицата на тази повърхност се наричат. ръбовете на M. u., горната част на върха на M. u. Многостенен ъгъл се нарича правилно... Математическа енциклопедия

Вижте Плътен ъгъл... Естествена наука. Енциклопедичен речник

многостенен ъгъл- математика. Част от пространството, ограничено от няколко равнини, минаващи през една точка (връх на ъгъл) ... Речник на много изрази

МНОГОЛИКА, многостранна, многостранна (книга). 1. Имащ няколко лица или страни. Многостранен камък. Многостенен ъгъл (част от пространството, ограничена от няколко равнини, пресичащи се в една точка; мат.). 2. трансфер...... РечникУшакова

- (мат.). Ако начертаем прави OA и 0B от точка O на дадена равнина, получаваме ъгъл AOB (фиг. 1). глупости. 1. Точка 0 извика върха на ъгъла и правите OA и 0B като страни на ъгъла. Да предположим, че са дадени два ъгъла ΒΟΑ и Β 1 Ο 1 Α 1, така че... ...

- (мат.). Ако начертаем прави OA и 0B от точка O на дадена равнина, получаваме ъгъл AOB (фиг. 1). глупости. 1. Точка 0 извика върха на ъгъла и правите OA и 0B като страни на ъгъла. Да предположим, че са дадени два ъгъла ΒΟΑ и Β1Ο1Α1. Нека ги насложим така, че върховете O... Енциклопедичен речник F.A. Брокхаус и И.А. Ефрон

Този термин има други значения, вижте Ъгъл (значения). Ъгъл ∠ Размер ° SI единици Радиан ... Wikipedia

плосък, геометрична фигура, образуван от два лъча (страни на повърхността), излизащи от една точка (върха на повърхността). Всеки U. имащ връх в центъра O на някакъв кръг (централен U.), определя върху кръга дъга AB, ограничена от... ... Велика съветска енциклопедия

МНОГОСТЪЛНИ ЪГЛИ

Многостенният ъгъл е пространственият аналог на многоъгълник. Спомнете си, че многоъгълник в равнина е фигура, образувана от проста затворена начупена линия и вътрешната област, ограничена от нея. Лъч в пространството ще считаме за аналог на точка от равнина, а плоския ъгъл в пространството за аналог на отсечка от равнина. Тогава аналогът на проста затворена начупена линия в равнината е повърхност, образувана от краен набор от равнинни ъглиА 1 S.A. 2 , А 2 S.A. 3 , …, A n -1 SA n, A n SA 1 с общ връхС (фиг. 1), в който съседните ъгли нямат общи точки, с изключение на точките на общ лъч, а несъседните ъгли нямат общи точки, с изключение на общия връх. Фигурата, образувана от посочената повърхност и една от двете части на пространството, ограничено от нея, се нарича със самолет BSC. След това, без да променяме получения двустенен ъгъл, го завъртаме около правата линия SC, така че равнината BSC да образува определен двустенен ъгъл с равнината CSD. Нека продължим това последователно въртене около всяка обща страна. Ако последната страна SF съвпадне с първата страна SA, тогава се образува фигура (фиг. 38), която се нарича. Общ връхСнаречен , а общият връх S-многостенен ъгъл. ЛъчиS.A. 1 , …, SA nсе наричат ребрамногостенен ъгъл и самите равнинни ъглиА 1 S.A. 2 , А 2 S.A. 3 , …, A n -1 SA n, A n SA 1 – илимногостенен ъгъл. Многостенният ъгъл е обозначен с буквитеS.A. 1 … A n, указващ върха и точките по ръбовете му. В зависимост от броя на лицата многостенните ъгли се наричат ​​тристенни, четиристенни, петостенни (фиг. 2) и др.

Многостенен ъгъл се нарича изпъкнал, ако е изпъкнала фигура, т.е. заедно с произволни две свои точки съдържа и тази, която ги свързвасегмент На фигура 2 тристенният и четиристенният ъгъл са изпъкнали, но петоъгълният ъгъл не е.
Нека разгледаме някои свойства на триъгълниците и подобни свойства на тристенните ъгли.
Имот 1(Неравенство на триъгълник). Всяка страна на триъгълник е по-малка от сумата на другите две страни.
Подобно свойство за тристенните ъгли е следното свойство.
Имот 1". Всеки плосък ъгъл на тристенен ъгъл е по-малък от сбора на другите му два равнинни ъгъла.
Доказателство. Помислете за тристенен ъгъл SABC . Нека най-големият от неговите равнинни ъгли е ъгълът A.S.C.. Тогава неравенствата са в сила

ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .

Така че остава да се докаже неравенството ASC< A.S.B.+ BSC.
Нека го поставим на ръба A.S.C.ъгъл A.S.D., равен A.S.B. , и точка бнека изберем така че SB = SD(фиг. 3). След това триъгълниците A.S.B.И A.S.D.равни (от двете страни и ъгъла между тях) и следователно, AB = AD. Нека използваме неравенството на триъгълника A.C.< AB + BC . Изваждане от двете му части AD = AB, получаваме неравенството DC< BC. В триъгълници DSCИ BSCедната страна е обща ( S.C.), SD = SBИ DC< BC. В случая против по-голяма страналежи под по-голям ъгъл и следователно DSC< BSC . Добавяне на ъгъла към двете страни на това неравенство A.S.D. , равен A.S.B., получаваме търсеното неравенство ASC< A.S.B.+ BSC.

Следствие 1.Сумата от равнинните ъгли на тристенен ъгъл е по-малка от 360° .
Доказателство. Нека SABC– даден тристенен ъгъл. Да разгледаме тристенен ъгъл с връх А, образувани от ръбове ABS, ACSи ъгъл BAC. Поради доказаното свойство неравенството е в сила BAC< БАН+ CAS. По същия начин за тристенни ъгли с върхове бИ СЪСима неравенства: ABC< ABS+ CBS, ACB< ACS+ BCS. Събирайки тези неравенства и вземайки предвид, че сумата от ъглите на триъгълник ABCравно на 180° , получаваме 180 ° < BAS+CAS+ ABS+CBS+BCS+ ACS= 180 ° - ASB+ 180° - BSC+ 180° - A.S.C.. следователно ASB+BSC+ASC< 360 ° .
Следствие 2.Сумата от равнинните ъгли на изпъкнал многостенен ъгъл е по-малка от 360.
Доказателството е подобно на предишното.
Следствие 3.Сумата от двустенните ъгли на тристенния ъгъл е по-голяма от 180° .
Доказателство. Нека SABC- триъгълен ъгъл. Да изберем някаква точка Пвътре в него и пуснете перпендикуляри от него PA 1 , П.Б. 1 , PC 1 на ръба (фиг. 4).

Плоски ъгли б 1 PC 1 , А 1 PC 1 , А 1 П.Б. 1 допълнете съответните двустенни ъгли с ръбове SA, SB, SCдо 180° . Следователно сумата от тези двустенни ъгли е 540° - ( б 1 PC 1 +А 1 PC 1 + А 1 П.Б. 1 ). Като се има предвид, че сумата от равнинните ъгли на тристен с връх Пъгъл по-малък от 360° , намираме, че сумата от двустенните ъгли на оригиналния тристенен ъгъл е по-голяма от 180° .
Имот 2.Симетралите на триъгълник се пресичат в една точка.
Имот 2".Симетралните равнини на двустенните ъгли на тристенния ъгъл се пресичат по една права линия.
Доказателството е подобно на случая със самолета. А именно нека SABC- триъгълен ъгъл. Бисектална равнина на двустенен ъгъл S.A.е GMT ​​на ъгъла, равноотдалечен от лицата му A.S.C.И A.S.B.. По същия начин равнината на ъглополовящата на двустенния ъгъл С.Б.е GMT ​​на ъгъла, равноотдалечен от лицата му B.S.A.И BSC . Линията на тяхното пресичане ТАКАще бъде на еднакво разстояние от всички страни на тристенния ъгъл и следователно равнината на ъглополовящата на двустенния ъгъл ще минава през него S.C. .
Имот 3.Перпендикулярните ъглополовящи на страните на триъгълника се пресичат в една точка.
Имот 3".Равнините, минаващи през ъглополовящите на лицата на тристенен ъгъл и перпендикулярни на тези лица, се пресичат по една права линия.
Доказателството е подобно на доказателството за предишното свойство.
Имот 4.Медианите на триъгълник се пресичат в една точка.
Имот 4".Равнините, минаващи през ръбовете на тристенен ъгъл и ъглополовящите на противоположни лица, се пресичат по една права линия.
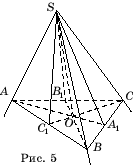
Доказателство. Помислете за тристенен ъгъл SABC,SA=SB=SC(фиг. 5). След това ъглополовящите S.A. 1 , С.Б. 1 , S.C. 1 ъгли BSC, ASC, ASB са медианите на съответните триъгълници. Ето защо А.А. 1 , BB 1 , CC 1 – медиани на триъгълник ABC. Нека О– точката на тяхното пресичане. Направо ТАКАсе съдържа и в трите разглеждани равнини и следователно е линията на тяхното пресичане.

Имот 5.Височините на триъгълник се пресичат в една точка.
Имот 5". Равнините, минаващи през ръбовете на тристенен ъгъл и перпендикулярни на противоположните лица, се пресичат по една права линия.
Доказателство. Да разгледаме тристенен ъгъл с връх Си ребра a, b, c.Нека обозначим а 1 , b 1 , c 1 – линии на пресичане на лица с равнини, минаващи през съответните ръбове и перпендикулярни на тези лица (фиг. 6). Нека оправим точката Вна ръба cи пуснете перпендикуляри от него C.A. 1 И C.B. 1 на прави линии а 1 и b 1 . Нека обозначим АИ бпресичания на линии C.A. 1 и C.B. 1 с прави линии аИ b. Тогава S.A. 1 е проекция А.А. 1 до ръба BSC. защото пр.н.е.перпендикулярен S.A. 1 , тогава тя е перпендикулярна и А.А. 1 . по същия начин, A.C.перпендикулярен BB 1 . по този начин А.А. 1 и BB 1 са височините на триъгълника ABC. Нека О– точката на тяхното пресичане. Самолети, преминаващи през линии аИ а 1 , bИ b 1 перпендикулярна на равнината ABCи следователно линията на тяхното пресичане ТАКАперпендикулярен ABC. означава, ТАКАперпендикулярен AB. от другата страна, COперпендикулярен AB. Следователно равнината, минаваща през ръба cИ ТАКАще бъде перпендикулярно на противоположното лице.
Свойство 6 (синусова теорема). В триъгълник ABCсъс страните a, b, cсъответно се получават равенствата а : грях А = б: грях B=c: грях В.
Имот 6".Нека a, b, g - плоски ъгли на тристенен ъгъл, a, b, c– двустенни ъгли срещу тях. Тогавагрях а : грях а= sin b : sin b= sin g : грях c.
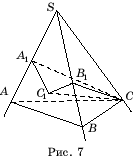
Доказателство.Нека SABC- триъгълен ъгъл. Да се ​​откажем от точката Вперпендикулярен CC 1 до самолета A.S.B.и перпендикулярно C.A. 1 на ръба S.A.(фиг. 7). След това ъгълът C.A. 1 В 1 ще линеен ъгълдвустенен ъгъл а. Ето защо CC 1 = C.A. 1 грях а = S.C.грях б грях а. По същия начин е показано, че CC 1 = CB 1 грях b = SCгрях грях b. Следователно равенството грях b грях а =грях а грях bи, следователно, равенството гряха : грях а= грях b : грях b. По подобен начин се доказва, че равенството sin b : грях b= sin g : грях c.

Имот 7.Ако в изпъкнал четириъгълникАко можете да впишете кръг, тогава сумите на противоположните страни са равни.
Имот 7".Ако една сфера може да бъде вписана в изпъкнал тетраедърен ъгъл, тогава сумите на противоположните равнинни ъгли са равни.

Литература
1. Адамард Дж. Елементарна геометрия. Част II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. добре елементарна геометрия. Част II. Геометрия в космоса. – М.-Л.: Гостехиздат, 1949.
3. Енциклопедия елементарна математика. Книга IV. Геометрия. - М.; 1963 г.
4. Смирнова И.М. В света на полиедрите. – М.: Образование, 1995.

ТЕКСТОВ ПРЕПИС НА УРОКА:

В планиметрията един от обектите на изследване е ъгъл.

Ъгълът е геометрична фигура, състояща се от точка - върха на ъгъла и два лъча, излизащи от тази точка.

Два ъгъла, едната страна на които е обща, а другите две са продължение един на друг, се наричат ​​съседни в планиметрията.

Компасът може да се разглежда като модел на равнинен ъгъл.

Нека си припомним понятието двустенен ъгъл.

Това е фигура, образувана от права a и две полуравнини c обща границаИ това, че не принадлежи към една и съща равнина в геометрията, се нарича двустенен ъгъл. Полуравнините са лицата на двустенния ъгъл. Правата a е ребро на двустенен ъгъл.

Покривът на къщата ясно демонстрира двустенния ъгъл.

Но покривът на къщата на фигура две е направен под формата на фигура, образувана от шест плоски ъгъла с общ връх, така че ъглите са взети на в определен реди всяка двойка съседни ъгли, включително първия и последния, има обща страна. Как се нарича тази форма на покрива?

В геометрията, фигура, съставена от ъгли

А ъглите, от които е съставен този ъгъл, се наричат ​​равнинни ъгли. Страните на равнинните ъгли се наричат ​​ръбове на многостенния ъгъл. Точка O се нарича връх на ъгъла.

Примери за многостенни ъгли могат да бъдат намерени в тетраедъра и паралелепипеда.

Лицата на тетраедъра DBA, ABC, DBC образуват многостенния ъгъл BADC. По-често се нарича тристенен ъгъл.

В паралелепипед лицата AA1D1D, ABCD, AA1B1B образуват тристенния ъгъл AA1DB.

Е, покривът на къщата е направен във формата на шестоъгълен ъгъл. Състои се от шест плоски ъгъла.

Редица свойства са верни за многостенния ъгъл. Нека ги формулираме и докажем. Тук се казва, че изявлението

Първо, за всеки изпъкнал полиедърен ъгъл има равнина, пресичаща всичките му ръбове.

За доказателство разгледайте многостенния ъгъл OA1A2 A3…An.

По условие той е изпъкнал. Ъгълът се нарича изпъкнал, ако лежи от едната страна на равнината на всеки от неговите равнинни ъгли.

Тъй като по условие този ъгъл е изпъкнал, то точките O, A1, A2, A3, An лежат от едната страна на равнината OA1A2

Нека изпълним средна линия KM на триъгълника OA1A2 и изберете от ръбовете OA3, OA4, OAn ръба, който образува най-малкия двустенен ъгъл с равнината OKM. Нека това е край OAi. (оа общо)

Нека разгледаме полуравнината α с границата CM, разделяща двустенния ъгъл OKMAi на два двустенни ъгъла. Всички върхове от A до An лежат от едната страна на равнината α, а точка O от другата страна. Следователно равнината α пресича всички ръбове на многостенния ъгъл. Твърдението е доказано.

Изпъкналите полиедрични ъгли имат друго важно свойство.

Сумата от равнинните ъгли на изпъкнал многостенен ъгъл е по-малка от 360°.

Да разгледаме изпъкнал многостенен ъгъл с връх в точка O. По силата на доказаното твърдение има равнина, която пресича всички негови ръбове.

Нека начертаем такава равнина α, нека тя пресича ръбовете на ъгъла в точки A1, A2, A3 и така нататък An.

Равнината α от външната област на равнинния ъгъл ще отреже триъгълника. Сборът на ъглите е 180°. Получаваме, че сумата от всички равнинни ъгли от A1OA2 до AnOA1 е равна на израза, трансформираме този израз, пренареждаме членовете, получаваме

IN този изразсумите, посочени в скоби, са суми от равнинните ъгли на тристенен ъгъл и както е известно, те са по-големи от третия равнинен ъгъл.

Това неравенство може да се напише за всички тристенни ъгли, образуващи даден многостенен ъгъл.

Следователно получаваме следното продължение на равенството

Отговорът доказва, че сборът от равнинните ъгли на изпъкнал многостенен ъгъл е по-малък от 360 градуса.