Определение: правильной n-угольной пирамидой называется такая пирамида, у которой в основании лежит правильный n-угольник, и высота проецируется в центр этого n-угольника (рис. 1).
Правильная треугольная пирамида
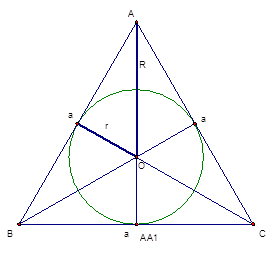
Для начала рассмотрим ∆ABC (рис. 2), в котором AB=BC=CA (то есть в основании пирамиды лежит правильный треугольник). У правильного треугольника центр вписанной и описанной окружности совпадают и являются центром самого треугольника. В данном случае центр находится следующим образом: находим середину АВ - С1, проводим отрезок СС1, который является медианой, биссектрисой и высотой; аналогично находим середину AC - B1 и проводим отрезок BB1. Пересечением BB1 и СС1 будет точка О, которая является центром ∆АВС.
Если соединить центр треугольника O с вершиной пирамиды S, то получим высоту пирамиды SO ⊥ ABC, SO = h.
Соединив точку S с точками А, В и С получим боковые ребра пирамиды.
Мы получили правильную треугольную пирамиду SABC (рис. 2).

2. Стандартные задания на пирамиды (Sосн,Sбок,ha)
Известны стороны основания - а и высота пирамиды - h. Необходимо найти:
Решение:
1. Найти S осн
Если есть ∆АВС (рис. 3), сторона которого равна а, то
![]()
2. Найти S бок , h а
Отрезок SC1 называется апофемой ha(рис. 2). Апофему найдем из прямоугольного треугольника SC1O. Известен катет SO=h, второй катет С1О найдем из ∆АВС (рис. 3).
Для начала найдем высоту АА1 из прямоугольного треугольника АА1С:
![]()
Высота АА1 состоит из радиуса вписанной окружности r=С1О и из радиуса описанной окружности R (причем R=2r).
Следовательно
![]()
Зная катеты ∆SC1O, мы можем найти гипотенузу

Найдя апофему haможно без труда найти
![]()
3. Стандартные задания на пирамиды (двухгранные углы)
Теорема о боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
![]()
3. Найти ∠ (АВ)
Двугранный угол при ребре АВ есть угол между плоскостями SAB и ABC. Обозначим его
![]() Избавимся от иррациональности в знаменателе путем умножения и деления выражения на
Избавимся от иррациональности в знаменателе путем умножения и деления выражения на
Зная тангенс угла, можем найти сам угол
![]()
5) ∠ 4. Найти (∠ (SC )
Проведем BP⊥SC и AP⊥SC ,SC, тогда ∠(SC)= ∠APB. Обозначим его как ∠α (рис. 4)

Для нахождения угла рассмотрим равнобедренный треугольник АРВ. Основание треугольника АВ=а, а боковые стороны найдем из ∆ACS (который тоже является равнобедреннымтреугольником) в).
B ∆SAC S известны основание АС = а и боковые стороны ![]() . Необходимо найти высоту,высоту, проведенную из точки А. Для этого нужно найти площадь треугольника:
. Необходимо найти высоту,высоту, проведенную из точки А. Для этого нужно найти площадь треугольника:
![]()
Из данного уравнения найдем АР:
По теореме косинусов
![]()
Косинус угла однозначно определяет угол в треугольнике, поэтому дальше задача очевидная.
4. Усеченная пирамида, понятие, свойства
Вспомним понятие n-угольной пирамиды на примере треугольной пирамиды. Задан треугольник АВС. Вне плоскости треугольника взята точка Р, соединенная с вершинами треугольника. Полученная многогранная поверхность и называется пирамидой (рис. 1).

Рис. 1. Треугольная пирамида
Рассечем пирамиду плоскостью , параллельной плоскости основания пирамиды . Полученная между этими плоскостями фигура и называется усеченной пирамидой (рис. 2).
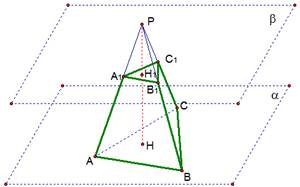
Рис. 2. Усеченная пирамида
Основные элементы:
Верхнее основание ;
Нижнее основание АВС;
Боковая грань ;
Если РН - высота исходной пирамиды, то - высота усеченной пирамиды.
Свойства усеченной пирамиды вытекают из способа ее построения, а именно из параллельности плоскостей оснований:
Все боковые грани усеченной пирамиды являются трапециями. Рассмотрим, например, грань . У нее по свойству параллельных плоскостей (поскольку плоскости параллельны, то боковую грань исходной пирамиды АВР они рассекают по параллельным прямым), в то же время и не параллельны. Очевидно, что четырехугольник является трапецией, как и все боковые грани усеченной пирамиды.
Отношение оснований одинаково для всех трапеций:
![]()
Имеем несколько пар подобных треугольников с одинаковым коэффициентом подобия. Например, треугольники и РАВ подобны в силу параллельности плоскостей и , коэффициент подобия:
![]()
В то же время подобны треугольники и РВС с коэффициентом подобия:
![]()
Очевидно, что коэффициенты подобия для всех трех пар подобных треугольников равны, поэтому отношение оснований одинаково для всех трапеций.
5. Правильная усеченная пирамида, понятие, основные определения
Правильной усеченной пирамидой называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию (рис. 3).

Рис. 3. Правильная усеченная пирамида
Определение.
Правильной называется пирамида, в основании которой лежит правильный n-угольник, а вершина проектируется в центр этого n-угольника (центр вписанной и описанной окружности).
В данном случае в основании пирамиды лежит квадрат, и вершина проектируется в точку пересечения его диагоналей. У полученной правильной четырехугольной усеченной пирамиды ABCD - нижнее основание, - верхнее основание. Высота исходной пирамиды - РО, усеченной пирамиды - (рис. 4).
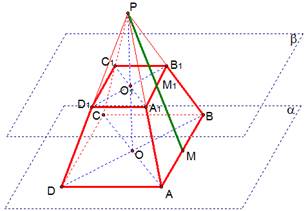
Рис. 4. Правильная четырехугольная усеченная пирамида
Определение.
Высота усеченной пирамиды - это перпендикуляр, проведенный из любой точки одного основания к плоскости второго основания.
Апофема исходной пирамиды - РМ (М - середина АВ), апофема усеченной пирамиды - (рис. 4).
Определение.
Апофема усеченной пирамиды - высота любой боковой грани.
Ясно, что все боковые ребра усеченной пирамиды равны между собой, то есть боковые грани - равные равнобедренные трапеции.
6. Теорема о площади боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.
Доказательство (для правильной четырехугольной усеченной пирамиды - рис. 4):
Итак, необходимо доказать:
Площадь боковой поверхности здесь будет состоять из суммы площадей боковых граней - трапеций. Поскольку трапеции одинаковы, имеем:
![]()
Площадь равнобедренной трапеции - это произведение полусуммы оснований и высоты, апофема является высотой трапеции. Имеем:
Что и требовалось доказать.
Для n-угольной пирамиды:
![]()
Где n - количество боковых граней пирамиды, a и b - основания трапеции, - апофема.
7. Решение задачи 1
Стороны основания правильной усеченной четырехугольной пирамиды ![]() равны 3 см и 9 см, высота - 4 см. Найти площадь боковой поверхности.
равны 3 см и 9 см, высота - 4 см. Найти площадь боковой поверхности.
МОУ «Гимназия» г.Черногорск
Маркелова Светлана Валериевна



В правильной четырехугольной пирамиде сторона основания равна 8 см, угол между боковым ребром и плоскостью основания равен 30 ◦ . Найдите высоту пирамиды, боковое ребро, угол между плоскостью основания и боковой гранью, двугранный угол при боковом ребре, площадь полной поверхности пирамиды.
В правильной треугольной пирамиде сторона основания равна 6 см, высота 12 см. Найдите боковое ребро пирамиды, угол между боковым ребром и плоскостью основания пирамиды, угол между боковой гранью и основанием пирамиды, двугранный угол при боковом ребре, площадь полной поверхности.


В правильной усечённой четырёхугольной пирамиде стороны оснований 6 см и 10 см. Плоский угол боковой грани 45°. Найти площадь полной поверхности пирамиды.
В правильной треугольной усеченной пирамиде стороны основания 4 и 8, а площадь сечения, проходящего через боковое ребро и середину противоположной стороны основания, равна 6 . Найти площадь полной поверхности пирамиды.

Задача 1: В правильной четырехугольной пирамиде сторона основания равна 8 см, угол между боковым ребром и плоскостью основания равен 30 ◦ . Найдите:
а) высоту пирамиды;
б) боковое ребро;
в) двугранный угол при основании;
д) площадь полной поверхности пирамиды.


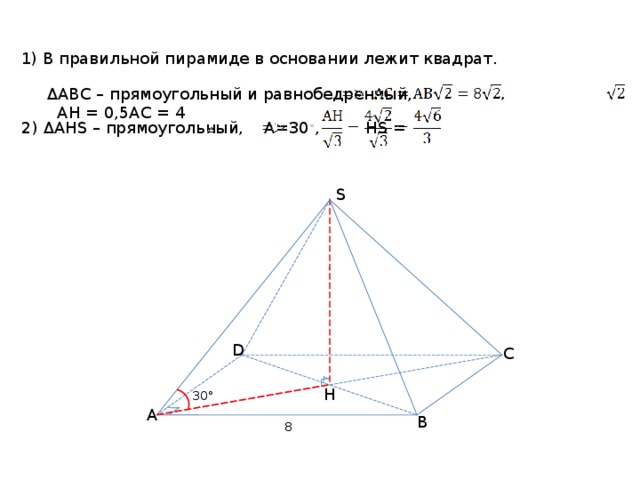
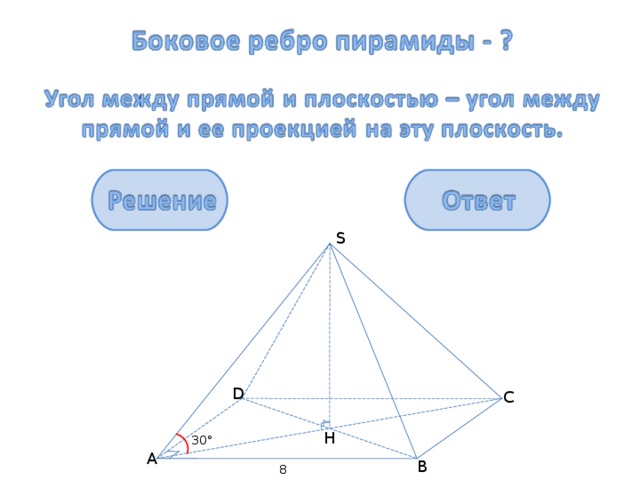


1) В правильной пирамиде в основании лежит квадрат.
Δ АВС – прямоугольный и равнобедренный, АН = 0,5АС = 4
2) Δ АН S – прямоугольный, А=30 ◦ , Н S =
3) А S = 2*Н S =


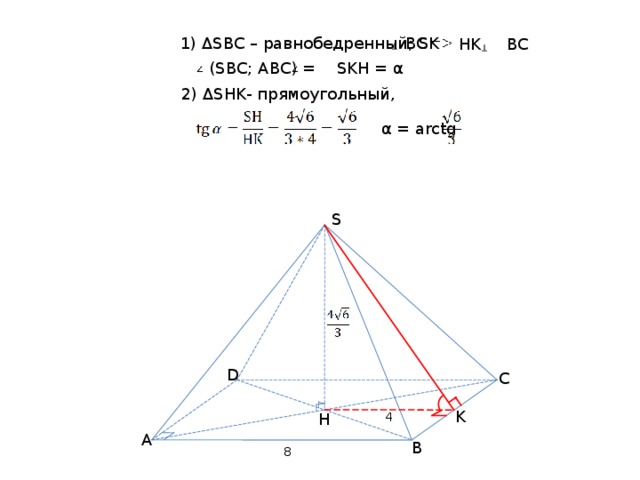
1) ΔSBC – равнобедренный; SK
(SBC ; АВС) = SKH = α
2) ΔSHK - прямоугольный,

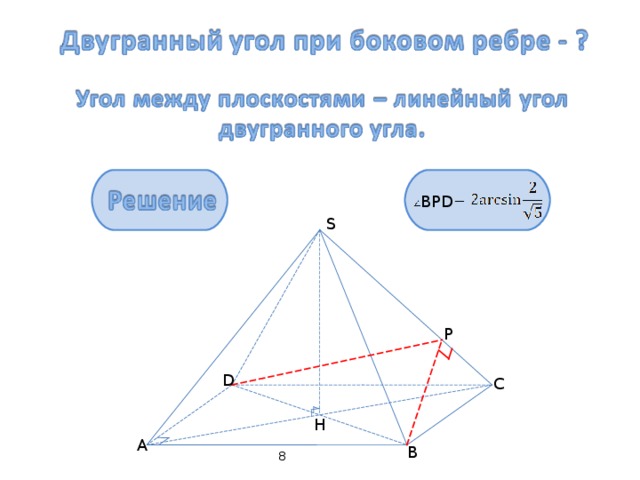

1) ΔSDC = ΔSC В – равнобедренные, BP ┴ SC, DP ┴ SC , (SDC ; S ВС) = BPD =
2) ΔDPB – равнобедренный, DB = , HB = , РН – медиана и высота,
3) по двум углам,
4) ΔPHB – прямоугольный,
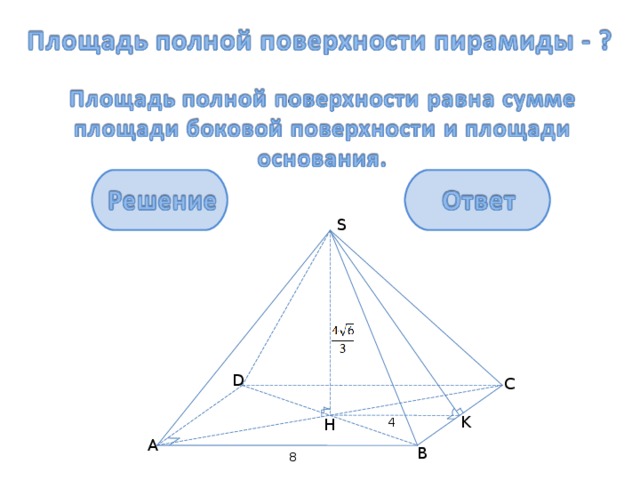


1) АВС D – квадрат, S осн = a 2 = 64.
2) И з ΔSHK по теореме Пифагора:
3) S б = 0,5*Р *SK = 0,5*32*4 = 64
4) S n = S б + S осн =

Задача 2: В правильной треугольной пирамиде сторона основания равна 6 см, высота 12 см. Найдите:
а) боковое ребро пирамиды;
б) угол между боковым ребром и плоскостью основания пирамиды;
в) угол между боковой гранью и основанием пирамиды;
г) двугранный угол при боковом ребре;
д) площадь полной поверхности.



1) Так как пирамида правильная, то точка пересечения медиан CC 1 и ВВ 1 является основанием высоты.
2) Δ НС 1 В – прямоугольный, В = 30 ◦ , С 1 В = 3, НС 1 = , НВ = 2 .
3) ΔS НВ – прямоугольный, по теореме Пифагора



1) (S В; АВС) = S ВН = α
2) ΔS ВН – прямоугольный,

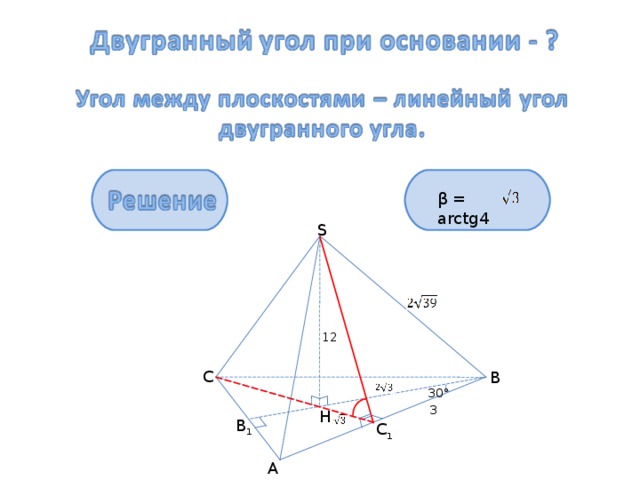

1) (S АВ; АВС) = НС 1 S = β



1) ΔS AВ = ΔSC В – равнобедренные, AM ┴ SB , CM ┴ SB (S АВ; S ВС) = AMC =
2) ΔAMC – равнобедренный, МВ 1 ┴ A C , ΔM В 1 А – прямоугольный и sin
3) ΔSHC 1 – прямоугольный, SC 1 = , где
HC 1 = * , SC 1 =
4) по двум углам,


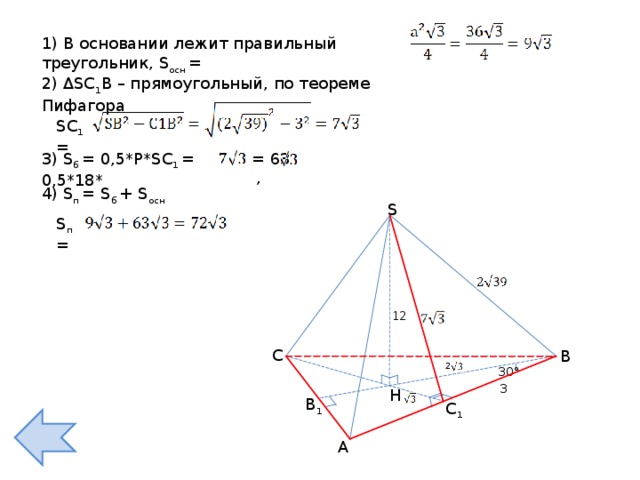
1) В основании лежит правильный треугольник, S осн =
2) ΔS С 1 В – прямоугольный, по теореме Пифагора
3) S б = 0,5*Р* S С 1 = 0,5*18*
4) S п = S б + S осн

Задача 1 : Основанием пирамиды является равнобедренный треугольник с углом 120 ° . Боковые ребра образуют с плоскостью основания углы по 30 ° . Высота равна 6 см. Найдите площадь полной поверхности пирамиды.

Задача 1 : Основанием пирамиды является равнобедренный треугольник с углом 120 ° . Боковые ребра образуют с плоскостью основания углы по 30 ° . Высота равна 6 см. Найдите площадь полной поверхности пирамиды.
Так как боковые ребра образуют с плоскостью основания равные углы, то основание высоты находится в центре окружности, описанной около Δ АВС. Центр окружности описанной около треугольника находится в точке пересечения серединных перпендикуляров. В треугольнике один из углов тупой, значит, точка пересечения серединных перпендикуляров лежит вне треугольника. SH ┴ пл(АВС), АН = СН = ВН = R .

1. Δ А SH – прямоугольный, А=30 ◦ и SH =6 АН = SH = 6 – радиус описанной окружности.
2. Δ А H С = Δ С H В – равносторонние АС = СВ = 6 см.
S АВС = см 2 .
AC = 3 , АК = СК* = *3 = 9 см.
3. Δ АСК – прямоугольный, С=60 ◦ , АС = 6 CK =
4. Δ А S С = Δ С S В, высоты, опущенные в этих треугольниках из вершины S будут равными. ΔS НР – прямоугольный, где Р – середина СВ, по теореме Пифагора:
S Р = = = см.
ΔS НК – прямоугольный, по теореме Пифагора:
6. S б = 2*S SCB + S ASB = 2*
S п = S б + S осн =

Задача 1:
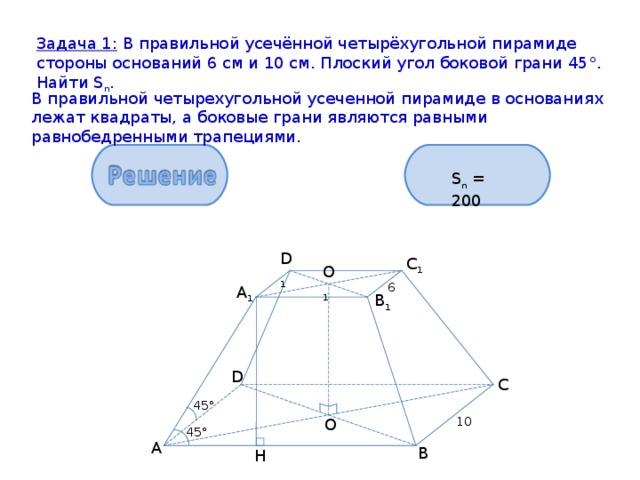
Задача 1: В правильной усечённой четырёхугольной пирамиде стороны оснований 6 см и 10 см. Плоский угол боковой грани 45°. Найти S n .
В правильной четырехугольной усеченной пирамиде в основаниях лежат квадраты, а боковые грани являются равными равнобедренными трапециями.

1) АА 1 В 1 В – равнобедренная трапеция; А 1 Н ┴ АВ Δ АНА 1 – прямоугольный и равнобедренный,
АН = А 1 Н = = 2 см.
2) S n = S 1 + S 2 + S б = 10 2 + 6 2 + 4 * = 136 + 64 = 200 см.

Задача

Задача 2: В правильной треугольной усеченной пирамиде стороны основания 4 и 8, а площадь сечения, проходящего через боковое ребро и середину противоположной стороны основания, равна 6 . Найти площадь полной поверхности пирамиды.
В правильной треугольной усеченной пирамиде в основаниях лежат правильные треугольники, а боковые грани являются равными равнобедренными трапециями.

1) S ABC = = 16 ; S A B C = = 4
2) КК 1 – высота боковой грани.
3) S сеч = h = = = 2
А 1 К 1 = ; АК =
4) К 1 Е ┴ АК и ЕК = ОК - ОЕ = ОК - О 1 К 1 ;
ОК = АК = * = ;
О 1 К 1 = А 1 К 1 = * = ;
5) Из прямоугольного Δ К 1 ЕК по теореме Пифагора:
6) S б = *К 1 К = =
7) S n = 16 + 4 + 24 = 44

Задача 3: Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 30 ◦ и 45 ◦ . Найдите площадь поверхности пирамиды.

Задача 3: Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 30 ◦ и 45 ◦ . Найдите площадь поверхности пирамиды.
Так как плоскости двух боковых граней перпендикулярны к плоскости основания, то боковое ребро, по которому пересекаются боковые грани также перпендикулярно к плоскости основания. Это боковое ребро является высотой пирамиды.
S пир = 8(3 + 3 + 3)
1) Предположим, что плоскости МАВ и MAD перпендикулярны к плоскости основания, тогда линия их пересечения МА перпендикулярна к плоскости основания, т. е. МА - высота пирамиды.
2) Так как СВ АВ, то СВ МВ по теореме о трех перпендикулярах, поэтому MBA - линейный угол двугранного угла при ребре СВ, MBA = 30°.
Аналогично AD DC , MD DC , MDA - линейный угол двугранного угла при ребре DC , MDA = 45°. Треугольники МВС и MDC прямоугольные.
3) Пусть MA = х см, тогда МВ = 2х см, АВ = х см. Из ΔMAD имеем: МА = AD = x см, MD = х см. Из Δ АВС получаем: АВ 2 + ВС 2 = АС 2 , 3х 2 + х 2 = 64, х 2 = 16, х = 4 (см).
4) Таким образом, МА = 4 см, АВ = DC = 4 см, МВ = 8 см, MD = 4 см, AD = BC = 4 см.
S бок = АВ*АМ + А D *АМ + ВС*ВМ + D С* D М =
= *4 *4 + *4*4 + *4*8 + *4 *4 = 24 + 8 +
S осн = 4 *4 = 16
S пир = 24 + 24 + 8 = 8(3 + 3 + 3)

Задача 2: Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.

Задача 2: Основанием пирамиды является треугольник со сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 45°. Найдите площадь боковой поверхности пирамиды.
Так как каждая боковая грань наклонена к основанию под одним и тем же углом, то основание высоты находится в центре вписанной окружности(точки пересечения биссектрис).

1) АВ = АС = 10 см, ВС = 12 см, МО - высота пирамиды, АЕ - высота и медиана к стороне ВС треугольника АВС. Из Δ АВЕ получаем: ВЕ = 6 см, АЕ = 8 см. S АВС = 6*8 = 48 см 2 .
2) Пусть OD и ОК - перпендикуляры к сторонам треугольника АВС, тогда МЕО, MDO , MKO - линейные углы двугранных углов, образованных плоскостями боковых граней и основанием пирамиды. МЕО = MDO = MKO = 45°, Δ МЕО = ΔMDO = Δ МКО (ПО катету МО и противолежащему острому углу в 45°), поэтому OE = OD = OK , т. е. точка О -
центр окружности, вписанной в основание пирамиды. Пусть ОЕ = г. Тогда r = = = 3 см (р - полупериметр Δ АВС).
3) Из Δ МОЕ получаем: ОЕ = 3 см, МЕ = = З см
MD = MK = ME = 3 см
4) S бок = (AB + BC + AC)*ME = (10 + 12 + 10)* З =

