Как найти радиус описанной окружности для трапеции?
В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.
I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции
Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.
В общем случае может быть найден по одной из формул
где a — сторона треугольника, α — противолежащий ей угол;
либо по формуле
где a, b, c — стороны, S — площадь треугольника.
Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:
где синус угла A можно найти из прямоугольного треугольника ABF:
III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров
Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).
Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.
Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить
и приравнять правые части
№ 3. Высота правильной четырехугольной призмы равна 8, а сторона основаня 6√2. Найти расстояние от вершины А до плоскости А1ВD.
Решение.
Т.к. призма правильная, то в основании - квадрат, значит диагонали перпендикулярны.
OA _|_ BD ; OA = AC/2 = BD/2;
В 3-ке DOA: OA 2 + OD 2 = DA 2 ; 2x 2 = 36*2; OA = x = 6.
В 3-ке АОА 1 проведем АК_|_ОА 1 , АК - расстояние до плоскости А 1 BD.
A 1 O = √(8 2 +6 2) = 10
AK*OA 1 = OA*AA 1 ; AK = 6*8/10 = 4,8.
Ответ: 4,8.
№ 4. Ребро куба равно 10 см. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
Решение,
В основании призмы - прямоугольный 3-к с катетами 5 и 5. Sосн= 1/2 * 5*5 = 12,5
Высота призмы равна длине ребра куба = 10. V призмы= 12,5*10=125
№ 5. Площадь основания правильной призмы ABCDA1B1C1D1 равна 0,5 кв.см. Высота призмы равна 9 см. Найдите площадь сечения A1B1CD.
Решение.
В основании правильной призмы лежит квадрат. Sосн= АВ 2 =0,5 --> AB=ВС=√0,5
Т.к. грань АА1D1D | DC, то А1D | DC --> сечение A1B1CD - прямоугольник.
Sсеч=А1D*DС. Найдем А1D из 3-ка АА1D по теореме Пифагора.
А1D 2 = АD 2 +АА1 2 = (√0,5 2 + 9 2) = 81,5
Sсеч=√(81,5*√0,5 =√40,75 ≈6,38
Пирамида, вписанная в сферу. Свойства пирамиды, вписанной в сферу
Определение 1. Пирамидой, вписанной в сферу, называют такую пирамиду , все вершины которой лежат на сфере (рис. 1).
Определение 2. Если пирамида вписана в сферу, то сферу называют описанной около пирамиды.
Теорема 1. Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.
Доказательство. Докажем сначала, что, если пирамида вписана в сферу, то около ее основания можно описать окружность. Для этого рассмотрим рисунок 2.
На рисунке 2 изображена пирамида SA 1 A 2 ... A n , вписанная в сферу. Плоскость основания пирамиды пересекает сферу по окружности, в которую вписан многоугольник A 1 A 2 ... A n - основание пирамиды. Доказано.
Теперь предположим, что около основания A 1 A 2 ... A n пирамиды SA 1 A 2 ... A n можно описать окружность. Докажем, что в этом случае около пирамиды SA 1 A 2 ... A n можно описать сферу. С этой целью обозначим центр окружности, описанной около многоугольника A 1 A 2 ... A n , символом O" и проведем прямую p, проходящую через точку O" и перпендикулярную к плоскости многоугольника A 1 A 2 ... A n (рис. 3).
Рассмотрим плоскость β, проходящую через середину отрезка SA n и перпендикулярную к этому отрезку . Если обозначить буквой O точку пересечения плоскости β с прямой p, то точка O и будет центром сферы, описанной около пирамиды SA 1 A 2 ... A n . Для того, чтобы это доказать, рассмотрим следующий рисунок 4.
Докажем, что точка O находится на одном и том же расстоянии от точек S, A 1 , A 2 , ... , A n . Поскольку точка O лежит на серединном перпендикуляре к отрезку SA n , то расстояния OS и OA n равны. С другой стороны, отрезки OA 1 , OA 2 , ... , OA n как гипотенузы в равных прямоугольных треугольниках OO"A 1 , OO"A 2 , ... , OO"A n . (Треугольники OO"A 1 , OO"A 2 , ... , OO"A n равны , так как у них катет OO" общий, а катеты O"A 1 , O"A 2 , ... , O"A n равны как радиусы окружности, описанной около многоугольника A 1 A 2 ... A n ).
Итак, мы доказали, что точка O находится на одном и том же расстоянии от всех вершин пирамиды SA 1 A 2 ... A n . Отсюда вытекает, что точка O является центром сферы, описанной около пирамиды SA 1 A 2 ... A n .
Для завершения доказательства теоремы остается лишь доказать, что плоскость β и прямая p действительно пересекаются. Если предположить, что это не так, то из такого предположения будет следовать, что плоскость β и прямая p параллельны, а, значит, точка S лежит в плоскости A 1 A 2 ... A n , что противоречит определению пирамиды .
Теорема доказана.
Следствие 1. Около любой правильной пирамиды можно описать сферу.
Следствие 2. Если у пирамиды все боковые ребра равны , то около нее можно описать сферу.
Указание. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее основания, является центром описанной около основания окружности. .
Радиус сферы, описанной около правильной n - угольной пирамиды
из формулы (1) получаем соотношение
Ответ.
Следствие 3. Радиус сферы, описанной около
РЕШЕНИЕ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
(по материалам ЕГЭ)
Задача №1 . Вычислите объём правильной треугольной пирамиды, если радиус описанной вокруг основания окружности равен , а высота пирамиды равна 4.
Р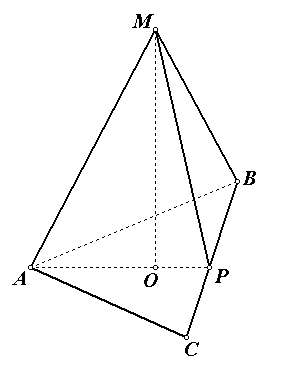
ешение.
.
, 
.
, 
.
3) вычислим объём пирамиды
.
Ответ. 9
Задача №2 . Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен , а боковые ребра пирамиды равны 6.
Решение.
, тогда 
.
, 
.
, 
.
по теореме Пифагора находим высоту пирамиды: 
, .
5) вычислим объём пирамиды
.
Ответ. 18
.
Задача №3 . Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен , а высота пирамиды равны 1.
Р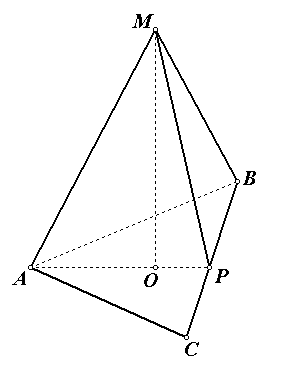
ешение.
1) найдем сторону основания правильной пирамиды по формуле , .
2) найдем периметр основания Р = 3 · а ,
Р = 9.
, тогда 
.
4) из прямоугольного треугольника
МОР
МР
: 
,
МР
= 
5) вычислим площадь боковой поверхности правильной пирамиды:
,
.
Ответ. 
.
Задача №4
. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна 
.
Решение. ,
1) найдем радиус описанной около основания и вписанной в основание окружностей: , 
то есть 
.
2) найдем площадь основания, как площадь правильного треугольника , 
.
МОР
, МО = 
.
= 
.
Ответ. 18.
Задача №5
. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна 
.
Решение.
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда 
.
2) найдем сторону основания правильной пирамиды по формуле , 
.
3) найдем площадь основания, как площадь правильного треугольника , 
.
4) вычислим объём правильной пирамиды: = 
.
Ответ. 36.
Задача №6
. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3.
Р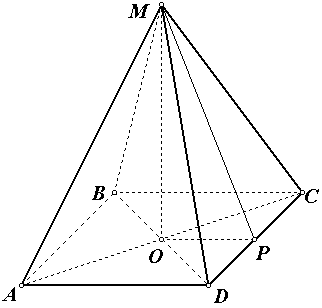
ешение
.
1) найдем сторону основания по формуле 
, т.е. 
.
2) найдем периметр основания: Р = 4 а ,
Р = 24.
3) из прямоугольного треугольника
М
D
Р
по теореме Пифагора находим апофему
МР
: 
,
DP
=
тогда:
МР
= 
.
4) вычислим площадь боковой поверхности пирамиды: = 
.
Ответ. 48.
Задача №7
. В правильной четырехугольной пирамиде площадь боковой поверхности равна 16, а площадь основания 4. Найдите высоту пирамиды.
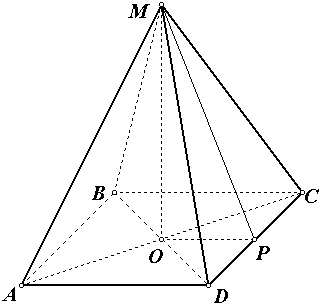
Решение .
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.
2) по условию = 16 т.е.
.
3) из прямоугольного треугольника
МОР
по теореме Пифагора находим высоту: , учитывая, что ОР = 
= 1, получаем: МО = 
.
Ответ. 
.
Задача №8
. Вычислите объём правильной шестиугольной пирамиды, если сторона основания равна 4, а боковые ребра пирамиды равны 5.
Решение.
1) сторона основания правильного шестиугольника равна радиусу описанной около него окружности т.е. 
, 
2) площадь правильного шестиугольника найдем по формуле 
или 
= 24.
3) из прямоугольного треугольника МОВ найдем высоту МО : .
4) вычисляем объём пирамиды: =
.
Ответ. 24.
Задача №9
. В правильной шестиугольной пирамиде сторона основания равна 2, а боковое ребро равно 2
. Найдите объём пирамиды.
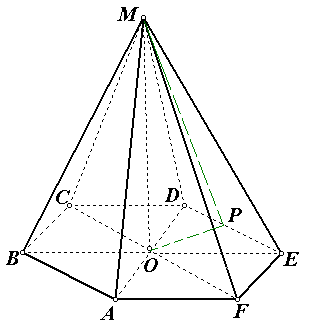
Решение.
1) найдем площадь правильного шестиугольника по формуле или = 12.
2) из прямоугольного треугольника
МОВ
найдем высоту
МО,
учитывая, что в правильном шестиугольнике : .
3) вычисляем объём пирамиды: =
.
Ответ: 24.
Задача № 10
. Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания
R
удовлетворяет уравнению
R
2
+
R
– 6 = 0. Найдите объём призмы.
Р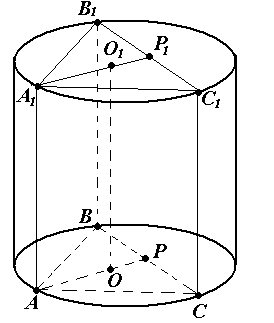
ешение.
V
=
S
·
H
1) так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, Н = 5.
2) по условию R удовлетворяет уравнению R 2 + R – 6 = 0, решая которое находим
R 1 = - 3, R 2 = 2, так как радиус величина положительная то -3 не удовлетворяет условию задачи.
3) найдем сторону вписанного правильного треугольника по формуле 
, 
.
4) найдем площадь основания правильной призмы, как площадь правильного треугольника: 
= 
5) вычислим объём призмы:
V
=
S
·
H
=
.
Ответ. 15.
Задача №11
. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно 
. Высота цилиндра равна трем его радиусам. Найдите объём призмы.
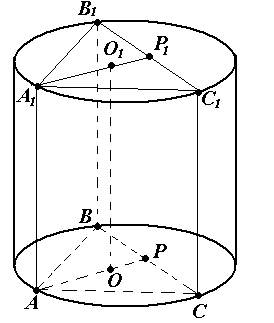
Решение. V = S · H
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра, по условию Н = 3 R ..
2) Расстояние между осью цилиндра и стороной основания призмы равно радиусу вписанной в треугольник
АВС
окружности, т.е. 
, и по условию равно .
3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. , тогда .
4) найдем сторону вписанного правильного треугольника по формуле , 
.
5) найдем площадь основания правильной призмы, как площадь правильного треугольника: = 
6) вычислим объём призмы:
V
=
S
·
H
=
S
·
3
·
R
=
162.
Ответ. 162.
Задача №12 . Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 . Найдите объём призмы, если сторона её основания равна 5.
Решение . V = S · H
2) Найдем площадь основания правильной призмы, как площадь правильного треугольника: =
.
3) Сторона вписанного правильного треугольника находится по формуле , тогда 
.
4) По условию площадь боковой поверхности цилиндра равна 16
·
т.е.
, откуда
Н
= 
= 
.
5) Вычислим объём призмы:
V
=
S
·
H
=
·
= 30.
Ответ. 30.
Задача №13 . Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20 . Найдите площадь боковой поверхности призмы.
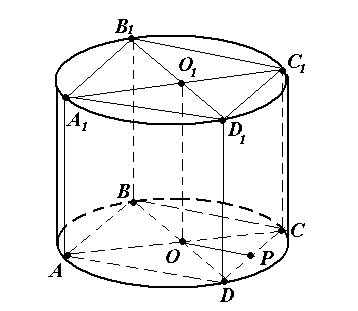Решение. 
1) Так как призма вписана в цилиндр, то высота призмы равна высоте цилиндра, а основание призмы вписано в основание цилиндра.
2) По условию площадь боковой поверхности цилиндра равна 20
, т.е. 
, 
.
. Найдите диагональ призмы.
,
ешение.
3) из прямоугольного треугольника DCC 1 найдем СС 1 = Н по теореме Пифагора:
Н =
.
4) приравняем значения для Н: 
,