Гипотеза: Если изучить движение графика при образовании уравнения функций то можно заметить что все графики подчиняются общим закономерностям поэтому можно сформулировать общие законы вне зависимости от функций, что позволит не только облегчить построение графиков различных функций, но и использовать их при решении задач.
Цель: Изучить движение графиков функций:
1)Задача изучение литературы
2) Научится строить графики различных функций
3) Научится преобразовывать графики линейных функций
4) Рассмотреть вопрос применения графиков при решении задач
Объект исследования: Графики функций
Предмет исследования: Движения графиков функций
Актуальность: Построение графиков функций, как правило занимает очень много времени и требует внимательности со стороны ученика, но зная правила преобразования графиков функций и графики основных функций можно достаточно быстро и легко построить графики функций что позволит не только выполнять задания на построения графиков функций, но и решать связанные с ним задачи (на нахождения максимально (минимально высоты времени и точки встречи))
Данный проект полезен всем ученикам школы.
Обзор литературы :
В литературе рассматриваются способы построения графика различных функций, а так же приведены примеры преобразования графиков этих функций. Графики практически всех основных функций используются в различных технических процессах, что позволяет более наглядно представить течение процесса и спрограммировать результат
Постоянная функция. Эта функция задана формулой у = b, где b – некоторое число. Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. Графиком функции у = 0 является ось абсцисс.
Виды функции 1Прямая пропорциональность. Эта функция задана формулой у = kx, где коэффициент пропорциональности k ≠ 0. Графиком прямой пропорциональности является прямая, проходящая через начало координат.
Линейная функция. Такая функция задана формулой у = kx + b, где k и b – действительные числа. Графиком линейной функции является прямая.
Графики линейных функций могут пересекаться или быть параллельными.
Так, прямые графиков линейных функций у = k 1 x + b 1 и у = k 2 x + b 2 пересекаются, если k 1 ≠ k 2 ; если же k 1 = k 2 , то прямые параллельны.
2Обратная пропорциональность – это функция, которая задана формулой у = k/x, где k ≠ 0. K называется коэффициентом обратной пропорциональности. Графиком обратной пропорциональности является гипербола.
Функция у = х 2 представлена графиком, получившим название парабола: на промежутке [-~; 0] функция убывает, на промежутке функция возрастает.
Функция у = х 3 возрастает на всей числовой прямой и графически представлена кубической параболой.
Степенная функция с натуральным показателем. Эта функция задана формулой у = х n , где n – натуральное число. Графики степенной функции с натуральным показателем зависят от n. Например, если n = 1, то графиком будет прямая (у = х), если n = 2, то графиком будет парабола и т.д.
Степенная функция с целым отрицательным показателем представлена формулой у = х -n , где n – натуральное число. Данная функция определена при всех х ≠ 0. График функции также зависит от показателя степени n.
Степенная функция с положительным дробным показателем. Эта функция представлена формулой у = х r , где r – положительная несократимая дробь. Данная функция также не является ни четной, ни нечетной.
График-линия которая отображает взаимосвязь зависимой и независимой переменных на координатной плоскости. График служит для наглядного отображения этих элементов
Независимая переменная это переменная которая может принимать любые значения в области определения функций (где данная функция имеет смысл(нельзя делить на нуль))
Чтобы построить график функций необходимо
1)Найти ОДЗ (область допустимых значений)
2)взять несколько произвольных значений для независимой переменной
3)Найти значен6ие зависимой переменной
4)Построить координатную плоскость отметить на ней данные точки
5) Соединить их линии при необходимости исследовать полученный график Преобразование графиков элементарных функций.
Преобразование графиков
В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат). К примеру, квадратичная функция формула представляет собой квадратичную параболу формула, сжатую втрое относительно оси ординат, симметрично отображенную относительно оси абсцисс, сдвинутую против направления этой оси на 2/3 единицы и сдвинутую по направлению оси ординат на 2 единицы.
Давайте разберемся в этих геометрических преобразованиях графика функции пошагово на конкретных примерах.
С помощью геометрических преобразований графика функции f(x) может быть построен график любой функции вида формула, где формула - коэффициенты сжатия или растяжения вдоль осей oy и ox соответственно, знаки «минус» перед коэффициентами формула и формула указывают на симметричное отображение графика относительно координатных осей, а и b определяют сдвиг относительно осей абсцисс и ординат соответственно.
Таким образом, различают три вида геометрических преобразований графика функции:
Первый вид - масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На необходимость масштабирования указывают коэффициенты формулы отличные от единицы, если число меньше 1 , то происходит сжатие графика относительно oy и растяжение относительно ox , если число больше 1, то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.
Второй вид - симметричное (зеркальное) отображение относительно координатных осей.
На необходимость этого преобразования указывают знаки «минус» перед коэффициентами формулы (в этом случае симметрично отображаем график относительно оси ox) и формула (в этом случае симметрично отображаем график относительно оси oy). Если знаков «минус» нет, то этот шаг пропускается.
В зависимости от условий протекания физических процессов одни величины принимают постоянные значения и называются константами, другие - изменяются в определенных условиях и называются переменными.
Внимательное изучение окружающей среды показывает, что физические величины зависимы друг от друга, т. е. изменение одних величин влечет за собой изменение других.
Математический анализ занимается изучением количественных соотношений взаимно -изменяющихся величин, отвлекаясь от конкретного физического смысла. Одним из основных понятий математического анализа есть понятие функции.
Рассмотрим элементы
множества
и элементы множества
(рис. 3.1).
Если устанавливается
некоторое соответствие между элементами
множеств
и
в виде правила
,
то тем самым отмечают, что определяется
функция
.
Определение
3.1.
Соответствие
,
которое связывает с каждым элементом
не пустого множества
некоторый, вполне определенный, элемент
не пустого множества
,называется функцией или отображением
в
.
Символически
отображение
в
записывается следующим образом:
.
При этом множество
называется областью определения функции
и обозначается
.
В
свою очередь, множество
называется областью значений функции
и обозначается
.
Кроме
того, необходимо отметить, что элементы
множества
называют независимыми переменными,
элементы множества
называют зависимыми переменными.
Способы задания функции
Функция может задаваться следующими основными способами: табличным, графическим, аналитическим.
Если на основании экспериментальных данных составляют таблицы, в которых содержатся значения функции и соответствующие им значения аргумента, то такой способ задания функции называют табличным.
В то же время, если некоторые исследования результата эксперимента выводят на регистратор (осциллограф, самописец и т. д.), то отмечают, что функция задается графически.
Наиболее распространенным есть аналитический способ задания функции, т.е. способ, при котором с помощью формулы связывают независимую и зависимую переменные. При этом существенную роль играет область определения функции:
разные, хотя они и задаются одинаковыми аналитическими соотношениями.
Если
задают только формулу функции
,
то считают, что область определения
этой функции совпадает с множеством
тех значений переменной
,
для которых выражение
имеет смысл. В этой связи особую роль
играет проблема нахождения области
определения функции.
Задача 3.1. Найти область определения функции
Решение
Первое
слагаемое принимает действительные
значения при
,а второе при.
Таким образом, для нахождения области
определения заданной функции необходимо
решить систему неравенств:
В
результате решения такой системы
получают
.
Следовательно, область определения
функции есть отрезок
.
Простейшие преобразования графиков функций
Построение графиков функций можно существенно упростить, если пользоваться известными графиками основных элементарных функций. Основными элементарными функциями называются следующие функции:
1)степенная функция
где
;
2)показательная функция
где
и
;
3)логарифмическая функция
,
где
-любое положительное число, отличное
от единицы:
и
;
4)тригонометрические функции
;
.
5)обратные
тригонометрические функции
;
;
;
.
Элементарными функциями называются функции, получающиеся из основных элементарных функций с помощью четырех арифметических действий и суперпозиций, примененных конечное число раз.
Простые геометрические преобразования также позволяют упростить процесс построения графика функций. Эти преобразования основываются на следующих утверждениях:
График функции y=f(x+a) есть графикy=f(x), сдвинутый (при a >0 влево, при a < 0 вправо) на |a| единиц параллельно осиOx.
График функции y=f(x) +bесть графикy=f(x), сдвинутый (приb>0 вверх, приb< 0 вниз) на |b| единиц параллельно осиOy.
График
функции y = mf(x) (m0)
есть график y = f(x), растянутый (приm>1) вmраз или сжатый
(при 0 График
функции y = f(kx) есть график y = f(x), сжатый
(при k >1) в k раз или растянутый (при
0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx)
есть зеркальное отображение графика
y = f(–kx) от оси Oy.
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.
Рассмотрим на примере квадратичной функции вида y = - 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х, причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:
Yandex.RTB R-A-339285-1
Геометрические преобразования графика функции
Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f (± k 2 · (x + a)) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 < k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 > 1 , k 2 > 1 вдоль О у и О х. Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у.
Определение 1
Существует 3 вида геометрических преобразований графика :
- Масштабирование вдоль О х и О у. На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 < k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 > 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х.
- Симметричное отображение относительно координатных осей. При наличии знака « - » перед k 1 симметрия идет относительно О х, перед k 2 идет относительно О у. Если « - » отсутствует, тогда пункт при решении пропускается;
- Параллельный перенос (сдвиг) вдоль О х и О у. Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у, что значит при положительном b функция движется вверх, при отрицательном – вниз.
Рассмотрим решения на примерах, начиная со степенной функции.
Пример 1
Преобразовать y = x 2 3 и построить график функции y = - 1 2 · 8 x - 4 2 3 + 3 .
Решение
Представим функции таким образом:
y = - 1 2 · 8 x - 4 2 3 + 3 = - 1 2 · 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3
Где k 1 = 2 , стоит обратить внимание на наличие « - » , а = - 1 2 , b = 3 . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х, сдвигается вправо на 1 2 и вверх на 3 единицы.
Если изобразить исходную степенную функцию, получим, что
при растягивании вдвое вдоль О у имеем, что
Отображение, симметричное относительно О х, имеет вид
а движение вправо на 1 2
движение на 3 единицы вверх имеет вид
Преобразования показательной функции рассмотрим на примерах.
Пример 2
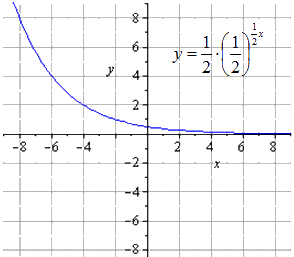
Произвести построение графика показательной функции y = - 1 2 1 2 (2 - x) + 8 .
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 · 1 2 - 1 2 x + 8
Отсюда видно, что получим цепочку преобразований y = 1 2 x:
y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = - 1 2 · 1 2 1 2 x → y = - 1 2 · 1 2 - 1 2 x → → y = - 1 2 · 1 2 - 1 2 x + 8
Получаем, что исходная показательная функция имеет вид
Сжимание вдвое вдоль О у дает
Растягивание вдоль О х
Симметричное отображение относительно О х
Отображение симметрично относительно О у
Сдвигание на 8 единиц вверх
Рассмотрим решение на примере логарифмической функции y = ln (x) .
Пример 3
Построить функцию y = ln e 2 · - 1 2 x 3 при помощи преобразования y = ln (x) .
Решение
Для решения необходимо использовать свойства логарифма, тогда получаем:
y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2
Преобразования логарифмической функции выглядят так:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2
Изобразим график исходной логарифмической функции
Производим сжимание строе по О у
Производим растягивание вдоль О х
Производим отображение относительно О у
Производим сдвигание вверх на 2 единицы, получаем
Для преобразования графиков тригонометрической функциинеобходимо подгонять под схему решения вида ± k 1 · f (± k 2 · (x + a)) + b . Необходимо, чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0 < k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.
Рассмотрим примеры решения заданий с преобразованиями y = sin x .
Пример 4
Построить график y = - 3 sin 1 2 x - 3 2 - 2 с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:
y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2
Видно, что k 1 = 3 , k 2 = 1 2 , a = - 3 , b = - 2 . Так как перед k 1 имеется « - » , а перед k 2 - нет, тогда получим цепочку преобразований вида:
y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2
Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin (x) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума - - π 2 + 2 π · k ; - 1 , k ∈ Z .
Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π - это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы - - π 2 + 2 π · k ; - 3 , k ∈ Z .
При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в - π + 4 π · k ; - 3 , k ∈ Z .
Изображение производится симметрично относительно О х. Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как - π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; - 3 , k ∈ Z .
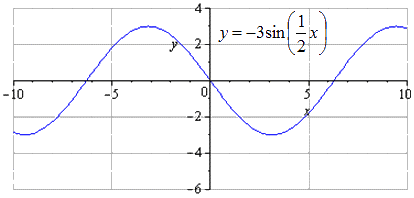
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки - π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов - π + 3 + 4 π · k ; - 5 , k ∈ Z .
На данном этапе график тригонометрической функции считается преобразованным.
Рассмотрим подробное преобразование функции y = cos x .
Пример 5
Построить график функции y = 3 2 cos 2 - 2 x + 1 при помощи преобразования функции вида y = cos x .
Решение
По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что
y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1
Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = - 1 , b = 1 , где k 2 имеет « - » , а перед k 1 он отсутствует.
Отсюда получаем, что получится график тригонометрической функции вида:
y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1)) → y = 3 2 cos - 2 (x - 1) + 1
Пошаговое преобразование косинусоиды с графической иллюстрацией.
При заданной графике y = cos (x) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; - 1 , k ∈ Z .
При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; - 3 2 , k ∈ Z .
При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов - π 2 + π · k ; - 3 2 , k ∈ Z .
Симметричное отображение относительно О у. Так как график нечетный, то он не будет изменяться.
При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов - π 2 + 1 + π · k ; - 3 2 , k ∈ Z .
При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; - 1 2 , k ∈ Z .
Преобразования функции косинуса завершено.
Рассмотрим преобразования на примере y = t g x .
Пример 6
Построить график функции y = - 1 2 t g π 3 - 2 3 x + π 3 при помощи преобразований функции y = t g (x) .
Решение
Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что
y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3
Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = - π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « - » . Значит, после преобразования тангенсоиды получаем
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3
Поэтапное преобразование тангенсоиды с графическим изображением.
Имеем, что исходный график – это y = t g (x) . Изменение положительного периода равняется T = π . Областью определения считается - π 2 + π · k ; π 2 + π · k , k ∈ Z .
Сжимаем в 2 раза вдоль О у. T = π считается наименьшим положительным периодом, где область определения имеет вид - π 2 + π · k ; π 2 + π · k , k ∈ Z .
Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами - 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.
Симметрия идет по сторону О х. Период не изменится в этот момент.
Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у, тогда преобразуем до исходной функции.
