క్రాస్ ఉత్పత్తి సున్నాకి ఎందుకు సమానం? క్రాస్ ఉత్పత్తి - నిర్వచనాలు, లక్షణాలు, సూత్రాలు, ఉదాహరణలు మరియు పరిష్కారాలు

7.1 క్రాస్ ఉత్పత్తి యొక్క నిర్వచనం

సూచించిన క్రమంలో తీసుకున్న మూడు నాన్-కోప్లానార్ వెక్టర్స్ a, b మరియు c, మూడవ వెక్టర్ c చివరి నుండి మొదటి వెక్టార్ నుండి రెండవ వెక్టర్ b వరకు అతి తక్కువ మలుపు కనిపించినట్లయితే, కుడి చేతి ట్రిపుల్‌గా ఏర్పడుతుంది. అపసవ్యదిశలో ఉండాలి మరియు సవ్యదిశలో ఉంటే ఎడమచేతి త్రిపాది (Fig. 16 చూడండి).

వెక్టర్ a మరియు వెక్టర్ b యొక్క వెక్టర్ ఉత్పత్తిని వెక్టర్ c అంటారు, ఇది:

1. వెక్టార్లకు లంబంగా a మరియు b, అంటే c ^ a మరియు c ^ b ;

2. వెక్టర్స్‌పై నిర్మించిన సమాంతర చతుర్భుజం వైశాల్యానికి సంఖ్యాపరంగా సమానమైన పొడవును కలిగి ఉంటుంది a మరియుబివైపులా (Fig. 17 చూడండి), అనగా.

3. వెక్టర్స్ a, b మరియు c కుడిచేతి ట్రిపుల్‌ను ఏర్పరుస్తాయి.

క్రాస్ ఉత్పత్తిని x b లేదా [a,b] అని సూచిస్తారు. వెక్టర్ ఉత్పత్తి యొక్క నిర్వచనం నుండి నేను నేరుగా అనుసరించే యూనిట్ వెక్టర్స్ మధ్య ఈ క్రింది సంబంధాలు, జెమరియు కె(అంజీర్ 18 చూడండి):

i x j = k, j x k = i, k x i = j.
ఉదాహరణకు, దానిని నిరూపిద్దాం i xj =k.

1) k ^ i, k ^ j ;

2) |k |=1, కానీ | i x j| = |i | |J | పాపం(90°)=1;

3) వెక్టర్స్ i, j మరియు కెకుడి ట్రిపుల్‌ను ఏర్పరుస్తుంది (Fig. 16 చూడండి).

7.2 క్రాస్ ఉత్పత్తి యొక్క లక్షణాలు

1. కారకాలను పునర్వ్యవస్థీకరించేటప్పుడు, వెక్టర్ ఉత్పత్తి గుర్తును మారుస్తుంది, అనగా. మరియు xb =(b xa) (Fig. 19 చూడండి).

వెక్టర్స్ a xb మరియు b xa కొలినియర్, ఒకే మాడ్యూల్‌లను కలిగి ఉంటాయి (సమాంతర చతుర్భుజం యొక్క వైశాల్యం మారదు), కానీ వ్యతిరేక దిశలో ఉంటాయి (ట్రిపుల్స్ a, b, a xb మరియు a, b, b x a వ్యతిరేక ధోరణి). అంటే axb = -(బి xa).

2. వెక్టార్ ఉత్పత్తి స్కేలార్ ఫ్యాక్టర్‌కు సంబంధించి సమ్మేళన లక్షణాన్ని కలిగి ఉంటుంది, అనగా l (a xb) = (l a) x b = a x (l b).

l >0ని అనుమతించండి. వెక్టర్ l (a xb) a మరియు b వెక్టర్‌లకు లంబంగా ఉంటుంది. వెక్టర్ ( ఎల్ a)x బివెక్టర్స్ a మరియు లంబంగా కూడా ఉంటుంది బి(వెక్టర్స్ a, ఎల్కానీ అదే విమానంలో పడుకోండి). దీని అర్థం వెక్టర్స్ ఎల్(a xb) మరియు ( ఎల్ a)x బికొలినియర్. వారి దిశలు ఏకీభవిస్తున్నాయని స్పష్టంగా తెలుస్తుంది. అవి ఒకే పొడవును కలిగి ఉంటాయి:

అందుకే ఎల్(a xb)= ఎల్ఒక xb. ఇది ఇదే విధంగా నిరూపించబడింది ఎల్<0.

3. రెండు సున్నా కాని వెక్టర్స్ a మరియు బివాటి వెక్టార్ ఉత్పత్తి సున్నా వెక్టార్‌కి సమానంగా ఉంటే మరియు మాత్రమే కొలినియర్‌గా ఉంటాయి, అనగా ఒక ||b<=>మరియు xb =0.

ముఖ్యంగా, i *i =j *j =k *k =0 .

4. వెక్టర్ ఉత్పత్తి పంపిణీ లక్షణాన్ని కలిగి ఉంది:

(a+b) xc = a xc + బి xs.

మేము రుజువు లేకుండా అంగీకరిస్తాము.

7.3 కోఆర్డినేట్‌ల పరంగా క్రాస్ ప్రోడక్ట్‌ను వ్యక్తీకరించడం

మేము వెక్టర్స్ i యొక్క క్రాస్ ప్రోడక్ట్ టేబుల్‌ని ఉపయోగిస్తాము, జెమరియు కె:

మొదటి వెక్టర్ నుండి రెండవది వరకు ఉన్న చిన్న మార్గం యొక్క దిశ బాణం యొక్క దిశతో సమానంగా ఉంటే, అప్పుడు ఉత్పత్తి మూడవ వెక్టర్‌కు సమానం; అది ఏకీభవించకపోతే, మూడవ వెక్టర్ మైనస్ గుర్తుతో తీసుకోబడుతుంది.

రెండు వెక్టర్స్ a =a x i +a y ఇవ్వబడనివ్వండి జె+a z కెమరియు b =b x i+బి వై జె+b z కె. ఈ వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తిని వాటిని బహుపదాలుగా గుణించడం ద్వారా కనుగొనండి (వెక్టార్ ఉత్పత్తి యొక్క లక్షణాల ప్రకారం):

ఫలిత సూత్రాన్ని మరింత క్లుప్తంగా వ్రాయవచ్చు:

సమానత్వం యొక్క కుడి వైపు (7.1) మొదటి వరుసలోని మూలకాల పరంగా మూడవ-ఆర్డర్ నిర్ణాయకం యొక్క విస్తరణకు అనుగుణంగా ఉంటుంది.సమానత్వం (7.2) గుర్తుంచుకోవడం సులభం.

7.4 క్రాస్ ప్రోడక్ట్ యొక్క కొన్ని అప్లికేషన్లు

వెక్టర్స్ యొక్క కోలినియారిటీని స్థాపించడం

సమాంతర చతుర్భుజం మరియు త్రిభుజం యొక్క వైశాల్యాన్ని కనుగొనడం

వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తి యొక్క నిర్వచనం ప్రకారం ఎమరియు బి |a xb | =|a | * |b |sin g, అనగా S జతల = |a x b |. మరియు, అందువలన, D S =1/2|a x b |.

ఒక పాయింట్ గురించి శక్తి యొక్క క్షణం యొక్క నిర్ణయం

పాయింట్ A వద్ద బలాన్ని వర్తింపజేయండి F = ABదాన్ని పోనివ్వు గురించి- అంతరిక్షంలో కొంత పాయింట్ (Fig. 20 చూడండి).

అని భౌతిక శాస్త్రం ద్వారా తెలిసింది శక్తి యొక్క క్షణం ఎఫ్ పాయింట్ కు సంబంధించి గురించివెక్టర్ అంటారు M,ఇది పాయింట్ గుండా వెళుతుంది గురించిమరియు:

1) పాయింట్ల గుండా వెళుతున్న విమానానికి లంబంగా O, A, B;

2) సంఖ్యాపరంగా ప్రతి చేతికి శక్తి యొక్క ఉత్పత్తికి సమానం

3) OA మరియు A B వెక్టర్‌లతో కుడి ట్రిపుల్‌ను ఏర్పరుస్తుంది.

కాబట్టి, M = OA x F.

సరళ భ్రమణ వేగాన్ని కనుగొనడం

వేగం vకోణీయ వేగంతో తిరిగే దృఢమైన శరీరం యొక్క పాయింట్ M wస్థిర అక్షం చుట్టూ, ఆయిలర్ సూత్రం v =w xr ద్వారా నిర్ణయించబడుతుంది, ఇక్కడ r =OM, ఇక్కడ O అనేది అక్షం యొక్క కొంత స్థిర బిందువు (Fig. 21 చూడండి).

వెక్టర్ ఉత్పత్తి యొక్క భావనను ఇవ్వడానికి ముందు, త్రిమితీయ స్థలంలో ఒక →, b →, c → యొక్క ఆర్డర్ చేయబడిన ట్రిపుల్ వెక్టర్స్ యొక్క విన్యాసాన్ని ప్రశ్నకు చూద్దాం.

ప్రారంభించడానికి, వెక్టర్స్ a → , b → , c → ఒక పాయింట్ నుండి పక్కన పెడదాం. ట్రిపుల్ a → , b → , c → యొక్క విన్యాసాన్ని వెక్టార్ c → యొక్క దిశను బట్టి కుడి లేదా ఎడమ కావచ్చు. ట్రిపుల్ a → , b → , c → రకం వెక్టార్ c → చివరి నుండి వెక్టర్ a → నుండి b → వరకు అతి తక్కువ మలుపు ఉండే దిశ నుండి నిర్ణయించబడుతుంది.

చిన్న మలుపు అపసవ్య దిశలో జరిగితే, అప్పుడు వెక్టర్స్ యొక్క ట్రిపుల్ a → , b → , c → అంటారు కుడి, సవ్యదిశలో ఉంటే - వదిలేశారు.

తరువాత, రెండు నాన్-కాలినియర్ వెక్టర్స్ a → మరియు b → తీసుకోండి. అప్పుడు A B → = a → మరియు A C → = b → అనే పాయింట్ నుండి వెక్టార్‌లను ప్లాట్ చేద్దాం. A B → మరియు A C → రెండింటికి ఏకకాలంలో లంబంగా ఉండే వెక్టర్ A D → = c →ని నిర్మిస్తాము. ఆ విధంగా, వెక్టార్‌ను నిర్మించేటప్పుడు A D → = c →, మనం రెండు పనులు చేయవచ్చు, దానికి ఒక దిశ లేదా వ్యతిరేకం (దృష్టాంతం చూడండి).

వెక్టార్ యొక్క ట్రిపుల్ యొక్క ఆర్డర్ a → , b → , c → అనేది వెక్టార్ యొక్క దిశను బట్టి మనం కనుగొన్నట్లుగా కుడి లేదా ఎడమ కావచ్చు.

పై నుండి మేము వెక్టర్ ఉత్పత్తి యొక్క నిర్వచనాన్ని పరిచయం చేయవచ్చు. త్రిమితీయ స్థలం యొక్క దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లో నిర్వచించబడిన రెండు వెక్టర్‌లకు ఈ నిర్వచనం ఇవ్వబడింది.

నిర్వచనం 1

a → మరియు b → అనే రెండు వెక్టార్ల వెక్టార్ ఉత్పత్తి త్రిమితీయ స్థలం యొక్క దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లో నిర్వచించబడిన అటువంటి వెక్టర్‌ని మేము పిలుస్తాము:

• వెక్టర్స్ a → మరియు b → కొలినియర్ అయితే, అది సున్నా అవుతుంది;
• ఇది వెక్టర్ a → మరియు వెక్టార్ b → రెండింటికి లంబంగా ఉంటుంది, అనగా. ∠ a → c → = ∠ b → c → = π 2 ;
• దాని పొడవు సూత్రం ద్వారా నిర్ణయించబడుతుంది: c → = a → · b → · sin ∠ a → , b → ;
• వెక్టర్స్ యొక్క ట్రిపుల్ a → , b → , c → ఇచ్చిన కోఆర్డినేట్ సిస్టమ్ వలె అదే ధోరణిని కలిగి ఉంటుంది.

వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి a → మరియు b → కింది సంజ్ఞామానాన్ని కలిగి ఉంది: a → × b →.

వెక్టర్ ఉత్పత్తి యొక్క కోఆర్డినేట్లు

ఏ వెక్టర్ కోఆర్డినేట్ సిస్టమ్‌లో నిర్దిష్ట కోఆర్డినేట్‌లను కలిగి ఉన్నందున, మేము వెక్టర్ ఉత్పత్తికి రెండవ నిర్వచనాన్ని పరిచయం చేయవచ్చు, ఇది వెక్టర్స్ యొక్క ఇచ్చిన కోఆర్డినేట్‌లను ఉపయోగించి దాని కోఆర్డినేట్‌లను కనుగొనడానికి అనుమతిస్తుంది.

నిర్వచనం 2

త్రిమితీయ స్థలం యొక్క దీర్ఘచతురస్రాకార కోఆర్డినేట్ వ్యవస్థలో రెండు వెక్టార్ల వెక్టర్ ఉత్పత్తి a → = (a x ; a y ; a z) మరియు b → = (b x ; b y ; b z) వెక్టర్ అంటారు c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , ఇక్కడ నేను → కోర్స్, j →

వెక్టార్ ఉత్పత్తిని థర్డ్-ఆర్డర్ స్క్వేర్ మ్యాట్రిక్స్ యొక్క డిటర్మినేట్‌గా సూచించవచ్చు, ఇక్కడ మొదటి వరుసలో వెక్టార్ వెక్టర్స్ i → , j → , k → , రెండవ వరుసలో వెక్టార్ యొక్క కోఆర్డినేట్‌లు a → , మరియు మూడవ వరుస ఉంటాయి ఇచ్చిన దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లో వెక్టర్ b → యొక్క కోఆర్డినేట్‌లను కలిగి ఉంటుంది, ఇది మాతృక యొక్క నిర్ణాయకం ఇలా కనిపిస్తుంది: c → = a → × b → = i → j → k → a x a y a z b z b x b y b

ఈ నిర్ణాయకాన్ని మొదటి వరుసలోని మూలకాలకు విస్తరించడం ద్వారా, మేము సమానత్వాన్ని పొందుతాము: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · ix → b z · x → b b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

క్రాస్ ఉత్పత్తి యొక్క లక్షణాలు

కోఆర్డినేట్‌లలోని వెక్టార్ ఉత్పత్తి మాతృక c → = a → × b → = i → j → k → a x a y a z b x b y b z , ఆ తర్వాత ఆధారంగా సూచించబడుతుందని తెలుసు మాతృక నిర్ణాయకం యొక్క లక్షణాలుకిందివి ప్రదర్శించబడతాయి వెక్టర్ ఉత్పత్తి యొక్క లక్షణాలు:

1. వ్యతిరేకత a → × b → = - b → × a → ;
2. పంపిణీ a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → లేదా a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. అసోసియేటివిటీ λ a → × b → = λ a → × b → లేదా a → × (λ b →) = λ a → × b →, ఇక్కడ λ అనేది ఏకపక్ష వాస్తవ సంఖ్య.

ఈ లక్షణాలకు సాధారణ ఆధారాలు ఉన్నాయి.

ఉదాహరణగా, మేము వెక్టర్ ఉత్పత్తి యొక్క యాంటీకమ్యుటేటివ్ ఆస్తిని నిరూపించగలము.

యాంటీకమ్యుటేటివిటీకి రుజువు

నిర్వచనం ప్రకారం, a → × b → = i → j → k → a x a y a z b x b y b z మరియు b → × a → = i → j → k → b x b y b z a x a y a z. మరియు మాతృక యొక్క రెండు అడ్డు వరుసలు మారినట్లయితే, అప్పుడు మాతృక యొక్క నిర్ణాయకం యొక్క విలువ వ్యతిరేకతకు మారాలి, కాబట్టి, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k z b x - b → × a → , ఇది మరియు వెక్టార్ ఉత్పత్తి యాంటీకమ్యుటేటివ్ అని రుజువు చేస్తుంది.

వెక్టర్ ఉత్పత్తి - ఉదాహరణలు మరియు పరిష్కారాలు

చాలా సందర్భాలలో, మూడు రకాల సమస్యలు ఉన్నాయి.

మొదటి రకం సమస్యలలో, రెండు వెక్టర్స్ యొక్క పొడవులు మరియు వాటి మధ్య కోణం సాధారణంగా ఇవ్వబడతాయి మరియు మీరు వెక్టర్ ఉత్పత్తి యొక్క పొడవును కనుగొనవలసి ఉంటుంది. ఈ సందర్భంలో, కింది సూత్రాన్ని ఉపయోగించండి c → = a → · b → · sin ∠ a → , b → .

ఉదాహరణ 1

మీకు a → = 3, b → = 5, ∠ a →, b → = π 4 తెలిస్తే వెక్టర్స్ a → మరియు b → వెక్టర్ ఉత్పత్తి పొడవును కనుగొనండి.

పరిష్కారం

వెక్టర్స్ a → మరియు b → వెక్టర్ ఉత్పత్తి పొడవును నిర్ణయించడం ద్వారా, మేము ఈ సమస్యను పరిష్కరిస్తాము: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

సమాధానం: 15 2 2 .

రెండవ రకానికి చెందిన సమస్యలు వెక్టర్స్ యొక్క కోఆర్డినేట్‌లతో కనెక్షన్ కలిగి ఉంటాయి, వాటిలో వెక్టర్ ఉత్పత్తి, దాని పొడవు మొదలైనవి. ఇచ్చిన వెక్టర్స్ యొక్క తెలిసిన కోఆర్డినేట్‌ల ద్వారా శోధించబడతాయి a → = (a x; a y; a z) మరియు b → = (b x ; b y ; b z) .

ఈ రకమైన సమస్య కోసం, మీరు చాలా టాస్క్ ఎంపికలను పరిష్కరించవచ్చు. ఉదాహరణకు, a → మరియు b → వెక్టార్‌ల కోఆర్డినేట్‌లను పేర్కొనలేము, కానీ రూపం యొక్క సమన్వయ వెక్టర్‌లుగా వాటి విస్తరణలు b → = b x · i → + b y · j → + b z · k → మరియు c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, లేదా వాటి వెక్టర్స్ a → మరియు b → యొక్క సమన్వయం ద్వారా ప్రారంభించవచ్చు మరియు ముగింపు పాయింట్లు.

కింది ఉదాహరణలను పరిశీలించండి.

ఉదాహరణ 2

దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లో, రెండు వెక్టర్స్ ఇవ్వబడ్డాయి: a → = (2; 1; - 3), b → = (0; - 1; 1). వారి క్రాస్ ఉత్పత్తిని కనుగొనండి.

పరిష్కారం

రెండవ నిర్వచనం ప్రకారం, మేము ఇచ్చిన కోఆర్డినేట్‌లలో రెండు వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తిని కనుగొంటాము: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

మేము మాతృక యొక్క డిటర్మినెంట్ ద్వారా వెక్టార్ ఉత్పత్తిని వ్రాస్తే, ఈ ఉదాహరణకి పరిష్కారం ఇలా కనిపిస్తుంది: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 -1 -1 1 = - 2 i → - 2 j → - 2 k → .

సమాధానం: a → × b → = - 2 i → - 2 j → - 2 k → .

ఉదాహరణ 3

i → - j → మరియు i → + j → + k → వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి పొడవును కనుగొనండి, ఇక్కడ i →, j →, k → దీర్ఘచతురస్రాకార కార్టీసియన్ కోఆర్డినేట్ సిస్టమ్ యొక్క యూనిట్ వెక్టర్స్.

పరిష్కారం

ముందుగా, ఇచ్చిన దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లో ఇవ్వబడిన వెక్టార్ ఉత్పత్తి i → - j → × i → + j → + k → యొక్క కోఆర్డినేట్‌లను కనుగొనండి.

వెక్టర్స్ i → - j → మరియు i → + j → + k → వరుసగా కోఆర్డినేట్‌లను (1; - 1; 0) మరియు (1; 1; 1) కలిగి ఉన్నాయని తెలుసు. మాతృక యొక్క నిర్ణయాధికారిని ఉపయోగించి వెక్టార్ ఉత్పత్తి యొక్క పొడవును కనుగొనండి, అప్పుడు మనకు i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

కాబట్టి, వెక్టార్ ఉత్పత్తి i → - j → × i → + j → + k → ఇచ్చిన కోఆర్డినేట్ సిస్టమ్‌లో కోఆర్డినేట్‌లు (- 1 ; - 1 ; 2) ఉన్నాయి.

మేము సూత్రాన్ని ఉపయోగించి వెక్టార్ ఉత్పత్తి యొక్క పొడవును కనుగొంటాము (వెక్టార్ యొక్క పొడవును కనుగొనే విభాగాన్ని చూడండి): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

సమాధానం: i → - j → × i → + j → + k → = 6 . .

ఉదాహరణ 4

దీర్ఘచతురస్రాకార కార్టీసియన్ కోఆర్డినేట్ సిస్టమ్‌లో, A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) అనే మూడు పాయింట్ల కోఆర్డినేట్‌లు ఇవ్వబడ్డాయి. అదే సమయంలో A B → మరియు A C → లంబంగా కొన్ని వెక్టర్‌లను కనుగొనండి.

పరిష్కారం

వెక్టర్స్ A B → మరియు A C → వరుసగా క్రింది కోఆర్డినేట్‌లను (- 1 ; 2 ; 2) మరియు (0 ; 4 ; 1) కలిగి ఉంటాయి. A B → మరియు A C → వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తిని కనుగొన్న తర్వాత, ఇది A B → మరియు A C → రెండింటికి నిర్వచనం ప్రకారం లంబ వెక్టార్ అని స్పష్టంగా తెలుస్తుంది, అంటే ఇది మన సమస్యకు పరిష్కారం. దానిని A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

సమాధానం: - 6 i → + j → - 4 k → . - లంబ వెక్టార్లలో ఒకటి.

మూడవ రకం యొక్క సమస్యలు వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తి యొక్క లక్షణాలను ఉపయోగించడంపై దృష్టి సారించాయి. దరఖాస్తు చేసిన తర్వాత, మేము ఇచ్చిన సమస్యకు పరిష్కారాన్ని పొందుతాము.

ఉదాహరణ 5

వెక్టర్స్ a → మరియు b → లంబంగా ఉంటాయి మరియు వాటి పొడవు వరుసగా 3 మరియు 4. వెక్టార్ ఉత్పత్తి పొడవును కనుగొనండి 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

పరిష్కారం

వెక్టార్ ఉత్పత్తి యొక్క డిస్ట్రిబ్యూటివ్ ప్రాపర్టీ ద్వారా, మనం 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 అని వ్రాయవచ్చు. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

అసోసియేటివిటీ యొక్క ఆస్తి ద్వారా, మేము చివరి వ్యక్తీకరణలో వెక్టర్ ఉత్పత్తుల సంకేతం నుండి సంఖ్యా గుణకాలను తీసుకుంటాము: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

వెక్టార్ ఉత్పత్తులు a → × a → మరియు b → × b → 0కి సమానం, ఎందుకంటే a → × a → = a → · a → · sin 0 = 0 మరియు b → × b → = b → · b → · sin 0 = 0, ఆపై 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → . × a → .

వెక్టార్ ఉత్పత్తి యొక్క యాంటీకమ్యుటాటివిటీ నుండి ఇది అనుసరిస్తుంది - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × బి → . .

వెక్టార్ ఉత్పత్తి యొక్క లక్షణాలను ఉపయోగించి, మేము సమానత్వం 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

షరతు ప్రకారం, a → మరియు b → వెక్టర్స్ లంబంగా ఉంటాయి, అంటే వాటి మధ్య కోణం π 2కి సమానం. కనుగొనబడిన విలువలను తగిన సూత్రాలలోకి మార్చడమే ఇప్పుడు మిగిలి ఉంది: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

సమాధానం: 3 a → - b → × a → - 2 b → = 60.

నిర్వచనం ప్రకారం వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి పొడవు a → × b → = a → · b → · sin ∠ a → , b → . త్రిభుజం యొక్క వైశాల్యం ఈ భుజాల మధ్య కోణం యొక్క సైన్ ద్వారా గుణించబడిన దాని రెండు భుజాల పొడవు యొక్క సగం ఉత్పత్తికి సమానం అని ఇప్పటికే (పాఠశాల కోర్సు నుండి) తెలిసినందున. పర్యవసానంగా, వెక్టర్ ఉత్పత్తి యొక్క పొడవు సమాంతర చతుర్భుజం యొక్క వైశాల్యానికి సమానంగా ఉంటుంది - రెట్టింపు త్రిభుజం, అవి వెక్టర్స్ రూపంలో భుజాల ఉత్పత్తి a → మరియు b →, ఒక పాయింట్ నుండి, సైన్ ద్వారా నిర్దేశించబడింది వాటి మధ్య కోణం పాపం ∠ a →, b →.

ఇది వెక్టార్ ఉత్పత్తి యొక్క రేఖాగణిత అర్థం.

వెక్టర్ ఉత్పత్తి యొక్క భౌతిక అర్థం

మెకానిక్స్‌లో, భౌతిక శాస్త్ర శాఖలలో ఒకటి, వెక్టర్ ఉత్పత్తికి ధన్యవాదాలు, మీరు అంతరిక్షంలో ఒక బిందువుకు సంబంధించి శక్తి యొక్క క్షణాన్ని నిర్ణయించవచ్చు.

నిర్వచనం 3

పాయింట్ Aకి సంబంధించి, పాయింట్ Bకి F → వర్తించే శక్తి యొక్క క్షణం ద్వారా, మేము క్రింది వెక్టార్ ఉత్పత్తి A B → × F →ని అర్థం చేసుకుంటాము.

మీరు టెక్స్ట్‌లో లోపాన్ని గమనించినట్లయితే, దయచేసి దాన్ని హైలైట్ చేసి, Ctrl+Enter నొక్కండి

వెక్టర్స్ మధ్య కోణం

మేము రెండు వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి యొక్క భావనను పరిచయం చేయడానికి, మేము మొదట ఈ వెక్టర్స్ మధ్య కోణం వంటి భావనను అర్థం చేసుకోవాలి.

మాకు $\overline(α)$ మరియు $\overline(β)$ అనే రెండు వెక్టర్లను ఇవ్వండి. స్పేస్‌లో $O$ పాయింట్‌ని తీసుకుని, దాని నుండి $\overline(α)=\overline(OA)$ మరియు $\overline(β)=\overline(OB)$, ఆపై కోణం $AOB$ని ప్లాట్ చేద్దాం. ఈ వెక్టర్స్ మధ్య కోణం అని పిలుస్తారు (Fig. 1).

సంజ్ఞామానం: $∠(\overline(α),\overline(β))$

వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తి యొక్క భావన మరియు కనుగొనే సూత్రం

నిర్వచనం 1

రెండు వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి రెండు వెక్టర్లకు లంబంగా ఉండే వెక్టార్, మరియు దాని పొడవు ఈ వెక్టర్స్ మధ్య కోణం యొక్క సైన్తో ఈ వెక్టర్స్ పొడవుల ఉత్పత్తికి సమానంగా ఉంటుంది మరియు రెండు ప్రారంభ వాటిని కలిగి ఉన్న ఈ వెక్టర్ కూడా కార్టీసియన్ కోఆర్డినేట్ సిస్టమ్ వలె అదే ధోరణి.

సంజ్ఞామానం: $\overline(α)х\overline(β)$.

గణితశాస్త్రపరంగా ఇది ఇలా కనిపిస్తుంది:

1. $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
3. $(\overline(α)х\overline(β),\overline(α),\overline(β))$ మరియు $(\overline(i),\overline(j),\overline(k))$ అదే ఓరియెంటెడ్ (Fig. 2)

సహజంగానే, వెక్టర్స్ యొక్క బయటి ఉత్పత్తి రెండు సందర్భాలలో సున్నా వెక్టర్‌తో సమానంగా ఉంటుంది:

1. ఒకటి లేదా రెండు వెక్టర్‌ల పొడవు సున్నా అయితే.
2. ఈ వెక్టర్‌ల మధ్య కోణం $180^\circ$ లేదా $0^\circ$కి సమానంగా ఉంటే (ఈ సందర్భంలో సైన్ సున్నా కాబట్టి).

వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి ఎలా కనుగొనబడుతుందో స్పష్టంగా చూడటానికి, పరిష్కారాల యొక్క క్రింది ఉదాహరణలను పరిగణించండి.

ఉదాహరణ 1

వెక్టార్ $\ఓవర్‌లైన్(δ)$ యొక్క పొడవును కనుగొనండి, ఇది వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి ఫలితంగా ఉంటుంది, $\overline(α)=(0,4,0)$ మరియు $\overline(β) =(3,0,0)$.

పరిష్కారం.

కార్టీసియన్ కోఆర్డినేట్ స్పేస్‌లో ఈ వెక్టర్‌లను వర్ణిద్దాం (Fig. 3):

మూర్తి 3. కార్టీసియన్ కోఆర్డినేట్ స్పేస్‌లోని వెక్టర్స్. రచయిత24 - విద్యార్థి రచనల ఆన్‌లైన్ మార్పిడి

ఈ వెక్టర్‌లు వరుసగా $Ox$ మరియు $Oy$ అక్షాలపై ఉన్నాయని మనం చూస్తాము. అందువల్ల, వాటి మధ్య కోణం $90^\circ$ అవుతుంది. ఈ వెక్టర్స్ యొక్క పొడవులను కనుగొనండి:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

అప్పుడు, నిర్వచనం 1 ద్వారా, మేము మాడ్యూల్ $|\overline(δ)|$ని పొందుతాము

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

సమాధానం: $12$.

వెక్టార్ కోఆర్డినేట్‌ల నుండి క్రాస్ ప్రొడక్ట్‌ను గణించడం

డెఫినిషన్ 1 వెంటనే రెండు వెక్టర్స్ కోసం వెక్టర్ ఉత్పత్తిని కనుగొనే పద్ధతిని సూచిస్తుంది. వెక్టర్, దాని విలువతో పాటు, దిశను కూడా కలిగి ఉంటుంది కాబట్టి, స్కేలార్ పరిమాణాన్ని ఉపయోగించి మాత్రమే దానిని కనుగొనడం అసాధ్యం. కానీ ఇది కాకుండా, కోఆర్డినేట్‌లను ఉపయోగించి మనకు ఇచ్చిన వెక్టర్‌లను కనుగొనడానికి ఒక మార్గం కూడా ఉంది.

మాకు $\ఓవర్‌లైన్(α)$ మరియు $\ఓవర్‌లైన్(β)$ వెక్టార్‌లను అందించండి, వీటిలో వరుసగా $(α_1,α_2,α_3)$ మరియు $(β_1,β_2,β_3)$ కోఆర్డినేట్‌లు ఉంటాయి. అప్పుడు క్రాస్ ఉత్పత్తి యొక్క వెక్టర్ (అవి దాని కోఆర్డినేట్లు) క్రింది సూత్రాన్ని ఉపయోగించి కనుగొనవచ్చు:

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

లేకపోతే, డిటర్మినెంట్‌ను విస్తరిస్తే, మేము ఈ క్రింది కోఆర్డినేట్‌లను పొందుతాము

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

ఉదాహరణ 2

$(0,3,3)$ మరియు $(-1,2,6)$ కోఆర్డినేట్‌లతో $\ఓవర్‌లైన్(α)$ మరియు $\overline(β)$ యొక్క వెక్టార్ ఉత్పత్తి యొక్క వెక్టర్‌ను కనుగొనండి.

పరిష్కారం.

పైన ఇచ్చిన ఫార్ములాను వాడుకుందాం. మాకు దొరికింది

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k )=(12,-3,3)$

సమాధానం: $(12,-3,3)$.

వెక్టర్స్ యొక్క వెక్టర్ ఉత్పత్తి యొక్క లక్షణాలు

ఏకపక్ష మిశ్రమ మూడు వెక్టర్స్ $\overline(α)$, $\overline(β)$ మరియు $\overline(γ)$, అలాగే $r∈R$ కోసం, క్రింది లక్షణాలు కలిగి ఉంటాయి:

ఉదాహరణ 3

$(3,0,0)$, $(0,0,0)$, $(0,8,0)$ మరియు $(3,8,0) కోఆర్డినేట్‌లను కలిగి ఉన్న సమాంతర చతుర్భుజ వైశాల్యాన్ని కనుగొనండి $.

పరిష్కారం.

ముందుగా, ఈ సమాంతర చతుర్భుజాన్ని కోఆర్డినేట్ స్పేస్‌లో వర్ణిద్దాం (Fig. 5):

మూర్తి 5. కోఆర్డినేట్ స్పేస్‌లో సమాంతర చతుర్భుజం. రచయిత24 - విద్యార్థి రచనల ఆన్‌లైన్ మార్పిడి

ఈ సమాంతర చతుర్భుజం యొక్క రెండు వైపులా $\overline(α)=(3,0,0)$ మరియు $\overline(β)=(0,8,0)$ కోఆర్డినేట్‌లతో కొలినియర్ వెక్టార్‌లను ఉపయోగించి నిర్మించబడిందని మేము చూస్తాము. నాల్గవ ఆస్తిని ఉపయోగించి, మేము పొందుతాము:

$S=|\overline(α)х\overline(β)|$

వెక్టర్ $\overline(α)х\overline(β)$ని కనుగొనండి:

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

అందుకే

$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$

సహజంగానే, వెక్టార్ ఉత్పత్తి విషయంలో, వెక్టర్స్ తీసుకునే క్రమం ముఖ్యమైనది, అంతేకాకుండా,

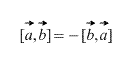
అలాగే, నిర్వచనం నుండి నేరుగా ఏదైనా స్కేలార్ ఫ్యాక్టర్ k (సంఖ్య) కోసం కిందిది నిజం అని అనుసరిస్తుంది:

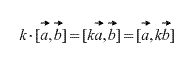
కొల్లినియర్ వెక్టర్స్ యొక్క క్రాస్ ప్రొడక్ట్ సున్నా వెక్టర్‌కి సమానం. అంతేకాకుండా, రెండు వెక్టర్స్ యొక్క క్రాస్ ప్రొడక్ట్ అవి కొలినియర్ అయితే మరియు మాత్రమే సున్నా. (వాటిలో ఒకటి సున్నా వెక్టార్ అయితే, సున్నా వెక్టర్ నిర్వచనం ప్రకారం ఏదైనా వెక్టర్‌కు కొలినియర్ అని గుర్తుంచుకోవాలి).

వెక్టర్ ఉత్పత్తి కలిగి ఉంది పంపిణీ ఆస్తి, అంటే

వెక్టార్ల కోఆర్డినేట్ల ద్వారా వెక్టర్ ఉత్పత్తిని వ్యక్తపరచడం.

రెండు వెక్టర్లను ఇవ్వనివ్వండి

(వెక్టార్ యొక్క ప్రారంభ మరియు ముగింపు యొక్క కోఆర్డినేట్‌ల నుండి వెక్టర్ యొక్క కోఆర్డినేట్‌లను ఎలా కనుగొనాలి - వెక్టర్స్ యొక్క డాట్ ఉత్పత్తి, అంశం డాట్ ఉత్పత్తి యొక్క ప్రత్యామ్నాయ నిర్వచనం లేదా వాటి కోఆర్డినేట్‌ల ద్వారా పేర్కొన్న రెండు వెక్టర్‌ల డాట్ ఉత్పత్తిని గణించడం అనే వ్యాసం చూడండి.)

మీకు వెక్టర్ ఉత్పత్తి ఎందుకు అవసరం?

క్రాస్ ఉత్పత్తిని ఉపయోగించడానికి అనేక మార్గాలు ఉన్నాయి, ఉదాహరణకు, పైన వ్రాసిన విధంగా, రెండు వెక్టర్స్ యొక్క క్రాస్ ఉత్పత్తిని లెక్కించడం ద్వారా మీరు అవి కొల్లినియర్ కాదా అని తెలుసుకోవచ్చు.

లేదా ఈ వెక్టర్స్ నుండి నిర్మించిన సమాంతర చతుర్భుజం యొక్క వైశాల్యాన్ని లెక్కించడానికి ఇది ఒక మార్గంగా ఉపయోగించవచ్చు. నిర్వచనం ఆధారంగా, ఫలిత వెక్టర్ యొక్క పొడవు ఇచ్చిన సమాంతర చతుర్భుజం యొక్క ప్రాంతం.

విద్యుత్ మరియు అయస్కాంతత్వంలో కూడా భారీ సంఖ్యలో అప్లికేషన్లు ఉన్నాయి.

ఆన్‌లైన్ వెక్టర్ ఉత్పత్తి కాలిక్యులేటర్.

ఈ కాలిక్యులేటర్‌ను ఉపయోగించి రెండు వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తిని కనుగొనడానికి, మీరు మొదటి పంక్తిలో మొదటి వెక్టర్ యొక్క కోఆర్డినేట్‌లను క్రమంలో నమోదు చేయాలి మరియు రెండవ వరుసలో రెండవది. వెక్టర్స్ యొక్క కోఆర్డినేట్‌లను వాటి ప్రారంభం మరియు ముగింపు యొక్క కోఆర్డినేట్‌ల నుండి లెక్కించవచ్చు (వ్యాసం చూడండి వెక్టర్స్ యొక్క డాట్ ఉత్పత్తి, అంశం డాట్ ఉత్పత్తికి ప్రత్యామ్నాయ నిర్వచనం లేదా వాటి కోఆర్డినేట్‌ల ద్వారా ఇవ్వబడిన రెండు వెక్టర్స్ యొక్క డాట్ ఉత్పత్తిని గణించడం.)

వెక్టర్ కళాకృతిత్రిమితీయ యూక్లిడియన్ స్పేస్‌లోని వెక్టర్‌లపై బైనరీ ఆపరేషన్ “వెక్టర్ గుణకారం” ఫలితంగా రెండు కారకాల నుండి నిర్మించబడిన సమతలానికి లంబంగా ఉండే సూడోవెక్టర్. వెక్టర్ ఉత్పత్తికి కమ్యుటాటివిటీ మరియు అసోసియేటివిటీ (ఇది యాంటీకమ్యుటేటివ్) యొక్క లక్షణాలను కలిగి ఉండదు మరియు వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తి వలె కాకుండా, వెక్టర్. అనేక ఇంజనీరింగ్ మరియు ఫిజిక్స్ అప్లికేషన్లలో విస్తృతంగా ఉపయోగించబడుతుంది. ఉదాహరణకు, కోణీయ మొమెంటం మరియు లోరెంజ్ ఫోర్స్ గణితశాస్త్రంలో వెక్టర్ ఉత్పత్తిగా వ్రాయబడ్డాయి. వెక్టర్స్ లంబంగా "కొలవడం" కోసం క్రాస్ ప్రోడక్ట్ ఉపయోగపడుతుంది - రెండు వెక్టర్స్ యొక్క క్రాస్ ప్రొడక్ట్ యొక్క మాడ్యులస్ లంబంగా ఉంటే వాటి మాడ్యులీల ఉత్పత్తికి సమానంగా ఉంటుంది మరియు వెక్టర్స్ సమాంతరంగా లేదా వ్యతిరేక సమాంతరంగా ఉంటే సున్నాకి తగ్గుతుంది.

వెక్టర్ ఉత్పత్తిని వివిధ మార్గాల్లో నిర్వచించవచ్చు మరియు సిద్ధాంతపరంగా, ఏదైనా పరిమాణం n యొక్క స్థలంలో, n-1 వెక్టర్స్ యొక్క ఉత్పత్తిని లెక్కించవచ్చు, తద్వారా వాటన్నింటికీ లంబంగా ఒకే వెక్టార్‌ని పొందవచ్చు. కానీ ఉత్పత్తి వెక్టార్ ఫలితాలతో నాన్-ట్రివియల్ బైనరీ ఉత్పత్తులకు పరిమితం అయితే, సాంప్రదాయ వెక్టర్ ఉత్పత్తి త్రిమితీయ మరియు ఏడు డైమెన్షనల్ ఖాళీలలో మాత్రమే నిర్వచించబడుతుంది. వెక్టార్ ఉత్పత్తి యొక్క ఫలితం, స్కేలార్ ఉత్పత్తి వలె, యూక్లిడియన్ స్థలం యొక్క మెట్రిక్‌పై ఆధారపడి ఉంటుంది.

త్రిమితీయ దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్‌లోని కోఆర్డినేట్‌ల నుండి స్కేలార్ ఉత్పత్తి వెక్టర్‌లను లెక్కించే ఫార్ములా కాకుండా, క్రాస్ ప్రోడక్ట్ సూత్రం దీర్ఘచతురస్రాకార కోఆర్డినేట్ సిస్టమ్ యొక్క విన్యాసాన్ని లేదా మరో మాటలో చెప్పాలంటే, దాని “చిరాలిటీ”పై ఆధారపడి ఉంటుంది.

నిర్వచనం:
స్పేస్ R3లో వెక్టర్ a మరియు వెక్టర్ b యొక్క వెక్టర్ ఉత్పత్తి క్రింది అవసరాలను తీర్చే వెక్టర్ c:
వెక్టార్ c యొక్క పొడవు వెక్టర్స్ a మరియు b మరియు వాటి మధ్య ఉన్న కోణం φ యొక్క పొడవు యొక్క ఉత్పత్తికి సమానం:
|c|=|a||b|sin φ;
వెక్టార్ c అనేది ప్రతి వెక్టర్స్‌కి ఆర్తోగోనల్‌గా ఉంటుంది a మరియు b;
వెక్టర్ c నిర్దేశించబడుతుంది, తద్వారా వెక్టర్స్ యొక్క ట్రిపుల్ abc కుడిచేతితో ఉంటుంది;
స్పేస్ R7 విషయంలో, a, b, c యొక్క ట్రిపుల్ వెక్టర్స్ యొక్క అనుబంధం అవసరం.
హోదా:
c===a × b

అన్నం. 1. సమాంతర చతుర్భుజం యొక్క వైశాల్యం వెక్టర్ ఉత్పత్తి యొక్క మాడ్యులస్‌కు సమానం

క్రాస్ ఉత్పత్తి యొక్క రేఖాగణిత లక్షణాలు:
రెండు నాన్ జీరో వెక్టర్స్ యొక్క కోలినియారిటీకి అవసరమైన మరియు తగినంత షరతు ఏమిటంటే వాటి వెక్టర్ ఉత్పత్తి సున్నాకి సమానం.

క్రాస్ ప్రొడక్ట్ మాడ్యూల్ విస్తీర్ణంతో సమానం ఎస్వెక్టర్స్‌పై నిర్మించిన సమాంతర చతుర్భుజం సాధారణ మూలానికి తగ్గించబడింది aమరియు బి(అంజీర్ 1 చూడండి).

ఉంటే ఇ- వెక్టార్లకు యూనిట్ వెక్టార్ ఆర్తోగోనల్ aమరియు బిమరియు మూడు కాబట్టి ఎంపిక a,b,e- కుడి, మరియు ఎస్వాటిపై నిర్మించిన సమాంతర చతుర్భుజం యొక్క వైశాల్యం (సాధారణ మూలానికి తగ్గించబడింది), అప్పుడు వెక్టర్ ఉత్పత్తికి సూత్రం చెల్లుతుంది:
= ఎస్ ఇ

Fig.2. వెక్టర్ యొక్క వెక్టర్ మరియు స్కేలార్ ఉత్పత్తిని ఉపయోగించి సమాంతర పైప్డ్ యొక్క వాల్యూమ్; చుక్కల పంక్తులు వెక్టర్ c యొక్క అంచనాలను a × b మరియు వెక్టర్ a b × c పై చూపుతాయి, మొదటి దశ స్కేలార్ ఉత్పత్తులను కనుగొనడం

ఉంటే సి- కొంత వెక్టర్, π - ఈ వెక్టర్‌ను కలిగి ఉన్న ఏదైనా విమానం, ఇ- యూనిట్ వెక్టర్ విమానంలో పడి ఉంది π మరియు ఆర్తోగోనల్ కు c,g- యూనిట్ వెక్టార్ విమానానికి ఆర్తోగోనల్ π మరియు వెక్టర్స్ యొక్క ట్రిపుల్ తద్వారా దర్శకత్వం వహించారు ఇసిజిసరైనది, అప్పుడు విమానంలో పడి ఉన్నవారికి π వెక్టర్ aసూత్రం సరైనది:
=Pr e a |c|g
ఇక్కడ Pr e a అనేది వెక్టార్ e యొక్క ప్రొజెక్షన్
|c|-వెక్టార్ యొక్క మాడ్యులస్ c

వెక్టర్ మరియు స్కేలార్ ఉత్పత్తులను ఉపయోగిస్తున్నప్పుడు, మీరు వెక్టర్స్‌పై నిర్మించిన సమాంతర పైప్డ్ వాల్యూమ్‌ను సాధారణ మూలానికి తగ్గించవచ్చు ఎ, బిమరియు సి. మూడు వెక్టర్స్ యొక్క అటువంటి ఉత్పత్తిని మిశ్రమం అంటారు.
V=|a (b×c)|
ఈ వాల్యూమ్‌ను రెండు విధాలుగా కనుగొనవచ్చని ఫిగర్ చూపిస్తుంది: "స్కేలార్" మరియు "వెక్టార్" ఉత్పత్తులను మార్చుకున్నప్పుడు కూడా రేఖాగణిత ఫలితం భద్రపరచబడుతుంది:
V=a×b c=a b×c

క్రాస్ ప్రొడక్ట్ యొక్క పరిమాణం అసలు వెక్టర్స్ మధ్య కోణం యొక్క సైన్ మీద ఆధారపడి ఉంటుంది, కాబట్టి క్రాస్ ప్రొడక్ట్ కూడా వెక్టర్స్ యొక్క "లంబంగా" డిగ్రీగా గుర్తించబడుతుంది, స్కేలార్ ఉత్పత్తిని "సమాంతరత" డిగ్రీగా చూడవచ్చు. ”. అసలు వెక్టర్స్ లంబంగా ఉంటే రెండు యూనిట్ వెక్టర్స్ యొక్క వెక్టార్ ఉత్పత్తి 1 (యూనిట్ వెక్టర్)కి సమానం మరియు వెక్టర్స్ సమాంతరంగా లేదా వ్యతిరేక సమాంతరంగా ఉంటే 0 (సున్నా వెక్టర్)కి సమానం.

కార్టీసియన్ కోఆర్డినేట్‌లలో క్రాస్ ప్రోడక్ట్ కోసం వ్యక్తీకరణ
రెండు వెక్టర్స్ ఉంటే aమరియు బివాటి దీర్ఘచతురస్రాకార కార్టీసియన్ కోఆర్డినేట్‌ల ద్వారా నిర్వచించబడింది లేదా మరింత ఖచ్చితంగా, ఆర్థోనార్మల్ ప్రాతిపదికన సూచించబడుతుంది
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
మరియు కోఆర్డినేట్ సిస్టమ్ కుడిచేతితో ఉంటుంది, అప్పుడు వారి వెక్టర్ ఉత్పత్తి రూపాన్ని కలిగి ఉంటుంది
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
ఈ సూత్రాన్ని గుర్తుంచుకోవడానికి:
i =∑ε ijk a jb k
ఎక్కడ ε ijk- లెవి-సివిటా యొక్క చిహ్నం.