Jedwali la viunga vya kazi za trigonometric. Kuunganisha vipengele vya trigonometric

Viunga vya kazi za trigonometric.
Mifano ya ufumbuzi

Katika somo hili tutaangalia viambatanisho vya kazi za trigonometric, ambayo ni, kujazwa kwa viunga kutakuwa sines, cosines, tangents na cotangents katika mchanganyiko mbalimbali. Mifano zote zitachambuliwa kwa undani, kupatikana na kueleweka hata kwa teapot.

Ili kusoma kwa mafanikio viunga vya kazi za trigonometric, lazima uwe na ufahamu mzuri wa viunga rahisi zaidi, na pia ujue mbinu kadhaa za ujumuishaji. Unaweza kufahamiana na nyenzo hizi kwenye mihadhara Muhimu usio na kikomo. Mifano ya ufumbuzi Na.

Na sasa tunahitaji: Jedwali la viungo, Jedwali la derivatives Na Orodha ya fomula za trigonometric. Vifaa vyote vya kufundishia vinaweza kupatikana kwenye ukurasa Fomula za hisabati na meza. Ninapendekeza kuchapisha kila kitu. Ninazingatia hasa fomula za trigonometric, zinapaswa kuwa mbele ya macho yako- bila hii, ufanisi wa kazi utapungua sana.

Lakini kwanza, kuhusu ni viungo gani katika makala hii Hapana. Hakuna viungo vya fomu, - kosine, sine, iliyozidishwa na aina fulani ya polynomial (mara nyingi kitu kilicho na tanjiti au cotangent). Viungo vile vinaunganishwa na sehemu, na kujifunza njia, tembelea somo Ujumuishaji kwa sehemu. Mifano ya suluhisho Pia hapa hakuna viambatanisho na "matao" - arctangent, arcsine, nk, pia mara nyingi huunganishwa na sehemu.

Wakati wa kupata viunga vya kazi za trigonometric, njia kadhaa hutumiwa:

(4) Tunatumia fomula ya jedwali , tofauti pekee ni kwamba badala ya "X" tuna usemi changamano.

Mfano 2

Mfano 3

Pata muunganisho usio na kikomo.

Aina ya asili kwa wale ambao wanazama kwenye shindano. Kama labda umegundua, katika jedwali la viunga hakuna muhimu ya tangent na cotangent, lakini, hata hivyo, viambatanisho kama hivyo vinaweza kupatikana.

(1) Tunatumia fomula ya trigonometric

(2) Tunaleta kazi chini ya ishara tofauti.

(3) Tunatumia jedwali muhimu .

Mfano 4

Pata muunganisho usio na kikomo.

Huu ni mfano wa suluhu la kujitegemea, suluhu kamili na jibu ziko mwishoni mwa somo.

Mfano 5

Pata muunganisho usio na kikomo.

Digrii zetu zitaongezeka polepole =).
Kwanza suluhisho:

(1) Tunatumia fomula

(2) Tunatumia utambulisho mkuu wa trigonometric , ambayo inafuata hiyo .

(3) Gawa nambari kwa neno denominata kwa muhula.

(4) Tunatumia sifa ya mstari wa kiunganishi kisichojulikana.

(5) Tunaunganisha kwa kutumia meza.

Mfano 6

Pata muunganisho usio na kikomo.

Huu ni mfano wa suluhu la kujitegemea, suluhu kamili na jibu ziko mwishoni mwa somo.

Pia kuna viungo vya tangents na cotangents, ambazo ziko katika mamlaka ya juu. Muhimu wa mchemraba wa tangent unajadiliwa katika somo Jinsi ya kuhesabu eneo la takwimu ya gorofa? Viunga vya tangent (cotangent) kwa nguvu ya nne na ya tano vinaweza kupatikana kwenye ukurasa Complex integrals.

Kupunguza kiwango cha integrand

Mbinu hii hufanya kazi wakati vitendakazi vya integrand vimejazwa na sines na kosini ndani hata digrii. Ili kupunguza kiwango, tumia fomula za trigonometric , na , na fomula ya mwisho mara nyingi hutumiwa kwa mwelekeo tofauti: .

Mfano 7

Pata muunganisho usio na kikomo.

Suluhisho:

Kimsingi, hakuna kitu kipya hapa, isipokuwa kwamba tulitumia fomula (kupunguza kiwango cha integrand). Tafadhali kumbuka kuwa nimefupisha suluhisho. Unapopata uzoefu, kiungo cha inaweza kupatikana kwa mdomo; hii inaokoa muda na inakubalika kabisa wakati wa kumaliza kazi. Katika kesi hii, ni vyema si kuelezea utawala , kwanza tunachukua kwa maneno kiungo cha 1, kisha cha .

Mfano 8

Pata muunganisho usio na kikomo.

Huu ni mfano wa suluhu la kujitegemea, suluhu kamili na jibu ziko mwishoni mwa somo.

Hili ndilo ongezeko la shahada lililoahidiwa:

Mfano 9

Pata muunganisho usio na kikomo.

Kwanza suluhisho, kisha maoni:

(1) Tayarisha muunganisho ili kutumia fomula .

(2) Kwa kweli tunatumia fomula.

(3) Sisi mraba denominator na kuchukua mara kwa mara nje ya ishara muhimu. Inaweza kufanywa tofauti kidogo, lakini, kwa maoni yangu, ilikuwa rahisi zaidi.

(4) Tunatumia fomula

(5) Katika muhula wa tatu sisi tena kupunguza shahada, lakini kwa kutumia formula .

(6) Tunawasilisha masharti yanayofanana (hapa nimegawanya neno kwa muda na alifanya nyongeza).

(7) Kwa kweli, tunachukua kanuni muhimu, kanuni ya mstari na njia ya kutekeleza kazi chini ya ishara tofauti inafanywa kwa mdomo.

(8) Kuchanganya jibu.

! Katika muunganisho usio na kipimo, jibu mara nyingi linaweza kuandikwa kwa njia kadhaa

Katika mfano uliozingatiwa hivi karibuni, jibu la mwisho lingeweza kuandikwa kwa njia tofauti - kufungua mabano na hata kufanya hivi kabla ya kuunganisha usemi, ambayo ni, mwisho ufuatao wa mfano unakubalika kabisa:

Inawezekana kwamba chaguo hili ni rahisi zaidi, nilielezea tu jinsi nilivyozoea kutatua mwenyewe). Hapa kuna mfano mwingine wa kawaida wa suluhisho la kujitegemea:

Mfano 10

Pata muunganisho usio na kikomo.

Mfano huu unaweza kutatuliwa kwa njia mbili, na unaweza kufanikiwa majibu mawili tofauti kabisa(kwa usahihi zaidi, wataonekana tofauti kabisa, lakini kutoka kwa mtazamo wa hisabati watakuwa sawa). Uwezekano mkubwa zaidi, hautaona njia ya busara zaidi na utateseka na kufungua mabano na kutumia fomula zingine za trigonometric. Suluhisho la ufanisi zaidi hutolewa mwishoni mwa somo.

Kwa muhtasari wa aya, tunahitimisha: kiungo chochote cha fomu , wapi na - hata nambari, hutatuliwa kwa njia ya kupunguza kiwango cha integrand.
Kwa mazoezi, nilikutana na viunga na digrii 8 na 10, na ilinibidi kutatua fujo zao mbaya kwa kupunguza digrii mara kadhaa, na kusababisha majibu marefu na marefu.

Njia ya Kubadilisha Tofauti

Kama ilivyoelezwa katika makala Njia ya kubadilisha inayoweza kubadilika katika muunganisho usiojulikana, sharti kuu la kutumia njia ya uingizwaji ni ukweli kwamba katika kiunganishi kuna kazi fulani na derivative yake:
(kazi si lazima katika bidhaa)

Mfano 11

Pata muunganisho usio na kikomo.

Tunaangalia jedwali la derivatives na tunaona fomula, , yaani, katika integrand yetu kuna kazi na derivative yake. Walakini, tunaona kwamba wakati wa kutofautisha, cosine na sine hubadilika kwa kila mmoja, na swali linatokea: jinsi ya kufanya mabadiliko ya kutofautisha na tunamaanisha nini kwa sine au cosine?! Swali linaweza kutatuliwa kwa kuchochewa kisayansi: ikiwa tutafanya uingizwaji vibaya, basi hakuna kitu kizuri kitatokea.

Mwongozo wa jumla: katika hali sawa, unahitaji kuteua kazi ambayo iko kwenye dhehebu.

Tunasumbua suluhisho na kufanya uingizwaji

Kila kitu ni sawa katika dhehebu, kila kitu kinategemea tu , sasa inabakia kujua nini kitageuka.
Ili kufanya hivyo, tunapata tofauti:

Au, kwa kifupi:
Kutoka kwa usawa unaosababishwa, kwa kutumia sheria ya uwiano, tunaelezea usemi tunaohitaji:

Kwa hivyo:

Sasa integrand yetu yote inategemea tu na tunaweza kuendelea kutatua

Tayari. Acha nikukumbushe kuwa madhumuni ya uingizwaji ni kurahisisha kiunganishi; katika kesi hii, kila kitu kilishuka ili kuunganisha kazi ya nguvu kulingana na jedwali.

Sio bahati mbaya kwamba nilielezea mfano huu kwa undani kama hii; hii ilifanywa kwa madhumuni ya kurudia na kuimarisha nyenzo za somo. Njia ya kubadilisha inayoweza kubadilika katika muunganisho usiojulikana.

Na sasa mifano miwili ya suluhisho lako mwenyewe:

Mfano 12

Pata muunganisho usio na kikomo.

Mfano 13

Pata muunganisho usio na kikomo.

Kamilisha masuluhisho na majibu mwishoni mwa somo.

Mfano 14

Pata muunganisho usio na kikomo.

Hapa tena, katika integrand, kuna sine na cosine (kazi yenye derivative), lakini katika bidhaa, na shida hutokea - tunamaanisha nini kwa sine au cosine?

Unaweza kujaribu kufanya uingizwaji kwa kutumia poking ya kisayansi, na ikiwa hakuna kitu kinachofanya kazi, basi iteue kama kazi nyingine, lakini kuna:

Mwongozo wa jumla: unahitaji kuteua kazi ambayo, kwa njia ya mfano, iko katika "nafasi isiyofaa".

Tunaona kwamba katika mfano huu, mwanafunzi cosine "anateseka" kutoka kwa shahada, na sine hukaa kwa uhuru, peke yake.

Kwa hivyo, wacha tufanye uingizwaji:

Ikiwa mtu yeyote bado ana shida na algorithm ya kuchukua nafasi ya kutofautisha na kupata tofauti, basi unapaswa kurudi kwenye somo. Njia ya kubadilisha inayoweza kubadilika katika muunganisho usiojulikana.

Mfano 15

Pata muunganisho usio na kikomo.

Wacha tuchambue kiunga, ni nini kinapaswa kuashiria?
Wacha tukumbuke miongozo yetu:
1) Kazi ina uwezekano mkubwa katika dhehebu;
2) Kazi iko katika "nafasi isiyofaa".

Kwa njia, miongozo hii halali sio tu kwa kazi za trigonometric.

Sine inafaa vigezo vyote viwili (haswa ya pili), kwa hivyo uingizwaji unajipendekeza. Kimsingi, uingizwaji unaweza tayari kufanywa, lakini kwanza itakuwa nzuri kujua nini cha kufanya na? Kwanza, "tunapunguza" cosine moja:

Tunahifadhi kwa tofauti yetu ya "baadaye".

Na tunaionyesha kupitia sine kwa kutumia kitambulisho cha msingi cha trigonometric:

Sasa hapa kuna mbadala:

Kanuni ya jumla: Ikiwa katika muunganisho moja ya vitendaji vya trigonometric (sine au cosine) iko ndani isiyo ya kawaida shahada, basi unahitaji "kuuma" kazi moja kutoka kwa digrii isiyo ya kawaida, na uteue kazi nyingine nyuma yake. Tunazungumza tu juu ya viambatanisho ambapo kuna cosines na sines.

Katika mfano uliozingatiwa, tulikuwa na kosine kwa nguvu isiyo ya kawaida, kwa hivyo tukang'oa kosini moja kutoka kwa nguvu, na tukaiweka kama sine.

Mfano 16

Pata muunganisho usio na kikomo.

Digrii zinaondoka =).
Huu ni mfano kwako kutatua peke yako. Suluhisho kamili na jibu mwishoni mwa somo.

Ubadilishaji wa trigonometric wa Universal

Ubadilishaji wa trigonometric wa Universal ni kesi ya kawaida ya mbinu ya uingizwaji tofauti. Unaweza kujaribu kuitumia wakati "hujui la kufanya." Lakini kwa kweli kuna miongozo ya matumizi yake. Viambatanisho vya kawaida ambapo uingizwaji wa trigonometriki zima unahitaji kutumika ni viambatanisho vifuatavyo: , , , na kadhalika.

Mfano 17

Pata muunganisho usio na kikomo.

Uingizwaji wa trigonometric wa ulimwengu wote katika kesi hii unatekelezwa kwa njia ifuatayo. Wacha tubadilishe:. Situmii herufi , lakini herufi , hii sio aina fulani ya sheria, ni kwamba, tena, nimezoea kutatua mambo kwa njia hii.

Hapa ni rahisi zaidi kupata tofauti; kwa hili, kutoka kwa usawa, ninaelezea:
Ninaambatisha arctangent kwa sehemu zote mbili:

Actangent na tangent kufuta kila mmoja nje:

Hivyo:

Kwa mazoezi, sio lazima kuielezea kwa undani kama hii, lakini tumia tu matokeo ya kumaliza:

! Usemi huo ni halali ikiwa tu chini ya sines na cosines tuna "X", kwa kiunganishi (ambayo tutazungumza baadaye) kila kitu kitakuwa tofauti kidogo!

Wakati wa kuchukua nafasi, sines na cosines hubadilika kuwa sehemu zifuatazo:
, , usawa huu ni msingi wa fomula zinazojulikana za trigonometric: ,

Kwa hivyo, muundo wa mwisho unaweza kuonekana kama hii:

Wacha tufanye uingizwaji wa trigonometric wa ulimwengu wote:

Fomula za msingi za trigonometric na mbadala za kimsingi zinawasilishwa. Njia za kuunganisha kazi za trigonometric zimeainishwa - ujumuishaji wa kazi za busara, bidhaa ya kazi za nguvu za sin x na cos x, bidhaa ya polynomial, kielelezo na sine au cosine, ujumuishaji wa kazi za trigonometric inverse. Njia zisizo za kawaida huathiriwa.

Maudhui

Mbinu za kawaida za kuunganisha kazi za trigonometric

Mbinu ya jumla

Kwanza, ikiwa ni lazima, integrand lazima ibadilishwe ili kazi za trigonometric hutegemea hoja moja, ambayo ni sawa na kutofautiana kwa ushirikiano.

Kwa mfano, ikiwa integrand inategemea dhambi(x+a) Na cos(x+b), basi unapaswa kufanya uongofu:
cos (x+b) = cos (x+a - (a-b)) = cos (x+a) cos (b-a) + dhambi ( x+a ) dhambi (b-a).
Kisha fanya uingizwaji z = x+a. Kwa hivyo, utendakazi wa trigonometriki zitategemea tu utofauti wa ujumuishaji z.

Wakati utendakazi wa trigonometriki hutegemea hoja moja inayoambatana na utofauti wa ujumuishaji (wacha tuseme ni z), yaani, kiunganishi kinajumuisha tu vitendaji kama vile. dhambi z, kwani z, tg z, ctg z, basi unahitaji kufanya badala
.
Uingizwaji kama huo husababisha kuunganishwa kwa kazi za busara au zisizo na maana (ikiwa kuna mizizi) na inaruhusu mtu kuhesabu muhimu ikiwa imeunganishwa katika kazi za msingi.

Hata hivyo, mara nyingi unaweza kupata njia nyingine zinazokuwezesha kutathmini muhimu kwa njia fupi, kwa kuzingatia maalum ya integrand. Chini ni muhtasari wa njia kuu kama hizo.

Mbinu za kuunganisha kazi za busara za sin x na cos x

Kazi za busara kutoka dhambi x Na kwani x ni kazi zinazoundwa kutoka dhambi x, kwani x na viambajengo vyovyote vinavyotumia utendakazi wa kujumlisha, kutoa, kuzidisha, kugawanya na kuongeza hadi nguvu kamili. Wameteuliwa kama ifuatavyo: R (dhambi x, cos x). Hii inaweza pia kujumuisha tanjiti na kotanji, kwani huundwa kwa kugawanya sine na kosine na kinyume chake.
Viunga vya kazi za busara vina fomu:
.

Mbinu za kuunganisha kazi za kimantiki za trigonometric ni kama ifuatavyo.
1) Ubadilishaji kila wakati husababisha ujumuishaji wa sehemu ya busara. Hata hivyo, katika baadhi ya matukio, kuna mbadala (hizi zimewasilishwa hapa chini) ambazo husababisha hesabu fupi.
2) ikiwa R (dhambi x, cos x) cos x → - cos x dhambi x.
3) ikiwa R (dhambi x, cos x) kuzidishwa na -1 wakati wa kubadilisha dhambi x → - dhambi x, kisha uingizwaji t = kwani x.
4) Ikiwa R (dhambi x, cos x) haibadiliki kama ilivyo kwa uingizwaji wa wakati mmoja cos x → - cos x, Na dhambi x → - dhambi x, kisha uingizwaji t = tg x au t = ctg x.

Mifano:
, , .

Bidhaa ya kazi za nguvu za cos x na sin x

Viunga vya fomu

ni viunga vya utendakazi wa kimantiki wa trigonometriki. Kwa hivyo, njia zilizoainishwa katika sehemu iliyopita zinaweza kutumika kwao. Mbinu kulingana na maalum ya viambatanisho vile vinajadiliwa hapa chini.

Ikiwa m na n ni nambari za busara, basi moja ya mbadala t = dhambi x au t = kwani x muhimu ni kupunguzwa kwa muhimu ya binomial tofauti.

Ikiwa m na n ni nambari kamili, basi ujumuishaji unafanywa kwa kutumia fomula za kupunguza:

;
;
;
.

Mfano:
.

Viunga vya bidhaa za polynomial na sine au cosine

Muunganisho wa fomu:
, ,
ambapo P(x) ni polynomial katika x, zimeunganishwa na sehemu. Hii inatoa fomula zifuatazo:

;
.

Mifano:
, .

Viunga vya bidhaa ya polynomial, kielelezo na sine au kosine

Muunganisho wa fomu:
, ,
ambapo P(x) ni polynomial katika x, iliyounganishwa kwa kutumia fomula ya Euler
e iax = cos ax + isin ax(ambapo mimi 2 = - 1 ).
Ili kufanya hivyo, kwa kutumia njia iliyoainishwa katika aya iliyotangulia, hesabu muhimu
.
Kwa kutenganisha sehemu za kweli na za kufikiria kutoka kwa matokeo, viunga vya asili hupatikana.

Mfano:
.

Mbinu zisizo za kawaida za kuunganisha kazi za trigonometric

Chini ni idadi ya mbinu zisizo za kawaida zinazokuwezesha kufanya au kurahisisha ujumuishaji wa kazi za trigonometric.

Utegemezi (a sin x + b cos x)

Ikiwa integrand inategemea tu a dhambi x + b cos x, basi ni muhimu kutumia formula:
,
Wapi.

Kwa mfano

Kusuluhisha sehemu kutoka kwa sine na kosini kuwa sehemu rahisi zaidi

Fikiria muhimu
.
Njia rahisi zaidi ya ujumuishaji ni kutenganisha sehemu kuwa rahisi zaidi kwa kutumia mabadiliko:
dhambi(a - b) = dhambi(x + a - (x + b)) = dhambi(x+a) cos(x+b) - cos(x+a) dhambi(x+b)

Kuunganisha sehemu za shahada ya kwanza

Wakati wa kuhesabu kiunga
,
ni rahisi kutenganisha sehemu kamili ya sehemu na derivative ya denominator
a 1 dhambi x + b 1 cos x = A (dhambi x + b cos x) + B (dhambi x + b cos x)′ .
Viunga vya A na B vinapatikana kwa kulinganisha pande za kushoto na kulia.

Marejeleo:
N.M. Gunter, R.O. Kuzmin, Mkusanyiko wa shida katika hisabati ya juu, "Lan", 2003.

Angalia pia:

Mifano ya ufumbuzi wa viambatanisho kwa sehemu huzingatiwa kwa undani, muunganisho wake ambao ni bidhaa ya polynomial kwa kielelezo (e kwa nguvu x) au kwa sine (sin x) au cosine (cos x).

Maudhui

Angalia pia: Njia ya kuunganishwa kwa sehemu
Jedwali la viambatanisho visivyo na kikomo
Mbinu za kuhesabu viambatanisho visivyo na kikomo
Kazi za msingi za msingi na mali zao

Mfumo wa kuunganishwa kwa sehemu

Wakati wa kutatua mifano katika sehemu hii, ujumuishaji na fomula ya sehemu hutumiwa:
;
.

Mifano ya viambatanisho vilivyo na bidhaa ya polynomial na sin x, cos x au e x

Hapa kuna mifano ya viungo vile:
, , .

Ili kuunganisha viambatanisho vile, polynomial inaashiria u, na sehemu iliyobaki na v dx. Ifuatayo, tumia ujumuishaji kwa fomula ya sehemu.

Chini ni suluhisho la kina kwa mifano hii.

Mifano ya kutatua viambatanisho

Mfano na kipeo, e kwa nguvu ya x

Amua muhimu:
.

Wacha tuanzishe kielezi chini ya ishara tofauti:
e - x dx = - e - x d(-x) = - d(e - x).

Wacha tuunganishe kwa sehemu.

Hapa
.
Pia tunaunganisha kiungo kilichobaki kwa sehemu.
.
.
.
Hatimaye tuna:
.

Mfano wa kufafanua kiungo na sine

Kuhesabu sehemu muhimu:
.

Wacha tuanzishe sine chini ya ishara ya kutofautisha:

Wacha tuunganishe kwa sehemu.

hapa u = x 2 , v = cos(2 x+3), du = ( x 2 )′ dx

Pia tunaunganisha kiungo kilichobaki kwa sehemu. Ili kufanya hivyo, anzisha cosine chini ya ishara tofauti.

hapa u = x, v = dhambi(2 x+3), du = dx

Hatimaye tuna:

Mfano wa bidhaa ya polynomial na cosine

Kuhesabu sehemu muhimu:
.

Wacha tuanzishe cosine chini ya ishara ya kutofautisha:

Wacha tuunganishe kwa sehemu.

hapa = x 2 + 3 x + 5, v = dhambi 2 x, du = ( x 2 + 3 x + 5 )′ dx

Pia kutakuwa na matatizo kwako kutatua peke yako, ambayo unaweza kuona majibu.

Mchanganyiko unaweza kubadilishwa kutoka kwa bidhaa ya kazi za trigonometric hadi jumla

Wacha tuzingatie viunga ambavyo kiunganishi ni bidhaa ya sines na cosines ya shahada ya kwanza ya x iliyozidishwa na sababu tofauti, ambayo ni, viunga vya fomu.

Kwa kutumia fomula za trigonometric zinazojulikana

(2)
(3)
(4)
mtu anaweza kubadilisha kila moja ya bidhaa katika viambatanisho vya fomu (31) kuwa jumla ya aljebra na kuunganisha kulingana na fomula.

(5)

(6)

Mfano 1. Tafuta

Suluhisho. Kwa mujibu wa fomula (2) katika

Mfano 2. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Kwa mujibu wa fomula (3) katika

Mfano 3. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Kwa mujibu wa fomula (4) katika tunapata mabadiliko yafuatayo ya integrand:

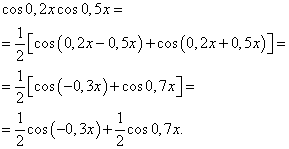
Kutumia formula (6), tunapata

Muunganisho wa bidhaa ya nguvu za sine na kosine ya hoja sawa

Wacha sasa tuzingatie viunga vya kazi ambavyo ni zao la nguvu za sine na cosine ya hoja sawa, i.e.

(7)

Katika hali maalum, moja ya viashiria ( m au n) inaweza kuwa sifuri.

Wakati wa kuunganisha kazi kama hizo, hutumiwa kwamba nguvu hata ya cosine inaweza kuonyeshwa kupitia sine, na tofauti ya sine ni sawa na cos. x dx(au hata nguvu ya sine inaweza kuonyeshwa kwa suala la cosine, na tofauti ya cosine ni sawa na - dhambi x dx ) .

Kesi mbili zinapaswa kutofautishwa: 1) angalau moja ya viashiria m Na n isiyo ya kawaida; 2) viashiria vyote viwili ni sawa.

Hebu kesi ya kwanza ifanyike, yaani kiashiria n = 2k+ 1 - isiyo ya kawaida. Kisha, kutokana na hilo

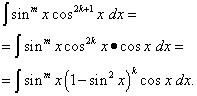
Kiunganishi kinawasilishwa kwa njia ambayo sehemu yake moja ni kazi ya sine tu, na nyingine ni tofauti ya sine. Sasa kwa kutumia uingizwaji tofauti t= dhambi x ufumbuzi hupunguza kuunganisha polynomial kwa heshima na t. Ikiwa tu digrii m ni isiyo ya kawaida, basi wanafanya vivyo hivyo, wakitenga sababu ya dhambi x, ikielezea sehemu iliyobaki katika suala la cos x na kuamini t=cos x. Mbinu hii pia inaweza kutumika wakati kuunganisha nguvu za mgawo wa sine na kosine , Lini angalau moja ya viashiria ni isiyo ya kawaida . Jambo zima ni hilo mgawo wa nguvu za sine na cosine ni kesi maalum ya bidhaa zao : Wakati kazi ya trigonometric iko katika denominator ya integrand, shahada yake ni hasi. Lakini pia kuna matukio ya kazi za sehemu ya trigonometric, wakati nguvu zao ni sawa tu. Kuhusu wao - katika aya inayofuata.

Ikiwa viashiria vyote viwili m Na n- hata, basi, kwa kutumia fomula za trigonometric

punguza vielelezo vya sine na cosine, baada ya hapo kiungo cha aina sawa na hapo juu hupatikana. Kwa hiyo, ushirikiano unapaswa kuendelea kulingana na mpango huo. Ikiwa moja ya vielelezo hata ni hasi, yaani, mgawo wa nguvu za sine na cosine huzingatiwa, basi mpango huu haufai. . Kisha mabadiliko ya kutofautiana hutumiwa kulingana na jinsi integrand inaweza kubadilishwa. Kesi kama hiyo itazingatiwa katika aya inayofuata.

Mfano 4. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Kipeo cha kosine si cha kawaida. Kwa hiyo, hebu fikiria

t= dhambi x(Kisha dt=cos x dx ) Kisha tunapata

Kurudi kwa tofauti ya zamani, hatimaye tunapata

Mfano 5. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Kipeo cha cosine, kama katika mfano uliopita, ni isiyo ya kawaida, lakini kubwa zaidi. Hebu fikiria

na kufanya mabadiliko ya kutofautiana t= dhambi x(Kisha dt=cos x dx ) Kisha tunapata

Hebu tufungue mabano

na tunapata

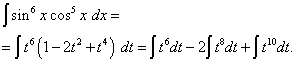
Kurudi kwa kutofautiana kwa zamani, tunapata suluhisho

Mfano 6. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Vielelezo vya sine na kosine ni sawa. Kwa hivyo, tunabadilisha kazi ya integrand kama ifuatavyo:

Kisha tunapata

Katika kiunga cha pili tunafanya mabadiliko ya kutofautisha, mpangilio t= dhambi2 x. Kisha (1/2)dt= cos2 x dx . Kwa hivyo,

Hatimaye tunapata

Kwa kutumia Njia ya Ubadilishaji Tofauti

Njia ya Kubadilisha Tofauti wakati wa kuunganisha kazi za trigonometric, inaweza kutumika katika hali ambapo kiunganishi kina sine au cosine pekee, bidhaa ya sine na kosine, ambamo sine au kosine iko katika digrii ya kwanza, tanjiti au cotangent, na vile vile sehemu ya hata nguvu za sine na cosine za hoja moja. Katika kesi hii, inawezekana kufanya vibali sio dhambi tu x = t na dhambi x = t, lakini pia tg x = t na ctg x = t .

Mfano 8. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Wacha tubadilishe utofauti: , basi . Mchanganyiko unaosababishwa unaweza kuunganishwa kwa urahisi kwa kutumia jedwali la viunga:

Mfano 9. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Wacha tubadilishe tangent kuwa uwiano wa sine na cosine:

Wacha tubadilishe utofauti: , basi . Mchanganyiko unaosababishwa ni meza muhimu na ishara ya kuondoa:

Kurudi kwa utofauti wa asili, hatimaye tunapata:

Mfano 10. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Wacha tubadilishe utofauti: , basi .

Hebu tubadilishe kiunganishi ili kutumia utambulisho wa trigonometric :

Tunabadilisha kutofautisha, bila kusahau kuweka ishara ya minus mbele ya kiunga (tazama hapo juu, ni nini sawa na dt) Ifuatayo, tunazingatia kiunga na kuunganisha kulingana na jedwali:

Kurudi kwa utofauti wa asili, hatimaye tunapata:

Pata kiunga cha kazi ya trigonometric mwenyewe, na kisha uangalie suluhisho

Ubadilishaji wa trigonometric wa Universal

Ubadilishaji wa trigonometric wa Universal inaweza kutumika katika hali ambapo integrand haingii chini ya kesi zilizojadiliwa katika aya zilizopita. Kimsingi, wakati sine au kosine (au zote mbili) ziko katika dhehebu la sehemu. Imethibitishwa kuwa sine na kosine zinaweza kubadilishwa na usemi mwingine ulio na tanjiti ya nusu ya pembe asili kama ifuatavyo:

Lakini kumbuka kuwa uingizwaji wa trigonometric wa ulimwengu wote mara nyingi hujumuisha mabadiliko changamano ya aljebra, kwa hivyo hutumiwa vyema wakati hakuna njia nyingine inayofanya kazi. Hebu tuangalie mifano ambapo, pamoja na uingizwaji wa trigonometric wa ulimwengu wote, uingizwaji chini ya ishara tofauti na njia ya coefficients isiyojulikana hutumiwa.

Mfano 12. Tafuta muhimu ya kazi ya trigonometric

Suluhisho. Suluhisho. Hebu kuchukua faida uingizwaji wa trigonometric zima. Kisha
.

Tunazidisha sehemu katika nambari na denominator kwa , na kuchukua mbili na kuiweka mbele ya ishara muhimu. Kisha

Jedwali la antiderivatives ("integrals"). Jedwali la viungo. Viunga visivyo na kikomo vya jedwali. (Viunga rahisi zaidi na viunga vilivyo na parameta). Fomula za kuunganishwa kwa sehemu. Fomula ya Newton-Leibniz.

Jedwali la antiderivatives ("integrals"). Viunga visivyo na kikomo vya jedwali. (Viunga rahisi zaidi na viunga vilivyo na parameta).
Muhimu wa utendaji kazi wa nguvu.	Muhimu wa utendaji kazi wa nguvu.
Kiunga ambacho kinapungua hadi muunganisho wa chaguo za kukokotoa za nguvu ikiwa x inaendeshwa chini ya ishara tofauti.

	Muunganisho wa kielelezo, ambapo a ni nambari isiyobadilika.
Muhtasari wa utendaji changamano wa kielelezo.	Muhtasari wa utendaji wa kipeo.

Muhimu sawa na logarithm asili.	Muhimu: "Logarithm ndefu".
	Muhimu: "Logarithm ndefu".
Muhimu: "Logarithm ya juu".	Kiunganishi, ambapo x katika nambari huwekwa chini ya ishara ya kutofautisha (kiashiria kisichobadilika chini ya ishara kinaweza kuongezwa au kupunguzwa), hatimaye ni sawa na kiunganishi sawa na logarithm asili.
Muhimu: "Logarithm ya juu".

Cosine muhimu.	Sine muhimu.
Muhimu sawa na tangent.	Muhimu sawa na kotangent.

Muhimu sawa na arcsine na arccosine
Sawa sawa na arcsine na arccosine.	Muhimu sawa na arctangent na arctangent.

Sahihi sawa na kosekanti.	Sahihi sawa na sekanti.
Muhimu sawa na arcsecant.	Muhimu sawa na arccosecant.
Muhimu sawa na arcsecant.	Muhimu sawa na arcsecant.

Sahihi sawa na sine hyperbolic.	Sahihi sawa na kosine ya hyperbolic.

Sahihi sawa na sine hyperbolic, ambapo sinhx ni sine hyperbolic katika toleo la Kiingereza.	Sahihi sawa na kosine lambano, ambapo sinhx ni sine ya hyperbolic katika toleo la Kiingereza.
Sahihi sawa na tanjiti ya hyperbolic.	Sahihi sawa na kotangenti ya hyperbolic.
Sahihi sawa na sekanti ya hyperbolic.	Sahihi sawa na kosekanti ya hyperbolic.

Fomula za kuunganishwa kwa sehemu. Sheria za ujumuishaji.

Fomula za kuunganishwa kwa sehemu. Fomula ya Newton-Leibniz. Kanuni za ujumuishaji.
Kuunganisha bidhaa (kazi) kwa mara kwa mara:
Kuunganisha jumla ya kazi:
viungo visivyo na kikomo:
Mfumo wa kuunganishwa kwa sehemu viungo dhahiri:
Fomula ya Newton-Leibniz viungo dhahiri:	Ambapo F(a),F(b) ni thamani za vizuia derivatives katika pointi b na a, mtawalia.

Jedwali la derivatives. Viingilio vya jedwali. Derivative ya bidhaa. Derivative ya mgawo. Inatokana na utendaji kazi changamano.

Ikiwa x ni tofauti huru, basi:

Jedwali la derivatives. Derivatives za tabular."derivative ya jedwali" - ndio, kwa bahati mbaya, hivi ndivyo hutafutwa kwenye mtandao.
	Inatokana na utendaji kazi wa nguvu

	Inatokana na kipeo
Nyingine ya utendaji changamano wa kielelezo	Nyingine ya utendaji wa kipeo

Nyingine ya kitendakazi cha logarithmic	Inatokana na logarithm asili
	Inatokana na logariti asilia ya chaguo za kukokotoa

Inatokana na sine	Derivative ya cosine
Inatokana na kosekanti	Inatokana na sekanti
Derivative ya arcsine	Derivative ya arc cosine
Derivative ya arcsine	Derivative ya arc cosine
Toleo la tangent	Derivative ya cotangent
Derivative ya arctangent	Derivative ya arc cotangent
Derivative ya arctangent	Derivative ya arc cotangent
Inatokana na arcsecant	Inatokana na arccosecant
Inatokana na arcsecant	Inatokana na arccosecant

Inatokana na sine hyperbolic Inatokana na sine hyperbolic katika toleo la Kiingereza	Imetoka kwa cosine ya hyperbolic Inatokana na hyperbolic cosine katika toleo la Kiingereza
Inatokana na tanjenti ya hyperbolic	Imetoka kwa kotangenti ya hyperbolic
Inatokana na sekanti ya hyperbolic	Inatokana na kosekanti ya hyperbolic

Kanuni za kutofautisha. Derivative ya bidhaa. Derivative ya mgawo. Inatokana na utendaji kazi changamano.
Inatokana na bidhaa (kazi) kwa mara kwa mara:
Inatokana na jumla (kazi):
Derivative ya bidhaa (kazi):
Inayotokana na mgawo (wa vitendaji):
Inayotokana na kazi ngumu:

Tabia za logarithm. Njia za kimsingi za logarithm. Desimali (lg) na logarithmu asili (ln).

Utambulisho wa msingi wa logarithmic
Wacha tuonyeshe jinsi utendakazi wowote wa umbo a b unavyoweza kufanywa kuwa kielelezo. Kwa kuwa kazi ya fomu e x inaitwa kielelezo, basi
Utendaji wowote wa fomu a b unaweza kuwakilishwa kama nguvu ya kumi

Logarithm asilia ln (logarithm kwa msingi e = 2.718281828459045...) ln(e)=1; ln(1)=0

Mfululizo wa Taylor. Upanuzi wa mfululizo wa Taylor wa chaguo za kukokotoa.

Ni zinageuka kuwa wengi kivitendo kukutana vipengele vya hisabati vinaweza kuwakilishwa kwa usahihi wowote katika eneo la sehemu fulani kwa njia ya mfululizo wa nishati iliyo na nguvu za mabadiliko katika mpangilio unaoongezeka. Kwa mfano, katika eneo la uhakika x=1:

Wakati wa kutumia mfululizo unaoitwa Safu za Taylor vitendaji mchanganyiko vilivyo na, tuseme, vitendakazi vya aljebra, trigonometriki na vipeo maalum vinaweza kuonyeshwa kama vitendakazi vya aljebra pekee. Kutumia mfululizo, mara nyingi unaweza kufanya utofautishaji na ujumuishaji haraka.

Msururu wa Taylor katika kitongoji cha point a una namna:

1) , ambapo f(x) ni chaguo la kukokotoa ambalo lina viasili vya maagizo yote kwa x = a. R n - neno lililosalia katika safu ya Taylor huamuliwa na usemi

Mgawo wa k-th (saa x k) wa mfululizo huamuliwa na fomula

3) Kesi maalum ya mfululizo wa Taylor ni mfululizo wa Maclaurin (=McLaren). (upanuzi hutokea karibu na uhakika a=0)

kwa = 0

wanachama wa mfululizo huamuliwa na fomula

Masharti ya kutumia mfululizo wa Taylor.

1. Ili chaguo za kukokotoa f(x) ipanuliwe kuwa mfululizo wa Taylor kwenye muda (-R;R), ni muhimu na inatosha kwamba neno linalosalia katika fomula ya Taylor (Maclaurin (=McLaren)) kwa hili. kitendakazi huwa na sifuri kama k →∞ kwa muda uliobainishwa (-R;R).

2. Ni muhimu kuwe na viasili vya kazi fulani katika sehemu iliyo karibu nayo ambayo tutaunda mfululizo wa Taylor.

Sifa za mfululizo wa Taylor.

Ikiwa f ni kazi ya uchanganuzi, basi mfululizo wake wa Taylor wakati wowote a katika kikoa cha ufafanuzi wa f hubadilika na kuwa f katika baadhi ya mtaa wa a.

Kuna vitendaji vinavyoweza kutofautishwa kabisa ambavyo mfululizo wa Taylor huungana, lakini wakati huo huo hutofautiana na utendaji kazi katika kitongoji chochote cha a. Kwa mfano:

Mfululizo wa Taylor hutumiwa katika ukadiriaji (ukadirio ni njia ya kisayansi ambayo inajumuisha kuchukua nafasi ya vitu vingine na vingine, kwa maana moja au nyingine karibu na vile vya asili, lakini rahisi zaidi) ya kazi na polynomia. Hasa, uwekaji mstari ((kutoka kwa mstari - mstari), moja ya njia za uwakilishi wa takriban wa mifumo iliyofungwa isiyo ya mstari, ambayo uchunguzi wa mfumo usio na mstari hubadilishwa na uchambuzi wa mfumo wa mstari, kwa maana fulani sawa na ule wa asili. .) milinganyo hutokea kwa kupanua katika mfululizo wa Taylor na kukata masharti yote juu ya mpangilio wa kwanza.

Kwa hivyo, karibu kazi yoyote inaweza kuwakilishwa kama polynomial kwa usahihi fulani.

Mifano ya baadhi ya upanuzi wa kawaida wa kazi za nguvu katika mfululizo wa Maclaurin (=McLaren, Taylor katika maeneo ya karibu ya uhakika 0) na Taylor katika maeneo ya karibu ya nukta 1. Masharti ya kwanza ya upanuzi wa kazi kuu katika mfululizo wa Taylor na McLaren.

Mifano ya upanuzi wa kawaida wa utendaji wa nishati katika mfululizo wa Maclaurin (=McLaren, Taylor katika maeneo ya karibu ya nukta 0)