After preliminary artillery preparation, examples with 3-4-5 nestings of functions will be less scary. The following two examples may seem complicated to some, but if you understand them (someone will suffer), then almost everything else in differential calculus will seem like a child's joke.
Example 2
Find the derivative of a function
As already noted, when finding the derivative of a complex function, first of all, it is necessary Right UNDERSTAND your investments. In cases where there are doubts, I remind you of a useful technique: we take the experimental value of “x”, for example, and try (mentally or in a draft) to substitute this value into the “terrible expression”.
1) First we need to calculate the expression, which means the sum is the deepest embedding.
2) Then you need to calculate the logarithm:
4) Then cube the cosine:
5) At the fifth step the difference:
6) And finally, the outermost function is the square root: 
Formula for differentiating a complex function 
are applied in reverse order, from the outermost function to the innermost. We decide:
It seems without errors:
1) Take the derivative of the square root.
2) Take the derivative of the difference using the rule 
3) The derivative of a triple is zero. In the second term we take the derivative of the degree (cube).
4) Take the derivative of the cosine.
6) And finally, we take the derivative of the deepest embedding.
It may seem too difficult, but this is not the most brutal example. Take, for example, Kuznetsov’s collection and you will appreciate all the beauty and simplicity of the analyzed derivative. I noticed that they like to give a similar thing in an exam to check whether a student understands how to find the derivative of a complex function or does not understand.
The following example is for you to solve on your own.
Example 3
Find the derivative of a function
Hint: First we apply the linearity rules and the product differentiation rule
Full solution and answer at the end of the lesson.
It's time to move on to something smaller and nicer.
It is not uncommon for an example to show the product of not two, but three functions. How to find the derivative of the product of three factors?
Example 4
Find the derivative of a function 
First we look, is it possible to turn the product of three functions into the product of two functions? For example, if we had two polynomials in the product, then we could open the brackets. But in the example under consideration, all the functions are different: degree, exponent and logarithm.
In such cases it is necessary sequentially apply the product differentiation rule 
twice
The trick is that by “y” we denote the product of two functions: , and by “ve” we denote the logarithm: . Why can this be done? Is it possible 
- this is not a product of two factors and the rule does not work?! There is nothing complicated:
Now it remains to apply the rule a second time to bracket:
You can also get twisted and put something out of brackets, but in this case it’s better to leave the answer exactly in this form - it will be easier to check.
The considered example can be solved in the second way:
Both solutions are absolutely equivalent.
Example 5
Find the derivative of a function
This is an example for an independent solution; in the sample it is solved using the first method.
Let's look at similar examples with fractions.
Example 6
Find the derivative of a function 
There are several ways you can go here:
Or like this:
But the solution will be written more compactly if we first use the rule of differentiation of the quotient 
, taking for the entire numerator:
In principle, the example is solved, and if it is left as is, it will not be an error. But if you have time, it is always advisable to check on a draft to see if the answer can be simplified?
Let's reduce the expression of the numerator to a common denominator and get rid of the three-story structure of the fraction:
The disadvantage of additional simplifications is that there is a risk of making a mistake not when finding the derivative, but during banal school transformations. On the other hand, teachers often reject the assignment and ask to “bring it to mind” the derivative.
A simpler example to solve on your own:
Example 7
Find the derivative of a function
We continue to master the methods of finding the derivative, and now we will consider a typical case when a “terrible” logarithm is proposed for differentiation
If g(x) And f(u) – differentiable functions of their arguments, respectively, at points x And u= g(x), then the complex function is also differentiable at the point x and is found by the formula
A typical mistake when solving derivative problems is mechanically transferring the rules for differentiating simple functions to complex functions. Let's learn to avoid this mistake.
Example 2. Find the derivative of a function
Wrong solution: calculate the natural logarithm of each term in parentheses and look for the sum of the derivatives:
Correct solution: again we determine where the “apple” is and where the “minced meat” is. Here the natural logarithm of the expression in parentheses is an “apple”, that is, a function over the intermediate argument u, and the expression in brackets is “minced meat”, that is, an intermediate argument u by independent variable x.
Then (using formula 14 from the derivatives table)
In many real-life problems, the expression with a logarithm can be somewhat more complicated, which is why there is a lesson
Example 3. Find the derivative of a function
Wrong solution:
Correct solution. Once again we determine where the “apple” is and where the “mincemeat” is. Here, the cosine of the expression in brackets (formula 7 in the table of derivatives) is an “apple”, it is prepared in mode 1, which affects only it, and the expression in brackets (the derivative of the degree is number 3 in the table of derivatives) is “minced meat”, it is prepared under mode 2, which affects only it. And as always, we connect two derivatives with the product sign. Result:
The derivative of a complex logarithmic function is a frequent task in tests, so we strongly recommend that you attend the lesson “Derivative of a logarithmic function.”
The first examples were on complex functions, in which the intermediate argument on the independent variable was a simple function. But in practical tasks it is often necessary to find the derivative of a complex function, where the intermediate argument is either itself a complex function or contains such a function. What to do in such cases? Find derivatives of such functions using tables and differentiation rules. When the derivative of the intermediate argument is found, it is simply substituted into the right place in the formula. Below are two examples of how this is done.
In addition, it is useful to know the following. If a complex function can be represented as a chain of three functions
then its derivative should be found as the product of the derivatives of each of these functions:
Many of your homework assignments may require you to open your guides in new windows. Actions with powers and roots And Operations with fractions .
Example 4. Find the derivative of a function
We apply the rule of differentiation of a complex function, not forgetting that in the resulting product of derivatives there is an intermediate argument with respect to the independent variable x does not change:
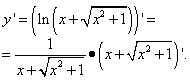
We prepare the second factor of the product and apply the rule for differentiating the sum:
The second term is the root, so
Thus, we found that the intermediate argument, which is a sum, contains a complex function as one of the terms: raising to a power is a complex function, and what is being raised to a power is an intermediate argument with respect to the independent variable x.
Therefore, we again apply the rule for differentiating a complex function:
We transform the degree of the first factor into a root, and when differentiating the second factor, do not forget that the derivative of the constant is equal to zero:
Now we can find the derivative of the intermediate argument needed to calculate the derivative of a complex function required in the problem statement y:
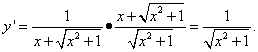
Example 5. Find the derivative of a function
First, we use the rule for differentiating the sum:
We obtained the sum of the derivatives of two complex functions. Let's find the first one:
Here, raising the sine to a power is a complex function, and the sine itself is an intermediate argument for the independent variable x. Therefore, we will use the rule of differentiation of a complex function, along the way taking the factor out of brackets :
Now we find the second term of the derivatives of the function y:
Here raising the cosine to a power is a complex function f, and the cosine itself is an intermediate argument in the independent variable x. Let us again use the rule for differentiating a complex function:
The result is the required derivative:
Table of derivatives of some complex functions
For complex functions, based on the rule of differentiation of a complex function, the formula for the derivative of a simple function takes a different form.
| 1. Derivative of a complex power function, where u x |  |
| 2. Derivative of the root of the expression | |
| 3. Derivative of an exponential function |  |
| 4. Special case of exponential function | |
| 5. Derivative of a logarithmic function with an arbitrary positive base A |  |
| 6. Derivative of a complex logarithmic function, where u– differentiable function of the argument x | |
| 7. Derivative of sine |  |
| 8. Derivative of cosine |  |
| 9. Derivative of tangent |  |
| 10. Derivative of cotangent |  |
| 11. Derivative of arcsine |  |
| 12. Derivative of arc cosine |  |
| 13. Derivative of arctangent |  |
| 14. Derivative of arc cotangent |  |
It is not entirely correct to call functions of a complex type the term “complex function”. For example, it looks very impressive, but this function is not complicated, unlike.
In this article, we will understand the concept of a complex function, learn how to identify it as part of elementary functions, give a formula for finding its derivative, and consider in detail the solution of typical examples.
When solving examples, we will constantly use the table of derivatives and differentiation rules, so keep them before your eyes.
Complex function is a function whose argument is also a function.
From our point of view, this definition is the most understandable. Conventionally, it can be denoted as f(g(x)) . That is, g(x) is like an argument of the function f(g(x)) .
For example, let f be the arctangent function and g(x) = lnx be the natural logarithm function, then the complex function f(g(x)) is arctan(lnx) . Another example: f is the function of raising to the fourth power, and 
is an entire rational function (see ), then 
.
In turn, g(x) can also be a complex function. For example, 
. Conventionally, such an expression can be denoted as 
. Here f is the sine function, is the square root function, 
- fractional rational function. It is logical to assume that the degree of nesting of functions can be any finite natural number.
You can often hear a complex function called composition of functions.
Formula for finding the derivative of a complex function.
Example.
Find the derivative of a complex function.
Solution.
In this example, f is the squaring function and g(x) = 2x+1 is the linear function.
Here is the detailed solution using the complex function derivative formula: 
Let's find this derivative by first simplifying the form of the original function.
Hence,
As you can see, the results are the same.
Try not to confuse which function is f and which is g(x) .
Let's illustrate this with an example to show your attention.
Example.
Find derivatives of complex functions and .
Solution.
In the first case, f is the squaring function and g(x) is the sine function, so
.
In the second case, f is a sine function, and is a power function. Therefore, by the formula for the product of a complex function we have
The derivative formula for a function has the form 
Example.
Differentiate function 
.
Solution.
In this example, the complex function can be conventionally written as 
, where is the sine function, the third power function, the base e logarithm function, the arctangent function and the linear function, respectively.
According to the formula for the derivative of a complex function 
Now we find
Let's put together the obtained intermediate results: 
There is nothing scary, analyze complex functions like nesting dolls.
This could be the end of the article, if not for one thing...
It is advisable to clearly understand when to apply the rules of differentiation and the table of derivatives, and when to apply the formula for the derivative of a complex function.
BE EXTREMELY CAREFUL NOW. We will talk about the difference between complex functions and complex functions. Your success in finding derivatives will depend on how much you see this difference.
Let's start with simple examples. Function 
can be considered as complex: g(x) = tanx , 
. Therefore, you can immediately apply the formula for the derivative of a complex function 
And here is the function 
It can no longer be called complex.
This function is the sum of three functions, 3tgx and 1. Although - is a complex function: - a power function (quadratic parabola), and f is a tangent function. Therefore, first we apply the sum differentiation formula: 
It remains to find the derivative of the complex function: 
That's why .
We hope you get the gist.
If we look more broadly, it can be argued that functions of a complex type can be part of complex functions, and complex functions can be components of functions of a complex type.
As an example, let us analyze the function into its component parts 
.
Firstly, this is a complex function that can be represented as , where f is the base 3 logarithm function, and g(x) is the sum of two functions 
And 
. That is, 
.
Secondly, let's deal with the function h(x) . It represents a relationship to 
.
This is the sum of two functions and 
, Where 
- a complex function with a numerical coefficient of 3. - cube function, - cosine function, - linear function.
This is the sum of two functions and , where 
- complex function, - exponential function, - power function.
Thus, .
Third, go to , which is the product of a complex function 
and the whole rational function
The squaring function is the logarithm function to base e.
Hence, .
Let's summarize: 
Now the structure of the function is clear and it has become clear which formulas and in what sequence to apply when differentiating it.
In the section on differentiating a function (finding the derivative) you can familiarize yourself with the solution to similar problems.
Derivative
Calculating the derivative of a mathematical function (differentiation) is a very common problem when solving higher mathematics. For simple (elementary) mathematical functions, this is a fairly simple matter, since tables of derivatives for elementary functions have long been compiled and are easily accessible. However, finding the derivative of a complex mathematical function is not a trivial task and often requires significant effort and time.
Find derivative online
Our online service allows you to get rid of pointless long calculations and find derivative online in one moment. Moreover, using our service located on the website www.site, you can calculate online derivative both from an elementary function and from a very complex one that does not have an analytical solution. The main advantages of our site compared to others are: 1) there are no strict requirements for the method of entering a mathematical function for calculating the derivative (for example, when entering the sine x function, you can enter it as sin x or sin(x) or sin[x], etc. d.); 2) online derivative calculation occurs instantly in the mode online and absolutely for free; 3) we allow you to find the derivative of a function any order, changing the order of the derivative is very easy and understandable; 4) we allow you to find the derivative of almost any mathematical function online, even very complex ones that cannot be solved by other services. The response provided is always accurate and cannot contain errors.
Using our server will allow you to 1) calculate the derivative online for you, eliminating time-consuming and tedious calculations during which you could make an error or typo; 2) if you calculate the derivative of a mathematical function yourself, then we provide you with the opportunity to compare the result obtained with the calculations of our service and make sure that the solution is correct or find an error that has crept in; 3) use our service instead of using tables of derivatives of simple functions, where it often takes time to find the desired function.
All that is required of you is to find derivative online- is to use our service on
Functions of a complex type do not always fit the definition of a complex function. If there is a function of the form y = sin x - (2 - 3) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11, then it cannot be considered complex, unlike y = sin 2 x.
This article will show the concept of a complex function and its identification. Let's work with formulas for finding the derivative with examples of solutions in the conclusion. The use of the derivative table and differentiation rules significantly reduces the time for finding the derivative.
Basic definitions
Definition 1A complex function is one whose argument is also a function.
It is denoted this way: f (g (x)). We have that the function g (x) is considered an argument f (g (x)).
Definition 2
If there is a function f and it is a cotangent function, then g(x) = ln x is the natural logarithm function. We find that the complex function f (g (x)) will be written as arctg(lnx). Or a function f, which is a function raised to the 4th power, where g (x) = x 2 + 2 x - 3 is considered an entire rational function, we obtain that f (g (x)) = (x 2 + 2 x - 3) 4 .
Obviously g(x) can be complex. From the example y = sin 2 x + 1 x 3 - 5 it is clear that the value of g has the cube root of the fraction. This expression can be denoted as y = f (f 1 (f 2 (x))). From where we have that f is a sine function, and f 1 is a function located under the square root, f 2 (x) = 2 x + 1 x 3 - 5 is a fractional rational function.
Definition 3
The degree of nesting is determined by any natural number and is written as y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .
Definition 4
The concept of function composition refers to the number of nested functions according to the conditions of the problem. To solve, use the formula for finding the derivative of a complex function of the form
(f (g (x))) " = f " (g (x)) g " (x)
Examples
Example 1Find the derivative of a complex function of the form y = (2 x + 1) 2.
Solution
The condition shows that f is a squaring function, and g(x) = 2 x + 1 is considered a linear function.
Let's apply the derivative formula for a complex function and write:
f " (g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f " (g (x)) g " (x) = 2 (2 x + 1) 2 = 8 x + 4
It is necessary to find the derivative with a simplified original form of the function. We get:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
From here we have that
y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4
The results were the same.
When solving problems of this type, it is important to understand where the function of the form f and g (x) will be located.
Example 2
You should find the derivatives of complex functions of the form y = sin 2 x and y = sin x 2.
Solution
The first function notation says that f is the squaring function and g(x) is the sine function. Then we get that
y " = (sin 2 x) " = 2 sin 2 - 1 x (sin x) " = 2 sin x cos x
The second entry shows that f is a sine function, and g(x) = x 2 denotes a power function. It follows that we write the product of a complex function as
y " = (sin x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)
The formula for the derivative y = f (f 1 (f 2 (f 3 (. . . (f n (x))))) will be written as y " = f " (f 1 (f 2 (f 3 (. . . ( f n (x))))) · f 1 " (f 2 (f 3 (. . . (f n (x)))) · · f 2 " (f 3 (. . . (f n (x))) )) · . . . fn "(x)
Example 3
Find the derivative of the function y = sin (ln 3 a r c t g (2 x)).
Solution
This example shows the difficulty of writing and determining the location of functions. Then y = f (f 1 (f 2 (f 3 (f 4 (x))))) denote where f , f 1 , f 2 , f 3 , f 4 (x) is the sine function, the function of raising to 3 degree, function with logarithm and base e, arctangent and linear function.
From the formula for defining a complex function we have that
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x)
We get what we need to find
- f " (f 1 (f 2 (f 3 (f 4 (x))))) as the derivative of the sine according to the table of derivatives, then f " (f 1 (f 2 (f 3 (f 4 (x)))) ) = cos (ln 3 a r c t g (2 x)) .
- f 1 " (f 2 (f 3 (f 4 (x)))) as the derivative of a power function, then f 1 " (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
- f 2 " (f 3 (f 4 (x))) as a logarithmic derivative, then f 2 " (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 " (f 4 (x)) as the derivative of the arctangent, then f 3 " (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
- When finding the derivative f 4 (x) = 2 x, remove 2 from the sign of the derivative using the formula for the derivative of a power function with an exponent equal to 1, then f 4 " (x) = (2 x) " = 2 x " = 2 · 1 · x 1 - 1 = 2 .
We combine the intermediate results and get that
y " = f " (f 1 (f 2 (f 3 (f 4 (x)))) f 1 " (f 2 (f 3 (f 4 (x)))) f 2 " (f 3 (f 4 (x)) f 3 " (f 4 (x)) f 4 " (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)
Analysis of such functions is reminiscent of nesting dolls. Differentiation rules cannot always be applied explicitly using a derivative table. Often you need to use a formula for finding derivatives of complex functions.
There are some differences between complex appearance and complex functions. With a clear ability to distinguish this, finding derivatives will be especially easy.
Example 4
It is necessary to consider giving such an example. If there is a function of the form y = t g 2 x + 3 t g x + 1, then it can be considered as a complex function of the form g (x) = t g x, f (g) = g 2 + 3 g + 1. Obviously, it is necessary to use the formula for a complex derivative:
f " (g (x)) = (g 2 (x) + 3 g (x) + 1) " = (g 2 (x)) " + (3 g (x)) " + 1 " = = 2 · g 2 - 1 (x) + 3 g " (x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x
A function of the form y = t g x 2 + 3 t g x + 1 is not considered complex, since it has the sum of t g x 2, 3 t g x and 1. However, t g x 2 is considered a complex function, then we obtain a power function of the form g (x) = x 2 and f, which is a tangent function. To do this, differentiate by amount. We get that
y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 cos 2 x
Let's move on to finding the derivative of a complex function (t g x 2) ":
f " (g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)
We get that y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Functions of a complex type can be included in complex functions, and complex functions themselves can be components of functions of a complex type.
Example 5
For example, consider a complex function of the form y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1)
This function can be represented as y = f (g (x)), where the value of f is a function of the base 3 logarithm, and g (x) is considered the sum of two functions of the form h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 and k (x) = ln 2 x · (x 2 + 1) . Obviously, y = f (h (x) + k (x)).
Consider the function h(x). This is the ratio l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 to m (x) = e x 2 + 3 3
We have that l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) is the sum of two functions n (x) = x 2 + 7 and p (x) = 3 cos 3 (2 x + 1) , where p (x) = 3 p 1 (p 2 (p 3 (x))) is a complex function with numerical coefficient 3, and p 1 is a cube function, p 2 by a cosine function, p 3 (x) = 2 x + 1 by a linear function.
We found that m (x) = e x 2 + 3 3 = q (x) + r (x) is the sum of two functions q (x) = e x 2 and r (x) = 3 3, where q (x) = q 1 (q 2 (x)) is a complex function, q 1 is a function with an exponential, q 2 (x) = x 2 is a power function.
This shows that h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3 (x))) q 1 (q 2 (x)) + r (x)
When moving to an expression of the form k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x), it is clear that the function is presented in the form of a complex s (x) = ln 2 x = s 1 ( s 2 (x)) with a rational integer t (x) = x 2 + 1, where s 1 is a squaring function, and s 2 (x) = ln x is logarithmic with base e.
It follows that the expression will take the form k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x).
Then we get that
y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)
Based on the structures of the function, it became clear how and what formulas need to be used to simplify the expression when differentiating it. To become familiar with such problems and for the concept of their solution, it is necessary to turn to the point of differentiating a function, that is, finding its derivative.
If you notice an error in the text, please highlight it and press Ctrl+Enter