As:
± d m … d 1 d 0 , d -1 d -2 …
where ± is the fraction sign: either +, or -,
, is a decimal point that serves as a separator between the integer and fractional parts of a number,
dk- decimal numbers.
In this case, the order of numbers before the decimal point (to the left of it) has an end (as min 1 per digit), and after the decimal point (to the right) it can be both finite (as an option, there may be no digits after the decimal point at all) and infinite.
Decimal value ± d m … d 1 d 0 , d -1 d -2 … is a real number:
which is equal to the sum of a finite or infinite number of terms.
Representing real numbers using decimal fractions is a generalization of writing integers in the decimal number system. The decimal representation of an integer has no digits after the decimal point, so the representation looks like this:
± d m … d 1 d 0 ,
And this coincides with writing our number in the decimal number system.
Decimal- this is the result of dividing 1 into 10, 100, 1000 and so on parts. These fractions are quite convenient for calculations, because they are based on the same positional system on which counting and recording of integers are based. Thanks to this, the notation and rules for working with decimal fractions are almost the same as for whole numbers.
When writing decimal fractions, you do not need to mark the denominator; it is determined by the place occupied by the corresponding digit. First we write the whole part of the number, then we put a decimal point on the right. The first digit after the decimal point indicates the number of tenths, the second - the number of hundredths, the third - the number of thousandths, and so on. The numbers that are located after the decimal point are decimals.
For example: 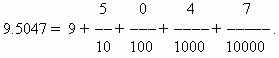
One of the advantages of decimal fractions is that they can very easily be reduced to ordinary fractions: the number after the decimal point (for us it is 5047) is numerator; denominator equals n-th power of 10, where n- the number of decimal places (for us this is n=4):

When there is no integer part in a decimal fraction, we put a zero before the decimal point:
Properties of decimal fractions.
1. The decimal does not change when zeros are added to the right:
13.6 =13.6000.
2. The decimal does not change when the zeros at the end of the decimal are removed:
0.00123000 = 0.00123.
Attention! You cannot remove zeros that are NOT located at the end of the decimal fraction!
3. The decimal fraction increases by 10, 100, 1000 and so on times when we move the decimal point to 1, 2, 2 and so on positions to the right, respectively:
3.675 → 367.5 (fraction increased a hundred times).
4. The decimal fraction becomes ten, one hundred, thousand, and so on times smaller when we move the decimal point to 1, 2, 3, and so on positions to the left, respectively:
1536.78 → 1.53678 (the fraction became a thousand times smaller).
Types of decimal fractions.
Decimal fractions are divided into final, endless And periodic decimals.
The final decimal fraction is this is a fraction containing a finite number of digits after the decimal point (or there are none at all), i.e. looks like that:
A real number can be represented as a finite decimal fraction only if this number is rational and when written as an irreducible fraction p/q denominator q has no prime factors other than 2 and 5.
Infinite decimal.
![]()
Contains an infinitely repeating group of numbers called period. The period is written in brackets. For example, 0.12345123451234512345… = 0.(12345).
Periodic decimal- this is an infinite decimal fraction in which the sequence of digits after the decimal point, starting from a certain place, is a periodically repeating group of digits. In other words, periodic fraction- a decimal fraction that looks like this:
Such a fraction is usually briefly written as follows:

Group of numbers b 1 … b l, which repeats, is period of the fraction, the number of digits in this group is period length.
When in a periodic fraction the period comes immediately after the decimal point, it means the fraction is pure periodic. When there are numbers between the decimal point and the 1st period, then the fraction is mixed periodic, and the group of digits after the decimal point up to the 1st digit of the period is fraction preperiod.
For example, the fraction 1,(23) = 1.2323... is pure periodic, and the fraction 0.1(23) = 0.12323... is mixed periodic.
The main property of periodic fractions, due to which they are distinguished from the entire set of decimal fractions, lies in the fact that periodic fractions and only they represent rational numbers. More precisely, the following occurs:
Any infinitely periodic decimal fraction represents a rational number. Conversely, when a rational number is expanded into an infinite decimal fraction, it means that this fraction will be periodic.
DECIMALS. OPERATIONS ON DECIMALS
(summarizing lesson)
Tumysheva Zamira Tansykbaevna, mathematics teacher, gymnasium school No. 2
Khromtau city, Aktobe region, Republic of Kazakhstan
This lesson development is intended as a generalization lesson for the chapter “Actions on decimals.” It can be used in both 5th and 6th grades. The lesson is conducted in a playful way.
Decimal fractions. Operations with decimal fractions.(summarizing lesson)
Target:
Practicing skills in addition, subtraction, multiplication and division of decimals by natural numbers and decimals
Creating conditions for the development of independent work skills, self-control and self-esteem, development of intellectual qualities: attention, imagination, memory, ability to analyze and generalize
Instill a cognitive interest in the subject and develop self-confidence
LESSON PLAN:
1. Organizational part.
3. The topic and purpose of our lesson.
4. Game “To the cherished flag!”
5. Game "Number Mill".
6. Lyrical digression.
7. Test work.
8. Game “Encryption” (work in pairs)
9. Summing up.
10. Homework.
1. Organizational part. Hello. Have a seat.
2. Review of the rules for performing arithmetic operations with decimals.
Rule for adding and subtracting decimals:
1) equalize the number of decimal places in these fractions;
2) write one below the other so that the comma is under the comma;
3) without noticing the comma, perform the action (addition or subtraction), and put a comma under the commas as a result.
3,455 + 0,45 = 3,905 3,5 + 4 = 7,5 15 – 7,88 = 7,12 4,57 - 3,2 = 1,37
3,455 + 3,5 _15,00 _ 4,57
0,450 4,0 7,88 3,20
3,905 7,5 7,12 1,37
When adding and subtracting, natural numbers are written as a decimal fraction with decimal places equal to zero
Rule for multiplying decimals:
1) without paying attention to the comma, multiply the numbers;
2) in the resulting product, separate as many digits from right to left with a comma as there are in decimal fractions separated by a comma.
When multiplying a decimal fraction by digit units (10, 100, 1000, etc.), the decimal point is moved to the right by as many numbers as there are zeros in the digit unit
4
17.25 4 = 69
x 1 7.2 5
4
6 9,0 0
15.256 100 = 1525.6
.5 · 0.52 = 2.35X 0.5 2
4,5
2 7 0
2 0 8__
2,3 5 0
When multiplying, natural numbers are written as natural numbers.
The rule for dividing decimal fractions by a natural number:
1) divide the whole part of the dividend, put a comma in the quotient;
2) continue division.
When dividing, we add only one number from the dividend to the remainder.
If in the process of dividing a decimal fraction there remains a remainder, then by adding the required number of zeros to it, we will continue division until the remainder is zero.
15,256: 100 = 0,15256
0,25: 1000 = 0,00025
When dividing a decimal fraction into digit units (10, 100, 1000, etc.), the comma is moved to the left by as many numbers as there are zeros in the digit unit.
18,4: 8 = 2,3
_ 18,4 І_8_
16 2,3
2 4
2 4
22,2: 25 = 0,88
22,2 І_25_
0 0,888
22 2
20 0
2 20
2 00
200
200
3,56: 4 = 0,89
3,56 І_4_
0 0,89
3 5
3 2
36
When dividing, natural numbers are written as natural numbers.
The rule for dividing decimals by decimals is:
1) move the comma in the divisor to the right so that we get a natural number;
2) move the comma in the dividend to the right as many numbers as were moved in the divisor;
3) divide the decimal fraction by a natural number.
3,76: 0,4 = 9, 4
_ 3,7,6 І_0,4,_
3 6 9, 4
1 6
1 6
0
Game “To the cherished flag!”
Rules of the game: From each team, one student is called to the board and performs an oral count from the bottom step. The person who solves one example marks the answer in the table. Then he is replaced by another team member. There is an upward movement - towards the coveted flag. Students in the field orally review their players' performance. If the answer is incorrect, another team member comes to the board to continue solving the problems. Team captains call students to work at the board. The team that reaches the flag first with the fewest number of students wins.
Game "Number Mill"
Rules of the game: The mill circles contain numbers. The arrows connecting the circles indicate actions. The task is to perform sequential actions, moving along the arrow from the center to the outer circle. By performing sequential actions along the indicated route, you will find the answer in one of the circles below. The result of performing actions on each arrow is recorded in the oval next to it.

Lyrical digression.
Lifshitz's poem "Three Tenths"
Who is this
From the briefcase
Throws it in frustration
Hateful problem book,
Pencil case and notebooks
And he puts in his diary.
Without blushing,
Under an oak sideboard.
To lie under the sideboard?..
Please meet:
Kostya Zhigalin.
Victim of eternal nagging, -
He failed again.
And hisses
To disheveled
Looking at the problem book:
I'm just unlucky!
I'm just a loser!
What is the reason
His grievances and annoyances?
That the answer didn't add up
Only three tenths.
This is a mere trifle!
And to him, of course,
Find fault
Strict
Marya Petrovna.
Three tenths...
Tell me about this mistake -
And, perhaps, on their faces
You will see a smile.
Three tenths...
And yet about this mistake
I ask you
Listen to me
No smile.
If only, building your house.
The one you live in.
Architect
A little bit
Wrong
In counting, -
What would happen?
Do you know, Kostya Zhigalin?
This house
Would have turned
Into a pile of ruins!
You step onto the bridge.
It is reliable and durable.
Don't be an engineer
Accurate in his drawings, -
Would you, Kostya,
Having fallen
into the cold river
I wouldn't say thank you
That man!
Here's the turbine.
She has a shaft
Wasted by turners.
If only the turner
In progress
Wasn't very accurate -
It would happen, Kostya,
Great misfortune:
It would blow the turbine apart
To small pieces!
Three tenths -
And the walls
Are being built
Koso!
Three tenths -
And they will collapse
Cars
Off the slope!
Make a mistake
Only three tenths
Pharmacy, -
The medicine will become poison
Will kill a person!
We smashed and drove
Fascist gang.
Your father served
Battery command.
He made a mistake when he arrived
At least three tenths, -
The shells wouldn't have reached me
Damned fascists.
Think about it
My friend, coolly
And tell me.
Wasn't it right?
Marya Petrovna?
Honestly
Just think about it, Kostya.
You won't lie down for long
To the diary under the buffet!
Test work on the topic “Decimals” (mathematics -5)
9 slides will appear on the screen in sequence. Students write down the option number and answers to the question in their notebooks. For example, Option 2
1. C; 2. A; and so on.
QUESTION 1
Option 1
When multiplying a decimal fraction by 100, you need to move the decimal point in this fraction:
A. to the left by 2 digits; B. to the right by 2 digits; C. do not change the place of the comma.
Option 2
When multiplying a decimal fraction by 10, you need to move the decimal point in this fraction:
A. to the right by 1 digit; B. to the left by 1 digit; C. do not change the place of the comma.
QUESTION 2
Option 1
The sum 6.27+6.27+6.27+6.27+6.27 as a product is written as follows:
A. 6.27 5; V. 6.27 · 6.27; P. 6.27 · 4.
Option 2
The sum 9.43+9.43+9.43+9.43 as a product is written as follows:
A. 9.43 · 9.43; V. 6 · 9.43; P. 9.43 · 4.
QUESTION 3
Option 1
In the product 72.43·18 after the decimal point there will be:
Option 2
In the product 12.453 35 after the decimal point there will be:
A. 2 digits; B. 0 digits; C. 3 digits.
QUESTION 4
Option 1
In the quotient 76.4: 2 after the decimal point it will be:
A. 2 digits; B. 0 digits; C. 1 digit.
Option 2
In the quotient 95.4: 6 after the decimal point it will be:
A. 1 digit; B. 3 digits; C. 2 digits.
QUESTION 5
Option 1
Find the value of the expression 34.5: x + 0.65· y, with x=10 y=100:
A. 35.15; V. 68.45; pp. 9.95.
Option 2
Find the value of the expression 4.9 x +525:y, with x=100 y=1000:
A. 4905.25; V. 529.9; pp. 490.525.
QUESTION 6
Option 1
The area of a rectangle with sides 0.25 and 12 cm is
A. 3; V. 0.3; P. 30.
Option 2
The area of a rectangle with sides 0.5 and 36 cm is equal to
A. 1.8; V. 18; S. 0.18.
QUESTION 7
Option 1
Two students left the school at the same time in opposite directions. The speed of the first student is 3.6 km/h, the speed of the second is 2.56 km/h. After 3 hours the distance between them will be equal:
A. 6.84 km; E. 18.48 km; N. 3.12 km
Option 2
Two cyclists left the school at the same time in opposite directions. The speed of the first is 11.6 km/h, the speed of the second is 13.06 km/h. After 4 hours the distance between them will be equal:
A. 5.84 km; E. 100.8 km; N. 98.64 km
Option 1
Option 2
Check your answers. Put “+” for a correct answer and “-” for an incorrect answer.
Game "Encryption"
Rules of the game: Each desk is given a card with a task that has a letter code. After completing the steps and receiving the result, write down the letter code of your card under the number corresponding to your answer.
As a result, we get the following sentence:
6,8
420
21,6
420
306
65,8
21,6
Summing up the lesson.
Grades for the test work are announced.
Homework No. 1301, 1308, 1309
Thank you for your attention!!!
This article is about decimals. Here we will understand the decimal notation of fractional numbers, introduce the concept of a decimal fraction and give examples of decimal fractions. Next we’ll talk about the digits of decimal fractions and give the names of the digits. After this, we will focus on infinite decimal fractions, let's talk about periodic and non-periodic fractions. Next we list the basic operations with decimal fractions. In conclusion, let us establish the position of decimal fractions on the coordinate beam.
Page navigation.
Decimal notation of a fractional number
Reading Decimals
Let's say a few words about the rules for reading decimal fractions.
Decimal fractions, which correspond to proper ordinary fractions, are read in the same way as these ordinary fractions, only “zero integer” is first added. For example, the decimal fraction 0.12 corresponds to the common fraction 12/100 (read “twelve hundredths”), therefore, 0.12 is read as “zero point twelve hundredths”.
Decimal fractions that correspond to mixed numbers are read exactly the same as these mixed numbers. For example, the decimal fraction 56.002 corresponds to a mixed number, so the decimal fraction 56.002 is read as “fifty-six point two thousandths.”
Places in decimals
In writing decimal fractions, as well as in writing natural numbers, the meaning of each digit depends on its position. Indeed, the number 3 in the decimal fraction 0.3 means three tenths, in the decimal fraction 0.0003 - three ten thousandths, and in the decimal fraction 30,000.152 - three tens of thousands. So we can talk about decimal places, as well as about the digits in natural numbers.
The names of the digits in the decimal fraction up to the decimal point completely coincide with the names of the digits in natural numbers. And the names of the decimal places after the decimal point can be seen from the following table.

For example, in the decimal fraction 37.051, the digit 3 is in the tens place, 7 is in the units place, 0 is in the tenths place, 5 is in the hundredths place, and 1 is in the thousandths place.
Places in decimal fractions also differ in precedence. If in writing a decimal fraction we move from digit to digit from left to right, then we will move from seniors To junior ranks. For example, the hundreds place is older than the tenths place, and the millions place is lower than the hundredths place. In a given final decimal fraction, we can talk about the major and minor digits. For example, in decimal fraction 604.9387 senior (highest) the place is the hundreds place, and junior (lowest)- ten-thousandths digit.
For decimal fractions, expansion into digits takes place. It is similar to expansion into digits of natural numbers. For example, the expansion into decimal places of 45.6072 is as follows: 45.6072=40+5+0.6+0.007+0.0002. And the properties of addition from the decomposition of a decimal fraction into digits allow you to move on to other representations of this decimal fraction, for example, 45.6072=45+0.6072, or 45.6072=40.6+5.007+0.0002, or 45.6072= 45.0072+0.6.
Ending decimals
Up to this point, we have only talked about decimal fractions, in the notation of which there is a finite number of digits after the decimal point. Such fractions are called finite decimals.
Definition.
Ending decimals- These are decimal fractions, the records of which contain a finite number of characters (digits).
Here are some examples of final decimal fractions: 0.317, 3.5, 51.1020304958, 230,032.45.
However, not every fraction can be represented as a final decimal. For example, the fraction 5/13 cannot be replaced by an equal fraction with one of the denominators 10, 100, ..., therefore, cannot be converted into a final decimal fraction. We will talk more about this in the theory section, converting ordinary fractions to decimals.
Infinite Decimals: Periodic Fractions and Non-Periodic Fractions
In writing a decimal fraction after the decimal point, you can assume the possibility of an infinite number of digits. In this case, we will come to consider the so-called infinite decimal fractions.
Definition.
Infinite decimals- These are decimal fractions, which contain an infinite number of digits.
It is clear that we cannot write down infinite decimal fractions in full form, so in their recording we limit ourselves to only a certain finite number of digits after the decimal point and put an ellipsis indicating an infinitely continuing sequence of digits. Here are some examples of infinite decimal fractions: 0.143940932…, 3.1415935432…, 153.02003004005…, 2.111111111…, 69.74152152152….
If you look closely at the last two infinite decimal fractions, then in the fraction 2.111111111... the endlessly repeating number 1 is clearly visible, and in the fraction 69.74152152152..., starting from the third decimal place, a repeating group of numbers 1, 5 and 2 is clearly visible. Such infinite decimal fractions are called periodic.
Definition.
Periodic decimals(or simply periodic fractions) are endless decimal fractions, in the recording of which, starting from a certain decimal place, some number or group of numbers is endlessly repeated, which is called period of the fraction.
For example, the period of the periodic fraction 2.111111111... is the digit 1, and the period of the fraction 69.74152152152... is a group of digits of the form 152.
For infinite periodic decimal fractions, a special form of notation is adopted. For brevity, we agreed to write down the period once, enclosing it in parentheses. For example, the periodic fraction 2.111111111... is written as 2,(1) , and the periodic fraction 69.74152152152... is written as 69.74(152) .
It is worth noting that different periods can be specified for the same periodic decimal fraction. For example, the periodic decimal fraction 0.73333... can be considered as a fraction 0.7(3) with a period of 3, and also as a fraction 0.7(33) with a period of 33, and so on 0.7(333), 0.7 (3333), ... You can also look at the periodic fraction 0.73333 ... like this: 0.733(3), or like this 0.73(333), etc. Here, in order to avoid ambiguity and discrepancies, we agree to consider as the period of a decimal fraction the shortest of all possible sequences of repeating digits, and starting from the closest position to the decimal point. That is, the period of the decimal fraction 0.73333... will be considered a sequence of one digit 3, and the periodicity starts from the second position after the decimal point, that is, 0.73333...=0.7(3). Another example: the periodic fraction 4.7412121212... has a period of 12, the periodicity starts from the third digit after the decimal point, that is, 4.7412121212...=4.74(12).
Infinite decimal periodic fractions are obtained by converting into decimal fractions ordinary fractions whose denominators contain prime factors other than 2 and 5.
Here it is worth mentioning periodic fractions with a period of 9. Let us give examples of such fractions: 6.43(9) , 27,(9) . These fractions are another notation for periodic fractions with period 0, and they are usually replaced by periodic fractions with period 0. To do this, period 9 is replaced by period 0, and the value of the next highest digit is increased by one. For example, a fraction with period 9 of the form 7.24(9) is replaced by a periodic fraction with period 0 of the form 7.25(0) or an equal final decimal fraction 7.25. Another example: 4,(9)=5,(0)=5. The equality of a fraction with period 9 and its corresponding fraction with period 0 is easily established after replacing these decimal fractions with equal ordinary fractions.
Finally, let's take a closer look at infinite decimal fractions, which do not contain an endlessly repeating sequence of digits. They are called non-periodic.
Definition.
Non-recurring decimals(or simply non-periodic fractions) are infinite decimal fractions that have no period.
Sometimes non-periodic fractions have a form similar to that of periodic fractions, for example, 8.02002000200002... is a non-periodic fraction. In these cases, you should be especially careful to notice the difference.
Note that non-periodic fractions do not convert to ordinary fractions; infinite non-periodic decimal fractions represent irrational numbers.
Operations with decimals
One of the operations with decimal fractions is comparison, and the four basic arithmetic functions are also defined operations with decimals: addition, subtraction, multiplication and division. Let's consider separately each of the actions with decimal fractions.
Comparison of decimals essentially based on comparison of ordinary fractions corresponding to the decimal fractions being compared. However, converting decimal fractions into ordinary fractions is a rather labor-intensive process, and infinite non-periodic fractions cannot be represented as an ordinary fraction, so it is convenient to use a place-wise comparison of decimal fractions. Place-wise comparison of decimal fractions is similar to comparison of natural numbers. For more detailed information, we recommend studying the article: comparison of decimal fractions, rules, examples, solutions.
Let's move on to the next step - multiplying decimals. Multiplication of finite decimal fractions is carried out similarly to subtraction of decimal fractions, rules, examples, solutions to multiplication by a column of natural numbers. In the case of periodic fractions, multiplication can be reduced to multiplication of ordinary fractions. In turn, the multiplication of infinite non-periodic decimal fractions after their rounding is reduced to the multiplication of finite decimal fractions. We recommend for further study the material in the article: multiplication of decimal fractions, rules, examples, solutions.
Decimals on a coordinate ray
There is a one-to-one correspondence between points and decimals.
Let's figure out how points on the coordinate ray are constructed that correspond to a given decimal fraction.
We can replace finite decimal fractions and infinite periodic decimal fractions with equal ordinary fractions, and then construct the corresponding ordinary fractions on the coordinate ray. For example, the decimal fraction 1.4 corresponds to the common fraction 14/10, so the point with coordinate 1.4 is removed from the origin in the positive direction by 14 segments equal to a tenth of a unit segment.

Decimal fractions can be marked on a coordinate ray, starting from the decomposition of a given decimal fraction into digits. For example, let us need to build a point with coordinate 16.3007, since 16.3007=16+0.3+0.0007, then we can get to this point by sequentially laying 16 unit segments from the origin of coordinates, 3 segments whose length equal to a tenth of a unit, and 7 segments, the length of which is equal to a ten-thousandth of a unit segment.
This method of constructing decimal numbers on a coordinate ray allows you to get as close as you like to the point corresponding to an infinite decimal fraction.
Sometimes it is possible to accurately plot the point corresponding to an infinite decimal fraction. For example, ![]() , then this infinite decimal fraction 1.41421... corresponds to a point on the coordinate ray, distant from the origin of coordinates by the length of the diagonal of a square with a side of 1 unit segment.
, then this infinite decimal fraction 1.41421... corresponds to a point on the coordinate ray, distant from the origin of coordinates by the length of the diagonal of a square with a side of 1 unit segment.
The reverse process of obtaining the decimal fraction corresponding to a given point on a coordinate ray is the so-called decimal measurement of a segment. Let's figure out how it is done.
Let our task be to get from the origin to a given point on the coordinate line (or to infinitely approach it if we can’t get to it). With the decimal measurement of a segment, we can sequentially lay off from the origin any number of unit segments, then segments whose length is equal to a tenth of a unit, then segments whose length is equal to a hundredth of a unit, etc. By recording the number of segments of each length laid aside, we obtain the decimal fraction corresponding to a given point on the coordinate ray.
For example, to get to point M in the above figure, you need to set aside 1 unit segment and 4 segments, the length of which is equal to a tenth of a unit. Thus, point M corresponds to the decimal fraction 1.4.
It is clear that the points of the coordinate ray, which cannot be reached in the process of decimal measurement, correspond to infinite decimal fractions.
Bibliography.
- Mathematics: textbook for 5th grade. general education institutions / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21st ed., erased. - M.: Mnemosyne, 2007. - 280 pp.: ill. ISBN 5-346-00699-0.
- Mathematics. 6th grade: educational. for general education institutions / [N. Ya. Vilenkin and others]. - 22nd ed., rev. - M.: Mnemosyne, 2008. - 288 p.: ill. ISBN 978-5-346-00897-2.
- Algebra: textbook for 8th grade. general education institutions / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; edited by S. A. Telyakovsky. - 16th ed. - M.: Education, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Mathematics (a manual for those entering technical schools): Proc. allowance.- M.; Higher school, 1984.-351 p., ill.
§ 31. Problems and examples for all operations with decimal fractions.
Follow these steps:

767. Find the quotient of division:

772. Calculate:
Find X , If:

776. The unknown number was multiplied by the difference between the numbers 1 and 0.57 and the product was 3.44. Find the unknown number.
777. The sum of the unknown number and 0.9 was multiplied by the difference between 1 and 0.4 and the product was 2.412. Find the unknown number.
778. Using the data from the diagram about iron smelting in the RSFSR (Fig. 36), create a problem to solve which you need to apply the actions of addition, subtraction and division.

779. 1) The length of the Suez Canal is 165.8 km, the length of the Panama Canal is 84.7 km less than the Suez Canal, and the length of the White Sea-Baltic Canal is 145.9 km more than the length of the Panama Canal. What is the length of the White Sea-Baltic Canal?
2) The Moscow metro (by 1959) was built in 5 stages. The length of the first stage of the metro is 11.6 km, the second -14.9 km, the length of the third is 1.1 km less than the length of the second stage, the length of the fourth stage is 9.6 km more than the third stage, and the length of the fifth stage is 11.5 km less fourth. What was the length of the Moscow metro at the beginning of 1959?
780. 1) The greatest depth of the Atlantic Ocean is 8.5 km, the greatest depth of the Pacific Ocean is 2.3 km greater than the depth of the Atlantic Ocean, and the greatest depth of the Arctic Ocean is 2 times less than the greatest depth of the Pacific Ocean. What is the greatest depth of the Arctic Ocean?
2) The Moskvich car consumes 9 liters of gasoline per 100 km, the Pobeda car consumes 4.5 liters more than the Moskvich, and the Volga is 1.1 times more than the Pobeda. How much gasoline does a Volga car consume per 1 km of travel? (Round answer to the nearest 0.01 l.)
781. 1) The student went to his grandfather during the holidays. He traveled by rail for 8.5 hours, and from the station by horse for 1.5 hours. In total he traveled 440 km. At what speed did the student travel on the railroad if he rode horses at a speed of 10 km per hour?
2) The collective farmer had to be at a point located at a distance of 134.7 km from his home. He rode the bus for 2.4 hours at an average speed of 55 km per hour, and walked the rest of the way at a speed of 4.5 km per hour. How long did he walk?
782. 1) Over the summer, one gopher destroys about 0.12 centners of bread. In the spring, the pioneers exterminated 1,250 ground squirrels on 37.5 hectares. How much bread did the schoolchildren save for the collective farm? How much saved bread is there per 1 hectare?
2) The collective farm calculated that by destroying gophers on an area of 15 hectares of arable land, schoolchildren saved 3.6 tons of grain. How many gophers are destroyed on average per 1 hectare of land if one gopher destroys 0.012 tons of grain over the summer?
783. 1) When grinding wheat into flour, 0.1 of its weight is lost, and when baking, a bake equal to 0.4 of the weight of flour is obtained. How much baked bread will be produced from 2.5 tons of wheat?
2) The collective farm collected 560 tons of sunflower seeds. How much sunflower oil will be produced from the collected grains if the weight of the grain is 0.7 of the weight of sunflower seeds and the weight of the resulting oil is 0.25 of the weight of the grain?
784. 1) The yield of cream from milk is 0.16 of the weight of milk, and the yield of butter from cream is 0.25 of the weight of cream. How much milk (by weight) is required to produce 1 quintal of butter?
2) How many kilograms of porcini mushrooms must be collected to obtain 1 kg of dried mushrooms, if during preparation for drying 0.5 of the weight remains, and during drying 0.1 of the weight of the processed mushroom remains?
785. 1) The land allocated to the collective farm is used as follows: 55% of it is occupied by arable land, 35% by meadow, and the rest of the land in the amount of 330.2 hectares is allocated for the collective farm garden and for the estates of collective farmers. How much land is there on the collective farm?
2) The collective farm sowed 75% of the total sown area with grain crops, 20% with vegetables, and the remaining area with forage grasses. How much sown area did the collective farm have if it sowed 60 hectares with fodder grasses?
786. 1) How many quintals of seeds will be required to sow a field shaped like a rectangle 875 m long and 640 m wide, if 1.5 quintals of seeds are sown per 1 hectare?
2) How many quintals of seeds will be required to sow a field shaped like a rectangle if its perimeter is 1.6 km? The field width is 300 m. To sow 1 hectare, 1.5 quintals of seeds are required.
787. How many square plates with a side of 0.2 dm will fit in a rectangle measuring 0.4 dm x 10 dm?
788. The reading room has dimensions of 9.6 m x 5 m x 4.5 m. How many seats is the reading room designed for if 3 cubic meters are needed for each person? m of air?
789. 1) What area of meadow will a tractor with a trailer of four mowers mow in 8 hours, if the working width of each mower is 1.56 m and the tractor speed is 4.5 km per hour? (Time for stops is not taken into account.) (Round the answer to the nearest 0.1 hectares.)
2) The working width of the tractor vegetable seeder is 2.8 m. What area can be sown with this seeder in 8 hours. work at a speed of 5 km per hour?
790. 1) Find the output of a three-furrow tractor plow in 10 hours. work, if the tractor speed is 5 km per hour, the grip of one body is 35 cm, and the waste of time was 0.1 of the total time spent. (Round the answer to the nearest 0.1 hectares.)
2) Find the output of a five-furrow tractor plow in 6 hours. work, if the tractor speed is 4.5 km per hour, the grip of one body is 30 cm, and the waste of time was 0.1 of the total time spent. (Round the answer to the nearest 0.1 hectares.)
791. The water consumption per 5 km of travel for a steam locomotive of a passenger train is 0.75 tons. The tender's water tank holds 16.5 tons of water. How many kilometers will the train have enough water to travel if the tank is filled to 0.9 of its capacity?
792. The siding can accommodate only 120 freight cars with an average car length of 7.6 m. How many four-axle passenger cars, each 19.2 m long, can fit on this track if 24 more freight cars are placed on this track?
793. To ensure the strength of the railway embankment, it is recommended to strengthen the slopes by sowing field grasses. For each square meter of embankment, 2.8 g of seeds are required, costing 0.25 rubles. for 1 kg. How much will it cost to sow 1.02 hectares of slopes if the cost of the work is 0.4 of the cost of the seeds? (Round the answer to the nearest 1 ruble.)
794. The brick factory delivered bricks to the railway station. 25 horses and 10 trucks worked to transport the bricks. Each horse carried 0.7 tons per trip and made 4 trips per day. Each vehicle transported 2.5 tons per trip and made 15 trips per day. The transportation lasted 4 days. How many bricks were delivered to the station if the average weight of one brick is 3.75 kg? (Round the answer to the nearest 1 thousand units.)
795. The flour stock was distributed among three bakeries: the first received 0.4 of the total stock, the second 0.4 of the remainder, and the third bakery received 1.6 tons less flour than the first. How much flour was distributed in total?
796. In the second year of the institute there are 176 students, in the third year there are 0.875 of this number, and in the first year there are one and a half times more than in the third year. The number of students in the first, second and third years was 0.75 of the total number of students of this institute. How many students were there at the institute?
___________
797. Find the arithmetic mean:
1) two numbers: 56.8 and 53.4; 705.3 and 707.5;
2) three numbers: 46.5; 37.8 and 36; 0.84; 0.69 and 0.81;
3) four numbers: 5.48; 1.36; 3.24 and 2.04.
798. 1) In the morning the temperature was 13.6°, at noon 25.5°, and in the evening 15.2°. Calculate the average temperature for this day.
2) What is the average temperature for the week, if during the week the thermometer showed: 21°; 20.3°; 22.2°; 23.5°; 21.1°; 22.1°; 20.8°?
799. 1) The school team weeded 4.2 hectares of beets on the first day, 3.9 hectares on the second day, and 4.5 hectares on the third. Determine the average output of the team per day.
2) To establish the standard time for manufacturing a new part, 3 turners were supplied. The first one produced the part in 3.2 minutes, the second in 3.8 minutes, and the third in 4.1 minutes. Calculate the time standard that was set for manufacturing the part.
800. 1) The arithmetic mean of two numbers is 36.4. One of these numbers is 36.8. Find something else.
2) The air temperature was measured three times a day: in the morning, at noon and in the evening. Find the air temperature in the morning if it was 28.4° at noon, 18.2° in the evening, and the average temperature of the day is 20.4°.
801. 1) The car traveled 98.5 km in the first two hours, and 138 km in the next three hours. How many kilometers did the average car travel per hour?
2) A test catch and weighing of yearling carp showed that out of 10 carp, 4 weighed 0.6 kg, 3 weighed 0.65 kg, 2 weighed 0.7 kg and 1 weighed 0.8 kg. What is the average weight of a yearling carp?
802. 1) For 2 liters of syrup costing 1.05 rubles. for 1 liter added 8 liters of water. How much does 1 liter of the resulting water with syrup cost?
2) The hostess bought a 0.5 liter can of canned borscht for 36 kopecks. and boiled with 1.5 liters of water. How much does a plate of borscht cost if its volume is 0.5 liters?
803. Laboratory work “Measuring the distance between two points”,
1st appointment. Measurement with a tape measure (measuring tape). The class is divided into units of three people each. Accessories: 5-6 poles and 8-10 tags.
Progress of work: 1) points A and B are marked and a straight line is drawn between them (see task 178); 2) lay the tape measure along the hung straight line and each time mark the end of the tape measure with a tag. 2nd appointment. Measurement, steps. The class is divided into units of three people each. Each student walks the distance from A to B, counting the number of his steps. By multiplying the average length of your step by the resulting number of steps, you find the distance from A to B.
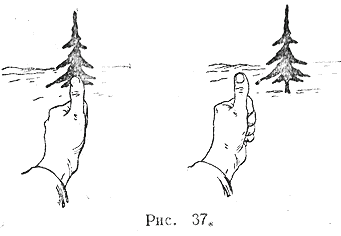
3rd appointment. Measuring by eye. Each student extends his left hand with his thumb raised (Fig. 37) and points his thumb at the pole at point B (a tree in the picture) so that the left eye (point A), thumb and point B are on the same straight line. Without changing position, close your left eye and look at your thumb with your right. Measure the resulting displacement by eye and increase it by 10 times. This is the distance from A to B.
_________________
804. 1) According to the 1959 census, the population of the USSR was 208.8 million people, and the rural population was 9.2 million more than the urban population. How many urban and how many rural population were there in the USSR in 1959?
2) According to the 1913 census, the population of Russia was 159.2 million people, and the urban population was 103.0 million less than the rural population. What was the urban and rural population in Russia in 1913?
805. 1) The length of the wire is 24.5 m. This wire was cut into two parts so that the first part was 6.8 m longer than the second. How many meters long is each part?
2) The sum of two numbers is 100.05. One number is 97.06 more than the other. Find these numbers.
806. 1) There are 8656.2 tons of coal in three coal warehouses, in the second warehouse there are 247.3 tons of coal more than in the first, and in the third there are 50.8 tons more than in the second. How many tons of coal are in each warehouse?
2) The sum of three numbers is 446.73. The first number is less than the second by 73.17 and more than the third by 32.22. Find these numbers.
807. 1) The boat moved along the river at a speed of 14.5 km per hour, and against the current at a speed of 9.5 km per hour. What is the speed of the boat in still water and what is the speed of the river current?
2) The steamer traveled 85.6 km along the river in 4 hours, and 46.2 km against the current in 3 hours. What is the speed of the steamboat in still water and what is the speed of the river flow?
_________
808. 1) Two steamships delivered 3,500 tons of cargo, and one steamship delivered 1.5 times more cargo than the other. How much cargo did each ship carry?
2) The area of two rooms is 37.2 square meters. m. The area of one room is 2 times larger than the other. What is the area of each room?
809. 1) From two settlements, the distance between which is 32.4 km, a motorcyclist and a cyclist simultaneously rode towards each other. How many kilometers will each of them travel before the meeting if the speed of the motorcyclist is 4 times the speed of the cyclist?
2) Find two numbers whose sum is 26.35, and the quotient of dividing one number by the other is 7.5.
810. 1) The plant sent three types of cargo with a total weight of 19.2 tons. The weight of the first type of cargo was three times the weight of the second type of cargo, and the weight of the third type of cargo was half as much as the weight of the first and second types of cargo combined. What is the weight of each type of cargo?
2) In three months, a team of miners extracted 52.5 thousand tons of iron ore. In March it was produced 1.3 times, in February 1.2 times more than in January. How much ore did the crew mine monthly?
811. 1) The Saratov-Moscow gas pipeline is 672 km longer than the Moscow Canal. Find the length of both structures if the length of the gas pipeline is 6.25 times greater than the length of the Moscow Canal.
2) The length of the Don River is 3.934 times greater than the length of the Moscow River. Find the length of each river if the length of the Don River is 1,467 km greater than the length of the Moscow River.
812. 1) The difference between two numbers is 5.2, and the quotient of one number divided by another is 5. Find these numbers.
2) The difference between two numbers is 0.96, and their quotient is 1.2. Find these numbers.
813. 1) One number is 0.3 less than the other and is 0.75 of it. Find these numbers.
2) One number is 3.9 more than another number. If the smaller number is doubled, it will be 0.5 of the larger one. Find these numbers.
814. 1) The collective farm sowed 2,600 hectares of land with wheat and rye. How many hectares of land were sown with wheat and how many with rye, if 0.8 of the area sown with wheat is equal to 0.5 of the area sown with rye?
2) The collection of two boys together amounts to 660 stamps. How many stamps does each boy's collection consist of if 0.5 of the first boy's stamps are equal to 0.6 of the second boy's collection?
815. Two students together had 5.4 rubles. After the first spent 0.75 of his money, and the second 0.8 of his money, they had the same amount of money left. How much money did each student have?
816. 1) Two steamships set out towards each other from two ports, the distance between which is 501.9 km. How long will it take them to meet if the speed of the first ship is 25.5 km per hour, and the speed of the second is 22.3 km per hour?
2) Two trains set off towards each other from two points, the distance between which is 382.2 km. How long will it take them to meet if the average speed of the first train was 52.8 km per hour, and the second one was 56.4 km per hour?
817. 1) Two cars left two cities at a distance of 462 km at the same time and met after 3.5 hours. Find the speed of each car if the speed of the first was 12 km per hour greater than the speed of the second car.
2) From two settlements, the distance between which is 63 km, a motorcyclist and a cyclist left at the same time towards each other and met after 1.2 hours. Find the speed of the motorcyclist if the cyclist was traveling at a speed 27.5 km per hour less than the speed of the motorcyclist.
818. The student noticed that a train consisting of a steam locomotive and 40 carriages passed by him for 35 seconds. Determine the speed of the train per hour if the length of the locomotive is 18.5 m and the length of the carriage is 6.2 m. (Give the answer accurate to 1 km per hour.)
819. 1) A cyclist left A for B at an average speed of 12.4 km per hour. After 3 hours 15 minutes. another cyclist rode out from B towards him at an average speed of 10.8 km per hour. After how many hours and at what distance from A will they meet if 0.32 the distance between A and B is 76 km?
2) From cities A and B, the distance between which is 164.7 km, a truck from city A and a car from city B drove towards each other. The speed of the truck is 36 km, and the speed of the car is 1.25 times higher. The passenger car left 1.2 hours later than the truck. After how much time and at what distance from city B will the passenger car meet the truck?
820. Two ships left the same port at the same time and are heading in the same direction. The first steamer travels 37.5 km every 1.5 hours, and the second steamer travels 45 km every 2 hours. How long will it take for the first ship to be 10 km from the second?
821. A pedestrian first left one point, and 1.5 hours after his exit a cyclist left in the same direction. At what distance from the point did the cyclist catch up with the pedestrian if the pedestrian was walking at a speed of 4.25 km per hour and the cyclist was traveling at a speed of 17 km per hour?
822. The train left Moscow for Leningrad at 6 o'clock. 10 min. morning and walked at an average speed of 50 km per hour. Later, a passenger plane took off from Moscow to Leningrad and arrived in Leningrad simultaneously with the arrival of the train. The average speed of the aircraft was 325 km per hour, and the distance between Moscow and Leningrad was 650 km. When did the plane take off from Moscow?
823. The steamer traveled along the river for 5 hours, and against the current for 3 hours and covered only 165 km. How many kilometers did he walk downstream and how many against the current, if the speed of the river flow is 2.5 km per hour?
824. The train has left A and must arrive at B at a certain time; having passed half the way and doing 0.8 km in 1 minute, the train was stopped for 0.25 hours; having further increased the speed by 100 m per 1 million, the train arrived at B on time. Find the distance between A and B.
825. From the collective farm to the city 23 km. A postman rode a bicycle from the city to the collective farm at a speed of 12.5 km per hour. 0.4 hours after this, the collective farm executive rode into the city on a horse at a speed equal to 0.6 of the postman’s speed. How long after his departure will the collective farmer meet the postman?
826. A car left city A for city B, 234 km away from A, at a speed of 32 km per hour. 1.75 hours after this, a second car left city B towards the first, the speed of which was 1.225 times greater than the speed of the first. How many hours after its departure will the second car meet the first?
827. 1) One typist can retype a manuscript in 1.6 hours, and another in 2.5 hours. How long will it take both typists to type this manuscript, working together? (Round the answer to the nearest 0.1 hour.)
2) The pool is filled with two pumps of different power. The first pump, working alone, can fill the pool in 3.2 hours, and the second in 4 hours. How long will it take to fill the pool if these pumps are running simultaneously? (Round answer to the nearest 0.1.)
828. 1) One team can complete an order in 8 days. The other one needs 0.5 time to complete this order. The third team can complete this order in 5 days. How many days will it take to complete the entire order if three teams work together? (Round answer to the nearest 0.1 day.)
2) The first worker can complete the order in 4 hours, the second 1.25 times faster, and the third in 5 hours. How many hours will it take to complete the order if three workers work together? (Round the answer to the nearest 0.1 hour.)
829. Two cars are working to clean the street. The first of them can clean the entire street in 40 minutes, the second requires 75% of the time of the first. Both machines started working at the same time. After working together for 0.25 hours, the second machine stopped working. How long after that did the first machine finish cleaning the street?
830. 1) One of the sides of the triangle is 2.25 cm, the second is 3.5 cm larger than the first, and the third is 1.25 cm smaller than the second. Find the perimeter of the triangle.
2) One of the sides of the triangle is 4.5 cm, the second is 1.4 cm less than the first, and the third side is equal to half the sum of the first two sides. What is the perimeter of the triangle?
831 . 1) The base of the triangle is 4.5 cm, and its height is 1.5 cm less. Find the area of the triangle.
2) The height of the triangle is 4.25 cm, and its base is 3 times larger. Find the area of the triangle. (Round answer to the nearest 0.1.)
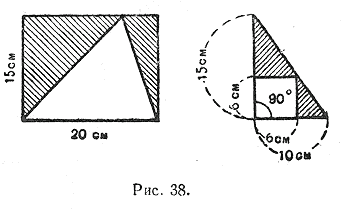
832. Find the area of the shaded figures (Fig. 38).
833. Which area is larger: a rectangle with sides 5 cm and 4 cm, a square with sides 4.5 cm, or a triangle whose base and height are each 6 cm?
834. The room is 8.5 m long, 5.6 m wide and 2.75 m high. The area of windows, doors and stoves is 0.1 of the total wall area of the room. How many pieces of wallpaper will be needed to cover this room if a piece of wallpaper is 7 m long and 0.75 m wide? (Round the answer to the nearest 1 piece.)
835. It is necessary to plaster and whitewash the outside of a one-story house, the dimensions of which are: length 12 m, width 8 m and height 4.5 m. The house has 7 windows measuring 0.75 m x 1.2 m each and 2 doors each measuring 0.75 m x 2.5 m. How much will the whole work cost if whitewashing and plastering is 1 sq. m. m costs 24 kopecks? (Round the answer to the nearest 1 ruble.)
836. Calculate the surface and volume of your room. Find the dimensions of the room by measuring.
837. The garden has the shape of a rectangle, the length of which is 32 m, the width is 10 m. 0.05 of the entire area of the garden is sown with carrots, and the rest of the garden is planted with potatoes and onions, and an area 7 times larger than with onions is planted with potatoes. How much land is individually planted with potatoes, onions and carrots?
838. The vegetable garden has the shape of a rectangle, the length of which is 30 m and the width of 12 m. 0.65 of the entire area of the vegetable garden is planted with potatoes, and the rest with carrots and beets, and 84 square meters are planted with beets. m more than carrots. How much land separately is there for potatoes, beets and carrots?
839. 1) The cube-shaped box was lined on all sides with plywood. How much plywood was used if the edge of the cube is 8.2 dm? (Round the answer to the nearest 0.1 sq. dm.)
2) How much paint will be needed to paint a cube with an edge of 28 cm, if per 1 sq. cm will 0.4 g of paint be used? (Answer, round to the nearest 0.1 kg.)
840. The length of a cast iron billet in the shape of a rectangular parallelepiped is 24.5 cm, width 4.2 cm and height 3.8 cm. How much do 200 cast iron billets weigh if 1 cubic. dm of cast iron weighs 7.8 kg? (Round answer to the nearest 1 kg.)
841. 1) The length of a box (with a lid) in the shape of a rectangular parallelepiped is 62.4 cm, width 40.5 cm, height 30 cm. How many square meters of boards were used to make the box, if waste boards amount to 0.2 of the surface area that should be covered with boards? (Round the answer to the nearest 0.1 sq. m.)
2) The bottom and side walls of the pit, which has the shape of a rectangular parallelepiped, must be covered with boards. The length of the pit is 72.5 m, width 4.6 m and height 2.2 m. How many square meters of boards were used for sheathing if the waste of boards constitutes 0.2 of the surface that should be sheathed with boards? (Round the answer to the nearest 1 sq.m.)
842. 1) The length of the basement, shaped like a rectangular parallelepiped, is 20.5 m, the width is 0.6 of its length, and the height is 3.2 m. The basement was filled with potatoes to 0.8 of its volume. How many tons of potatoes fit in the basement if 1 cubic meter of potatoes weighs 1.5 tons? (Round answer to the nearest 1 thousand.)
2) The length of the tank, shaped like a rectangular parallelepiped, is 2.5 m, the width is 0.4 of its length, and the height is 1.4 m. The tank is filled with kerosene to 0.6 of its volume. How many tons of kerosene are poured into the tank if the weight of kerosene in a volume is 1 cubic meter? m equals 0.9 t? (Round answer to the nearest 0.1 t.)
843. 1) How long can it take to renew the air in a room that is 8.5 m long, 6 m wide and 3.2 m high, if through a window in 1 second. passes 0.1 cubic meters. m of air?
2) Calculate the time required to refresh the air in your room.
844. The dimensions of the concrete block for building walls are as follows: 2.7 m x 1.4 m x 0.5 m. The void makes up 30% of the volume of the block. How many cubic meters of concrete will be required to make 100 such blocks?
845. Grader-elevator (machine for digging ditches) in 8 hours. The work makes a ditch 30 cm wide, 34 cm deep and 15 km long. How many diggers does such a machine replace if one digger can remove 0.8 cubic meters? m per hour? (Round the result.)
846. The bin in the shape of a rectangular parallelepiped is 12 m long and 8 m wide. In this bin, grain is poured to a height of 1.5 m. In order to find out how much all the grain weighs, they took a box 0.5 m long, 0.5 m wide and 0.4 m high, filled it with grain and weighed it. How much did the grain in the bin weigh if the grain in the box weighed 80 kg?

849. Construct a linear diagram of the growth of the urban population in the USSR, if in 1913 the urban population was 28.1 million people, in 1926 - 24.7 million, in 1939 - 56.1 million and in 1959 - 99, 8 million people.
850. 1) Make an estimate for the renovation of your classroom, if you need to whitewash the walls and ceiling, and paint the floor. Find out the data for drawing up an estimate (class size, cost of whitewashing 1 sq. m, cost of painting the floor 1 sq. m) from the school caretaker.
2) For planting in the garden, the school bought seedlings: 30 apple trees for 0.65 rubles. per piece, 50 cherries for 0.4 rubles. per piece, 40 gooseberry bushes for 0.2 rubles. and 100 raspberry bushes for 0.03 rubles. for a bush. Write an invoice for this purchase using the following example:

ANSWERS

In this article we will understand what a decimal fraction is, what features and properties it has. Go! 🙂
A decimal fraction is a special case of ordinary fractions (where the denominator is a multiple of 10).
Definition
Decimals are fractions whose denominators are numbers consisting of one and a number of zeros following it. That is, these are fractions with a denominator of 10, 100, 1000, etc. Otherwise, a decimal fraction can be characterized as a fraction with a denominator of 10 or one of the powers of ten.
Examples of fractions:
, ,
Decimal fractions are written differently than ordinary fractions. Operations with these fractions are also different from operations with ordinary ones. The rules for operations with them are largely similar to the rules for operations with integers. This, in particular, explains their demand for solving practical problems.
Representation of fractions in decimal notation
The decimal fraction does not have a denominator; it displays the number of the numerator. In general, a decimal fraction is written according to the following scheme:
where X is the integer part of the fraction, Y is its fractional part, “,” is the decimal point.
To correctly represent a fraction as a decimal, it requires that it be a regular fraction, that is, with the integer part highlighted (if possible) and a numerator that is less than the denominator. Then in decimal notation the integer part is written before the decimal point (X), and the numerator of the common fraction is written after the decimal point (Y).
If the numerator contains a number with fewer digits than the number of zeros in the denominator, then in part Y the missing number of digits in the decimal notation is filled with zeros ahead of the numerator digits.
Example: ![]()
If a common fraction is less than 1, i.e. does not have an integer part, then for X in decimal form write 0.
In the fractional part (Y), after the last significant (non-zero) digit, an arbitrary number of zeros can be entered. This does not affect the value of the fraction. Conversely, all zeros at the end of the fractional part of the decimal can be omitted.
Reading Decimals
Part X is generally read as follows: “X integers.”
The Y part is read according to the number in the denominator. For denominator 10 you should read: “Y tenths”, for denominator 100: “Y hundredths”, for denominator 1000: “Y thousandths” and so on... 😉
Another approach to reading, based on counting the number of digits of the fractional part, is considered more correct. To do this, you need to understand that the fractional digits are located in a mirror image with respect to the digits of the whole part of the fraction.
The names for correct reading are given in the table:

Based on this, reading should be based on compliance with the name of the digit of the last digit of the fractional part.
- 3.5 is read as "three point five"
- 0.016 reads "zero point sixteen thousandths"
Converting an arbitrary fraction to a decimal
If the denominator of a common fraction is 10 or some power of ten, then the conversion of the fraction is performed as described above. In other situations, additional transformations are required.
There are 2 translation methods.
First transfer method
The numerator and denominator must be multiplied by such an integer that the denominator produces the number 10 or one of the powers of ten. And then the fraction is represented in decimal notation.
This method is applicable for fractions whose denominator can only be expanded into 2 and 5. So, in the previous example ![]() . If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
. If the expansion contains other prime factors (for example, ), then you will have to resort to the 2nd method.
Second translation method
The 2nd method is to divide the numerator by the denominator in a column or on a calculator. The whole part, if any, does not participate in the transformation.
The rule for long division that results in a decimal fraction is described below (see Division of decimals).
Converting a decimal fraction to a common fraction
To do this, you should write down its fractional part (to the right of the decimal point) as the numerator, and the result of reading the fractional part as the corresponding number in the denominator. Next, if possible, you need to reduce the resulting fraction.
![]()
Finite and infinite decimal fraction
A decimal fraction is called a final fraction, the fractional part of which consists of a finite number of digits.
All the examples above contain final decimal fractions. However, not every ordinary fraction can be represented as a final decimal. If the 1st conversion method is not applicable for a given fraction, and the 2nd method demonstrates that the division cannot be completed, then only an infinite decimal fraction can be obtained.
It is impossible to write an infinite fraction in its complete form. In incomplete form, such fractions can be represented:
- as a result of reduction to the desired number of decimal places;
- as a periodic fraction.
A fraction is called periodic if after the decimal point it is possible to distinguish an endlessly repeating sequence of digits.
The remaining fractions are called non-periodic. For non-periodic fractions, only the 1st method of representation (rounding) is allowed.
An example of a periodic fraction: 0.8888888... Here there is a repeating number 8, which, obviously, will be repeated ad infinitum, since there is no reason to assume otherwise. This figure is called period of the fraction.
Periodic fractions can be pure or mixed. A pure decimal fraction is one whose period begins immediately after the decimal point. A mixed fraction has 1 or more digits before the decimal point.
54.33333… – periodic pure decimal fraction
2.5621212121… – periodic mixed fraction
Examples of writing infinite decimal fractions:
The 2nd example shows how to correctly format a period in writing a periodic fraction.
Converting periodic decimal fractions to ordinary fractions
To convert a pure periodic fraction into an ordinary period, write it into the numerator, and write a number consisting of nines in an amount equal to the number of digits in the period into the denominator.
![]()
The mixed periodic decimal fraction is translated as follows:
- you need to form a number consisting of the number after the decimal point before the period and the first period;
- From the resulting number, subtract the number after the decimal point before the period. The result will be the numerator of the common fraction;
- in the denominator you need to enter a number consisting of a number of nines equal to the number of digits of the period, followed by zeros, the number of which is equal to the number of digits of the number after the decimal point before the 1st period.
![]()
![]()
Comparison of decimals
Decimal fractions are compared initially by their whole parts. The fraction whose whole part is larger is greater.
If the integer parts are the same, then compare the digits of the corresponding digits of the fractional part, starting from the first (from the tenths). The same principle applies here: the larger fraction is the one with more tenths; if the tenths digits are equal, the hundredths digits are compared, and so on.
Because the
![]() , since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
, since with equal whole parts and equal tenths in the fractional part, the 2nd fraction has a larger hundredths figure.
Adding and subtracting decimals
Decimals are added and subtracted in the same way as whole numbers by writing the corresponding digits below each other. To do this, you need to have decimal points below each other. Then the units (tens, etc.) of the integer part, as well as the tenths (hundredths, etc.) of the fractional part, will be in accordance. The missing digits of the fractional part are filled with zeros. Directly The process of addition and subtraction is carried out in the same way as for integers.
Multiplying Decimals
To multiply decimals, you need to write them one below the other, aligned with the last digit and not paying attention to the location of the decimal points. Then you need to multiply the numbers in the same way as when multiplying whole numbers. After receiving the result, you should recalculate the number of digits after the decimal point in both fractions and separate the total number of fractional digits in the resulting number with a comma. If there are not enough digits, they are replaced with zeros.

Multiplying and dividing decimals by 10n
These actions are simple and boil down to moving the decimal point. P When multiplying, the decimal point is moved to the right (the fraction is increased) by a number of digits equal to the number of zeros in 10n, where n is an arbitrary integer power. That is, a certain number of digits are transferred from the fractional part to the whole part. When dividing, accordingly, the comma is moved to the left (the number decreases), and some of the digits are transferred from the integer part to the fractional part. If there are not enough numbers to transfer, then the missing bits are filled with zeros.
Dividing a decimal and a whole number by a whole number and a decimal
Dividing a decimal by an integer is similar to dividing two integers. Additionally, you only need to take into account the position of the decimal point: when removing the digit of a place followed by a comma, you must place a comma after the current digit of the generated answer. Next you need to continue dividing until you get zero. If there are not enough signs in the dividend for complete division, zeros should be used as them.

Similarly, 2 integers are divided into a column if all the digits of the dividend are removed and the complete division is not yet completed. In this case, after removing the last digit of the dividend, a decimal point is placed in the resulting answer, and zeros are used as the removed digits. Those. the dividend here is essentially represented as a decimal fraction with a zero fractional part.

To divide a decimal fraction (or an integer) by a decimal number, you must multiply the dividend and divisor by the number 10 n, in which the number of zeros is equal to the number of digits after the decimal point in the divisor. In this way, you get rid of the decimal point in the fraction you want to divide by. Further, the division process coincides with that described above.
Graphical representation of decimal fractions
Decimal fractions are represented graphically using a coordinate line. To do this, individual segments are further divided into 10 equal parts, just as centimeters and millimeters are marked simultaneously on a ruler. This ensures that decimals are displayed accurately and can be compared objectively.
In order for the divisions on individual segments to be identical, you should carefully consider the length of the single segment itself. It should be such that the convenience of additional division can be ensured.
