I denne artikel taler en matematik- og fysikvejleder om, hvordan man udfører elementære operationer med almindelige brøker: addition og subtraktion, multiplikation og division. Lær, hvordan du repræsenterer et blandet tal som en uægte brøk og omvendt, samt hvordan du reducerer brøker.
Tilføjelse og subtrahering af almindelige brøker
Lad os minde dig om det nævner brøk er det tal, der er nedefra, A tæller- nummeret, der er placeret over fra brøklinjen. For eksempel i en brøk er tallet tælleren, og tallet er nævneren.
Fællesnævner er det mindst mulige tal, der er deleligt med både nævneren i den første brøk og nævneren i den anden brøk.
Eksempel 1. Tilføj to brøker:.
Lad os bruge algoritmen beskrevet ovenfor:
1) Det mindste tal, der er deleligt med både nævneren i den første brøk og nævneren i den anden brøk, er lig med . Dette tal vil være fællesnævneren. Nu skal du bringe begge brøker til en fællesnævner.
2) Tilføj de resulterende fraktioner: ![]() .
.
Multiplikation af almindelige brøker
Med andre ord gælder følgende lighed for alle reelle tal , , , :
![]()
Eksempel 2. Gang brøker:.
For at løse dette problem bruger vi formlen præsenteret ovenfor: ![]() .
.
Opdeling af brøker
Med andre ord gælder følgende lighed for alle reelle tal , , , , :

Eksempel 3. Divider brøker:.
For at løse dette problem bruger vi ovenstående formel: ![]() .
.
Repræsenterer et blandet tal som en uægte brøk
Lad os nu finde ud af, hvad vi skal gøre, hvis du skal udføre en operation med brøker præsenteret i form af blandede tal. I dette tilfælde skal du først repræsentere blandede tal som ukorrekte brøker og derefter udføre den nødvendige handling.
Lad os minde dig om det forkert En brøk, hvis tæller er større end eller lig med dens nævner kaldes.
Husk også, at et blandet tal har brøkdel Og hele delen. For eksempel har et blandet tal en brøkdel lig med , og en heltalsdel lig .
Eksempel 4. Udtryk et blandet tal som en uægte brøk.
Lad os bruge algoritmen præsenteret ovenfor: ![]() .
.
Eksempel 5. Repræsenter en uægte brøk som et blandet tal.
Brøk- en form for at repræsentere et tal i matematik. Brøklinjen angiver divisionsoperationen. Tæller brøk kaldes udbyttet, og nævner- skillevæg. For eksempel, i en brøk er tælleren 5 og nævneren er 7.
Korrekt En brøk kaldes, hvor tællerens modul er større end nævnerens modul. Hvis en brøk er rigtig, så er modulet af dens værdi altid mindre end 1. Alle andre brøker er forkert.
Brøken kaldes blandet, hvis det skrives som et heltal og en brøk. Dette er det samme som summen af dette tal og brøken:
Hovedegenskaben ved en brøk
Hvis en brøks tæller og nævner ganges med det samme tal, så ændres brøkens værdi ikke, dvs. f.eks.
![]()
Reduktion af brøker til en fællesnævner
For at bringe to brøker til en fællesnævner skal du bruge:
- Multiplicer tælleren for den første brøk med nævneren af den anden
- Gang tælleren for den anden brøk med nævneren af den første
- Udskift nævnerne for begge fraktioner med deres produkt
Operationer med brøker
Tilføjelse. For at tilføje to brøker skal du bruge
- Tilføj de nye tællere for begge brøker og lad nævneren være uændret
Eksempel:
Subtraktion. For at trække en brøk fra en anden, skal du bruge
- Reducer brøker til en fællesnævner
- Træk tælleren for den anden fra tælleren i den første brøk, og lad nævneren være uændret
Eksempel:
![]()
Multiplikation. For at gange en brøk med en anden skal du gange deres tællere og nævnere:
![]()
Division. For at dividere en brøk med en anden skal du gange tælleren for den første brøk med nævneren af den anden og gange nævneren af den første brøk med tælleren i den anden:
![]()
Lad os blive enige om, at "handlinger med brøker" i vores lektion vil betyde handlinger med almindelige brøker. En almindelig brøk er en brøk, der har attributter som en tæller, en brøklinje og en nævner. Dette adskiller en almindelig brøk fra en decimal, som fås fra en almindelig brøk ved at reducere nævneren til et multiplum af 10. Decimalbrøken skrives med et komma, der adskiller hele delen fra brøkdelen. Vi vil tale om operationer med almindelige brøker, da det er dem, der forårsager de største vanskeligheder for elever, der har glemt det grundlæggende i dette emne, dækket i første halvdel af skolens matematikkursus. Når man transformerer udtryk i højere matematik, er det samtidig hovedsageligt operationer med almindelige brøker, der bruges. Alene brøkforkortelserne er det værd! Decimalbrøker volder ikke særlige vanskeligheder. Så gå videre!
To brøker siges at være lige, hvis .
For eksempel siden
Brøker og (siden), og (siden) er også lige.
Det er klart, at begge brøker og er lige store. Det betyder, at hvis tælleren og nævneren for en given brøk ganges eller divideres med det samme naturlige tal, får man en brøk, der er lig med den givne: .
Denne egenskab kaldes den grundlæggende egenskab for en brøk.
Den grundlæggende egenskab for en brøk kan bruges til at ændre fortegnene for tælleren og nævneren for en brøk. Hvis tælleren og nævneren af en brøk ganges med -1, får vi . Det betyder, at værdien af en brøk ikke ændres, hvis fortegnene for tæller og nævner ændres på samme tid. Hvis du kun ændrer tegnet for tælleren eller kun nævneren, vil brøken ændre sit fortegn:
Reducerende brøker
Ved at bruge en brøks grundegenskab kan du erstatte en given brøk med en anden brøk, der er lig med den givne, men med en mindre tæller og nævner. Denne substitution kaldes fraktionsreduktion.
Lad for eksempel få en brøk. Tallene 36 og 48 har en største fælles divisor på 12. Så
![]() .
.
Generelt er det altid muligt at reducere en brøk, hvis tælleren og nævneren ikke er indbyrdes primtal. Hvis tælleren og nævneren er indbyrdes primtal, så kaldes brøken irreducerbar.
Så at reducere en brøk betyder at dividere brøkens tæller og nævner med en fælles faktor. Alt ovenstående gælder også for brøkudtryk, der indeholder variable.
Eksempel 1. Reducer fraktion
Løsning. For at faktorisere tælleren skal du først præsentere monomialet - 5 xy som en sum - 2 xy - 3xy, vi får

For at faktorisere nævneren bruger vi kvadratforskellens formel:
Som resultat
![]() .
.
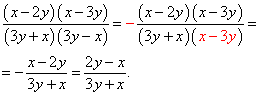
Reduktion af brøker til en fællesnævner
Lad to brøker og . De har forskellige nævnere: 5 og 7. Ved at bruge brøkernes grundlæggende egenskab kan du erstatte disse brøker med andre, der er lig med dem, og sådan at de resulterende brøker får de samme nævnere. Multiplicerer tælleren og nævneren af brøken med 7, får vi
Hvis vi multiplicerer brøkens tæller og nævner med 5, får vi
Så brøkerne reduceres til en fællesnævner:
![]() .
.
Men dette er ikke den eneste løsning på problemet: for eksempel kan disse brøker også reduceres til en fællesnævner på 70:
![]() ,
,
![]()
og generelt til enhver nævner, der kan divideres med både 5 og 7.
Lad os overveje et andet eksempel: lad os bringe brøkerne og til en fællesnævner. Argumenterer som i det foregående eksempel, får vi
![]() ,
,
![]() .
.
Men i dette tilfælde er det muligt at reducere brøkerne til en fællesnævner, der er mindre end produktet af disse brøkers nævnere. Lad os finde det mindste fælles multiplum af tallene 24 og 30: LCM(24, 30) = 120.
Da 120:4 = 5, for at skrive en brøk med nævneren 120, skal du gange både tælleren og nævneren med 5, dette tal kaldes en ekstra faktor. Midler ![]() .
.
Dernæst får vi 120:30=4. Hvis vi multiplicerer brøkens tæller og nævner med en ekstra faktor på 4, får vi ![]() .
.
Så disse brøker er reduceret til en fællesnævner.
Det mindste fælles multiplum af disse brøkers nævnere er den mindst mulige fællesnævner.
For brøkudtryk, der involverer variable, er fællesnævneren et polynomium, der er divideret med nævneren for hver brøk.
Eksempel 2. Find fællesnævneren for brøkerne og.
Løsning. Fællesnævneren for disse brøker er et polynomium, da det er deleligt med både og. Dette polynomium er dog ikke det eneste, der kan være en fællesnævner for disse brøker. Det kan også være et polynomium ![]() og polynomium
og polynomium ![]() og polynomium
og polynomium ![]() etc. Normalt tager de sådan en fællesnævner, at enhver anden fællesnævner divideres med den valgte uden en rest. Denne nævner kaldes den laveste fællesnævner.
etc. Normalt tager de sådan en fællesnævner, at enhver anden fællesnævner divideres med den valgte uden en rest. Denne nævner kaldes den laveste fællesnævner.
I vores eksempel er den laveste fællesnævner . Fik:
![]() ;
;
![]() .
.
Vi var i stand til at reducere brøker til deres laveste fællesnævner. Dette skete ved at gange tælleren og nævneren af den første brøk med , og tælleren og nævneren i den anden brøk med . Polynomier kaldes yderligere faktorer for henholdsvis første og anden brøk.
Addere og trække brøker fra
Addition af fraktioner er defineret som følger:
![]() .
.
For eksempel,
![]() .
.
Hvis b = d, At
![]() .
.
Det betyder, at for at tilføje brøker med samme nævner, er det nok at tilføje tællere og lade nævneren være den samme. For eksempel,
![]() .
.
Tilføjer man brøker med forskellige nævnere, reducerer man normalt brøkerne til den laveste fællesnævner, og lægger derefter tællerne sammen. For eksempel,
![]() .
.
Lad os nu se på et eksempel på tilføjelse af brøkudtryk med variable.
Eksempel 3. Konverter udtryk til én brøk
![]() .
.
Løsning. Lad os finde den laveste fællesnævner. For at gøre dette faktoriserer vi først nævnerne.
Eksempler med brøker er et af de grundlæggende elementer i matematik. Der findes mange forskellige typer ligninger med brøker. Nedenfor er detaljerede instruktioner til løsning af eksempler af denne type.
Sådan løses eksempler med brøker - generelle regler
For at løse eksempler med brøker af enhver type, det være sig addition, subtraktion, multiplikation eller division, skal du kende de grundlæggende regler:
- For at tilføje brøkudtryk med samme nævner (nævneren er tallet nederst i brøken, tælleren øverst), skal du tilføje deres tællere og lade nævneren være den samme.
- For at trække et andet brøkudtryk (med samme nævner) fra en brøk, skal du trække deres tællere fra og lade nævneren være den samme.
- For at tilføje eller trække brøker med forskellige nævnere, skal du finde den laveste fællesnævner.
- For at finde et brøkprodukt skal du gange tællere og nævnere og, hvis det er muligt, reducere.
- For at dividere en brøk med en brøk, gange du den første brøk med den anden brøk omvendt.
Sådan løses eksempler med brøker - øv dig
Regel 1, eksempel 1:
Beregn 3/4 +1/4.
Ifølge regel 1, hvis to (eller flere) brøker har samme nævner, tilføjer du blot deres tællere. Vi får: 3/4 + 1/4 = 4/4. Hvis en brøk har samme tæller og nævner, vil brøken være lig med 1.
Svar: 3/4 + 1/4 = 4/4 = 1.
Regel 2, eksempel 1:
Beregn: 3/4 – 1/4
Ved at bruge regel nummer 2 skal du for at løse denne ligning trække 1 fra 3 og lade nævneren være den samme. Vi får 2/4. Da to 2 og 4 kan reduceres, reducerer vi og får 1/2.
Svar: 3/4 – 1/4 = 2/4 = 1/2.
Regel 3, eksempel 1
Beregn: 3/4 + 1/6
Løsning: Ved hjælp af den 3. regel finder vi den laveste fællesnævner. Den mindste fællesnævner er det tal, der er deleligt med nævnerne for alle brøkudtryk i eksemplet. Vi skal således finde det mindste tal, der vil være deleligt med både 4 og 6. Dette tal er 12. Vi skriver 12 som nævner. Divider 12 med nævneren af den første brøk, vi får 3, gang med 3, skriv 3 i tælleren *3 og + tegnet. Divider 12 med nævneren af den anden brøk, vi får 2, gange 2 med 1, skriv 2*1 i tælleren. Så vi får en ny brøk med en nævner lig med 12 og en tæller lig med 3*3+2*1=11. 11/12.
Svar: 11/12
Regel 3, eksempel 2:
Beregn 3/4 – 1/6. Dette eksempel ligner meget det forrige. Vi udfører alle de samme trin, men i tælleren i stedet for +-tegnet skriver vi et minustegn. Vi får: 3*3-2*1/12 = 9-2/12 = 7/12.
Svar: 7/12
Regel 4, eksempel 1:
Beregn: 3/4 * 1/4
Ved at bruge den fjerde regel multiplicerer vi nævneren i den første brøk med nævneren i den anden og tælleren i den første brøk med tælleren i den anden. 3*1/4*4 = 3/16.
Svar: 16/3
Regel 4, eksempel 2:
Beregn 2/5 * 10/4.
Denne fraktion kan reduceres. I tilfælde af et produkt annulleres tælleren for den første brøk og nævneren i den anden og tælleren i den anden brøk og nævneren i den første.
2 aflysninger fra 4. 10 aflysninger fra 5. Vi får 1 * 2/2 = 1*1 = 1.
Svar: 2/5 * 10/4 = 1
Regel 5, eksempel 1:
Beregn: 3/4: 5/6
Ved at bruge den 5. regel får vi: 3/4: 5/6 = 3/4 * 6/5. Vi reducerer brøken efter princippet i det foregående eksempel og får 9/10.
Svar: 9/10.


Sådan løses eksempler med brøker - brøkligninger
Brøkligninger er eksempler, hvor nævneren indeholder en ukendt. For at løse en sådan ligning skal du bruge visse regler.
Lad os se på et eksempel:
Løs ligningen 15/3x+5 = 3
Lad os huske, at du ikke kan dividere med nul, dvs. nævnerværdien må ikke være nul. Ved løsning af sådanne eksempler skal dette angives. Til dette formål er der en OA (tilladt værdiområde).
Så 3x+5 ≠ 0.
Derfor: 3x ≠ 5.
x ≠ 5/3
Ved x = 5/3 har ligningen simpelthen ingen løsning.
Efter at have specificeret ODZ, er den bedste måde at løse denne ligning på at slippe af med brøkerne. For at gøre dette præsenterer vi først alle ikke-brøkværdier som en brøk, i dette tilfælde tallet 3. Vi får: 15/(3x+5) = 3/1. For at slippe af med brøker skal du gange hver af dem med den laveste fællesnævner. I dette tilfælde vil det være (3x+5)*1. Rækkefølge:
- Multiplicer 15/(3x+5) med (3x+5)*1 = 15*(3x+5).
- Åbn parenteserne: 15*(3x+5) = 45x + 75.
- Vi gør det samme med højre side af ligningen: 3*(3x+5) = 9x + 15.
- Sæt lighedstegn mellem venstre og højre side: 45x + 75 = 9x +15
- Flyt X'erne til venstre, tallene til højre: 36x = – 50
- Find x: x = -50/36.
- Vi reducerer: -50/36 = -25/18
Svar: ODZ x ≠ 5/3. x = -25/18.


Sådan løses eksempler med brøker - brøkuligheder
Fraktionelle uligheder af typen (3x-5)/(2-x)≥0 løses ved hjælp af talaksen. Lad os se på dette eksempel.
Rækkefølge:
- Vi sætter lighedstegn mellem tæller og nævner til nul: 1. 3x-5=0 => 3x=5 => x=5/3
2. 2-x=0 => x=2 - Vi tegner en talakse og skriver de resulterende værdier på den.
- Tegn en cirkel under værdien. Der er to typer cirkler - fyldte og tomme. En udfyldt cirkel betyder, at den givne værdi er inden for løsningsområdet. En tom cirkel angiver, at denne værdi ikke er inkluderet i løsningsområdet.
- Da nævneren ikke kan være lig med nul, vil der være en tom cirkel under 2'eren.


- For at bestemme fortegnene erstatter vi et hvilket som helst tal større end to i ligningen, for eksempel 3. (3*3-5)/(2-3)= -4. værdien er negativ, hvilket betyder at vi skriver et minus over arealet efter de to. Erstat derefter X med enhver værdi af intervallet fra 5/3 til 2, for eksempel 1. Værdien er igen negativ. Vi skriver et minus. Vi gentager det samme med området placeret op til 5/3. Vi erstatter et hvilket som helst tal mindre end 5/3, for eksempel 1. Igen minus.


- Da vi er interesseret i værdierne af x, hvor udtrykket vil være større end eller lig med 0, og der ikke er sådanne værdier (der er minusser overalt), har denne ulighed ingen løsning, det vil sige x = Ø (et tomt sæt).
Svar: x = Ø
Lektionens indhold
Tilføjelse af brøker med ens nævnere
Der er to typer addition af fraktioner:
- Tilføjelse af brøker med ens nævnere;
- Tilføjelse af brøker med forskellige nævnere.
Lad os først studere tilføjelsen af brøker med ens nævnere. Alt er enkelt her. For at tilføje brøker med de samme nævnere, skal du tilføje deres tællere og lade nævneren være uændret.
Lad os f.eks. tilføje brøkerne og . Tilføj tællere og lad nævneren være uændret:

Dette eksempel kan let forstås, hvis vi husker pizzaen, som er opdelt i fire dele. Tilføjer du pizza til pizza, får du pizza:

Eksempel 2. Tilføj brøker og .

Svaret viste sig at være en upassende brøk. Når slutningen af opgaven kommer, er det sædvanligt at slippe af med ukorrekte fraktioner. For at slippe af med en ukorrekt fraktion skal du vælge hele delen af den. I vores tilfælde er hele delen let isoleret - to divideret med to vil være en:

Dette eksempel kan let forstås, hvis vi husker om en pizza, der er opdelt i to dele. Tilføjer du mere pizza til pizzaen, får du en hel pizza:

Eksempel 3. Tilføj brøker og .
Igen lægger vi tællerne sammen og lader nævneren være uændret:
![]()
Dette eksempel kan let forstås, hvis vi husker pizzaen, som er opdelt i tre dele. Tilføjer du mere pizza til pizzaen, får du pizza:

Eksempel 4. Find værdien af et udtryk 
Dette eksempel er løst på nøjagtig samme måde som de foregående. Tællerne skal tilføjes og nævneren forblive uændret:
Lad os prøve at skildre vores løsning ved hjælp af en tegning. Tilføjer du pizzaer til en pizza og tilføjer flere pizzaer, får du 1 hel pizza og flere pizzaer.

Som du kan se, er der ikke noget kompliceret ved at tilføje brøker med de samme nævnere. Det er nok at forstå følgende regler:
- For at tilføje brøker med de samme nævnere, skal du tilføje deres tællere og lade nævneren være uændret;
Tilføjelse af brøker med forskellige nævnere
Lad os nu lære, hvordan man tilføjer brøker med forskellige nævnere. Ved sammenlægning af brøker skal nævnerne for brøkerne være de samme. Men de er ikke altid ens.
For eksempel kan brøker tilføjes, fordi de har de samme nævnere.
Men brøker kan ikke tilføjes med det samme, da disse brøker har forskellige nævnere. I sådanne tilfælde skal brøker reduceres til samme (fælles)nævner.
Der er flere måder at reducere brøker til den samme nævner. I dag vil vi kun se på en af dem, da de andre metoder kan virke komplicerede for en begynder.
Essensen af denne metode er, at først LCM af nævnerne af begge fraktioner søges. LCM divideres derefter med nævneren af den første brøk for at opnå den første yderligere faktor. De gør det samme med den anden brøk - LCM divideres med nævneren af den anden brøk, og en anden yderligere faktor opnås.
Brøkernes tællere og nævnere ganges derefter med deres yderligere faktorer. Som et resultat af disse handlinger bliver brøker, der havde forskellige nævnere, til brøker, der har de samme nævnere. Og vi ved allerede, hvordan man tilføjer sådanne brøker.
Eksempel 1. Lad os tilføje brøkerne og
Først og fremmest finder vi det mindste fælles multiplum af nævnerne i begge brøker. Nævneren i den første brøk er tallet 3, og nævneren i den anden brøk er tallet 2. Det mindste fælles multiplum af disse tal er 6
LCM (2 og 3) = 6
Lad os nu vende tilbage til brøker og . Del først LCM med nævneren af den første brøk og få den første ekstra faktor. LCM er tallet 6, og nævneren i den første brøk er tallet 3. Divider 6 med 3, så får vi 2.
Det resulterende tal 2 er den første ekstra multiplikator. Vi skriver det ned til den første brøk. For at gøre dette skal du lave en lille skrå linje over brøken og nedskrive den ekstra faktor, der findes over den:
Vi gør det samme med den anden brøk. Vi dividerer LCM med nævneren af den anden brøk og får den anden ekstra faktor. LCM er tallet 6, og nævneren i den anden brøk er tallet 2. Divider 6 med 2, så får vi 3.
Det resulterende tal 3 er den anden ekstra multiplikator. Vi skriver det ned til den anden brøk. Igen laver vi en lille skrå linje over den anden brøk og skriver den ekstra faktor, der findes over den, ned:
Nu har vi alt klar til tilføjelse. Det er tilbage at gange brøkernes tællere og nævnere med deres yderligere faktorer:

Se nøje på, hvad vi er kommet til. Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde samme nævnere. Og vi ved allerede, hvordan man tilføjer sådanne brøker. Lad os tage dette eksempel til slutningen:

Dette fuldender eksemplet. Det viser sig at tilføje .
Lad os prøve at skildre vores løsning ved hjælp af en tegning. Tilføjer du pizza til en pizza, får du en hel pizza og en anden sjettedel af en pizza:

Reduktion af brøker til den samme (fælles)nævner kan også afbildes ved hjælp af et billede. Ved at reducere brøkerne og til en fællesnævner fik vi brøkerne og . Disse to fraktioner vil være repræsenteret af de samme stykker pizza. Den eneste forskel vil være, at de denne gang bliver delt i lige store andele (reduceret til samme nævner).

Den første tegning repræsenterer en brøk (fire stykker ud af seks), og den anden tegning repræsenterer en brøkdel (tre stykker ud af seks). Tilføjelse af disse stykker får vi (syv stykker ud af seks). Denne brøkdel er ukorrekt, så vi fremhævede hele delen af den. Som et resultat fik vi (en hel pizza og en anden sjette pizza).
Bemærk venligst, at vi har beskrevet dette eksempel for meget detaljeret. I uddannelsesinstitutioner er det ikke sædvanligt at skrive så detaljeret. Du skal hurtigt kunne finde LCM for både nævnere og yderligere faktorer til dem, samt hurtigt gange de fundne yderligere faktorer med dine tællere og nævnere. Hvis vi var i skole, skulle vi skrive dette eksempel som følger:

Men der er også en anden side af mønten. Hvis du ikke tager detaljerede noter i de første faser af at studere matematik, begynder spørgsmål af den slags at dukke op. "Hvor kommer det tal fra?", "Hvorfor bliver brøker pludselig til helt andre brøker? «.
For at gøre det nemmere at tilføje brøker med forskellige nævnere kan du bruge følgende trinvise instruktioner:
- Find LCM for nævnerne af brøker;
- Divider LCM med nævneren af hver brøk og få en ekstra faktor for hver brøk;
- Multiplicer tællere og nævnere af brøker med deres yderligere faktorer;
- Tilføj brøker, der har de samme nævnere;
- Hvis svaret viser sig at være en ukorrekt brøk, så vælg hele dens del;
Eksempel 2. Find værdien af et udtryk  .
.
Lad os bruge instruktionerne ovenfor.
Trin 1. Find LCM for nævnerne af brøkerne
Find LCM for nævnerne af begge brøker. Nævnerne for brøker er tallene 2, 3 og 4

Trin 2. Divider LCM med nævneren for hver brøk og få en ekstra faktor for hver brøk
Divider LCM med nævneren af den første brøk. LCM er tallet 12, og nævneren for den første brøk er tallet 2. Divider 12 med 2, vi får 6. Vi fik den første ekstra faktor 6. Vi skriver den over den første brøk:
Nu dividerer vi LCM med nævneren af den anden brøk. LCM er tallet 12, og nævneren for den anden brøk er tallet 3. Divider 12 med 3, vi får 4. Vi får den anden yderligere faktor 4. Vi skriver den over den anden brøk:
Nu dividerer vi LCM med nævneren af den tredje brøk. LCM er tallet 12, og nævneren for den tredje brøk er tallet 4. Divider 12 med 4, vi får 3. Vi får den tredje ekstra faktor 3. Vi skriver den over den tredje brøk:
Trin 3. Multiplicer brøkernes tællere og nævnere med deres yderligere faktorer
Vi multiplicerer tællere og nævnere med deres yderligere faktorer:
Trin 4. Tilføj brøker med de samme nævnere
Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde de samme (fælles)nævnere. Tilbage er blot at tilføje disse fraktioner. Tilføj det:

Tilføjelsen passede ikke på én linje, så vi flyttede det resterende udtryk til den næste linje. Dette er tilladt i matematik. Når et udtryk ikke passer på én linje, flyttes det til næste linje, og det er nødvendigt at sætte et lighedstegn (=) i slutningen af den første linje og i begyndelsen af den nye linje. Lighedstegnet på den anden linje indikerer, at dette er en fortsættelse af det udtryk, der var på den første linje.
Trin 5. Hvis svaret viser sig at være en ukorrekt brøk, så vælg hele delen af det
Vores svar viste sig at være en ukorrekt brøkdel. Vi skal fremhæve en hel del af det. Vi fremhæver:

Vi fik svar
At trække brøker fra med ens nævnere
Der er to typer subtraktion af brøker:
- At trække brøker fra med ens nævnere
- Fratræk brøker med forskellige nævnere
Lad os først lære, hvordan man trækker brøker fra med ens nævnere. Alt er enkelt her. For at trække en anden fra en brøk, skal du trække tælleren for den anden brøk fra tælleren i den første brøk, men lade nævneren være den samme.
Lad os f.eks. finde værdien af udtrykket . For at løse dette eksempel skal du trække tælleren for den anden brøk fra tælleren i den første brøk og lade nævneren være uændret. Lad os gøre det:

Dette eksempel kan let forstås, hvis vi husker pizzaen, som er opdelt i fire dele. Hvis du skærer pizzaer fra en pizza, får du pizzaer:

Eksempel 2. Find værdien af udtrykket.
Igen, fra tælleren for den første brøk, trækker du tælleren fra den anden brøk, og lad nævneren være uændret:

Dette eksempel kan let forstås, hvis vi husker pizzaen, som er opdelt i tre dele. Hvis du skærer pizzaer fra en pizza, får du pizzaer:

Eksempel 3. Find værdien af et udtryk 
Dette eksempel er løst på nøjagtig samme måde som de foregående. Fra tælleren for den første brøk skal du trække tællerne for de resterende brøker fra:

Som du kan se, er der ikke noget kompliceret ved at trække brøker fra med de samme nævnere. Det er nok at forstå følgende regler:
- For at trække en anden fra en brøk, skal du trække tælleren for den anden brøk fra tælleren i den første brøk og lade nævneren være uændret;
- Hvis svaret viser sig at være en ukorrekt brøkdel, skal du fremhæve hele delen af det.
Fratræk brøker med forskellige nævnere
For eksempel kan du trække en brøk fra en brøk, fordi brøkerne har de samme nævnere. Men du kan ikke trække en brøk fra en brøk, da disse brøker har forskellige nævnere. I sådanne tilfælde skal brøker reduceres til samme (fælles)nævner.
Fællesnævneren findes ved at bruge det samme princip, som vi brugte, når vi tilføjede brøker med forskellige nævnere. Først og fremmest skal du finde LCM for nævnerne af begge brøker. Derefter divideres LCM med nævneren af den første brøk, og den første yderligere faktor opnås, som er skrevet over den første brøk. På samme måde divideres LCM med nævneren for den anden brøk, og der opnås en anden yderligere faktor, som er skrevet over den anden brøk.
Brøkerne ganges derefter med deres yderligere faktorer. Som et resultat af disse operationer konverteres brøker, der havde forskellige nævnere, til brøker, der har de samme nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra.
Eksempel 1. Find betydningen af udtrykket:
Disse brøker har forskellige nævnere, så du skal reducere dem til den samme (fælles)nævner.
Først finder vi LCM for nævnerne af begge brøker. Nævneren i den første brøk er tallet 3, og nævneren i den anden brøk er tallet 4. Det mindste fælles multiplum af disse tal er 12
LCM (3 og 4) = 12
Lad os nu vende tilbage til brøker og
Lad os finde en ekstra faktor for den første brøk. For at gøre dette skal du dividere LCM med nævneren af den første brøk. LCM er tallet 12, og nævneren for den første brøk er tallet 3. Divider 12 med 3, vi får 4. Skriv en firer over den første brøk:
Vi gør det samme med den anden brøk. Divider LCM med nævneren af den anden brøk. LCM er tallet 12, og nævneren for den anden brøk er tallet 4. Divider 12 med 4, vi får 3. Skriv en treer over den anden brøk:
Nu er vi klar til subtraktion. Det er tilbage at gange brøkerne med deres yderligere faktorer:

Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde samme nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra. Lad os tage dette eksempel til slutningen:

Vi fik svar
Lad os prøve at skildre vores løsning ved hjælp af en tegning. Hvis du skærer pizza fra en pizza, får du pizza

Dette er den detaljerede version af løsningen. Hvis vi var i skolen, skulle vi løse dette eksempel kortere. En sådan løsning vil se sådan ud:

Reduktion af brøker til en fællesnævner kan også afbildes ved hjælp af et billede. Reducerer disse brøker til en fællesnævner, fik vi brøkerne og . Disse brøker vil være repræsenteret af de samme pizzaskiver, men denne gang vil de blive opdelt i lige store dele (reduceret til samme nævner):

Det første billede viser en brøk (otte stykker ud af tolv), og det andet billede viser en brøk (tre stykker ud af tolv). Ved at skære tre stykker fra otte stykker får vi fem stykker ud af tolv. Brøken beskriver disse fem stykker.
Eksempel 2. Find værdien af et udtryk 
Disse brøker har forskellige nævnere, så først skal du reducere dem til den samme (fælles) nævner.
Lad os finde LCM for nævnerne af disse brøker.
Brøkernes nævnere er tallene 10, 3 og 5. Det mindste fælles multiplum af disse tal er 30
LCM(10; 3; 5) = 30
Nu finder vi yderligere faktorer for hver brøkdel. For at gøre dette skal du dividere LCM med nævneren for hver brøk.
Lad os finde en ekstra faktor for den første brøk. LCM er tallet 30, og nævneren for den første brøk er tallet 10. Divider 30 med 10, vi får den første ekstra faktor 3. Vi skriver den over den første brøk:
Nu finder vi en ekstra faktor for den anden fraktion. Divider LCM med nævneren af den anden brøk. LCM er tallet 30, og nævneren for den anden brøk er tallet 3. Divider 30 med 3, vi får den anden ekstra faktor 10. Vi skriver den over den anden brøk:
Nu finder vi en ekstra faktor for den tredje fraktion. Divider LCM med nævneren af den tredje brøk. LCM er tallet 30, og nævneren for den tredje brøk er tallet 5. Divider 30 med 5, vi får den tredje ekstra faktor 6. Vi skriver den over den tredje brøk:
Nu er alt klar til subtraktion. Det er tilbage at gange brøkerne med deres yderligere faktorer:
Vi kom til den konklusion, at brøker, der havde forskellige nævnere, blev til brøker, der havde de samme (fælles)nævnere. Og vi ved allerede, hvordan man trækker sådanne brøker fra. Lad os afslutte dette eksempel.
Fortsættelsen af eksemplet vil ikke passe på én linje, så vi flytter fortsættelsen til næste linje. Glem ikke lighedstegnet (=) på den nye linje:

Svaret viste sig at være en almindelig brøkdel, og alt ser ud til at passe os, men det er for besværligt og grimt. Vi bør gøre det enklere. Hvad kan gøres? Du kan forkorte denne brøkdel.
For at reducere en brøk skal du dividere dens tæller og nævner med (GCD) af tallene 20 og 30.
Så vi finder gcd af tallene 20 og 30:

Nu vender vi tilbage til vores eksempel og dividerer brøkens tæller og nævner med den fundne gcd, det vil sige med 10

Vi fik svar
At gange en brøk med et tal
For at gange en brøk med et tal, skal du gange brøkens tæller med det tal og lade nævneren være uændret.
Eksempel 1. Gang en brøkdel med tallet 1.
Gang brøkens tæller med tallet 1
![]()
Optagelsen kan forstås som at den tager halv 1 gang. Tager du fx pizza én gang, får du pizza

Fra multiplikationslovene ved vi, at hvis multiplikaden og faktoren byttes om, vil produktet ikke ændre sig. Hvis udtrykket skrives som , så vil produktet stadig være lig med . Igen fungerer reglen for at gange et helt tal og en brøk:
![]()
Denne notation kan forstås som at tage halvdelen af en. For eksempel, hvis der er 1 hel pizza, og vi tager halvdelen af den, så vil vi have pizza:

Eksempel 2. Find værdien af et udtryk
Gang brøkens tæller med 4
![]()
Svaret var en upassende brøk. Lad os fremhæve hele delen af det:
![]()
Udtrykket kan forstås som at det tager to kvarter 4 gange. Tager du for eksempel 4 pizzaer, får du to hele pizzaer

Og hvis vi bytter multiplikanten og multiplikatoren, får vi udtrykket . Det vil også være lig med 2. Dette udtryk kan forstås som at tage to pizzaer fra fire hele pizzaer:

Tallet ganges med brøken og nævneren for brøken opløses, hvis de har en fælles faktor større end én.
For eksempel kan et udtryk evalueres på to måder.
Første vej. Gang tallet 4 med brøkens tæller, og lad brøkens nævner være uændret:
![]()
Anden vej. De fire ganges og de fire i brøkens nævner kan reduceres. Disse firere kan reduceres med 4, da den største fælles divisor for to firere er de fire selv:

Vi fik det samme resultat 3. Efter at have reduceret firerne, dannes der nye tal i deres sted: to enere. Men at gange en med tre og derefter dividere med en ændrer ikke noget. Derfor kan løsningen kort skrives:
Reduktionen kan udføres, selv når vi besluttede at bruge den første metode, men på tidspunktet for at gange tallet 4 og tælleren 3 besluttede vi at bruge reduktionen:

Men for eksempel kan udtrykket kun beregnes på den første måde - gange 7 med nævneren af brøken, og lad nævneren være uændret:
![]()
Dette skyldes, at tallet 7 og brøkens nævner ikke har en fælles divisor, der er større end én, og derfor ikke annullerer.
Nogle elever forkorter fejlagtigt tallet, der ganges, og tælleren for brøken. Du kan ikke gøre dette. For eksempel er følgende indtastning ikke korrekt:
At reducere en brøk betyder det både tæller og nævner vil blive divideret med det samme tal. I situationen med udtrykket udføres division kun i tælleren, da at skrive dette er det samme som at skrive . Vi ser, at division kun udføres i tælleren, og der sker ingen division i nævneren.
Multiplikation af brøker
For at gange brøker skal du gange deres tællere og nævnere. Hvis svaret viser sig at være en ukorrekt brøkdel, skal du fremhæve hele den del af det.
Eksempel 1. Find værdien af udtrykket.
![]()
Vi fik svar. Det er tilrådeligt at reducere denne fraktion. Fraktionen kan reduceres med 2. Så vil den endelige opløsning have følgende form:

Udtrykket kan forstås som at tage en pizza fra en halv pizza. Lad os sige, at vi har en halv pizza:
Hvordan tager man to tredjedele fra denne halvdel? Først skal du dele denne halvdel i tre lige store dele:

Og tag to fra disse tre stykker:

Vi laver pizza. Husk hvordan pizza ser ud, når den er opdelt i tre dele:

Et stykke af denne pizza og de to stykker, vi tog, vil have samme dimensioner:

Vi taler med andre ord om pizza af samme størrelse. Derfor er værdien af udtrykket

Eksempel 2. Find værdien af et udtryk
Multiplicer tælleren for den første brøk med tælleren i den anden brøk og nævneren for den første brøk med nævneren i den anden brøk:

Svaret var en upassende brøk. Lad os fremhæve hele delen af det:
![]()
Eksempel 3. Find værdien af et udtryk
Multiplicer tælleren for den første brøk med tælleren i den anden brøk og nævneren for den første brøk med nævneren i den anden brøk:
![]()
Svaret viste sig at være en almindelig brøk, men det ville være godt, hvis det blev forkortet. For at reducere denne brøk skal du dividere tælleren og nævneren for denne brøk med den største fælles divisor (GCD) af tallene 105 og 450.
Så lad os finde gcd'en for tallene 105 og 450:

Nu dividerer vi tælleren og nævneren for vores svar med den gcd, som vi nu har fundet, det vil sige med 15
Repræsenterer et helt tal som en brøk
Ethvert helt tal kan repræsenteres som en brøk. For eksempel kan tallet 5 repræsenteres som . Dette vil ikke ændre betydningen af fem, da udtrykket betyder "tallet fem divideret med en", og dette er, som vi ved, lig med fem:
Gensidige tal
Nu vil vi stifte bekendtskab med et meget interessant emne i matematik. Det kaldes "omvendte tal".
Definition. Vend til nummer-en er et tal, der ganges med-en giver en.
Lad os erstatte i denne definition i stedet for variablen -en nummer 5 og prøv at læse definitionen:
Vend til nummer 5 er et tal, der ganges med 5 giver en.
Er det muligt at finde et tal, der, når det ganges med 5, giver et? Det viser sig, at det er muligt. Lad os forestille os fem som en brøk:
Derefter ganges denne brøk med sig selv, bare skift tæller og nævner. Med andre ord, lad os gange brøken med sig selv, kun på hovedet:
Hvad vil der ske som følge af dette? Hvis vi fortsætter med at løse dette eksempel, får vi et:
![]()
Det betyder, at det omvendte af tallet 5 er tallet, da når du gange 5 med, får du en.
Den reciproke af et tal kan også findes for ethvert andet heltal.
Du kan også finde den reciproke af enhver anden brøk. For at gøre dette skal du bare vende den om.
At dividere en brøk med et tal
Lad os sige, at vi har en halv pizza:
Lad os dele det ligeligt mellem to. Hvor meget pizza får hver person?

Det kan ses, at man efter at have delt halvdelen af pizzaen opnåede to lige store stykker, som hver udgør en pizza. Så alle får en pizza.
