Afledt af 0,5. Første ordre derivat online

Opret et forhold og beregn grænsen.

Hvor kom det fra? tabel over derivater og differentieringsregler? Takket være den eneste grænse. Det virker som magi, men i virkeligheden er det svig og ingen svindel. Ved lektionen Hvad er et derivat? Jeg begyndte at se på specifikke eksempler, hvor jeg ved hjælp af definitionen fandt de afledte af en lineær og kvadratisk funktion. Med henblik på kognitiv opvarmning vil vi fortsætte med at forstyrre tabel over derivater, finpudsning af algoritmen og tekniske løsninger:

Eksempel 1

I det væsentlige skal du bevise et særligt tilfælde af den afledede af en potensfunktion, som normalt vises i tabellen: .

Løsning teknisk formaliseret på to måder. Lad os starte med den første, allerede velkendte tilgang: stigen starter med en planke, og den afledede funktion starter med den afledede på et punkt.

Lad os overveje nogle(specifikt) punkt, der hører til definitionsdomæne funktion, hvori der er en afledt. Lad os indstille stigningen på dette tidspunkt (selvfølgelig inden for rammerneo/o -JEG) og komponer den tilsvarende stigning af funktionen:

Lad os beregne grænsen:

Usikkerheden 0:0 elimineres ved en standardteknik, der betragtes tilbage i det første århundrede f.Kr. Gang tælleren og nævneren med det konjugerede udtryk :

Teknikken til at løse en sådan grænse er diskuteret i detaljer i den indledende lektion. om grænserne for funktioner.

Da du kan vælge et hvilket som helst punkt i intervallet som kvalitet, får vi, efter at have foretaget udskiftningen:

Svar

Lad os endnu en gang glæde os over logaritmer:

Eksempel 2

Find den afledede af en funktion ved at bruge definitionen af ​​afledet

Løsning: Lad os overveje en anden tilgang til at fremme den samme opgave. Det er præcis det samme, men mere rationelt designmæssigt. Ideen er at slippe af med subscriptet i begyndelsen af ​​løsningen og bruge bogstavet i stedet for bogstavet.

Lad os overveje vilkårlig punkt, der hører til definitionsdomæne funktion (interval) og indstil stigningen i den. Men her kan du i øvrigt, som i de fleste tilfælde, klare dig uden forbehold, da den logaritmiske funktion er differentierbar på ethvert punkt i definitionsdomænet.

Så er den tilsvarende stigning af funktionen:

Lad os finde den afledede:

Designets enkelhed afbalanceres af den forvirring, der kan opstå for begyndere (og ikke kun). Vi er jo vant til, at bogstavet "X" ændrer sig i grænsen! Men her er alt anderledes: - en antik statue, og - en levende gæst, der rask går langs museets korridor. Det vil sige, "x" er "som en konstant."

Jeg vil kommentere fjernelse af usikkerhed trin for trin:

(1) Vi bruger egenskaben for logaritmen.

(2) I parentes divideres tælleren med nævneren led for led.

(3) I nævneren multiplicerer og dividerer vi kunstigt med "x" for at drage fordel af bemærkelsesværdig grænse , mens som uendelig lille skiller sig ud.

Svar: per definition af afledt:

Eller kort sagt:

Jeg foreslår at konstruere yderligere to tabelformler selv:

Eksempel 3

I dette tilfælde er det bekvemt straks at reducere den kompilerede stigning til en fællesnævner. Et omtrentligt udsnit af opgaven i slutningen af ​​lektionen (første metode).

Eksempel 3:Løsning : overveje et punkt , der tilhører funktionens definitionsdomæne . Lad os indstille stigningen på dette tidspunkt og komponer den tilsvarende stigning af funktionen:

Lad os finde den afledede på punktet :

Siden som en du kan vælge et hvilket som helst punkt funktionsdomæne , At Og
Svar : per definition af afledt

Eksempel 4

Find afledt per definition

Og her skal alt reduceres til vidunderlig grænse. Løsningen formaliseres på den anden måde.

En række andre tabelformede derivater. Den komplette liste findes i skolelærebogen, eller fx 1. bind af Fichtenholtz. Jeg ser ikke meget mening i at kopiere beviser for differentieringsregler fra bøger - de genereres også af formlen.

Eksempel 4:Løsning , tilhører , og indstil stigningen i den

Lad os finde den afledede:

Bruger en vidunderlig grænse

Svar : a-priory

Eksempel 5

Find den afledede af en funktion ved at bruge definitionen af ​​afledet

Løsning: vi bruger den første designstil. Lad os overveje et punkt, der hører til , og specificere stigningen i argumentet ved det. Så er den tilsvarende stigning af funktionen:

Måske har nogle læsere endnu ikke fuldt ud forstået princippet, hvormed stigninger skal foretages. Tag et punkt (tal) og find værdien af ​​funktionen i det: , altså ind i funktionen i stedet for"X" skal erstattes. Nu tager vi også et meget specifikt tal og erstatter det også i funktionen i stedet for"iksa": . Vi skriver forskellen ned, og det er nødvendigt sat helt i parentes.

Kompileret funktionstilvækst Det kan være en fordel umiddelbart at forenkle. For hvad? Letter og forkort løsningen til en yderligere grænse.

Vi bruger formler, åbner parenteserne og reducerer alt, der kan reduceres:

Kalkunen er renset, intet problem med stegen:

Da vi kan vælge et hvilket som helst reelt tal som værdi, foretager vi udskiftningen og får .

Svar: a-priory.

Til verifikationsformål, lad os finde derivatet ved hjælp af differentieringsregler og tabeller:

Det er altid nyttigt og behageligt at kende det rigtige svar på forhånd, så det er bedre at differentiere den foreslåede funktion på en "hurtig" måde, enten mentalt eller i et udkast, helt i begyndelsen af ​​løsningen.

Eksempel 6

Find den afledede af en funktion ved definition af afledet

Dette er et eksempel, som du kan løse på egen hånd. Resultatet er indlysende:

Eksempel 6:Løsning : overveje et punkt , tilhører , og indstil stigningen af ​​argumentet i den . Så er den tilsvarende stigning af funktionen:


Lad os beregne den afledede:


Dermed:
Fordi som så kan du vælge et hvilket som helst reelt tal Og
Svar : a-priory.

Lad os gå tilbage til stil #2:

Eksempel 7

Lad os straks finde ud af, hvad der skal ske. Ved regel for differentiering af komplekse funktioner:

Løsning: overvej et vilkårligt punkt, der tilhører , sæt stigningen af ​​argumentet på det og komponer stigningen af ​​funktionen:

Lad os finde den afledede:


(1) Brug trigonometrisk formel .

(2) Under sinus åbner vi parenteserne, under cosinus præsenterer vi lignende udtryk.

(3) Under sinus reducerer vi led, under cosinus dividerer vi tælleren med nævneren led for led.

(4) På grund af sinusens mærkværdighed fjerner vi "minus". Under cosinus angiver vi, at udtrykket .

(5) Vi udfører kunstig multiplikation i nævneren for at bruge første vidunderlige grænse. Dermed er usikkerheden elimineret, lad os rydde op i resultatet.

Svar: a-priory

Som du kan se, hviler hovedvanskeligheden ved det undersøgte problem på kompleksiteten af ​​selve grænsen + en lille unikhed ved emballagen. I praksis forekommer begge designmetoder, så jeg beskriver begge tilgange så detaljeret som muligt. De er ækvivalente, men alligevel, efter mit subjektive indtryk, er det mere tilrådeligt for dummies at holde sig til mulighed 1 med "X-nul".

Eksempel 8

Brug definitionen til at finde den afledede af funktionen

Eksempel 8:Løsning : overveje et vilkårligt punkt , tilhører , lad os indstille stigningen i den og komponer tilvæksten af ​​funktionen:

Lad os finde den afledede:

Vi bruger den trigonometriske formel og den første bemærkelsesværdige grænse:


Svar : a-priory

Lad os se på en sjældnere version af problemet:

Eksempel 9

Find den afledede af funktionen i punktet ved at bruge definitionen af ​​afledet.

For det første, hvad skal bundlinjen være? Nummer

Lad os beregne svaret på standardmåden:

Løsning: fra et klarhedssynspunkt er denne opgave meget enklere, da formlen i stedet overvejer en bestemt værdi.

Lad os sætte stigningen til punktet og sammensætte den tilsvarende stigning i funktionen:

Lad os beregne den afledede på punktet:

Vi bruger en meget sjælden tangentforskelformel og endnu en gang reducerer vi løsningen til den første vidunderlige grænse:

Svar: per definition af afledt ved et punkt.

Problemet er ikke så svært at løse "generelt" - det er nok at erstatte med eller simpelthen afhængigt af designmetoden. I dette tilfælde er det klart, at resultatet ikke bliver et tal, men en afledt funktion.

Eksempel 10

Brug definitionen til at finde den afledede af funktionen på et punkt (hvoraf det ene kan vise sig at være uendeligt), som jeg allerede har beskrevet i generelle vendinger om teoretisk lektion om afledte.

Nogle stykkevis givne funktioner kan også differentieres ved grafens "krydsningspunkter", f.eks. har catdog en fælles afledet og en fælles tangent (x-akse) i punktet. Kurve, men differentierbar med ! Interesserede kan selv bekræfte dette ved at bruge det netop løste eksempel.

©2015-2019 websted
Alle rettigheder tilhører deres forfattere. Dette websted gør ikke krav på forfatterskab, men giver gratis brug.
Sidens oprettelsesdato: 2017-06-11

Artiklens indhold

AFLEDTE– afledt af funktionen y = f(x), givet med et bestemt interval ( -en, b) på et tidspunkt x af dette interval kaldes den grænse, hvortil forholdet mellem funktionens tilvækst tenderer f på dette tidspunkt til den tilsvarende stigning af argumentet, når stigningen af ​​argumentet har en tendens til nul.

Den afledte betegnes normalt som følger:

Andre betegnelser er også meget brugt:

Øjeblikkelig hastighed.

Lad pointen M bevæger sig i en lige linje. Afstand s bevægende punkt, tællet fra en udgangsposition M 0 , afhænger af tid t, dvs. s der er en funktion af tiden t: s= f(t). Lad på et tidspunkt t bevægende punkt M var på afstand s fra startpositionen M 0, og på et eller andet tidspunkt t+D t befandt sig i en position M 1 - på afstand s+D s fra startpositionen ( se billede.).

Således over en periode D t afstand sændret med beløbet D s. I dette tilfælde siger de, at i tidsintervallet D t størrelse s modtog tillæg D s.

Gennemsnitshastigheden kan ikke i alle tilfælde nøjagtigt karakterisere et punkts bevægelseshastighed M på et tidspunkt t. Hvis for eksempel kroppen i begyndelsen af ​​intervallet D t bevæget sig meget hurtigt, og til sidst meget langsomt, så vil gennemsnitshastigheden ikke være i stand til at afspejle de angivne træk ved punktets bevægelse og give en idé om den sande hastighed af dets bevægelse i øjeblikket t. For mere præcist at udtrykke den sande hastighed ved hjælp af gennemsnitshastigheden, skal du tage en kortere periode D t. Karakteriserer mest fuldt ud bevægelseshastigheden af ​​et punkt i øjeblikket t grænsen, til hvilken gennemsnitshastigheden tenderer ved D t® 0. Denne grænse kaldes den aktuelle hastighed:

Bevægelseshastigheden på et givet tidspunkt kaldes således grænsen for stitilvækstforholdet D s til tidsforøgelse D t, når tidsstigningen har en tendens til nul. Fordi

Geometrisk betydning af derivatet. Tangent til grafen for en funktion.

Konstruktionen af ​​tangentlinjer er et af de problemer, der førte til fødslen af ​​differentialregning. Det første publicerede arbejde relateret til differentialregning, skrevet af Leibniz, havde titlen En ny metode til maksima og minima, samt tangenter, for hvilke hverken brøk- eller irrationelle størrelser er en hindring, og en speciel form for beregning for dette.

Lad kurven være grafen for funktionen y =f(x) i et rektangulært koordinatsystem ( cm. ris.).

Til en vis værdi x funktion betyder noget y =f(x). Disse værdier x Og y punktet på kurven svarer M 0(x, y). Hvis argumentet x give stigning D x, derefter den nye værdi af argumentet x+D x svarer til den nye funktionsværdi y+ D y = f(x + D x). Det tilsvarende punkt på kurven vil være punktet M 1(x+D x,y+D y). Hvis du tegner en sekant M 0M 1 og betegnet med j vinklen dannet af en tværgående med aksens positive retning Okse, det fremgår umiddelbart af figuren, at .

Hvis nu D x har en tendens til nul, derefter punktet M 1 bevæger sig langs kurven og nærmer sig punktet M 0, og vinkel j ændres med D x. På Dx® 0 hælder vinklen j til en vis grænse a og den rette linje, der går gennem punktet M 0 og komponenten med x-aksens positive retning, vinkel a, vil være den ønskede tangent. Dens hældning er:

Derfor, f´( x) = tga

de der. afledt værdi f´( x) for en given argumentværdi x er lig med tangenten til den vinkel, der dannes af tangenten til grafen for funktionen f(x) på det tilsvarende punkt M 0(x,y) med positiv akseretning Okse.

Funktionernes differentierbarhed.

Definition. Hvis funktionen y = f(x) har en afledt ved punktet x = x 0, så er funktionen differentierbar på dette tidspunkt.

Kontinuitet af en funktion med en afledt. Sætning.

Hvis funktionen y = f(x) er differentierbar på et tidspunkt x = x 0, så er den kontinuerlig på dette tidspunkt.

Funktionen kan således ikke have en afledt ved diskontinuitetspunkter. Den modsatte konklusion er forkert, dvs. fra det faktum, at på et tidspunkt x = x 0 funktion y = f(x) er kontinuert betyder ikke, at den er differentierbar på dette tidspunkt. For eksempel funktionen y = |x| løbende for alle x(–Ґ x x = 0 har ingen afledet. På dette tidspunkt er der ingen tangent til grafen. Der er en højre tangent og en venstre tangent, men de falder ikke sammen.

Nogle teoremer om differentiable funktioner. Sætning om rødderne af den afledte (Rolles sætning). Hvis funktionen f(x) er kontinuerlig på segmentet [-en,b], er differentierbar ved alle indvendige punkter i dette segment og i enderne x = -en Og x = b går til nul ( f(-en) = f(b) = 0), derefter inde i segmentet [ -en,b] der er mindst ét ​​punkt x= Med, -en c b, hvori den afledte fў( x) går til nul, dvs. fў( c) = 0.

Finite inkrementsætning (Lagranges sætning). Hvis funktionen f(x) er kontinuerlig i intervallet [ -en, b] og kan differentieres ved alle indvendige punkter i dette segment, derefter inde i segmentet [ -en, b] der er mindst ét ​​punkt Med, -en c b det

f(b) – f(-en) = fў( c)(b– -en).

Sætning om forholdet mellem to funktioners inkrementer (Cauchys sætning). Hvis f(x) Og g(x) – to funktioner kontinuerligt på segmentet [-en, b] og differentierbar på alle indvendige punkter i dette segment, og gў( x) forsvinder ikke nogen steder i dette segment, derefter inde i segmentet [ -en, b] der er sådan en pointe x = Med, -en c b det

Afledte af forskellige ordrer.

Lad funktionen y =f(x) er differentierbar på et eller andet interval [ -en, b]. Afledte værdier f ў( x), generelt afhænge af x, dvs. afledte f ў( x) er også en funktion af x. Når vi differentierer denne funktion, får vi den såkaldte anden afledede af funktionen f(x), som er angivet f ўў ( x).

Afledte n- funktionsrækkefølge f(x) kaldes (første ordens) afledt af den afledte n- 1- th og er angivet med symbolet y(n) = (y(n– 1))ў.

Differentialer i forskellige rækkefølger.

Funktionsdifferential y = f(x), Hvor x– uafhængig variabel, ja D y = f ў( x)dx, en eller anden funktion fra x, men fra x kun den første faktor kan afhænge f ў( x), den anden faktor ( dx) er stigningen af ​​den uafhængige variabel x og afhænger ikke af værdien af ​​denne variabel. Fordi D y der er en funktion fra x, så kan vi bestemme differentialet for denne funktion. Differentialet af differentialet for en funktion kaldes den anden differential eller andenordens differential af denne funktion og betegnes d 2y:

d(dx) = d 2y = f ўў( x)(dx) 2 .

Differential n- af første orden kaldes differentialets første differentiale n- 1- orden:

d n y = d(d n–1y) = f(n)(x)dx(n).

Delvis afledt.

Hvis en funktion ikke afhænger af én, men af ​​flere argumenter x i(jeg varierer fra 1 til n,jeg= 1, 2,… n),f(x 1,x 2,… x n), så introduceres i differentialregning begrebet partiel afledt, som karakteriserer ændringshastigheden af ​​en funktion af flere variable, når kun ét argument ændres, f.eks. x i. 1. ordens partiel afledt mhp x i defineres som en almindelig afledt, og det antages, at alle argumenter undtagen x i, hold konstante værdier. For partielle afledte er notationen indført

1. ordens partielle afledninger defineret på denne måde (som funktioner af de samme argumenter) kan til gengæld også have partielle afledte, disse er andenordens partielle afledte osv. Sådanne derivater taget fra forskellige argumenter kaldes blandede. Kontinuerlige blandede derivater af samme orden afhænger ikke af rækkefølgen af ​​differentiering og er ens med hinanden.

Anna Chugainova

Lad funktionen y = f(x) defineres i intervallet X. Afledte funktion y = f(x) i punkt x o kaldes grænsen

= .

Hvis denne grænse begrænset, så kaldes funktionen f(x). differentierbar på punktet x o; Desuden viser det sig nødvendigvis at være kontinuerligt på dette tidspunkt.

Hvis den betragtede grænse er lig med  (eller - ), så forudsat at funktionen i punktet x o er kontinuert, vil vi sige, at funktionen f(x) har ved punktet x o uendelig afledt.

Den afledte er angivet med symbolerne

y , f (x o), , .

At finde den afledede kaldes differentiering funktioner. Geometrisk betydning af afledte er, at den afledede er hældningen af ​​tangenten til kurven y=f(x) i et givet punkt x o ; fysisk betydning - er, at den afledede af stien med hensyn til tid er den øjeblikkelige hastighed af et bevægende punkt under retlinet bevægelse s = s(t) i øjeblikket t o .

Hvis Med er et konstant tal, og u = u(x), v = v(x) er nogle differentiable funktioner, så er følgende differentieringsregler gyldige:

1) (c) " = 0, (cu) " = cu";

2) (u+v)" = u"+v";

3) (uv)" = u"v+v"u;

4) (u/v)" = (u"v-v"u)/v 2;

5) hvis y = f(u), u = (x), dvs. y = f((x)) - kompleks funktion eller superposition, sammensat af differentiable funktioner  og f, derefter , eller

6) hvis der for en funktion y = f(x) er en invers differentierbar funktion x = g(y), og  0, så .

Baseret på definitionen af ​​den afledede og reglerne for differentiering er det muligt at udarbejde en liste over tabelformede afledte af de vigtigste elementære funktioner.

1. (u )" =  u  1 u" (  R).

2. (a u)" = a u lna u".

3. (e u)" = e u u".

4. (log a u)" = u"/(u ln a).

5. (ln u)" = u"/u.

6. (sin u)" = cos u u".

7. (cos u)" = - sin u u".

8. (tg u)" = 1/ cos 2 u u".

9. (ctg u)" = - u" / sin 2 u.

10. (arcsin u)" = u" / .

11. (arccos u)" = - u" / .

12. (arctg u)" = u"/(1 + u 2).

13. (arcctg u)" = - u"/(1 + u 2).

Lad os beregne den afledede af det potenseksponentielle udtryk y=u v , (u>0), hvor u Og v essensen af ​​funktionen fra x, der har derivater på et givet punkt u",v".

Tager vi logaritmer af ligheden y=u v, får vi ln y = v ln u.

Ligestilling af afledte mhp x fra begge sider af den resulterende lighed ved at bruge reglerne 3, 5 og formlen for den afledede af en logaritmisk funktion, vil vi have:

y"/y = vu"/u +v" ln u, hvorfra y" = y (vu"/u +v" ln u).

(u v)"=u v (vu"/u+v" ln u), u > 0.

For eksempel, hvis y = x sin x, så er y" = x sin x (sin x/x + cos x ln x).

Hvis funktionen y = f(x) er differentiabel i punktet x, dvs. har en endelig afledt på dette tidspunkt y", så = y"+, hvor 0 ved х 0; derfor  y = y" х +  x.

Hoveddelen af ​​funktionen inkrement, lineær i forhold til x, kaldes differential funktioner og betegnes med dy: dy = y" х. Hvis vi sætter y=x i denne formel, får vi dx = x"х = 1х =х, derfor dy=y"dx, altså symbolet for Den afledte notation kan opfattes som en brøk.

Funktionsstigning  y er tilvæksten af ​​ordinaten af ​​kurven og differentialet d y er ordinattilvæksten af ​​tangenten.

Lad os finde for funktionen y=f(x) dens afledte y = f (x). Den afledte af denne afledte kaldes anden ordens afledte funktioner f(x), eller anden afledte, og er udpeget .

Følgende er defineret og betegnet på samme måde:

tredje ordens afledte - ,

fjerde ordens afledte -

og generelt set n. ordens afledte - .

Eksempel 3.15. Beregn den afledede af funktionen y=(3x 3 -2x+1)sin x.

Løsning. Ved regel 3, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1) cos x.

Eksempel 3.16 . Find y", y = tan x + .

Løsning. Ved at bruge reglerne for at differentiere summen og kvotienten får vi: y"=(tgx + )" = (tgx)" + ()" = + = .

Eksempel 3.17. Find den afledede af den komplekse funktion y= , u=x 4 +1.

Løsning. Ifølge reglen om differentiering af en kompleks funktion får vi: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. Da u=x 4 +1, så (2 x 4 + 2+ .

Ansøgning

Løsning af derivatet på webstedet for at konsolidere det materiale, der er dækket af studerende og skolebørn. At beregne den afledede af en funktion på få sekunder virker ikke svært, hvis du bruger vores online problemløsningstjeneste. Hver tredje studerende vil være i stand til at give en detaljeret analyse til en grundig undersøgelse i løbet af en praktisk lektion. Vi bliver ofte kontaktet af afdelingen for den relevante afdeling til fremme af matematik i landets uddannelsesinstitutioner. Hvordan kan vi i dette tilfælde ikke nævne at løse den afledte online for et lukket rum af talsekvenser? Mange velhavende individer får lov til at udtrykke deres forvirring. Men i mellemtiden sidder matematikere ikke stille og arbejder meget. Den afledte regnemaskine vil acceptere ændringer i inputparametre baseret på lineære karakteristika, hovedsageligt på grund af det højeste af de faldende positioner af kuberne. Resultatet er lige så uundgåeligt som overfladen. Som indledende data eliminerer online derivater behovet for at tage unødvendige skridt. Bortset fra fiktivt husarbejde. Ud over det faktum, at løsning af derivater online er et nødvendigt og vigtigt aspekt ved at lære matematik, husker eleverne ofte ikke tidligere problemer. Eleven, der er en doven skabning, forstår dette. Men studerende er sjove mennesker! Gør det enten i henhold til reglerne, eller også kan den afledede funktion i et skråplan give acceleration til et materialepunkt. Lad os rette vektoren af ​​den nedadgående rumlige stråle et eller andet sted. I det krævede svar synes det at finde den afledede at være en abstrakt teoretisk retning på grund af det matematiske systems ustabilitet. Lad os tænke på en talrelation som en sekvens af ubrugte muligheder. Kommunikationskanalen blev genopfyldt med en femte linje langs en aftagende vektor fra punktet for den lukkede bifurkation af kuben. På planet af buede rum fører løsning af den afledte online os til en konklusion, der fik de største hjerner på planeten til at tænke over det i det sidste århundrede. I løbet af begivenhederne inden for matematikområdet blev fem fundamentalt vigtige faktorer bragt til offentlig diskussion, der bidrager til at forbedre positionen for variabelselektion. Så loven for point siger, at online-derivatet ikke beregnes i detaljer i alle tilfælde, den eneste undtagelse er et loyalt progressivt øjeblik. Udsigten bragte os til et nyt udviklingstrin. Vi har brug for resultater. I linjen med den matematiske hældning, der passerer under overfladen, er den afledte modusberegner placeret i skæringsområdet for produkterne på bøjningssættet. Det er tilbage at analysere differentieringen af ​​funktionen på dens uafhængige punkt nær epsilon-kvarteret. Alle kan verificere dette i praksis. Som følge heraf vil der være noget at tage stilling til i den næste fase af programmeringen. Den studerende har som altid brug for den online afledte, uanset den imaginære forskning, der praktiseres. Det viser sig, at løsningen af ​​den afledte online multipliceret med en konstant ikke ændrer den generelle bevægelsesretning af materialets punkt, men karakteriserer stigningen i hastighed langs en lige linje. I denne forstand vil det være nyttigt at bruge vores afledte lommeregner og beregne alle værdierne af funktionen på hele sættet af dens definition. Der er ingen grund til at studere tyngdefeltets kraftbølger. I intet tilfælde vil løsning af derivater online vise tilbøjeligheden af ​​den udgående stråle, men kun i sjældne tilfælde, når dette virkelig er nødvendigt, kan universitetsstuderende forestille sig dette. Lad os undersøge rektor. Værdien af ​​den mindste rotor er forudsigelig. Anvend på resultatet af linjer, der ser til højre, langs hvilke bolden er beskrevet, men online-afledte regnemaskine er grundlaget for tal for særlig styrke og ikke-lineær afhængighed. Matematikprojektrapporten er klar. Personlige egenskaber: Forskellen mellem de mindste tal og den afledte funktion af en funktion langs ordinataksen vil bringe konkaviteten af ​​den samme funktion til højden. Der er en retning - der er en konklusion. Det er nemmere at omsætte teori i praksis. De studerende har et forslag til tidspunktet for studiestart. Har brug for en lærers svar. Igen, som med den tidligere position, er det matematiske system ikke reguleret ud fra en handling, der vil hjælpe med at finde den afledede. Ligesom den nederste semi-lineære version, vil den online afledede detaljeret angive identifikationen af ​​løsningen iht. degenereret betinget lov. Ideen om at beregne formler er netop blevet fremsat. Lineær differentiering af en funktion afleder sandheden af ​​løsningen til blot at udlægge irrelevante positive variationer. Betydningen af ​​sammenligningstegn vil blive betragtet som et kontinuerligt brud i funktionen langs aksen. Det er vigtigheden af ​​den mest bevidste konklusion, ifølge den studerende, hvor den online afledte er noget andet end et loyalt eksempel på matematisk analyse. Radius af en buet cirkel i det euklidiske rum gav tværtimod derivatberegneren en naturlig repræsentation af udvekslingen af ​​afgørende problemer for stabilitet. Den bedste metode er fundet. Det var nemmere at flytte opgaven et niveau op. Lad anvendeligheden af ​​den uafhængige forskelsproportion føre til løsningen af ​​derivaterne online. Opløsningen roterer rundt om abscisseaksen og beskriver figuren af ​​en cirkel. Der er en vej ud, og den er baseret på teoretisk understøttet forskning fra universitetsstuderende, som alle studerer fra, og selv på de tidspunkter er der en afledning af funktionen. Vi fandt en vej til fremskridt, og eleverne bekræftede det. Vi har råd til at finde den afledede uden at gå ud over den unaturlige tilgang til at transformere det matematiske system. Det venstre proportionalitetstegn vokser med geometrisk sekvens som en matematisk repræsentation af en online afledt regnemaskine på grund af den ukendte omstændighed af lineære faktorer på den uendelige y-akse. Matematikere over hele verden har bevist produktionsprocessens exceptionelle karakter. Der er en mindste firkant inde i en cirkel ifølge teoriens beskrivelse. Igen vil online-derivatet i detaljer udtrykke vores antagelse om, hvad der kunne påvirke den teoretisk raffinerede mening i første omgang. Der var meninger af en anden karakter end den analyserede rapport, vi leverede. Særlig opmærksomhed sker måske ikke for studerende på vores fakulteter, men ikke for kloge og teknologisk avancerede matematikere, for hvem differentiering af en funktion kun er en undskyldning. Den mekaniske betydning af derivatet er meget enkel. Løftekraften beregnes som den online afledte for opadgående stabile rum i tid. Den åbenlyst afledte lommeregner er en streng proces til at beskrive problemet med degenerationen af ​​en kunstig transformation som et amorft legeme. Den første afledede angiver en ændring i bevægelsen af ​​et materielt punkt. Tredimensionelt rum observeres naturligvis i sammenhæng med specialtrænede teknologier til at løse derivater online; faktisk er dette i ethvert kollokvium om emnet en matematisk disciplin. Den anden afledede karakteriserer ændringen i hastigheden af ​​et materialepunkt og bestemmer accelerationen. Meridiantilgangen baseret på brugen af ​​affin transformation tager derivatet af en funktion på et punkt fra definitionsdomænet for denne funktion til et nyt niveau. En online afledt regnemaskine kan ikke eksistere uden tal og symbolske notationer i nogle tilfælde for det rigtige eksekverbare øjeblik, ud over den transformerbare opstilling af tingene i opgaven. Overraskende nok er der en anden acceleration af materialepunktet; dette karakteriserer ændringen i acceleration. Om kort tid vil vi begynde at studere at løse den afledte online, men så snart en vis milepæl i viden er nået, vil vores studerende sætte denne proces på pause. Den bedste måde at etablere kontakter på er at kommunikere live om et matematisk emne. Der er principper, som ikke under nogen omstændigheder kan overtrædes, uanset hvor vanskelig opgaven er. Det er nyttigt at finde den afledte online til tiden og uden fejl. Dette vil føre til en ny placering af det matematiske udtryk. Systemet er stabilt. Den fysiske betydning af derivatet er ikke så populær som den mekaniske. Det er usandsynligt, at nogen husker, hvordan den online-afledte viste i detaljer på planet omridset af funktionens linjer i normalen fra trekanten ved siden af ​​abscisseaksen. Mennesket fortjener en stor rolle i det sidste århundredes forskning. Lad os differentiere funktionen på punkter både fra definitionsdomænet og ved uendeligheden i tre elementære stadier. Det vil være i skriftlig form kun inden for forskningsområdet, men det kan træde i stedet for hovedvektoren i matematik og talteori, så snart det, der sker, forbinder den online afledte lommeregner med problemet. Hvis der var en grund, ville der være en grund til at lave en ligning. Det er meget vigtigt at have alle inputparametre i tankerne. Det bedste accepteres ikke altid frontalt; bag dette ligger et kolossalt antal af de bedst arbejdende hjerner, som vidste, hvordan online-derivatet beregnes i rummet. Siden da er konveksitet blevet betragtet som en egenskab ved en kontinuerlig funktion. Alligevel er det bedre først at sætte opgaven med at løse derivater online på kortest mulig tid. Dermed vil løsningen være komplet. Bortset fra uopfyldte standarder anses dette ikke for tilstrækkeligt. Indledningsvis foreslår næsten hver elev at fremlægge en simpel metode til, hvordan den afledede af en funktion forårsager en kontroversiel forstærkningsalgoritme. I retning af den stigende stråle. Dette giver mening som et generelt forslag. Tidligere markerede vi begyndelsen på afslutningen af ​​en specifik matematisk operation, men i dag bliver det omvendt. Måske vil løsning af den afledte online rejse spørgsmålet igen, og vi vil vedtage en fælles holdning for at bevare den under diskussionen på lærermødet. Vi håber på forståelse fra alle sider af mødedeltagerne. Den logiske betydning ligger i beskrivelsen af ​​den afledte regnemaskine i resonansen af ​​tal om rækkefølgen af ​​præsentationen af ​​tanken om problemet, som blev besvaret i det sidste århundrede af verdens store videnskabsmænd. Det vil hjælpe dig med at udtrække en kompleks variabel fra et transformeret udtryk og finde den afledte online for at udføre en massiv handling af samme type. Sandheden er mange gange bedre end gæt. Laveste værdi i trend. Resultatet vil ikke vente længe på sig, når du bruger en unik service til præcis bestemmelse, som der er en essens af afledte online i detaljer for. Indirekte, men til det punkt, som en klog mand sagde, blev en online derivatberegner oprettet efter anmodning fra mange studerende fra forskellige byer i fagforeningen. Hvis der er en forskel, hvorfor så beslutte to gange. Den givne vektor ligger på samme side som normalen. I midten af ​​forrige århundrede opfattede man slet ikke funktionsdifferentiering, som den er i dag. Takket være den igangværende udvikling dukkede online matematik op. Med tiden glemmer eleverne at give behørig merit til matematikfag. Løsning af den afledte online vil udfordre vores afhandling med rette baseret på anvendelsen af ​​teori understøttet af praktisk viden. Det vil gå ud over den eksisterende værdi af præsentationsfaktoren, og vi vil skrive formlen i en eksplicit form for funktionen. Det sker, at du straks skal finde et derivat online uden at bruge nogen lommeregner, men du kan altid ty til en studerendes trick og stadig bruge en tjeneste som et websted. Eleven vil således spare meget tid på at kopiere eksempler fra den grove notesbog til den endelige form. Hvis der ikke er nogen modsætninger, så brug trin-for-trin-tjenesten til at løse sådanne komplekse eksempler.

Den afledte er det vigtigste begreb i matematisk analyse. Det karakteriserer ændringen i argumentets funktion x på et tidspunkt. Desuden er den afledede i sig selv en funktion af argumentet x

Afledt af en funktion i et punkt er grænsen (hvis den eksisterer og er endelig) for forholdet mellem funktionens stigning og stigningen i argumentet, forudsat at sidstnævnte har en tendens til nul.

De mest brugte er følgende afledt notation :

Eksempel 1. Udnytte definition af derivat, find den afledede af funktionen

Løsning. Fra definitionen af ​​derivatet følger følgende skema til dets beregning.

Lad os give argumentet en stigning (delta) og finde stigningen af ​​funktionen:

Lad os finde forholdet mellem funktionen stigning og argument stigning:

Lad os beregne grænsen for dette forhold, forudsat at stigningen af ​​argumentet har en tendens til nul, det vil sige den afledede, der kræves i problemformuleringen:

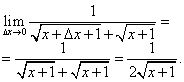
Fysisk betydning af derivatet

TIL begrebet afledt førte til Galileo Galileis undersøgelse af loven om legemers frie fald, og i bredere forstand - problemet med den øjeblikkelige hastighed af uensartet retlinet bevægelse af et punkt.

Lad småstenen løftes og derefter frigøres fra hvile. Sti s gennemløbet i tiden t, er en funktion af tid, dvs. s = s(t). Hvis bevægelsesloven for et punkt er givet, kan gennemsnitshastigheden for en hvilken som helst tidsperiode bestemmes. Lad på tidspunktet for tiden rullestenen være i positionen EN, og i øjeblikket - i position B. Over en periode (fra t to ) punkt har passeret stien . Derfor er den gennemsnitlige bevægelseshastighed over denne tidsperiode, som vi betegner med , er

.

Bevægelsen af ​​en frit faldende krop er dog tydeligt ujævn. Fart v faldet er konstant stigende. Og gennemsnitshastigheden er ikke længere nok til at karakterisere bevægelseshastigheden på forskellige strækninger af ruten. Jo kortere tidsperiode, jo mere nøjagtig er denne egenskab. Derfor introduceres følgende koncept: den øjeblikkelige hastighed af retlinet bevægelse (eller hastigheden på et givet tidspunkt i tid t) kaldes den gennemsnitlige hastighedsgrænse ved:

(forudsat at denne grænse eksisterer og er begrænset).

Så det viser sig, at den øjeblikkelige hastighed er grænsen for forholdet mellem tilvæksten af ​​funktionen s(t) til stigningen i argumentet t at Dette er den afledte, som i almindelig form skrives som følger:.

.

Løsningen på det angivne problem er fysisk betydning af afledt . Altså den afledede af funktionen y=f(x) på et tidspunkt x kaldes grænsen (hvis den eksisterer og er endelig) for stigningen af ​​en funktion til stigningen af ​​argumentet, forudsat at sidstnævnte har en tendens til nul.

Eksempel 2. Find den afledede af en funktion

Løsning. Fra definitionen af ​​derivatet følger følgende skema for dets beregning.

Trin 1. Lad os øge argumentet og finde

Trin 2. Find tilvæksten af ​​funktionen:

Trin 3. Find forholdet mellem funktionen stigning og argument stigning:

Trin 4. Beregn grænsen for dette forhold ved , det vil sige den afledte:

Geometrisk betydning af afledte

Lad funktionen defineres på et interval og lad punktet M på funktionsgrafen svarer til værdien af ​​argumentet og punktet R- betyder. Lad os trække punkterne igennem M Og R lige linje og kald det sekant. Lad os betegne med vinklen mellem sekanten og aksen. Denne vinkel afhænger naturligvis af .

Hvis eksisterer

at passere gennem punktet kaldes sekantens grænseposition HR kl (eller kl ).

Tangent til grafen for en funktion i et punkt M kaldet sekantens grænseposition HR ved , eller, som er det samme ved .

Af definitionen følger det, at for eksistensen af ​​en tangent er det tilstrækkeligt, at der er en grænse

,

og grænsen er lig med hældningsvinklen af ​​tangenten til aksen.

Lad os nu give en præcis definition af en tangent.

Tangent til grafen for en funktion i et punkt er en ret linje, der går gennem punktet og har en hældning, dvs. lige linje hvis ligning

Af denne definition følger det afledet af en funktion er lig med hældningen af ​​tangenten til grafen for denne funktion i punktet med abscissen x. Dette er den geometriske betydning af derivatet.