الموسوعة الكبرى للنفط والغاز

سوف نقوم بالرد لفظيا! هل صحيح أنه يمكن وصف الكرة حول أي هرم ثلاثي؟ هل من الممكن وصف كرة حول أي هرم رباعي الزوايا؟ ما هي الخصائص التي يجب أن يتمتع بها الهرم ليتمكن من وصف الكرة المحيطة به؟ الهرم منقوش في كرة، حافتها الجانبية متعامدة مع القاعدة. كيفية العثور على مركز الكرة؟ يتم وصف الكرة بالقرب من الهرم العادي. وكيف يقع مركزها بالنسبة لعناصر الهرم؟

الشريحة 17من العرض "مشاكل الهندسة" الصف الحادي عشر. حجم الأرشيف مع العرض التقديمي هو 1032 كيلو بايت.

الهندسة الصف الحادي عشر

ملخص العروض الأخرى

"مفهوم التناظر المركزي" - رسم الفضاء على نفسه. التماثل المركزي. هذا الرقم يسمى متماثل. التماثل المركزي هو الحركة. حركة الفضاء. تسمى النقطتان M و M1 بالتناظر. ملكية. الحركات. لقد أصبحنا على دراية بتحركات الطائرة. مهمة. التماثل المركزي هو حالة خاصة من الدوران.

"مشاكل في حساب مساحة المثلث" - إيفان نيفن. حل مشكلة واحدة. شعار الدرس. أهداف شخصية. أوجد مساحة الشكل. الإملاء الرياضي. طرق إيجاد مساحة المثلث. حدد بيان. دقيقة التربية البدنية. احسب مساحة الشكل. مساحة الشكل. التحقق من التقدم. مربع.

"المهام في القياس المجسم" - أوجد مربع المسافة بين القمم. مهام. قطر كرة الرصاص. حجم الكرة وأجزائها. أوجد زاوية متعدد السطوح. أوجد حجم الهرم. أوجد إحداثيات النقطة أ. القطاع الدائري. أوجد الحجم V للأسطوانة. أوجد مساحة سطح متعدد السطوح. أوجد مساحة شبه المنحرف. محيط.

"احسب حجم الجسم الدوار" - المجال. اسطوانة ومخروط. مخروط. الاسطوانات موجودة في كل مكان حولنا. الحجم الخامس من المخروط. مكعب تعريف المخروط. أنواع الأجسام الدورانية. كرة. مجلدات جثث الثورة. شكل. ابحث عن الحجم. وعاء أسطواني. تعريف الاسطوانة . نصف القطر. اسطوانة. حجم المخروط.

"أحجام وأسطح أجسام الثورة" - اقتراح واختبار الفرضيات. تلخيص المعرفة. أحجام وأسطح أجسام الثورة. التعرف على الشكل الهندسي. صياغة المشكلة. مشكلة. أمثلة من الأنشطة العملية. لماذا يسخن خزان ميزان الحرارة بشكل أسرع؟ إبريق الشاي على شكل كرة له أصغر مساحة سطحية. أحجام.

"الأجسام التي تدور حولنا" - الأجسام التي تدور حولنا. معدات صناعية. العثور على أجسام الدوران. شجرة التنوب المخروطية للغابات. البرج المائل في إيطاليا. في الفضاء الخارجي. منزل ميلنيكوف. مخروط. أبراج مستديرة. تاريخ المبنى الدائري. الأجسام الكونية.

مجموعات من متعددات الوجوه والأجسام المستديرة

مفاهيم الكرة والكرة.

جسم كرويهو شكل يتكون من مجموعة من جميع النقاط في الفضاء، والمسافة من كل منها إلى نقطة معينة O تساوي رقمًا موجبًا معينًا r. تسمى النقطة O مركزالكرة، والقطعة التي تربط نقطة بأي نقطة على الكرة هي نصف القطر. جميع أنصاف أقطار الكرة لها طول r. الرقم r يسمى نصف قطر الكرة.

تقسم الكرة مجموعة جميع النقاط في الفضاء التي لا تنتمي إليها إلى مجموعتين فرعيتين: داخليو خارجيالمساحة بالنسبة للكرة. وتشمل المنطقة الداخلية تلك النقاط في الفضاء، المسافة من كل منها إلى المركز أقل من نصف القطر، والمنطقة الخارجية تشمل تلك النقاط، المسافة من كل منها إلى المركز أكبر من نصف القطر.

كرةهو شكل يتكون من مجموعة من جميع النقاط في الفضاء، والمسافة من كل منها إلى نقطة معينة O ليست أكبر من رقم موجب معين r. تسمى النقطة O مركزالكرة، والرقم r هو لها نصف القطر. تسمى الكرة التي مركزها O ونصف قطرها r سطحأو حدود الكرة. جميع نقاط الكرة التي لا تنتمي إلى سطحها تسمى النقاط الداخلية للكرة أو النقاط الموجودة داخل الكرة. وبالتالي، فإن الكرة هي شكل يتكون من اتحاد جميع نقاط الكرة (سطح الكرة) ومجموعة جميع النقاط الداخلية المتعلقة بهذه الكرة.

يسمى المستوى المماس لسطح الكرة طائرة تماسيةإلى الكرة. يكون المستوى مماسًا للكرة إذا وفقط إذا مرت عبر نقطة على سطح الكرة عموديًا على نصف القطر المرسوم على هذه النقطة. لاحظ أيضًا أنه من خلال كل نقطة على سطح الكرة يمر مستوى واحد فقط مماس للكرة.

كرة محاطة بمتعدد السطوح.

تعريف.يسمى المجال الموصوفة حول متعدد السطوح، إذا كانت جميع رؤوس متعدد السطوح تقع على الكرة.

النظرية 1.يمكن وصف الكرة حول أي هرم ثلاثي.

مجموعة النقاط المتساوية البعد عن رؤوس قاعدة الهرم هي خط عمودي مرسوم من مركز الدائرة المحددة بالقرب من القاعدة (يوجد GMT في الفضاء المتساوي البعد عن رؤوس مضلع معين إذا أمكن وصف دائرة حولها هذا المضلع، ويوجد عمودي مرسوم على مستوى هذا المضلع عبر مركز الدائرة المحددة). مركز الدائرة المحيطة هو نقطة تقاطع المنصفين المتعامدين لقاعدة الهرم.

للعثور على مركز الكرة المقيدة، ارسم مستوى عبر النقطة M - منتصف الحافة الجانبية AD. سوف يتقاطع هذا المستوى مع العمودي (المشار إليه سابقًا) عند النقطة S. ومن خلال البناء SA=SB=SC، وأيضًا من حقيقة أن المثلث ASD متساوي الساقين (أيضًا من خلال البناء) يترتب على ذلك أن SA=SD. ولذلك فإن المسافات من جميع رؤوس الهرم إلى النقطة S متساوية، وهذه المسافة تساوي نصف قطر الكرة المحصورة بالقرب من الهرم ABCD (SA=SB=SC=SD=R).

مثال 1 . أوجد نصف قطر الكرة المحصورة حول رباعي منتظم.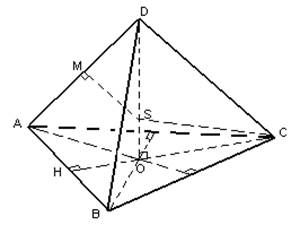

خذ بعين الاعتبار المثلث SOC. سيكون مستطيلًا بزاوية قائمة O (حسب البناء، سيكون OD هو ارتفاع الهرم).

لأن O هي نقطة تقاطع المتوسطات.

، حيث DO هو ارتفاع الهرم.

ثم من خلال نظرية فيثاغورس يتبع ذلك أو

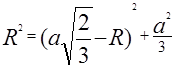
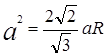
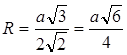
الإجابة: نصف قطر الكرة المحصورة حول رباعي منتظم يساوي

النظرية 2. إذا كان من الممكن وصف دائرة حول قاعدة الهرم، فيمكن وصف كرة حول الهرم.

لقد نظرنا بالفعل في حالة خاصة. وعلى العموم فالدليل مشابه.

النظرية 3 . من المستحيل وصف كرة بالقرب من منشور مائل؛ بالقرب من المنشور المستقيم يمكنك وصف الكرة، إذا كان بالقرب من قاعدة المنشور يمكنك وصف الدائرة.

1) دعونا نفكر أولاً في الحالة التي يكون فيها المنشور مائلًا (لنأخذ المنشور الثلاثي كمثال). النقطة المتساوية البعد عن النقاط A وB وC ستكون على الخط المستقيم OS 1 المتعامد على مستوى المثلث ABC وقاعدة المتعامد تكون عند نقطة تقاطع المتعامدين المنصفين المرسومين على جوانب المثلث ABC .

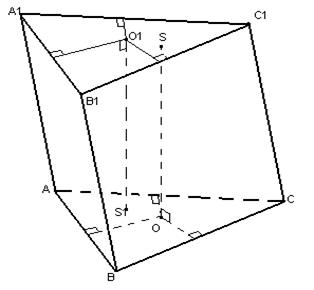
وبالمثل، فإن النقاط المتساوية البعد عن النقاط A 1، B 1، C 1 تقع على خط عمودي على مستوى المثلث A 1 B 1 C 1 – O 1 S. وبما أن المنشور مائل، فإن الخطوط OS 1 و O 1 S سوف تكون تكون متوازية، ولكن غير متطابقة. وهذا يعني أنه لن يكون لديهم نقاط مشتركة، وبالتالي: لا توجد نقطة تكون فيها المسافة إلى جميع رؤوس المنشور هي نفسها، وهو ما يشبه استحالة بناء كرة موصوفة حول منشور مائل.

2) خذ بعين الاعتبار منشورًا مستقيمًا يمكن وصف دائرة بالقرب من قاعدته. النقطتان O وO 1 هما مراكز الدوائر المقيدة بالقرب من القاعدتين السفلية والعلوية، على التوالي. بما أن المنشور مستقيم، فإن الخط المستقيم OO 1 سيكون متعامدًا مع مستويات القاعدة.

بعد ذلك، سيكون المستوى الذي يمر عبر منتصف الأضلاع الجانبية موازيًا لمستوى القاعدة ويتقاطع مع OO 1 عند النقطة S - منتصف OO 1. بعد ذلك، ستكون المسافة من جميع رؤوس المنشور إلى عربة اليد S هي نفسها (حسب البناء)، وبالتالي فإن S هو مركز الكرة الموصوف حول المنشور العادي.

لذلك، نحن مقتنعون بأنه من المستحيل وصف المجال بالقرب من المنشور المائل، ولكن بالقرب من المنشور المستقيم من الممكن إذا كان من الممكن وصف الدائرة بالقرب من قاعدتها.

النظرية 4. يمكن وصف الكرة حول هرم مقطوع إذا وفقط إذا أمكن وصف الدوائر حول قواعده وكان الخط المستقيم الذي يصل بين مراكز هذه الدوائر متعامدًا مع مستويات القواعد.

الشرط الأول يعني أن المتعامدين، وهما HMT، للقواعد المتساوية البعد عن رؤوس المضلعات ستكون موجودة، والثاني - أن تكونا متطابقتين، وبالتالي ستكون هناك نقطة متساوية البعد عن جميع رؤوس المضلعات. الهرم المقطوع.

المؤتمر الخامس عشر المفتوح للطلاب

"مثقفو القرن الحادي والعشرين"

القسم: الرياضيات

المنطقة الموصوفة في الأولمبياد وامتحان الدولة الموحدة

كييفا آنا أناتوليفنا

أورينبورغ – 2008

1.2 النطاق الموصوف

1.2.1 الخصائص والتعاريف الأساسية

1.2.2 تركيبة الهرم

1.2.3 الجمع مع المنشور

1.2.4 تركيبة مع الاسطوانة

1.2.5 تركيبة مع المخروط

2 أمثلة على مهام الأولمبياد

2.1 أمثلة على مهام الأولمبياد بالهرم

2.2 أمثلة على مهام الأولمبياد بالمنشور

2.3 أمثلة على مهام الأولمبياد باستخدام الأسطوانة

2.4 أمثلة على مهام الأولمبياد ذات المخروط

3.3 أمثلة على مهام امتحان الدولة الموحدة باستخدام الاسطوانة

3.4 أمثلة على مهام امتحان الدولة الموحدة باستخدام المخروط

مقدمة

يتم تنفيذ هذا العمل كجزء من مشروع إنشاء صفحة رياضية لأطفال المدارس على الموقع الإلكتروني للمدرسة الداخلية وسيتم نشره في قسم "الطرق الرياضية".

هدفالعمل - إنشاء كتاب مرجعي مخصص لطريقة حل المشكلات الهندسية مع المجال الموصوف في الأولمبياد وامتحان الدولة الموحدة.

لتحقيق هذا الهدف، كان علينا حل ما يلي مهام :

1) التعرف على مفهوم المجال الموصوف؛

2) دراسة ميزات مجموعات الكرة الموصوفة مع الهرم والمنشور والأسطوانة والمخروط؛

3) من بين المشاكل الهندسية، حدد تلك التي تحتوي على شرط وجود المجال الموصوف؛

4) تحليل وتنظيم وتصنيف المواد التي تم جمعها؛

5) قم باختيار المشاكل لحلها بشكل مستقل؛

6) عرض نتيجة البحث في شكل ملخص.

أهمية عملية– يمكن استخدام المواد التي أعددناها في إعداد تلاميذ المدارس للأولمبياد، ولامتحان الدولة الموحدة والدراسات اللاحقة في الجامعة.

1 المجال والكرة

1.1 الكرة والكرة: المفاهيم والتعاريف الأساسية

جسم كرويهو سطح يتكون من جميع نقاط الفضاء الواقعة على مسافة معينة من نقطة معينة.

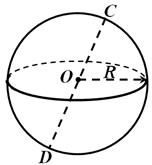
هذه النقطة تسمى مركز الكرة(نقطة عنفي التين. 1) وهذه المسافة نصف قطر الكرة. أي جزء يربط المركز بأي نقطة في الكرة يسمى أيضًا نصف قطر الكرة. يسمى الجزء المستقيم الذي يربط بين نقطتين على الكرة ويمر بمركزها قطر المجال(القطعة المستقيمة العاصمةفي التين. 1). لاحظ أنه يمكن الحصول على الكرة عن طريق تدوير نصف دائرة حول قطرها.

كرةيسمى الجسم الذي يحده المجال. يُطلق على مركز الكرة ونصف قطرها وقطرها أيضًا اسم مركز , نصف القطرو قطر الكرة. من الواضح أنها كرة نصف قطرها رتتمركز في عنيحتوي على جميع النقاط في الفضاء التي تقع من النقطة عنعلى مسافة لا تتجاوز ر(بما في ذلك النقطة عن)، ولا يحتوي على نقاط أخرى. كرةويسمى أيضًا شكل دوران نصف دائرة حول قطره. شريحة الكرة- جزء من الكرة مقطوع عنها بواسطة طائرة ما. كل جزء من الكرة بجوار المستوى هو دائرة. مركز هذه الدائرة هو قاعدة العمود المرسوم من مركز الكرة على مستوى القطع. تسمى الطائرة التي تمر عبر مركز الكرة طائرة قطرية.يُسمى الجزء الذي يقع على مستوى قطر الكرة دائرة كبيرة، وقسم الكرة هو دائرة كبيرة. قطاع الكرة –جسم هندسي يتم الحصول عليه عن طريق تدوير قطاع دائري بزاوية أقل من 90 درجة حول خط مستقيم يحتوي على أحد أنصاف الأقطار التي تحدد القطاع الدائري. يتكون القطاع الكروي من قطعة كروية ومخروط ذو قاعدة مشتركة.

مساحة سطح الكرة:

س = 4π ر 2 ,

أين ر- نصف قطر الكرة، س- مساحة الكرة.

حجم المجال

أين الخامس– حجم الكرة

حجم قطاع الكرة

الخامس – حجم الجزء الكروي.

مساحة السطح القطاعية

- ارتفاع القطعة، مساحة السطح القطعية

نصف قطر قاعدة القطعة

، - نصف قطر قاعدة القطعة، - ارتفاع القطعة، 0<ح < 2ر .

مساحة السطح الكروية لقطعة الكرة

- مساحة السطح الكروي للقطعة الكروية.

في الفضاء، بالنسبة للكرة والطائرة، هناك ثلاث حالات محتملة:

1) إذا كانت المسافة من مركز الكرة إلى المستوى أكبر من نصف قطر الكرة، فإن الكرة والمستوى ليس لهما نقاط مشتركة.

2) إذا كانت المسافة من مركز الكرة إلى المستوى تساوي نصف قطر الكرة، فإن المستوى لديه نقطة مشتركة واحدة فقط مع الكرة والكرة المحيطة بها.

3) إذا كانت المسافة من مركز الكرة إلى المستوى أقل من نصف قطر الكرة فإن تقاطع الكرة مع المستوى يكون دائرة. مركز هذه الدائرة هو إسقاط مركز الكرة على مستوى معين. تقاطع المستوى مع الكرة هو محيط الدائرة المحددة.

1.2 المجال الموصوف

1.2.1 التعاريف والخصائص

يسمى المجال الموصوفة حول متعدد السطوح(والمتعدد السطوح هو المدرجة في المجال)، إذا كانت جميع رؤوس متعدد السطوح تقع على الكرة.

هناك حقيقتان تتبعان تعريف المجال الموصوف:

1) جميع رؤوس متعدد السطوح المدرج في الكرة متساوية البعد من نقطة معينة (من مركز الكرة المحصورة)؛

2) كل وجه من وجوه متعدد السطوح منقوش في كرة هو مضلع منقوش في دائرة معينة، على وجه التحديد في الدائرة التي يتم الحصول عليها في قسم الكرة بواسطة مستوى الوجه؛ وفي هذه الحالة تكون قاعدة المتعامدين النازلين من مركز الكرة المحصورة على مستوى الوجوه هي مراكز الدوائر المحصورة حول الوجوه.

النظرية 1 . يمكن وصف الكرة حول متعدد السطوح إذا وفقط إذا تم استيفاء أي من الشروط التالية:

أ) يمكن وصف الدائرة حول أي وجه لمتعدد السطوح، وتتقاطع محاور الدوائر الموصوفة حول وجوه متعدد السطوح عند نقطة واحدة؛

ب) تتقاطع المستويات المتعامدة مع حواف متعدد السطوح وتمر عبر نقاط المنتصف عند نقطة واحدة؛

ج) توجد نقطة واحدة متساوية البعد عن جميع رؤوس متعدد السطوح.

دليل.

ضروري.دع الكرة توصف حول متعدد السطوح. دعونا نثبت أن الشرط أ) مستوفي. في الواقع، نظرًا لأن مستوى وجه معين لمتعدد السطوح يتقاطع مع الكرة على طول الدائرة، فإن رؤوس الوجه التي تنتمي إلى الكرة ومستوى الوجه تنتمي إلى خط تقاطعهما - الدائرة. وبما أن مركز الكرة متساوي البعد عن جميع رءوس وجه معين، فإنه يقع على عمودي على هذا الوجه المرسوم عبر مركز الدائرة المحيطة بالوجه.

قدرة.دع الشرط أ) يكون راضيا. دعونا نثبت أنه يمكن وصف الكرة حول متعدد السطوح. في الواقع، بما أن النقطة المشتركة للمتعامدين على الوجوه المرسومة من خلال مراكز الدوائر المحيطة بالأوجه متساوية البعد عن جميع رؤوس متعدد السطوح، فقد تم وصف كرة مركزها عند هذه النقطة حول متعدد السطوح.

الشرط أ) في هذه الحالة يعادل الشرطين ب) و ج).

إذا كانت الكرة محاطة بمتعدد السطوح، فإن: أ) قاعدة المتعامد الذي يسقط من مركز الكرة على أي وجه هي مركز دائرة محيطة بهذا الوجه (مثل قاعدة ارتفاع الهرم الذي يساويه الحواف الجانبية - نصف قطر الكرة المرسومة من مركزها إلى رؤوس وجه معين)؛ ب) يمكن أن يقع مركز الكرة المحصورة حول متعدد السطوح داخل متعدد السطوح، على سطحه (في وسط دائرة محاطة بوجه، على وجه الخصوص، في منتصف بعض الحواف)، خارج متعدد السطوح.

1.2.2 الكرة والهرم المحيطان

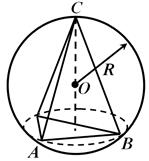
نظرية 2 . يمكن وصف الكرة حول الهرم فقط إذا أمكن وصف الدائرة حول قاعدتها.

دليل.دع الدائرة توصف حول قاعدة الهرم. ثم تحدد هذه الدائرة ونقطة خارج مستوى هذه الدائرة - قمة الهرم - مجالًا واحدًا يحيط بالهرم. والعودة. إذا كانت الكرة محاطة حول هرم، فإن قسم الكرة على مستوى قاعدة الهرم يكون دائرة محاطة بالقاعدة.

النتيجة الطبيعية 1.يمكن وصف الكرة حول أي رباعي الاسطح.

النتيجة الطبيعية 2.حول أي هرم منتظم يمكن وصف كرة يقع مركزها عند ارتفاع الهرم أو امتداده.

قد يكون مركز الكرة الموصوفة بالقرب من الهرم:

· مع وجود قمة الهرم على أحد جانبي مستوى قاعدته - داخل الهرم، في مستوى الوجه الجانبي (في وسط الدائرة الموصوفة حول هذا الوجه)، خارج الهرم؛

· في مستوى القاعدة - في وسط الدائرة الموصوفة بالقرب من القاعدة؛

· أن تكون قمة الهرم على طرفي نقيض من مستوى قاعدته.

النظرية 3 . إذا كانت الحواف الجانبية للهرم مائلة بالتساوي على مستوى قاعدته، فيمكن وصف كرة حول الهرم.

دليل.وبما أن الحواف الجانبية تميل بشكل متساوٍ إلى مستوى قاعدة الهرم، فيمكن وصف دائرة بالقرب من قاعدة الهرم، ومن ثم يمكن وصف كرة بالقرب من الهرم.

يمكن صياغة هذه النظرية بشكل مختلف: إذا كان للهرم حواف جانبية متساوية، فيمكن وصف الكرة حول الهرم.

نظرية العكس غير صحيح

النظرية 4. إذا تم وصف الكرة بالقرب من الهرم، فإن مركزها هو نقطة تقاطع جميع المستويات المرسومة من خلال نقاط منتصف حواف الهرم المتعامدة مع هذه الحواف.

دليل.وفي الواقع، فإن أي نقطة متساوية البعد من رأسي هرم مجاورة لإحدى حافتيه تقع في مستوى مرسوم بشكل عمودي على هذه الحافة من الهرم من خلال منتصفه. ولذلك، فإن مركز الكرة المحددة، كونه على مسافة متساوية من جميع رؤوس الهرم، يجب أن يقع في كل من هذه المستويات، أي. إنها نقطة تقاطع كل هذه المستويات. عند الرسم، غالبًا ما يضع تلاميذ المدارس مركز الكرة الموصوفة بشكل عشوائي، دون أن يتخيلوا التكوين المكاني المحدد جيدًا، وخاصة دون إجراء أي تفكير حول موضع هذا المركز. في هذه الحالة، كقاعدة عامة، يتم وضع المركز داخل الهرم. وفي الوقت نفسه، يمكن أن يقع مركز الكرة الموصوفة داخل الهرم أو خارجه أو على سطحه (حسب نوع الهرم المحدد).

النظرية 5 . يمكن وصف الكرة حول الهرم المقطوع فقط إذا تم استيفاء أي من الشروط التالية:

أ) تم وصف الدوائر بالقرب من قواعد الهرم، والتي يكون خط مراكزها متعامدًا مع مستوياتها؛

ب) جميع الحواف الجانبية للهرم مائلة بالتساوي على مستوى إحدى القواعد؛

ج) جميع الحواف الجانبية للهرم متساوية مع بعضها البعض؛

د) جميع الوجوه الجانبية للهرم هي شبه منحرفة متساوية الأضلاع.

دليل.لنفترض أنه يمكن وصف الدوائر بالقرب من قواعد هرم مقطوع معين، وأن مستويات هذه الدوائر متعامدة مع خط مراكزها. ومن ثم، كما هو معروف، فإن هاتين الدائرتين تحددان كرة واحدة، والتي سيتم تحديدها حول هذا الهرم.

لنفترض، على العكس من ذلك، أن الكرة موصوفة حول هرم مقطوع معين. ثم تكون أقسام الكرة حسب مستويات قواعد الهرم دوائر موصوفة حول القواعد. إضافي. الخط المستقيم المتعامد مع مستويات قواعد الهرم ويمر بمركز الكرة يمر بمراكز الدوائر الموصوفة حول القواعد.

حالة أ) يعادل الشروط ب), ج), د).

عاقبة.يمكن وصف الكرة حول أي هرم منتظم مقطوع.

1.2.3 المجال المحصور والمنشور

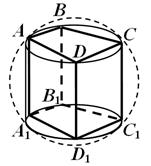
النظرية 6. يمكن وصف الكرة حول منشور إذا وفقط إذا كان المنشور مستقيمًا ويمكن وصف دائرة حول قاعدته.

دليل.

ضروري.إذا كان المنشور منقوشًا في كرة، فكل وجه من وجوهه منقوش في دائرة - جزء من الكرة بجوار مستوى هذا الوجه. وهذا يعني أنه يمكن وصف دائرة بالقرب من قاعدة المنشور، وجميع الوجوه الجانبية للمنشور تشبه متوازيات الأضلاع المنقوشة في الدوائر - مستطيلات وبالتالي يكون المنشور مستقيما.

قدرة.ليكن المنشور مستقيما وترسم دائرة حول قاعدته. ثم إن الدوائر المحصورة حول قواعد المنشور، والتي تكون مستوياتها متعامدة مع خط مراكزها، تحدد كرة واحدة، تكون محاطة حول المنشور.

عواقب:

أ) يمكن وصف الكرة حول أي منشور منتظم؛

ب) يمكن وصف الكرة حول أي منشور ثلاثي قائم؛

ج) يمكن وصف الكرة حول أي متوازي مستطيلات؛

مركز الكرة المحيط بالمنشور يكون على مسافة متساوية من مستويات قواعد المنشور ويمكن أن يقع داخل المنشور، على وجهه الجانبي (في وسط الدائرة الموصوفة حول الوجه)، خارج المنشور.

1.2.4 المجال والأسطوانة المقيدة

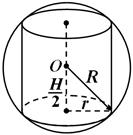
يسمى المجال وصف حول الاسطوانةإذا كانت دوائر قواعد الاسطوانة تقع عليها (الشكل 4). يمكنك دائمًا وصف كرة حول أسطوانة.

1.2.5 المجال المحدود والمخروط

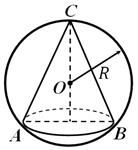
يسمى المجال الموصوفة حول المخروطإذا كان قمة المخروط ودائرة قاعدة المخروط يقعان عليه (الشكل 5). من الممكن دائمًا وصف كرة حول مخروط؛ نصف قطرها يساوي نصف قطر الدائرة الموصوفة حول القسم المحوري للمخروط. يسمى المخروط المقطوع منقوشةإلى كرة إذا كانت قاعدتها عبارة عن أجزاء من سطح الكرة.

2 أمثلة على مهام الأولمبياد

2.1 أمثلة على مهام الأولمبياد بالهرم

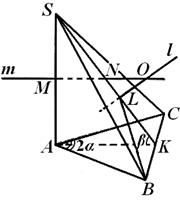
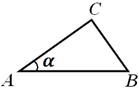
مثال 1. في الهرم الثلاثي س ABC edge BC يساوي حافة AB=AC س وعموديًا على قاعدة الهرم ABC، تكون الزاوية ثنائية السطوح عند الحافة س أ يساوي 2α , وعلى الحافة BC يساوي β (الشكل 6) . أوجد نصف قطر الكرة المقيدة.

حل.النظر في الهرم س ABC,والتي تمت مناقشتها في بيان المشكلة. منذ الحافة S. A.عمودي على مستوى القاعدة، ثم

فرجينيا س = CAS= 90 درجة، وبالتالي الزاوية أنتهي بالضبط الزاوية الخطية للزاوية ثنائية السطوح عند الحافة S. A.. وهكذا، في قاعدة الهرم يوجد مثلث متساوي الساقين بزاوية 2 α في الأعلى، ويتوافق ارتفاع الهرم مع حافته س أ.

منذ نتوءات الأضلاع الجانبية إس بي.و س مععلى مستوى القاعدة متساوية، فإن هذه الحواف نفسها متساوية. وبالتالي الحافة في س مع- مثلث متساوي الساقين، ويكون ارتفاعه أقل من قمة الرأس س، يقع في المنتصف لضلوع شمس.بواسطة نظرية الثلاثة المتعامدين أك- ارتفاع المثلث أنت.ومن هذا يتضح أن الزاوية س كاليفورنيا- الزاوية الخطية للزاوية ثنائية السطوح عند الحافة شمس،أي.

س كاليفورنيا = β .

يقع مركز الكرة المقيدة عند تقاطع الخط ل، عمودي على الطائرة في س معويمر بمركز الدائرة المحيطة بالمثلث في س مع،مع مرور الطائرة في منتصف الحافة أ سعمودي عليه. مستقيم ليكمن في الطائرة أ س ل:في الواقع، الطائرة في س معيمر عبر خط مستقيم شمس،عمودي على الطائرة أ س ل، أي الطائرات في س معو أ س لعمودي؛ في نفس الوقت على التوالي لعمودي على الطائرة في س معويمر بخط تقاطع هذه المستويات، بحيث يقع في المستوى أ س ل .

لذا فإن مركز الكرة يقع في المستوى أ س ل. لنأخذ هذه الطائرة إلى رسم خاص. مركز الكرة عنسوف تقع بعد ذلك عند تقاطع الخط لومستقيم م، عمودي أ سويمر في وسطه. ولكن، بشكل عام، هناك ثلاثة احتمالات قد تطرح نفسها: المباشر لو تتتقاطع داخل المثلث أو خارجه أ س لأو إلى جانبه، وعلينا أن نأخذ في الاعتبار كل هذه الاحتمالات (انظر الشكل 7، 8، 9). أدناه، في سياق الحسابات، سنبين أن اثنين منهم لم يتم تنفيذهما فعليا. نحن مهتمون بنصف القطر رالكرة المقيدة، أي. المسافة من النقطة عن- نقاط تقاطع الخطوط العمودية تو لإلى جانبي الزاوية ل س أ- الى حد، الى درجة س، رؤوس هذه الزاوية. أولا وقبل كل شيء، دعونا نجد إس إل- إسقاط المسافة المطلوبة على الجانب إس.ك.مثلث كاس. منذ في مثلث أك ب(الشكل 6) نعرف الساق فك =

أوالزاوية كاف = α،الذي - التي أك= أ ctg α .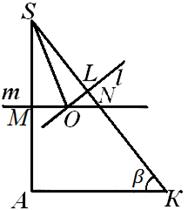

إس.ك. =

لأن ل- المركز الموصوف حول المثلث في س معالدوائر إذن إل إس. = ل في،ا لأنه من المثلث VC لنجد ذلك ( س ل- إس إل ) 2 +HF 2 = ب ل 2 , أي.

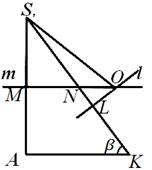
مع ملاحظة أن حسابات المقطع إس إللا يعتمد بأي شكل من الأشكال على موقع المركز عنالكرة الموصوفة، دعنا نعود إلى الشكل. 7، 8، 9. دعونا نشير بـ ننقطة تقاطع الخط ممع الجانب س ل.فمن الواضح أن على التوالي لو تتتقاطع الخارجمثلث كاليفورنيا س , لو SN <إس إل(الشكل 8)؛ لو س ن> إس إل , ثم أشر عنيقع داخل هذا المثلث (الشكل 7)؛ أخيرا، إذا SN = إس إل , ثم أشر عنيقع على الجانب س لهذا المثلث (الشكل 9). دعونا معرفة أي من هذه الأحكام يحدث بالفعل.

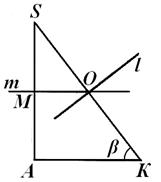
لأن مينيسوتا كاليفورنيا س , الذي - التي SN =

س ل. مقارنة أطوال القطاعات SNو إس إل، يمكننا بسهولة إثبات ذلك لأي شخص أ، ألفاو

(من الاعتبارات الهندسية يتبع ذلك أ> 0.0 درجة<

< 90 درجة و 0 درجة< β < 90°). Следовательно, каковы бы ни были размеры أ , α و β الأهرامات س ABC,مركز عنفالكرة المقيدة تقع دائمًا خارج الهرم. وهذا بدوره يعني أن التكوين المسطح الذي أخرجناه في المستوى كاليفورنيا سيمكن أن يكون لها النموذج الموضح في الشكل 8 فقط؛ المواقع الموضحة في الشكل 7 و9 لا يمكن أن يحدثا بالفعل. النظر إلى الشكل. 8، يمكننا بسهولة أن نبين أن = β ، وبالتالي L.O. = NL tg β = (إس إل -س ن) tg β. استبدال هنا التعبيرات التي تم الحصول عليها أعلاه ل إس إلو س ن، نحصل على حسابات واضحة:

ل يا =

أ tg α خطيئة β .

وأخيرا، من المثلث الأيمن عن إل إس.نجد

= .

كما ترون، تبين أن الحسابات في المشكلة بسيطة - تكمن الصعوبة الرئيسية للحل في المنطق الذي يحدد موضع مركز الكرة المقيدة.

إجابة: ر =

مثال 2. هرم مثلثي منتظم بزاوية مسطحة  عند قمته محفور في كرة نصف قطرها R. أوجد حجم الهرم، وكذلك السطح الجانبي للمخروط الموصوف حول الهرم المشار إليه .

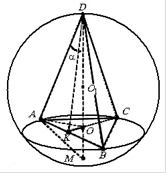
حل.دع جانب قاعدة الهرم يكون أفإن نصف قطر قاعدة المخروط الموصوف حول هذا الهرم يساوي ص، ثم

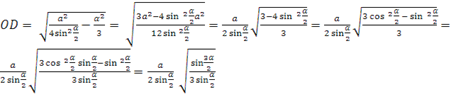(الشكل 10). وجوه الهرم مثلثات متساوية الساقين. ثم لا أعرف- الارتفاع والوسيط والمنصف  عبد. من المثلث الأيمن أدكلدينا . أوجد ارتفاع الهرم من المثلث القائم AOD : ,

مارك ألماني- قطر الكرة . ثم في قسم الكرة التي تمر عبر القطر مارك ألمانيوالفترة أ، نحصل على مثلث قائم الزاوية أيه إم دي. من العلاقات المترية في المثلث الأيمن لدينا

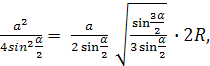أين

ثم نجد مساحة القاعدة باستخدام الصيغة:

ومن الصيغة

أوجد حجم الهرم : .

حافة إعلانبحكم التعريف، المخروط المحدود هو مولده. ثم نجد السطح الجانبي للمخروط المحدد باستخدام الصيغة سالجانب =  ص ل :

إجابة:

;

مثال 3. يوجد في قاعدة الهرم مربع طول ضلعه أ. ويمر ارتفاع الهرم بمنتصف أحد حواف القاعدة ويساوي

. أوجد نصف قطر الكرة المحيطة بالهرم.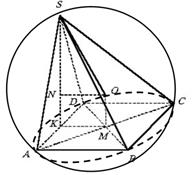

حل.من الأخطاء النموذجية عند حل هذه المشكلة القول بأن مركز الكرة الموصوفة يقع على الحافة اس بي سي(الشكل 11). في الواقع موقف هذه النقطة عنغير متصل بالحافة اس بي سي.

بسبب تساوي النقطة عنمن القمم س، أ، ب، ج، ديتبع ذلك أوابكد- هرم رباعي منتظم. لذلك، إلى حافة الهاوية ا ب ت ثنقطة عنالمتوقعة إلى حد ما م- نقطة تقاطع الأقطار. مثلث أ.س.د.متساوي الساقين ثم ارتفاع الهرم إس.ك.هو متوسط المثلث أ.س.د. ,

. من المثلث الأيمن ش.م.ك.سوف نجد S. A. :

وبالتالي المثلث حزين.- متساوي الأضلاع و OASD- الهرم الثلاثي المنتظم . ثم أشر عنالمتوقعة إلى حافة الهاوية حزين.إلى وسط المثلث حزين.. من هنا

من مثلث ابنالعثور على نصف القطر المطلوب لذا،

إجابة:

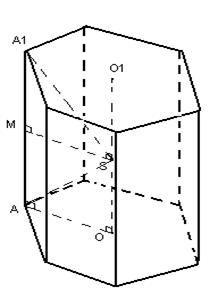
مثال 4. إلى كرة نصف قطرها ر تم نقش هرم مقطوع سداسي منتظم، يمر فيه مستوى القاعدة السفلية بمركز الكرة، وتشكل الحافة الجانبية زاوية مقدارها 60 مع مستوى القاعدة

. تحديد حجم الهرم.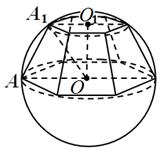

حل.بالشرط،

الزراعة العضوية 1 = 60 (الشكل 12)؛ وسائل، عن 1 الزراعة العضوية 1 = 30 و أ 1 عن 1 = أ 1 يا = ,O. O. 1 = .

سأسفل القاعدة = 6

, سقمة أساسي = أقل أساسي .

أخيرا وصلنا

إجابة:

2.2 أمثلة على مهام الأولمبياد بالمنشور

مثال 1. في كرة حجمها يساوي الخامس , تم نقش المنشور الثلاثي الأيمن. قاعدة المنشور عبارة عن مثلث قائم الزاوية حاد الزوايا

، ووجهه الجانبي الأكبر مربع. أوجد حجم المنشور.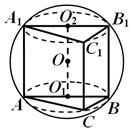

حل.أولًا، نحدد موضع مركز الكرة بالنسبة للمنشور. أقسام الكرة حسب مستويات قواعد المنشور هي الدوائر التي نقشت فيها هذه القواعد (شكل 13)، وبما أن قواعد المنشور متساوية، فإن دوائر الأقسام متساوية ومتباعدة بشكل متساوٍ عن مركز الكرة. كل مركز عن 1 و عن 2 يتزامن مع منتصف الوتر المقابل.

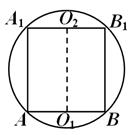
من خواص مقاطع الكرة على المستوى يعرف أن العمودي يرسم من مركز الكرة عنيمر مستوى دائرة المقطع العرضي بمركز هذه الدائرة. لذلك، عن 1 عن

طائرة اي بي سي.مستقيم عن 1 عنيمر أيضا من خلال يا 2 وعمودي على المستوى وبذلك يقع مركز الكرة على الوجه في منتصف القطعة يا 1 يا. جميع الوجوه الجانبية للمنشور مستطيلة، والوجه - أعظمهم (منذ أب -الوتر للمثلث أ شمس). هذا الوجه هو حسب الاتفاقية مربع. إن قسم الكرة بجوار مستوى الوجه عبارة عن دائرة كبيرة من الكرة، وبالتالي فإن نصف قطر الدائرة الموضح في الشكل. 14، يساوي نصف قطر الكرة ر . لاحظ أن ارتفاع المنشور أأ 1 = أ 4 = . الآن كل ما تبقى هو العثور على مساحة القاعدة:

س أ ب مع =

. من (الشكل 15)

لدينا أس = أب

, وسائل،

س أ ب مع =

الآن نحصل على:

الخامسجائزة.

بالشرط،

ر 3 = الخامس ,

أين ر 3 =

،لذلك،

الخامسجائزة.

إجابة: الخامسجائزة.

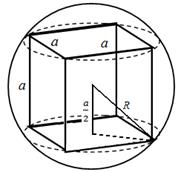
مثال 2. أوجد نسبة سطح الكرة وحجمها، على التوالي، إلى سطح وحجم المكعب المنقوش

حل.دع نصف قطر الكرة يكون ر , حافة المكعب تساوي أ؛

ثم ر 2 -

، أين أ= .

دعونا نشير إلى أحجام وأسطح الكرة والمكعب، على التوالي، بواسطة الخامس 1 , الخامس 2 , و س 1 , س 2 .

, الخامس 2 = = , س 1 =4, س 2 = 6أ 2 =8ر 2 , الخامس 2 = , س 1 س 2 = .

إجابة: الخامس 1

الخامس 2 = , س 1 س 2 = .

2.3 أمثلة على مهام الأولمبياد باستخدام الأسطوانة

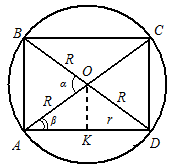
مثال. أوجد نسبة حجم الكرة إلى حجم الأسطوانة الدائرية القائمة المنقوشة في هذه الكرة، إذا علم أن الزاوية الصغرى بين قطري المقطع المحوري للأسطوانة تساوي

وقطر القاعدة أكبر من ارتفاع الاسطوانة (شكل 18).

حل.نحن نعرف حجم الكرة

، ونجد حجم الاسطوانة باستخدام الصيغة، ولكن، لذلك

يترك ا ب ت ث- القسم المحوري للأسطوانة (انظر الشكل 18). وبما أن قطر القاعدة أكبر من ارتفاع الاسطوانة

- الزاوية AOB.من مثلث أبوويترتب على ذلك ارتفاع الاسطوانة

نصف قطر قاعدة الاسطوانة

. .

لقد أتضح أن

دعنا نستبدل البيانات التي تم العثور عليها في صيغة حجم الأسطوانة:

;

هكذا،

دعونا نجد العلاقة

إجابة:

2.4 أمثلة على مهام الأولمبياد مع مخروط

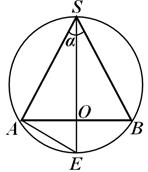
مثال 1. إلى كرة نصف قطرها ر مخروط دائري منقوش. الزاوية بين مولدات المخروط في القسم المحوري تساوي α. أوجد الارتفاع الذي يشكل نصف قطر قاعدة المخروط.

حل.الجزء الذي يمر عبر محور المخروط من الكرة هو الدائرة الكبرى للكرة التي يقع فيها

أ.ب س(الشكل 19)، حيث أ في- قطر قاعدة المخروط . دعنا نواصل ارتفاع (محور) المخروط لذاحتى يتقاطع مع الدائرة الكبرى عند هذه النقطة هوالنظر ه س أ:

في هذا المثلث

جنوب شرق. = 2ر ,

س إى = 90° و أ س ه= .

أ س = 2ر

الآن من

أ نظام التشغيلنجد

أ عن = ص = 2ر

, لذا = ح= 2ر

إجابة : لذا= 2ر

أ س = 2ر , أ عن =.

مثال 2. النسبة بين ارتفاع المخروط إلى نصف قطر الكرة المحيط به تساوي ك . أوجد النسبة بين أحجام هذه الأجسام. اكتشف ماذا ك المهمة منطقية.

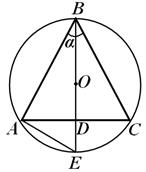
حل.لنفكر في القسم المحوري للمخروط (الشكل 20). يترك ح- ارتفاع المخروط، ر- نصف قطر الكرة محاط بالمخروط. ثم حسب الشرط

=ك، أي. ح = ك ر .

دعونا نعبر عن نصف القطر صقاعدة المخروط من خلال ر; بعد أن نظرت في الحبال تكييفو يكون،نحن نحصل:

في د

د ه = أ د د مع(لأن م = العاصمة ,
- مستطيلي، إعلان – انخفض الارتفاع من قمة الزاوية اليمنى).

(لذلك، ك < 2).

الخامسث =

; الخامسك ==

هكذا،

، (في 0< ك < 2).

إجابة:

، (في 0< ك < 2).

مثال 3. في المخروط المقطوع، يكون نصف قطر القاعدتين السفلية والعلوية متساويتين، على التوالي ص 1 و ص 2 ، ويميل المولد للمخروط إلى مستوى القاعدة السفلية بزاوية α (الشكل 21). أوجد نصف قطر الكرة التي تم إدراج المخروط المقطوع فيها.

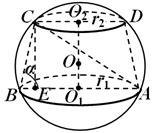
حل.في قسم الكرة الذي يمر عبر محور المخروط المقطوع، يتم الحصول على دائرة كبيرة من الكرة، يتم فيها نقش شبه منحرف اي بي سي د. دعونا نفكر

أ شمس،وهو مكتوب أيضًا في الدائرة الكبرى للكرة. الزاوية في هذا المثلث معروفة مع بكالوريوس. = α . بحكم نظرية الجيب، تكييف = 2ر. وهكذا لتحديد ريكفي أن تجد تكييف.دعونا نسقط من هذه النقطة مععمودي SEعلى أ.ب.بوضوح،

أ = ص 1 + ص 2 ,كن = ص 1 - ص 2، أ م = ( ص 1 - ص 2 )

لذلك، وفقا لنظرية فيثاغورس

= = = من أين ر =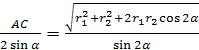

إجابة: ر

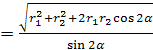3 أمثلة على مهام امتحان الدولة الموحدة

3.1 أمثلة على مهام امتحان الدولة الموحدة ذات الهرم

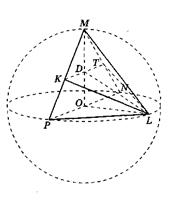
مثال 1. الجزء P ن , يساوي 8، وهو قطر الكرة. النقاط م، ل استلقي على الكرة بحيث يكون حجم الهرم P ن م ل الأكبر (الشكل 22). أوجد مساحة المثلث K ل تي، حيث K و T هما نقطتا المنتصف لحواف PM و ن م على التوالى.

حل.يترك عنهو مركز الكرة، و ر- نصف قطرها. بسبب ال ر ن = 2ر= 8 والنقاط مو لالاستلقاء على الكرة، ثم أو = س ل = ا ن = أوم = ر = 4. أقسام الكرة بالطائرات ر إل إنو آر إم ن- شعاع الدائرة ر = 4،وصف عن المثلثات ر إل إنو آر إم ن , و

آر إم ن = ر إل إن= 90 درجة، كزوايا منقوشة على أساس القطر ر ن .

يترك ن- ارتفاع الهرم منخفضا من الأعلى م، أ ح- ارتفاع المثلث ر إل إن , عقد على الجانب ر ن . منذ هذه النقطة متقع على المجال، والطائرة ر إل إنيحتوي على مركز الكرة، إذن ن

ر , و ن = ر , لو شهر ر NL . وبالمثل، منذ هذه النقطة لتقع على الكرة، ثم ح ر , و ح = ر , لو ل عن ر ن .

وبالتالي لحجم الهرم ر ن م للدينا

, .

هكذا الهرم ر ن م للديه أكبر حجم إذا كانت المثلثات ر إل إنو آر إم نمستطيل، متساوي الساقين مع الوتر المشترك ر ن، ملقاة في طائرات متعامدة بشكل متبادل. منذ المثلثات ل عن ن , ل أو، ل أوم، مدمج، ن أوممتساويان على قدمين، ثم المثلثان ل م نو ل السيدالصحيح مع الجانب

NL = ف ل = على

ويترتب على ذلك أن الوسطاء ل لو ل تهذه المثلثات متساوية، و

ل ل =

= 2.

مثلث ل ل تمتساوي الساقين، وارتفاعه إل ديهو متوسط المثلث متساوي الساقين الأيمن ل أوم.من هنا

إل دي =

= 2.

ط م- الخط الأوسط للمثلث آر إم نوبالتالي ط م = 0,5ر ن =ر . ولذلك المنطقة س ل ل ت =

ط م إل دي = 4.

إجابة: 4

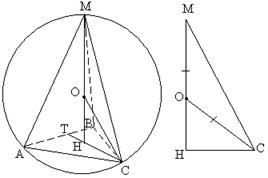
مثال 2. في الهرم الثلاثي المنتظم يكون طول ضلع القاعدة 5، وتكون أضلاعه الجانبية مائلة على القاعدة بزاوية 60يا. أوجد نصف قطر الكرة المحيطة بالهرم.

حل.يترك ABCMالهرم المشار إليه (انظر الشكل 23) يقع مركز الكرة الموصوفة عند ارتفاع الهرم، حيث أن الهرم منتظم.

قاعدة ارتفاع الهرم هي مركز المثلث اي بي سي، أي نقطة تقاطع المتوسطات. ثم:

ست =

CH= = = .

الآن فكر في المثلث MNS.هنا الزاوية ام اس انتساوي 60 درجة، وهي الزاوية بين الحافة الجانبية آنسةوالأساس اي بي سي. ركن NMSيساوي 30

. مو = نظام التشغيلمثل نصف القطر. إذن فهو مثلث موسمتساوي الساقين. كما تعلم، في المثلث متساوي الساقين تكون زوايا القاعدة متساوية. لذلك، OSM = التأمين الطبي الإلزامي = 30, أو إس إن = ام اس ان - مكو = 60 - 30= 30.

من المثلث الأيمن أو إس إندعونا نحدد الوتر نظام التشغيلباستخدام العلاقة بين الدوال المثلثية في المثلث القائم:

إجابة: أوك. =

3.2 أمثلة على مهام الاستخدام بالمنشور

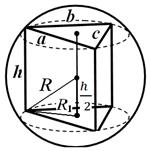
مثال 1. قاعدة المنشور عبارة عن مثلث له جوانب أ , ب , ج . ارتفاع المنشور ح (الشكل 25). أوجد نصف قطر الكرة المقيدة.

حل.وبما أن الكرة محاطة حول المنشور، فإن المنشور مستقيم وحافته الجانبية تساوي ارتفاعه. يتم حساب نصف قطر الدائرة الموصوفة حول قاعدة المنشور بواسطة الصيغة

إجابة:

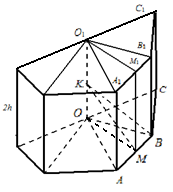
مثال 2. نصف قطر الكرة ر . منشور ذو عدد n منتظم ارتفاعه 2 محفور في كرة. ح (الشكل 26). أوجد جانب قاعدة المنشور.

حل.يترك ل- مركز الكرة المقيدة. لدينا: ك.ب. = ر , نعم = ح. يترك أوم

أ.ب، ثم

أو.ب. =

(من المثلث أوكي بي).

من مثلث مكتب الإدارة والميزانيةنجد

أ = 2م.ب. = 2أو.ب.

لذا، أ =

إجابة: أ =

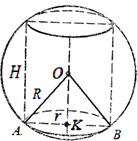
3.3 أمثلة على مهام امتحان الدولة الموحدة باستخدام الاسطوانة

مثال 1. ارتفاع أسطوانة دائرية أكبر بمقدار 10 من نصف قطر قاعدتها، ومساحة سطحها الإجمالية 144

. أوجد نصف قطر الكرة المقيدة.

حل.نصف قطر الكرة المقيدة

(الشكل 27).

مساحة سطح الاسطوانة

, 144,

دعونا نبسط هذا التعبير:

نحصل على معادلة تربيعية

دعونا نجد جذور هذه المعادلة

، غير مناسب لأنه سلبي. ارتفاع

لنجد نصف قطر الكرة المقيدة:

إجابة:

مثال 2. أسطوانة دائرية مستقيمة محفورة في كرة (الشكل 28). كم مرة يكون حجم الكرة أكبر من حجم الاسطوانة إذا علم أن نسبة نصف قطر الكرة إلى نصف قطر قاعدة الاسطوانة هي نصف نسبة سطح الكرة؟ المجال إلى السطح الجانبي للأسطوانة.

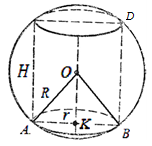
حل.نسبة حجم الكرة إلى حجم الأسطوانة المنقوشة

وبالشرط معروف ذلك

; –

متساوي الاضلاع

دعونا نوجد النسبة بين حجم الكرة والأسطوانة المنقوشة

إجابة: 16:9.

3.4 أمثلة على مهام امتحان الدولة الموحدة باستخدام المخروط

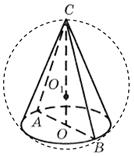
مثال 1. يبلغ قطر قاعدة المخروط 6 أمتار، ويميل المولد إلى مستوى القاعدة بزاوية 60 درجة (الشكل 29). أوجد مساحة الكرة المحصورة حول المخروط.

سيارة أجرةتساوي الزاوية بين مولد المخروط ومساحة قاعدته. لهذا الكابينة = 60 درجة ومثلث متساوي الساقين اي بي سي -صحيح. إنه يتبع هذا

CA = AB = BC= 6 م.

دعونا نجد موضع مركز الكرة المحيط بالمخروط. وبتعريف مثل هذه الكرة، فإن محيط قاعدة المخروط هو جزء من الكرة المقيدة، ورأس المخروط يقع على هذه الكرة. بحسب خاصية قطر الكرة التي تمر بمركز أي قسم منها الخط المستقيم شركةعمودي على مستوى قاعدة المخروط وبالتالي المركز عن 1 من الكرة المقيدة تقع على خط مستقيم شركةويترتب على ذلك المركز عن 1 للكرة المحصورة حول المخروط هو مركز الدائرة المحاطة بقسمها المحوري.

في المثلث الأيمن

اي بي سي ر = يا 1 ج =

(م)

لنجد مساحة الكرة:

(م2).

إجابة: 48

م 2.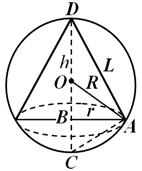

مثال 2. إلى كرة نصف قطرها ر = مخروط منقوش بارتفاع 6 سم ح (الشكل 30). عبر عن الحجم والسطح الجانبي للمخروط كدالة للوسيط ح .

حل.لدينا:

أين ص - نصف القطر الأساسي, ل- تشكيل مخروط.

معتبرا أن ص = فرجينيا –الارتفاع الذي تم إنزاله من رأس الزاوية القائمة إلى الوتر، لدينا: و . أو ص 2 و

, .

الآن نحصل على:

, .

إجابة:

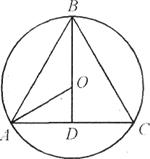
مثال 3. يتم إدراج مخروط في الكرة، ومولدها يساوي قطر القاعدة (الشكل 31). أوجد نسبة سطح المخروط إلى سطح الكرة.

حل.دعونا نصور القسم المحوري للمخروط الذي سيمر عبر مركز الكرة. نظرًا لأن قطر قاعدة المخروط يساوي المولد، في القسم نحصل على مثلث منتظم منقوش في دائرة (الشكل 31). دع نصف قطر الكرة يساوي ر : ثم

أ.ب =ر

, أ د =

دعونا نشير إلى السطح الكلي للمخروط بواسطة س 1، وسطح الكرة من خلال س 2. لدينا

أين س 1: س 2 = 9:16.

إجابة: س 1: س 2 = 9:16.

خاتمة

أثناء البحث، اكتشفنا أن المشكلات المتعلقة بالمنطقة الموصوفة يتم تقديمها في كثير من الأحيان لأطفال المدارس في امتحان الدولة الموحدة، وبالتالي فإن القدرة على حل المهام من هذا النوع تلعب دورًا مهمًا للغاية في اجتياز الامتحانات بنجاح. أيضًا، غالبًا ما توجد مشاكل في المنطقة الموصوفة في أولمبياد الرياضيات على مستويات مختلفة. وترد الأمثلة ذات الصلة في عملنا. في هذه المرحلة، اقتصرنا على النظر في المسائل التي تتضمن اتحاد كرة محددة مع الهرم، والمنشور، والأسطوانة، والمخروط. مهام مختارة للعمل المستقل. في عملية تنفيذ العمل، استخدمنا الأساليب التالية: العمل مع الأدبيات العلمية والشعبية، وجمع المعلومات على الإنترنت، والتحليل والتنظيم والتصنيف والمعالجة على جهاز كمبيوتر. يتم عرض النتائج حاليا في شكل مجردة. ومن المخطط في المستقبل استكمال العمل بمهام جديدة.

فهرس

1. أبراموفيتش إم. آي.، ستارودوبتسيف إم. تي. الرياضيات (الهندسة والدوال المثلثية). الكتاب المدرسي للأقسام التحضيرية بالجامعات - م: المدرسة العليا 1976. - 304 ص.

2. فويتوفيتش إف إس. تركيبات الأجسام الهندسية: (الأفلاك المنقوشة والمحدودة): كتاب للطلاب. – مينسك: نارودنايا أسفيتا، 1992. – 160 ص.

3. جوفوروف في إم، ديبوف بي تي، ميروشين إن في وغيرها قائمة المشاكل التنافسية في الرياضيات (مع تعليمات وحلول منهجية): كتاب مدرسي. – الطبعة الثانية – م: ناوكا، 1986. – 384 ص.

4. دينيشيفا إل.أو.، بيزروكوفا جي.ك.، بويشينكو إي.إم. وغيرها امتحان الدولة الموحد رياضيات مواد قياس كنترول - م : تربية 2005 - 80 ص .

5. Denishcheva L.O.، Glazkov Yu.A.، Krasnyanskaya K.A. وغيرها امتحان الدولة الموحدة. الرياضيات. مواد تعليمية وتدريبية لإعداد الطلاب / FIPI - م: مركز الفكر، 2008. - 240 ص.

6. دوروفييف جي في، بوتابوف كيه إم، روزوف إن. دليل الرياضيات للمقبلين على الجامعات – م: ناوكا 1972. – 528 ص.

7. إيجيريف في.ك.، زايتسيف في.في.، كورديمسكي بي.إيه. وغيرها 2500 مسألة في الرياضيات مع الحلول للمقبلين على الجامعات: - م: دار النشر ذات المسؤولية المحدودة "ONICS 21st Century": دار النشر ذات المسؤولية المحدودة "العالم والتعليم"، 2002. - 912 ص.

8. زفافيتش إل.إي.، ريازانوفسكي أ.ر. الهندسة في الجداول - م: بوستارد 2007. - 128 ص.

9. كليمين إس في، سترونكينا تي في، بانتيليفا إي. وغيرها امتحان الدولة الموحدة مهام اختبارية - م : تربية 2002 - 24 ص .

10. Modenov V.P.، Dorofeev G.V.، Novoselov S.I. وغيرها دليل في الرياضيات - م: دار النشر بجامعة موسكو، 1972. - 404 ص.

11. شوفالوفا إي. زد، كابلون في. آي. الهندسة: كتاب مدرسي للأقسام التحضيرية بالجامعات - م: المدرسة العليا 1980. - 265 ص.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

طلب. مهام الحل المستقل

1. في الهرم فابكحواف ABFو اي بي سيعمودي، ب.ف. :F. A. = 15:11. ظل الزاوية المحصورة بين خط مستقيم قبل الميلادوالطائرة ABFيساوي 5. نقطة ممختارة على الحافة قبل الميلادلذا ب م :م ج = 4:11. نقطة تتقع على خط مستقيم F. A.وعلى مسافة متساوية من النقاط مو في.مركز الكرة المحاطة بالهرم فابك , تقع على الحافة أ.ب، مساحة هذه الكرة 36

. أوجد حجم الهرم ASMT. (إجابة: 6)

2. قاعدة الهرم فابكدهو مستطيل ا ب ت ث . طائرة الاتحاد الآسيوي.عمودي على الطائرة اي بي سي , ظل الزاوية القوات المسلحة الكونغوليةيساوي

، ظل الزاوية المحصورة بين الخط قبل الميلادوالطائرة الاتحاد الآسيوي.يساوي . نقطة متقع على الحافة قبل الميلاد ، في إم =قبل الميلاد . نقطة لتقع على خط مستقيم F. A.وعلى مسافة متساوية من النقاط مو ج . حجم الهرم ل في د ميساوي 72. مركز الكرة المحيطة بالهرم فابكد , تقع على مستوى قاعدتها. أوجد نصف قطر هذه الكرة. (إجابة: 5)

3. بالقرب من الهرم العادي فابكيصف الكرة التي يقع مركزها في مستوى القاعدة اي بي سيالأهرامات. نقطة متقع على الحافة أ.بلذا أ م :م ب=1:3. نقطة تتقع على خط مستقيم F. A.وعلى مسافة متساوية من النقطة مو في. حجم الهرم TVSMيساوي

. أوجد نصف قطر الكرة التي يحدها الهرم فابك . (إجابة: )

4. القطعة المستقيمة أ.ب– قطر الكرة . نقاط مع، د ا ب ت ثأعظم. أوجد جيب تمام الزاوية بين السطور سمو أب،لو م- وسط الضلع دينار بحريني . (إجابة:

)

5. القطعة المستقيمة ر ن , يساوي 8، وهو قطر الكرة. نقطة م، لالاستلقاء على الكرة بحيث يكون حجم الهرم ر ن م لأعظم. أوجد مساحة المثلث KLT , أين كو ت – منتصف الأضلاع آر إمو ن معلى التوالى. (إجابة: 4

)

6. بالنظر إلى كرة نصف قطرها 6. الجزء المستوي من الكرة عبارة عن دائرة يبلغ قطرها ط م. تتم إزالة مستوى القسم من مركز الكرة على مسافة 5. نقطة ريتم تحديده على المجال، والنقطة ل ر.ك ل تأعظم. أوجد الزاوية المحصورة بين الخط المستقيم إل إم.والطائرة بي تي كيه , لو مالضلع الأوسط ر.ك. (إجابة: 30

)

7. من خلال المركز عن Fيتم تحديده على المجال، والنقاط أ , ب , ج , د – فابكدأعظم. نقاط م، ت، ل – منتصف الأضلاع فيسبوك , قرص مضغوطو إعلانعلى التوالى. مساحة المثلث ملتيساوي 64

. أوجد نصف قطر الكرة. (إجابة: 2)

8. من خلال المركز عنيتكون قسم من هذا المجال. نقطة Fيتم تحديده على المجال، والنقاط أ , ب , ج , د – بالتتابع على دائرة المقطع العرضي بحيث يكون حجم الهرم فابكدأعظم. أوجد جيب الزاوية المحصورة بين الخط أكونوالطائرة ب.ف.د. . (إجابة:

)

9. بالنظر إلى كرة نصف قطرها 10. الجزء المستوي من هذه الكرة عبارة عن دائرة يبلغ قطرها أ.ب.تتم إزالة مستوى القسم من مركز الكرة على مسافة 8. نقطة ديتم تحديده على المجال، والنقطة مع– على محيط مقطعه بحيث يكون حجم الهرم اي بي سي دأعظم. العثور على مساحة الوجه حوار التعاون الآسيوي .(إجابة: 27

)

10. قاعدة الهرم مستطيلة. الطائرة عمودي على الطائرة اي بي سي، ظل الزاوية المحصورة بين الخط شمسوالطائرة القوات المسلحة الكونغوليةيساوي 2. نقطة متقع على الحافة شمسو إم في =

نقطة لتقع على خط مستقيم F. A.وعلى مسافة متساوية من النقاط مو مع. مركز الكرة المحاطة بالهرم F. A. في قرص مضغوطتقع في مستوى قاعدة الهرم، ونصف قطر هذه الكرة هو 4. أوجد حجم الهرم لوس أنجلوس آنسة. (إجابة: 48)

11. في الكرة، نصف قطرها 2

ABCA 1 في 1 مع 1 . مستقيم تكييف 1 أشكال مع الطائرة ايه بي بي (إجابة: 288)

12. منشور ثلاثي منتظم منقوش في كرة ABCA 1 في 1 مع 1، حجمها 4.5. مستقيم فرجينيا 1 أشكال مع الطائرة VSS 1 زاوية45

. أوجد مساحة سطح الكرة. (إجابة: 11)

13. في كرة ذات نصف قطر

تم نقش المنشور الثلاثي العادي ABCA 1 في 1 مع 1 . مستقيم أ.ب 1 أشكال مع الطائرة لجنة التنسيق الإدارية 1 زاوية 45. أوجد حجم المنشور. (إجابة: 36)

14. احسب حواف المنشور الثلاثي المنتظم، مع معرفة نصف القطر رالكرة المقيدة وزاوية الميل α نصف قطر هذه الكرة المرسومة إلى قمة المنشور، إلى الوجه الجانبي الذي يحتوي على هذه القمة. (إجابة: 2

)

15. إلى كرة نصف قطرها رتم نقش مخروط دائري صحيح. أوجد السطح الجانبي للمخروط إذا كان ارتفاعه ح . (إجابة:

)

16. مخروط منقوش في المجال. مساحة المقطع العرضي المحوري للمخروط تساوي س. الزاوية بين ارتفاعه والمولد تساوي α . أوجد حجم الكرة. (إجابة:

)

17. حدد السطح الجانبي للمخروط بمعرفة طول نصف القطر رالكرة المحصورة حوله والزاوية α, والتي بموجبها يمكن رؤية مولد المخروط من وسط الكرة. (إجابة:

)

18. أوجد نسبة المساحة السطحية الكلية للمخروط القائم المدرج في كرة إلى مساحة سطح هذه الكرة، إذا كانت الزاوية عند قمة المقطع المحوري للمخروط تساوي α و

. (إجابة:

)

19. يتم رسم مخروط في كرة بحيث يتم تقسيم ارتفاعه على مركز الكرة بنسبة المتوسط والأقصى. أوجد الزاوية عند قمة المقطع المحوري للمخروط. حدد عدد المرات التي يكون فيها حجم الكرة أكبر من حجم المخروط. (إجابة:

; 4 مرات )

مثال 2.في الهرم الثلاثي المنتظم يكون طول ضلع القاعدة 5، وتكون أضلاعه الجانبية مائلة على القاعدة بزاوية 60يا. أوجد نصف قطر الكرة المحيطة بالهرم.

حل.يترك ABCMالهرم المشار إليه (انظر الشكل 23) يقع مركز الكرة الموصوفة عند ارتفاع الهرم، حيث أن الهرم منتظم.

قاعدة ارتفاع الهرم هي مركز المثلث اي بي سي، أي نقطة تقاطع المتوسطات. ثم:

CH= ست = CH= = = .

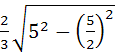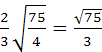الآن فكر في المثلث MNS.هنا الزاوية ام اس انتساوي 60 درجة، وهي الزاوية بين الحافة الجانبية آنسةوالأساس اي بي سي. ركن NMSيساوي 30. مو = نظام التشغيلمثل نصف القطر. إذن فهو مثلث موسمتساوي الساقين. كما تعلم، في المثلث متساوي الساقين تكون زوايا القاعدة متساوية. لذلك،

OSM = التأمين الطبي الإلزامي = 30, أو إس إن = ام اس ان - مكو = 60 - 30= 30.

نظام التشغيل= = .

إجابة: أوك.= .

3.2 أمثلة على مهام الاستخدام بالمنشور

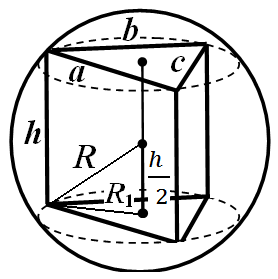
مثال 1.قاعدة المنشور عبارة عن مثلث له جوانبأ, ب, ج. ارتفاع المنشورح(الشكل 25). أوجد نصف قطر الكرة المقيدة.

إجابة:

مثال 2.نصف قطر الكرةر. منشور ذو عدد n منتظم ارتفاعه 2 محفور في كرة.ح(الشكل 26). أوجد جانب قاعدة المنشور.

حل.يترك ل- مركز الكرة المقيدة. لدينا: ك.ب.= ر, نعم= ح. يترك أومأ.ب، ثم

أو.ب.=

(من المثلث أوكي بي).

من مثلث مكتب الإدارة والميزانيةنجد

أ= 2م.ب.= 2أو.ب..

لذا، أ= .

إجابة: أ= .

3.3 أمثلة على مهام امتحان الدولة الموحدة باستخدام الاسطوانة

مثال 1.ارتفاع أسطوانة دائرية أكبر بمقدار 10 من نصف قطر قاعدتها، ومساحة سطحها الإجمالية 144. أوجد نصف قطر الكرة المقيدة.

حل.نصف قطر الكرة المقيدة

مساحة سطح الاسطوانة

دعونا نبسط هذا التعبير:

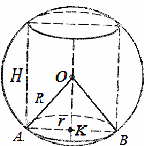
نحصل على معادلة تربيعية

دعونا نجد جذور هذه المعادلة

الجذر غير مناسب لأنه سلبي. ارتفاع

لنجد نصف قطر الكرة المقيدة:

إجابة: .

مثال 2.أسطوانة دائرية مستقيمة محفورة في كرة (الشكل 28). كم مرة يكون حجم الكرة أكبر من حجم الاسطوانة إذا علم أن نسبة نصف قطر الكرة إلى نصف قطر قاعدة الاسطوانة هي نصف نسبة سطح الكرة؟ المجال إلى السطح الجانبي للأسطوانة.

حل.نسبة حجم الكرة إلى حجم الأسطوانة المنقوشة

وبالشرط معروف ذلك

متساوي الاضلاع

دعونا نوجد النسبة بين حجم الكرة والأسطوانة المنقوشة

إجابة: 16:9.

3.4 أمثلة على مهام امتحان الدولة الموحدة باستخدام المخروط

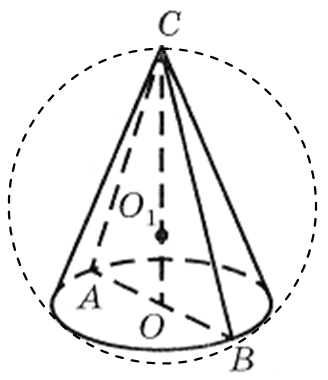
مثال 1.يبلغ قطر قاعدة المخروط 6 أمتار، ويميل المولد إلى مستوى القاعدة بزاوية 60 درجة (الشكل 29). أوجد مساحة الكرة المحصورة حول المخروط.

حل.يترك مع -الجزء العلوي من المخروط عن -مركز قاعدته، مطار الدوحة الدولي -القسم المحوري للمخروط. بما أن مولد المخروط يميل إلى مستوى القاعدة بزاوية 60 درجة و شركةهو ارتفاع المخروط، ثم الخط المستقيم أب -الإسقاط المباشر ساعلى مستوى قاعدة المخروط. لذلك، سيارة أجرةتساوي الزاوية بين مولد المخروط ومساحة قاعدته. لهذا الكابينة = 60 درجة ومثلث متساوي الساقين اي بي سي -صحيح. إنه يتبع هذا

CA = AB = BC= 6 م.

دعونا نجد موضع مركز الكرة المحيط بالمخروط. وبتعريف مثل هذه الكرة، فإن محيط قاعدة المخروط هو جزء من الكرة المقيدة، ورأس المخروط يقع على هذه الكرة. بحسب خاصية قطر الكرة التي تمر بمركز أي قسم منها الخط المستقيم شركةعمودي على مستوى قاعدة المخروط وبالتالي المركز عن 1 من الكرة المقيدة تقع على خط مستقيم شركةويترتب على ذلك المركز عن 1 الكرة المحصورة حول المخروط هي مركز الدائرة المحصورة حول قسمها المحوري.

في المثلث الأيمن

اي بي سير= يا 1 ج= (م)

مثال 3.يتم إدراج مخروط في الكرة، ومولدها يساوي قطر القاعدة (الشكل 31). أوجد نسبة سطح المخروط إلى سطح الكرة.

أ.ب= ر , أد =

دعونا نشير إلى السطح الكلي للمخروط بواسطة س 1، وسطح الكرة من خلال س 2. لدينا

أين س 1: س 2 = 9:16.

إجابة:س 1: س 2 = 9:16.

خاتمة

فهرس

أبراموفيتش إم آي، ستارودوبتسيف إم تي. الرياضيات (الهندسة والدوال المثلثية). الكتاب المدرسي للأقسام التحضيرية بالجامعات - م: المدرسة العليا 1976. - 304 ص.

فويتوفيتش إف إس. تركيبات الأجسام الهندسية: (الأفلاك المنقوشة والمحدودة): كتاب للطلاب. – مينسك: نارودنايا أسفيتا، 1992. – 160 ص.

جوفوروف في إم، ديبوف بي تي، ميروشين إن في وغيرها قائمة المشاكل التنافسية في الرياضيات (مع تعليمات وحلول منهجية): كتاب مدرسي. – الطبعة الثانية – م: ناوكا، 1986. – 384 ص.

Denishcheva L.O.، Bezrukova G.K.، Boychenko E.M. وغيرها امتحان الدولة الموحد رياضيات مواد قياس كنترول - م : تربية 2005 - 80 ص .

Denishcheva L.O.، Glazkov Yu.A.، Krasnyanskaya K.A. وغيرها امتحان الدولة الموحدة. الرياضيات. مواد تعليمية وتدريبية لإعداد الطلاب / FIPI - م: مركز الفكر، 2008. - 240 ص.

Dorofeev G.V.، Potapov K.M.، Rozov N.Kh. دليل الرياضيات للمقبلين على الجامعات – م: ناوكا 1972. – 528 ص.

Egerev V.K.، Zaitsev V.V.، Kordemsky B.A. وغيرها 2500 مسألة في الرياضيات مع الحلول للمقبلين على الجامعات: - م: دار النشر ذات المسؤولية المحدودة "ONICS 21st Century": دار النشر ذات المسؤولية المحدودة "العالم والتعليم"، 2002. - 912 ص.

زفافيتش إل.إي.، ريازانوفسكي أ.ر. الهندسة في الجداول - م: بوستارد 2007. - 128 ص.

Klimin S.V.، Strunkina T.V.، Panteleeva E.I. وغيرها امتحان الدولة الموحدة مهام اختبارية - م : تربية 2002 - 24 ص .

Modenov V.P.، Dorofeev G.V.، Novoselov S.I. وغيرها دليل في الرياضيات - م: دار النشر بجامعة موسكو، 1972. - 404 ص.

شوفالوفا إي. زد، كابلون في. آي. الهندسة: كتاب مدرسي للأقسام التحضيرية بالجامعات - م: المدرسة العليا 1980. - 265 ص.

http :// الكم. مرآة1. com.mccme. رو/ بي دي إف/2000/06/ كيلو فولت0600 solut. بي دي إف

http :// رو. ويكيبيديا. ORG/ ويكي/% د0%9 F% د0% يكون% د1%80% د1%82% د0% ب0% د0% ب:% د0%9 د% د0% ب0% د1%83% د0% بكالوريوس.% د0% ب0

rgp . نانومتر. رو/ هندسة/ praktika11/ زاداتشا119. لغة البرمجة

طلب. مهام الحل المستقل

يعد موضوع "المسائل المختلفة حول متعددات الوجوه والأسطوانة والمخروط والكرة" من أصعب المواضيع في مقرر الهندسة للصف الحادي عشر. قبل حل المشكلات الهندسية، يقومون عادةً بدراسة الأقسام ذات الصلة من النظرية التي يتم الرجوع إليها عند حل المشكلات. في الكتاب المدرسي الذي كتبه S. Atanasyan وآخرون حول هذا الموضوع (ص 138) يمكن للمرء أن يجد فقط تعريفات لمتعدد السطوح الموصوف حول كرة، ومتعدد السطوح منقوش في كرة، وكرة منقوشة في متعدد السطوح، وكرة موصوفة حول كرة. متعدد السطوح. التوصيات المنهجية لهذا الكتاب المدرسي (انظر كتاب "دراسة الهندسة في الصفوف 10-11" للكاتب S. M. Sahakyan و V. F. Butuzov، ص 159) تقول ما هي مجموعات الأجسام التي يتم أخذها في الاعتبار عند حل المشكلات رقم 629-646، ويتم لفت الانتباه إلى حقيقة أنه "عند حل مشكلة معينة، أولاً وقبل كل شيء، من الضروري التأكد من أن الطلاب لديهم فهم جيد للمواضع النسبية للأجسام المشار إليها في الحالة". وفيما يلي حل المسألتين رقم 638(أ) ورقم 640.

وبالنظر إلى كل ما سبق، وحقيقة أن أصعب المشاكل التي يواجهها الطلاب هي الجمع بين الكرة والأجسام الأخرى، فمن الضروري تنظيم المبادئ النظرية ذات الصلة وإيصالها إلى الطلاب.

تعريفات.

1. تسمى الكرة منقوشة في متعدد السطوح، ويتم وصف متعدد السطوح حول الكرة إذا لامس سطح الكرة جميع وجوه متعدد السطوح.

2. تسمى الكرة محصورة حول متعدد السطوح، ومتعددة السطوح محفورة في الكرة، إذا كان سطح الكرة يمر عبر جميع رؤوس متعدد السطوح.

3. يقال إن الكرة مكتوبة في أسطوانة مخروط مقطوع (مخروط) ويقال إن أسطوانة مخروط مقطوع (مخروط) مكتوب حول الكرة إذا لامس سطح الكرة القواعد (القاعدة) وكل شيء مولدات الاسطوانة، المخروط المقطوع (المخروط).

(يترتب على هذا التعريف أنه يمكن إدراج الدائرة الكبرى للكرة في أي قسم محوري من هذه الأجسام).

4. يقال إن الكرة محاطة حول أسطوانة، مخروط مقطوع (مخروط)، إذا كانت دوائر القواعد (دائرة القاعدة والقمة) تنتمي إلى سطح الكرة.

(من هذا التعريف يترتب على أنه يمكن وصف دائرة أكبر من الكرة حول أي قسم محوري من هذه الأجسام).

ملاحظات عامة حول موضع مركز الكرة.

1. يقع مركز الكرة المنقوشة في متعدد السطوح عند نقطة تقاطع المستويات المنصف لجميع زوايا ثنائي السطوح في متعدد السطوح. يقع فقط داخل متعدد السطوح.

2. يقع مركز الكرة المحاطة بمتعدد السطوح عند نقطة تقاطع المستويات المتعامدة مع جميع حواف متعدد السطوح ويمر عبر نقاط منتصفها. يمكن أن يكون موجودًا داخل المجسم متعدد السطوح أو على السطح أو خارجه.

مزيج من المجال والمنشور.

1. كرة منقوشة في منشور مستقيم.

النظرية 1. يمكن رسم كرة في منشور مستقيم إذا أمكن فقط كتابة دائرة عند قاعدة المنشور، وكان ارتفاع المنشور يساوي قطر هذه الدائرة.

النتيجة الطبيعية 1.يقع مركز الكرة المنقوشة في المنشور القائم عند منتصف ارتفاع المنشور المار بمركز الدائرة المنقوشة في القاعدة.

النتيجة الطبيعية 2.يمكن رسم الكرة، على وجه الخصوص، في خطوط مستقيمة: مثلثة، منتظمة، رباعية الزوايا (حيث يكون مجموع الأضلاع المتقابلة للقاعدة متساويًا مع بعضها البعض) تحت الشرط H = 2r، حيث H هو ارتفاع الكرة. المنشور، r هو نصف قطر الدائرة المدرج في القاعدة.

2. كرة محاطة بالمنشور.

النظرية 2. يمكن وصف الكرة حول منشور إذا وفقط إذا كان المنشور مستقيمًا ويمكن وصف دائرة حول قاعدته.

النتيجة الطبيعية 1. يقع مركز الكرة المحصورة حول منشور مستقيم عند منتصف ارتفاع المنشور المرسوم عبر مركز دائرة محيطة بالقاعدة.

النتيجة الطبيعية 2.يمكن وصف الكرة، على وجه الخصوص، بالقرب من منشور ثلاثي قائم، بالقرب من منشور منتظم، بالقرب من متوازي مستطيلات، بالقرب من منشور رباعي الزوايا قائم، حيث يكون مجموع الزوايا المتقابلة للقاعدة يساوي 180 درجة.

من كتاب L. S. Atanasyan، يمكن اقتراح المسائل رقم 632، 633، 634، 637(أ)، 639(أ،ب) للجمع بين الكرة والمنشور.

مزيج من الكرة مع الهرم.

1. كرة موصوفة بالقرب من الهرم.

النظرية 3. يمكن وصف الكرة حول الهرم إذا أمكن وصف دائرة حول قاعدتها فقط.

النتيجة الطبيعية 1.يقع مركز الكرة المحيطة بالهرم عند نقطة تقاطع خط مستقيم عمودي على قاعدة الهرم ويمر بمركز دائرة محيطة بهذه القاعدة ومستوى متعامد مع أي حافة جانبية مرسومة في منتصف الهرم. هذه الحافة.

النتيجة الطبيعية 2.إذا كانت الحواف الجانبية للهرم متساوية مع بعضها البعض (أو مائلة بالتساوي على مستوى القاعدة)، فيمكن وصف كرة حول هذا الهرم، ويقع مركز هذه الكرة في هذه الحالة عند نقطة تقاطع الهرم. ارتفاع الهرم (أو امتداده) مع محور تناظر الحافة الجانبية الواقعة في مستوى الحافة الجانبية والارتفاع.

النتيجة الطبيعية 3.يمكن وصف الكرة، على وجه الخصوص، بالقرب من هرم ثلاثي، بالقرب من هرم منتظم، بالقرب من هرم رباعي الزوايا يكون فيه مجموع الزوايا المتقابلة 180 درجة.

2. كرة منقوشة في الهرم.

النظرية 4. إذا كانت الجوانب الجانبية للهرم مائلة بالتساوي إلى القاعدة، فيمكن إدراج كرة في هذا الهرم.

النتيجة الطبيعية 1.يقع مركز الكرة المنقوشة في الهرم الذي أوجهه الجانبية متساوية في الميل على القاعدة عند نقطة تقاطع ارتفاع الهرم مع منصف الزاوية الخطية لأي زاوية ثنائية السطوح عند قاعدة الهرم، الجانب منها ارتفاع الوجه الجانبي المرسوم من أعلى الهرم.

النتيجة الطبيعية 2.يمكنك وضع كرة في هرم عادي.

من الكتاب المدرسي لـ L. S. Atanasyan، يمكن اقتراح المشكلات رقم 635، 637(ب)، 638، 639(ج)، 640، 641 لدمج الكرة مع الهرم.

مزيج من الكرة مع الهرم المقطوع.

1. كرة محاطة حول هرم منتظم مقطوع.

النظرية 5. يمكن وصف الكرة حول أي هرم منتظم مقطوع. (هذا الشرط كاف وليس ضروريا)

2. كرة منقوشة في هرم منتظم مقطوع.

النظرية 6. يمكن كتابة كرة في هرم منتظم مقطوع إذا وفقط إذا كان قياس الهرم مساويًا لمجموع قياسات القواعد.

هناك مشكلة واحدة فقط في الجمع بين الكرة والهرم المقطوع في كتاب L. S. Atanasyan المدرسي (رقم 636).

مزيج من الكرة مع الأجسام المستديرة.

النظرية 7. يمكن وصف الكرة حول أسطوانة، أو مخروط مقطوع (دائري مستقيم)، أو مخروط.

النظرية 8. يمكن إدراج الكرة في أسطوانة (دائرية مستقيمة) إذا كانت الأسطوانة متساوية الأضلاع وفقط.

النظرية 9. يمكنك وضع كرة في أي مخروط (دائري مستقيم).

النظرية 10. يمكن إدراج الكرة في مخروط مقطوع (دائري مستقيم) إذا وفقط إذا كان مولدها يساوي مجموع أنصاف أقطار القواعد.

من الكتاب المدرسي لـ L. S. Atanasyan، يمكن اقتراح المشكلات رقم 642، 643، 644، 645، 646 لدمج الكرة مع الأجسام المستديرة.

لدراسة المواد حول هذا الموضوع بنجاح أكبر، من الضروري تضمين المهام الشفهية في الدروس:

1. حافة المكعب تساوي أ. أوجد أنصاف أقطار الكرات: المنقوشة في المكعب والمحددة حوله. (ص = أ/2، ص = a3).

2. هل من الممكن وصف كرة (كرة) حول: أ) مكعب؛ ب) متوازي مستطيل. ج) متوازي سطوح مائل وفي قاعدته مستطيل؛ د) متوازي مستقيم. ه) متوازي السطوح المائل؟ (أ) نعم؛ ب) نعم؛ ج) لا؛ د) لا؛ د) لا)

3. هل صحيح أنه يمكن وصف الكرة حول أي هرم ثلاثي؟ (نعم)

4. هل من الممكن وصف كرة حول أي هرم رباعي الزوايا؟ (لا، ليس بالقرب من أي هرم رباعي الزوايا)

5. ما هي الخصائص التي يجب أن يتمتع بها الهرم حتى يتمكن من وصف الكرة المحيطة به؟ (يجب أن يكون في قاعدتها مضلع يمكن وصف الدائرة حوله)

6. الهرم منقوش في كرة تكون حافتها الجانبية متعامدة مع القاعدة. كيفية العثور على مركز الكرة؟ (مركز الكرة هو نقطة التقاطع بين موضعين هندسيين من النقاط في الفضاء. الأول عمودي مرسوم على مستوى قاعدة الهرم، عبر مركز دائرة محيطة به. والثاني مستوى عمودي على حافة جانبية معينة ومرسومة من وسطها)

7. تحت أي ظروف يمكنك وصف كرة حول منشور يوجد في قاعدته شبه منحرف؟ (أولا يجب أن يكون المنشور مستقيما وثانيا يجب أن يكون شبه المنحرف متساوي الساقين حتى يمكن وصف الدائرة حوله)

8. ما هي الشروط التي يجب أن يستوفيها المنشور حتى يمكن وصف الكرة حوله؟ (يجب أن يكون المنشور مستقيماً، وأن تكون قاعدته مضلعاً يمكن وصف الدائرة حوله)

9. يتم وصف الكرة حول منشور ثلاثي يقع مركزه خارج المنشور. أي مثلث هو قاعدة المنشور؟ (مثلث منفرج الزاوية)

10. هل من الممكن وصف كرة حول منشور مائل؟ (لا لا يمكنك)

11. في أي حالة يقع مركز الكرة المحصورة حول المنشور الثلاثي القائم على أحد الوجوه الجانبية للمنشور؟ (القاعدة مثلث قائم الزاوية)

12. قاعدة الهرم عبارة عن شبه منحرف متساوي الساقين، والإسقاط المتعامد لأعلى الهرم على مستوى القاعدة هو نقطة تقع خارج شبه المنحرف. هل من الممكن وصف كرة حول شبه منحرف كهذا؟ (نعم، يمكنك ذلك. لا يهم حقيقة أن الإسقاط المتعامد لأعلى الهرم يقع خارج قاعدته. من المهم أن يوجد في قاعدة الهرم شبه منحرف متساوي الساقين - وهو مضلع يمكن أن تدور حوله دائرة موصوف)

13. تم وصف الكرة بالقرب من هرم منتظم. وكيف يقع مركزها بالنسبة لعناصر الهرم؟ (يكون مركز الكرة عموديا على مستوى القاعدة مرورا بمركزها)

14. تحت أي حالة يقع مركز الكرة الموصوفة حول المنشور الثلاثي القائم: أ) داخل المنشور؛ ب) خارج المنشور؟ (عند قاعدة المنشور: أ) مثلث حاد الزوايا؛ ب) مثلث منفرج)

15. تم وصف الكرة حول متوازي مستطيلات أبعاد حوافه 1 dm، 2 dm، 2 dm. احسب نصف قطر الكرة. (1.5 ديسيمتر)

16. ما هو المخروط المقطوع الذي يمكن أن تتناسب معه الكرة؟ (في المخروط المقطوع، في القسم المحوري الذي يمكن كتابة دائرة منه. القسم المحوري للمخروط هو شبه منحرف متساوي الساقين، يجب أن يكون مجموع قواعده مساويًا لمجموع جوانبه الجانبية. وبعبارة أخرى، يجب أن يكون مجموع أنصاف أقطار قواعد المخروط مساوياً للمولد)

17. كرة منقوشة في مخروط مقطوع. في أي زاوية يمكن رؤية المولد المولد للمخروط من مركز الكرة؟ (90 درجة)

18. ما هي الخاصية التي يجب أن يتمتع بها المنشور المستقيم لكي تُدرج فيه الكرة؟ (أولاً، عند قاعدة المنشور المستقيم، يجب أن يكون هناك مضلع يمكن كتابة دائرة فيه، وثانيًا، يجب أن يكون ارتفاع المنشور مساويًا لقطر الدائرة المنقوشة في القاعدة)

19. أعط مثالا على الهرم الذي لا يمكن أن يصلح للكرة؟ (على سبيل المثال، هرم رباعي الزوايا به مستطيل أو متوازي أضلاع في قاعدته)

20. يوجد في قاعدة المنشور المستقيم معين. هل من الممكن تركيب كرة في هذا المنشور؟ (لا، هذا مستحيل، لأنه بشكل عام من المستحيل وصف دائرة حول معين)

21. في أي حالة يمكن رسم كرة في المنشور الثلاثي القائم؟ (إذا كان ارتفاع المنشور ضعف نصف قطر الدائرة الموضحة في القاعدة)

22. في أي حالة يمكن كتابة كرة في هرم رباعي الزوايا منتظم؟ (إذا كان المقطع العرضي لهرم معين عبارة عن مستوى يمر عبر منتصف جانب القاعدة المتعامد عليه، فهو شبه منحرف متساوي الساقين يمكن كتابة دائرة فيه)

23. تم نقش كرة في هرم مثلث مقطوع. أي نقطة من الهرم هي مركز الكرة؟ (مركز الكرة المنقوشة في هذا الهرم يقع عند تقاطع ثلاث مستويات منقسمة للزوايا تشكلها الوجوه الجانبية للهرم مع القاعدة)

24. هل من الممكن وصف كرة حول أسطوانة (الدائرية اليمنى)؟ (نعم يمكنك)

25. هل من الممكن وصف كرة حول مخروط، مخروط مقطوع (دائري مستقيم)؟ (نعم يمكنك في كلتا الحالتين)

26. هل يمكن كتابة كرة في أي أسطوانة؟ ما هي الخصائص التي يجب أن تتمتع بها الأسطوانة لتتمكن من وضع كرة داخلها؟ (لا، ليس في كل مرة: يجب أن يكون القسم المحوري للأسطوانة مربعا)

27. هل يمكن نقش كرة في أي مخروط؟ كيفية تحديد موضع مركز الكرة المدرج في المخروط؟ (نعم بالتأكيد. يقع مركز الكرة المنقوشة عند تقاطع ارتفاع المخروط ومنصف زاوية ميل المولد إلى مستوى القاعدة)

يعتقد المؤلف أنه من بين دروس التخطيط الثلاثة حول موضوع "المشكلات المختلفة حول متعددات الوجوه والأسطوانة والمخروط والكرة"، يُنصح بتخصيص درسين لحل المشكلات المتعلقة بدمج الكرة مع الأجسام الأخرى. لا ينصح بإثبات النظريات المذكورة أعلاه بسبب عدم كفاية الوقت في الفصل. يمكنك دعوة الطلاب الذين لديهم المهارات الكافية لإثبات ذلك من خلال الإشارة (حسب تقدير المعلم) إلى الدورة التدريبية أو خطة الإثبات.