لماذا يساوي المنتج الاتجاهي الصفر؟ المنتج المتقاطع - التعاريف والخصائص والصيغ والأمثلة والحلول

7.1. تعريف المنتج المتقاطع

ثلاثة نواقل غير متحدة المستوى أ، ب، ج، مأخوذة بالترتيب المشار إليه، تشكل ثلاثية يمينية إذا شوهد من نهاية المتجه الثالث ج، أقصر دورة من المتجه الأول أ إلى المتجه الثاني ب تكون عكس اتجاه عقارب الساعة، وثلاثية أعسر إذا كانت في اتجاه عقارب الساعة (انظر الشكل 16).

يسمى المنتج المتجه للمتجه أ والمتجه ب المتجه ج، والذي:

1. عمودي على المتجهين a وb، أي c ^ a وc ^ ب ؛

2. له طول يساوي عدديًا مساحة متوازي الأضلاع المبني على المتجهات a وبكما في الجوانب (انظر الشكل 17)، أي.

3. تشكل المتجهات a وb وc ثلاثية قائمة.

يُشار إلى المنتج المتقاطع بـ x b أو [a,b]. العلاقات التالية بين متجهات الوحدات أتبعها مباشرة من تعريف حاصل الضرب المتجه، يو ك(انظر الشكل 18):

i x j = k، j x k = i، k x i = j.
دعونا نثبت ذلك، على سبيل المثالأنا xj = ك.

1) ك ^ ط، ك ^ ي ;

2) |ك |=1، لكن | ط س ي| = |أنا | |ي | الخطيئة (90 درجة) = 1؛

3) المتجهات ط، ي و كشكل ثلاثيًا قائمًا (انظر الشكل 16).

7.2. خصائص المنتج المتقاطع

1. عند إعادة ترتيب العوامل، تتغير إشارة المنتج المتجه، أي. و xb =(b xa) (انظر الشكل 19).

المتجهات a xb و b xa متداخلة، ولها نفس الوحدات (تبقى مساحة متوازي الأضلاع دون تغيير)، ولكنها موجهة بشكل معاكس (ثلاثية a، b، a xb و a، b، b x a ذات اتجاه معاكس). إنه com.axb = -(ب أ).

2. المنتج المتجه له خاصية الدمج فيما يتعلق بالعامل العددي، أي l (a xb) = (l a) x b = a x (l b).

دع ل> 0. المتجه l (a xb) متعامد مع المتجهين a وb. المتجه ( لفأس بهو أيضا عمودي على المتجهات و ب(المتجهات أ، لولكن تكمن في نفس الطائرة). وهذا يعني أن المتجهات ل(أ إكس ب) و ( لفأس بعلى استطراد. ومن الواضح أن اتجاهاتهم متطابقة. لديهم نفس الطول:

لهذا ل(أ إكس ب)= لإكس بي. وقد ثبت بطريقة مماثلة ل ل<0.

3. متجهان غير صفريين a و بتكون على خط مستقيم إذا وفقط إذا كان منتجها المتجه يساوي المتجه الصفري، أي a ||b<=>وكسب = 0.

على وجه الخصوص، i *i =j *j =k *k =0 .

4. المنتج المتجه له خاصية التوزيع:

(أ+ب)س ج = أ س ج + ب xs.

سوف نقبل بدون دليل.

7.3. التعبير عن المنتج الاتجاهي بدلالة الإحداثيات

سوف نستخدم جدول الضرب الاتجاهي للمتجهات i، يو ك:

إذا كان اتجاه أقصر مسار من المتجه الأول إلى الثاني يتطابق مع اتجاه السهم، فإن حاصل الضرب يساوي المتجه الثالث، وإذا لم يتطابق، يؤخذ المتجه الثالث بعلامة الطرح.

دع المتجهين a =a x i +a y معطى ي+أ ض كو ب = ب س أنا+ب ي ي+ب ض ك. دعونا نجد المنتج المتجه لهذه المتجهات عن طريق ضربها في كثيرات الحدود (وفقًا لخصائص المنتج المتجه):

يمكن كتابة الصيغة الناتجة بشكل أكثر إيجازًا:

حيث أن الجانب الأيمن من المساواة (7.1) يتوافق مع مفكوك محدد الدرجة الثالثة بدلالة عناصر الصف الأول، ومن السهل تذكر المساواة (7.2).

7.4. بعض تطبيقات المنتج المتقاطع

إنشاء علاقة خطية متداخلة من المتجهات

إيجاد مساحة متوازي الأضلاع والمثلث

حسب تعريف المنتج المتجه للمتجهات أوب |أ إكس بي | =|أ | * |b |sin g، أي أزواج S = |a x b |. وبالتالي، D S =1/2|a x b |.

تحديد عزم القوة حول نقطة ما

دع القوة تطبق عند النقطة A و = أ بدعها تذهب عن- نقطة ما في الفضاء (انظر الشكل 20).

ومن المعروف من الفيزياء أن لحظة القوة F نسبة إلى النقطة عنيسمى ناقل م،الذي يمر عبر النقطة عنو:

1) عمودي على المستوى الذي يمر عبر النقاط يا، أ، ب؛

2) يساوي عدديًا حاصل ضرب القوة لكل ذراع

3) يشكل ثلاثيًا قائمًا مع المتجهات OA وAB.

لذلك، M = الزراعة العضوية × F.

إيجاد سرعة الدوران الخطية

سرعة الخامسالنقطة M لجسم صلب يدور بسرعة زاوية ثحول محور ثابت، يتم تحديده بواسطة صيغة أويلر v =w xr، حيث r =OM، حيث O هي نقطة ثابتة في المحور (انظر الشكل 21).

قبل إعطاء مفهوم المنتج المتجه، دعونا ننتقل إلى مسألة اتجاه ثلاثية مرتبة من المتجهات a →، b →، c → في الفضاء ثلاثي الأبعاد.

في البداية، دعونا نضع جانبًا المتجهات a → , b → , c → من نقطة واحدة. يمكن أن يكون اتجاه الثلاثي a → , b → , c → يمينًا أو يسارًا، اعتمادًا على اتجاه المتجه c → نفسه. سيتم تحديد نوع الثلاثي a → , b → , c → من الاتجاه الذي يتم فيه أقصر دورة من المتجه a → إلى b → من نهاية المتجه c → .

إذا تم تنفيذ أقصر دورة عكس اتجاه عقارب الساعة، فسيتم استدعاء ثلاثية المتجهات a → , b → , c → يمين، إذا كان في اتجاه عقارب الساعة - غادر.

بعد ذلك، خذ متجهين غير خطيين a → وb →. دعونا بعد ذلك نرسم المتجهات A B → = a → و A C → = b → من النقطة A. لنقم ببناء المتجه A D → = c →، والذي يكون متعامدًا في الوقت نفسه على كل من A B → وAC →. وهكذا، عند بناء المتجه نفسه A D → = c →، يمكننا أن نفعل شيئين، نعطيه إما اتجاه واحد أو الاتجاه المعاكس (انظر الشكل التوضيحي).

يمكن لثلاثية المتجهات المرتبة a → , b → , c → أن تكون، كما اكتشفنا، يمينًا أو يسارًا اعتمادًا على اتجاه المتجه.

مما سبق يمكننا تقديم تعريف المنتج المتجه. يتم تقديم هذا التعريف لمتجهين محددين في نظام إحداثيات مستطيل لمساحة ثلاثية الأبعاد.

التعريف 1

المنتج المتجه لمتجهين a → و b → سوف نسمي هذا المتجه المحدد في نظام إحداثيات مستطيل لمساحة ثلاثية الأبعاد مثل:

إذا كان المتجهان a → و b → على خط واحد، فسيكون صفرًا؛
سيكون عموديًا على كل من المتجه a → والمتجه b → أي. ∠ أ → ج → = ∠ ب → ج → = π 2 ;
يتم تحديد طوله بالصيغة: c → = a → · b → · sin ∠ a → , b → ;
ثلاثية المتجهات a → , b → , c → لها نفس اتجاه نظام الإحداثيات المحدد.

المنتج المتجه للمتجهات a → و b → له الترميز التالي: a → × b →.

إحداثيات المنتج المتجه

نظرًا لأن أي متجه له إحداثيات معينة في نظام الإحداثيات، فيمكننا تقديم تعريف ثانٍ لمنتج المتجهات، مما سيسمح لنا بإيجاد إحداثياته باستخدام الإحداثيات المعطاة للمتجهات.

التعريف 2

في نظام إحداثي مستطيل للفضاء ثلاثي الأبعاد المنتج المتجه لمتجهين a → = (a x ; a y ; a z) و b → = (b x ; b y ; b z) يسمى المتجه c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → حيث i → , j → , k → هي متجهات إحداثية.

يمكن تمثيل حاصل الضرب المتجه كمحدد لمصفوفة مربعة من الدرجة الثالثة، حيث يحتوي الصف الأول على المتجهات المتجهة i → , j → , k → , ويحتوي الصف الثاني على إحداثيات المتجه a → , والصف الثالث يحتوي على إحداثيات المتجه b → في نظام إحداثيات مستطيل معين، وهذا هو محدد المصفوفة كما يلي: c → = a → × b → = i → j → k → a x a y a z b x b y b z

بتوسيع هذا المحدد إلى عناصر الصف الأول، نحصل على المساواة: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × ب → = (أ ذ ب ض - أ ض ب ذ) i → + (أ ض ب س - أ س ب ض) ي → + (أ س ب ص - أ ذ ب س) ك →

خصائص المنتج المتقاطع

من المعروف أن حاصل الضرب المتجه في الإحداثيات يتم تمثيله كمحدد للمصفوفة c → = a → × b → = i → j → k → a x a y a z b x b y b z ، ثم على الأساس خصائص محدد المصفوفةيتم عرض ما يلي خصائص المنتج المتجه:

مضاد التبادل أ → × ب → = - ب → × أ → ;
التوزيعية أ (1) → + أ (2) → × ب = أ (1) → × ب → + أ (2) → × ب → أو أ → × ب (1) → + ب (2) → = أ → × ب (1) → + أ → × ب (2) → ;
الترابط π a → × b → = π a → × b → أو a → × (lect b →) = π a → × b →، حيث π هو رقم حقيقي تعسفي.

هذه الخصائص لها براهين بسيطة.

على سبيل المثال، يمكننا إثبات الخاصية المضادة للتبديل للمنتج المتجه.

إثبات مضاد التبديل

حسب التعريف، a → × b → = i → j → k → a x a y a z b x b y b z و b → × a → = i → j → k → b x b y b z a x a y a z . وإذا تم تبديل صفين من المصفوفة، فيجب أن تتغير قيمة محدد المصفوفة إلى العكس، وبالتالي، a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → والذي يثبت أن المنتج المتجه مضاد للتبادل.

منتج المتجهات - الأمثلة والحلول

في معظم الحالات، هناك ثلاثة أنواع من المشاكل.

في المسائل من النوع الأول، عادةً ما يتم إعطاء طولي متجهين والزاوية بينهما، وتحتاج إلى إيجاد طول حاصل ضرب المتجه. في هذه الحالة، استخدم الصيغة التالية c → = a → · b → · sin ∠ a → , b → .

مثال 1

أوجد طول حاصل ضرب المتجهات للمتجهين a → وb → إذا كنت تعرف a → = 3، b → = 5، ∠ a →، b → = π 4.

حل

من خلال تحديد طول المنتج المتجه للمتجهين a → و b →، نحل هذه المشكلة: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .

إجابة: 15 2 2 .

مشاكل النوع الثاني لها علاقة بإحداثيات المتجهات، حيث يوجد منتج المتجهات وطوله وما إلى ذلك. يتم البحث من خلال الإحداثيات المعروفة للمتجهات المعطاة أ → = (أ س؛ أ ص؛ أ ض) و ب → = (ب س ; ب ص ; ب ض) .

بالنسبة لهذا النوع من المشاكل، يمكنك حل الكثير من خيارات المهام. على سبيل المثال، لا يمكن تحديد إحداثيات المتجهين a → وb →، ولكن يمكن تحديد توسعاتهم في المتجهات الإحداثية للنموذج ب → = ب س · أنا → + ب ذ · ي → + ب ض · ك → و c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →، أو يمكن تحديد المتجهات a → و b → بإحداثيات بدايتها ونقاط النهاية.

النظر في الأمثلة التالية.

مثال 2

في نظام الإحداثيات المستطيل، يتم إعطاء متجهين: a → = (2; 1; - 3)، b → = (0; - 1; 1). ابحث عن منتجهم المتقاطع.

حل

بالتعريف الثاني، نجد حاصل الضرب المتجه لمتجهين في الإحداثيات المعطاة: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( أ س · ب ص - أ ص · ب س) · ك → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · ي → + (2) · (- 1) - 1 · 0) · ك → = = - 2 ط → - 2 ي → - 2 ك → .

إذا كتبنا حاصل الضرب المتجه من خلال محدد المصفوفة، فإن حل هذا المثال يبدو كما يلي: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 ط → - 2 ي → - 2 ك → .

إجابة: أ → × ب → = - 2 ط → - 2 ي → - 2 ك → .

مثال 3

أوجد طول حاصل ضرب المتجهات للمتجهات i → - j → وi → + j → + k →، حيث i →، j →، k → هي متجهات الوحدة لنظام الإحداثيات الديكارتية المستطيل.

حل

أولاً، دعونا نوجد إحداثيات منتج متجه معين i → - j → × i → + j → + k → في نظام إحداثيات مستطيل معين.

من المعروف أن المتجهات i → - j → و i → + j → + k → لها إحداثيات (1؛ - 1؛ 0) و (1؛ 1؛ 1)، على التوالي. دعونا نوجد طول حاصل الضرب المتجه باستخدام محدد المصفوفة، ثم لدينا i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - ي → + 2 ك → .

ولذلك، فإن المنتج المتجه i → - j → × i → + j → + k → له إحداثيات (- 1 ; - 1 ; 2) في نظام الإحداثيات المحدد.

نجد طول حاصل ضرب المتجه باستخدام الصيغة (انظر القسم الخاص بإيجاد طول المتجه): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

إجابة: أنا → - ي → × أنا → + ي → + ك → = 6 . .

مثال 4

في نظام الإحداثيات الديكارتي المستطيل، يتم إعطاء إحداثيات ثلاث نقاط A (1، 0، 1)، B (0، 2، 3)، C (1، 4، 2). أوجد متجهًا متعامدًا على A B → و A C → في نفس الوقت.

حل

المتجهان A B → و A C → لهما الإحداثيات التالية (- 1 ; 2 ; 2) و (0 ; 4 ; 1) على التوالي. بعد العثور على المنتج المتجه للمتجهين A B → و A C →، فمن الواضح أنه متجه عمودي حسب التعريف لكل من A B → و A C →، أي أنه حل لمشكلتنا. لنجدها A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

إجابة: - 6 ط → + ي → - 4 ك → . - أحد المتجهات المتعامدة.

وتتركز مشاكل النوع الثالث على استخدام خصائص المنتج المتجه للمتجهات. وبعد تطبيق ذلك سنحصل على حل للمشكلة المحددة.

مثال 5

المتجهان a → و b → متعامدان وأطوالهما هي 3 و 4 على التوالي. أوجد طول المنتج المتجه 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · أ → × - 2 · ب → + - ب → × أ → + - ب → × - 2 · ب → .

حل

من خلال الخاصية التوزيعية للمنتج المتجه، يمكننا كتابة 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 أ → × أ → + 3 أ → × - 2 ب → + - ب → × أ → + - ب → × - 2 ب →

بواسطة خاصية الترابط، نخرج المعاملات العددية من إشارة نواتج المتجهات في التعبير الأخير: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - ب → × - 2 · ب → = = 3 · أ → × أ → + 3 · (- 2) · أ → × ب → + (- 1) · ب → × أ → + (- 1) · (- 2) · ب → × ب → = = 3 أ → × أ → - 6 أ → × ب → - ب → × أ → + 2 ب → × ب →

منتجات المتجهات a → × a → و b → × b → تساوي 0، حيث أن a → × a → = a → · a → · sin 0 = 0 و b → × b → = b → · b → · sin 0 = 0، ثم 3 · أ → × أ → - 6 · أ → × ب → - ب → × أ → + 2 · ب → × ب → = - 6 · أ → × ب → - ب → × أ → . .

من عكسية المنتج المتجه يتبع - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ب → . .

باستخدام خصائص المنتج المتجه، نحصل على المساواة 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

حسب الحالة، يكون المتجهان a → و b → متعامدين، أي أن الزاوية بينهما تساوي π 2. الآن كل ما تبقى هو استبدال القيم التي تم العثور عليها في الصيغ المناسبة: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → ب → · الخطيئة (أ → ، ب →) = 5 · 3 · 4 · الخطيئة π 2 = 60 .

إجابة: 3 أ → - ب → × أ → - 2 ب → = 60.

طول المنتج المتجه للمتجهات حسب التعريف يساوي a → × b → = a → · b → · sin ∠ a → , b → . حيث أنه من المعروف (من المقرر الدراسي) أن مساحة المثلث تساوي نصف حاصل ضرب طولي ضلعيه مضروباً في جيب الزاوية الواقعة بين هذين الضلعين. وبالتالي، فإن طول منتج المتجه يساوي مساحة متوازي الأضلاع - مثلث مضاعف، أي منتج الجوانب في شكل ناقلات a → و b →، المنصوص عليها من نقطة واحدة، بواسطة جيب الزاوية بينهما الخطيئة ∠ أ →، ب →.

هذا هو المعنى الهندسي للمنتج المتجه.

المعنى المادي للمنتج ناقلات

في الميكانيكا، أحد فروع الفيزياء، بفضل المنتج المتجه، يمكنك تحديد عزم القوة بالنسبة إلى نقطة ما في الفضاء.

التعريف 3

بحلول لحظة تطبيق القوة F → على النقطة B، بالنسبة إلى النقطة A، سوف نفهم المنتج المتجه التالي A B → × F →.

إذا لاحظت وجود خطأ في النص، فيرجى تحديده والضغط على Ctrl+Enter

الزاوية بين المتجهات

لكي نتمكن من تقديم مفهوم حاصل الضرب المتجه لمتجهين، علينا أولًا أن نفهم مفهومًا مثل الزاوية بين هذين المتجهين.

دعونا نحصل على متجهين $\overline(α)$ و $\overline(β)$. دعونا نأخذ نقطة ما $O$ في الفضاء ونرسم منها المتجهات $\overline(α)=\overline(OA)$ و $\overline(β)=\overline(OB)$ منها، ثم الزاوية $AOB$ سيتم تسميتها بالزاوية بين هذه المتجهات (الشكل 1).

تدوين: $∠(\overline(α),\overline(β))$

مفهوم المنتج المتجه للمتجهات وصيغة البحث

التعريف 1

حاصل الضرب المتجه لمتجهين هو متجه متعامد على كلا المتجهين المعطاين، وسيكون طوله مساويًا لمنتج أطوال هذين المتجهين مع جيب الزاوية بين هذين المتجهين، وأيضًا هذا المتجه ذو المتجهين الأوليين له نفس اتجاه نظام الإحداثيات الديكارتية.

تدوين: $\overline(α)x\overline(β)$.

رياضيا يبدو مثل هذا:

$|\overline(α)x\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
$\overline(α)x\overline(β)⊥\overline(α)$, $\overline(α)x\overline(β)⊥\overline(β)$
$(\overline(α)x\overline(β),\overline(α),\overline(β))$ و $(\overline(i),\overline(j),\overline(k))$ هي نفس التوجه (الشكل 2)

ومن الواضح أن المنتج الخارجي للمتجهات سوف يساوي المتجه الصفري في حالتين:

إذا كان طول أحد المتجهين أو كليهما يساوي صفرًا.
إذا كانت الزاوية بين هذه المتجهات تساوي $180^\circ$ أو $0^\circ$ (حيث أن جيب الجيب في هذه الحالة هو صفر).

لكي ترى بوضوح كيف يتم العثور على المنتج المتجه للمتجهات، فكر في الأمثلة التالية للحلول.

مثال 1

أوجد طول المتجه $\overline(δ)$، الذي سيكون نتيجة حاصل ضرب المتجهات للمتجهات، بإحداثيات $\overline(α)=(0,4,0)$ و $\overline(β) =(3,0,0 )$.

حل.

دعونا نصور هذه المتجهات في مساحة الإحداثيات الديكارتية (الشكل 3):

الشكل 3. المتجهات في مساحة الإحداثيات الديكارتية. Author24 - تبادل أعمال الطلاب عبر الإنترنت

نرى أن هذه المتجهات تقع على المحورين $Ox$ و$Oy$، على التوالي. وبالتالي فإن الزاوية بينهما ستكون $90^\circ$. لنجد أطوال هذه المتجهات:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

ومن ثم، من خلال التعريف 1، نحصل على الوحدة النمطية $|\overline(δ)|$

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

الجواب: 12 دولاراً.

حساب المنتج الاتجاهي من إحداثيات المتجهات

يتضمن التعريف 1 على الفور طريقة للعثور على المنتج المتجه لمتجهين. نظرًا لأن المتجه، بالإضافة إلى قيمته، له اتجاه أيضًا، فمن المستحيل العثور عليه فقط باستخدام كمية قياسية. لكن بالإضافة إلى ذلك، هناك أيضًا طريقة للعثور على المتجهات المعطاة لنا باستخدام الإحداثيات.

دعونا نحصل على المتجهات $\overline(α)$ و$\overline(β)$، والتي سيكون لها إحداثيات $(α_1,α_2,α_3)$ و$(β_1,β_2,β_3)$، على التوالي. ثم يمكن العثور على متجه الضرب الاتجاهي (أي إحداثياته) باستخدام الصيغة التالية:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

بخلاف ذلك، بتوسيع المحدد، نحصل على الإحداثيات التالية

$\overline(α)x\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

مثال 2

أوجد متجه المنتج المتجه للمتجهات الخطية $\overline(α)$ و$\overline(β)$ بالإحداثيات $(0,3,3)$ و$(-1,2,6)$.

حل.

دعونا نستخدم الصيغة المذكورة أعلاه. نحن نحصل

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18) -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$

الجواب: $(12,-3,3)$.

خصائص المنتج المتجه للنواقل

بالنسبة إلى المتجهات الثلاثة المختلطة التعسفية $\overline(α)$ و$\overline(β)$ و$\overline(γ)$، بالإضافة إلى $r∈R$، فإن الخصائص التالية تحمل:

مثال 3

أوجد مساحة متوازي الأضلاع الذي إحداثيات رؤوسه $(3,0,0)$، $(0,0,0)$، $(0,8,0)$ و$(3,8,0) $.

حل.

أولاً، دعونا نصور متوازي الأضلاع هذا في مساحة الإحداثيات (الشكل 5):

الشكل 5. متوازي الأضلاع في مساحة الإحداثيات. Author24 - تبادل أعمال الطلاب عبر الإنترنت

نرى أن جانبي متوازي الأضلاع هذا تم إنشاؤهما باستخدام متجهات خطية متداخلة بإحداثيات $\overline(α)=(3,0,0)$ و $\overline(β)=(0,8,0)$. وباستخدام الخاصية الرابعة نحصل على:

$S=|\overline(α)x\overline(β)|$

دعونا نجد المتجه $\overline(α)x\overline(β)$:

$\overline(α)x\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (ط)-0\overline(j)+24\overline(k)=(0,0,24)$

لذلك

$S=|\overline(α)x\overline(β)|=\sqrt(0+0+24^2)=24$

من الواضح، في حالة المنتج المتجه، أن الترتيب الذي يتم به أخذ المتجهات مهم، علاوة على ذلك،

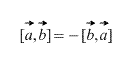
أيضًا، مباشرة من التعريف يترتب على ذلك بالنسبة لأي عامل عددي k (رقم) ما يلي صحيح:

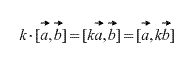
المنتج الاتجاهي للمتجهات الخطية يساوي المتجه الصفري. علاوة على ذلك، يكون الضرب الاتجاهي لمتجهين صفرًا إذا كانا على خط واحد فقط. (في حالة كون أحدهما متجهًا صفرًا، فمن الضروري أن نتذكر أن المتجه الصفري يكون على خط مستقيم مع أي متجه حسب التعريف).

المنتج ناقلات لديه خاصية التوزيع، إنه

التعبير عن منتج المتجه من خلال إحداثيات المتجهات.

دعونا نعطي ناقلين

(كيفية العثور على إحداثيات المتجه من إحداثيات بدايته ونهايته - راجع المقالة المنتج النقطي للمتجهات، البند التعريف البديل للمنتج النقطي، أو حساب المنتج النقطي لمتجهين محددين بإحداثياتهما.)

لماذا تحتاج إلى منتج متجه؟

هناك العديد من الطرق لاستخدام حاصل الضرب الاتجاهي، على سبيل المثال، كما هو مكتوب أعلاه، من خلال حساب حاصل الضرب الاتجاهي لمتجهين يمكنك معرفة ما إذا كانا على خط واحد.

أو يمكن استخدامه كوسيلة لحساب مساحة متوازي الأضلاع المبني من هذه المتجهات. وبناء على التعريف، فإن طول المتجه الناتج هو مساحة متوازي الأضلاع المحدد.

هناك أيضًا عدد كبير من التطبيقات في الكهرباء والمغناطيسية.

آلة حاسبة لمنتج المتجهات عبر الإنترنت.

للعثور على المنتج القياسي لمتجهين باستخدام هذه الآلة الحاسبة، عليك إدخال إحداثيات المتجه الأول في السطر الأول بالترتيب، والثاني في السطر الثاني. يمكن حساب إحداثيات المتجهات من إحداثيات بدايتها ونهايتها (انظر المقالة المنتج النقطي للمتجهات، البند تعريف بديل للمنتج النقطي، أو حساب المنتج النقطي لمتجهين معطيين بإحداثياتهما.)

ناقلات العمل الفنيهو متجه كاذب متعامد على مستوى مكون من عاملين، وهو نتيجة العملية الثنائية "ضرب المتجهات" على المتجهات في الفضاء الإقليدي ثلاثي الأبعاد. لا يمتلك المنتج المتجه خصائص التبادلية والترابطية (وهو مضاد للإبدال)، وعلى عكس المنتج القياسي للمتجهات، فهو متجه. تستخدم على نطاق واسع في العديد من التطبيقات الهندسية والفيزيائية. على سبيل المثال، يتم كتابة الزخم الزاوي وقوة لورنتز رياضيا كمنتج متجه. يعتبر الضرب الاتجاهي مفيدًا في "قياس" عمودي المتجهات - معامل الضرب الاتجاهي لمتجهين يساوي منتج معامليهما إذا كانا متعامدين، وينخفض إلى الصفر إذا كانت المتجهات متوازية أو غير متوازية.

يمكن تعريف حاصل الضرب المتجه بطرق مختلفة، ومن الناحية النظرية، في الفضاء بأي بعد n، يمكن للمرء حساب حاصل ضرب المتجهات n-1، وبالتالي الحصول على متجه واحد عمودي عليهم جميعًا. ولكن إذا كان المنتج يقتصر على المنتجات الثنائية غير التافهة ذات النتائج المتجهة، فإن المنتج المتجه التقليدي يتم تعريفه فقط في الفضاءات ثلاثية الأبعاد وسبعة الأبعاد. تعتمد نتيجة الضرب المتجه، مثل المنتج العددي، على قياس الفضاء الإقليدي.

على عكس صيغة حساب متجهات المنتج العددية من الإحداثيات في نظام إحداثيات مستطيل ثلاثي الأبعاد، تعتمد صيغة المنتج الاتجاهي على اتجاه نظام الإحداثيات المستطيل، أو بعبارة أخرى، "لامركزية".

تعريف:
المنتج المتجه للمتجه a والمتجه b في الفضاء R3 هو المتجه c الذي يلبي المتطلبات التالية:
طول المتجه c يساوي حاصل ضرب أطوال المتجهين a و b وجيب الزاوية φ بينهما:
|ج|=|أ||ب|الخطيئة φ;
المتجه c متعامد مع كل من المتجهين a و b؛
يتم توجيه المتجه c بحيث يكون ثلاثي المتجهات abc أيمنًا؛
في حالة الفضاء R7، يلزم وجود ترابط ثلاثي المتجهات a، b، c.
تعيين:
ج===أ × ب

أرز. 1. مساحة متوازي الأضلاع تساوي معامل المنتج المتجه

الخصائص الهندسية للمنتج المتقاطع:
الشرط الضروري والكافي للعلاقة الخطية المتداخلة بين متجهين غير صفريين هو أن حاصل ضربهما المتجه يساوي صفرًا.

وحدة المنتجات المتقاطعة يساوي المساحة سمتوازي الأضلاع مبني على ناقلات مختزلة إلى أصل مشترك أو ب(انظر الشكل 1).

لو ه- وحدة المتجهات متعامدة مع المتجهات أو بواختار بحيث ثلاثة أ، ب، ه- صحيح، و سهي مساحة متوازي الأضلاع المبنية عليها (مختزلة إلى أصل مشترك)، فإن صيغة حاصل الضرب المتجه تكون صالحة:
=س ه

الصورة 2. حجم متوازي السطوح باستخدام المتجه والمنتج العددي للمتجهات؛ توضح الخطوط المنقطة إسقاطات المتجه c على a × b والمتجه a على b × c، والخطوة الأولى هي العثور على المنتجات العددية

لو ج- بعض المتجهات، π - أي طائرة تحتوي على هذا المتجه، ه- متجه الوحدة ملقاة في الطائرة π ومتعامد ل ج، ز- متجه الوحدة المتعامد مع المستوى π وتوجيهها بحيث الثلاثي من النواقل تخطيط القلبهو الصحيح، ثم لأي الكذب في الطائرة π المتجه أالصيغة صحيحة:
=Pr e a |c|g
حيث Pr e a هو إسقاط المتجه e على a
|c|-معامل المتجه c

عند استخدام المنتجات المتجهة والعددية، يمكنك حساب حجم متوازي السطوح المبني على ناقلات مختزلة إلى أصل مشترك أ، بو ج. يسمى هذا المنتج المكون من ثلاثة نواقل مختلطًا.
V=|أ (ب×ج)|
يوضح الشكل أنه يمكن العثور على هذا الحجم بطريقتين: يتم الحفاظ على النتيجة الهندسية حتى عند تبديل المنتجات "العددية" و"المتجهة":
V=أ×ب ج=أ ب×ج

يعتمد مقدار حاصل الضرب الاتجاهي على جيب الزاوية بين المتجهات الأصلية، لذلك يمكن إدراك حاصل الضرب الاتجاهي على أنه درجة "تعامد" المتجهات، تمامًا كما يمكن رؤية حاصل الضرب القياسي على أنه درجة "التوازي" ". يساوي حاصل الضرب المتجه لمتجهي وحدة 1 (متجه الوحدة) إذا كانت المتجهات الأصلية متعامدة، ويساوي 0 (متجه صفر) إذا كانت المتجهات متوازية أو غير متوازية.

التعبير عن المنتج الاتجاهي في الإحداثيات الديكارتية
إذا اثنين من المتجهات أو بمحددة بإحداثياتها الديكارتية المستطيلة، أو بشكل أكثر دقة، ممثلة على أساس متعامد
أ=(أ س ,أ ص ,أ ض)
ب=(ب س،ب ذ،ب ض)
وإذا كان النظام الإحداثي أيمن، فإن حاصل الضرب المتجه له الشكل
=(أ y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
لتذكر هذه الصيغة:
ط =∑ε ijk أ ي ب ك
أين ε إيك- رمز ليفي سيفيتا.