Chỉ có “X” và chỉ có trục x, nhưng bây giờ “Y” được thêm vào và trường hoạt động mở rộng ra toàn bộ mặt phẳng tọa độ. Hơn nữa, trong văn bản, cụm từ “bất đẳng thức tuyến tính” được hiểu theo nghĩa hai chiều, điều này sẽ trở nên rõ ràng sau vài giây.
Ngoài hình học giải tích, tài liệu này còn liên quan đến một số vấn đề trong phân tích toán học cũng như mô hình kinh tế và toán học, vì vậy tôi khuyên bạn nên nghiên cứu bài giảng này một cách nghiêm túc.
Bất đẳng thức tuyến tính
Có hai loại bất đẳng thức tuyến tính:
1) Nghiêm ngặt bất đẳng thức: .
2) lỏng lẻo bất đẳng thức: .
Ý nghĩa hình học của những bất đẳng thức này là gì? Nếu một phương trình tuyến tính xác định một đường thẳng thì bất đẳng thức tuyến tính xác định nửa mặt phẳng.
Để hiểu được thông tin dưới đây, bạn cần biết các loại đường thẳng trên mặt phẳng và có thể dựng được đường thẳng. Nếu bạn gặp bất kỳ khó khăn nào trong phần này, hãy đọc phần trợ giúp Đồ thị và tính chất của hàm– đoạn văn về hàm tuyến tính.
Hãy bắt đầu với những bất đẳng thức tuyến tính đơn giản nhất. Ước mơ của mọi học sinh nghèo là một mặt phẳng tọa độ trên đó không có gì:

Như bạn đã biết, trục x được cho bởi phương trình - “y” luôn (đối với bất kỳ giá trị nào của “x”) bằng 0
Hãy xem xét sự bất bình đẳng. Làm thế nào để hiểu nó một cách chính thức? “Y” luôn luôn (với bất kỳ giá trị nào của “x”) dương. Rõ ràng, bất đẳng thức này xác định nửa mặt phẳng trên - xét cho cùng, tất cả các điểm có “trò chơi” dương đều nằm ở đó.
Trong trường hợp bất đẳng thức không nghiêm ngặt, đến nửa mặt phẳng trên thêm vào đó trục chính nó được thêm vào.
Tương tự: bất đẳng thức được thỏa mãn bởi mọi điểm của nửa mặt phẳng dưới; bất đẳng thức không chặt tương ứng với nửa mặt phẳng dưới + trục.
Câu chuyện tầm thường tương tự cũng xảy ra với trục y:
– bất đẳng thức xác định nửa mặt phẳng bên phải;
– bất đẳng thức xác định nửa mặt phẳng bên phải, kể cả trục hoành;
– bất đẳng thức xác định nửa mặt phẳng bên trái;
– bất đẳng thức xác định nửa mặt phẳng bên trái, kể cả trục hoành.
Trong bước thứ hai, chúng ta xem xét các bất đẳng thức trong đó thiếu một trong các biến.
Thiếu chữ "Y":
Hoặc không có chữ “x”:
Những bất bình đẳng này có thể được giải quyết theo hai cách: vui lòng xem xét cả hai cách tiếp cận. Trong quá trình thực hiện, chúng ta hãy ghi nhớ và củng cố các hoạt động của trường với những bất bình đẳng đã được thảo luận trên lớp. Miền chức năng.
Ví dụ 1
Giải bất đẳng thức tuyến tính:
Việc giải bất đẳng thức tuyến tính có ý nghĩa gì?
Giải bất đẳng thức tuyến tính có nghĩa là tìm nửa mặt phẳng, điểm của nó thỏa mãn bất đẳng thức này (cộng với chính đường thẳng đó, nếu bất đẳng thức không nghiêm ngặt). Giải pháp, như một quy luật, đồ họa.
Sẽ thuận tiện hơn khi thực hiện ngay bản vẽ và sau đó nhận xét mọi thứ: 
a) Giải bất đẳng thức
Phương pháp một
Phương pháp này rất gợi nhớ đến câu chuyện với các trục tọa độ mà chúng ta đã thảo luận ở trên. Ý tưởng là biến đổi bất đẳng thức - để lại một biến ở vế trái mà không có bất kỳ hằng số nào, trong trường hợp này là biến “x”.
Luật lệ: Trong một bất đẳng thức, các số hạng được chuyển từ phần này sang phần khác bằng cách đổi dấu, còn dấu của chính bất đẳng thức đó không thay đổi(ví dụ: nếu có dấu "nhỏ hơn" thì nó sẽ vẫn là "nhỏ hơn").
Chúng ta di chuyển số “năm” sang bên phải bằng cách đổi dấu:
Luật lệ TÍCH CỰC không thay đổi.
Bây giờ vẽ một đường thẳng (đường chấm màu xanh). Đường thẳng được vẽ là đường chấm chấm vì bất đẳng thức nghiêm ngặt, và các điểm thuộc đường này chắc chắn sẽ không được đưa vào lời giải.
Ý nghĩa của sự bất bình đẳng là gì? “X” luôn luôn (đối với bất kỳ giá trị nào của “Y”) nhỏ hơn . Rõ ràng phát biểu này được thỏa mãn bởi mọi điểm của nửa mặt phẳng bên trái. Về nguyên tắc, nửa mặt phẳng này có thể được tô bóng, nhưng tôi sẽ hạn chế sử dụng những mũi tên nhỏ màu xanh lam để không biến bức vẽ thành một bảng màu nghệ thuật.
Phương pháp hai
Đây là một phương pháp phổ quát. ĐỌC RẤT CẨN THẬN!
Đầu tiên chúng ta vẽ một đường thẳng. Nhân tiện, để rõ ràng, nên trình bày phương trình ở dạng .
Bây giờ chọn bất kỳ điểm nào trên mặt phẳng, không trực tiếp. Tất nhiên, trong hầu hết các trường hợp, điểm tốt nhất là. Hãy thay tọa độ của điểm này vào bất đẳng thức: ![]()
Đã nhận bất đẳng thức sai(nói một cách đơn giản, điều này không thể xảy ra), điều này có nghĩa là điểm không thỏa mãn bất đẳng thức.
Nguyên tắc chính của nhiệm vụ của chúng tôi:
không thỏa mãn thì bất bình đẳng TẤT CẢ các điểm của nửa mặt phẳng cho trước không thỏa mãn sự bất bình đẳng này.
– Nếu bất kỳ điểm nào của nửa mặt phẳng (không thuộc đường thẳng) thỏa mãn thì bất bình đẳng TẤT CẢ các điểm của nửa mặt phẳng cho trước thỏa mãn sự bất bình đẳng này.
Bạn có thể kiểm tra: bất kỳ điểm nào ở bên phải của đường thẳng sẽ không thỏa mãn bất đẳng thức.
Kết luận từ thí nghiệm với điểm là gì? Không có nơi nào để đi, bất đẳng thức được thỏa mãn bởi tất cả các điểm của nửa mặt phẳng bên kia (bạn cũng có thể kiểm tra).
b) Giải bất đẳng thức
Phương pháp một
Hãy biến đổi bất đẳng thức:
Luật lệ: Cả hai vế của bất đẳng thức có thể được nhân (chia) cho TIÊU CỰC số có dấu bất đẳng thức THAY ĐỔI ngược lại (ví dụ: nếu có dấu "lớn hơn hoặc bằng" thì nó sẽ trở thành "nhỏ hơn hoặc bằng").
Ta nhân cả hai vế của bất đẳng thức với:
Hãy vẽ một đường thẳng (màu đỏ) và vẽ một đường liền nét, vì chúng ta có bất đẳng thức không nghiêm ngặt, và đường thẳng hiển nhiên thuộc nghiệm.
Sau khi phân tích bất đẳng thức thu được, chúng ta đi đến kết luận rằng nghiệm của nó là nửa mặt phẳng dưới (+ chính đường thẳng).
Chúng tôi tô bóng hoặc đánh dấu nửa mặt phẳng thích hợp bằng mũi tên.
Phương pháp hai
Hãy vẽ một đường thẳng. Ví dụ: hãy chọn một điểm tùy ý trên mặt phẳng (không thuộc một đường thẳng) và thay tọa độ của nó vào bất đẳng thức của chúng ta: ![]()
Đã nhận sự bất bình đẳng thực sự, có nghĩa là điểm thỏa mãn bất đẳng thức và nói chung, TẤT CẢ các điểm của nửa mặt phẳng dưới đều thỏa mãn bất đẳng thức này.
Ở đây, với điểm thực nghiệm, chúng ta “đánh trúng” nửa mặt phẳng mong muốn.
Giải pháp cho vấn đề này được biểu thị bằng đường màu đỏ và mũi tên màu đỏ.
Cá nhân tôi thích giải pháp đầu tiên hơn vì giải pháp thứ hai trang trọng hơn.
Ví dụ 2
Giải bất đẳng thức tuyến tính:
Đây là ví dụ để bạn tự giải quyết. Cố gắng giải quyết vấn đề theo hai cách (nhân tiện, đây là một cách tốt để kiểm tra lời giải). Đáp án cuối bài sẽ chỉ có hình vẽ cuối cùng.
Tôi nghĩ rằng sau tất cả các hành động được thực hiện trong các ví dụ, bạn sẽ phải kết hôn với họ; sẽ không khó để giải bất đẳng thức đơn giản nhất như v.v.
Chúng ta hãy chuyển sang xem xét trường hợp thứ ba, trường hợp tổng quát, khi cả hai biến đều có mặt trong bất đẳng thức:
Ngoài ra, thuật ngữ tự do “ce” có thể bằng 0.
Ví dụ 3
Tìm nửa mặt phẳng ứng với các bất đẳng thức sau:
Giải pháp: Phương pháp giải phổ quát với sự thay thế điểm được sử dụng ở đây.
a) Hãy xây dựng một phương trình cho đường thẳng và đường thẳng phải được vẽ dưới dạng đường chấm chấm, vì bất đẳng thức là nghiêm ngặt và bản thân đường thẳng đó sẽ không được đưa vào nghiệm.
Ví dụ: chúng tôi chọn một điểm thử nghiệm của mặt phẳng không thuộc một đường thẳng nhất định và thay thế tọa độ của nó vào bất đẳng thức của chúng tôi:
Đã nhận bất đẳng thức sai, có nghĩa là điểm và TẤT CẢ các điểm của nửa mặt phẳng đã cho không thỏa mãn bất đẳng thức. Giải pháp cho bất đẳng thức sẽ là một nửa mặt phẳng khác, chúng ta chiêm ngưỡng tia sét xanh: 
b) Hãy giải bất đẳng thức. Đầu tiên, hãy xây dựng một đường thẳng. Điều này không khó thực hiện; chúng ta có tỷ lệ trực tiếp chuẩn mực. Chúng tôi vẽ đường liên tục, vì bất đẳng thức không nghiêm ngặt.
Ta chọn một điểm tùy ý trên mặt phẳng không thuộc đường thẳng. Tôi muốn sử dụng lại nguồn gốc, nhưng than ôi, bây giờ nó không phù hợp. Vì vậy, bạn sẽ phải làm việc với một người bạn khác. Sẽ có lợi hơn nếu lấy một điểm có giá trị tọa độ nhỏ, chẳng hạn như . Hãy thay thế tọa độ của nó vào bất đẳng thức của chúng ta:
Đã nhận sự bất bình đẳng thực sự, có nghĩa là điểm và tất cả các điểm của nửa mặt phẳng đã cho thỏa mãn bất đẳng thức . Nửa mặt phẳng mong muốn được đánh dấu bằng mũi tên màu đỏ. Ngoài ra, giải pháp bao gồm chính đường thẳng.
Ví dụ 4
Tìm nửa mặt phẳng ứng với các bất đẳng thức:
Đây là ví dụ để bạn tự giải quyết. Giải pháp hoàn chỉnh, mẫu gần đúng của thiết kế cuối cùng và đáp án ở cuối bài.
Hãy xem xét vấn đề nghịch đảo:
Ví dụ 5
a) Cho một đường thẳng. Định nghĩa nửa mặt phẳng chứa điểm, còn đường thẳng phải được đưa vào nghiệm.
b) Cho một đường thẳng. Định nghĩa nửa mặt phẳng chứa điểm đó. Bản thân đường thẳng không được đưa vào giải pháp.
Giải pháp: Không cần phải vẽ ở đây và giải pháp sẽ mang tính phân tích. Không có gì khó khăn:
a) Hãy tạo một đa thức phụ trợ ![]() và tính giá trị của nó tại điểm:
và tính giá trị của nó tại điểm:
. Do đó, bất đẳng thức mong muốn sẽ có dấu “nhỏ hơn”. Theo điều kiện, đường thẳng được đưa vào nghiệm nên bất đẳng thức sẽ không chặt chẽ:
b) Hãy soạn một đa thức và tính giá trị của nó tại điểm:
. Như vậy, bất đẳng thức mong muốn sẽ có dấu “lớn hơn”. Theo điều kiện, đường thẳng không có trong nghiệm nên bất đẳng thức sẽ nghiêm ngặt: .
Trả lời:
Ví dụ sáng tạo cho việc tự học:
Ví dụ 6
Cho điểm và đường thẳng. Trong số các điểm được liệt kê, hãy tìm những điểm cùng với gốc tọa độ nằm trên cùng một phía của đường thẳng đã cho.
Một gợi ý nhỏ: trước tiên, bạn cần tạo một bất đẳng thức xác định nửa mặt phẳng chứa gốc tọa độ. Giải pháp phân tích và đáp án cuối bài.
Hệ thống bất đẳng thức tuyến tính
Như bạn hiểu, hệ bất đẳng thức tuyến tính là một hệ bao gồm nhiều bất đẳng thức. Lol, à, mình đưa ra định nghĩa rồi =)) Nhím là nhím, dao là dao. Nhưng đó là sự thật – hóa ra nó đơn giản và dễ tiếp cận! Không, nghiêm túc mà nói, tôi không muốn đưa ra bất kỳ ví dụ chung chung nào, vì vậy hãy đi thẳng vào vấn đề cấp bách:
Việc giải một hệ bất phương trình tuyến tính có ý nghĩa gì?
Giải hệ bất phương trình tuyến tính- điều này có nghĩa là tìm tập hợp các điểm trên mặt phẳng, thỏa mãn tới mọi người sự bất bình đẳng của hệ thống.
Là những ví dụ đơn giản nhất, hãy xem xét các hệ bất đẳng thức xác định các phần tọa độ của hệ tọa độ hình chữ nhật (“hình ảnh những học sinh kém” ở ngay đầu bài học):
Hệ bất đẳng thức xác định quý tọa độ thứ nhất (phía trên bên phải). Tọa độ của bất kỳ điểm nào trong quý đầu tiên, ví dụ: ![]() vân vân. thỏa mãn tới mọi người sự bất bình đẳng của hệ thống này.
vân vân. thỏa mãn tới mọi người sự bất bình đẳng của hệ thống này.
Tương tự:
– hệ bất đẳng thức xác định quý tọa độ thứ hai (phía trên bên trái);
– hệ bất đẳng thức xác định quý tọa độ thứ ba (phía dưới bên trái);
– hệ bất đẳng thức xác định phần tư tọa độ thứ tư (phía dưới bên phải).
Một hệ bất đẳng thức tuyến tính có thể không có nghiệm, nghĩa là, trở thành không khớp. Một lần nữa ví dụ đơn giản nhất: . Rõ ràng là “x” không thể đồng thời lớn hơn ba và nhỏ hơn hai.
Nghiệm của hệ bất phương trình có thể là đường thẳng, ví dụ: . Một con thiên nga, một con tôm, không có chó, kéo xe về hai hướng khác nhau. Đúng, mọi thứ vẫn còn đó - giải pháp cho hệ thống này là đường thẳng.
Nhưng trường hợp phổ biến nhất là khi giải pháp cho hệ thống là một số vùng mặt phẳng. Khu vực giải pháp Có lẽ không giới hạn(ví dụ: khu tọa độ) hoặc giới hạn. Vùng nghiệm giới hạn được gọi là hệ thống giải pháp đa giác.
Ví dụ 7
Giải hệ bất phương trình tuyến tính
Trong thực tế, trong hầu hết các trường hợp, chúng ta phải giải các bất đẳng thức yếu nên các em sẽ là người dẫn dắt các bước nhảy vòng trong phần còn lại của bài học.
Giải pháp: Việc có quá nhiều bất bình đẳng không đáng sợ. Có thể có bao nhiêu bất bình đẳng trong hệ thống? Vâng, bao nhiêu tùy thích. Điều chính là tuân thủ một thuật toán hợp lý để xây dựng vùng giải pháp:
1) Đầu tiên chúng ta xét các bất đẳng thức đơn giản nhất. Các bất đẳng thức xác định phần tư tọa độ đầu tiên, bao gồm cả ranh giới của các trục tọa độ. Mọi việc đã dễ dàng hơn nhiều vì khu vực tìm kiếm đã được thu hẹp đáng kể. Trong hình vẽ, ta đánh dấu ngay các nửa mặt phẳng tương ứng bằng mũi tên (mũi tên đỏ và xanh)
2) Bất đẳng thức đơn giản thứ hai là không có chữ “Y” ở đây. Đầu tiên, chúng ta tự xây dựng đường thẳng và thứ hai, sau khi chuyển đổi bất đẳng thức sang dạng , ngay lập tức thấy rõ rằng tất cả các chữ “X” đều nhỏ hơn 6. Chúng ta đánh dấu nửa mặt phẳng tương ứng bằng các mũi tên màu xanh lá cây. Chà, khu vực tìm kiếm thậm chí còn trở nên nhỏ hơn - một hình chữ nhật như vậy không bị giới hạn ở phía trên.
3) Ở bước cuối cùng, chúng ta giải các bất đẳng thức “với đầy đủ đạn dược”: . Chúng tôi đã thảo luận chi tiết về thuật toán giải pháp trong đoạn trước. Nói tóm lại: đầu tiên chúng ta xây dựng một đường thẳng, sau đó, sử dụng một điểm thử nghiệm, chúng ta tìm thấy nửa mặt phẳng mà chúng ta cần.
Các em hãy đứng lên, đứng thành vòng tròn: 
Vùng giải pháp của hệ thống là một đa giác; trong bản vẽ, nó được viền bằng một đường màu đỏ thẫm và được tô bóng. Tôi đã làm quá nó một chút =) Trong sổ ghi chép, chỉ cần tô bóng vùng giải pháp hoặc phác thảo nó đậm hơn bằng bút chì đơn giản là đủ.
Bất kỳ điểm nào của đa giác đều thỏa mãn MỌI bất đẳng thức của hệ thống (bạn có thể kiểm tra nó cho vui).
Trả lời: Nghiệm của hệ là đa giác.
Khi xin một bản sao rõ ràng, bạn nên mô tả chi tiết những điểm nào bạn đã sử dụng để dựng các đường thẳng (xem bài học Đồ thị và tính chất của hàm) và cách xác định các nửa mặt phẳng (xem đoạn đầu tiên của bài học này). Tuy nhiên, trên thực tế, trong hầu hết các trường hợp, bạn sẽ chỉ được ghi nhận nếu có bản vẽ đúng. Bản thân việc tính toán có thể được thực hiện trên bản nháp hoặc thậm chí bằng miệng.
Ngoài đa giác lời giải của hệ thống, trong thực tế, mặc dù ít thường xuyên hơn, vẫn có một vùng mở. Hãy cố gắng tự mình hiểu ví dụ sau. Mặc dù, vì mục đích chính xác, không có sự tra tấn nào ở đây - thuật toán xây dựng giống nhau, chỉ là diện tích sẽ không giới hạn.
Ví dụ 8
Giải quyết hệ thống
Đáp án và đáp án ở cuối bài. Rất có thể bạn sẽ có các tên chữ cái khác nhau cho các đỉnh của vùng kết quả. Điều này không quan trọng, cái chính là tìm đúng các đỉnh và xây dựng diện tích một cách chính xác.
Không có gì lạ khi các bài toán không chỉ yêu cầu xây dựng miền nghiệm của hệ thống mà còn phải tìm tọa độ các đỉnh của miền. Trong hai ví dụ trước, tọa độ của những điểm này rất rõ ràng, nhưng trên thực tế, mọi thứ đều không có băng:
Ví dụ 9
Giải hệ và tìm tọa độ các đỉnh của vùng kết quả
Giải pháp: Chúng ta hãy mô tả trong bản vẽ vùng giải pháp của hệ thống này. Bất đẳng thức xác định nửa mặt phẳng bên trái với trục hoành, và ở đây không còn phần tự do nào nữa. Sau khi tính toán các bản sao/bản nháp cuối cùng hoặc quá trình suy nghĩ sâu sắc, chúng tôi nhận được các giải pháp sau: 
Trong bài viết này, tôi trả lời một câu hỏi khác từ những người đăng ký của tôi. Các câu hỏi đến theo nhiều cách khác nhau. Không phải tất cả chúng đều được xây dựng chính xác. Và một số trong số chúng được xây dựng theo cách mà không rõ tác giả muốn hỏi ngay điều gì. Vì vậy, trong số rất nhiều câu hỏi được gửi đi, tôi phải chọn ra những câu hỏi thực sự thú vị, chẳng hạn như những “viên ngọc trai”, câu trả lời không chỉ thú vị mà còn hữu ích, đối với tôi, đối với những độc giả khác của tôi. Và hôm nay tôi trả lời một trong những câu hỏi này. Làm thế nào để mô tả tập hợp các giải pháp cho một hệ bất đẳng thức?
Đây thực sự là một câu hỏi hay. Bởi vì phương pháp giải các bài toán bằng đồ thị trong toán học là một phương pháp rất có tác dụng. Một người được thiết kế theo cách thuận tiện hơn cho anh ta trong việc tiếp nhận thông tin với sự trợ giúp của nhiều tài liệu trực quan khác nhau. Vì vậy, nếu bạn thành thạo phương pháp này thì tin tôi đi, nó sẽ không thể thiếu đối với bạn khi giải các bài tập trong Kỳ thi Thống nhất, đặc biệt là từ phần thứ hai, các kỳ thi khác cũng như khi giải các bài toán tối ưu hóa, v.v. .
Vì vậy, nó ở đây. Làm thế nào chúng ta có thể trả lời câu hỏi này? Hãy bắt đầu đơn giản. Giả sử hệ bất đẳng thức chỉ chứa một biến.
| Ví dụ 1. Vẽ tập nghiệm của hệ bất phương trình: Title="Được kết xuất bởi QuickLaTeX.com">!} |
Hãy đơn giản hóa hệ thống này. Để làm điều này, hãy cộng 7 vào cả hai vế của bất đẳng thức thứ nhất và chia cả hai vế cho 2 mà không làm thay đổi dấu của bất đẳng thức, vì 2 là một số dương. Chúng ta cộng 4 vào cả hai vế của bất đẳng thức thứ hai, kết quả là chúng ta thu được hệ bất đẳng thức sau:
Title="Được kết xuất bởi QuickLaTeX.com">!}
Thông thường một vấn đề như vậy được gọi là một chiều. Tại sao? Có, bởi vì để mô tả nhiều giải pháp của nó, nó đủ trực tiếp. Nói chính xác là một dòng số. Hãy đánh dấu điểm 6 và 8 trên trục số này. Rõ ràng là điểm 8 sẽ ở xa hơn về bên phải so với điểm 6, vì trên trục số, số lớn hơn nằm bên phải số nhỏ hơn. Ngoài ra, điểm 8 sẽ được tô màu vì theo ký hiệu của bất đẳng thức thứ nhất, nó được đưa vào nghiệm của nó. Ngược lại, điểm 6 sẽ không được tô đậm vì nó không nằm trong nghiệm của bất đẳng thức thứ hai:
Bây giờ chúng ta hãy đánh dấu bằng một mũi tên phía trên các giá trị nhỏ hơn hoặc bằng 8, theo yêu cầu của bất đẳng thức đầu tiên của hệ thống và bằng một mũi tên bên dưới - các giá trị lớn hơn 6, theo yêu cầu của bất đẳng thức thứ hai của hệ:
Vẫn còn phải trả lời câu hỏi các nghiệm của hệ bất đẳng thức nằm ở đâu trên trục số. Hãy nhớ một lần và mãi mãi. Ký hiệu của hệ thống - dấu ngoặc nhọn - trong toán học thay thế cho liên từ “I”. Tức là, dịch ngôn ngữ của công thức sang ngôn ngữ của con người, chúng ta có thể nói rằng chúng ta bắt buộc phải chỉ ra các giá trị lớn hơn 6 VÀ nhỏ hơn hoặc bằng 8. Tức là khoảng yêu cầu nằm ở giao điểm của dấu được đánh dấu khoảng thời gian:
Như vậy ta đã biểu diễn tập nghiệm của hệ bất phương trình trên trục số trong trường hợp hệ bất phương trình chỉ chứa một biến. Khoảng bóng mờ này bao gồm tất cả các giá trị thỏa mãn tất cả các bất đẳng thức được ghi trong hệ thống.
Bây giờ chúng ta hãy xem xét một trường hợp phức tạp hơn. Giả sử hệ của chúng ta chứa các bất đẳng thức với hai biến và . Trong trường hợp này, sẽ không thể chỉ sử dụng một đường thẳng để mô tả nghiệm của một hệ thống như vậy. Chúng tôi vượt ra ngoài thế giới một chiều và thêm một chiều khác vào đó. Ở đây chúng ta cần cả một chiếc máy bay. Hãy xem xét tình huống bằng một ví dụ cụ thể.
Vậy làm thế nào để biểu diễn tập nghiệm của một hệ bất phương trình hai biến cho trước trong hệ tọa độ chữ nhật trên mặt phẳng? Hãy bắt đầu với điều đơn giản nhất. Chúng ta hãy tự hỏi vùng nào của mặt phẳng này được xác định bởi bất đẳng thức. Phương trình xác định đường thẳng vuông góc với trục CON BÒ ĐỰC qua điểm (0;0). Tức là đường thẳng này trùng với trục ôi. Chà, vì chúng ta quan tâm đến các giá trị lớn hơn hoặc bằng 0, nên toàn bộ nửa mặt phẳng nằm bên phải đường thẳng là phù hợp:
Hơn nữa, mọi điểm nằm trên trục ôi, cũng phù hợp với ta vì bất đẳng thức không chặt chẽ.
Để hiểu diện tích nào trên mặt phẳng tọa độ mà bất đẳng thức thứ ba xác định, bạn cần vẽ đồ thị của hàm. Đây là một đường thẳng đi qua gốc tọa độ và, ví dụ, điểm (1;1). Đó là, trên thực tế, nó là một đường thẳng chứa đường phân giác của góc tạo thành một phần tư tọa độ thứ nhất.
Bây giờ chúng ta hãy nhìn vào bất đẳng thức thứ ba trong hệ và suy nghĩ. Chúng ta cần tìm khu vực nào? Chúng ta hãy xem: . Dấu lớn hơn hoặc bằng. Đó là, tình huống tương tự như trong ví dụ trước. Chỉ ở đây “nhiều hơn” không có nghĩa là “nhiều hơn về bên phải”, mà là “cao hơn”. Bởi vì ôi- đây là trục thẳng đứng của chúng tôi. Nghĩa là, diện tích được xác định trên mặt phẳng theo bất đẳng thức thứ ba là tập hợp các điểm nằm phía trên đường thẳng hoặc trên đường thẳng đó:
Với bất đẳng thức thứ nhất, hệ thống kém thuận tiện hơn một chút. Nhưng sau khi chúng ta có thể xác định diện tích được xác định bởi bất đẳng thức thứ ba, tôi nghĩ chúng ta đã rõ cách hành động.
Cần phải trình bày sự bất đẳng thức này sao cho chỉ có biến ở bên trái và chỉ có biến ở bên phải. Để làm điều này, hãy trừ cả hai vế của bất đẳng thức và chia cả hai vế cho 2 mà không thay đổi dấu của bất đẳng thức, vì 2 là một số dương. Kết quả là, chúng ta có được bất đẳng thức sau:
Việc còn lại là vẽ một đường thẳng trên mặt phẳng tọa độ cắt trục ôi tại điểm A(0;4) và đường thẳng tại điểm . Tôi đã học được điều sau bằng cách đánh đồng vế phải của phương trình đường thẳng và thu được phương trình. Từ phương trình này, tọa độ của điểm giao nhau được tìm thấy và tọa độ, tôi nghĩ bạn đã đoán được, bằng tọa độ. Dành cho những ai vẫn chưa đoán được, điều này là do chúng ta có phương trình của một trong các đường thẳng giao nhau: .
Ngay sau khi vẽ đường thẳng này, chúng ta có thể đánh dấu ngay vùng mong muốn. Dấu bất đẳng thức ở đây là “nhỏ hơn hoặc bằng”. Điều này có nghĩa là vùng mong muốn nằm bên dưới hoặc ngay trên đường thẳng được mô tả:
Vâng, câu hỏi cuối cùng. Đâu là vùng mong muốn thỏa mãn cả ba bất đẳng thức của hệ thống? Rõ ràng, nó nằm ở giao điểm của cả ba khu vực được đánh dấu. Lại vượt qua! Hãy nhớ: ký hiệu hệ thống trong toán học có nghĩa là giao lộ. Đây rồi, khu vực này:
Vâng, ví dụ cuối cùng. Thậm chí còn tổng quát hơn. Bây giờ chúng ta hãy giả sử rằng chúng ta không có một hoặc hai biến trong hệ thống mà có đến ba biến!
Vì có ba biến, để mô tả tập nghiệm của hệ bất đẳng thức như vậy, chúng ta sẽ cần một chiều thứ ba ngoài hai chiều mà chúng ta đã làm việc trong ví dụ trước. Tức là chúng ta bước ra khỏi mặt phẳng vào không gian và mô tả một hệ tọa độ không gian có ba chiều: X, Y Và Z. Tương ứng với chiều dài, chiều rộng và chiều cao.
Hãy bắt đầu bằng cách mô tả trong hệ tọa độ này bề mặt được xác định bởi phương trình. Về hình thức, nó rất giống với phương trình đường tròn trên mặt phẳng, chỉ thêm một số hạng nữa với biến . Dễ dàng đoán rằng đây là phương trình của một hình cầu có tâm tại điểm (1;3;2), bình phương có bán kính là 4. Tức là bán kính của chính nó là 2.
Sau đó là một câu hỏi. Vậy thì bản thân sự bất bình đẳng đặt ra điều gì? Đối với những người đang bối rối trước câu hỏi này, tôi đề xuất lý do như sau. Dịch ngôn ngữ của các công thức sang ngôn ngữ của con người, chúng ta có thể nói rằng cần phải chỉ ra tất cả các hình cầu có tâm tại điểm (1;3;2), bán kính của chúng nhỏ hơn hoặc bằng 2. Nhưng rồi tất cả những quả cầu này sẽ nằm bên trong quả cầu được mô tả! Trên thực tế, bất đẳng thức này xác định toàn bộ vùng bên trong của hình cầu được mô tả. Nếu bạn muốn, một quả bóng được xác định, giới hạn bởi hình cầu được mô tả:
Bề mặt được xác định bởi phương trình x+y+z=4 là mặt phẳng cắt các trục tọa độ tại các điểm (0;0;4), (0;4;0) và (4;0;0). Chà, rõ ràng là số ở bên phải của dấu bằng càng lớn thì các điểm giao nhau của mặt phẳng này với các trục tọa độ sẽ càng xa tâm tọa độ. Tức là, bất đẳng thức thứ hai xác định một nửa không gian nằm “phía trên” một mặt phẳng cho trước. Sử dụng thuật ngữ thông thường “cao hơn”, ý tôi là xa hơn theo hướng tăng giá trị tọa độ dọc theo các trục.
Mặt phẳng này cắt hình cầu được mô tả. Trong trường hợp này, phần giao nhau là một hình tròn. Bạn thậm chí có thể tính toán khoảng cách từ tâm của hệ tọa độ đến tâm của vòng tròn này. Nhân tiện, ai đoán được cách thực hiện thì hãy viết đáp án và câu trả lời của bạn vào phần bình luận. Do đó, hệ bất đẳng thức ban đầu xác định một vùng không gian nằm xa mặt phẳng này theo hướng tọa độ tăng dần, nhưng được bao bọc trong hình cầu được mô tả:
Đây là cách mô tả nhiều nghiệm của một hệ bất bình đẳng. Nếu có nhiều biến trong hệ thống hơn 3 (ví dụ: 4), sẽ không thể mô tả rõ ràng tập hợp các giải pháp được nữa. Bởi vì điều này sẽ yêu cầu hệ tọa độ 4 chiều. Nhưng một người bình thường không thể tưởng tượng được 4 trục tọa độ vuông góc với nhau có thể được đặt như thế nào. Mặc dù tôi có một người bạn tuyên bố rằng anh ấy có thể làm điều này một cách dễ dàng. Tôi không biết liệu anh ấy có nói sự thật hay không, có lẽ anh ấy đang nói sự thật. Tuy nhiên, trí tưởng tượng bình thường của con người không cho phép thực hiện được điều này.
Tôi hy vọng bạn thấy bài học hôm nay hữu ích. Để kiểm tra xem bạn đã hiểu nó đến mức nào, hãy làm bài tập về nhà dưới đây.
Vẽ tập nghiệm của hệ bất phương trình:
ql-right-eqno"> title="Rendered by QuickLaTeX.com">!}
Tài liệu được chuẩn bị bởi Serge Valerievich
Giải bất đẳng thức hai biến, và thậm chí còn hơn thế nữa hệ bất đẳng thức hai biến, có vẻ là một việc khá khó khăn. Tuy nhiên, có một thuật toán đơn giản giúp giải quyết những vấn đề tưởng chừng như rất phức tạp thuộc loại này một cách dễ dàng và không cần tốn nhiều công sức. Hãy cố gắng tìm ra nó.
Cho ta có bất đẳng thức với hai biến thuộc một trong các loại sau:
y > f(x); y ≥ f(x); y< f(x); y ≤ f(x).
Để mô tả tập nghiệm của bất đẳng thức đó trên mặt phẳng tọa độ, hãy tiến hành như sau:
1. Chúng ta xây dựng đồ thị của hàm y = f(x), chia mặt phẳng thành hai vùng.
2. Chúng tôi chọn bất kỳ khu vực kết quả nào và xem xét một điểm tùy ý trong đó. Chúng tôi kiểm tra tính khả thi của bất đẳng thức ban đầu cho điểm này. Nếu thử nghiệm cho kết quả bất đẳng thức số đúng thì chúng ta kết luận rằng bất đẳng thức ban đầu được thỏa mãn trong toàn bộ vùng mà điểm được chọn thuộc về. Do đó, tập nghiệm của bất đẳng thức là miền chứa điểm được chọn. Nếu kết quả kiểm tra là một bất đẳng thức số không chính xác thì tập hợp nghiệm của bất đẳng thức sẽ là vùng thứ hai mà điểm được chọn không thuộc về.
3.
Nếu bất đẳng thức là nghiêm ngặt thì ranh giới của vùng, tức là các điểm của đồ thị của hàm y = f(x), không được đưa vào tập nghiệm và ranh giới được biểu thị bằng một đường chấm. Nếu bất đẳng thức không nghiêm ngặt thì ranh giới của vùng, tức là các điểm của đồ thị của hàm y = f(x), được đưa vào tập nghiệm của bất đẳng thức này và ranh giới trong trường hợp này được mô tả như một đường liền nét.
Bây giờ chúng ta hãy xem xét một số vấn đề về chủ đề này.
Nhiệm vụ 1.
Tập hợp điểm nào được cho bởi bất đẳng thức x · y 4?
Giải pháp.
1) Chúng ta xây dựng đồ thị của phương trình x · y = 4. Để làm điều này, trước tiên chúng ta biến đổi nó. Rõ ràng, x trong trường hợp này không chuyển sang 0, vì nếu không thì chúng ta sẽ có 0 · y = 4, điều này không đúng. Điều này có nghĩa là chúng ta có thể chia phương trình của mình cho x. Chúng ta nhận được: y = 4/x. Đồ thị của hàm này là một hyperbol. Nó chia toàn bộ mặt phẳng thành hai vùng: vùng nằm giữa hai nhánh của hyperbol và vùng nằm ngoài chúng.
2) Hãy chọn một điểm tùy ý từ vùng đầu tiên, gọi là điểm (4; 2).
Hãy kiểm tra bất đẳng thức: 4 · 2 ≤ 4 – sai.
Điều này có nghĩa là các điểm của miền này không thỏa mãn bất đẳng thức ban đầu. Khi đó chúng ta có thể kết luận rằng tập nghiệm của bất đẳng thức sẽ là vùng thứ hai mà điểm được chọn không thuộc về.
3) Vì bất đẳng thức không chặt chẽ nên ta vẽ các điểm biên, tức là các điểm của đồ thị hàm số y = 4/x, bằng một đường liền nét.
Hãy tô màu vàng cho tập hợp các điểm xác định bất đẳng thức ban đầu (Hình 1).
Nhiệm vụ 2.
Vẽ diện tích được hệ thống xác định trên mặt phẳng tọa độ
( y > x 2 + 2;
(y + x > 1;
( x 2 + y 2 ≤ 9.
Giải pháp.
Để bắt đầu, chúng ta xây dựng đồ thị của các hàm sau (Hình 2):
y = x 2 + 2 – parabol,
y + x = 1 – đường thẳng
x 2 + y 2 = 9 – đường tròn.

1) y > x 2 + 2.
Chúng ta lấy điểm (0; 5), nằm phía trên đồ thị của hàm.
Hãy kiểm tra bất đẳng thức: 5 > 0 2 + 2 – đúng.
Do đó, mọi điểm nằm phía trên parabol y = x 2 + 2 đã cho đều thỏa mãn bất đẳng thức thứ nhất của hệ. Hãy sơn chúng màu vàng.
2) y + x > 1.
Chúng ta lấy điểm (0; 3), nằm phía trên đồ thị của hàm.
Kiểm tra bất đẳng thức: 3 + 0 > 1 – đúng.
Do đó, mọi điểm nằm phía trên đường thẳng y + x = 1 đều thỏa mãn bất đẳng thức bậc hai của hệ. Hãy sơn chúng với màu xanh lá cây.
3) x 2 + y 2 ≤ 9.
Lấy điểm (0; -4) nằm ngoài đường tròn x 2 + y 2 = 9.
Hãy kiểm tra bất đẳng thức: 0 2 + (-4) 2 ≤ 9 – sai.
Do đó, mọi điểm nằm ngoài đường tròn x 2 + y 2 = 9,  không thỏa mãn bất đẳng thức thứ ba của hệ. Khi đó ta có thể kết luận rằng mọi điểm nằm trong đường tròn x 2 + y 2 = 9 đều thỏa mãn bất đẳng thức thứ ba của hệ. Hãy sơn chúng với màu tím.
không thỏa mãn bất đẳng thức thứ ba của hệ. Khi đó ta có thể kết luận rằng mọi điểm nằm trong đường tròn x 2 + y 2 = 9 đều thỏa mãn bất đẳng thức thứ ba của hệ. Hãy sơn chúng với màu tím.
Đừng quên rằng nếu bất đẳng thức nghiêm ngặt thì đường biên tương ứng phải được vẽ bằng đường chấm. Chúng ta có được hình ảnh sau (Hình 3).

(Hình 4).
Nhiệm vụ 3.
Vẽ diện tích được xác định trên mặt phẳng tọa độ theo hệ thống:
(x 2 + y 2 ≤ 16;
(x ≥ -y;
(x 2 + y 2 ≥ 4.
Giải pháp.
Để bắt đầu, chúng ta xây dựng đồ thị của các hàm sau: 
x 2 + y 2 = 16 – đường tròn,
x = -y – đường thẳng
x 2 + y 2 = 4 – đường tròn (Hình 5).
Bây giờ chúng ta hãy xem xét từng bất đẳng thức riêng biệt.
1) x 2 + y 2 ≤ 16.
Lấy điểm (0; 0), nằm bên trong đường tròn x 2 + y 2 = 16.
Hãy kiểm tra bất đẳng thức: 0 2 + (0) 2 16 – đúng.
Do đó, mọi điểm nằm trong đường tròn x 2 + y 2 = 16 đều thỏa mãn bất đẳng thức thứ nhất của hệ.
Hãy sơn chúng với màu đỏ. 
Chúng ta lấy điểm (1; 1), nằm phía trên đồ thị của hàm số.
Kiểm tra bất đẳng thức: 1 ≥ -1 – true.
Do đó, mọi điểm nằm trên đường x = -y đều thỏa mãn bất đẳng thức thứ hai của hệ. Hãy sơn chúng với màu xanh lam.
3) x 2 + y 2 ≥ 4.
Lấy điểm (0; 5), nằm ngoài đường tròn x 2 + y 2 = 4.
Kiểm tra bất đẳng thức: 0 2 + 5 2 ≥ 4 – true.
Do đó, mọi điểm nằm ngoài đường tròn x 2 + y 2 = 4 đều thỏa mãn bất đẳng thức thứ ba của hệ. Hãy sơn chúng màu xanh.
Trong bài toán này, mọi bất đẳng thức đều không chặt chẽ, có nghĩa là chúng ta vẽ mọi ranh giới bằng một đường liền nét. Chúng ta có được hình ảnh sau (Hình 6).
Vùng tìm kiếm là vùng mà cả ba vùng màu giao nhau (Hình 7).

Vẫn còn thắc mắc? Bạn chưa biết cách giải hệ bất phương trình hai biến?
Để nhận được sự giúp đỡ từ một gia sư -.
Bài học đầu tiên là miễn phí!
blog.site, khi sao chép toàn bộ hoặc một phần tài liệu, cần có liên kết đến nguồn gốc.
, giáo viên toán, Cơ sở giáo dục thành phố "Trường trung học cơ bản Upsha"
Giải pháp đồ họa cho sự bất bình đẳngvới hai biến
Thường cần vẽ trên mặt phẳng tọa độ tập nghiệm của bất đẳng thức hai biến. Hãy nhớ lại rằng nghiệm của bất đẳng thức hai biến là một cặp giá trị của các biến này để biến bất đẳng thức đã cho thành bất đẳng thức số thực.
Ví dụ 1
Xét sự bất đẳng thức
Một cặp giá trị biến (-1; 1) biến bất đẳng thức này thành
đúng bất đẳng thức số 2< 8, и является решением неравенства. Пара значений (2; 1) приводит к неверному числовому неравенству 11 < 8, и не является решением данного неравенства.
Bằng cách sử dụng các ví dụ, chúng ta sẽ xem xét cách mô tả tập nghiệm của bất đẳng thức hai biến trên mặt phẳng tọa độ.
Ví dụ 2
Hãy biểu diễn trên mặt phẳng tọa độ tập nghiệm của nertiền bản quyền 2у+ Zx< 6.
Đầu tiên hãy dựng một đường thẳng
Nó chia tập hợp tất cả các điểm của mặt phẳng tọa độ thành các điểm nằm trên nó và các điểm nằm dưới nó.
Hãy lấy từ mỗi khu vực điểm kiểm soát , Ví dụ A (1; 1) và B (1; 3)
tọa độ điểm MỘT thỏa mãn bất đẳng thức này 2у+ Zx< 6, т. е. 2 1 + 3 1 < 6.
tọa độ điểm TRONG không thỏa mãn bất đẳng thức này 2∙3 + 3∙1< 6.
Vì bất đẳng thức này có thể đổi dấu trên đường thẳng 2у+ 3x = 6 thì bất đẳng thức được thỏa mãn bởi tập hợp các điểm trong vùng chứa điểm A.
Như vậy ta đã vẽ được tập nghiệm của bất đẳng thức 2у+ Zx< 6.
Ví dụ 3
Hãy vẽ tập nghiệm của bất đẳng thức x2 + 2x + y2- 4у + 1 > 0trên mặt phẳng tọa độ.
Trước tiên chúng ta hãy xây dựng đồ thị của phương trình x2 + 2x + y2 - 4y + 1 = 0. Hãy bôi đen phương trình đường tròn trong phương trình này: (x2 + 2x + 1) + (y2 - 4y + 4) = 4, hoặc (x + 1)2 + ( y - 2)2 = 22.
Đây là phương trình của đường tròn có tâm tại điểm 0 (-1; 2) và bán kính R = 2. Hãy dựng đường tròn này.

Vì bất đẳng thức này là nghiêm ngặt và các điểm nằm trên đường tròn không thỏa mãn bất đẳng thức nên ta dựng đường tròn bằng một đường chấm chấm.
Dễ dàng kiểm tra được tọa độ tâm VỀđường tròn không thỏa mãn bất đẳng thức này. Biểu thức x2 + 2x + y2 - 4y+ 1 đổi dấu trên đường tròn dựng sẵn. Khi đó bất đẳng thức được thỏa mãn bởi các điểm nằm ngoài đường tròn. Những điểm này được tô bóng.
Ví dụ 4
Hãy vẽ trên mặt phẳng tọa độ tập nghiệm của bất phương trình
(y - x2)(y- x - 3)< 0.
Đầu tiên hãy vẽ biểu thức (y - x2)(y- x - 3) = 0. Là parabol Tại= x2 và đường thẳng y = x+ 3. Hãy dựng các dòng này và lưu ý rằng việc thay đổi dấu của biểu thức (y - x2)(y- x - 3) chỉ xảy ra trên những dòng này. Đối với điểm A (0; 5), chúng ta xác định dấu của biểu thức này: - 3) > 0 (tức là bất đẳng thức này không đúng). Bây giờ thật dễ dàng để đánh dấu tập hợp các điểm thỏa mãn bất đẳng thức này (các vùng này được tô màu).
Bất đẳng thức là hai số hoặc biểu thức toán học được kết nối bằng một trong các dấu: > (lớn hơn, trong trường hợp bất đẳng thức nghiêm ngặt),< (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Bất bình đẳng là tuyến tính trong cùng điều kiện như phương trình: nó chỉ chứa các biến ở bậc một và không chứa tích của các biến.
Lời giải của bất đẳng thức tuyến tính và hệ bất phương trình tuyến tính gắn bó chặt chẽ với ý nghĩa hình học của chúng: lời giải của bất đẳng thức tuyến tính là một nửa mặt phẳng nhất định trong đó toàn bộ mặt phẳng được chia cho một đường thẳng, phương trình xác định bất đẳng thức tuyến tính . Nửa mặt phẳng này, và trong trường hợp hệ bất đẳng thức tuyến tính, phần của mặt phẳng giới hạn bởi một số đường thẳng, phải được tìm thấy trong hình vẽ.
Nhiều bài toán kinh tế, đặc biệt là các bài toán quy hoạch tuyến tính, trong đó yêu cầu tìm cực đại hoặc cực tiểu của một hàm, được quy giản thành việc giải các hệ bất phương trình tuyến tính với một số lượng lớn biến.
Giải hệ bất phương trình tuyến tính với số ẩn bất kỳ
Đầu tiên, chúng ta hãy xem xét các bất đẳng thức tuyến tính trong mặt phẳng. Xét một bất đẳng thức có hai biến và:
![]() ,
,
đâu là hệ số của các biến (một số số), là số hạng tự do (cũng là một số số).
Một bất đẳng thức có hai ẩn số, giống như một phương trình, có vô số nghiệm. Lời giải của bất đẳng thức này là một cặp số thỏa mãn bất đẳng thức này. Về mặt hình học, tập nghiệm của bất đẳng thức được biểu diễn dưới dạng nửa mặt phẳng giới hạn bởi một đường thẳng
![]() ,
,
mà chúng ta sẽ gọi là đường ranh giới.
Bước 1. Xây dựng đường thẳng giới hạn tập nghiệm của bất đẳng thức tuyến tính
Để làm điều này, bạn cần biết hai điểm bất kỳ trên đường này. Hãy tìm giao điểm của các trục tọa độ. Tọa độ giao lộ MỘT bằng 0 (Hình 1). Các giá trị số trên các trục trong hình này đề cập đến ví dụ 1 mà chúng tôi sẽ phân tích ngay sau chuyến tham quan lý thuyết này.

Chúng ta tìm hoành độ bằng cách giải phương trình đường thẳng với phương trình trục như một hệ.
Hãy tìm giao điểm với trục:

Thay giá trị vào phương trình đầu tiên, chúng ta nhận được
Ở đâu .
Như vậy ta đã tìm được hoành độ của điểm MỘT .
Hãy tìm tọa độ giao điểm với trục.
chấm trục hoành B bằng không. Giải phương trình đường biên bằng phương trình trục tọa độ:
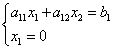
![]() ,
,
do đó tọa độ của điểm B: .
Bước 2. Vẽ đường thẳng giới hạn tập nghiệm của bất đẳng thức. Biết các điểm MỘT Và B giao điểm của đường biên với các trục tọa độ, ta vẽ được đường này. Một đường thẳng (lại là Hình 1) chia toàn bộ mặt phẳng thành hai phần nằm ở bên phải và bên trái (trên và dưới) của đường thẳng này.
Bước 3. Xác định nửa mặt phẳng nào là nghiệm của bất đẳng thức này.Để làm điều này, bạn cần thay thế gốc tọa độ (0; 0) vào bất đẳng thức này. Nếu tọa độ gốc thỏa mãn bất đẳng thức thì nghiệm của bất đẳng thức là nửa mặt phẳng chứa gốc tọa độ. Nếu tọa độ không thỏa mãn bất đẳng thức thì nghiệm của bất đẳng thức là một nửa mặt phẳng không chứa gốc tọa độ. Nửa mặt phẳng của nghiệm của bất đẳng thức sẽ được biểu thị bằng các nét từ đường thẳng vào nửa mặt phẳng, như trên Hình 1.
Nếu chúng ta giải hệ bất đẳng thức tuyến tính, thì mỗi bước được thực hiện cho từng bất đẳng thức của hệ.
Ví dụ 1. Giải bất đẳng thức
Giải pháp. Hãy vẽ một đường thẳng
Thay một đường thẳng vào phương trình, ta được , và thay , ta được . Do đó, tọa độ các giao điểm với các trục sẽ là MỘT(3; 0) , B(0; 2) . Hãy vẽ một đường thẳng đi qua những điểm này (một lần nữa, Hình 1).

Hãy chọn nửa mặt phẳng nghiệm của bất đẳng thức. Để làm điều này, chúng ta thay tọa độ gốc (0; 0) vào bất đẳng thức:
chúng ta thu được , tức là tọa độ gốc thỏa mãn bất đẳng thức này. Do đó, nghiệm của bất đẳng thức là nửa mặt phẳng chứa gốc tọa độ, tức là nửa mặt phẳng bên trái (hay còn gọi là phía dưới).
Nếu bất đẳng thức này là nghiêm ngặt thì nó sẽ có dạng
thì các điểm của đường biên sẽ không phải là nghiệm vì chúng không thỏa mãn bất đẳng thức.
Bây giờ hãy xem xét một hệ bất đẳng thức tuyến tính với hai ẩn số:

Mỗi bất đẳng thức của hệ này trên mặt phẳng xác định một nửa mặt phẳng. Một hệ bất đẳng thức tuyến tính được gọi là nhất quán nếu nó có ít nhất một nghiệm và không nhất quán nếu nó không có nghiệm. Nghiệm của hệ bất phương trình tuyến tính là bất kỳ cặp số () nào thỏa mãn mọi bất phương trình đã cho.
Về mặt hình học, nghiệm của một hệ bất đẳng thức tuyến tính là tập hợp các điểm thỏa mãn tất cả các bất đẳng thức của hệ, tức là phần chung của các nửa mặt phẳng thu được. Do đó, về mặt hình học, trong trường hợp tổng quát, nghiệm có thể được biểu diễn dưới dạng một số đa giác; trong trường hợp cụ thể, nó có thể là một đường thẳng, một đoạn hoặc thậm chí là một điểm. Nếu một hệ bất đẳng thức tuyến tính không nhất quán thì không có một điểm nào trên mặt phẳng thỏa mãn tất cả các bất đẳng thức của hệ.
Ví dụ 2.
Giải pháp. Vì vậy, chúng ta cần tìm ra nhiều nghiệm cho hệ bất đẳng thức này. Hãy dựng một đường biên cho bất đẳng thức thứ nhất, tức là một đường thẳng, và một đường biên cho bất đẳng thức thứ hai, tức là một đường thẳng.
Chúng tôi thực hiện việc này từng bước một, như đã trình bày trong tài liệu tham khảo lý thuyết và trong ví dụ 1, đặc biệt vì trong ví dụ 1, chúng tôi đã xây dựng đường ranh giới cho bất đẳng thức, đây là đường ranh giới đầu tiên trong hệ thống này.

Nửa mặt phẳng nghiệm tương ứng với các bất đẳng thức của hệ này được tô bóng vào trong trong Hình 2. Phần chung của nửa mặt phẳng nghiệm là góc mở ABC. Điều này có nghĩa là tập hợp các điểm trong mặt phẳng tạo thành một góc mở ABC, là nghiệm của cả bất đẳng thức thứ nhất và bất đẳng thức thứ hai của hệ, tức là nó là nghiệm của hệ gồm hai bất đẳng thức tuyến tính. Nói cách khác, tọa độ của bất kỳ điểm nào trong tập hợp này đều thỏa mãn cả hai bất đẳng thức của hệ.
Ví dụ 3. Giải hệ bất phương trình tuyến tính
Giải pháp. Hãy xây dựng các đường biên tương ứng với các bất đẳng thức của hệ. Chúng tôi thực hiện điều này bằng cách làm theo các bước được đưa ra trong phần trợ giúp lý thuyết cho từng bất đẳng thức. Bây giờ chúng ta xác định nửa mặt phẳng nghiệm của từng bất đẳng thức (Hình 3).

Các nửa mặt phẳng nghiệm tương ứng với các bất đẳng thức của một hệ đã cho được tô bóng vào trong. Giao điểm của nửa mặt phẳng của các giải pháp được mô tả, như trong hình, dưới dạng một hình tứ giác ABCE. Ta thấy đa giác nghiệm của hệ bất phương trình tuyến tính hai biến là một tứ giác ABCE .
Mọi điều được mô tả ở trên về hệ bất đẳng thức tuyến tính với hai ẩn số cũng áp dụng cho hệ bất đẳng thức với số ẩn bất kỳ, với điểm khác biệt duy nhất là nghiệm của bất đẳng thức với N những điều chưa biết sẽ là tổng thể N các số () thỏa mãn mọi bất đẳng thức và thay vì đường biên sẽ có siêu phẳng biên N-không gian chiều. Lời giải sẽ là một nghiệm đa diện (đơn hình) được giới hạn bởi các siêu phẳng.
