Tạo tỉ số và tính giới hạn.
Nó đến từ đâu? bảng đạo hàm và quy tắc đạo hàm? Nhờ giới hạn duy nhất. Nó có vẻ giống như một phép thuật, nhưng thực tế nó chỉ là sự khéo léo và không hề có sự lừa đảo. trong lớp Một dẫn xuất là gì? Tôi bắt đầu xem xét các ví dụ cụ thể trong đó, bằng cách sử dụng định nghĩa, tôi đã tìm thấy đạo hàm của hàm tuyến tính và hàm bậc hai. Với mục đích khởi động nhận thức, chúng tôi sẽ tiếp tục làm phiền bảng dẫn xuất, hoàn thiện thuật toán và giải pháp kỹ thuật:
Ví dụ 1
Về cơ bản, bạn cần chứng minh một trường hợp đặc biệt của đạo hàm hàm lũy thừa, trường hợp này thường xuất hiện trong bảng: .
Giải phápđược chính thức hóa về mặt kỹ thuật theo hai cách. Hãy bắt đầu với cách tiếp cận đầu tiên, vốn đã quen thuộc: bậc thang bắt đầu bằng một tấm ván và hàm đạo hàm bắt đầu bằng đạo hàm tại một điểm.
Hãy xem xét một số(cụ thể) điểm thuộc về miền định nghĩa hàm trong đó có đạo hàm. Chúng ta hãy đặt mức tăng tại thời điểm này (tất nhiên là trong phạm vio/o
-TÔI) và soạn phần tăng tương ứng của hàm:
Hãy tính giới hạn:
Độ không đảm bảo 0:0 được loại bỏ bằng một kỹ thuật tiêu chuẩn, được xem xét từ thế kỷ thứ nhất trước Công nguyên. Nhân tử số và mẫu số với biểu thức liên hợp 
:
Kỹ thuật giải giới hạn như vậy sẽ được thảo luận chi tiết trong bài học giới thiệu. về giới hạn của hàm.
Vì bạn có thể chọn BẤT KỲ điểm nào của khoảng làm chất lượng, nên sau khi thực hiện thay thế, chúng tôi nhận được:
Trả lời
Một lần nữa chúng ta hãy vui mừng với logarit:
Ví dụ 2
Tìm đạo hàm của hàm số bằng cách sử dụng định nghĩa đạo hàm
Giải pháp: Hãy xem xét một cách tiếp cận khác để thúc đẩy cùng một nhiệm vụ. Nó hoàn toàn giống nhau nhưng hợp lý hơn về mặt thiết kế. Ý tưởng là loại bỏ chỉ số dưới ở đầu lời giải và sử dụng chữ cái thay vì chữ cái.
Hãy xem xét tùy tiệnđiểm thuộc về miền định nghĩa hàm (khoảng) và đặt mức tăng trong đó. Nhưng ở đây, nhân tiện, như trong hầu hết các trường hợp, bạn có thể thực hiện mà không cần đặt trước, vì hàm logarit có khả vi tại bất kỳ điểm nào trong miền định nghĩa.
Khi đó mức tăng tương ứng của hàm là:
Hãy tìm đạo hàm:
Sự đơn giản của thiết kế được cân bằng bởi sự nhầm lẫn có thể nảy sinh đối với người mới bắt đầu (và không chỉ). Rốt cuộc, chúng ta đã quen với việc chữ “X” thay đổi trong giới hạn! Nhưng ở đây mọi thứ đều khác: - một bức tượng cổ, và - một du khách còn sống đang bước nhanh dọc hành lang của bảo tàng. Nghĩa là, “x” là “giống như một hằng số”.
Tôi sẽ bình luận về việc loại bỏ sự không chắc chắn từng bước:
(1) Chúng tôi sử dụng tính chất của logarit.
(2) Trong ngoặc đơn, chia tử số cho số hạng mẫu số cho số hạng.
(3) Ở mẫu số, chúng ta nhân chia giả tạo cho “x” để tận dụng giới hạn đáng chú ý 
, trong khi như vô cùng nhỏ nổi bật.
Trả lời: theo định nghĩa đạo hàm:
Hay nói ngắn gọn là:
Tôi đề xuất tự mình xây dựng thêm hai công thức bảng:
Ví dụ 3
Trong trường hợp này, sẽ thuận tiện hơn nếu giảm ngay số gia đã biên dịch xuống mẫu số chung. Mẫu bài tập gần đúng ở cuối bài (phương pháp đầu tiên).
Ví dụ 3:Giải pháp
: xem xét một số điểm
, thuộc miền định nghĩa của hàm số
. Chúng ta hãy đặt mức tăng tại thời điểm này
và soạn phần tăng tương ứng của hàm:
Hãy tìm đạo hàm tại điểm
:
Vì với tư cách là một
bạn có thể chọn bất kỳ điểm nào
miền chức năng
, Cái đó
Và
Trả lời
:
theo định nghĩa đạo hàm
Ví dụ 4
Tìm đạo hàm theo định nghĩa
Và ở đây mọi thứ cần được giảm xuống giới hạn tuyệt vời. Giải pháp được chính thức hóa theo cách thứ hai.
Một số khác dẫn xuất dạng bảng. Danh sách đầy đủ có thể được tìm thấy trong sách giáo khoa của trường, hoặc, ví dụ, tập 1 của Fichtenholtz. Tôi không thấy có ích lợi gì khi sao chép bằng chứng về các quy tắc vi phân từ sách - chúng cũng được tạo ra bởi công thức.
Ví dụ 4:Giải pháp
, thuộc về
và đặt mức tăng trong đó
Hãy tìm đạo hàm:
Sử dụng một giới hạn tuyệt vời
Trả lời
:
theo định nghĩa
Ví dụ 5
Tìm đạo hàm của hàm số bằng cách sử dụng định nghĩa đạo hàm
Giải pháp: chúng tôi sử dụng phong cách thiết kế đầu tiên. Hãy xem xét một số điểm thuộc về , và xác định mức tăng của đối số tại đó. Khi đó mức tăng tương ứng của hàm là:
Có lẽ một số độc giả vẫn chưa hiểu hết nguyên tắc cần phải tăng dần. Lấy một điểm (số) và tìm giá trị của hàm số trong đó: 
, tức là vào hàm thay vì"X" nên được thay thế. Bây giờ chúng ta cũng lấy một số rất cụ thể và thay thế nó vào hàm thay vì"iksa": . Chúng tôi viết ra sự khác biệt, và nó là cần thiết đặt hoàn toàn trong ngoặc.
Tăng hàm được biên dịch Việc đơn giản hóa ngay lập tức có thể có ích. Để làm gì? Tạo điều kiện thuận lợi và rút ngắn giải pháp đến một giới hạn hơn nữa.
Chúng tôi sử dụng công thức, mở ngoặc và rút ngắn mọi thứ có thể rút ngắn: 
Gà tây rút ruột, nướng không vấn đề gì:
Vì chúng ta có thể chọn bất kỳ số thực nào làm giá trị nên chúng ta thực hiện thay thế và nhận được 
.
Trả lời: theo định nghĩa.
Với mục đích xác minh, hãy tìm đạo hàm bằng cách sử dụng quy tắc và bảng phân biệt:
Việc biết trước câu trả lời chính xác luôn hữu ích và dễ chịu, vì vậy tốt hơn là bạn nên phân biệt chức năng được đề xuất một cách “nhanh chóng”, trong đầu hoặc trong bản nháp, ngay khi bắt đầu giải pháp.
Ví dụ 6
Tìm đạo hàm của hàm số theo định nghĩa đạo hàm
Đây là ví dụ để bạn tự giải quyết. Kết quả là rõ ràng:
Ví dụ 6:Giải pháp
: xem xét một số điểm
, thuộc về
và đặt mức tăng của đối số trong đó
. Khi đó mức tăng tương ứng của hàm là:
Hãy tính đạo hàm:
Như vậy: 
Bởi vì như
bạn có thể chọn bất kỳ số thực nào, sau đó
Và
Trả lời
:
theo định nghĩa.
Hãy quay lại phong cách số 2:
Ví dụ 7
Chúng ta hãy tìm hiểu ngay điều gì sẽ xảy ra. Qua quy tắc đạo hàm của hàm phức:
Giải pháp: xem xét một điểm tùy ý thuộc về , đặt mức tăng của đối số tại đó và tính mức tăng của hàm:
Hãy tìm đạo hàm: 
(1) Sử dụng công thức lượng giác 
.
(2) Dưới sin chúng ta mở ngoặc, dưới cos chúng ta trình bày các thuật ngữ tương tự.
(3) Theo sin chúng ta rút gọn các số hạng, dưới cosin chúng ta chia tử số cho số hạng mẫu số cho số hạng.
(4) Do tính chất kỳ lạ của sin nên chúng ta bỏ “dấu trừ”. Theo cosin, chúng tôi chỉ ra rằng số hạng .
(5) Chúng ta thực hiện phép nhân nhân tạo ở mẫu số để sử dụng giới hạn tuyệt vời đầu tiên. Vì vậy, sự không chắc chắn đã được loại bỏ, hãy thu thập kết quả.
Trả lời: theo định nghĩa
Như bạn có thể thấy, khó khăn chính của vấn đề đang được xem xét nằm ở độ phức tạp của chính giới hạn + tính độc đáo nhỏ của bao bì. Trong thực tế, cả hai phương pháp thiết kế đều xảy ra, vì vậy tôi mô tả cả hai phương pháp càng chi tiết càng tốt. Chúng tương đương nhau, nhưng theo ấn tượng chủ quan của tôi, những người giả nên chọn phương án 1 với “X-zero” sẽ tốt hơn.
Ví dụ 8
Sử dụng định nghĩa, tìm đạo hàm của hàm số
Ví dụ 8:Giải pháp
: xét một điểm tùy ý
, thuộc về
, chúng ta hãy đặt mức tăng trong đó
và soạn phần tăng của hàm:
Hãy tìm đạo hàm:
Chúng tôi sử dụng công thức lượng giác
và giới hạn đáng chú ý đầu tiên:
Trả lời
:
theo định nghĩa
Hãy xem xét một phiên bản hiếm hơn của vấn đề:
Ví dụ 9
Tìm đạo hàm của hàm số tại điểm bằng cách sử dụng định nghĩa đạo hàm.
Đầu tiên, điểm mấu chốt nên là gì? Con số
Hãy tính đáp án theo cách chuẩn: 
Giải pháp: từ quan điểm rõ ràng, nhiệm vụ này đơn giản hơn nhiều vì thay vào đó, công thức xem xét một giá trị cụ thể.
Hãy đặt mức tăng tại điểm và soạn mức tăng tương ứng của hàm:
Hãy tính đạo hàm tại một điểm:
Chúng tôi sử dụng một công thức hiệu tiếp tuyến rất hiếm 
và một lần nữa chúng tôi giảm giải pháp xuống giới hạn tuyệt vời đầu tiên:
Trả lời: theo định nghĩa đạo hàm tại một điểm.
Vấn đề không quá khó để giải quyết “nói chung” - chỉ cần thay thế hoặc đơn giản là tùy thuộc vào phương pháp thiết kế. Tất nhiên, trong trường hợp này, kết quả không phải là một con số mà là một hàm dẫn xuất.
Ví dụ 10
Sử dụng định nghĩa, tìm đạo hàm của hàm số 
tại một điểm (một trong số đó có thể là vô hạn), mà tôi đã mô tả một cách tổng quát về bài giảng lý thuyết về đạo hàm.
Một số hàm đã cho từng phần cũng khả vi tại các điểm “giao” của đồ thị, ví dụ, catdog có đạo hàm chung và một tiếp tuyến chung (trục x) tại điểm đó. Đường cong, nhưng có thể phân biệt bằng ! Những người quan tâm có thể tự mình xác minh điều này bằng cách sử dụng ví dụ vừa giải quyết.
©2015-2019 trang web
Tất cả các quyền thuộc về tác giả của họ. Trang web này không yêu cầu quyền tác giả nhưng cung cấp quyền sử dụng miễn phí.
Ngày tạo trang: 2017-06-11
Nội dung của bài viết
PHÁT SINH– đạo hàm của hàm y = f(x), cho trên một khoảng nhất định ( Một, b) tại điểm x của khoảng này được gọi là giới hạn mà tỷ số của độ tăng của hàm có xu hướng f tại thời điểm này với mức tăng tương ứng của đối số khi mức tăng của đối số có xu hướng bằng 0.
Đạo hàm thường được ký hiệu như sau:
Các chỉ định khác cũng được sử dụng rộng rãi:
Tốc độ tức thời.
Hãy để điểm M chuyển động theo đường thẳng. Khoảng cách Sđiểm chuyển động, được tính từ một số vị trí ban đầu M 0 , phụ thuộc vào thời gian t, tức là S có một hàm của thời gian t: S= f(t). Hãy để vào một thời điểm nào đó tđiểm chuyển động Mđã ở một khoảng cách S từ vị trí bắt đầu M 0 và tại một thời điểm tiếp theo t+D t thấy mình ở một vị trí M 1 – ở khoảng cách xa S+D S từ vị trí ban đầu ( xem ảnh.).
Như vậy trong khoảng thời gian D t khoảng cách S thay đổi một lượng D S. Trong trường hợp này họ nói rằng trong khoảng thời gian D t kích cỡ S nhận được số tiền tăng D S.
Tốc độ trung bình trong mọi trường hợp không thể mô tả chính xác tốc độ chuyển động của một điểm M tại một thời điểm t. Ví dụ: nếu cơ thể ở đầu khoảng D t di chuyển rất nhanh và cuối cùng rất chậm, khi đó tốc độ trung bình sẽ không thể phản ánh các đặc điểm đã chỉ ra về chuyển động của điểm và đưa ra ý tưởng về tốc độ thực sự của chuyển động của điểm đó vào lúc này t. Để thể hiện chính xác hơn tốc độ thực bằng tốc độ trung bình, bạn cần lấy một khoảng thời gian ngắn hơn D t. Mô tả đầy đủ nhất tốc độ chuyển động của một điểm tại thời điểm này t giới hạn mà tốc độ trung bình có xu hướng ở D t® 0. Giới hạn này được gọi là tốc độ hiện tại:
Do đó, tốc độ chuyển động tại một thời điểm nhất định được gọi là giới hạn của tỷ lệ tăng đường đi D S tăng dần theo thời gian D t, khi mức tăng thời gian có xu hướng bằng không. Bởi vì
Ý nghĩa hình học của đạo hàm. Tiếp tuyến với đồ thị của hàm số.
Việc xây dựng các đường tiếp tuyến là một trong những vấn đề dẫn đến sự ra đời của phép tính vi phân. Tác phẩm được xuất bản đầu tiên liên quan đến phép tính vi phân của Leibniz có tựa đề Một phương pháp mới về cực đại và cực tiểu, cũng như các tiếp tuyến, mà cả đại lượng phân số và đại lượng vô tỷ đều không phải là trở ngại và một loại phép tính đặc biệt cho phương pháp này.
Gọi đường cong là đồ thị của hàm số y =f(x) trong hệ tọa độ chữ nhật ( cm. cơm.).
Ở một giá trị nào đó x vấn đề chức năng y =f(x). Những giá trị này x Và yđiểm trên đường cong tương ứng M 0(x, y). Nếu lập luận xđưa cho tăng D x, thì giá trị mới của đối số x+D x tương ứng với giá trị hàm mới y+ D y = f(x + D x). Điểm tương ứng của đường cong sẽ là điểm M 1(x+D x,y+D y). Nếu bạn vẽ một cát tuyến M 0M 1 và ký hiệu là j góc tạo bởi một đường ngang với hướng dương của trục Con bò đực, từ hình vẽ có thể thấy ngay rằng .
Nếu bây giờ D x có xu hướng về 0 thì điểm M 1 di chuyển dọc theo đường cong, tiến đến điểm M 0 và góc j thay đổi với D x. Tại Dx® 0 góc j tiến tới một giới hạn nhất định a và đường thẳng đi qua điểm M 0 và thành phần có hướng dương của trục x, góc a, sẽ là tiếp tuyến mong muốn. Độ dốc của nó là:
Kể từ đây, f´( x) = tga
những thứ kia. giá trị phái sinh f´( x) cho một giá trị đối số nhất định x bằng tiếp tuyến của góc tạo bởi tiếp tuyến của đồ thị hàm số f(x) tại điểm tương ứng M 0(x,y) với hướng trục dương Con bò đực.
Tính khả vi của các chức năng.
Sự định nghĩa. Nếu chức năng y = f(x) có đạo hàm tại điểm x = x 0 thì hàm số khả vi tại điểm này.
Tính liên tục của hàm số có đạo hàm. Định lý.
Nếu chức năng y = f(x) khả vi tại một số điểm x = x 0 thì nó liên tục tại điểm này.
Vì vậy, hàm số không thể có đạo hàm tại các điểm gián đoạn. Kết luận ngược lại là sai, tức là từ thực tế là tại một thời điểm nào đó x = x 0 chức năng y = f(x) liên tục không có nghĩa là nó khả vi tại điểm này. Ví dụ, chức năng y = |x| liên tục cho mọi người x(–Ґ x x = 0 không có đạo hàm. Lúc này đồ thị không có tiếp tuyến. Có tiếp tuyến phải và tiếp tuyến trái nhưng không trùng nhau.
Một số định lý về hàm khả vi. Định lý về nghiệm của đạo hàm (định lý Rolle). Nếu chức năng f(x) liên tục trên đoạn [Một,b], khả vi tại tất cả các điểm trong của đoạn này và tại các điểm cuối x = Một Và x = b tiến về 0 ( f(Một) = f(b) = 0), thì bên trong đoạn [ Một,b] có ít nhất một điểm x= Với, Một c b, trong đó đạo hàm fў( x) tiến tới 0, tức là fў( c) = 0.
Định lý gia tăng hữu hạn (định lý Lagrange). Nếu chức năng f(x) liên tục trên khoảng [ Một, b] và khả vi tại tất cả các điểm bên trong của đoạn thẳng này, rồi bên trong đoạn [ Một, b] có ít nhất một điểm Với, Một cb cái đó
f(b) – f(Một) = fў( c)(b– Một).
Định lý về tỉ số gia số của hai hàm số (định lý Cauchy). Nếu như f(x) Và g(x) – hai hàm liên tục trên đoạn [Một, b] và khả vi tại tất cả các điểm bên trong của đoạn này, và gў( x) không biến mất ở bất kỳ đâu bên trong đoạn này, thì bên trong đoạn [ Một, b] có một điểm như vậy x = Với, Một cb cái đó
Công cụ phái sinh của các đơn đặt hàng khác nhau.
Hãy để chức năng y =f(x) khả vi trên một khoảng [ Một, b]. Giá trị đạo hàm f ў( x), nói chung là phụ thuộc vào x, tức là phái sinh f ў( x) cũng là một hàm của x. Khi đạo hàm hàm này, ta thu được cái gọi là đạo hàm bậc hai của hàm f(x), được ký hiệu f ўў ( x).
phái sinh N- thứ tự chức năng f(x) được gọi là đạo hàm (bậc 1) của đạo hàm N- 1- th và được ký hiệu bằng ký hiệu y(N) = (y(N– 1))ў.
Sự khác biệt của các đơn đặt hàng khác nhau.
Hàm vi phân y = f(x), Ở đâu x– biến độc lập, có nhuộm = f ў( x)dx, một số chức năng từ x, nhưng từ x chỉ có yếu tố đầu tiên có thể phụ thuộc f ў( x), yếu tố thứ hai ( dx) là mức tăng của biến độc lập x và không phụ thuộc vào giá trị của biến này. Bởi vì nhuộm có một chức năng từ x, thì chúng ta có thể xác định được vi phân của hàm này. Vi phân của vi phân của một hàm số gọi là vi phân bậc hai hoặc vi phân bậc hai của hàm số đó và được ký hiệu là d 2y:
d(dx) = d 2y = f ўў( x)(dx) 2 .
vi sai N- bậc thứ nhất được gọi là vi phân bậc nhất của vi phân N- 1- thứ tự:
d n y = d(d n–1y) = f(N)(x)dx(N).
Đạo hàm một phần.
Nếu một hàm không phụ thuộc vào một mà phụ thuộc vào nhiều đối số x tôi(Tôi thay đổi từ 1 đến N,Tôi= 1, 2,… N),f(x 1,x 2,… x n), thì trong phép tính vi phân, khái niệm đạo hàm riêng được đưa ra, đặc trưng cho tốc độ thay đổi của hàm nhiều biến khi chỉ có một đối số thay đổi, ví dụ: x tôi. Đạo hàm riêng bậc 1 đối với x tôiđược định nghĩa là đạo hàm thông thường và giả định rằng tất cả các đối số ngoại trừ x tôi, giữ nguyên giá trị Đối với đạo hàm riêng, ký hiệu được đưa vào
Đạo hàm riêng bậc 1 được định nghĩa theo cách này (là hàm của cùng một đối số) cũng có thể có đạo hàm riêng, đây là đạo hàm riêng bậc hai, v.v. Các dẫn xuất như vậy được lấy từ các đối số khác nhau được gọi là hỗn hợp. Các đạo hàm hỗn hợp liên tục cùng cấp không phụ thuộc vào thứ tự vi phân và bằng nhau.
Anna Chugainova
Giả sử hàm y = f(x) được xác định trong khoảng X. phái sinh hàm số y = f(x) tại điểm x o được gọi là giới hạn
=
.
Nếu giới hạn này hữu hạn, thì hàm f(x) được gọi có thể phân biệt được tại điểm x ồ;
Hơn nữa, hóa ra nó nhất thiết phải liên tục vào thời điểm này. Nếu giới hạn đang xét bằng (hoặc - ), thì với điều kiện là hàm số tại điểm ồ X Nếu giới hạn đang xét bằng (hoặc - ), thì với điều kiện là hàm số tại điểm ồ là liên tục, ta sẽ nói rằng hàm số f(x) có tại điểm.
đạo hàm vô hạn
Đạo hàm được ký hiệu bằng ký hiệu
y , f (x o), , . Việc tìm đạo hàm được gọi là sự khác biệt chức năng.Ý nghĩa hình học của đạo hàm Nếu giới hạn đang xét bằng (hoặc - ), thì với điều kiện là hàm số tại điểm ồ ; là đạo hàm là độ dốc của tiếp tuyến với đường cong y=f(x) tại một điểm cho trướcý nghĩa vật lý -
là đạo hàm của đường đi theo thời gian là tốc độ tức thời của một điểm chuyển động trong quá trình chuyển động thẳng s = s(t) tại thời điểm t. Với Nếu như
là một số không đổi và u = u(x), v = v(x) là một số hàm khả vi, khi đó các quy tắc đạo hàm sau là đúng:
1)(c)” = 0, (cu) “= cu”;
2) (u+v)" = u"+v";
3) (uv)" = u"v+v"u;
4) (u/v)" = (u"v-v"u)/v 2; 5) nếu y = f(u), u = (x), tức là y = f((x)) - hàm phức tạp hoặc sự chồng chất
, bao gồm các hàm khả vi và f, khi đó , hoặc
6) nếu với hàm y = f(x) có hàm khả vi nghịch đảo x = g(y) và 0, thì .
Dựa vào định nghĩa đạo hàm và quy tắc đạo hàm có thể biên soạn được danh sách đạo hàm dạng bảng của các hàm cơ bản chính. 1. (u )" = u 1 u" ( ).
R
2. (a u)" = a u lna u".
3. (e u)" = e u u".
4. (log a u)" = u"/(u ln a).
5. (ln u)" = u"/u.
6. (sin u)" = cos u u".
7. (cos u)" = - sin u u".
8. (tg u)" = 1/ cos 2 u u".
9. (ctg u)" = - u" / sin 2 u.
10. (arcsin u)" = u" / .
11. (arccos u)" = - u" / .
12. (arctg u)" = u"/(1 + u 2).
13. (arcctg u)" = - u"/(1 + u 2). Hãy tính đạo hàm của biểu thức lũy thừa y=u v , (u>0), trong đó bạn Và v Nếu giới hạn đang xét bằng (hoặc - ), thì với điều kiện là hàm số tại điểm bản chất của chức năng từ , có đạo hàm tại một điểm cho trước,bạn".
v"
Lấy logarit của đẳng thức y=u v , ta thu được ln y = v ln u. Nếu giới hạn đang xét bằng (hoặc - ), thì với điều kiện là hàm số tại điểm từ cả hai vế của đẳng thức thu được bằng cách sử dụng quy tắc 3, 5 và công thức đạo hàm của hàm logarit, chúng ta sẽ có:
y"/y = vu"/u +v" ln u, từ đó y" = y (vu"/u +v" ln u).
(u v)"=u v (vu"/u+v" ln u), u > 0.
Ví dụ, nếu y = x sin x, thì y" = x sin x (sin x/x + cos x ln x).
Nếu hàm y = f(x) khả vi tại điểm x, tức là có đạo hàm hữu hạn tại điểm này ừ", thì = y"+, trong đó 0 tại х 0; do đó y = y" х + x.
Phần chính của hàm tăng, tuyến tính đối với x, được gọi là sự khác biệt chức năng và được ký hiệu là dy: dy = y" х. Nếu đặt y=x vào công thức này, chúng ta nhận được dx = x"х = 1х =х, do đó dy=y"dx, tức là ký hiệu for Ký hiệu đạo hàm có thể được coi là một phân số.
Hàm tăng y là độ tăng của tọa độ của đường cong và vi phân d y là gia số thứ cấp của tiếp tuyến.
Chúng ta hãy tìm đạo hàm y=f(x) của hàm số y = f (x). Đạo hàm của đạo hàm này được gọi làđạo hàm bậc hai hàm f(x), hoặcđạo hàm bậc hai, 
.
và được chỉ định
Sau đây được định nghĩa và chỉ định theo cùng một cách:
-
,
đạo hàm bậc ba
đạo hàm bậc bốn - và nói chung
-
.
đạo hàm cấp n.15. Ví dụ 3
Tính đạo hàm của hàm số y=(3x 3 -2x+1)sin x. Giải pháp.
Theo quy tắc 3, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x +1)cos x. 3.16 Ví dụ
Tính đạo hàm của hàm số y=(3x 3 -2x+1)sin x.. 
=
.
đạo hàm cấp n.17. Tìm y”, y = tan x + .
Tính đạo hàm của hàm số y=(3x 3 -2x+1)sin x. Sử dụng quy tắc phân biệt tổng và thương, ta thu được: y"=(tgx + )" = (tgx)" + ()" = + 
.
78875C8D xỨng dụng x
Đạo hàm là khái niệm quan trọng nhất trong phân tích toán học. Nó đặc trưng cho sự thay đổi chức năng của đối số tại một số điểm. Hơn nữa, bản thân đạo hàm cũng là một hàm của đối số
Đạo hàm của hàm tại một điểm là giới hạn (nếu nó tồn tại và hữu hạn) của tỷ lệ giữa mức tăng của hàm và mức tăng của đối số, với điều kiện là giá trị sau có xu hướng bằng 0. :
Được sử dụng phổ biến nhất là sau đây ký hiệu phái sinh Ví dụ 1. Lợi dụng
định nghĩa đạo hàm
, tìm đạo hàm của hàm số
Giải pháp. Từ định nghĩa của đạo hàm, sơ đồ tính toán sau đây được thực hiện.
Chúng ta hãy tính giới hạn của tỷ lệ này với điều kiện là mức tăng của đối số có xu hướng bằng 0, tức là đạo hàm cần có trong câu lệnh bài toán:
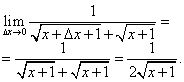
Ý nghĩa vật lý của đạo hàm
ĐẾN khái niệm đạo hàm dẫn đến nghiên cứu của Galileo Galilei về định luật rơi tự do của các vật thể, và theo nghĩa rộng hơn - vấn đề về tốc độ tức thời của chuyển động thẳng không đều của một điểm.
Hãy để hòn sỏi được nâng lên rồi thả ra khỏi trạng thái đứng yên. Con đường S vượt qua thời gian t, nghĩa là một hàm của thời gian. s = s(t). Nếu định luật chuyển động của một điểm được đưa ra thì có thể xác định được tốc độ trung bình trong một khoảng thời gian bất kỳ. Hãy để tại thời điểm đó viên sỏi ở đúng vị trí MỘT, và tại thời điểm này - ở vị trí B. Trong một khoảng thời gian (từ t tới ) điểm đã đi qua đường dẫn . Do đó, tốc độ chuyển động trung bình trong khoảng thời gian này, mà chúng ta biểu thị bằng , là
.
Tuy nhiên, chuyển động của một vật rơi tự do rõ ràng là không đều. Tốc độ Và mùa thu không ngừng tăng lên. Và tốc độ trung bình không còn đủ để mô tả tốc độ di chuyển trên các đoạn khác nhau của tuyến đường. Khoảng thời gian càng ngắn thì đặc tính này càng chính xác. Do đó, khái niệm sau được đưa ra: tốc độ tức thời của chuyển động thẳng (hoặc tốc độ tại một thời điểm nhất định) t) được gọi là tốc độ giới hạn trung bình tại:
(với điều kiện là giới hạn này tồn tại và hữu hạn).
Vì vậy, hóa ra tốc độ tức thời là giới hạn của tỷ lệ tăng của hàm S(t) theo sự gia tăng của đối số t tại Đây là đạo hàm, ở dạng tổng quát được viết như sau:.
.
Giải pháp cho vấn đề được chỉ ra là ý nghĩa vật lý của đạo hàm . Vì vậy, đạo hàm của hàm y=f(x) tại điểm xđược gọi là giới hạn (nếu nó tồn tại và hữu hạn) của mức tăng của hàm đối với mức tăng của đối số, với điều kiện là giá trị sau có xu hướng bằng 0.
Ví dụ 2. Tìm đạo hàm của một hàm số
Giải pháp. Từ định nghĩa của đạo hàm, sơ đồ sau đây để tính toán nó như sau.
Bước 1. Hãy tăng đối số và tìm
Bước 2. Tìm số gia của hàm:
Bước 3. Tìm tỷ lệ giữa phần tăng của hàm và phần tăng của đối số:
Bước 4. Tính giới hạn của tỷ số này tại , tức là đạo hàm:
Ý nghĩa hình học của đạo hàm
Hãy để hàm được xác định trên một khoảng và để điểm M trên đồ thị của hàm tương ứng với giá trị của đối số và điểm R- nghĩa. Hãy vẽ qua các điểm M Và Rđường thẳng và gọi nó cát tuyến. Chúng ta hãy biểu thị bằng góc giữa cát tuyến và trục. Rõ ràng góc này phụ thuộc vào .
Nếu tồn tại
đi qua điểm gọi là vị trí giới hạn của cát tuyến ÔNG tại (hoặc tại ).
Tiếp tuyến với đồ thị của hàm số tại một điểm M gọi là vị trí giới hạn của cát tuyến ÔNG tại , hoặc, giống nhau tại .
Từ định nghĩa suy ra rằng để tồn tại một tiếp tuyến chỉ cần có một giới hạn
,
và giới hạn này bằng góc nghiêng của tiếp tuyến với trục.
Bây giờ hãy đưa ra một định nghĩa chính xác về tiếp tuyến.
Đường tiếp tuyếnĐồ thị của hàm số tại một điểm là một đường thẳng đi qua điểm đó và có độ dốc, tức là đường thẳng có phương trình
Từ định nghĩa này suy ra rằng đạo hàm của hàm bằng độ dốc của tiếp tuyến với đồ thị của hàm số này tại điểm có hoành độ x. Đây là ý nghĩa hình học của đạo hàm.