“Miền định nghĩa hàm số” - Miền định nghĩa hàm số bậc hai là số thực bất kỳ. Một hàm được gọi là logarit nếu giá trị của biến nằm dưới dấu logarit. Hàm logarit. Hàm có biến nằm trong số mũ được gọi là hàm mũ. Hàm bậc hai.
“Tính chất chung của hàm số” - Tính chất chung của hàm số. Tìm miền định nghĩa của hàm số. Chức năng chẵn. Hàm số này là chẵn hay lẻ. Sử dụng đồ thị, xác định tập hợp các giá trị của hàm. Sử dụng đồ thị hãy xác định các giá trị của X. Sử dụng đồ thị hãy xác định các khoảng để hàm số giảm. Hàm f(x) đang tăng. Hàm y=f(x) đã cho.
“Hàm tăng giảm” - Hàm sin tăng giảm. Hãy xem một ví dụ khác. Các khoảng cosin giảm là các đoạn, n là số nguyên. Ví dụ, giả sử hàm f chẵn và tăng trong khoảng mà b>a?0. Chức năng tăng và giảm. Hàm cosin tăng và giảm. Hình bên dưới hiển thị đồ thị của hàm được xác định trên khoảng [-1;10].
“Ứng dụng tính liên tục” - Ý nghĩa biểu hiện. Ý nghĩa hình học của đạo hàm. Phương pháp ngắt quãng. Viết phương trình tiếp tuyến của đồ thị hàm số. Tiếp tuyến với đồ thị của hàm số. Đồ thị gần với một tiếp tuyến. Công thức. Hãy tính toán bằng công thức. Tiếp tuyến của đường cong tại điểm M cho trước là vị trí giới hạn của cát tuyến NM. Hyperbol.
“Chức năng vượt trội” - Sự phụ thuộc của áp suất khí vào nhiệt độ. Đề bài: “Dấu hiệu của hàm số tăng, hàm giảm. Bài kiểm tra. Sự thay đổi cường độ dòng điện khi mạch hở. Nghiên cứu hàm số tới cực trị”. Sự thay đổi dòng điện xoay chiều. Sơ đồ: Sự phụ thuộc của dòng điện vào điện áp. Sự phụ thuộc của áp suất khí vào thể tích. Đề tài: “Dấu hiệu của hàm tăng, hàm giảm.
“Các hàm và thuộc tính của chúng” - Biến độc lập được gọi là đối số. Tăng chức năng. Định nghĩa của một chức năng. Hàm chẵn và hàm lẻ. Tính đơn điệu của hàm số. Các giá trị của biến phụ thuộc được gọi là giá trị của hàm. Tất cả các giá trị của biến độc lập tạo thành miền định nghĩa của hàm -D (f). 1. Các giá trị của hàm đều dương.
Tổng cộng có 23 bài thuyết trình
Đề tài: Phương pháp sử dụng hàm giới hạn.
Cuộc sống tốt đẹp vì những gì trong đó
bạn có thể làm toán
(Leonard Euler)Bàn thắng: phát triển tư duy độc đáo mới, có thể áp dụng thành công trong các lĩnh vực hoạt động khác của con người (điều khiển học, công nghệ máy tính, kinh tế, vật lý phóng xạ, hóa học, v.v.).
Nhiệm vụ: - rèn luyện khả năng đánh giá độ khó khách quan, chủ quan của nhiệm vụ và lựa chọn sáng suốt các nhiệm vụ này trong kỳ thi;
Tạo ra một “con heo đất” với những lý luận độc đáo và khác thường.
Tiến độ bài học:
Tổ chức chốc lát. Học sinh xây dựng chủ đề của bài học bằng cách hoàn thành các bài tập A và B của Kỳ thi Thống nhất phần A và B và giải mã chủ đề theo thứ tự đáp án nhận được giảm dần. (Mã hóa 12 thẻ đánh số từ -2 đến 10 làm chữ) (Phụ lục 1 và 2)
hạn chế
2. Chia học sinh thành 2 nhóm, giao bộ “Lý thuyết + 10 nhiệm vụ” (Phụ lục 3 và 4), yêu cầu các em chọn những nhiệm vụ có thể hoàn thành phần lý thuyết này và giải thích cho sự lựa chọn của mình.3. HS trình bày tiến độ thực hiện các nhiệm vụ này lên bảng: Noskova K., Dedevshin I., Veselov I.4. Chia các nhiệm vụ trong thẻ thành 2 nhóm để giải, sau đó tự kiểm tra bằng tờ giấy có sẵn lời giải. (Phụ lục 5)5. Phát cho các nhóm tờ mô tả các phương pháp mới không chuẩn để giải phương trình, bất phương trình để chọn chủ đề tiếp theo (làm bài tập về nhà, tìm các bài toán trong tuyển tập Đề thi Thống nhất có thể giải được bằng phương pháp này) (Phụ lục 6)6. Phản ánh của học sinh (điền vào bảng) F.I. học sinhPhụ lục 1.
Giải các nhiệm vụ này và sắp xếp các câu trả lời theo thứ tự giảm dần, thu thập chủ đề bài học của chúng ta dựa trên các câu trả lời.
Tìm hoành độ của điểm trong đồ thị hàm số y=3x 2 -7x+7, trong đó tiếp tuyến của góc tiếp tuyến bằng -1.
Phụ lục 2.
9 2 0 7Nghiên cứu hàm số sử dụng đạo hàm. 10 5 1 -1Phương pháp sử dụng hàm giới hạn. 4 -2 8 12Giải bất phương trình bằng đồ thị.
3 11 6Giải phương trình hàm số.
Học
Phụ lục 3.
Một trong những phương pháp hiệu quả để giải phương trình hoặc bất phương trình là phương pháp dựa trên việc sử dụng hàm giới hạn. Ví dụ, các hàm giới hạn được biết đến nhiều nhất bao gồm một số hàm lượng giác; hàm lượng giác nghịch đảo; các hàm chứa mô đun, bậc, căn bậc chẵn và các hàm khác.
Các bất đẳng thức phổ biến nhất là:
│f(x) │≥
0, -1
≤
tội lỗi ≤
1, -1
≤
cosx ≤
1, -
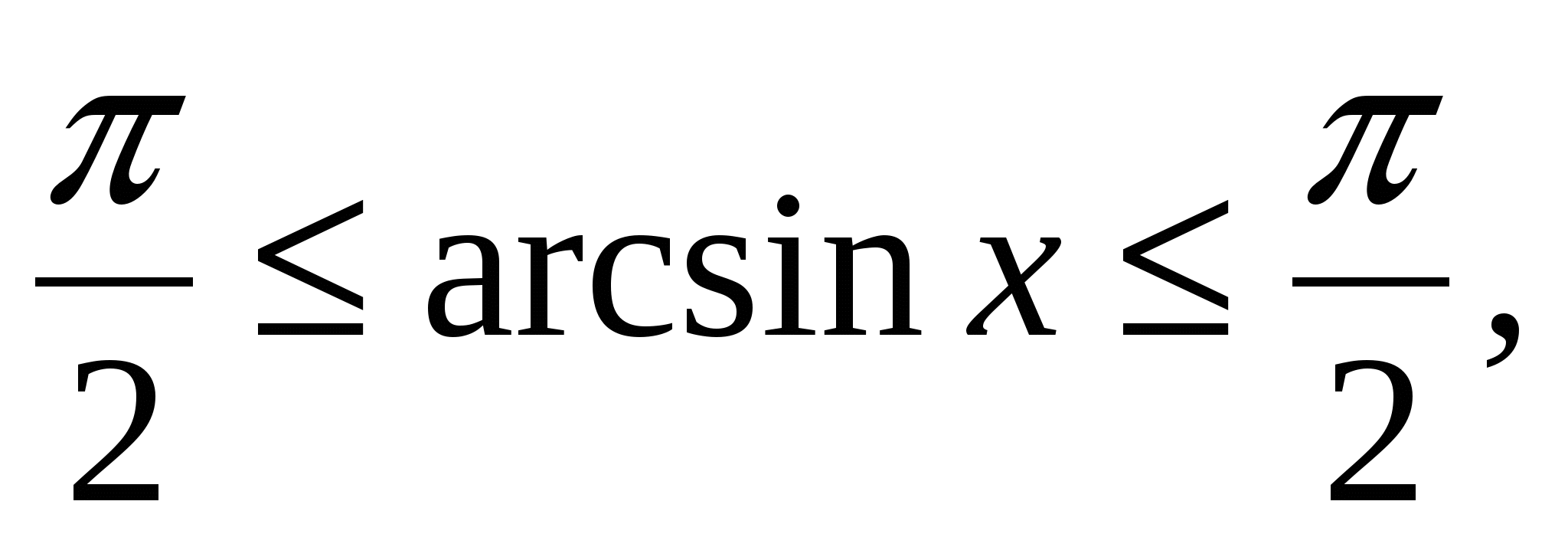
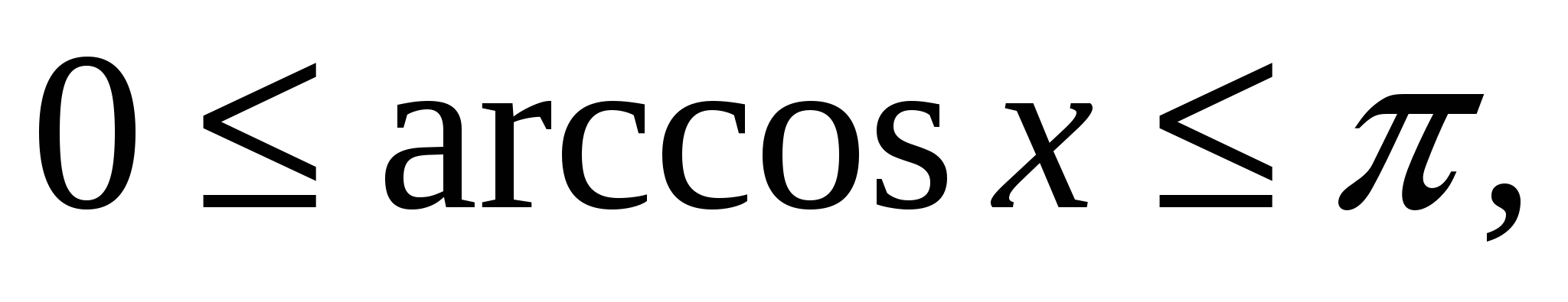 -
-

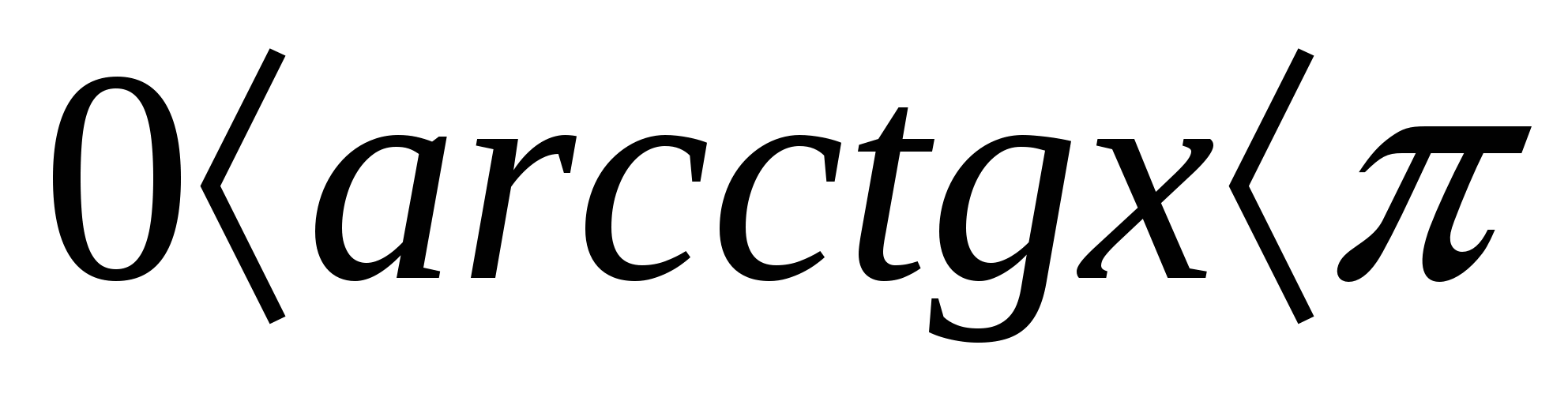 ,
Một f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
,
Một f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
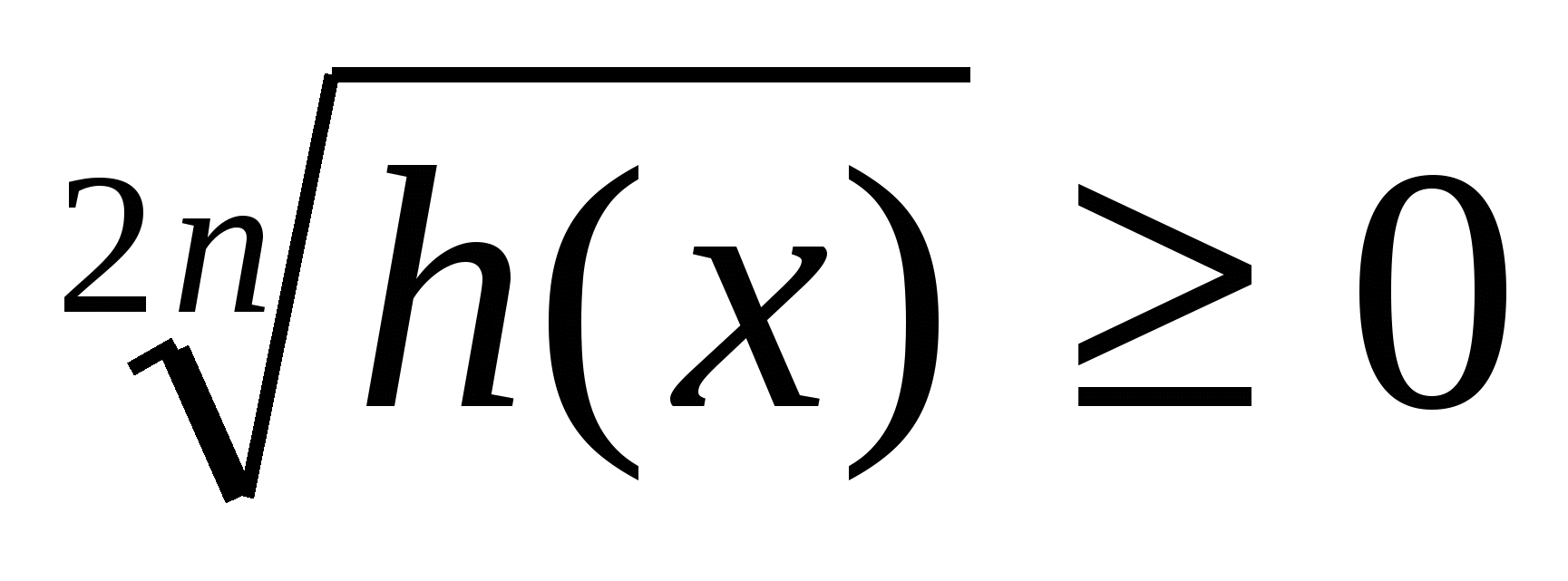 ,
Một+
≥
2,
b+
≤
-2
và nhiều người khác. Đây N - số tự nhiên, h(x) ≥
0,
Một>0,
b
0.
,
Một+
≥
2,
b+
≤
-2
và nhiều người khác. Đây N - số tự nhiên, h(x) ≥
0,
Một>0,
b
0.
Ngoài những bất đẳng thức đơn giản nhất nêu trên, còn có những bất đẳng thức phức tạp hơn, cụ thể là các bất đẳng thức lượng giác -,
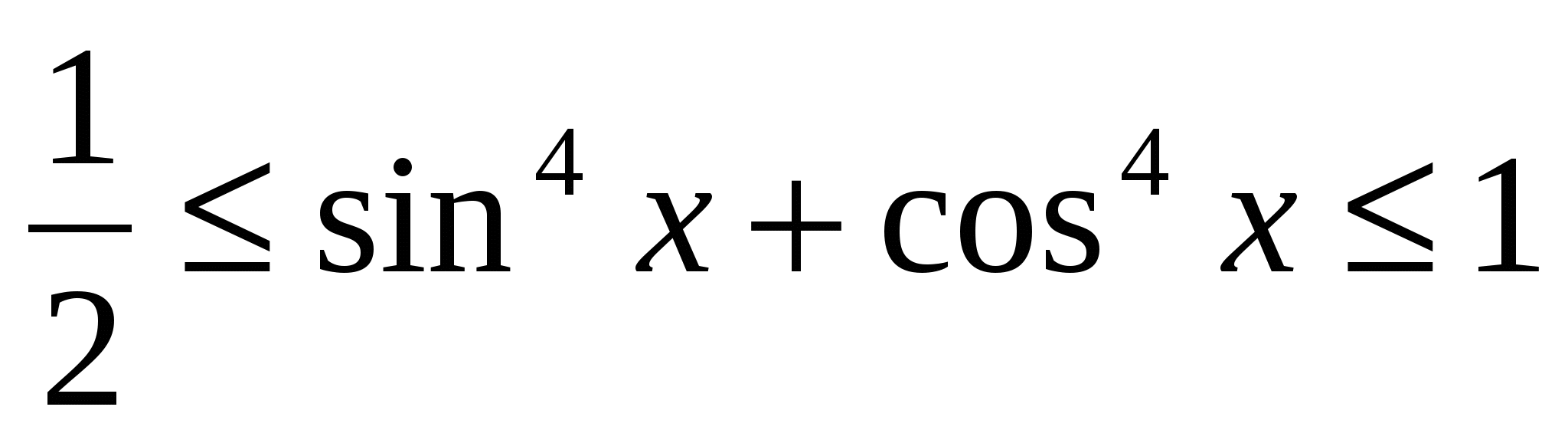 ,
,
và bất đẳng thức với các môđun có dạng 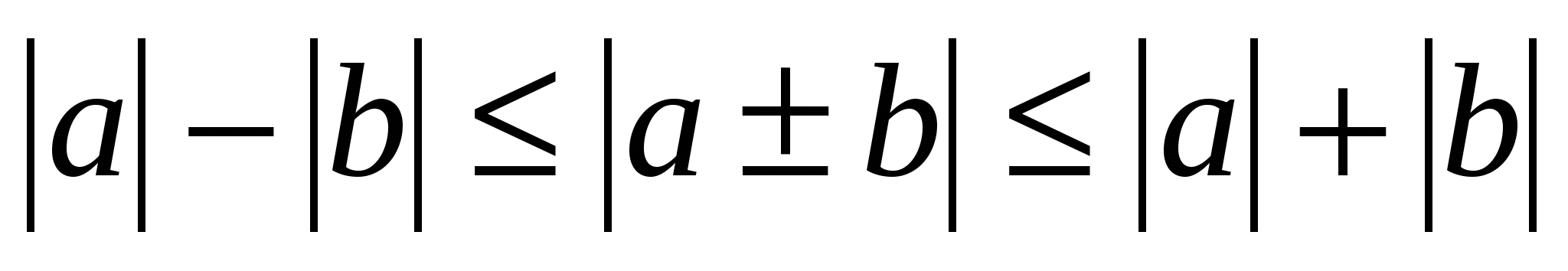 .
.
Ví dụ 1.Giải phương trình: 
Giải pháp:
Hãy chọn một hình vuông hoàn chỉnh ở phía bên phải của phương trình, tức là . Nó theo sau đó 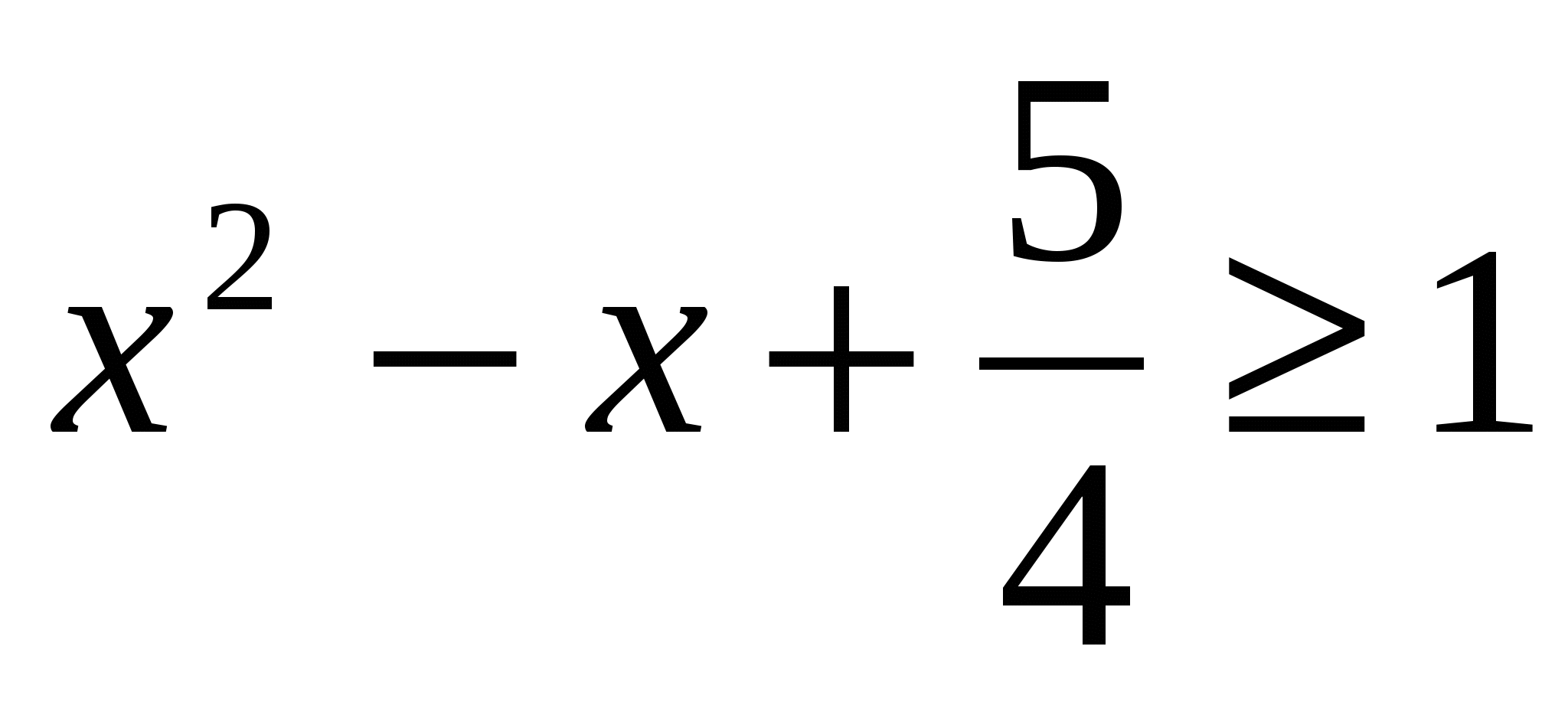 . Vì trong trường hợp này tội lỗi x ≤
1 thì ta thu được hệ phương trình
. Vì trong trường hợp này tội lỗi x ≤
1 thì ta thu được hệ phương trình 
Giải phương trình thứ hai của hệ ta được x=. Bằng cách thay thế vào phương trình đầu tiên, chúng ta đảm bảo rằng giá trị tìm thấy của x là một nghiệm của hệ, và do đó là một nghiệm của phương trình ban đầu.
Trả lời: x=.
Ví dụ 2.Giải phương trình: 
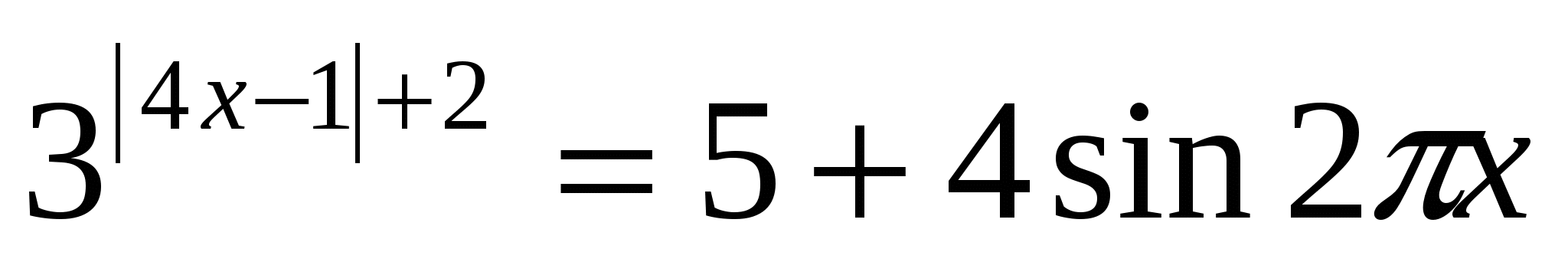
Giải pháp: vì Tuy nhiên sin2 π x ≤
1. Do đó, 5+4 sin2 π x ≤
9. Như vậy ta thu được hệ phương trình: 
Từ đây ta thu được hệ phương trình  , từ phương trình đầu tiên chúng ta tìm thấy x=. Hãy thay nó vào phương trình thứ hai của hệ và đảm bảo rằng x = là nghiệm của hệ, và do đó là nghiệm của phương trình ban đầu.
, từ phương trình đầu tiên chúng ta tìm thấy x=. Hãy thay nó vào phương trình thứ hai của hệ và đảm bảo rằng x = là nghiệm của hệ, và do đó là nghiệm của phương trình ban đầu.
Trả lời: x=
Phụ lục 4.
Từ danh sách các nhiệm vụ được đề xuất, hãy chọn những nhiệm vụ có thể giải quyết bằng phương pháp hàm giới hạn.
1. Giải phương trình x 2 -4 x=(2-cos  2. Tìm số nghiệm nguyên của bất đẳng thức x 2ctg 2
2. Tìm số nghiệm nguyên của bất đẳng thức x 2ctg 2 3. Giải phương trình
3. Giải phương trình 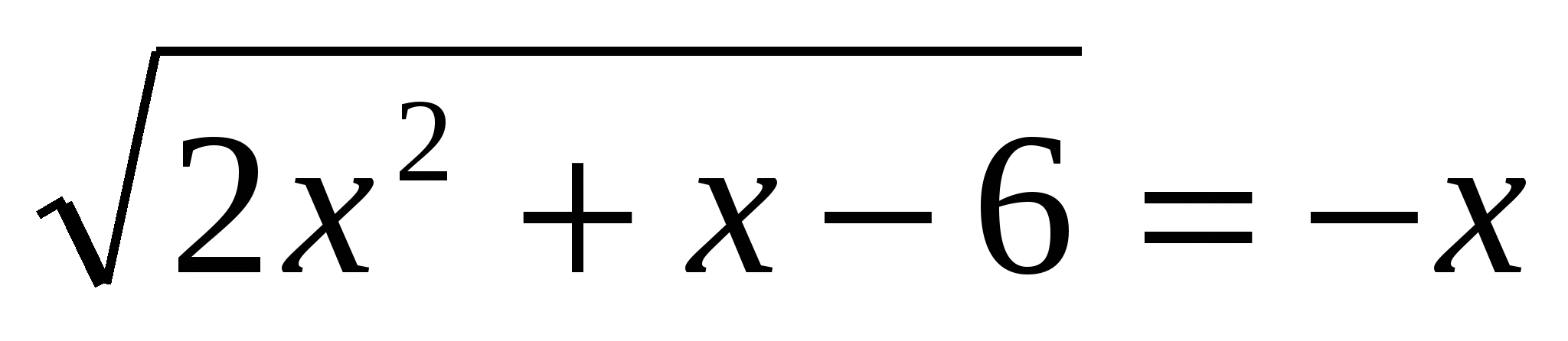 4. Giải phương trình 3-(5. Tìm số nghiệm nguyên của bất đẳng thức 16 2 ≥0 thỏa mãn điều kiện 3 tg 2
4. Giải phương trình 3-(5. Tìm số nghiệm nguyên của bất đẳng thức 16 2 ≥0 thỏa mãn điều kiện 3 tg 2  6. Giải phương trình
6. Giải phương trình  7. Giải phương trình -25x 2 +40x-23=( vì
7. Giải phương trình -25x 2 +40x-23=( vì 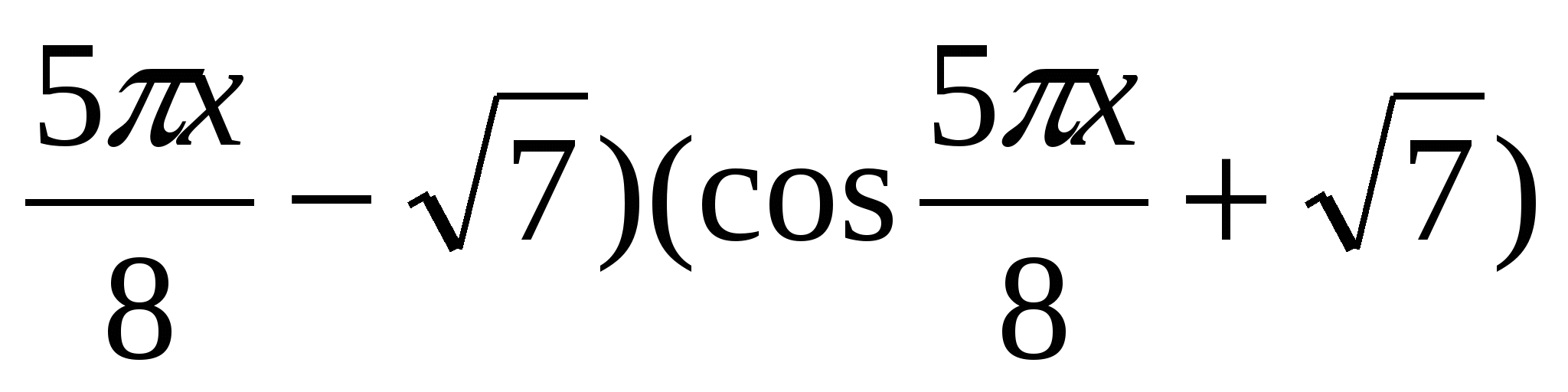 8. Tìm tích các nghiệm của phương trình x
8. Tìm tích các nghiệm của phương trình x  9. Giải phương trình
9. Giải phương trình  10. Giải phương trình 3- cos 2
10. Giải phương trình 3- cos 2 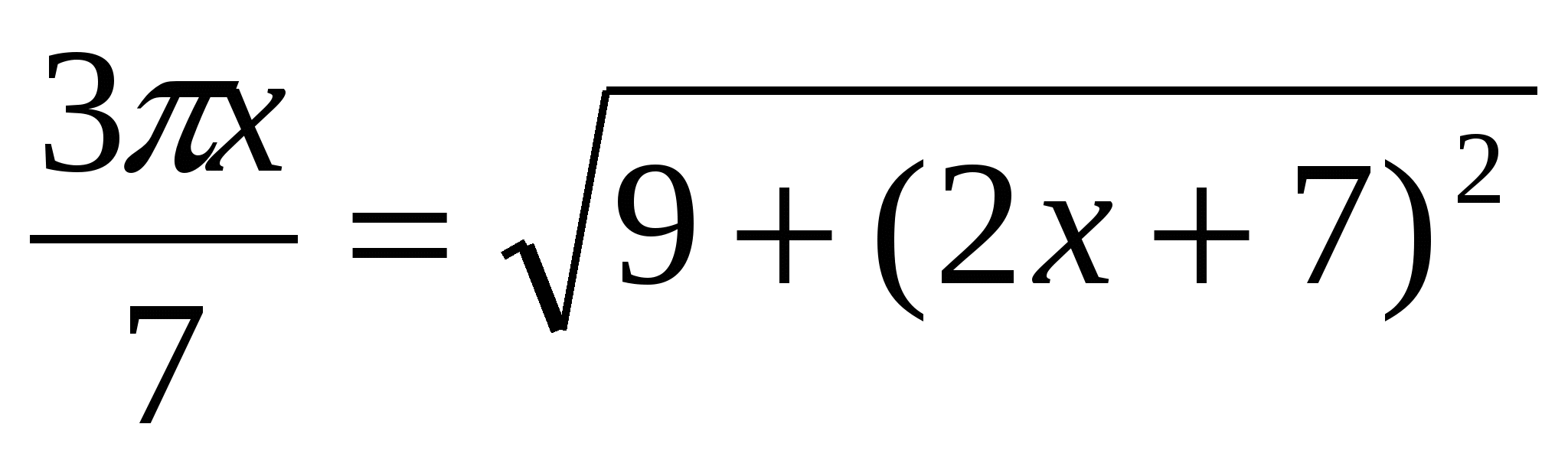
Phiếu tự kiểm tra.
Phụ lục 5.
1. Giải phương trình
Giải: vì , thì bởi vì và sau đó
chúng ta thu được hệ phương trình
giải phương trình thứ nhất, lấy x=, thay giá trị này vào phương trình thứ hai
2 . Giải phương trình 3-
cos 2 Giải: vì , thì bởi vì và sau đó
chúng ta thu được hệ phương trình
giải phương trình thứ hai, lấy x=, thay giá trị này vào phương trình thứ nhất
điều này có nghĩa là x= là nghiệm của phương trình ban đầu. Đáp án: x=
3. Tìm số nghiệm nguyên của bất đẳng thức x 2
+7x-8<0, thỏa mãn điều kiện ctg 2 Giải pháp: bởi vì và sau đó với bất kỳ giá trị chấp nhận được nào của x, chúng ta sẽ tìm các số 0 của tam thức bậc hai, sử dụng định lý Vieta, chúng ta sẽ giải bất đẳng thức bằng phương pháp khoảng
Cái đó. chúng tôi biết điều đó
các giá trị nguyên của x là các số bị loại Đáp án: 8 nghiệm số nguyên 4. Tìm số nghiệm nguyên của bất đẳng thức 16 2 ≥0 thỏa mãn điều kiện 3 tg 2 Giải pháp: bởi vì và sau đó với bất kỳ giá trị cho phép nào của x, chúng ta tìm các số 0 của biểu thức x = và x = Giải bất đẳng thức bằng phương pháp khoảng
Cái đó. chúng tôi biết điều đó
giá trị nguyên của x là số bị loại Đáp án: 7 nghiệm số nguyên
Phụ lục 6.
Phương pháp sử dụng tính đơn điệu của hàm số. Khi giải một phương trình như f(x)=g(x) trong một số trường hợp, một phương pháp hiệu quả là sử dụng tính đơn điệu của các hàm y= f(x) và y= g(x). Nếu hàm y= f(x) là liên tục và tăng (giảm) trên đoạn Một≤ x ≤ b, và hàm số у= g(x) liên tục và giảm (tăng) trên cùng một đoạn thì phương trình f(x)=g(x) trên đoạn đó Một≤ x ≤ b không thể có nhiều hơn một nghiệm, điều đó có nghĩa là cần phải cố gắng tìm nghiệm duy nhất của phương trình bằng cách chọn hoặc chứng minh rằng nghiệm đó không tồn tại. Phương pháp này đặc biệt hiệu quả trong trường hợp cả hai vế của phương trình f(x) = g(x) đều là những hàm “không thuận tiện” cho việc nghiên cứu chung. Bình luận: Nếu hàm y= f(x) tăng và hàm y= g(x) giảm đối với Một≤ x ≤ b Và cùng lúc f(a)>g(MỘT), thì nghiệm của phương trình nằm trong số Một≤ x ≤ b KHÔNG.
Ví dụ: Giải phương trìnhGiải pháp: Khoảng giá trị chấp nhận được của phương trình là x 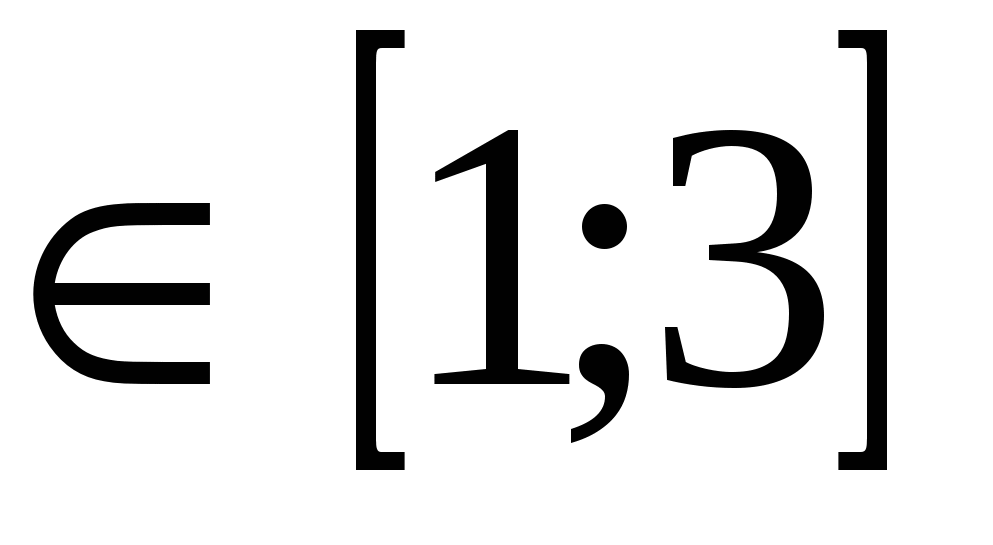 . Dễ dàng nhận thấy rằng trong vùng này, vế trái của phương trình tăng và vế phải giảm, tức là chức năngf(x)=
. Dễ dàng nhận thấy rằng trong vùng này, vế trái của phương trình tăng và vế phải giảm, tức là chức năngf(x)= ngày càng tăng và hàm sốg(x)=
ngày càng tăng và hàm sốg(x)= - giảm dần. Về vấn đề này, phương trình ban đầu chỉ có thể có một nghiệm (nếu có). Bằng cách chọn lọc, chúng ta tìm thấy nghiệm này của phương trình x = 2.Trả lời: x=2
- giảm dần. Về vấn đề này, phương trình ban đầu chỉ có thể có một nghiệm (nếu có). Bằng cách chọn lọc, chúng ta tìm thấy nghiệm này của phương trình x = 2.Trả lời: x=2
Phương pháp giải phương trình hàm số.
Trong số những bài toán khó nhất trong Kỳ thi Thống nhất là những bài toán mà lời giải của nó tập trung vào việc xem xét các phương trình hàm có dạng f(f(….f(x)…))=x hoặc f(g(x))=f(h(x)), trong đó f(x),g(x),h(x) là một số hàm và n ≥ 2
Phương pháp giải các phương trình hàm này dựa trên việc áp dụng nhiều định lý, hãy xem xét một trong số đó.
Định lý 1. Căn nguyên của phương trình
f(x)=0 là nghiệm của phương trình f(f(….f(x)…))=x
Ví dụ: Giải phương trình x= 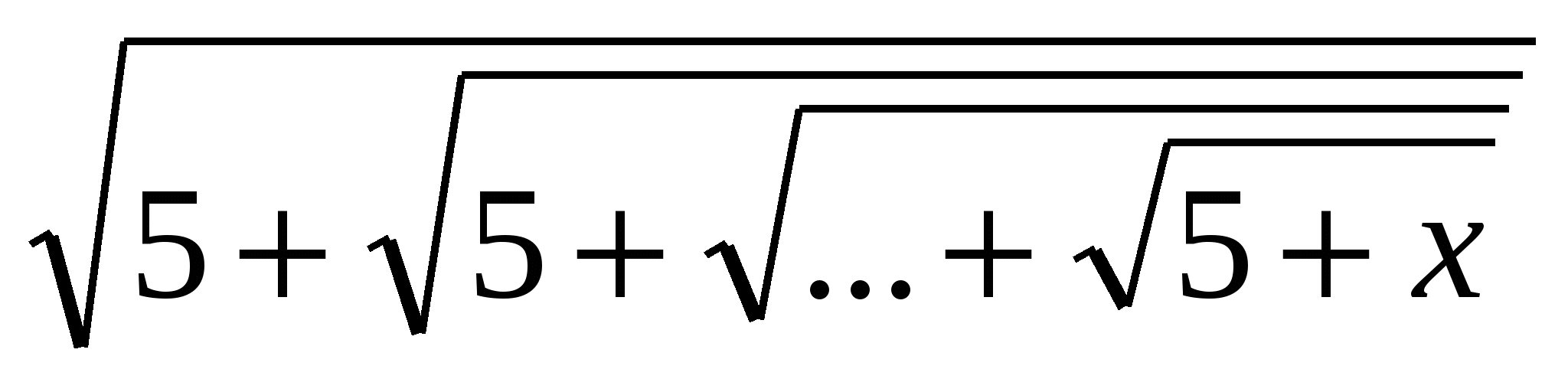 ,
căn bậc hai được lấy ở đâu?Nmột lần vàN≥
1
Giải pháp: Từ điều kiện bài toán suy ra x>
0. Hãy đểf(x)=
,
căn bậc hai được lấy ở đâu?Nmột lần vàN≥
1
Giải pháp: Từ điều kiện bài toán suy ra x>
0. Hãy đểf(x)=
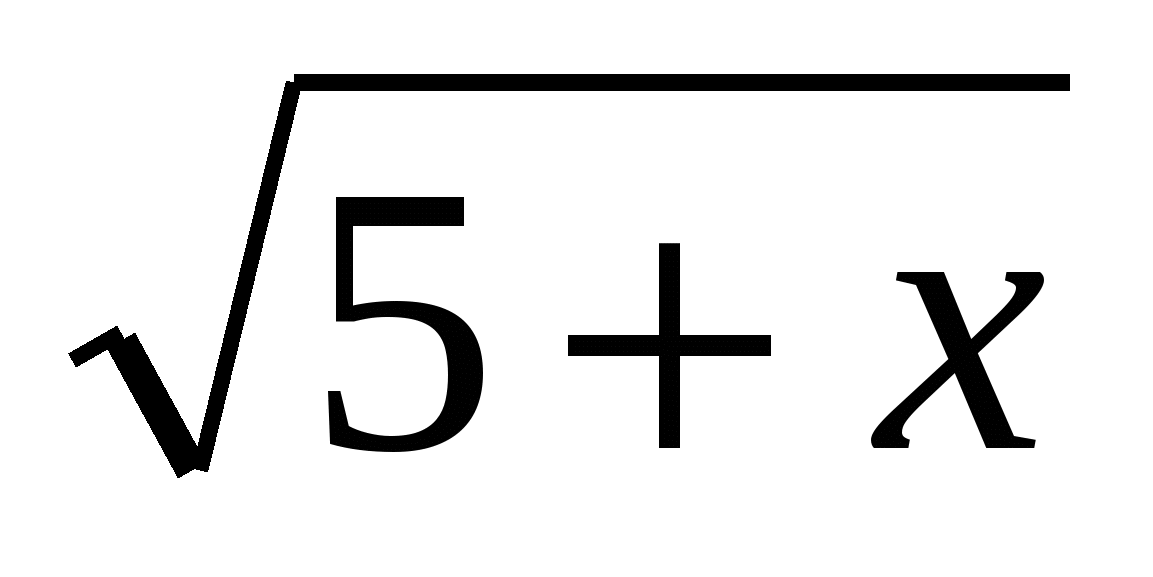 , thì phương trình của chúng ta có thể được biểu diễn dưới dạng hàm
f(
f(….
f(
x)…))=
x.
Vì tại x>
0 chức năngf(x)=
tăng vàf(x)
>
0 thì phương trình x= tương đương với phương trìnhf(x)=
x, tức là
=x, nghiệm dương của nó là x=
, thì phương trình của chúng ta có thể được biểu diễn dưới dạng hàm
f(
f(….
f(
x)…))=
x.
Vì tại x>
0 chức năngf(x)=
tăng vàf(x)
>
0 thì phương trình x= tương đương với phương trìnhf(x)=
x, tức là
=x, nghiệm dương của nó là x=  Trả lời: x=
Trả lời: x=
Galaeva Ekaterina, học sinh lớp 11 trường trung học MAOU số 149 ở Nizhny Novgorod
Công việc vừa mang tính ứng dụng vừa mang tính chất nghiên cứu. Để hoàn thiện nghiên cứu, các câu hỏi sau đây đã được xem xét:
– Tính chất của hàm số được thể hiện như thế nào khi giải phương trình, bất phương trình?
– Giải các phương trình, bất phương trình nào bằng cách xác định các tính chất của miền định nghĩa, tập giá trị, bất biến?
– Thuật toán giải là gì?
– Xem xét các nhiệm vụ có tham số được đề xuất trong tài liệu KIM để chuẩn bị cho Kỳ thi Thống nhất.
Trong công việc của mình, Ekaterina đã xem xét nhiều nhiệm vụ khác nhau và hệ thống hóa chúng theo hình thức bên ngoài.
Tải xuống:
Xem trước:
https://accounts.google.com
Chú thích slide:
Giải bất đẳng thức Giải. Hàm f(x) = tăng đơn điệu trên toàn bộ trục số và hàm g(x) = giảm đơn điệu trên toàn bộ miền định nghĩa. Do đó, bất đẳng thức f (x) > g (x) được thỏa mãn nếu x >
Cảm ơn bạn đã quan tâm!
Xem trước:
Để sử dụng bản xem trước bản trình bày, hãy tạo tài khoản Google và đăng nhập vào tài khoản đó: https://accounts.google.com
Chú thích slide:
Ứng dụng tính chất của hàm khi giải phương trình và bất phương trình Đã hoàn thành bài viết: Trường THCS Galaeva Ekaterina MBU số 149 Quận Moskovsky Học sinh lớp 11 “A” Người hướng dẫn khoa học: Fadeeva I. A. Giáo viên toán
Hướng chính: Nghiên cứu các tính chất của hàm: tính đơn điệu, giới hạn, miền định nghĩa và bất biến Tìm hiểu các câu lệnh cơ bản thường được sử dụng nhất khi giải phương trình, bất phương trình và hệ Giải các bài toán từ tài liệu CMM để chuẩn bị cho Kỳ thi Trạng thái Thống nhất
Tính đơn điệu Một hàm tăng nếu giá trị lớn hơn của đối số tương ứng với giá trị lớn hơn của hàm. Hàm giảm nếu giá trị lớn hơn của đối số tương ứng với giá trị nhỏ hơn của hàm. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Phát biểu 1. Nếu hàm y = f(x) là đơn điệu thì phương trình f(x) = c có nhiều nhất một nghiệm. x =2 f(x) = - giảm đơn điệu, tức là không còn nghiệm nào khác. Đáp án: x =2
Phát biểu 2. Nếu hàm y = f(x) tăng đơn điệu và hàm y = g(x) giảm đơn điệu thì phương trình f(x) = g(x) có nhiều nhất một nghiệm. 2 - x = log (x +11) + 1 g (x) = 2 - x đang giảm đơn điệu, và hàm f (x) = log (x + 11) + 1 đang tăng đơn điệu trên miền định nghĩa, mà có nghĩa là phương trình f (x ) = g (x) có nhiều nhất một nghiệm. Bằng cách lựa chọn, chúng tôi xác định rằng x = -1. Tuyên bố trên chứng minh tính duy nhất của giải pháp.
a) f (x) ≤ g (x) khi và chỉ khi x ϵ (- ∞ ; x 0 ]; b) f (x) ≥ g (x) khi và chỉ khi x ϵ [x 0 ; +∞). Ý nghĩa hình ảnh của phát biểu này là hiển nhiên Phát biểu 3. Nếu hàm số y = f(x) tăng đơn điệu trên toàn bộ trục số thì hàm y = g(x) giảm đơn điệu trên toàn bộ trục số và f(x 0) = g (x 0), thì các khẳng định sau là đúng:
Giải bất đẳng thức Giải. Hàm f(x) = tăng đơn điệu trên toàn bộ trục số và hàm g(x) = giảm đơn điệu trên toàn bộ miền định nghĩa. Do đó, bất đẳng thức f (x) > g (x) được thỏa mãn nếu x > 2. Ta hãy cộng miền định nghĩa của bất đẳng thức. Như vậy ta thu được hệ đáp án: (2; 5).
Phát biểu 4. Nếu hàm y = f (x) tăng đơn điệu thì các phương trình f (x) = x và f (f (x)) = x có cùng một tập nghiệm, bất kể số lượng nhúng. Kết quả. Nếu n là số tự nhiên và hàm y = f(x) tăng đơn điệu thì các phương trình f(x) = x và n lần có cùng một tập nghiệm.
Giải phương trình. Trả lời: Giải pháp. Với x ≥1, vế phải của phương trình không nhỏ hơn 1 và vế trái nhỏ hơn 1. Do đó, nếu phương trình có nghiệm thì bất kỳ nghiệm nào cũng nhỏ hơn 1. Với x ≤0, vế phải vế của phương trình không dương và vế trái là dương, do thực tế là . Do đó, bất kỳ nghiệm nào của phương trình này đều thuộc khoảng (0; 1). Nhân cả hai vế của phương trình này với x rồi chia tử số và mẫu số của vế trái cho x, ta được.
Từ = . Ký hiệu là t, trong đó t 0, ta thu được phương trình = t. Chúng ta hãy xem xét hàm f (t)= 1+ tăng trên miền định nghĩa của nó. Phương trình thu được có thể được viết dưới dạng f (f (f (f (t))))= t, và theo hệ quả tất yếu của Câu 4, nó có cùng tập nghiệm như phương trình f (t)= t, tức là phương trình 1 + = t, từ đâu ra. Căn dương duy nhất của phương trình tương đối bình phương này là. Điều này có nghĩa là ở đâu, tức là , hoặc. Trả lời:
Phát biểu 1. Nếu max f(x) = с và min g(x) = с thì phương trình f(x) = g(x) có cùng tập nghiệm như hệ B. Giá trị cực đại của vế trái là 1 và giá trị tối thiểu ở vế phải là 1, có nghĩa là nghiệm của phương trình được rút gọn về hệ phương trình: , từ phương trình thứ hai, chúng ta tìm thấy một ứng cử viên có thể là x=0, và chúng ta tin rằng đó là một nghiệm đến phương trình đầu tiên. Trả lời: x=1 .
Giải phương trình Giải. Vì sin3x<1 và cos4x<1, vế trái của phương trình này không vượt quá 7. Nó có thể bằng 7 khi và chỉ khi trong đó k , n ϵ Z . Vẫn còn phải xác định xem có số nguyên k và n mà hệ sau có nghiệm hay không. Trả lời: Z
Trong các bài toán có ẩn số x và tham số a, miền định nghĩa được hiểu là tập hợp tất cả các cặp số có thứ tự (x; a), mỗi cặp số sau khi thay các giá trị tương ứng của x và a vào mọi quan hệ được đưa vào vấn đề, chúng sẽ được xác định. Ví dụ 1. Với mỗi giá trị của tham số a, giải bất đẳng thức. Chúng ta hãy tìm miền định nghĩa của bất đẳng thức này. Từ đó rõ ràng là hệ thống không có giải pháp. Điều này có nghĩa là miền định nghĩa của bất đẳng thức không chứa bất kỳ cặp số x và a nào, và do đó bất đẳng thức không có nghiệm. Trả lời phạm vi:
Bất biến, tức là sự bất biến của một phương trình hoặc bất đẳng thức đối với việc thay thế một biến bằng một biểu thức đại số nào đó cho biến này. Ví dụ đơn giản nhất về tính bất biến là tính chẵn lẻ: nếu là hàm chẵn thì phương trình là bất biến dưới sự thay đổi của x và – x, vì = 0.
Tìm nghiệm nguyên của phương trình. Giải pháp. Lưu ý rằng cặp này bất biến khi thay thế. Thay vào đẳng thức, ta được. Bằng cách nhân cả hai vế của đẳng thức này với 2 và trừ số hạng đẳng thức theo số hạng từ đẳng thức thu được, chúng ta tìm được 3, từ đó. Bây giờ tất cả những gì còn lại là giải phương trình, từ đó gốc của phương trình là các số. Trả lời: .
Tìm tất cả các giá trị của a sao cho phương trình có nhiều hơn ba nghiệm khác nhau. Giải quyết vấn đề với thuộc tính tham số Monotonicity
|x|= dương X= |x|= Để hai nghiệm tồn tại, tử số phải dương. Do đó, khi nghiệm của phương trình thứ nhất và thứ hai trùng nhau, không thỏa mãn yêu cầu của điều kiện: có nhiều hơn ba nghiệm. Trả lời: .
Tìm tất cả các giá trị của a sao cho phương trình có hai nghiệm. Hãy chuyển phương trình về dạng Và xét hàm f(x) = xác định và liên tục trên toàn bộ trục số. Đồ thị của hàm này là một đường gãy bao gồm các đoạn thẳng và tia, mỗi đoạn liên kết của chúng là một phần của đường thẳng có dạng y= kt+l. f(x)= Với bất kỳ giá trị nào, việc bộc lộ mô đun của biểu thức k thứ nhất không vượt quá 8, do đó việc tăng giảm của hàm f(x) sẽ phụ thuộc vào việc bộc lộ mô đun thứ hai. Tại x f(x) sẽ giảm và tại x nó sẽ tăng. Nghĩa là, tại x=3 hàm số sẽ nhận giá trị lớn nhất. Để một phương trình có hai nghiệm thì cần phải có tính chất đơn điệu f(3)
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a Đáp án: a
Tìm tất cả các giá trị của tham số a, với mỗi giá trị mà bất đẳng thức đúng với bất kỳ giá trị thực nào của x. Chúng ta hãy viết lại bất đẳng thức dưới dạng, giới thiệu một biến mới t = và xem xét hàm f (t) =, được xác định. và liên tục trên trục số. Đồ thị của hàm này là một đường đứt nét bao gồm các đoạn thẳng và tia, mỗi liên kết của chúng là một phần của một đường có dạng, trong đó
Vì, thì t ϵ [-1; 1]. Do sự giảm đơn điệu của hàm y = f(t), việc kiểm tra cạnh trái của đoạn này là đủ. Z. A đúng Điều này có nghĩa là điều đó chỉ có thể xảy ra nếu các số và và v cùng dấu hoặc một trong số chúng bằng 0. , = () () 0. Phân tích thành nhân tử của các tam thức bậc hai, ta thu được bất đẳng thức (, từ đó ta tìm được a ϵ (-∞; -1] U (2) U [ 4; +∞). Trả lời: (- ∞; - 1] U (2) U )
