7.1. Định nghĩa sản phẩm chéo
Ba vectơ không đồng phẳng a, b và c, được sắp xếp theo thứ tự đã cho, tạo thành một bộ ba thuận nếu, từ điểm cuối của vectơ thứ ba c, đường quay ngắn nhất từ vectơ a đầu tiên đến vectơ thứ hai b được nhìn thấy là ngược chiều kim đồng hồ và bộ ba thuận tay trái nếu theo chiều kim đồng hồ (xem Hình .16).
Tích vectơ của vectơ a và vectơ b được gọi là vectơ c, trong đó:
1. Vuông góc với vectơ a và b, tức là c ^ a và c ^ b ;
2. Có chiều dài bằng diện tích hình bình hành dựng trên vectơ a vàb như ở các bên (xem Hình 17), tức là
3. Các vectơ a, b và c tạo thành bộ ba thuận tay phải.


Tích chéo được ký hiệu là a x b hoặc [a,b]. Các mối quan hệ sau đây giữa các vectơ đơn vị tôi rút ra trực tiếp từ định nghĩa của tích vectơ, j Và k
(xem Hình 18):
i x j = k, j x k = i, k x i = j. Hãy để chúng tôi chứng minh, ví dụ, rằng
tôi xj =k. ^ 1) k^i, k
j ; 2) |k |=1, nhưng | tôi x j
| = |tôi | Và|J | sin(90°)=1;
3) vectơ i, j và
tạo thành bộ ba bên phải (xem Hình 16).
7.2. Thuộc tính của sản phẩm chéo = -(1. Khi sắp xếp lại các thừa số, tích vectơ đổi dấu, tức là).
và xb =(b xa) (xem Hình 19).

Các vectơ a xb và b xa thẳng hàng, có cùng mô đun (diện tích hình bình hành không đổi) nhưng có hướng ngược nhau (bộ ba a, b, a xb và a, b, b x a ngược hướng). Vì thế axb b xa b 2. Tích vectơ có tính chất kết hợp đối với thừa số vô hướng, tức là l (a xb) = (l a) x b = a x (l b). bĐặt l > 0. Vector l (a xb) vuông góc với vectơ a và b. Vectơ ( axb tôi axb a)x axb b xa b cũng vuông góc với vectơ a và
(vectơ a, axb nhưng nằm trong cùng một mặt phẳng). Điều này có nghĩa là các vectơ axb(a xb) và ( axb<0.
thẳng hàng. Rõ ràng là hướng của họ trùng nhau. Chúng có cùng độ dài: bĐó là lý do tại sao<=>(a xb)=

một xb. Nó được chứng minh một cách tương tự cho
3. Hai vectơ khác 0 a và
(thẳng hàng khi và chỉ nếu tích vectơ của chúng bằng vectơ 0, tức là a ||b và xb = 0. b Cụ thể, i *i =j *j =k *k =0 .
4. Tích vector có tính chất phân phối:
7.3. Biểu diễn tích chéo theo tọa độ
Chúng ta sẽ sử dụng bảng tích chéo của vectơ i, Các mối quan hệ sau đây giữa các vectơ đơn vị tôi rút ra trực tiếp từ định nghĩa của tích vectơ, và k:

nếu hướng của đường đi ngắn nhất từ vectơ thứ nhất đến vectơ thứ hai trùng với hướng của mũi tên thì tích bằng vectơ thứ ba, nếu không trùng nhau thì vectơ thứ ba lấy dấu trừ;
Cho hai vectơ a =a x i +a y Các mối quan hệ sau đây giữa các vectơ đơn vị tôi rút ra trực tiếp từ định nghĩa của tích vectơ,+a z Và và b = b x Tôi+b y Các mối quan hệ sau đây giữa các vectơ đơn vị tôi rút ra trực tiếp từ định nghĩa của tích vectơ,+bz Và. Hãy tìm tích vectơ của các vectơ này bằng cách nhân chúng dưới dạng đa thức (theo tính chất của tích vectơ):

![]()
Công thức kết quả có thể được viết ngắn gọn hơn:

vì vế phải của đẳng thức (7.1) tương ứng với việc khai triển định thức bậc ba theo các phần tử của hàng đầu tiên. Đẳng thức (7.2) rất dễ nhớ.
7.4. Một số ứng dụng của tích chéo
Thiết lập sự cộng tuyến của các vectơ

Tìm diện tích hình bình hành và hình tam giác
Theo định nghĩa tích vectơ của vectơ MỘT và b |a xb | =|a | * |b |sin g, tức là S cặp = |a x b |. Và do đó, D S =1/2|a x b |.
Xác định mô men lực đối với một điểm
Cho một lực tác dụng vào điểm A F =AB và để VỀ- một số điểm trong không gian (xem Hình 20).

Người ta biết từ vật lý rằng khoảnh khắc của lực lượng F so với điểm VỀ gọi là vectơ M,đi qua điểm VỀ Và:
1) vuông góc với mặt phẳng đi qua các điểm O, A, B;
2) về số lượng bằng tích của lực trên mỗi cánh tay
3) tạo thành bộ ba bên phải với các vectơ OA và A B.
Do đó, M = OA x F.
Tìm tốc độ quay tuyến tính
Tốc độ vđiểm M của một vật rắn quay với vận tốc góc w quanh một trục cố định, được xác định theo công thức Euler v =w xr, trong đó r =OM, trong đó O là một điểm cố định nào đó của trục (xem Hình 21).

Trước khi đưa ra khái niệm tích vectơ, chúng ta hãy quay lại câu hỏi về hướng của bộ ba vectơ a →, b →, c → trong không gian ba chiều.
Để bắt đầu, hãy đặt các vectơ a → , b → , c → từ một điểm. Hướng của bộ ba a → , b → , c → có thể sang phải hoặc sang trái, tùy thuộc vào hướng của vectơ c → chính nó. Loại bộ ba a → , b → , c → sẽ được xác định từ hướng rẽ ngắn nhất từ vectơ a → đến b → từ điểm cuối của vectơ c → .
Nếu thực hiện vòng quay ngắn nhất ngược chiều kim đồng hồ thì bộ ba vectơ a → , b → , c → được gọi là Phải, nếu theo chiều kim đồng hồ – bên trái.
Tiếp theo, lấy hai vectơ không thẳng hàng a → và b →. Sau đó, chúng ta hãy vẽ các vectơ A B → = a → và A C → = b → từ điểm A. Hãy dựng một vectơ A D → = c →, vuông góc đồng thời với cả A B → và A C →. Như vậy, khi dựng vectơ A D → = c →, chúng ta có thể thực hiện theo hai cách, cho nó một hướng hoặc ngược lại (xem hình minh họa).

Như chúng ta đã tìm ra, một bộ ba vectơ a → , b → , c → có thể ở bên phải hoặc bên trái tùy thuộc vào hướng của vectơ.
Từ những điều trên chúng ta có thể đưa ra định nghĩa về tích vector. Định nghĩa này được đưa ra cho hai vectơ được xác định trong hệ tọa độ hình chữ nhật của không gian ba chiều.
Định nghĩa 1
Tích vectơ của hai vectơ a → và b → chúng ta sẽ gọi một vectơ như vậy được xác định trong hệ tọa độ hình chữ nhật của không gian ba chiều sao cho:
- nếu các vectơ a → và b → thẳng hàng thì nó sẽ bằng 0;
- nó sẽ vuông góc với cả hai vectơ a → và vectơ b → tức là. ∠ a → c → = ∠ b → c → = π 2 ;
- chiều dài của nó được xác định theo công thức: c → = a → · b → · sin ∠ a → , b → ;
- bộ ba vectơ a → , b → , c → có cùng hướng với hệ tọa độ đã cho.
Tích vectơ của các vectơ a → và b → có ký hiệu sau: a → × b →.
Tọa độ của tích vectơ
Vì bất kỳ vectơ nào cũng có tọa độ nhất định trong hệ tọa độ, nên chúng ta có thể đưa ra định nghĩa thứ hai về tích vectơ, định nghĩa này sẽ cho phép chúng ta tìm tọa độ của nó bằng cách sử dụng tọa độ đã cho của vectơ.
Định nghĩa 2
Trong hệ tọa độ chữ nhật của không gian ba chiều tích vectơ của hai vectơ a → = (a x ; a y ; a z) và b → = (b x ; b y ; b z) được gọi là vectơ c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , trong đó i → , j → , k → là các vectơ tọa độ.
Tích vectơ có thể được biểu diễn dưới dạng định thức của ma trận vuông bậc ba, trong đó hàng đầu tiên chứa các vectơ vectơ i → , j → , k → , hàng thứ hai chứa tọa độ của vectơ a → , và hàng thứ ba chứa tọa độ của vectơ b → trong một hệ tọa độ hình chữ nhật nhất định, đây là định thức của ma trận có dạng như sau: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Khai triển định thức này thành các phần tử của hàng đầu tiên, chúng ta thu được đẳng thức: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Thuộc tính của sản phẩm chéo
Được biết, tích vectơ trong tọa độ được biểu diễn dưới dạng định thức của ma trận c → = a → × b → = i → j → k → a x a y a z b x b y b z , khi đó trên cơ sở tính chất của định thức ma trận những điều sau đây được hiển thị Tính chất của tích vectơ:
- tính phản giao hoán a → × b → = - b → × a → ;
- độ phân phối a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → hoặc a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- tính kết hợp λ a → × b → = λ a → × b → hoặc a → × (λ b →) = λ a → × b →, trong đó λ là số thực tùy ý.
Những tính chất này có bằng chứng đơn giản.
Ví dụ, chúng ta có thể chứng minh tính chất phản giao hoán của tích vectơ.
Bằng chứng về tính phản giao hoán
Theo định nghĩa, a → × b → = i → j → k → a x a y a z b x b y b z và b → × a → = i → j → k → b x b y b z a x a y a z . Và nếu hai hàng của ma trận được hoán đổi cho nhau thì giá trị của định thức của ma trận sẽ thay đổi theo chiều ngược lại, do đó a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , điều này chứng tỏ rằng tích vectơ có tính phản giao hoán.
Sản phẩm Vector - ví dụ và giải pháp
Trong hầu hết các trường hợp, có ba loại vấn đề.
Trong các bài toán loại thứ nhất, độ dài của hai vectơ và góc giữa chúng thường được cho trước và bạn cần tìm độ dài của tích vectơ. Trong trường hợp này, hãy sử dụng công thức sau c → = a → · b → · sin ∠ a → , b → .
Ví dụ 1
Tìm độ dài tích vectơ của các vectơ a → và b →, nếu biết a → = 3, b → = 5, ∠ a →, b → = π 4.
Giải pháp
Bằng cách xác định độ dài tích vectơ của các vectơ a → và b →, ta giải được bài toán này: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Trả lời: 15 2 2 .
Các bài toán loại thứ hai có mối liên hệ với tọa độ của vectơ, trong đó tích vectơ, độ dài của nó, v.v. được tìm kiếm thông qua tọa độ đã biết của các vectơ đã cho a → = (a x; a y; a z) Và b → = (b x ; b y ; b z) .
Đối với loại vấn đề này, bạn có thể giải quyết rất nhiều phương án nhiệm vụ. Ví dụ, không thể xác định được tọa độ của các vectơ a → và b → mà là sự khai triển của chúng thành các vectơ tọa độ có dạng b → = b x · i → + b y · j → + b z · k → và c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, hoặc các vectơ a → và b → có thể được xác định bằng tọa độ điểm bắt đầu của chúng và điểm cuối.
Hãy xem xét các ví dụ sau.
Ví dụ 2
Trong hệ tọa độ hình chữ nhật, có hai vectơ: a → = (2; 1; - 3), b → = (0; - 1; 1). Tìm sản phẩm chéo của họ.
Giải pháp
Theo định nghĩa thứ hai, ta tìm tích vectơ của hai vectơ trong tọa độ cho trước: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .
Nếu chúng ta viết tích vectơ thông qua định thức của ma trận, thì nghiệm của ví dụ này sẽ như sau: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .
Trả lời: a → × b → = - 2 i → - 2 j → - 2 k → .
Ví dụ 3
Tìm độ dài tích vectơ của các vectơ i → - j → và i → + j → + k →, trong đó i →, j →, k → là các vectơ đơn vị của hệ tọa độ Descartes hình chữ nhật.
Giải pháp
Đầu tiên, chúng ta hãy tìm tọa độ của một tích vectơ cho trước i → - j → × i → + j → + k → trong một hệ tọa độ hình chữ nhật nhất định.
Được biết, các vectơ i → - j → và i → + j → + k → lần lượt có tọa độ (1; - 1; 0) và (1; 1; 1). Hãy tìm độ dài của tích vectơ bằng định thức của ma trận, khi đó ta có i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Do đó, tích vectơ i → - j → × i → + j → + k → có tọa độ (- 1 ; - 1 ; 2) trong hệ tọa độ đã cho.
Chúng ta tìm độ dài của tích vectơ bằng công thức (xem phần tìm độ dài của vectơ): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Trả lời: i → - j → × i → + j → + k → = 6 . .
Ví dụ 4
Trong hệ tọa độ Descartes hình chữ nhật, tọa độ của ba điểm A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) được cho trước. Tìm một số vectơ vuông góc với A B → và A C → đồng thời.
Giải pháp
Các vectơ A B → và A C → có tọa độ lần lượt là (- 1 ; 2 ; 2) và (0 ; 4 ; 1). Khi đã tìm được tích vectơ của các vectơ A B → và A C →, rõ ràng nó là vectơ vuông góc theo định nghĩa với cả A B → và A C →, tức là nó là nghiệm của bài toán của chúng ta. Hãy tìm nó A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Trả lời: - 6 i → + j → - 4 k → . - một trong các vectơ vuông góc.
Các bài toán loại thứ ba tập trung vào việc sử dụng các tính chất tích vectơ của vectơ. Sau khi áp dụng, chúng ta sẽ thu được giải pháp cho vấn đề đã cho.
Ví dụ 5
Các vectơ a → và b → vuông góc và độ dài của chúng lần lượt là 3 và 4. Tìm độ dài của tích vectơ 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Giải pháp
Theo tính chất phân phối của tích vectơ, ta có thể viết 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
Theo tính chất kết hợp, chúng ta lấy các hệ số số ra khỏi dấu của tích vectơ trong biểu thức cuối cùng: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
Tích vectơ a → × a → và b → × b → bằng 0, vì a → × a → = a → · a → · sin 0 = 0 và b → × b → = b → · b → · sin 0 = 0 thì 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
Từ tính phản giao hoán của tích vectơ suy ra - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Sử dụng các tính chất của tích vectơ, ta thu được đẳng thức 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .
Theo điều kiện, các vectơ a → và b → vuông góc, nghĩa là góc giữa chúng bằng π 2. Bây giờ tất cả những gì còn lại là thay thế các giá trị tìm được vào các công thức thích hợp: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Trả lời: 3 a → - b → × a → - 2 b → = 60.
Độ dài tích vectơ của các vectơ theo định nghĩa bằng a → × b → = a → · b → · sin ∠ a → , b → . Vì người ta đã biết (từ khóa học ở trường) rằng diện tích của một hình tam giác bằng một nửa tích độ dài hai cạnh của nó nhân với sin của góc giữa các cạnh này. Do đó, chiều dài của tích vectơ bằng diện tích của hình bình hành - một tam giác nhân đôi, cụ thể là tích của các cạnh dưới dạng vectơ a → và b →, đặt từ một điểm, theo sin của góc giữa chúng sin ∠ a →, b →.
Đây là ý nghĩa hình học của tích vector.

Ý nghĩa vật lý của sản phẩm vector
Trong cơ học, một trong những nhánh của vật lý, nhờ tích vectơ, bạn có thể xác định mômen của lực so với một điểm trong không gian.
Định nghĩa 3
Đến thời điểm lực F → tác dụng lên điểm B tương ứng với điểm A, ta sẽ hiểu tích vectơ sau A B → × F →.
Nếu bạn thấy văn bản có lỗi, vui lòng đánh dấu nó và nhấn Ctrl+Enter
Góc giữa các vectơ
Để giới thiệu khái niệm tích vectơ của hai vectơ, trước tiên chúng ta phải hiểu khái niệm đó là góc giữa các vectơ này.
Giả sử chúng ta có hai vectơ $\overline(α)$ và $\overline(β)$. Chúng ta hãy lấy một điểm $O$ trong không gian và vẽ các vectơ $\overline(α)=\overline(OA)$ và $\overline(β)=\overline(OB)$ từ đó, sau đó là góc $AOB$ sẽ được gọi là góc giữa các vectơ này (Hình 1).
Ký hiệu: $∠(\overline(α),\overline(β))$
Khái niệm tích vectơ của vectơ và công thức tìm
Định nghĩa 1
Tích vectơ của hai vectơ là vectơ vuông góc với cả hai vectơ đã cho và chiều dài của nó sẽ bằng tích độ dài của các vectơ này với sin góc giữa các vectơ này và vectơ này với hai vectơ ban đầu có cùng hướng với hệ tọa độ Descartes.
Ký hiệu: $\overline(α)х\overline(β)$.
Về mặt toán học nó trông như thế này:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ và $(\overline(i),\overline(j),\overline(k))$ là cùng định hướng (Hình 2)
Hiển nhiên, tích ngoài của vectơ sẽ bằng vectơ 0 trong hai trường hợp:
- Nếu độ dài của một hoặc cả hai vectơ bằng không.
- Nếu góc giữa các vectơ này bằng $180^\circ$ hoặc $0^\circ$ (vì trong trường hợp này sin bằng 0).
Để thấy rõ cách tìm tích vectơ của vectơ, hãy xem xét các ví dụ về giải pháp sau đây.
Ví dụ 1
Tìm độ dài của vectơ $\overline(δ)$, đây sẽ là kết quả của tích vectơ của các vectơ, với tọa độ $\overline(α)=(0,4,0)$ và $\overline(β) =(3,0,0 )$.
Giải pháp.
Hãy mô tả các vectơ này trong không gian tọa độ Descartes (Hình 3):
Hình 3. Các vectơ trong không gian tọa độ Descartes. Author24 - trao đổi trực tuyến các tác phẩm của sinh viên
Chúng ta thấy rằng các vectơ này lần lượt nằm trên trục $Ox$ và $Oy$. Do đó, góc giữa chúng sẽ là $90^\circ$. Hãy tìm độ dài của các vectơ này:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Sau đó, theo Định nghĩa 1, chúng ta thu được mô-đun $|\overline(δ)|$
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Trả lời: $12$.
Tính tích tích chéo từ tọa độ vectơ
Định nghĩa 1 ngay lập tức ngụ ý một phương pháp tìm tích vectơ của hai vectơ. Vì một vectơ, ngoài giá trị của nó, còn có hướng, nên không thể tìm thấy nó chỉ bằng đại lượng vô hướng. Nhưng bên cạnh đó, còn có một cách để tìm các vectơ được cung cấp cho chúng ta bằng cách sử dụng tọa độ.
Giả sử chúng ta có các vectơ $\overline(α)$ và $\overline(β)$, sẽ có tọa độ lần lượt là $(α_1,α_2,α_3)$ và $(β_1,β_2,β_3)$. Khi đó, vectơ của tích chéo (cụ thể là tọa độ của nó) có thể được tìm thấy bằng công thức sau:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
Ngược lại, khi khai triển định thức, ta thu được tọa độ sau
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Ví dụ 2
Tìm vectơ tích vectơ của các vectơ thẳng hàng $\overline(α)$ và $\overline(β)$ có tọa độ $(0,3,3)$ và $(-1,2,6)$.
Giải pháp.
Hãy sử dụng công thức đã cho ở trên. chúng tôi nhận được
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k )=(12,-3,3)$
Trả lời: $(12,-3,3)$.
Tính chất tích vectơ của vectơ
Đối với ba vectơ được trộn tùy ý $\overline(α)$, $\overline(β)$ và $\overline(γ)$, cũng như $r∈R$, các thuộc tính sau giữ nguyên:
Ví dụ 3
Tìm diện tích hình bình hành có các đỉnh có tọa độ $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ và $(3,8,0) $.
Giải pháp.
Đầu tiên, hãy mô tả hình bình hành này trong không gian tọa độ (Hình 5):
Hình 5. Hình bình hành trong không gian tọa độ. Author24 - trao đổi trực tuyến các tác phẩm của sinh viên
Chúng ta thấy rằng hai cạnh của hình bình hành này được dựng bằng các vectơ thẳng hàng có tọa độ $\overline(α)=(3,0,0)$ và $\overline(β)=(0,8,0)$. Sử dụng tính chất thứ tư, ta có:
$S=|\overline(α)х\overline(β)|$
Hãy tìm vectơ $\overline(α)х\overline(β)$:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Kể từ đây
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
Rõ ràng, trong trường hợp tích vectơ, thứ tự các vectơ được lấy là quan trọng, hơn nữa,
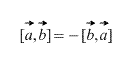
Ngoài ra, trực tiếp từ định nghĩa, đối với bất kỳ hệ số vô hướng k (số) nào thì điều sau đây là đúng:
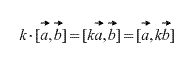
Tích chéo của các vectơ cộng tuyến bằng vectơ 0. Hơn nữa, tích chéo của hai vectơ bằng 0 khi và chỉ nếu chúng thẳng hàng. (Trong trường hợp một trong số chúng là vectơ 0, cần nhớ rằng vectơ 0 theo định nghĩa thẳng hàng với bất kỳ vectơ nào).

Sản phẩm vectơ có tài sản phân phối, đó là

Biểu diễn tích vectơ thông qua tọa độ của vectơ.
Cho hai vectơ

(cách tìm tọa độ của một vectơ từ tọa độ đầu và cuối của nó - xem bài Tích vô hướng của vectơ, mục Định nghĩa thay thế của tích vô hướng hoặc tính tích vô hướng của hai vectơ được chỉ định bởi tọa độ của chúng.)

Tại sao bạn cần một sản phẩm vector?
Có nhiều cách để sử dụng tích chéo, ví dụ như đã viết ở trên, bằng cách tính tích chéo của hai vectơ bạn có thể biết được chúng có thẳng hàng hay không.

Hoặc nó có thể được sử dụng như một cách để tính diện tích hình bình hành được xây dựng từ các vectơ này. Dựa trên định nghĩa, độ dài của vectơ kết quả là diện tích của hình bình hành đã cho.
Ngoài ra còn có một số lượng lớn các ứng dụng trong điện và từ tính.Máy tính sản phẩm vector trực tuyến.
Để tìm tích vô hướng của hai vectơ bằng máy tính này, bạn cần nhập tọa độ của vectơ đầu tiên ở dòng đầu tiên theo thứ tự và vectơ thứ hai ở dòng thứ hai. Tọa độ của vectơ có thể được tính từ tọa độ điểm đầu và điểm cuối của chúng (xem bài Tích vô hướng của vectơ, mục Một định nghĩa thay thế của tích vô hướng hoặc tính tích vô hướng của hai vectơ cho bởi tọa độ của chúng.)
tác phẩm nghệ thuật vector là một giả vectơ vuông góc với một mặt phẳng được xây dựng từ hai thừa số, là kết quả của phép toán nhị phân “nhân vectơ” trên các vectơ trong không gian Euclide ba chiều. Tích vectơ không có tính chất giao hoán và kết hợp (nó phản giao hoán) và, không giống như tích vô hướng của vectơ, là một vectơ. Được sử dụng rộng rãi trong nhiều ứng dụng kỹ thuật và vật lý. Ví dụ, động lượng góc và lực Lorentz được viết dưới dạng tích vectơ. Tích chéo rất hữu ích cho việc "đo" độ vuông góc của vectơ - mô đun tích chéo của hai vectơ bằng tích mô đun của chúng nếu chúng vuông góc và giảm về 0 nếu vectơ song song hoặc phản song song.
Tích vectơ có thể được định nghĩa theo nhiều cách khác nhau và về mặt lý thuyết, trong không gian có chiều n bất kỳ, người ta có thể tính tích của n-1 vectơ, từ đó thu được một vectơ duy nhất vuông góc với tất cả chúng. Nhưng nếu sản phẩm bị giới hạn ở các sản phẩm nhị phân không tầm thường có kết quả vectơ, thì sản phẩm vectơ truyền thống chỉ được xác định trong không gian ba chiều và bảy chiều. Kết quả của tích vectơ, giống như tích vô hướng, phụ thuộc vào số liệu của không gian Euclide.
Không giống như công thức tính vectơ tích vô hướng từ tọa độ trong hệ tọa độ hình chữ nhật ba chiều, công thức tính tích chéo phụ thuộc vào hướng của hệ tọa độ hình chữ nhật, hay nói cách khác là “độ chirality” của nó.
Sự định nghĩa:
Tích vectơ của vectơ a và vectơ b trong không gian R3 là vectơ c thỏa mãn các yêu cầu sau:
độ dài của vectơ c bằng tích độ dài của vectơ a và b và sin của góc φ giữa chúng:
|c|=|a||b|sin φ;
vectơ c trực giao với mỗi vectơ a và b;
vectơ c có hướng sao cho bộ ba vectơ abc thuận tay phải;
trong trường hợp không gian R7 cần phải có tính kết hợp của bộ ba vectơ a, b, c.
Chỉ định:
c===a × b

Cơm. 1. Diện tích hình bình hành bằng mô đun tích vectơ
Tính chất hình học của tích chéo:
Điều kiện cần và đủ để hai vectơ khác 0 cộng tuyến là tích vectơ của chúng bằng 0.
Mô-đun sản phẩm chéo diện tích bằng S hình bình hành được xây dựng trên các vectơ thu gọn về một gốc chung Một Và b(xem hình 1).
Nếu như e- vectơ đơn vị trực giao với vectơ Một Và b và được chọn sao cho ba a,b,e- đúng rồi, và S là diện tích của hình bình hành dựng trên chúng (rút gọn về một gốc tọa độ chung), thì công thức cho tích vectơ là hợp lệ:
=S e
Hình 2. Thể tích của hình bình hành sử dụng vectơ và tích vô hướng của vectơ; các đường chấm chấm biểu diễn hình chiếu của vectơ c lên a × b và vectơ a lên b × c, bước đầu tiên là tìm tích vô hướng
Nếu như c- một số vectơ, π
- bất kỳ mặt phẳng nào chứa vectơ này, e- vectơ đơn vị nằm trong mặt phẳng π
và vuông góc với c, g- vectơ đơn vị trực giao với mặt phẳng π
và có hướng sao cho bộ ba vectơ điện tâm đồ là đúng, vậy với bất kỳ ai nằm trên máy bay π
vectơ Một công thức là đúng:
=Pr e a |c|g
trong đó Pr e a là hình chiếu của vectơ e lên a
|c|-mô đun của vectơ c
Khi sử dụng tích vectơ và vô hướng, bạn có thể tính thể tích của một hình bình hành được xây dựng trên các vectơ giảm về một gốc chung một, b Và c. Tích của ba vectơ như vậy được gọi là hỗn hợp.
V=|a (b×c)|
Hình vẽ cho thấy khối lượng này có thể được tìm thấy theo hai cách: kết quả hình học được giữ nguyên ngay cả khi các tích “vô hướng” và “vectơ” được hoán đổi:
V=a×b c=a b×c
Độ lớn của tích chéo phụ thuộc vào sin của góc giữa các vectơ ban đầu, do đó tích chéo có thể được coi là mức độ “vuông góc” của các vectơ, giống như tích vô hướng có thể được coi là mức độ “song song” ”. Tích vectơ của hai vectơ đơn vị bằng 1 (vectơ đơn vị) nếu các vectơ gốc vuông góc và bằng 0 (vectơ 0) nếu các vectơ song song hoặc phản song song.
Biểu thức tích chéo trong tọa độ Descartes
Nếu hai vectơ Một Và bđược xác định bởi tọa độ Descartes hình chữ nhật của chúng, hay chính xác hơn, được biểu diễn dưới dạng cơ sở trực giao
a=(a x ,a y ,a z)
b=(b x ,b y ,b z)
và hệ tọa độ thuận tay phải thì tích vectơ của chúng có dạng
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Để nhớ công thức này:
i =∑ε ijk a j b k
Ở đâu ε ijk- biểu tượng của Levi-Civita.
