Hướng dẫn. Để giải trực tuyến, bạn cần chọn loại phương trình và đặt chiều của ma trận tương ứng.
trong đó A, B, C là ma trận được chỉ định, X là ma trận mong muốn. Các phương trình ma trận dạng (1), (2) và (3) được giải thông qua ma trận nghịch đảo A -1. Nếu đã cho biểu thức A·X - B = C thì trước tiên cần cộng các ma trận C + B và tìm nghiệm cho biểu thức A·X = D, trong đó D = C + B(). Nếu biểu thức A*X = B 2 được đưa ra thì ma trận B trước tiên phải bình phương. Bạn cũng nên làm quen với các thao tác cơ bản trên ma trận.Ví dụ số 1. Bài tập. Tìm nghiệm của phương trình ma trận
Giải pháp. Hãy biểu thị:
Khi đó phương trình ma trận sẽ được viết dưới dạng: A·X·B = C.
Định thức của ma trận A bằng detA=-1
Vì A là ma trận không suy biến nên có ma trận nghịch đảo A -1 . Nhân cả hai vế của phương trình bên trái với A -1: Nhân cả hai vế của phương trình này với A -1 và bên phải với B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Vì A A -1 = B B -1 = E và E X = X E = X nên X = A -1 C B -1
Ma trận nghịch đảo A -1: ![]()
Hãy tìm ma trận nghịch đảo B -1.
Ma trận chuyển vị B T:
Ma trận nghịch đảo B -1: ![]()
Ta tìm ma trận X theo công thức: X = A -1 ·C·B -1 ![]()
Trả lời:
Ví dụ số 2. Bài tập. Giải phương trình ma trận ![]()
Giải pháp. Hãy biểu thị:
Khi đó phương trình ma trận sẽ được viết dưới dạng: A·X = B.
Định thức của ma trận A là detA=0
Vì A là ma trận đơn (định thức bằng 0) nên phương trình vô nghiệm.
Ví dụ số 3. Bài tập. Tìm nghiệm của phương trình ma trận
Giải pháp. Hãy biểu thị:
Khi đó phương trình ma trận sẽ được viết dưới dạng: X A = B.
Định thức của ma trận A là detA=-60
Vì A là ma trận không suy biến nên có ma trận nghịch đảo A -1 . Hãy nhân cả hai vế của phương trình bên phải với A -1: X A A -1 = B A -1, từ đó ta tìm thấy X = B A -1
Hãy tìm ma trận nghịch đảo A -1 .
Ma trận chuyển vị A T: 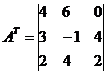
Ma trận nghịch đảo A -1: 
Ta tìm ma trận X theo công thức: X = B A -1 
Trả lời: > 
Bằng cách sử dụng máy tính ma trận trực tuyến, bạn có thể nếp gấp, trừ đi, nhân lên, chuyển đổi ma trận, tính toán đảo ngược ma trận, giả nghịch đảo ma trận, thứ hạng ma trận, yếu tố quyết định ma trận, m-norm và l-norm của ma trận, nâng ma trận lên lũy thừa, nhân ma trận với số, LÀM sự phân hủy xương ma trận, xóa các hàng phụ thuộc tuyến tính khỏi ma trận hoặc cột phụ thuộc tuyến tính, chỉ đạo loại trừ Gaussian, giải phương trình ma trận AX=B, phân tích LU của ma trận,tính toán hạt nhân (khoảng trống) của ma trận, LÀM Trực giao hóa Gram-Schmidt và trực giao hóa Gram-Schmidt.
Máy tính ma trận trực tuyến không chỉ hoạt động với số thập phân mà còn hoạt động với phân số. Để nhập phân số, bạn cần nhập ma trận ban đầu và nhập số có dạng Một hoặc Một/b, Ở đâu Một Và b số nguyên hoặc số thập phân ( b số dương). Ví dụ 12/67, -67,78/7,54, 327,6, -565.
Nút ở góc trên bên trái của ma trận sẽ mở ra một menu (Hình 1) để chuyển đổi ma trận gốc (tạo ma trận đơn vị, ma trận 0 hoặc xóa nội dung của các ô).

Trong quá trình tính toán, một ô trống được coi là 0.
Đối với các phép toán ma trận đơn (tức là chuyển vị, nghịch đảo, giả nghịch đảo, phân tách khung, v.v.), trước tiên hãy chọn một ma trận cụ thể bằng nút radio.
Các nút Fn1, Fn2 và Fn3 chuyển đổi các nhóm chức năng khác nhau.
Bằng cách nhấp vào các ma trận đã tính, một menu sẽ mở ra (Hình 2), cho phép bạn viết ma trận này thành các ma trận ban đầu và , cũng như chuyển đổi các phần tử của ma trận tại chỗ thành một phân số chung, một phân số hỗn hợp hoặc một phân số số thập phân.
Tính tổng, hiệu, tích của ma trận trực tuyến
tổng, hiệu hoặc tích của ma trận. Để tính tổng hoặc hiệu các ma trận cần phải có cùng thứ nguyên và để tính tích của các ma trận thì số cột của ma trận thứ nhất phải bằng số hàng của ma trận thứ hai.
Để tính tổng, hiệu hoặc tích của ma trận:
Tính toán nghịch đảo ma trận trực tuyến
Một máy tính ma trận trực tuyến có thể được sử dụng để tính ma trận nghịch đảo. Để tồn tại ma trận nghịch đảo, ma trận ban đầu phải là ma trận vuông không suy biến.
Để tính ma trận nghịch đảo:
Để tính toán ma trận nghịch đảo chi tiết từng bước, hãy sử dụng máy tính nghịch đảo ma trận này. Xem lý thuyết tính ma trận nghịch đảo.
Tính định thức của ma trận trực tuyến
Có thể sử dụng máy tính ma trận trực tuyến để tính định thức của ma trận. Để định thức ma trận tồn tại, ma trận ban đầu phải là ma trận vuông không suy biến.
Để tính định thức của ma trận:
Để tính toán chi tiết từng bước định thức của ma trận, hãy sử dụng máy tính này để tính định thức của ma trận. Xem lý thuyết tính định thức của ma trận.
Tính thứ hạng ma trận trực tuyến
Một máy tính ma trận trực tuyến có thể được sử dụng để tính thứ hạng của ma trận.
Để tính thứ hạng của ma trận:
Để tính toán thứ hạng ma trận một cách chi tiết từng bước, hãy sử dụng máy tính thứ hạng ma trận này. Xem lý thuyết tính hạng của ma trận.
Tính toán ma trận giả nghịch đảo trực tuyến
Một máy tính ma trận trực tuyến có thể được sử dụng để tính ma trận giả nghịch đảo. Luôn tồn tại một nghịch đảo giả của một ma trận nhất định.
Để tính ma trận giả nghịch đảo:
Loại bỏ các hàng hoặc cột ma trận phụ thuộc tuyến tính trực tuyến
Máy tính ma trận trực tuyến cho phép bạn xóa các hàng hoặc cột phụ thuộc tuyến tính khỏi ma trận, tức là. tạo ma trận xếp hạng đầy đủ.
Để loại bỏ các hàng hoặc cột ma trận phụ thuộc tuyến tính:
Phân hủy ma trận xương trực tuyến
Để thực hiện phân rã ma trận xương trực tuyến
Giải phương trình ma trận hoặc hệ phương trình tuyến tính AX=B trực tuyến
Sử dụng máy tính ma trận trực tuyến, bạn có thể giải phương trình ma trận AX=B đối với ma trận X. Trong trường hợp đặc biệt, nếu ma trận B là vectơ cột thì X sẽ là nghiệm của hệ phương trình tuyến tính AX= B.
Để giải phương trình ma trận:
Xin lưu ý rằng ma trận và phải có số hàng bằng nhau.
Loại bỏ Gaussian hoặc giảm ma trận thành dạng tam giác (bước) trực tuyến
Máy tính ma trận trực tuyến thực hiện phép loại bỏ Gaussian cho cả ma trận vuông và ma trận hình chữ nhật ở bất kỳ hạng nào. Đầu tiên, phương pháp Gaussian thông thường được thực hiện. Nếu ở một giai đoạn nào đó phần tử dẫn đầu bằng 0 thì một biến thể khác của phép loại bỏ Gaussian sẽ được chọn, chọn phần tử dẫn đầu lớn nhất trong cột.
Để loại bỏ Gaussian hoặc giảm ma trận về dạng tam giác
Phân tách LU hoặc phân tách LUP của ma trận trực tuyến
Máy tính ma trận này cho phép bạn thực hiện phân tách LU của ma trận (A=LU) hoặc phân tách LUP của ma trận (PA=LU), trong đó L là ma trận tam giác dưới, U là ma trận tam giác trên (hình thang), P là ma trận tam giác ma trận hoán vị. Đầu tiên, chương trình thực hiện phân tách LU, tức là một sự phân tách như vậy trong đó P=E, trong đó E là ma trận đồng nhất (tức là PA=EA=A). Nếu điều này là không thể thì việc phân tách LUP sẽ được thực hiện. Ma trận A có thể là ma trận hình vuông hoặc hình chữ nhật ở cấp bất kỳ.
Đối với phân tách LU(LUP):
Xây dựng kernel (khoảng trống) của ma trận trực tuyến
Sử dụng máy tính ma trận, bạn có thể xây dựng không gian rỗng (hạt nhân) của ma trận.
Để xây dựng không gian rỗng (kernel) của ma trận.
>Xin chào mọi người!!! Có công thức nào giúp bạn có thể loại bỏ tỷ lệ khỏi ma trận mà không cần biết hệ số tỷ lệ không ???
Chúng tôi nhớ ngay đến sự phân hủy cực. Chà, ma trận M được biểu diễn dưới dạng O * P. Trong đó O là trực giao và P là xác định dương, đối xứng - nghĩa là ma trận nén hoặc ma trận giãn nở. Ở đây chúng ta sẽ lấy ma trận O.
Câu hỏi đặt ra. Và nếu chúng ta khai triển M ở phía bên kia, chúng ta sẽ có P’ * O’. Sự phân rã theo một thứ tự khác, với các ma trận tiên nghiệm khác nhau. Tại sao không lấy O'? Tôi vật lộn với câu hỏi trong khoảng năm phút cho đến khi nhớ ra mình đã khiến học sinh thất bại trong vấn đề này như thế nào. Ma trận O' thực sự trùng với ma trận O. Nếu bạn vừa tốt nghiệp đại học hoặc vẫn đang đi học, bạn thậm chí có thể cố gắng chứng minh sự thật này.
Vì vậy, sự mở rộng cực:
Để tìm căn bậc hai dương của một ma trận, khoa học thực chứng đề xuất tính toán các giá trị riêng. Với mỗi giá trị riêng, hãy tìm không gian con riêng của nó, sau đó cẩn thận tạo căn bậc hai thực của toán tử.
Khi tưởng tượng điều gì sẽ xảy ra với một ma trận gần với ma trận đồng nhất, tôi rùng mình. Mọi thứ sẽ chết do sự thiếu chính xác của chiếc phao, thứ hạng của các ma trận sẽ giảm xuống - một sự sụp đổ hoàn toàn hứa hẹn sẽ xảy ra.
Tại sao những người cao quý không thử những phép lặp được cho là thần thánh?
Ở đây, căn nguyên của một số được tìm thấy bằng phương pháp của Newton. Dãy số a_(i+1) = 0,5 * (a_i + x / a_i); tự hào hội tụ về căn bậc hai của x. Để thử nghiệm, tôi đã lấy thư viện của ai đó về mat3x3 và tạo ra một ma trận tương tự.
Một phương pháp tương tự trực tiếp của phương pháp Newton nhanh chóng hội tụ sau 3-4 lần lặp, các bài kiểm tra trôi qua nhanh như gió. Kết quả là sự phân rã cực của ma trận; hiệu quả của thuật toán là hiển nhiên từ lý thuyết phổ cơ bản của các toán tử. Rõ ràng sau nửa giờ vắt óc.
Vì vậy, chúng tôi đã tìm thấy sự phân hủy cực. Câu hỏi là - tại sao? Và ở đây tôi buộc phải chuyển sang điểm chính của báo cáo của mình. Dạy học là điều ác. Thời gian bạn dành để ghi nhớ lý thuyết toán tử quang phổ đã bị lãng phí một cách thành công.
Phân tách quy mô Shear Rotate được tìm kiếm một lần. Chúng tôi áp dụng quá trình trực giao hóa và trực giao hóa cho ma trận. Theo cột. Chúng tôi nhận được một ma trận tuyệt vời. Và tại sao kết quả sẽ tồi tệ hơn? Không có gì!
Tôi đã thấy một bài đăng có mã bằng Pascal tính toán phép phân tách Xoay cắt tỷ lệ tương tự này và đột nhiên tôi nhận ra rằng tôi không có đối số nào cho việc phân tách cực. Điều này đòi hỏi ai phải biết loại công nghệ máy tính nào.
Tất nhiên, có những phản đối nhỏ, gần như ngụy biện. Ví dụ, không gian tiếp tuyến dễ được coi là trực giao hơn. Tính toán đơn giản hơn. Thông thường chúng ta xem xét dPosition/du, pháp tuyến và vectơ thứ ba được lấy vuông góc với cặp này. Rõ ràng là phương pháp này không đối xứng đối với tọa độ kết cấu; cái nào trong số chúng là thứ nhất và cái nào là thứ hai là hoàn toàn không rõ ràng. Có vẻ đúng khi áp dụng phân rã cực cho ma trận biến đổi cục bộ.
Bạn có thể nhận thấy sự khác biệt giữa quá trình phân rã cực “đúng” và quá trình trực giao hóa cột “không chính xác”. Có thể bạn sẽ không để ý. Và hình ảnh chắc chắn sẽ không khá hơn chút nào.
tái bút Việc lưu trữ hình ảnh động trong Xoay cắt tỷ lệ cũng rất thú vị. Ba vectơ, một quaternion. Lực cắt hầu như luôn bằng 0, Tỷ lệ hầu như luôn bằng 1, các đường ray liên tục có thể bị loại bỏ. Và ở những nơi có các bản nhạc không liên tục, có một cách để loại bỏ nó bằng cách chuyên biệt hóa mẫu. Hoặc một cái gì đó khác.
1)
Đầu tiên chúng ta xét ma trận thực. Giả sử rằng gốc được trích xuất từ ma trận $%A$%, tức là. có một ma trận $%B$% sao cho $%B \cdot B=A$%. Chúng ta cũng giả sử rằng ma trận $%B$% có thể được rút gọn về dạng đường chéo, tức là có một ma trận $%S$% sao cho $%S^(-1)BS=B"$%, trong đó $%B"$% là ma trận đường chéo. Từ các đẳng thức $%B"B"=S^(-1)BSS^(-1)BS=S^(-1)BBS=S^(-1)AS$% suy ra $%A"=S ^ (-1)AS$% cũng là một ma trận đường chéo, tức là các ma trận $%A$% và $%B$% được rút gọn về dạng đường chéo bằng cùng một phép biến đổi vì các phần tử của ma trận nguyên tố là các giá trị riêng của những cái không có mồi, thì các kết luận sau đây rút ra từ những cân nhắc ở trên.
1.1)Nếu ma trận $%A$% là ma trận xác định dương đối xứng thì nghiệm được rút ra từ nó dưới dạng ma trận thực.
1.2) Thuật toán tính nghiệm của ma trận như sau: giải bài toán giá trị riêng, trích rút các nghiệm từ các giá trị riêng, soạn ma trận đường chéo từ chúng, áp dụng cho nó một phép biến đổi nghịch đảo với phép biến đổi chuyển đổi ma trận $%A$% sang dạng đường chéo.
1.3) Số lượng ma trận khác nhau $%B$% bằng $%2^n$%, bởi vì Đối với mỗi giá trị riêng có 2 giá trị gốc - dương và âm.
2) Đối với ma trận phức, suy luận sẽ vẫn đúng nếu chúng ta thay thế tính đối xứng bằng tính đơn nhất. Yêu cầu về tính xác định tích cực đương nhiên sẽ bị loại bỏ.
3)
Giải pháp cho trường hợp tổng quát. Chúng ta hãy giả sử rằng phép biến đổi $%S$% đưa ma trận $%B$% không phải theo đường chéo mà thành dạng tam giác trên, tức là. ma trận $%B"$% là tam giác trên. Phép biến đổi như vậy tồn tại đối với bất kỳ ma trận vuông nào. Dễ dàng xác minh rằng ma trận $%A"$% cũng sẽ trở thành tam giác trên và các phần tử đường chéo của ma trận $%A"$% sẽ là các hình vuông tương ứng với các phần tử đường chéo của ma trận $%B"$%. Điều này cho phép bạn tìm tất cả các phần tử đường chéo của ma trận $%B"$% bằng cách lấy phần gốc của các phần tử đường chéo của ma trận $%A"$%, sau đó, dọc theo chuỗi, tìm tất cả các phần tử khác của ma trận $%B"$%. Từ đây rút ra các kết luận sau.
3.1) Một nghiệm được trích ra từ ma trận phức bất kỳ; trong trường hợp tổng quát, các nghiệm đó là $%2^n$%, nhưng có thể có (nhiều) nghiệm trùng nhau giữa chúng.
3.2) Thuật toán tính nghiệm như sau: chuyển ma trận $%A$% về dạng tam giác trên, tìm ma trận $%B"$% bằng thuật toán đã lập và thực hiện phép biến đổi ngược.
3.3) Điều kiện cần và đủ để tồn tại các nghiệm của ma trận thực là các phần tử đường chéo không âm sau khi biến ma trận thành dạng tam giác. Tính không âm của định thức là điều kiện cần nhưng chưa đủ.
Phụ lục 1 (trả lời bình luận). Bạn có nghĩa là "với một cái nhìn hình tam giác". Nói chung, trong đoạn văn. 1, 2, mọi thứ đều hoàn toàn rõ ràng, nhưng có vẻ như điểm 3 cần phải suy nghĩ thêm. Vấn đề là phương pháp Gaussian có thể không được rút gọn thành phép biến đổi $%S^(-1)AS$%, và bằng chứng dựa trên điều này. Những thứ kia. cách chứng minh chỉ áp dụng cho những ma trận có thể rút gọn về dạng tam giác bằng phép biến đổi $%S^(-1)AS$%.
Phụ lục 2. Có vẻ như trong đoạn 3, nói chung, mọi thứ đều đúng, bạn chỉ cần sử dụng phép biến đổi ma trận $%A$% sang dạng Jordan - đối với phép biến đổi này luôn có một ma trận thu được từ việc giải bài toán giá trị riêng. Vấn đề là bình phương của ma trận Jordan không phải là ma trận Jordan (mặc dù nó là hình tam giác và thậm chí là hai đường chéo). Sự biện minh chặt chẽ của thuật toán đòi hỏi phải chứng minh định lý sau: “Nếu $%A"=B"^2$% và $%A"$% là ma trận Jordan, thì $%B"$% là ma trận tam giác. " Tuyên bố này có vẻ đúng, nhưng tôi chưa biết làm thế nào để chứng minh điều đó.
