Khái niệm kim tự tháp

Định nghĩa 1

Một hình hình học được tạo thành bởi một đa giác và một điểm không nằm trong mặt phẳng chứa đa giác này, nối với tất cả các đỉnh của đa giác, được gọi là hình chóp (Hình 1).

Đa giác mà từ đó hình chóp được tạo ra được gọi là đáy của hình chóp; các hình tam giác thu được, khi nối với một điểm, là các mặt bên của hình chóp, các cạnh của hình tam giác là các cạnh của hình chóp và điểm chung cho tất cả các hình tam giác là đỉnh của kim tự tháp.

Các loại kim tự tháp

Tùy thuộc vào số góc ở đáy của kim tự tháp, nó có thể được gọi là hình tam giác, hình tứ giác, v.v. (Hình 2).

Hình 2.

Một loại kim tự tháp khác là kim tự tháp thông thường.

Hãy để chúng tôi giới thiệu và chứng minh tính chất của một kim tự tháp đều.

Định lý 1

Tất cả các mặt bên của một hình chóp đều là các tam giác cân bằng nhau.

Bằng chứng.

Xét một hình chóp $n-$giác đều có đỉnh $S$ có chiều cao $h=SO$. Chúng ta hãy vẽ một vòng tròn xung quanh đế (Hình 4).

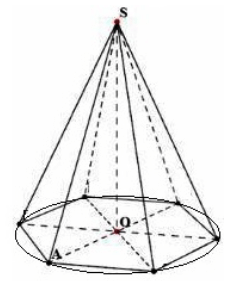
Hình 4.

Xét tam giác $SOA$. Theo định lý Pytago, ta có

Rõ ràng, bất kỳ cạnh bên nào cũng sẽ được xác định theo cách này. Do đó, tất cả các cạnh bên đều bằng nhau, nghĩa là tất cả các mặt bên đều là tam giác cân. Hãy chứng minh rằng chúng bằng nhau. Vì đáy là một đa giác đều nên các đáy của tất cả các mặt bên đều bằng nhau. Do đó, tất cả các mặt bên đều bằng nhau theo tiêu chuẩn III về sự bằng nhau của các tam giác.

Định lý đã được chứng minh.

Bây giờ chúng ta hãy giới thiệu định nghĩa sau đây liên quan đến khái niệm kim tự tháp đều.

Định nghĩa 3

Đỉnh của một kim tự tháp thông thường là chiều cao của mặt bên của nó.

Rõ ràng, theo Định lý 1, tất cả các trung đoạn đều bằng nhau.

Định lý 2

Diện tích bề mặt bên của một hình chóp thông thường được xác định bằng tích của bán chu vi của đáy và đường trung đoạn.

Bằng chứng.

Chúng ta hãy biểu thị cạnh đáy của hình chóp hình chóp $n-$giác bằng $a$, và trung điểm là $d$. Do đó diện tích của mặt bên bằng

Vì theo Định lý 1, tất cả các cạnh đều bằng nhau nên

Định lý đã được chứng minh.

Một loại kim tự tháp khác là kim tự tháp cắt ngắn.

Định nghĩa 4

Nếu một mặt phẳng song song với đáy của nó được vẽ thông qua một hình chóp thông thường, thì hình tạo thành giữa mặt phẳng này và mặt phẳng của đáy được gọi là hình chóp cụt (Hình 5).

Hình 5. Hình chóp cụt

Các mặt bên của hình chóp cụt là các hình thang.

Định lý 3

Diện tích bề mặt bên của một hình chóp cắt cụt đều được xác định bằng tích của tổng bán chu vi của các đáy và trung đoạn.

Bằng chứng.

Chúng ta hãy ký hiệu các cạnh của các đáy của hình chóp giác ngộ $n-$ lần lượt là $a\ và\ b$, và trung điểm là $d$. Do đó, diện tích của mặt bên bằng

Vì tất cả các cạnh đều bằng nhau nên

Định lý đã được chứng minh.

Nhiệm vụ mẫu

Ví dụ 1

Tìm diện tích bề mặt bên của một hình chóp tam giác cụt nếu nó được lấy từ một hình chóp đều có cạnh đáy 4 và trung điểm 5 bằng cách cắt một mặt phẳng đi qua đường giữa của các mặt bên.

Giải pháp.

Sử dụng định lý đường giữa, chúng ta thấy rằng đáy trên của hình chóp cụt bằng $4\cdot \frac(1)(2)=2$, và trung điểm bằng $5\cdot \frac(1)(2) = 2,5$.

Khi đó, theo Định lý 3, ta có

Kim tự tháp. Kim tự tháp cắt ngắn

kim tự tháp là một khối đa diện, một trong các mặt của nó là đa giác ( căn cứ ) và tất cả các mặt còn lại đều là những tam giác có chung một đỉnh ( mặt bên ) (Hình 15). Kim tự tháp được gọi là Chính xác , nếu đáy của nó là một đa giác đều và đỉnh của kim tự tháp được chiếu vào tâm của đế (Hình 16). Hình chóp tam giác có tất cả các cạnh bằng nhau được gọi là tứ diện .

Sườn bên của hình chóp là cạnh của mặt bên không thuộc đáy Chiều cao kim tự tháp là khoảng cách từ đỉnh của nó đến mặt phẳng đáy. Tất cả các cạnh bên của một hình chóp đều bằng nhau, tất cả các mặt bên đều là các tam giác cân bằng nhau. Chiều cao của mặt bên của hình chóp đều vẽ từ đỉnh được gọi là huyền thoại . Mặt cắt chéo được gọi là một phần của hình chóp bởi một mặt phẳng đi qua hai cạnh bên không thuộc cùng một mặt.

Diện tích bề mặt bên kim tự tháp là tổng diện tích của tất cả các mặt bên. Tổng diện tích bề mặt được gọi là tổng diện tích các mặt bên và đáy.

Định lý

1. Nếu trong một hình chóp, tất cả các cạnh bên đều nghiêng bằng nhau với mặt phẳng của đáy thì đỉnh của hình chóp được chiếu vào tâm của vòng tròn ngoại tiếp gần chân đế.

2. Nếu trong một hình chóp, tất cả các cạnh bên đều có độ dài bằng nhau thì đỉnh của hình chóp được chiếu vào tâm của một vòng tròn ngoại tiếp gần đáy.

3. Nếu tất cả các mặt của một hình chóp đều nghiêng bằng nhau với mặt phẳng của đáy thì đỉnh của hình chóp được chiếu vào tâm của một vòng tròn nội tiếp ở đáy.

Để tính thể tích của một hình chóp tùy ý, công thức đúng là:

Ở đâu V.- âm lượng;

Đế chữ S- diện tích cơ sở;

H- chiều cao của kim tự tháp.

Đối với một kim tự tháp thông thường, các công thức sau đây là đúng:

Ở đâu P- chu vi đáy;

ha– châm ngôn;

H- chiều cao;

đầy đủ

bên S

Đế chữ S- diện tích cơ sở;

V.- thể tích của hình chóp đều.

Kim tự tháp cắt ngắn gọi là phần kim tự tháp được bao bọc giữa đế và mặt phẳng cắt song song với đáy kim tự tháp (Hình 17). Kim tự tháp cắt ngắn thông thường gọi là phần của hình chóp đều được bao bọc giữa đáy và mặt phẳng cắt song song với đáy của hình chóp.

Lý do kim tự tháp cắt ngắn - đa giác tương tự. Mặt bên – hình thang. Chiều cao của một hình chóp cụt là khoảng cách giữa các đáy của nó. Đường chéo hình chóp cụt là đoạn nối các đỉnh của nó không nằm trên cùng một mặt. Mặt cắt chéo là một phần của hình chóp cụt bởi một mặt phẳng đi qua hai cạnh bên không thuộc cùng một mặt.

Đối với hình chóp cụt, các công thức sau là hợp lệ:

(4)

Ở đâu S 1 , S 2 – diện tích đáy trên và đáy dưới;

đầy đủ- tổng diện tích bề mặt;

bên S- diện tích bề mặt bên;

H- chiều cao;

V.- thể tích của hình chóp cụt.

Đối với một kim tự tháp cắt cụt thông thường, công thức là đúng:

Ở đâu P 1 , P 2 – chu vi của các căn cứ;

ha– đỉnh của một kim tự tháp cắt cụt thông thường.

Ví dụ 1. Trong một hình chóp tam giác đều, góc nhị diện ở đáy là 60°. Tìm tiếp tuyến của góc nghiêng của cạnh bên với mặt phẳng đáy.

Giải pháp. Hãy vẽ một bức tranh (Hình 18).

Kim tự tháp đều, có nghĩa là ở đáy có một tam giác đều và tất cả các mặt bên đều là các tam giác cân bằng nhau. Góc nhị diện ở đáy là góc nghiêng của mặt bên của hình chóp với mặt phẳng của đế. Góc tuyến tính là góc Một giữa hai đường vuông góc: v.v. Đỉnh của kim tự tháp chiếu vào tâm của tam giác (tâm của đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác) ABC). Góc nghiêng của cạnh bên (ví dụ S.B.) là góc giữa cạnh đó và hình chiếu của nó lên mặt phẳng đáy. Đối với xương sườn S.B. góc này sẽ là góc SBD. Để tìm tiếp tuyến bạn cần biết chân VÌ THẾ Và O.B.. Cho độ dài của đoạn BD bằng 3 MỘT. chấm VỀđoạn BDđược chia thành nhiều phần: và Từ chúng tôi tìm thấy VÌ THẾ: Từ đó chúng tôi tìm thấy:

Trả lời:

Ví dụ 2. Tìm thể tích của một hình chóp tứ giác cắt cụt đều nếu các đường chéo của đáy bằng cm và cm và chiều cao của nó là 4 cm.

Giải pháp.Để tìm thể tích của hình chóp cụt, chúng ta sử dụng công thức (4). Để tìm diện tích của các đáy, bạn cần tìm các cạnh của các hình vuông đáy, biết các đường chéo của chúng. Các cạnh của các đáy tương ứng là 2 cm và 8 cm. Điều này có nghĩa là diện tích của các đáy và thay thế tất cả dữ liệu vào công thức, chúng ta tính thể tích của hình chóp cụt:

Trả lời: 112cm3.

Ví dụ 3. Tìm diện tích mặt bên của một hình chóp tam giác đều có cạnh đáy là 10 cm và 4 cm, chiều cao của hình chóp là 2 cm.

Giải pháp. Hãy vẽ một bức tranh (Hình 19).

Mặt bên của kim tự tháp này là một hình thang cân. Để tính diện tích hình thang, bạn cần biết đáy và chiều cao. Các căn cứ được đưa ra theo điều kiện, chỉ có chiều cao là không rõ. Chúng ta sẽ tìm thấy cô ấy từ đâu MỘT 1 E vuông góc từ một điểm MỘT 1 trên mặt phẳng của đế dưới, MỘT 1 D- vuông góc với MỘT 1 mỗi AC. MỘT 1 E= 2 cm, vì đây là chiều cao của kim tự tháp. Để tìm DE Hãy tạo một bản vẽ bổ sung hiển thị góc nhìn từ trên xuống (Hình 20). chấm VỀ- hình chiếu tâm của đáy trên và đáy dưới. vì (xem Hình 20) và Mặt khác ĐƯỢC RỒI- bán kính nội tiếp trong đường tròn và ôi- Bán kính nội tiếp đường tròn:

MK = DE.

Theo định lý Pythagore từ

Diện tích mặt bên:

Trả lời:

Ví dụ 4. Dưới đáy của kim tự tháp là một hình thang cân, các đáy của nó MỘT Và b (Một> b). Mỗi mặt bên tạo thành một góc bằng mặt phẳng đáy của kim tự tháp j. Tìm tổng diện tích bề mặt của kim tự tháp.

Giải pháp. Hãy vẽ một bức tranh (Hình 21). Tổng diện tích bề mặt của kim tự tháp SABCD bằng tổng diện tích và diện tích hình thang ABCD.

Chúng ta hãy sử dụng phát biểu rằng nếu tất cả các mặt của hình chóp đều nghiêng với mặt phẳng của đáy thì đỉnh được chiếu vào tâm của đường tròn nội tiếp ở đáy. chấm VỀ– phép chiếu đỉnh Sở đáy kim tự tháp. Tam giác SOD là hình chiếu trực giao của tam giác CSD tới mặt phẳng của đáy. Áp dụng định lý về diện tích hình chiếu trực giao của hình phẳng, ta thu được:

Tương tự như vậy nó có nghĩa là Như vậy, bài toán đã được rút gọn thành việc tìm diện tích hình thang ABCD. Hãy vẽ một hình thang ABCD riêng biệt (Hình 22). chấm VỀ- tâm của đường tròn nội tiếp hình thang.

Vì một đường tròn có thể nội tiếp trong một hình thang nên hoặc Từ định lý Pythagore chúng ta có

Video hướng dẫn này sẽ giúp người dùng hình dung về chủ đề Kim tự tháp. Đúng kim tự tháp. Trong bài học này chúng ta sẽ làm quen với khái niệm kim tự tháp và đưa ra định nghĩa về nó. Chúng ta hãy xem kim tự tháp thông thường là gì và nó có những đặc tính gì. Sau đó, chúng ta chứng minh định lý về bề mặt bên của một hình chóp đều.

Trong bài học này chúng ta sẽ làm quen với khái niệm kim tự tháp và đưa ra định nghĩa về nó.

Hãy xem xét một đa giác A 1 A 2...MỘT, nằm trong mặt phẳng α và điểm P, không nằm trong mặt phẳng α (Hình 1). Hãy kết nối các dấu chấm P với đỉnh A 1, A 2, A 3, … MỘT. chúng tôi nhận được N hình tam giác: A 1 A 2 R, A 2 A 3 R và vân vân.

Sự định nghĩa. đa diện RA 1 A 2 ...A n, tạo thành từ N-quảng trường A 1 A 2...MỘT Và N hình tam giác RA 1 A 2, RA 2 A 3 …RA và A n-1 được gọi N-kim tự tháp than. Cơm. 1.

Cơm. 1

Hãy xem xét một kim tự tháp tứ giác PABCD(Hình 2).

R- đỉnh của kim tự tháp.

ABCD- đáy của kim tự tháp.

RA- sườn bên.

AB- sườn cơ bản.

Từ điểm R hãy bỏ đường vuông góc RNđến mặt phẳng cơ sở ABCD. Đường vuông góc được vẽ là chiều cao của kim tự tháp.

Cơm. 2

Bề mặt đầy đủ của kim tự tháp bao gồm bề mặt bên, nghĩa là diện tích của tất cả các mặt bên và diện tích của đế:

S đầy đủ = S bên + S chính

Một kim tự tháp được gọi là đúng nếu:

• đáy của nó là một đa giác đều;
• đoạn nối đỉnh của kim tự tháp với tâm của đế là chiều cao của nó.

Giải thích bằng ví dụ về hình chóp tứ giác đều

Xét một hình chóp tứ giác đều PABCD(Hình 3).

R- đỉnh của kim tự tháp. Cơ sở của kim tự tháp ABCD- một tứ giác đều, nghĩa là một hình vuông. chấm VỀ, giao điểm của hai đường chéo là tâm của hình vuông. Có nghĩa, RO là chiều cao của kim tự tháp.

Cơm. 3

Giải thích: đúng N Trong một tam giác, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp trùng nhau. Tâm này được gọi là tâm của đa giác. Đôi khi họ nói rằng đỉnh được chiếu vào tâm.

Chiều cao của mặt bên của một hình chóp đều vẽ từ đỉnh của nó được gọi là huyền thoại và được chỉ định ha.

1. tất cả các cạnh bên của hình chóp đều bằng nhau;

2. Các mặt bên là các tam giác cân bằng nhau.

Chúng tôi sẽ đưa ra bằng chứng về các tính chất này bằng ví dụ về hình chóp tứ giác đều.

Được cho: PABCD- kim tự tháp tứ giác đều,

ABCD- quảng trường,

RO- chiều cao của kim tự tháp.

Chứng minh:

1. RA = PB = RS = PD

2.∆ABP = ∆BCP =∆CDP =∆DAP Xem Hình 2. 4.

Cơm. 4

Bằng chứng.

RO- chiều cao của kim tự tháp. Tức là thẳng RO vuông góc với mặt phẳng ABC, và do đó trực tiếp CTCP, VÕ, SO Và LÀM nằm trong đó. Vậy hình tam giác ROA, ROV, ROS, ROD- hình chữ nhật.

Hãy xem xét một hình vuông ABCD. Từ các tính chất của hình vuông suy ra rằng AO = VO = CO = LÀM.

Khi đó các tam giác vuông ROA, ROV, ROS, ROD chân RO- nói chung và chân CTCP, VÕ, SO Và LÀM bằng nhau, nghĩa là các tam giác này có hai cạnh bằng nhau. Từ sự bằng nhau của các tam giác dẫn đến sự bằng nhau của các đoạn thẳng, RA = PB = RS = PD.Điểm 1 đã được chứng minh.

Phân đoạn AB Và Mặt trời bằng nhau vì chúng là các cạnh của cùng một hình vuông, RA = PB = RS. Vậy hình tam giác AVR Và VSR - cân và bằng nhau ở ba cạnh.

Theo cách tương tự, chúng ta thấy rằng các tam giác ABP, VCP, CDP, DAP là cân và bằng nhau, như yêu cầu chứng minh ở đoạn 2.

Diện tích bề mặt bên của một hình chóp đều bằng một nửa tích của chu vi đáy và trung đoạn:

Để chứng minh điều này, hãy chọn một hình chóp tam giác đều.

Được cho: RAV- hình chóp tam giác đều.

AB = BC = AC.

RO- chiều cao.

Chứng minh: . Xem hình. 5.

Cơm. 5

Bằng chứng.

RAV- hình chóp tam giác đều. Đó là AB= AC = BC. Cho phép VỀ- tâm của tam giác ABC, Sau đó RO là chiều cao của kim tự tháp. Dưới chân kim tự tháp có một hình tam giác đều ABC. Lưu ý rằng .

Hình tam giác RAV, RVS, RSA- tam giác cân bằng nhau (theo tính chất). Hình chóp tam giác có ba mặt: RAV, RVS, RSA. Điều này có nghĩa là diện tích bề mặt bên của kim tự tháp là:

Bên S = 3S RAW

Định lý đã được chứng minh.

Bán kính của một vòng tròn được ghi ở đáy của một kim tự tháp tứ giác đều là 3 m, chiều cao của kim tự tháp là 4 m. Tìm diện tích bề mặt bên của kim tự tháp.

Được cho: hình chóp tứ giác đều ABCD,

ABCD- quảng trường,

r= 3 m,

RO- chiều cao của kim tự tháp,

RO= 4m.

Tìm thấy: Bên S. Xem hình. 6.

Cơm. 6

Giải pháp.

Theo định lý đã được chứng minh thì .

Đầu tiên chúng ta hãy tìm cạnh của đáy AB. Chúng ta biết rằng bán kính của hình tròn nội tiếp đáy của một hình chóp tứ giác đều là 3 m.

Sau đó, tôi.

Tìm chu vi của hình vuông ABCD có cạnh 6m:

Hãy xem xét một hình tam giác BCD. Cho phép M- giữa bên DC. Bởi vì VỀ- ở giữa BD, Cái đó (m).

Tam giác DPC- cân. M- ở giữa DC. Đó là, RM- đường trung tuyến và do đó là chiều cao trong tam giác DPC. Sau đó RM- apothem của kim tự tháp.

RO- chiều cao của kim tự tháp. Sau đó, thẳng RO vuông góc với mặt phẳng ABC, và do đó trực tiếp ôi, nằm trong đó. Chúng ta hãy tìm apothem RM từ một tam giác vuông ROM.

Bây giờ chúng ta có thể tìm thấy bề mặt bên của kim tự tháp:

Trả lời: 60 m2.

Bán kính của hình tròn ngoại tiếp đáy của một hình chóp tam giác đều bằng m. Diện tích bề mặt bên là 18 m 2. Tìm độ dài của trung đoạn.

Được cho: ABCP- hình chóp tam giác đều,

AB = BC = SA,

R= m,

Cạnh S = 18 m2.

Tìm thấy: . Xem hình. 7.

Cơm. 7

Giải pháp.

Trong một tam giác vuông ABC Bán kính của đường tròn ngoại tiếp đã cho. Hãy tìm một bên AB tam giác này bằng cách sử dụng định luật sin.

Biết cạnh của một tam giác đều (m), chúng ta tìm được chu vi của nó.

Theo định lý về diện tích xung quanh của hình chóp đều, trong đó ha- apothem của kim tự tháp. Sau đó:

Trả lời: 4m.

Vì vậy, chúng ta đã xem kim tự tháp là gì, kim tự tháp đều là gì, và chúng ta đã chứng minh định lý về bề mặt bên của một kim tự tháp đều. Trong bài học tiếp theo chúng ta sẽ làm quen với hình chóp cụt.

Tài liệu tham khảo

1. Hình học. Lớp 10-11: Sách giáo khoa dành cho học sinh các cơ sở giáo dục phổ thông (cấp độ cơ bản và chuyên ngành) / I. M. Smirnova, V. A. Smirnov. - Tái bản lần thứ 5, tái bản. và bổ sung - M.: Mnemosyne, 2008. - 288 tr.: ốm.
2. Hình học. Lớp 10-11: Sách giáo khoa phổ thông / Sharygin I. F. - M.: Bustard, 1999. - 208 tr.: ill.
3. Hình học. Lớp 10: Sách giáo khoa dành cho cơ sở giáo dục phổ thông nghiên cứu chuyên sâu và chuyên sâu về toán/E. V. Potoskuev, L. I. Zvalich. - tái bản lần thứ 6, khuôn mẫu. - M.: Bustard, 008. - 233 tr.: ốm.

1. Cổng thông tin Internet "Yaklass" ()
2. Cổng thông tin điện tử “Ngày hội tư tưởng sư phạm “Ngày đầu tháng 9” ()
3. Cổng thông tin Internet “Slideshare.net” ()

bài tập về nhà

1. Một đa giác đều có thể là đáy của một kim tự tháp không đều không?
2. Chứng minh rằng các cạnh rời nhau của một hình chóp đều vuông góc.
3. Tìm giá trị của góc nhị diện ở cạnh đáy của một hình chóp tứ giác đều nếu đường trung bình của hình chóp bằng cạnh đáy của nó.
4. RAV- hình chóp tam giác đều. Xây dựng góc tuyến tính của góc nhị diện ở đáy kim tự tháp.

Trong đó một trong các gân bên vuông góc với đế.

Trong trường hợp này, cạnh này sẽ là chiều cao của kim tự tháp.

Thuộc tính của kim tự tháp.

1. Khi tất cả các cạnh bên có cùng kích thước thì:

• thật dễ dàng để mô tả một vòng tròn gần đáy của kim tự tháp, và đỉnh của kim tự tháp sẽ được chiếu vào tâm của vòng tròn này;
• các gân bên tạo thành các góc bằng nhau với mặt phẳng của đế;
• Hơn nữa, điều ngược lại cũng đúng, tức là khi các gân bên tạo thành các góc bằng nhau với mặt phẳng của đáy hoặc khi có thể mô tả một hình tròn xung quanh đáy hình chóp và đỉnh của hình chóp sẽ chiếu vào tâm của hình tròn này, điều đó có nghĩa là tất cả các cạnh bên của kim tự tháp có cùng kích thước.

2. Khi các mặt bên có một góc nghiêng so với mặt phẳng đáy có cùng giá trị thì:

• thật dễ dàng để mô tả một vòng tròn gần đáy của kim tự tháp, và đỉnh của kim tự tháp sẽ được chiếu vào tâm của vòng tròn này;
• chiều cao của các mặt bên có chiều dài bằng nhau;
• diện tích của mặt bên bằng ½ tích của chu vi đáy và chiều cao của mặt bên.

3. Một hình cầu có thể được mô tả xung quanh một kim tự tháp nếu ở đáy của hình chóp có một đa giác xung quanh có thể mô tả một hình tròn (điều kiện cần và đủ). Tâm của hình cầu sẽ là điểm giao nhau của các mặt phẳng đi qua tâm của các cạnh của hình chóp vuông góc với chúng. Từ định lý này, chúng ta kết luận rằng một hình cầu có thể được mô tả xung quanh bất kỳ hình tam giác nào và xung quanh bất kỳ hình chóp đều nào;

4. Một hình cầu có thể nội tiếp vào hình chóp nếu các mặt phẳng phân giác của các góc nhị diện trong của hình chóp cắt nhau tại điểm thứ nhất (điều kiện cần và đủ). Điểm này sẽ trở thành tâm của hình cầu.

5. Hình nón sẽ nội tiếp trong hình chóp khi các đỉnh của chúng trùng nhau và đáy của hình nón sẽ nội tiếp ở đáy hình chóp. Trong trường hợp này, chỉ có thể ghép một hình nón vào một hình chóp nếu các đường trung đoạn của hình chóp có kích thước bằng nhau (điều kiện cần và đủ);

6. Hình nón sẽ được mô tả gần đáy của hình chóp nếu các đỉnh của chúng trùng nhau và đáy của hình nón sẽ được mô tả gần đáy của hình chóp. Trong trường hợp này, chỉ có thể mô tả một hình nón gần hình chóp nếu tất cả các cạnh bên của hình chóp có cùng giá trị (điều kiện cần và đủ). Chiều cao của các hình nón và kim tự tháp này là như nhau.

7. Một hình trụ được gọi là hình chóp nếu một trong các đáy của nó trùng với một đường tròn nội tiếp trong tiết diện hình chóp bằng một mặt phẳng song song với đáy và đáy thứ hai thuộc về đáy của hình chóp.

8. Hình trụ sẽ được mô tả gần kim tự tháp khi đỉnh của kim tự tháp thuộc về một trong các đáy của nó, và đáy thứ hai của hình trụ sẽ được mô tả gần đáy của kim tự tháp. Trong trường hợp này, chỉ có thể mô tả một hình trụ gần một kim tự tháp nếu đáy của hình chóp là một đa giác nội tiếp (điều kiện cần và đủ).

Công thức xác định thể tích và diện tích của hình chóp hình chữ nhật.

V.- khối lượng của kim tự tháp,

S- diện tích đáy của kim tự tháp,

h- chiều cao của kim tự tháp,

sb- diện tích bề mặt bên của kim tự tháp,

Một- apothem (đừng nhầm lẫn với α ) kim tự tháp,

P- chu vi đáy của kim tự tháp,

N- số cạnh của đáy kim tự tháp,

b- chiều dài cạnh bên của kim tự tháp,

α - góc phẳng ở đỉnh kim tự tháp.

Tại đây bạn có thể tìm thấy thông tin cơ bản về kim tự tháp cũng như các công thức và khái niệm liên quan. Tất cả đều được học với một gia sư toán để chuẩn bị cho Kỳ thi Thống nhất.

Xét một mặt phẳng, một đa giác , nằm trong nó và một điểm S, không nằm trong đó. Hãy nối S với tất cả các đỉnh của đa giác. Khối đa diện kết quả được gọi là kim tự tháp. Các đoạn được gọi là gân bên. Đa giác được gọi là đáy và điểm S là đỉnh của hình chóp. Tùy thuộc vào số n, hình chóp được gọi là hình tam giác (n=3), hình tứ giác (n=4), hình ngũ giác (n=5), v.v. Một tên thay thế cho hình chóp tam giác là tứ diện. Chiều cao của hình chóp là đường vuông góc đi từ đỉnh của nó xuống mặt phẳng đáy.

Một kim tự tháp được gọi là đều đặn nếu một đa giác đều, và đáy của đường cao của kim tự tháp (gốc của đường vuông góc) là tâm của nó.

Lời bình của gia sư:
Đừng nhầm lẫn giữa khái niệm “kim tự tháp đều” và “tứ diện đều”. Trong một hình chóp đều, các cạnh bên không nhất thiết phải bằng các cạnh của đáy, nhưng trong một tứ diện đều thì cả 6 cạnh đều bằng nhau. Đây là định nghĩa của anh ấy. Dễ dàng chứng minh đẳng thức suy ra tâm P của đa giác trùng nhau có chiều cao đáy nên tứ diện đều là hình chóp đều.

apothem là gì?
Đỉnh của kim tự tháp là chiều cao của mặt bên của nó. Nếu kim tự tháp đều đặn thì tất cả các đường trung đoạn của nó đều bằng nhau. Điều ngược lại là không đúng.

Một gia sư toán về thuật ngữ của mình: 80% bài tập về kim tự tháp được xây dựng thông qua hai loại hình tam giác:
1) Chứa trung điểm SK và chiều cao SP
2) Chứa cạnh bên SA và hình chiếu PA của nó

Để đơn giản hóa việc tham chiếu đến các hình tam giác này, sẽ thuận tiện hơn cho gia sư toán gọi hình đầu tiên trong số đó vô thường, và thứ hai ven biển. Thật không may, bạn sẽ không tìm thấy thuật ngữ này trong bất kỳ cuốn sách giáo khoa nào và giáo viên phải đơn phương giới thiệu nó.

Công thức tính thể tích của kim tự tháp:
1) , diện tích đáy của kim tự tháp là bao nhiêu và chiều cao của kim tự tháp là bao nhiêu
2) , ở đâu là bán kính của hình cầu nội tiếp và là diện tích tổng bề mặt của kim tự tháp.
3) , trong đó MN là khoảng cách giữa hai cạnh giao nhau bất kỳ và là diện tích hình bình hành được tạo bởi trung điểm của bốn cạnh còn lại.

Tính chất đáy của chiều cao của kim tự tháp:

Điểm P (xem hình) trùng với tâm của đường tròn nội tiếp ở đáy hình chóp nếu đáp ứng một trong các điều kiện sau:
1) Tất cả các trung đoạn đều bằng nhau
2) Tất cả các mặt bên đều nghiêng bằng nhau so với đáy
3) Tất cả các đường trung đoạn đều nghiêng như nhau theo chiều cao của kim tự tháp
4) Chiều cao của hình chóp nghiêng bằng nhau đối với tất cả các mặt bên

Lời nhận xét của gia sư toán: Xin lưu ý rằng tất cả các điểm được thống nhất bởi một đặc tính chung: bằng cách này hay cách khác, các mặt bên đều có liên quan ở mọi nơi (các đoạn trung đoạn là các phần tử của chúng). Vì vậy, gia sư có thể đưa ra một công thức kém chính xác hơn nhưng thuận tiện hơn cho việc học: điểm P trùng với tâm của đường tròn nội tiếp, đáy của hình chóp, nếu có bất kỳ thông tin nào bằng nhau về các mặt bên của nó. Để chứng minh điều đó, chỉ cần chứng minh rằng mọi tam giác trung điểm đều bằng nhau là đủ.

Điểm P trùng với tâm của đường tròn ngoại tiếp gần đáy kim tự tháp nếu một trong ba điều kiện đúng:
1) Tất cả các cạnh bên đều bằng nhau
2) Tất cả các gân bên đều nghiêng bằng nhau so với đế
3) Tất cả các gân bên đều nghiêng bằng nhau theo chiều cao