Велика енциклопедія нафти та газу

Відповімо усно! Чи справедливе твердження, що біля будь-якої трикутної піраміди можна описати сферу? Чи можна описати сферу біля будь-якої чотирикутної піраміди? Які властивості має піраміда, щоб біля неї можна було описати сферу? У сферу вписана піраміда, бічне ребро якої перпендикулярне до основи. Як знайти центр сфери? При правильної піраміди описано світ. Як розташований її центр щодо елементів піраміди?

Слайд 17із презентації ««Завдання з геометрії» 11 клас». Розмір архіву із презентацією 1032 КБ.

Геометрія 11 клас

короткий зміст інших презентацій

"Поняття центральної симетрії" - Відображення простору на себе. Центральна симетрія. Фігура називається симетричною. Центральна симетрія є рухом. Рух простору. Точки М та М1 називаються симетричними. Властивість. Рухи. Ми знайомилися з рухами площини. Завдання. Центральна симетрія є окремим випадком повороту.

"Завдання на обчислення площі трикутника" - Айвен Нівен. Розв'язання одного завдання. Девіз уроку. Особистісні цілі. Знайти площу фігури. Математичний диктант. Способи знаходження площі трикутника. Виберіть затвердження. Фізкультхвилинка. Обчислити площу фігури. Площа фігури. Перевірка виконання. Площа.

"Завдання по стереометрії" - Знайдіть квадрат відстані між вершинами. Завдання. Діаметр свинцевої кулі. Об'єм кулі та її частин. Знайдіть кут багатогранника. Знайдіть обсяг піраміди. Знайдіть ординату точки A. Круговий сектор. Знайдіть об'єм V частини циліндра. Знайдіть площу поверхні багатогранника. Знайдіть площу трапеції. Довжина кола.

"Обчислити обсяг тіла обертання" - Сфера. Циліндр та конус. Конус. Циліндри довкола нас. Об'єм V конуса. Куб. Визначення конусу. Види тіл обертання. Куля. Об'єми тіл обертання. Фігура. Знайдіть обсяг. Циліндричний посуд. Визначення циліндра. Радіуси. Циліндр. Об'єм конуса.

«Обсяги та поверхні тіл обертання» - Висунення та перевірка гіпотез. Узагальнити знання. Об'єми та поверхні тіл обертання. Виявити геометричну форму. Формулювання проблеми. Проблема. Приклади із практичної діяльності. Чому резервуар градусника швидше нагрівається? Чайник у формі кулі має найменшу поверхню. Об'єми.

"Тіла обертання навколо нас" - Тіла обертання навколо нас. Промислове встаткування. Знайти тіла обертання. Ялина конусна лісова. Башта падіння в Італії. У космічному просторі. Будинок Мельникова. Конус. Круглі башти. Історія Круглої будівлі. Космічні тіла.

Комбінації багатогранників та круглих тіл

Поняття сфери та кулі.

Сфероюназивається фігура, що складається з безлічі всіх точок простору, відстань від кожної з яких до цієї точки дорівнює даному позитивному числу r. Точка О називається центромсфери, а відрізок, що з'єднує точку з будь-якою точкою сфери, – її радіусом. Усі радіуси сфери мають довжину r. Число r називається радіусом сфери.

Сфера розбиває безліч усіх точок простору, що не належать їй, на дві підмножини: внутрішнюі зовнішнюобласті щодо сфери. Внутрішній області належать ті точки простору, відстань від кожної з яких до центру менша за радіус, а зовнішньої області – ті точки, відстань від кожної з яких до центру більша за радіус.

Кулькоюназивається фігура, що складається з безлічі всіх точок простору, відстань від кожної з яких до даної точки не більше даного позитивного числа r. Точка О називається центромкулі, а число r – його радіусом. Сфера з центром Про радіус r називається поверхнеючи межею кулі. Усі точки кулі, що не належать його поверхні, називаються внутрішніми точками кулі або точками, що лежать усередині кулі. Таким чином, куля є фігура, що складається з об'єднання всіх точок сфери (поверхні кулі) та безлічі всіх внутрішніх точок щодо цієї сфери.

Дотична площина до поверхні кулі називається дотичною площиноюдо кулі. Площина є дотичною до кулі тоді і тільки тоді, коли вона проходить через точку поверхні кулі перпендикулярно радіусу, проведеному в цю точку. Зазначимо також, що через кожну точку поверхні кулі проходить одна і лише одна площина, яка стосується кулі.

Сфера, описана у багатогранника.

Визначення.Сфера називається описаної біля багатогранникаякщо всі вершини багатогранника лежать на сфері.

Теорема 1.Біля будь-якої трикутної піраміди можна описати сферу.

Багато точок, рівновіддалених від вершин основи піраміди є перпендикуляр, проведений з центру описаного кола біля основи (ГМТ у просторі рівновіддалених від вершин даного багатокутника існує, якщо біля цього багатокутника можна описати коло, і є перпендикуляр, проведений до площини цього багатокутника через центр описаного кола ). Центром описаного кола є точка перетину серединних перпендикулярів основи піраміди.

Щоб знайти центр описаної сфери, проведемо площину через точку М – середину бокового ребра AD. Ця площина перетне перпендикуляр (зазначений раніше) у точці S. За побудовою SA = SB = SC, а також з того, що трикутник ASD рівнобедрений (також за побудовою) слідує, що SA = SD. Отже, відстані від усіх вершин піраміди до точки S рівні, і ця відстань дорівнює радіусу описаної сфери біля ABCD піраміди (SA=SB=SC=SD=R).

Приклад 1 . Визначити радіус сфери, описаної у правильного тетраедра.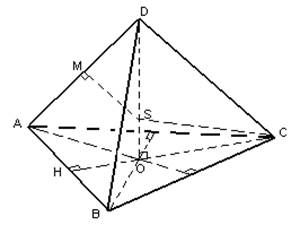

Розглянемо трикутник SOC. Він буде прямокутним з прямим кутом O (за побудовою OD буде висотою піраміди).

, оскільки О – точка перетину медіан.

де DO – висота піраміди.

Тоді за теоремою Піфагора випливає, що або

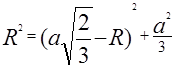
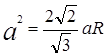
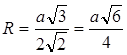
Відповідь: Радіус сфери, описаної у правильного тетраедра дорівнює

Теорема 2. Якщо біля основи піраміди можна описати коло, то біля піраміди можна описати сферу.

Ми вже розглянули окремий випадок. У випадку доводиться аналогічно.

Теорема 3 . При похилій призмі описати сферу не можна; біля прямої призми можна описати сферу, якщо біля підстави призми можна описати коло.

1) Розглянемо спочатку випадок, коли призма похила (як приклад візьмемо трикутну призму). Точка, рівновіддалена від точок А, В і С буде перебувати на прямій OS 1 яка перпендикулярна площині трикутника АВС і основа перпендикуляра знаходиться в точці перетину серединних перпендикулярів, проведених до сторін трикутника АВС.

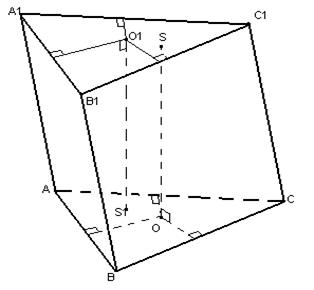
Аналогічно, точки, рівновіддалені від точок А 1 , В 1 , С 1 лежать на перпендикулярі до площини трикутника А 1 В 1 С 1 - О 1 S. Оскільки призма похила, то прямі OS 1 і О 1 S будуть паралельними, але не збігаються. А це означає, що вони не матимуть спільних точок, отже: не знайдеться такої точки, відстань від якої до всіх вершин призми була б однаковою, що аналогічно до неможливості побудови сфери, описаної біля похилої призми.

2) Розглянемо пряму призму, біля основи якої можна описати коло. Точки О і О 1 – центри описаних кіл біля нижньої та верхньої основи відповідно. Так як призма пряма, то пряма ГО 1 буде перпендикуляром до площин основи.

Тоді площина, що проходить через середини бічних ребер, буде паралельна площині основи і перетинатиме ГО 1 у точці S – середині ГО 1 . Тоді відстань від усіх вершин призми до тачки S буде однаковою (за побудовою), отже, S – центр сфери, описаної біля правильної призми.

Отже, ми переконалися, що біля похилої призми описати сферу не можна, а біля прямої призми – можливо, якщо біля її заснування можна описати коло.

Теорема 4. Біля зрізаної піраміди можна описати сферу тоді і тільки тоді, коли біля її основ можна описати кола і пряма, що з'єднує центри цих кіл, перпендикулярна до площин основ.

Перша умова означає, що перпендикуляри, які є ГМТ, рівновіддалених від вершин багатокутників основ будуть існувати, а друга – що вони збігаються, отже, знайдеться така точка, яка буде рівновіддалена від усіх вершин усіченої піраміди.

XV МІСЬКА ВІДКРИТА КОНФЕРЕНЦІЯ УЧНІВ

«ІНТЕЛЕКТУАЛИ XXI СТОЛІТТЯ»

Секція: МАТЕМАТИКА

Описана сфера на олімпіадах та ЄДІ

Кияєва Ганна Анатоліївна

Оренбург – 2008

1.2 Описана сфера

1.2.1 Основні властивості та визначення

1.2.2 Комбінація із пірамідою

1.2.3 Комбінація із призмою

1.2.4 Комбінація із циліндром

1.2.5 Комбінація з конусом

2 Приклади олімпіадних завдань

2.1 Приклади олімпіадних завдань із пірамідою

2.2 Приклади олімпіадних завдань із призмою

2.3 Приклади олімпіадних завдань із циліндром

2.4 Приклади олімпіадних завдань із конусом

3.3 Приклади завдань ЄДІ із циліндром

3.4 Приклади завдань ЄДІ з конусом

Вступ

Ця робота виконується в рамках проекту зі створення математичної сторінки для школярів на сайті ліцею-інтернату та буде розміщена у розділі «Математичні методи».

Цільроботи – створення довідника, присвяченого методу вирішення геометричних завдань із описаною сферою на олімпіадах та ЄДІ.

Для досягнення цієї мети нам необхідно було вирішити такі завдання :

1) ознайомитись із поняттям описаної сфери;

2) вивчити особливості комбінацій описаної сфери з пірамідою, призмою, циліндром та конусом;

3) серед геометричних завдань вибрати ті, що містять умову наявності описаної сфери;

4) проаналізувати, систематизувати та прокласифікувати зібраний матеріал;

5) зробити добірку завдань для самостійного розв'язання;

6) оформити результат дослідження як реферата.

Практична значимість– підготовлені нами матеріали можуть бути використані при підготовці школярів до олімпіад, ЄДІ та подальшого навчання у вузі.

1 Сфера та куля

1.1 Сфера та куля: основні поняття та визначення

Сфероюназивається поверхня, що складається всіх точок простору, розташованих на даній відстані від цієї точки.

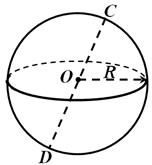
Ця точка називається центром сфери(точка Прона рис. 1), а дана відстань радіусом сфери. Будь-який відрізок, що з'єднує центр і якусь точку сфери, також називається радіусом сфери. Відрізок, що з'єднує дві точки сфери і проходить її центр, називається діаметром сфери(відрізок DCна рис. 1). Зазначимо, що сфера може бути отримана обертанням півкола навколо її діаметра.

Кулькоюназивається тіло, обмежене сферою. Центр, радіус та діаметр сфери називаються також центром , радіусомі діаметром кулі. Очевидно, куля радіусу Rз центром у Промістить усі точки простору, які розташовані від точки Прона відстані, що не перевищує R(включаючи точку Про), і не містить інших точок. Кулькоютакож називають фігуру обертання півкола навколо його діаметра. Кульовий сегмент– частина кулі, що відсікається від нього якоюсь площиною. Будь-який переріз кулі площиною є коло. Центр цього кола є підставою перпендикуляра, опущеного з центру кулі на площину, що сить. Площина, що проходить через центри кулі, називається діаметральною площиною.Перетин кулі діаметральною площиною називається великим колом, а переріз сфери - великим колом. Кульовий сектор -геометричне тіло, яке виходить при обертанні кругового сектора з кутом, меншим 90 про навколо прямий, що містить один з обмежують круговий сектор радіусів. Кульовий сектор складається з кульового сегмента та конуса із загальною основою.

Площа поверхні сфери:

S = 4π R 2 ,

де R- Радіус кулі, S- Площу сфери.

Обсяг сфери

де V- Обсяг кулі

Обсяг кульового сектора

V – об'єм кульового сегмента.

Площа сегментальної поверхні

- Висота сегмента, площа сегментальної поверхні

Радіус основи сегмента

, - Радіус основи сегмента, - висота сегмента, 0<H < 2R .

Площа сферичної поверхні кульового сегмента

- Площа сферичної поверхні кульового сегмента.

У просторі для кулі та площини можливі три випадки:

1) Якщо відстань від центру кулі до площини більша за радіус кулі, то куля і площина не мають спільних точок.

2) Якщо відстань від центру кулі до площини дорівнює радіусу кулі, то площина має з кулею і сферою, що обмежує її, тільки одну загальну точку.

3) Якщо відстань від центру кулі до площини менша за радіус кулі, то перетин кулі з площиною є коло. Центр цього кола є проекцією центру кулі на дану площину. Перетин площини зі сферою є коло зазначеного кола.

1.2 Описана сфера

1.2.1 Визначення та властивості

Сфера називається описаної біля багатогранника(а багатогранник - вписаним у сферу), якщо всі вершини багатогранника лежать у сфері.

З визначення описаної сфери випливають два факти:

1) всі вершини вписаного у сферу багатогранника рівновіддалені від певної точки (від центру описаної сфери);

2) кожна грань вписаного у сферу багатогранника є вписаним у деяке коло багатокутником, саме в те коло, яке виходить у перерізі сфери площиною грані; при цьому основа перпендикулярів, опущених із центру описаної сфери на площині граней, є центрами описаних біля граней кіл.

Теорема 1 . Біля багатогранника можна описати сферу, якщо і тільки якщо виконується будь-яка з умов:

а) біля будь-якої грані багатогранника можна описати коло, і осі кіл, описаних біля граней багатогранника, перетинаються в одній точці;

б) площини, перпендикулярні до ребрів багатогранника і які проходять їх середини, перетинаються у одній точці;

в) існує єдина точка, рівновіддалена від усіх вершин багатогранника.

Доказ.

Необхідність.Нехай у багатогранника описана сфера. Доведемо, що виконується умова а). Дійсно, оскільки площина даної грані багатогранника перетинає сферу по колу, то вершини грані, що належать сфері та площині грані, належать лінії їхнього перетину - колу. Оскільки центр сфери рівновіддалений від усіх вершин цієї грані, він лежить на перпендикулярі до цієї грані, проведеному через центр описаної біля грані кола.

Достатність.Нехай виконується умова а). Доведемо, що біля багатогранника можна описати сферу. Справді, оскільки загальна точка перпендикулярів до граней, проведених через центри описаних біля граней кіл, рівновіддалена від усіх вершин багатогранника, біля багатогранника описується сфера з центром у цій точці.

Умова а) у разі рівносильна умовам б) і в).

Якщо сфера описана біля багатогранника, то: а) основа перпендикуляра, опущеного з центру сфери на будь-яку межу, є центром кола, описаного біля цієї грані (як основа висоти піраміди з рівними бічними ребрами - радіусами сфери, проведеними з її центру на вершини даної грані ); б) центр сфери, описаної біля багатогранника, може перебувати всередині багатогранника, на його поверхні (в центрі описаної біля грані кола, зокрема - у середині деякого ребра), поза багатогранником.

1.2.2 Описана сфера та піраміда

Теорема 2 . Біля піраміди можна описати сферу, якщо й тільки якщо біля її основи можна описати коло.

Доказ.Нехай біля основи піраміди описується коло. Тоді це коло і точка поза площиною цього кола - вершина піраміди - визначають єдину сферу, яка і буде описана біля піраміди. І назад. Якщо у піраміди описана сфера, то переріз сфери площиною основи піраміди є коло, описане біля основи.

Наслідок 1.Біля будь-якого тетраедра можна описати сферу.

Наслідок 2.Біля будь-якої правильної піраміди можна описати сферу, центр якої лежить на висоті або її продовженні.

Центр сфери, описаної біля піраміди, може бути:

· З вершиною піраміди по одну сторону від площини її основи - всередині піраміди, в площині бічної грані (в центрі описаної біля цієї грані кола), поза пірамідою;

· У площині основи - в центрі описаної біля основи кола;

· З вершиною піраміди по різні боки від площини її основи.

Теорема 3 . Якщо бічні ребра піраміди рівнонахилені до поверхні її основи, то біля піраміди можна описати сферу.

Доказ.Оскільки бічні ребра рівнонахилені до площини основи піраміди, то біля основи піраміди можна описати коло, а тоді піраміди можна описати сферу.

Цю теорему можна сформулювати інакше: якщо піраміда має рівні бічні ребра, біля піраміди можна описати сферу.

Зворотна теорема не вірна

Теорема 4. Якщо близько піраміди описана куля, його центр є точкою перетинів всіх площин, проведених через середини ребер піраміди перпендикулярно до цих ребрів.

Доказ.Насправді, будь-яка точка, рівновіддалена від двох вершин піраміди, що прилягають до одного ребра, лежить у площині, проведеній перпендикулярно до цього ребра піраміди через його середину. Тому центр описаної кулі, будучи рівновіддаленим від усіх вершин піраміди, повинен перебувати у кожній з таких площин, тобто. він є точкою перетину всіх цих площин. При виконанні креслення школярі часто поміщають центр описаної кулі навмання, не уявивши досить цієї просторової конфігурації і тим більше не проводячи жодних міркувань про становище цього центру. У цьому, зазвичай, центр ставиться всередині піраміди. Тим часом центр описаної кулі може лежати і всередині, і назовні, і на поверхні піраміди (залежно від конкретного виду піраміди).

Теорема 5 . Біля зрізаної піраміди можна описати сферу, якщо і тільки якщо виконується будь-яка з умов:

a) біля основ піраміди описуються кола, лінія центрів яких перпендикулярна їх площин;

b) всі бічні ребра піраміди рівнонахилені до площини однієї з основ;

c) всі бічні ребра піраміди рівні між собою;

d) всі бічні грані піраміди – рівнобічні трапеції.

Доказ.Нехай біля основ цієї усіченої піраміди можна описати кола, і площини цих кіл перпендикулярні лінії їх центрів. Тоді, як відомо, такі два кола визначають єдину сферу, яка і буде описана біля даної піраміди.

Нехай, навпаки, у цієї зрізаної піраміди описана світ. Тоді перерізи сфери площинами основ піраміди будуть кола, описані біля основ. Далі. Пряма, перпендикулярна площин основ піраміди і проходить через центр сфери, пройде через центри кіл, описаних біля основ.

Умова a) рівносильно умовам b), c), d).

Слідство.Біля будь-якої правильної усіченої піраміди можна описати сферу.

1.2.3 Описана сфера та призма

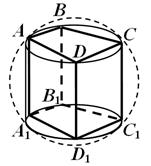
Теорема 6. Біля призми можна описати сферу, якщо тільки якщо призма пряма і біля її заснування можна описати коло.

Доказ.

Необхідність.Якщо призма вписана у сферу, то кожна її грань вписана в коло – перетин сфери площиною цієї грані. Значить, біля основи призми можна описати коло, і всі бічні грані призми як паралелограми, вписані в колі, - прямокутники і тому пряма призма.

Достатність.Нехай призма пряма і біля її основи описується коло. Тоді кола, описані біля підстав призми, площини яких перпендикулярні до лінії їх центрів, визначають єдину сферу, яка і буде описаною біля призми.

Наслідки:

а) при будь-якій правильній призмі можна описати сферу;

б) біля будь-якої прямої трикутної призми можна описати сферу;

в) біля будь-якого прямокутного паралелепіпеда можна описати сферу;

Центр описаної біля призми сфери рівновіддалений від площин підстав призми і може знаходитися всередині призми, на її бічній грані (в центрі описаної біля грані кола), поза призмою.

1.2.4 Описана сфера та циліндр

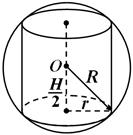
Сфера називається описаної біля циліндра, якщо на ній лежать кола основ циліндра (рис. 4). Біля циліндра можна описати сферу.

1.2.5 Описана сфера та конус

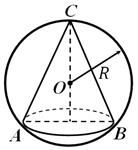
Сфера називається описаної біля конуса, якщо на ній лежать вершина та коло основи конуса (рис. 5). Біля конуса завжди можна описати сферу; її радіус дорівнює радіусу кола, описаного біля осьового перерізу конуса. Усічений конус називається вписаниму кулю, якщо її основи є перерізами поверхні кулі.

2 Приклади олімпіадних завдань

2.1 Приклади олімпіадних завдань із пірамідою

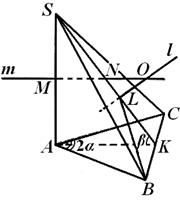
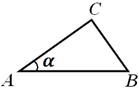
приклад 1. У трикутній піраміді S АВС ребро ВС дорівнює а, АВ = АС, ребро S А перпендикулярно до основи АВС піраміди, двогранний кут при ребрі S А дорівнює 2α , а при ребрі ВС дорівнює β (рис. 6) . Знайти радіус описаної кулі.

Рішення.Розглянемо піраміду S АВС,про яку йдеться за умови завдання. Оскільки ребро SAперпендикулярно до площини основи, то

ВА S = CAS= 90 °, а тому кут ВАСякраз і є лінійним кутом двогранного кута при ребрі SA. Таким чином, в основі піраміди лежить рівнобедрений трикутник з кутом 2 α при вершині, а висота піраміди збігається з рубом S А.

Оскільки проекції бічних ребер SBі S Зна площину основи рівні, і самі ці ребра рівні. Тому грань У S З- рівнобедрений трикутник, та його висота, опущена з вершини S, потрапляє до середини Доребра НД.За теоремою про три перпендикуляри АК- Висота трикутника ВАС.Звідси зрозуміло, що кут S КА- Лінійний кут двогранного кута при ребрі НД,тобто.

S КА = β .

Центр описаної кулі лежить на перетині прямої l, перпендикулярної до площини У S Зі проходить через центр кола, описаного біля трикутника У S З,з площиною, що проходить через середину ребра А Sперпендикулярно до нього. Пряма lлежить у площині А S До:насправді, площина У S Зпроходить через пряму НД,перпендикулярну до площини А S До, Т. е. площині У S Зі А S Доперпендикулярні; водночас пряма lперпендикулярна до площини У S Зі проходить через лінію перетину цих площин, так що вона лежить у площині А S До .

Отже, центр кулі лежить у площині А S До. Винесемо цю площину на спеціальне креслення. Центр кулі Пробуде тоді лежати на перетині прямої lі прямий m, перпендикулярної до А Sі проходить через його середину. Але, взагалі кажучи, можуть з'явитися три можливості: прямі lі тперетинаються всередині, або поза трикутником А S Доабо на його боці, і нам доведеться розглянути всі ці можливості (див. мал. 7, 8, 9). Нижче під час викладок ми покажемо, що дві з них насправді не здійснюються. Нас цікавить радіус Rописаного кулі, тобто. відстань від точки Про- точки перетину перпендикулярів ті lдо сторон кута До S А- До точки S, вершини цього кута. Насамперед знайдемо SL- Проекцію шуканої відстані на бік SKтрикутника KAS. Бо у трикутнику АК B(Мал. 6) нам відомий катет ВК=

ата кут КАВ = α,то АК= а ctg α .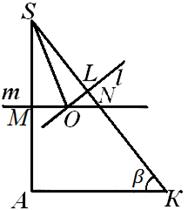

SK =

Оскільки L- центр описаної біля трикутника У S Зкола, то LS = L В,а тому з трикутника ВК Lзнаходимо, що ( S К- SL ) 2 +КВ 2 =В L 2 , тобто.

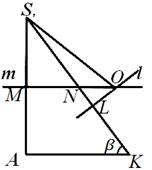
Зазначивши, що проведені обчислення відрізка SLніяк не залежали від розташування центру Проописаної кулі, повернемося до рис. 7, 8, 9. Позначимо через Nточку перетину прямий mзі стороною S До.Зрозуміло, що прямі lі тперетинаються позатрикутника КА S , якщо SN <SL(Рис. 8); якщо ж S N > SL , то крапка Пролежить усередині цього трикутника (рис. 7); нарешті, якщо SN = SL , то крапка Пролежить на боці S Доцього трикутника (рис. 9). З'ясуємо, яке із цих положень має місце насправді.

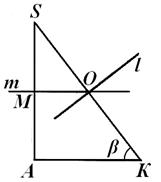
Оскільки МN КА S , то SN =

S До. Порівнюючи довжини відрізків SNі SL, легко доведемо, що за будь-яких а, αі

(З геометричних міркувань випливає, що а> 0, 0°<

< 90° та 0°< β < 90°). Следовательно, каковы бы ни были размеры а , α і β піраміди S АВС,центр Проописаної кулі завжди лежить поза пірамідою. Це своє чергу означає, що винесена нами пласка конфігурація у площині КА Sможе мати вигляд, зазначений на рис 8; розташування, зображені на рис. 7 та 9, насправді мати місця не можуть. Розглядаючи рис. 8, легко покажемо, що = β , а тому LO = NL tg β = (SL -S N) tg β. Підставляючи сюди отримані вище вирази для SLі S N, отримуємо після очевидних обчислень:

L О =

а tg α sin β .

Нарешті, із прямокутного трикутника Про LSзнаходимо

= .

Як бачимо, викладки в задачі виявилися простими - головна складність рішення лежить у міркуваннях, що встановлюють положення центру описаної кулі.

Відповідь: R =

приклад 2. У шар радіуса R вписано правильну трикутну піраміду з плоским кутом  при вершині. Знайти об'єм піраміди, а також бічну поверхню конуса, описаного біля зазначеної піраміди .

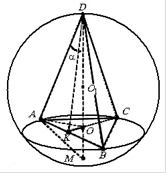
Рішення.Нехай сторона основи піраміди дорівнює a, радіус основи конуса, описаного у цієї піраміди дорівнює rтоді

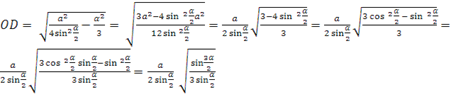(Рис. 10). Грані піраміди – рівнобедрені трикутники. Тоді DK– висота, медіана та бісектриса  ABD. З прямокутного трикутника ADKмаємо. Висоту піраміди знайдемо із прямокутного трикутника AOD : ,

DM- Діаметр кулі. Тоді в перерізі кулі, що проходить через діаметр DMі точку А, Отримаємо прямокутний трикутник AMD. З метричних співвідношень у прямокутному трикутнику маємо

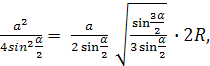звідки

Тоді площу основи знайдемо за формулою:

І з формули

знаходимо обсяг піраміди: .

Ребро ADза визначенням описаного конуса є його твірною. Тоді знайдемо бічну поверхню описаного конуса за формулою Sбік =  r l :

Відповідь:

;

приклад 3. В основі піраміди лежить квадрат зі стороною а. Висота піраміди проходить через середину одного з ребер основи і дорівнює

. Знайти радіус сфери, описаної біля піраміди.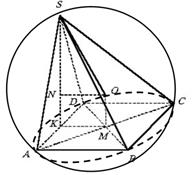

Рішення.Типовою помилкою при вирішенні цього завдання є твердження про те, що центр описаної сфери знаходиться на межі SBC(Рис. 11). Насправді положення точки Проне пов'язано з гранню SBC.

З огляду на рівновіддаленість точки Провід вершин S, A, B, C, Dслід, що OABCD- Правильна чотирикутна піраміда. Отже, на межу ABCDкрапка Пропроектується в крапку М– точку перетину діагоналей. Трикутник ASDрівнобедрений, тоді висота піраміди SKє медіаною трикутника ASD ,

. З прямокутного трикутника SAKзнайдемо SA :

Отже, трикутник SAD– рівносторонній та OASD- Правильна трикутна піраміда. Тоді точка Пропроектується на межу SADу центр трикутника SAD. Звідси

З трикутника SONзнаходимо шуканий радіус SO,

Відповідь:

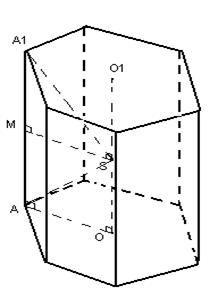
приклад 4. У кулю радіусу R вписана правильна шестикутна усічена піраміда, у якої площина нижньої основи проходить через центр кулі, а бічне ребро складає з площиною основи кут 60

. Визначити об'єм піраміди.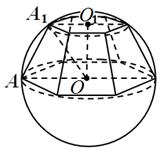

Рішення.За умовою,

OAA 1 = 60 (рис. 12); значить, Про 1 ОА 1 = 30 і А 1 Про 1 = А 1 О = ,OO 1 = .

Sнижн.осн. = 6

, Sверхн. осн. = нижня. осн. .

Остаточно отримаємо

Відповідь:

2.2 Приклади олімпіадних завдань із призмою

приклад 1. У кулю, обсяг якої дорівнює V , вписано пряму трикутну призму. Підставою призми є прямокутний трикутник з гострим кутом

а найбільша її бічна грань є квадрат. Знайти обсяг призми.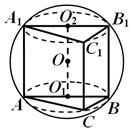

Рішення.Спочатку визначимо положення центру кулі щодо призми. Перетин кулі площинами основ призми - кола, в які вписані ці основи (рис. 13), а оскільки основи призми рівні, то рівні і однаково віддалені від центру кулі кола перерізів. Кожен із центрів Про 1 та Про 2 збігається із серединою відповідної гіпотенузи.

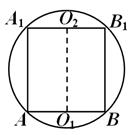
З властивостей перерізів кулі площиною відомо, що перпендикуляр, проведений із центру кулі Продоплощини кола перерізу, проходить через центр цього кола. Отже, Про 1 Про

площині АВС.Пряма Про 1 Пропроходить також через O 2 і перпендикулярна площині Таким чином, центр кулі лежить на межі в середині відрізка O 1 O. Усі бічні грані призми - прямокутники, причому грань - найбільша з них (бо АВ -гіпотенуза трикутника A НД). Ця грань за умовою – квадрат. Перетин кулі площиною грані - велике коло кулі, тому радіус кола, зображеного на рис. 14, дорівнює радіусу кулі R . Зауважимо, що висота призми АА 1 = a 4 = . Тепер залишається знайти площу основи:

S А B З =

. З (рис. 15)

маємо АС = АВ

, значить,

S А B З =

Тепер отримуємо:

Vприз.

За умовою,

R 3 = V ,

звідки R 3 =

,Отже,

Vприз.

Відповідь: Vприз.

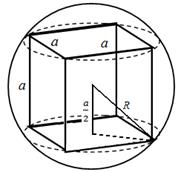
приклад 2. Знайти відношення поверхні та об'єму кулі відповідно до поверхні та об'єму вписаного куба

Рішення.Нехай радіус кулі дорівнює R , ребро куба одно а;

тоді R 2 -

, звідки а= .

Позначимо об'єми та поверхні кулі та куба відповідно через V 1 , V 2 , і S 1 , S 2 .

, V 2 = = , S 1 =4, S 2 = 6а 2 =8R 2 , V 2 = , S 1 S 2 = .

Відповідь: V 1

V 2 = , S 1 S 2 = .

2.3 Приклади олімпіадних завдань із циліндром

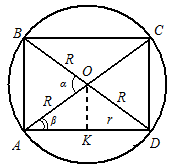
приклад. Знайдіть відношення об'єму кулі до об'єму прямого кругового циліндра, вписаного в цю кулю, якщо відомо, що менший кут між діагоналями осьового перерізу циліндра дорівнює

і діаметр основи більший за висоту циліндра (рис. 18).

Рішення.Об'єм кулі нам відомий

, а об'єм циліндра знайдемо за формулою , але тому

Нехай ABCD- осьовий переріз циліндра (див. рис. 18). Так як діаметр основи, більше висоти циліндра, то

- Кут АОВ.З трикутника АВОслід, що висота циліндра

Радіус основи циліндра

. .

Виходить, що

Підставимо знайдені дані у формулу об'єму циліндра:

;

Таким чином,

Знайдемо відношення

Відповідь:

2.4 Приклади олімпіадних завдань з конусом

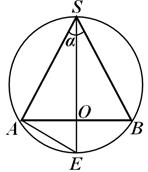
приклад 1. У кулю радіусу R вписаний круговий конус; кут між утворюючими конуса в осьовому перерізі дорівнює α. Знайти висоту, що утворює і радіус основи конуса.

Рішення.Перетин кулі, що проходить через вісь конуса, - це велике коло кулі, в яку вписано

АВ S(рис. 19), де A У- Діаметр основи конуса. Продовжимо висоту (вісь) конуса SOдо перетину з колом великого кола в точці Еі розглянемо Е S А:

у цьому трикутнику

SE = 2R ,

S АЕ = 90° і А S Е= .

А S = 2R

Тепер із

А OSзнаходимо

A Про = r = 2R

, SO = h= 2R

Відповідь : SO= 2R

А S = 2R , A Про =.

приклад 2. Відношенню висоти конуса до радіусу описаної навколо нього кулі дорівнює k . Знайти відношення обсягів цих тіл. З'ясувати за яких k завдання має сенс.

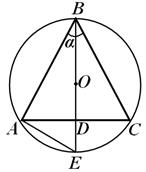
Рішення.Розглянемо осьовий перетин конуса (рис. 20). Нехай h- Висота конуса, R- Радіус кулі, описаної біля конуса. Тоді, за умовою,

=k, тобто. h = kR .

Виразимо радіус rпідстави конуса через R; розглянувши хорди АСі ВЕ,отримаємо:

У D

D Е = А D D З(Т.к. AD=DC ,
- Прямокутний, AD – висота опущеного з вершини прямого кута).

(отже, k < 2).

Vш =

; Vдо ==

Таким чином,

, (при 0< k < 2).

Відповідь:

, (при 0< k < 2).

приклад 3. У зрізаному конусі радіуси нижньої та верхньої основ рівні відповідно r 1 і r 2 а утворююча конуса нахилена до площини нижньої основи під кутом α (рис. 21). Знайти радіус кулі, в яку вписаний цей усічений конус.

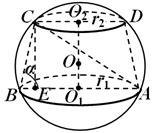
Рішення.У перерізі кулі, що проходить через вісь усіченого конуса, виходить велике коло кулі, в яку вписана трапеція АВС D. Розглянемо

A НД,який також вписаний у велике коло кулі. У цьому трикутнику відомий кут З BA = α . В силу теореми синусів, АС = 2R. Таким чином, для визначення Rдостатньо знайти АС.Опустимо з точки Зперпендикуляр РЄна АВ.Очевидно,

АЕ= r 1 + r 2 ,ВЕ = r 1 - r 2, а РЄ = ( r 1 - r 2 )

Тому з теореми Піфагора

= = =, звідки R =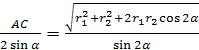

Відповідь: R

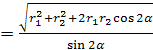3 Приклади завдань ЄДІ

3.1 Приклади завдань ЄДІ із пірамідою

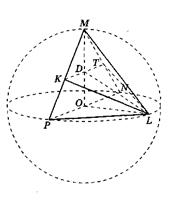
приклад 1. Відрізок Р N , рівний 8 - діаметр сфери. Точки М, L лежать у сфері отже обсяг піраміди Р N М L найбільший (рис. 22). Знайдіть площу трикутника К L Т, де К і Т - середини ребер РМ та N М відповідно.

Рішення.Нехай Про- центр сфери, а R- її радіус. Оскільки Р N = 2R= 8 та точки Мі Lлежать на сфері, то ОР = О L = Про N = ЗМ = R = 4. Перетин сфери площинами Р LNі РМ N- Кола радіусу R = 4,описані біля трикутників Р LNі РМ N , причому

РМ N = Р LN= 90°, як вписані кути, що спираються на діаметр Р N .

Нехай Н- Висота піраміди, опущена з вершини М, а h- Висота трикутника Р LN , проведена до сторони Р N . Оскільки точка Млежить на сфері, а площина Р LNмістить центр сфери, то Н

R , причому Н = R , якщо МО Р NL . Аналогічно, оскільки точка Lлежить на сфері, то h R , причому h = R , якщо L Про Р N .

Звідси для обсягу піраміди Р N М Lмаємо

, .

Таким чином, піраміда Р N М Lмає найбільший обсяг, якщо трикутники Р LNі РМ Nпрямокутні, рівнобедрені із загальною гіпотенузою Р N, що лежать у взаємно перпендикулярних площинах Оскільки трикутники L Про N , L ОР, L ОМ, РОМ, N ОМрівні по двох катетах, то трикутники L М Nі L МРправильні зі стороною

NL =Р L = ON

Звідси випливає, що медіани L Доі L Тцих трикутників рівні, причому

L До =

= 2.

Трикутник До L Трівнобедрений, та його висота LDє медіаною прямокутного рівнобедреного трикутника L ЗМ.Звідси

LD =

= 2.

КТ- Середня лінія трикутника РМ Nі тому КТ = 0,5Р N =R . Отже, площа S До L Т =

КТ LD = 4.

Відповідь: 4

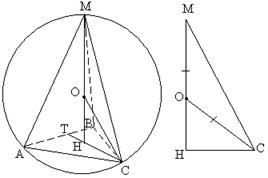
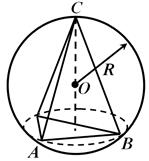
приклад 2. У правильній трикутній піраміді сторона основи дорівнює 5, а бічні ребра нахилені до основи під кутом 60о. Знайдіть радіус, описаний навколо піраміди сфери.

Рішення.Нехай АВСМвказана піраміда (див. рис. 23) Центр описаної сфери лежить на висоті піраміди, тому що піраміда правильна.

Основа висоти піраміди – центр трикутника АВС, Т. е. Точка перетину медіан. Тоді:

СТ =

СН= = = .

Тепер розглянемо трикутник МНС.Тут кут МСПдорівнює 60 про, як кут між бічним ребром МСта основою АВС. Кут НМСрівний30

. МО = ОСяк радіуси. Отже, трикутник МОСрівнобедрений. Як відомо, в рівнобедреному трикутнику кути при основі рівні. Отже, ОСМ = ЗМС = 30, ОСН = МСП - МСО = 60 - 30= 30.

З прямокутного трикутника ОСНвизначимо гіпотенузу ОС, використовуючи зв'язок тригонометричних функцій у прямокутному трикутнику:

Відповідь: OC =

3.2 Приклади завдань ЄДІ із призмою

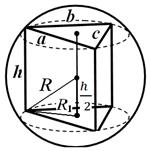
приклад 1. Підставою призми є трикутник зі сторонами a , b , c . Висота призми h (Рис 25). Знайти радіус описаної галузі.

Рішення.Оскільки біля призми описана сфера, то призма пряма та її бічне ребро дорівнює висоті. Радіус кола, описаного біля основи призми, обчислюється за формулою

Відповідь:

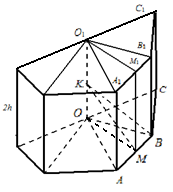
приклад 2. Радіус кулі R . У кулю вписана правильна п-вугільна призма, висота якої 2 h (Рис 26). Знайти бік заснування призми.

Рішення.Нехай До- Центр описаної кулі. Маємо: KB = R , OK = h. Нехай ОМ

АВтоді

OB =

(з трикутника OKB).

З трикутника OMBзнаходимо

a = 2MB = 2OB

Отже, a =

Відповідь: a =

3.3 Приклади завдань ЄДІ із циліндром

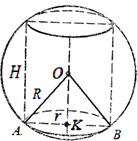
приклад 1. Висота кругового циліндра на 10 більша за радіус основи, а площа повної поверхні дорівнює 144

. Знайдіть радіус описаної галузі.

Рішення.Радіус описаної сфери

(Рис. 27).

Площа поверхні циліндра

, 144,

спростимо цей вислів:

Отримаємо квадратне рівняння

Знайдемо коріння цього рівняння

, не підходить, оскільки він негативний. Висота

Знайдемо радіус описаної сфери:

Відповідь:

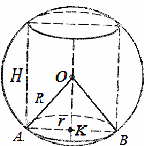
приклад 2. У кулю вписано прямий круговий циліндр (рис. 28). У скільки разів об'єм кулі більший за об'єм циліндра, якщо відомо, що відношення радіуса кулі до радіуса основи циліндра вдвічі менше, ніж відношення поверхні кулі до бічної поверхні циліндра.

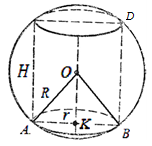
Рішення.Відношення об'єму кулі до об'єму вписаного циліндра

За умовою відомо, що

; –

рівносторонній

Знайдемо відношення об'ємів кулі та вписаного циліндра

Відповідь: 16:9.

3.4 Приклади завдань ЄДІ з конусом

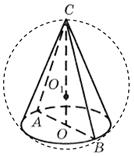
приклад 1. Діаметр основи конуса дорівнює 6 м, що утворює нахилену до площини основи під кутом 60° (рис. 29). Знайдіть площу описаної біля конуса сфери.

САВдорівнює куту між утворюючим конусом і площею його основи. Тому САВ = 60° та рівнобедрений трикутник АВС -правильний. Звідси випливає, що

СА = АВ = ВС= 6м.

Знайдемо положення центру сфери, що описана біля конуса. За визначенням такої сфери, коло основи конуса - перетин описаної сфери та вершина конуса лежить на цій сфері. За якістю діаметра сфери, що проходить через центр будь-якого її перерізу, пряма СОперпендикулярна площині основи конуса і тому центр Про 1 описаної сфери лежить на прямій СО.Звідси випливає, що центр Про 1 сфери, описаної біля конуса, є центр кола, описаної біля його осьового перерізу.

У правильному трикутнику

АВС R = O 1 C =

(м)

Знайдемо площу сфери:

(М2).

Відповідь: 48

м2.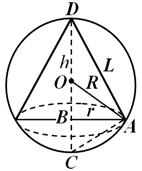

приклад 2. У кулю радіусу R = 6 см вписаний конус заввишки h (Рис. 30). Виразити об'єм та бічну поверхню конуса як функції аргументу h .

Рішення.Маємо:

де r - радіус основи, L- Утворює конуса.

враховуючи, що r = ВА –висота, опущена з вершини прямого кута на гіпотенузу, маємо: і . Або r 2 та

, .

Тепер отримуємо:

, .

Відповідь:

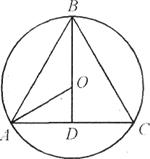
приклад 3. У кулю вписано конус, що утворює якого дорівнює діаметру основи (рис 31). Знайти відношення поверхні конуса до поверхні кулі.

Рішення.Зобразимо осьовий переріз конуса, який пройде крізь центр кулі. Так як діаметр основи конуса дорівнює твірній, то в перерізі отримаємо правильний трикутник, вписаний в коло (рис. 31). Нехай радіус кулі дорівнює R : тоді

АВ =R

, А D =

Позначимо повну поверхню конуса через S 1 , а поверхня кулі через S 2 . Маємо

звідки S 1: S 2 = 9:16.

Відповідь: S 1: S 2 = 9:16.

Висновок

У процесі дослідження ми з'ясували, що завдання з описаною сферою досить часто пропонуються школярам на ЄДІ, тому вміння розв'язувати задачі даного типу відіграє важливу роль у успішному складанні іспитів. Також завдання з описаною сферою часто зустрічаються на олімпіадах з математики різного рівня. Відповідні приклади наведено у нашій роботі. На цьому етапі ми обмежилися розглядом завдань на комбінацію описаної сфери з пірамідою, призмою, циліндром, конусом. Підібрано завдання для самостійної роботи. У процесі виконання роботи нами були використані такі методи: робота з науковою та науково-популярною літературою, збирання інформації в мережі Internet, аналіз, систематизація, класифікація та обробка на комп'ютері. На даний момент результати представлені у вигляді реферату. Надалі планується доповнити роботу новими завданнями.

Список литературы

1. Абрамович М.І., Стародубцев М.Т. Математика (геометрія та тригонометричні функції). Навчальний посібник для підготовчих відділень вузів - М.: Вища школа, 1976. - 304 с.

2. Войтович Ф.С. Комбінації геометричних тіл: (вписані та описані кулі): Книга для учнів. - Мінськ: Народна освіта, 1992. - 160 с.

3. Говоров В.М., Дибов П.Т., Мирошин Н.В. та ін. Список конкурсних завдань з математики (з методичними вказівками та рішеннями): навчальний посібник. - Друге видання - М: Наука, 1986. - 384 с.

4. Денищева Л.О., Безрукова Г.К., Бойченко О.М. та ін Єдиний державний іспит, математика, контрольні вимірювальні матеріали - М: Просвітництво 2005. - 80 с.

5. Денищева Л.О., Глазков Ю.А., Краснянська К.А. та ін Єдиний державний іспит. Математика. Навчально-тренувальні матеріали для підготовки учнів/ФІПД – М: Інтелект-Центр, 2008. – 240 с.

6. Дорофєєв Г.В., Потапов К.М., Розов Н.Х. Допомога з математики для вступників до вузів - М: Наука 1972. - 528 с.

7. Єгерєв В.К., Зайцев В.В., Кордемський Б.А. та ін. 2500 завдань з математики з рішеннями для вступників до вузів: - М: ТОВ «Видавничий дім «ОНІКС 21 століття»: ТОВ «Видавництво «Світ та Освіта», 2002. - 912 с.

8. Звавіч Л.І., Рязановський А.Р. Геометрія у таблицях - М: Дрофа 2007. - 128 с.

9. Клімін С.В., Стрункіна Т.В., Пантелєєва Є.І. та ін Єдиний державний іспит, тестові завдання - М: Просвітництво 2002. - 24 с.

10. Моденов В.П., Дорофєєв Г.В., Новосьолов С.І. та ін Посібник з математики - М: Видавництво Московського університету, 1972. - 404 с.

11. Шувалова Е.З., Каплун В.І. Геометрія: навчальний посібник для підготовчих відділень вузів - М.: Вища школа, 1980. - 265 с.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ua.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

Програма. Завдання для самостійного вирішення

1. У піраміді FABCграні ABFі ABCперпендикулярні, BF :FA = 15:11. Тангенс кута між прямою BCта площиною ABFдорівнює 5. Крапка Мобрана на ребрі BCтак, що B М :М C = 4:11. Крапка Тлежить на прямій FAі рівновіддалена від точок Мі Ст.Центр сфери, описаної біля піраміди FABC , лежить на ребрі AB, площа цієї сфери дорівнює 36

. Знайдіть обсяг піраміди АСМТ. (Відповідь: 6)

2. Підставою піраміди FABCDє прямокутник ABCD . Площина AFCперпендикулярно до площини ABC , тангенс кута FACдорівнює

, тангенс кута між прямою BCта площиною AFCдорівнює. Крапка Млежить на ребрі BC , ВМ =BC . Крапка Lлежить на прямій FAі рівновіддалена від точок Мі C . Об'єм піраміди L У D Мдорівнює 72. Центр сфери, описаної біля піраміди FABCD , лежить на поверхні її основи. Знайдіть радіус цієї галузі. (Відповідь: 5)

3. Біля правильної піраміди FABCописана сфера, центр якої лежить у площині основи ABCпіраміди. Крапка Млежить на ребрі ABтак, що A М :М B=1:3. Крапка Тлежить на прямій FAі рівновіддалена від точки Мі У. Об'єм піраміди ТВСМдорівнює

. Знайдіть радіус сфери, описаної біля піраміди FABC . (Відповідь: )

4. Відрізок AB- Діаметр сфери. Крапки З, D ABCDнайбільший. Знайдіть косинус кута між прямими СМі АВ,якщо М- середина ребра BD . (Відповідь:

)

5. Відрізок Р N , рівний 8, - Діаметр сфери. Крапка М, Lлежать на сфері так, що обсяг піраміди Р N М Lнайбільший. Знайдіть площу трикутника KLT , де Kі T – середини ребер РМі N Мвідповідно. (Відповідь: 4

)

6. Дана сфера радіусу 6. Перерізом сфери площиною є коло з діаметром КТ. Площина перерізу віддалена від центру сфери на відстань 5. Точка Робрана на сфері, а точка L РК L Тнайбільший. Знайдіть кут між прямою LMта площиною PTK , якщо Мсередина ребра РК. (Відповідь: 30

)

7. Через центр Про Fобрана на сфері, а точки A , B , C , D – FABCDнайбільший. Крапки М, Т, L – середини ребер FB , CDі ADвідповідно. Площа трикутника MLTдорівнює 64

. Знайдіть радіус сфери. (Відповідь: 2)

8. Через центр Проданої сфери проведено переріз. Крапка Fобрана на сфері, а точки A , B , C , D – послідовно на колі перерізу так, що обсяг піраміди FABCDнайбільший. Знайдіть синус кута між прямою АМта площиною BFD . (Відповідь:

)

9. Дана сфера радіусом 10. Перерізом цієї сфери площиною є коло з діаметром АВ.Площина перерізу віддалена від центру сфери на відстань 8. Точка Dобрана на сфері, а точка З– на колі перерізу так, що об'єм піраміди АВС Dнайбільший. Знайдіть площу грані ACD .(Відповідь: 27

)

10. Підставою піраміди є прямокутник. Площина перпендикулярна до площини АВС, тангенс кута між прямою НДта площиною FACдорівнює 2. Крапка Млежить на ребрі НДі МВ =

Крапка Lлежить на прямій FAі рівновіддалена від точок Мі З. Центр сфери, описаної біля піраміди FA У CD, лежить у площині основи піраміди, радіус цієї сфери дорівнює 4. Знайдіть об'єм піраміди LA МС. (Відповідь: 48)

11. У кулю, радіусом 2

АВСА 1 У 1 З 1 . Пряма АС 1 Утворює з площиною АВВ (Відповідь: 288)

12. У кулю вписано правильну трикутну призму АВСА 1 У 1 З 1 об'єм якої дорівнює 4,5. Пряма ВА 1 утворює з площиною ВСС 1 кут45

. Знайдіть площу поверхні кулі. (Відповідь: 11)

13. У кулю радіусом

вписано правильну трикутну призму АВСА 1 У 1 З 1 . Пряма АВ 1 утворює з площиною АСВ 1 кут 45. Знайдіть обсяг призми. (Відповідь: 36)

14. Обчислити ребра правильної трикутної призми, знаючи радіус Rописаної кулі та кут нахилу α радіуса цієї кулі, проведеної у вершину призми, до бічної грані, що містить цю вершину. (Відповідь: 2

)

15. У кулю радіусу Rвписано прямий круговий конус. Знайти бічну поверхню конуса, якщо його висота дорівнює h . (Відповідь:

)

16. У кулю вписано конус. Площа осьового перерізу конуса дорівнює S. Кут між його висотою і твірною дорівнює α . Знайдіть об'єм кулі. (Відповідь:

)

17. Визначте бічну поверхню конуса, знаючи довжину радіусу Rописаної навколо нього кулі та кут α, під яким з центру кулі видно конуса, що утворює. (Відповідь:

)

18. Знайдіть відношення площі повної поверхні прямого конуса, вписаного в кулю, до площі поверхні цієї кулі, якщо кут при вершині осьового перерізу конуса дорівнює α і

. (Відповідь:

)

19. У кулю вписано конус так, що його висота ділиться центром кулі в середньому та крайньому відношенні. Знайти кут при вершині осьового перерізу конуса. Визначити, у скільки разів об'єм кулі більший за об'єм конуса. (Відповідь:

; у 4 рази )

приклад 2.У правильній трикутній піраміді сторона основи дорівнює 5, а бічні ребра нахилені до основи під кутом 60о. Знайдіть радіус, описаний навколо піраміди сфери.

Основа висоти піраміди – центр трикутника АВС, Т. е. Точка перетину медіан. Тоді:

СН= СТ = СН= = = .

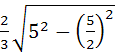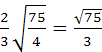Тепер розглянемо трикутник МНС.Тут кут МСПдорівнює 60 про, як кут між бічним ребром МСта основою АВС. Кут НМСдорівнює 30. МО = ОСяк радіуси. Отже, трикутник МОСрівнобедрений. Як відомо, в рівнобедреному трикутнику кути при основі рівні. Отже,

ОСМ = ЗМС = 30, ОСН = МСП - МСО = 60 - 30= 30.

ОС= = .

Відповідь: OC= .

3.2 Приклади завдань ЄДІ із призмою

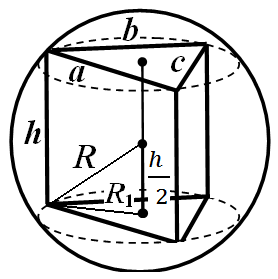
приклад 1.Підставою призми є трикутник зі сторонамиa, b, c. Висота призмиh(Рис 25). Знайти радіус описаної галузі.

Відповідь:

приклад 2.Радіус куліR. У кулю вписана правильна п-вугільна призма, висота якої 2h(Рис 26). Знайти бік заснування призми.

Рішення.Нехай До- Центр описаної кулі. Маємо: KB= R, OK= h. Нехай ОМАВтоді

OB=

(з трикутника OKB).

З трикутника OMBзнаходимо

a= 2MB= 2OB.

Отже, a= .

Відповідь: a= .

3.3 Приклади завдань ЄДІ із циліндром

приклад 1.Висота кругового циліндра на 10 більша за радіус основи, а площа повної поверхні дорівнює 144. Знайдіть радіус описаної галузі.

Рішення.Радіус описаної сфери

Площа поверхні циліндра

спростимо цей вислів:

Отримаємо квадратне рівняння

Знайдемо коріння цього рівняння

Корінь не підходить, тому що він негативний. Висота

Знайдемо радіус описаної сфери:

Відповідь: .

приклад 2.У кулю вписано прямий круговий циліндр (рис. 28). У скільки разів об'єм кулі більший за об'єм циліндра, якщо відомо, що відношення радіуса кулі до радіуса основи циліндра вдвічі менше, ніж відношення поверхні кулі до бічної поверхні циліндра.

Рішення.Відношення об'єму кулі до об'єму вписаного циліндра

За умовою відомо, що

рівносторонній

Знайдемо відношення об'ємів кулі та вписаного циліндра

Відповідь: 16:9.

3.4 Приклади завдань ЄДІ з конусом

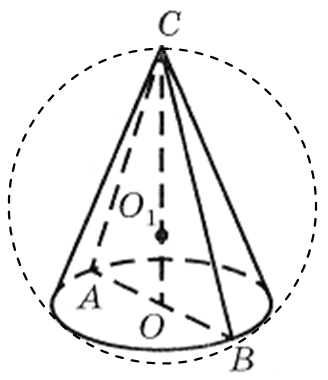
приклад 1.Діаметр основи конуса дорівнює 6 м, що утворює нахилену до площини основи під кутом 60° (рис. 29). Знайдіть площу описаної біля конуса сфери.

Рішення.Нехай З -вершина конуса, Про -центр його заснування, АСВ -осьовий переріз конуса. Оскільки утворююча конуса нахилена до площини основи під кутом 60° СО- Висота конуса, то пряма АВ -проекція пряма САна площину основи конуса. Отже, САВдорівнює куту між утворюючим конусом і площею його основи. Тому САВ = 60° та рівнобедрений трикутник АВС -правильний. Звідси випливає, що

СА = АВ = ВС= 6м.

У правильному трикутнику

АВСR= O 1 C= (м)

приклад 3.У кулю вписано конус, що утворює якого дорівнює діаметру основи (рис 31). Знайти відношення поверхні конуса до поверхні кулі.

АВ= R , АD =

Позначимо повну поверхню конуса через S 1 , а поверхня кулі через S 2 . Маємо

звідки S 1: S 2 = 9:16.

Відповідь:S 1: S 2 = 9:16.

Висновок

Список литературы

Абрамович М.І., Стародубцев М.Т. Математика (геометрія та тригонометричні функції). Навчальний посібник для підготовчих відділень вузів - М.: Вища школа, 1976. - 304 с.

Войтович Ф.С. Комбінації геометричних тіл: (вписані та описані кулі): Книга для учнів. - Мінськ: Народна освіта, 1992. - 160 с.

Говоров В.М., Дибов П.Т., Мирошин Н.В. та ін. Список конкурсних завдань з математики (з методичними вказівками та рішеннями): навчальний посібник. - Друге видання - М: Наука, 1986. - 384 с.

Деніщева Л.О., Безрукова Г.К., Бойченко О.М. та ін Єдиний державний іспит, математика, контрольні вимірювальні матеріали - М: Просвітництво 2005. - 80 с.

Деніщева Л.О., Глазков Ю.А., Краснянська К.А. та ін Єдиний державний іспит. Математика. Навчально-тренувальні матеріали для підготовки учнів/ФІПД – М: Інтелект-Центр, 2008. – 240 с.

Дорофєєв Г.В., Потапов К.М., Розов Н.Х. Допомога з математики для вступників до вузів - М: Наука 1972. - 528 с.

Єгерєв В.К., Зайцев В.В., Кордемський Б.А. та ін. 2500 завдань з математики з рішеннями для вступників до вузів: - М: ТОВ «Видавничий дім «ОНІКС 21 століття»: ТОВ «Видавництво «Світ та Освіта», 2002. - 912 с.

Звавіч Л.І., Рязановський А.Р. Геометрія у таблицях - М: Дрофа 2007. - 128 с.

Клімін С.В., Стрункіна Т.В., Пантелєєва Є.І. та ін Єдиний державний іспит, тестові завдання - М: Просвітництво 2002. - 24 с.

Моденов В.П., Дорофєєв Г.В., Новосьолов С.І. та ін Посібник з математики - М: Видавництво Московського університету, 1972. - 404 с.

Шувалова Е.З., Каплун В.І. Геометрія: навчальний посібник для підготовчих відділень вузів - М.: Вища школа, 1980. - 265 с.

http :// kvant. mirror1. mccme. ru/ pdf/2000/06/ kv0600 solut. pdf

http :// ru. wikipedia. org/ wiki/% D0%9 F% D0% BE% D1%80% D1%82% D0% B0% D0% BB:% D0%9 D% D0% B0% D1%83% D0% BA% D0% B0

rgp . nm. ru/ geometria/ praktika11/ zadatcha119. html

Програма. Завдання для самостійного вирішення

Тема "Різні завдання на багатогранники, циліндр, конус і куля" є однією з найскладніших в курсі геометрії 11 класу. Перед тим, як вирішувати геометричні завдання, зазвичай вивчають відповідні розділи теорії, на які посилаються під час вирішення завдань. У підручнику С.Атанасяна та ін. на цю тему (стор. 138) можна знайти лише визначення багатогранника, описаного біля сфери, багатогранника, вписаного в сферу, сфери, вписаної в багатогранник, та сфери, описаної біля багатогранника. У методичних рекомендаціях до цього підручника (див. книгу "Вивчення геометрії в 10-11-х класах" С.М.Саакяна і В.Ф.Бутузова, стор.159) сказано, які комбінації тіл розглядаються при вирішенні завдань № 629-646 , і звертається увага, що “при вирішенні тієї чи іншої завдання передусім потрібно домогтися, щоб учні добре представляли взаємне розташування зазначених у умов тіл”. Далі наводиться вирішення завдань №638(а) та №640.

Враховуючи все вище сказане, і те, що найважчими для учнів є завдання на комбінацію кулі з іншими тілами, необхідно систематизувати відповідні теоретичні положення та повідомити їх учнів.

Визначення.

1. Куля називається вписаною в багатогранник, а багатогранник описаним біля кулі, якщо поверхня кулі стосується всіх граней багатогранника.

2. Куля називається описаною біля багатогранника, а багатогранник вписаним у кулю, якщо поверхня кулі проходить через усі вершини багатогранника.

3. Куля називається вписаною в циліндр, усічений конус (конус), а циліндр, усічений конус (конус) - описаним біля кулі, якщо поверхня кулі стосується підстав (основи) і всіх утворюють циліндра, усіченого конуса (конуса).

(З цього визначення випливає, що в будь-який осьовий переріз цих тіл може бути вписано коло великого кола кулі).

4. Куля називається описаною біля циліндра, усіченого конуса (конуса), якщо кола основ (коло основи і вершина) належать поверхні кулі.

(З цього визначення випливає, що біля будь-якого осьового перерізу цих тіл може бути описано коло більшого кола кулі).

Загальні зауваження щодо положення центру кулі.

1. Центр кулі, вписаної в багатогранник, лежить у точці перетину бісекторних площин всіх двогранних кутів багатогранника. Він розташований лише всередині багатогранника.

2. Центр кулі, описаної біля багатогранника, лежить у точці перетину площин, перпендикулярних всім ребрам багатогранника і проходять через їх середини. Він може бути розташований усередині, на поверхні та поза багатогранником.

Комбінація кулі із призмою.

1. Куля, вписана в пряму призму.

Теорема 1. Кулю можна вписати в пряму призму в тому і тільки в тому випадку, якщо в основу призми можна вписати коло, а висота призми дорівнює діаметру цього кола.

Наслідок 1.Центр кулі, вписаної в пряму призму, лежить у середині висоти призми, що проходить через центр кола, вписаного в основу.

Наслідок 2.Кулю, зокрема, можна вписати у прямі: трикутну, правильну, чотирикутну (у якої суми протилежних сторін основи рівні між собою) за умови Н = 2r, де Н – висота призми, r – радіус кола, вписаного в основу.

2. Куля, описана біля призми.

Теорема 2. Кулю можна описати біля призми в тому і тільки в тому випадку, якщо призма пряма і біля її основи можна описати коло.

Наслідок 1. Центр кулі, описаної біля прямої призми, лежить на середині висоти призми, проведеної через центр кола, описаного біля основи.

Наслідок 2.Кулю, зокрема, можна описати: біля прямої трикутної призми, біля правильної призми, прямокутного паралелепіпеда, біля прямої чотирикутної призми, у якої сума протилежних кутів основи дорівнює 180 градусів.

З підручника Л.С.Атанасяна на комбінацію кулі із призмою можна запропонувати завдання № 632, 633, 634, 637(а), 639(а,б).

Комбінація кулі із пірамідою.

1. Куля, описана біля піраміди.

Теорема 3. Біля піраміди можна описати кулю в тому і тільки в тому випадку, якщо біля її основи можна описати коло.

Наслідок 1.Центр кулі, описаної біля піраміди, лежить у точці перетину прямої, перпендикулярної основи піраміди, що проходить через центр кола, описаної біля цієї основи, і площині, перпендикулярній будь-якому бічному ребру, проведеної через середину цього ребра.

Наслідок 2.Якщо бічні ребра піраміди рівні між собою (або одно нахилені до площини основи), то біля такої піраміди можна описати кулю. бічного ребра та висоти.

Наслідок 3.Кулю, зокрема, можна описати: біля трикутної піраміди, біля правильної піраміди, біля чотирикутної піраміди, у якої сума протилежних кутів дорівнює 180 градусів.

2. Куля, вписана в піраміду.

Теорема 4. Якщо бічні грані піраміди однаково нахилені до основи, то таку піраміду можна вписати кулю.

Наслідок 1.Центр кулі, вписаної в піраміду, у якої бічні грані однаково нахилені до основи, лежить у точці перетину висоти піраміди з бісектрисою лінійного кута будь-якого двогранного кута на підставі піраміди, стороною якого служить висота бічної грані, проведена з вершини піраміди.

Наслідок 2.У правильну піраміду можна вписати шар.

З підручника Л.С.Атанасяна на комбінацію кулі з пірамідою можна запропонувати завдання № 635, 637(б), 638, 639(в),640, 641.

Комбінація кулі з усіченою пірамідою.

1. Куля, описана при правильній зрізаної піраміди.

Теорема 5. Біля будь-якої правильної зрізаної піраміди можна описати кулю. (Ця умова є достатньою, але не є необхідною)

2. Куля, вписана в правильну усічену піраміду.

Теорема 6. У правильну зрізану піраміду можна вписати кулю в тому і тільки в тому випадку, якщо апофема піраміди дорівнює сумі апофем основ.

На комбінацію кулі з усіченою пірамідою в підручнику Л.С.Атанасяна є лише одне завдання (№ 636).

Комбінація кулі з круглими тілами.

Теорема 7. Біля циліндра, зрізаного конуса (прямих кругових), конуса можна описати кулю.

Теорема 8. У циліндр (прямий круговий) можна вписати кулю в тому і тільки в тому випадку, якщо рівномірний циліндр.

Теорема 9. У будь-який конус (прямий круговий) можна вписати кулю.

Теорема 10. У зрізаний конус (прямий круговий) можна вписати кулю в тому і тільки в тому випадку, якщо його утворює дорівнює сумі радіусів основ.

З підручника Л.С.Атанасяна на комбінацію кулі із круглими тілами можна запропонувати завдання № 642, 643, 644, 645, 646.

Для успішного вивчення матеріалу цієї теми необхідно включати у хід уроків усні завдання:

1. Ребро куба дорівнює а. Знайти радіуси куль: вписаного в куб і описаного біля нього. (r = a/2, R = a3).

2. Чи можна описати сферу (кулю) близько: а) куба; б) прямокутного паралелепіпеда; в) похилого паралелепіпеда, в основі якого лежить прямокутник; г) прямого паралелепіпеда; д) похилого паралелепіпеда? (а) так; б) так; в) ні; г) ні; д) ні)

3. Чи справедливе твердження, що біля будь-якої трикутної піраміди можна описати сферу? (Так)

4. Чи можна описати сферу біля будь-якої чотирикутної піраміди? (Ні, не біля кожної чотирикутної піраміди)

5. Які властивості має піраміда, щоб біля неї можна було описати сферу? (У її основі має лежати багатокутник, біля якого можна описати коло)

6. У сферу вписана піраміда, бічне ребро якої перпендикулярно до основи. Як знайти центр сфери? (Центр сфери – точка перетину двох геометричних місць точок в просторі. Перше – перпендикуляр, проведений до площини основи піраміди, через центр кола, описаного біля нього. Друге – площина перпендикулярна даному бічному ребру і проведена через його середину)

7. За яких умов можна описати сферу біля призми, на основі якої – трапеція? (По-перше, призма має бути прямою, і, по-друге, трапеція має бути рівнобедреною, щоб біля неї можна було описати коло)

8. Яким умовам має задовольняти призма, щоб у неї можна було описати сферу? (Призма має бути прямою, і її основою повинен бути багатокутник, біля якого можна описати коло)

9. Біля трикутної призми описана сфера, центр якої лежить поза призмою. Який трикутник є основою призми? (Тупокутний трикутник)

10. Чи можна описати сферу біля похилої призми? (Ні, не можна)

11. За якої умови центр сфери, описаної біля прямої трикутної призми, буде на одній із бічних граней призми? (В основі лежить прямокутний трикутник)

12. Основа піраміди – рівнобедрена трапеція. Ортогональна проекція вершини піраміди на площину основи – точка, розташована поза трапецією. Чи можна при такій трапеції описати сферу? (Так, можна. Те, що ортогональна проекція вершини піраміди розташована поза її основою, не має значення. Важливо, що в основі піраміди лежить рівнобедрена трапеція – багатокутник, біля якого можна описати коло)

13. При правильної піраміди описана сфера. Як розташований її центр щодо елементів піраміди? (Центр сфери знаходиться на перпендикулярі, проведеному до площини основи через його центр)

14. За якої умови центр сфери, описаної біля прямої трикутної призми, лежить: а) усередині призми; б) поза призмою? (В основі призми: а) гострокутний трикутник; б) тупокутний трикутник)

15. Біля прямокутного паралелепіпеда, ребра якого дорівнюють 1 дм, 2 дм та 2 дм, описана сфера. Обчисліть радіус сфери. (1,5 дм)

16. У який зрізаний конус можна вписати сферу? (У усічений конус, в осьовий переріз якого можна вписати коло. Осьовим перетином конуса є рівнобедрена трапеція, сума її підстав повинна дорівнювати сумі її бічних сторін. Інакше кажучи, у конуса сума радіусів підстав повинна дорівнювати твірної)

17. У усічений конус вписано сферу. Під яким кутом утворююча конуса видно з центру сфери? (90 градусів)

18. Яка властивість повинна мати пряму призму, щоб у неї можна було вписати сферу? (По-перше, в основі прямої призми повинен лежати багатокутник, в який можна вписати коло, і, по-друге, висота призми повинна дорівнювати діаметру вписаного в основу кола)

19. Наведіть приклад піраміди, куди не можна вписати сферу? (Наприклад, чотирикутна піраміда, в основі якої лежить прямокутник або паралелограм)

20. В основі прямої призми лежить ромб. Чи можна до цієї призму вписати сферу? (Ні, не можна, тому що біля ромба в загальному випадку не можна описати коло)

21. За якої умови у пряму трикутну призму можна вписати сферу? (Якщо висота призми вдвічі більша за радіус кола, вписаного в основу)

22. За якої умови у правильну чотирикутну усічену піраміду можна вписати сферу? (Якщо перетином даної піраміди площиною, що проходить через середину сторони основи перпендикулярно до неї, є рівнобедрена трапеція, в яку можна вписати коло)

23. У трикутну усічену піраміду вписано сферу. Яка точка піраміди є осередком сфери? (Центр вписаної в цю піраміду сфери знаходиться на перетині трьох біссектральних площин кутів, утворених бічними гранями піраміди з основою)

24. Чи можна описати сферу біля циліндра прямого кругового? (Так, можна)

25. Чи можна описати сферу біля конуса, усіченого конуса (прямих кругових)? (Так, можна, в обох випадках)

26. У будь-який циліндр можна вписати сферу? Якими властивостями повинен мати циліндр, щоб у нього можна було вписати сферу? (Ні, не у всякий: осьовий переріз циліндра має бути квадратом)

27. У будь-який конус можна вписати сферу? Як визначити становище центру сфери, вписаної в конус? (Так, у всякий. Центр вписаної сфери знаходиться на перетині висоти конуса і бісектриси кута нахилу, що утворює до площини основи)

Автор вважає, що з трьох уроків, які відводяться за плануванням на тему “Різні завдання на багатогранники, циліндр, конус та кулю”, два уроки доцільно відвести на вирішення задач на комбінацію кулі з іншими тілами. Теореми, наведені вище, через недостатню кількість часу під час уроків доводити не рекомендується. Можна запропонувати учням, які володіють достатніми для цього навичками, довести їх, вказавши (за смиренням вчителя) перебіг чи план доказу.