"Область визначення функції" - Область визначення квадратичної функції - будь-яке дійсне число. Функція називається логарифмічною, якщо змінна величина стоїть під знаком логарифму. Логарифмічна функція. Функція, змінна величина якої перебуває у показнику ступеня, називається показовою. Квадратична функція.
"Загальні властивості функцій" - Загальні властивості функцій. Знайти область визначення функції. Парна функція. Чи є ця функція парною чи непарною. За графіком визначте безліч значень функції. За графіком визначте значення Х. За графіком визначте проміжки зменшення функції. Функція f(x) зростаюча. Дано функцію y=f(x).
«Зростання та зменшення функції» - Зростання та зменшення функції синус. Розглянемо ще один приклад. Проміжками зменшення косинуса є відрізки , n - ціле. Нехай, наприклад, функція f парна і зростає на проміжку , де a?0. Зростання та зменшення функцій. Зростання та зменшення функції косинус. На малюнку нижче зображено графік функції, визначеної на відрізку [-1; 10].
«Застосування безперервності» – значення виразу. Геометричний зміст похідної. Метод інтервалів. Скласти рівняння щодо графіку функції. Дотична до графіка функції. Графік близький до дотичної. Формули. Обчислимо за такою формулою. Стосовною кривою в даній точці M називається граничне положення січної NM. Гіперболу.
"Екстремум функції" - Залежність тиску газу від температури. Тема уроку: «Ознаки зростання та зменшення функції. Тест. Зміна сили струму під час розмикання ланцюга. Дослідження функції на екстремум». Зміна змінного струму. План: Залежність сили струму від напруги. Залежність тиску газу від об'єму. Тема: «Ознаки зростання та зменшення функції.
«Функції та його властивості» - Незалежну змінну називають - аргумент. Зростаюча функція. Визначення функції. Парні та непарні функції. Монотонність функції. Значення залежної змінної називають значеннями функції. Усі значення незалежної змінної утворюють область визначення функції -D(f). 1. Значення функції позитивні.
Всього у темі 23 презентації
Тема: Методи використання обмеженості функцій.
Життя хороше тим, що в ньому
можна займатися математикою.
(Леонард Ейлер)Цілі: розвиток нового нешаблонного мислення, яке можна успішно застосовувати і в інших сферах людської діяльності (кібернетика, обчислювальна техніка, економіка, радіофізика, хімія та ін.).
Завдання: - навчання оцінки об'єктивної та суб'єктивної проблеми завдань і, розумному вибору цих завдань на іспиті;
Створення «скарбнички» нетрадиційних та незвичайних міркувань.
Хід уроку:
Орг. момент. Формулювання учнями теми уроку за допомогою виконання завдань ЄДІ частини А та В та розшифровування теми щодо спадання отриманих відповідей. (Як передбачуваних слів зашифрувати 12 карток під номерами від -2 до 10) (додаток 1 та 2)
обмеженості
2. Розділити учнів на 2 групи, вручити їм набір «Теорія + 10 завдань» (додатки 3 і 4), попросити вибрати ті завдання, які можна виконати з даної теоретичної частини, обґрунтувати свій вибір.3. Показати хід виконання цих завдань на дошці учнями: Носкова К., Дедевшин І., Веселов І.4. Розділити завдання з картки на 2 групи на вирішення їх із наступною самоперевіркою по аркушу готових решений. (Додаток 5)5. Роздати групам листи з описом нових нестандартних методів розв'язання рівнянь і нерівностей для вибору наступної теми (як дом. завдання знайти у збірниках ЄДІ завдання, які можна вирішувати цим методом) (додаток 6)6. Рефлексія учнів (заповнення таблички)Ф.І. учняДодаток 1.
Розв'яжіть ці завдання та розмістіть відповіді в порядку спадання, зберіть за відповідями тему нашого заняття.
Знайти абсцис точки графіка функції у=3х 2 -7х+7, в якій тангенс кута дотичної дорівнює -1.
Додаток 2.
9 2 0 7Дослідження функцій за допомогою похідної. 10 5 1 -1Метод використання обмеженості функцій. 4 -2 8 12Рішення нерівностей графічним способом.
3 11 6Рішення функціональних рівнянь.
Дослідження
Додаток 3.
Одним із ефективних методів розв'язання рівнянь чи нерівностей є метод, заснований на використанні обмеженості функцій. До найбільш відомих обмежених функцій відносяться, наприклад, деякі тригонометричні; зворотні тригонометричні функції; функції, що містять модуль, ступінь, корінь з парним ступенем та інші.
Найбільш поширеними нерівностями є такі:
│f(x) │≥
0, -1
≤
sinx ≤
1, -1
≤
cosx ≤
1, -
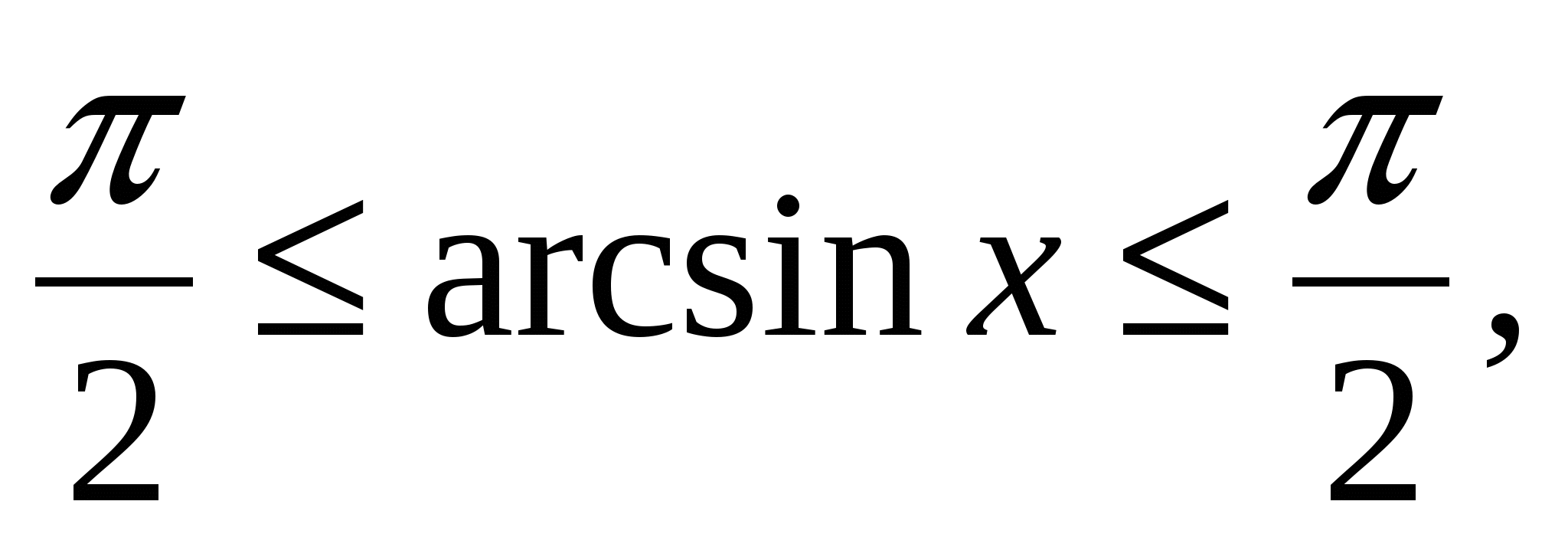
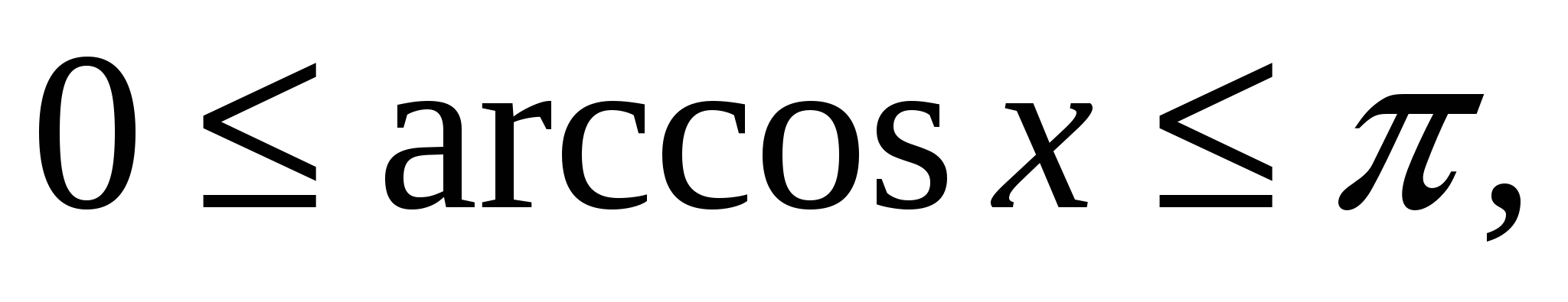 -
-

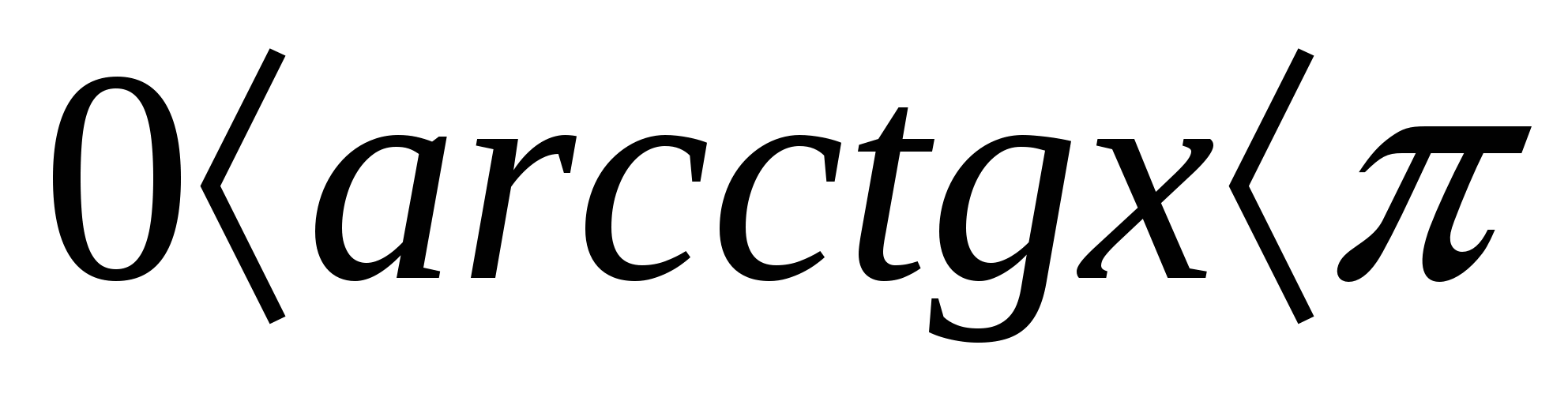 ,
a f (x) >0, (f(x) ±
g(x)) 2 n ≥
0,
,
a f (x) >0, (f(x) ±
g(x)) 2 n ≥
0,
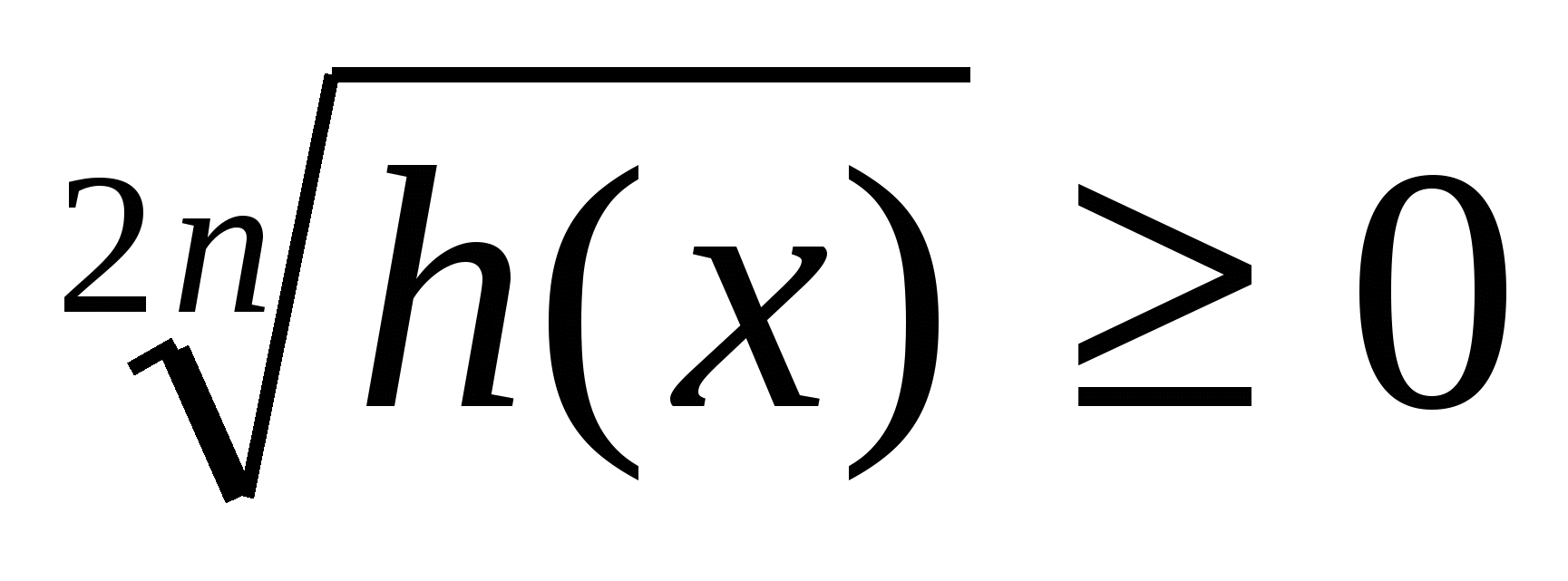 ,
a+
≥
2,
b+
≤
-2
та багато інших. Тут n -натуральне число, h(x) ≥
0,
a>0,
b
0.
,
a+
≥
2,
b+
≤
-2
та багато інших. Тут n -натуральне число, h(x) ≥
0,
a>0,
b
0.
Крім наведених найпростіших нерівностей є і складніші, зокрема, тригонометричні нерівності -,
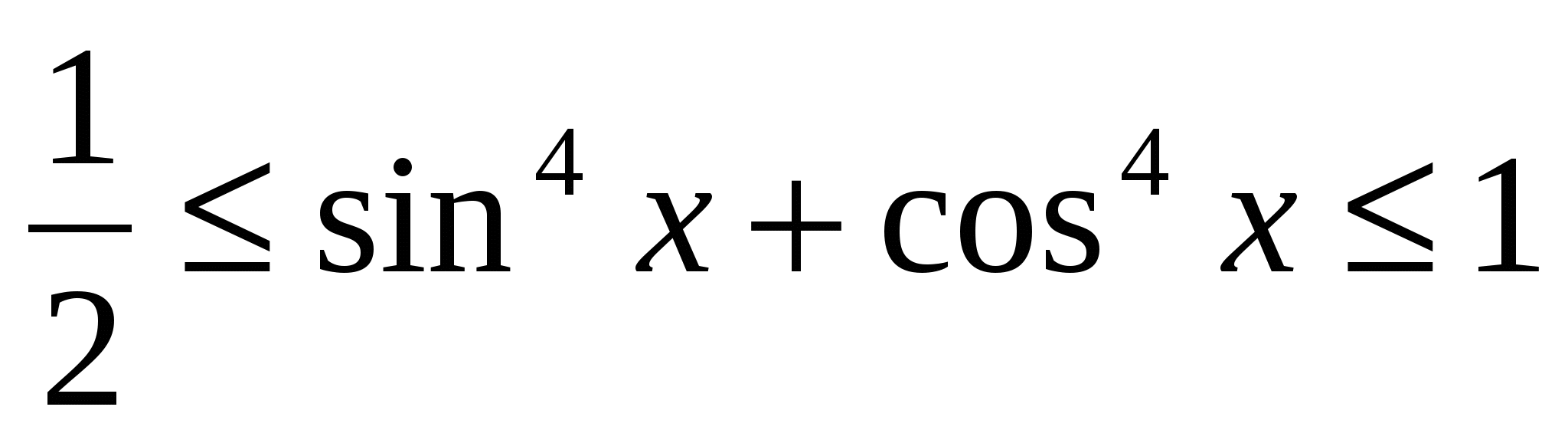 ,
,
та нерівності з модулями виду 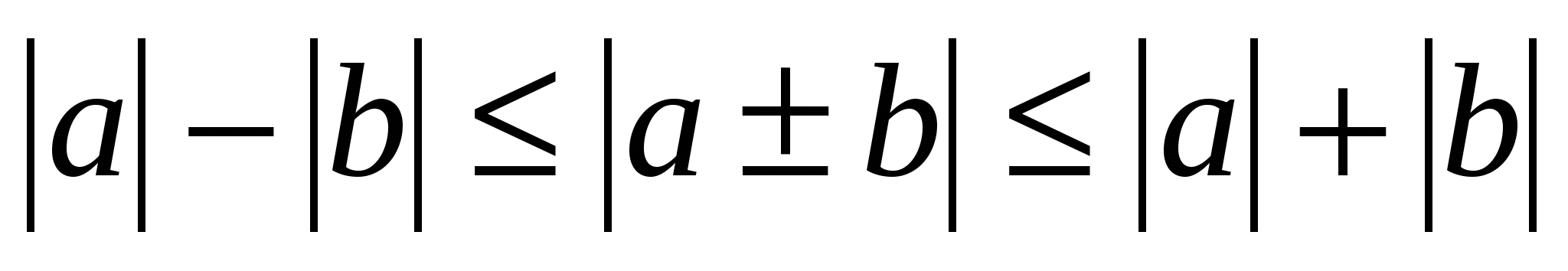 .
.
приклад 1.Розв'язати рівняння: 
Рішення:
виділимо повний квадрат у правій частині рівняння, тобто. . Звідси випливає, що 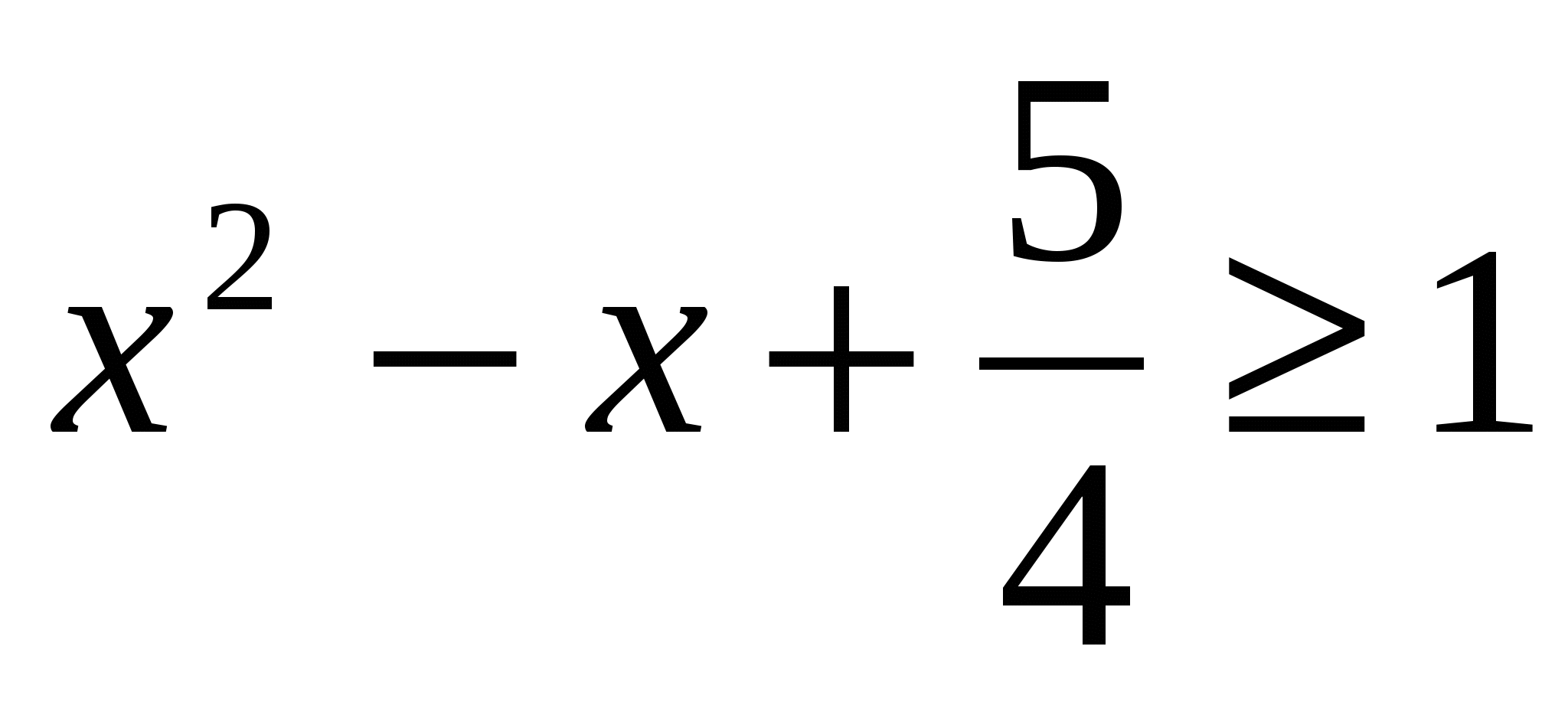 . Бо при цьому sinπ x ≤
1, то отримуємо систему рівнянь
. Бо при цьому sinπ x ≤
1, то отримуємо систему рівнянь 
Вирішуючи друге рівняння системи, отримуємо що х =. Підстановкою в перше рівняння переконуємося, що знайдене значення х є розв'язком системи, отже, є рішенням вихідного рівняння.
Відповідь:х =.
приклад 2.Розв'язати рівняння: 
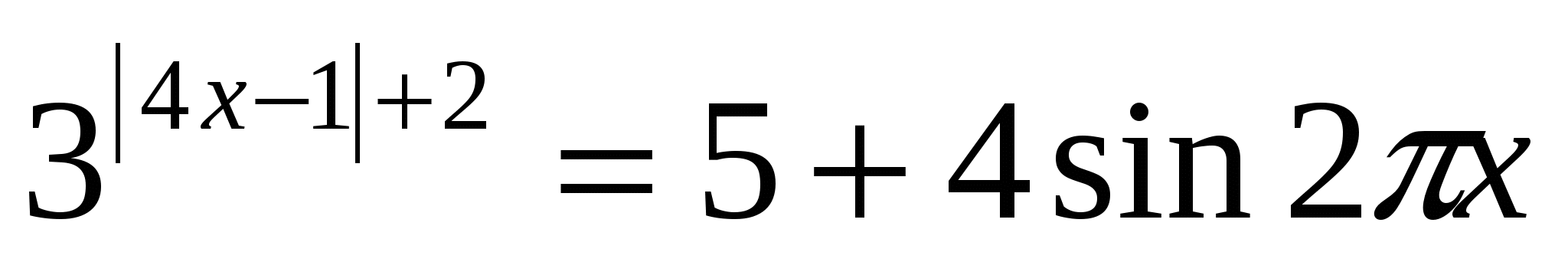
Рішення: оскільки Sin2 π x ≤
1. Тому, 5+4 sin2 π x ≤
9. Таким чином, отримуємо систему рівнянь: 
Звідси отримуємо систему рівнянь  , З першого рівняння знайдемо х =. Підставимо його у друге рівняння системи та переконаємося, що х= є розв'язком системи, а отже, є розв'язком вихідного рівняння.
, З першого рівняння знайдемо х =. Підставимо його у друге рівняння системи та переконаємося, що х= є розв'язком системи, а отже, є розв'язком вихідного рівняння.
Відповідь:х=
Додаток 4.
Виберіть із запропонованого списку завдань ті, які можна вирішити і за допомогою методу обмеженості функцій.
1. Розв'язати рівняння х 2 -4 x=(2-cos  2. Знайти кількість цілих рішень нерівності х 2 ctg 2
2. Знайти кількість цілих рішень нерівності х 2 ctg 2 3. Розв'язати рівняння
3. Розв'язати рівняння 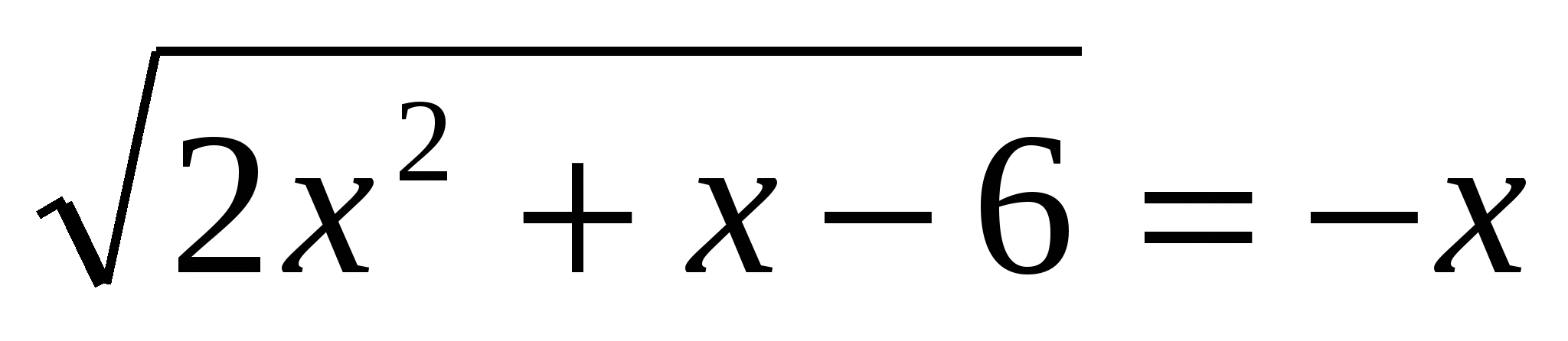 4. Розв'язати рівняння 3-(5. Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2
4. Розв'язати рівняння 3-(5. Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2  6. Розв'язати рівняння
6. Розв'язати рівняння  7. Розв'язати рівняння -25х2+40х-23=( cos
7. Розв'язати рівняння -25х2+40х-23=( cos 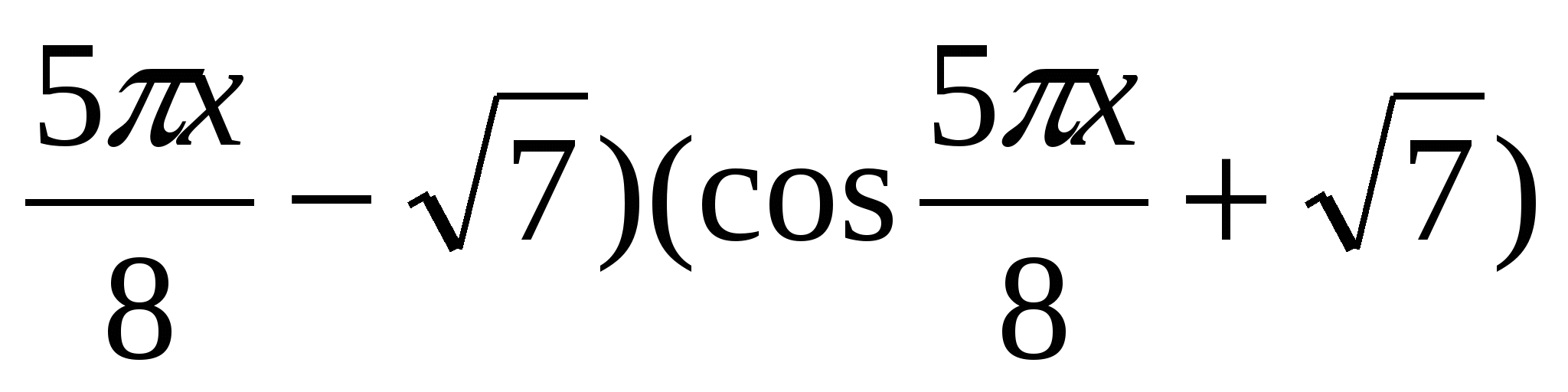 8. Знайти добуток коренів рівняння х
8. Знайти добуток коренів рівняння х  9. Розв'язати рівняння
9. Розв'язати рівняння  10. Розв'язати рівняння 3- cos 2
10. Розв'язати рівняння 3- cos 2 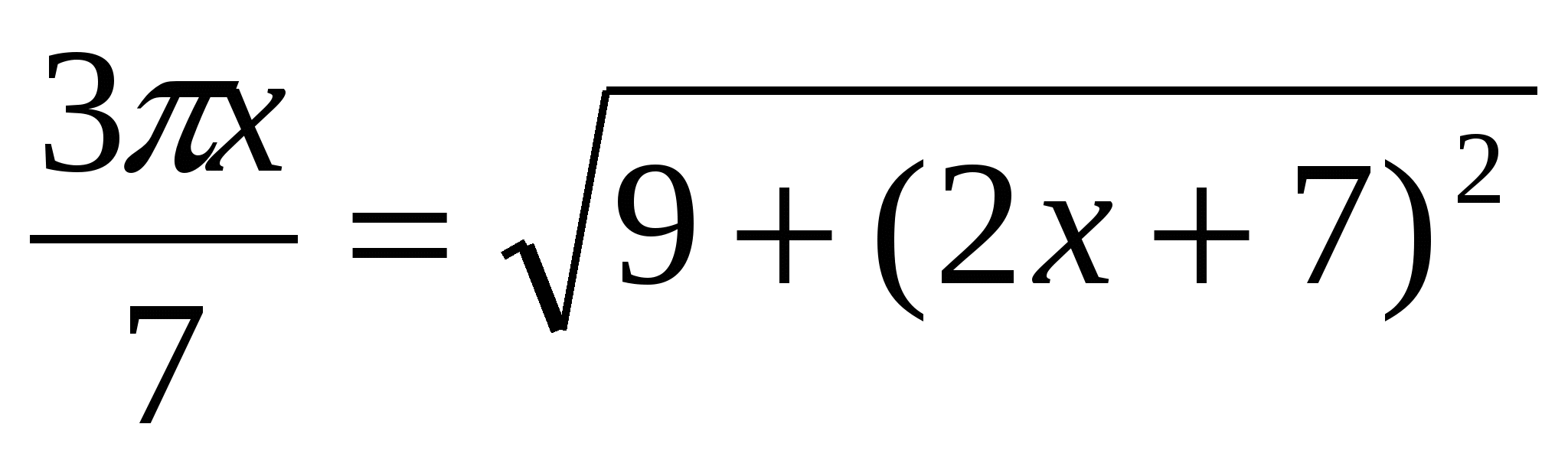
Аркуш самоперевірки.
Додаток 5.
1. Розв'язати рівняння
Рішення: т.к. , То т.к. і, то
отримуємо систему рівнянь
вирішуємо перше рівняння, отримуємо х = , підставимо це значення у друге рівняння
2 . Розв'язати рівняння 3-
cos 2 Рішення: т.к. , То т.к. і, то
отримуємо систему рівнянь
вирішуємо друге рівняння, отримуємо х = , підставимо це значення у перше рівняння
отже х= є рішенням вихідного рівняння. Відповідь: х=
3 . Знайти кількість цілих рішень нерівності х 2
+7х-8≤0, що задовольняють умові ctg 2 Рішення: т.к. і то за будь-яких допустимих значень хЗнайдемо нулі квадратного тричлена, за теоремою ВієтаРешим нерівність методом інтервалів
т.ч. хзнаємо, що
цілочисельні значення х - це числа виключаємо Відповідь: 8 цілих рішень 4 . Знайти кількість цілих рішень нерівності 16-х 2 ≥0, що задовольняють умові 3 tg 2 Рішення: т.к. і то за будь-яких допустимих значень хЗнайдемо нулі вирази, х= і х=Розв'яжемо нерівність методом інтервалів
т.ч. хзнаємо, що
цілочисельні значення х - це числа виключаємо Відповідь: 7 цілих рішень
Додаток 6.
Метод використання монотонності функцій. При вирішенні рівняння типу f(x)=g(x) у ряді випадків ефективним є метод, який використовує монотонність функцій у = f (x) і у = g (x). Якщо функція у = f (x) безперервна і зростає (зменшується) на відрізку a≤ x ≤ b, а функція у = g(x) безперервна і зменшується (зростає) цьому ж відрізку, то рівняння f(x)=g(x) на відрізку a≤ x ≤ b може мати не більше одного кореня, отже необхідно або спробувати підбір знайти єдиний корінь рівняння, або показати, що такого кореня не існує. Особливо цей метод ефективний у тому випадку, коли обидві частини рівняння f(x)=g(x) є «незручними» для спільного дослідження функції. Примітка:Якщо функція у = f(x) зростає, а функція у = g(x) зменшується для a≤ x ≤ b і при цьому f(а)>g(а), то коріння рівняння серед a≤ x ≤ bні.
приклад: Розв'язати рівнянняРішення: Областю допустимих значень рівняння є х 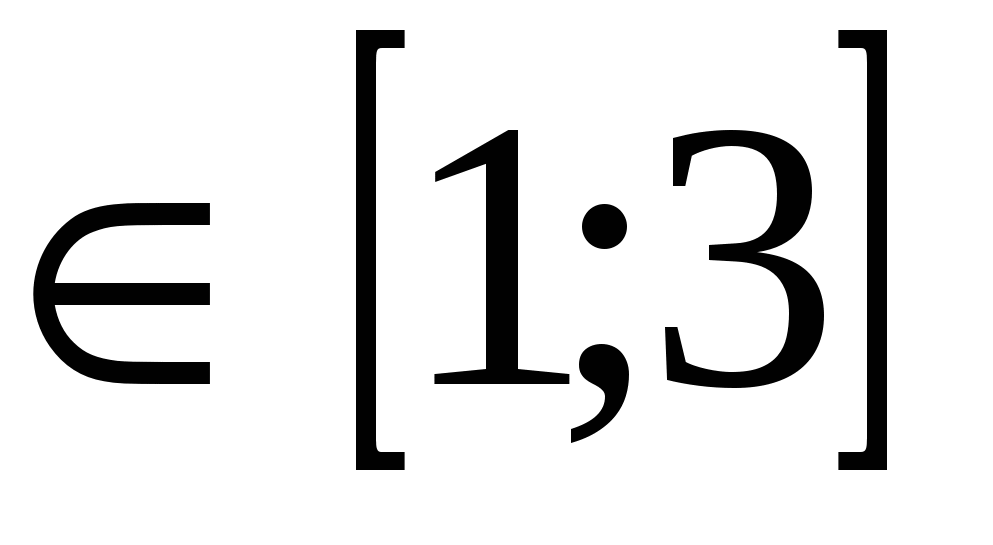 . Неважко бачити, що у цій галузі ліва частина рівняння зростає, а права - зменшується, тобто. функціяf(x)=
. Неважко бачити, що у цій галузі ліва частина рівняння зростає, а права - зменшується, тобто. функціяf(x)= є зростаючою, а функціяg(x)=
є зростаючою, а функціяg(x)= - спадна. У зв'язку з цим вихідне рівняння може мати лише один корінь (якщо він є). Підбором знаходимо цей корінь рівняння х = 2.Відповідь: х = 2
- спадна. У зв'язку з цим вихідне рівняння може мати лише один корінь (якщо він є). Підбором знаходимо цей корінь рівняння х = 2.Відповідь: х = 2
Метод розв'язання функціональних рівнянь.
До найбільш складних завдань на ЄДІ відносяться завдання, вирішення яких зводиться до розгляду функціональних рівнянь виду f(f(….f(x)…))=x або f(g(x))=f(h(x)), де f(x),g(x),h(x)- деякі функції та n≥ 2
Методи вирішення цих функціональних рівнянь ґрунтуються на застосуванні багатьох теорем, розглянемо одну з них.
Теорема1. Коріння рівняння
f(x)=0 є корінням рівняння f(f(….f(x)…))=x
приклад: Розв'язати рівняння х= 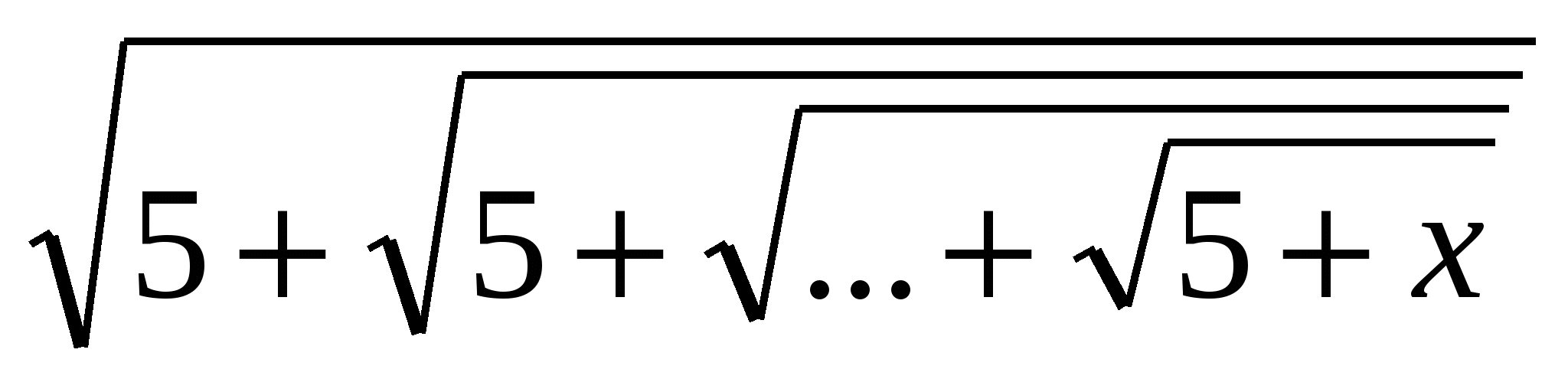 ,
де квадратний корінь беретьсяnраз іn≥
1
Рішення: З умови завдання випливає, що х>
0. Нехайf(x)=
,
де квадратний корінь беретьсяnраз іn≥
1
Рішення: З умови завдання випливає, що х>
0. Нехайf(x)=
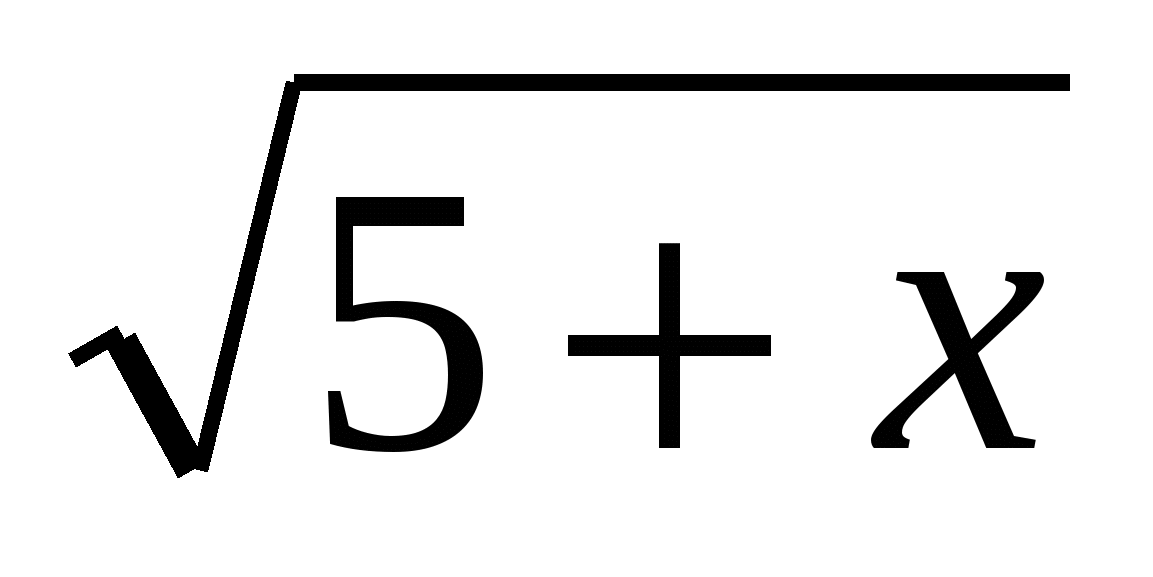 тоді наше рівняння можна представити у вигляді функціонального
f(
f(….
f(
x)…))=
x.
Бо при х>
0 функціяf(x)=
зростає іf(x)
>
0, то рівняння х = рівносильне рівняннюf(x)=
x, тобто.
=х, позитивним рішенням якого є х=
тоді наше рівняння можна представити у вигляді функціонального
f(
f(….
f(
x)…))=
x.
Бо при х>
0 функціяf(x)=
зростає іf(x)
>
0, то рівняння х = рівносильне рівняннюf(x)=
x, тобто.
=х, позитивним рішенням якого є х=  Відповідь:х=
Відповідь:х=
Галаєва Катерина, учениця 11 класу МАОУ ЗОШ №149 м Нижнього Новгорода
Робота носить одночасно і прикладний та дослідницький характер. Для повноти дослідження було розглянуто такі вопросы:
– Як відбиваються властивості функції під час вирішення рівнянь і нерівностей?
– Які рівняння та нерівності вирішуються через визначення властивостей галузі визначення, безлічі значень, інваріантності?
– Який алгоритм розв'язання?
– Розглянуто завдання з параметром, пропонованим у матеріалах КІМ під час підготовки до ЄДІ.
Діяльність Катерина досліджувала велике коло завдань і систематизував їх за зовнішнім виглядом.
Завантажити:
Попередній перегляд:
https://accounts.google.com
Підписи до слайдів:
Розв'язати нерівність Розв'язання. Функція f(х) = монотонно зростає на всій числовій прямій, а функція g(x) = монотонно зменшується на всій ділянці визначення. Тому нерівність f(х) > g(x) виконується, якщо х >
Дякую за увагу!
Попередній перегляд:
Щоб скористатися попереднім переглядом презентацій, створіть собі обліковий запис Google і увійдіть до нього: https://accounts.google.com
Підписи до слайдів:
Використання властивостей функції при розв'язанні рівнянь та нерівностей Виконала роботу: Галаєва Катерина МБОУ ЗОШ №149 Московського району Учениці 11 «А» класу Науковий керівник: Фадєєва І. А. Вчитель математики
Основні напрямки: Вивчення властивостей функції: монотонність, обмеженість, область визначення та інваріантність Дізнатись основні твердження, які найчастіше використовуються при вирішенні рівнянь, нерівностей та систем
Монотонність Функція зростає, якщо більше значення аргументу відповідає більше значення функції. Функція зменшується, якщо більшому значенню аргументу відповідає менше значення функції. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Твердження 1. Якщо функція у = f(x) монотонна, то рівняння f(x) = с має не більше одного кореня. x =2 f(x) = - монотонно спадаюча, отже, інших рішень немає. Відповідь: x = 2
Твердження 2. Якщо функція у = f(x) монотонно зростає, а функція у = g(x) монотонно зменшується, то рівняння f(x) = g(x) має не більше одного кореня. 2 - x = lg (x +11) + 1 g (x) = 2 - x є монотонно спадаючою, а функція f (x) = lg (x + 11) + 1 монотонно зростаючою на області визначення означає рівняння f (х ) = g(x) має не більше одного кореня. Підбором визначаємо, що х = -1. Вище викладене твердження доводить єдиність рішення.
а) f (х) ≤ g (x) у тому і тільки в тому випадку, коли х ϵ (- ∞ ; x 0 ]; б) f (х) ≥ g (x) у тому і тільки в тому випадку, х ϵ [х 0; +∞). Наочний зміст цього твердження очевидний Твердження 3. Якщо функція у = f (х) монотонно зростає на всій числовій прямій, функція у = g (x) монотонно зменшується на всій числовій прямій і f (х 0) = g (x 0), то справедливі такі твердження:
Розв'язати нерівність Розв'язання. Функція f(х) = монотонно зростає на всій числовій прямій, а функція g(x) = монотонно зменшується на всій ділянці визначення. Тому нерівність f(х) > g(x) виконується, якщо х > 2. Додамо область визначення нерівності. Отже, отримаємо систему Ответ: (2; 5).
Твердження 4. Якщо функція у = f(х) монотонно зростає, то рівняння f(х)=х і f(f(х))=х мають одну й ту саму безліч коренів, незалежно від кількості вкладень. Слідство. Якщо n - натуральне число, а функція у = f (х) монотонно зростає, то рівняння f (х) = х і n разів мають одне й те саме безліч коренів.
Вирішити рівняння. Відповідь: Рішення. При x ≥1 права частина рівняння не менше 1, а ліва частина менше 1. Отже, якщо рівняння має коріння, то будь-який з них менше 1. При x ≤0 права частина рівняння непозитивна, а ліва частина позитивна, тому що . Таким чином, будь-який корінь даного рівняння належить інтервалу (0; 1) Помноживши обидві частини даного рівняння на х, розділивши на x чисельник і знаменник лівої частини, отримаємо
Звідки =. Позначивши через t де t 0, отримаємо рівняння = t . Розглянемо зростаючу у своїй області визначення функцію f (t)= 1+ . Отримане рівняння можна записати як f (f (f (f (t))))= t , і за наслідком затвердження 4 воно має таку ж безліч рішень, як і рівняння f (t)= t , тобто. рівняння 1 + = t, звідки. Єдиним позитивним коренем цього квадратного щодо рівняння є. Отже, звідки, тобто. , або. Відповідь:
Твердження 1. Якщо max f (x) = с і min g (x) = с, то рівняння f (x) = g (x) має те ж безліч рішень, що і система Обмеженість Максимальне значення лівої частини дорівнює 1 і мінімальне значення правої частини 1 , отже, рішення рівняння зводитися до системи рівнянь: , з другого рівняння знаходимо можливий претендент x = 0 і переконуємося, що він є рішенням і першого рівняння. Відповідь: x=1.
Розв'язати рівняння Розв'язання. Так як sin3x≤1 і cos4x≤1, ліва частина даного рівняння не перевищує 7. Рівною 7 вона може бути в тому і тільки тому випадку, якщо звідки де k n Z Z . Залишається встановити, чи існують ці цілі k і n , при яких остання система має рішення. Відповідь: Z
У задачах з невідомими x і параметром a під областю визначення розуміють безліч всіх упорядкованих пар чисел (x ; a) , кожна з яких така, що після підстановки відповідних значень x і a у всі співвідношення співвідношення будуть визначені. Приклад 1. При кожному значення параметра a усуньте нерівність Рішення. Знайдемо область визначення цієї нерівності. З яких видно, що система не має рішень. Отже, область визначення нерівності немає жодних пар чисел x і a , тому нерівність немає рішень. Область визначення Відповідь:
Інваріантність, тобто. незмінність рівняння чи нерівності щодо заміни змінної будь-яким алгебраїчним виразом від цієї змінної. Найпростішим прикладом інваріантності є парність: якщо – парна функція, то рівняння інваріантне щодо заміни x та – x, оскільки = 0. Інваріантність
Знайти коріння рівняння. Рішення. Зауважимо, що пара інваріанту щодо заміни. Замінивши на рівність, отримаємо. Помноживши обидві частини даної рівності на 2 і віднімаючи з отриманої рівності почленно рівність, знаходимо 3 звідки. Тепер залишилося вирішити рівняння, звідки корінням рівняння є числа. Відповідь: .
Знайти всі значення a для кожного з яких рівняння має більше трьох різних рішень. Розв'язання задач із параметром Властивість монотонності
|x|= позитивно X= |x|= Для двох коренів чисельник може бути позитивний. Тому при корінні першого і другого рівняння збігаються, що не відповідає вимогі умови: наявність більше трьох коренів. Відповідь: .
Знайти всі значення a, при кожному з яких рівняння має два корені. Перетворимо рівняння до виду І розглянемо функцію f(x)= певну та безперервну на всій числовій прямій. Графік цієї функції є ламаною, що складається з відрізків прямих і променів, кожна ланка якої є частиною прямої виду y= kt+l . f(x)= При будь-якому розкриття модуля першого виразу k не перевищує 8, тому зростання та зменшення функції f(x) буде залежати від розкриття другого модуля. При x f (x) буде спадати, а за x зростати. Тобто, при x=3 функція прийматиме найбільше значення. Для того, щоб рівняння мало два корені, необхідно, щоб f(3) Властивість монотонності
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Відповідь: a
Знайти всі значення параметра а, при кожному з яких для будь-якого дійсного значення х виконано нерівність Перепишемо нерівність у вигляді, введемо нову змінну t = і розглянемо функцію f (t) = , визначену і безперервну на всій числовій прямій. Графік цієї функції є ламаною, що складається з відрізків прямих і променів, кожна ланка якої є частиною прямої виду, де до
Оскільки, то t ϵ [-1; 1]. В силу монотонного зменшення функції у = f (t) достатньо перевірити лівий край даного відрізка. З. А істинним є значить, що можливе, тільки якщо числа і і v одного знака або якесь з них дорівнює нулю. , = () () 0. Розклавши квадратні тричлени на множники, отримаємо нерівність (з якої знаходимо, що а ϵ (-∞; -1] U (2) U [ 4; +∞).Відповідь: (-∞; - 1] U (2) U )
