Інструкція. Для онлайн рішення необхідно вибрати вид рівняння та задати розмірність відповідних матриць.
де А, В, С - матриці, що задаються, Х - шукана матриця. Матричні рівняння виду (1), (2) та (3) вирішуються через зворотну матрицю A-1. Якщо задано вираз AX - B = C , то необхідно спочатку скласти матриці C + B і знаходити рішення для вираження A X = D , де D = C + B (). Якщо вираз A*X = B 2 , то попередньо матрицю B треба звести у квадрат . Рекомендується також ознайомитись з основними діями над матрицями.Приклад №1. Завдання. Знайти рішення матричного рівняння
Рішення. Позначимо:
Тоді матричне рівняння запишеться як: A·X·B = C.
Визначник матриці А дорівнює detA=-1
Оскільки A невироджена матриця, існує зворотна матриця A -1 . Помножимо зліва обидві частини рівняння на A -1: Помножуємо обидві частини цієї рівності зліва на A -1 і праворуч на B -1: A -1 · A · X · B · B -1 = A -1 · C · B -1 . Оскільки A·A -1 = B·B -1 = E і E·X = X·E = X, то X = A -1 ·C·B -1
Зворотна матриця A-1: ![]()
Знайдемо зворотну матрицю B-1.
Транспонована матриця B T:
Зворотна матриця B-1: ![]()
Матрицю X шукаємо за формулою: X = A -1 · C · B -1 ![]()
Відповідь:
Приклад №2. Завдання.Розв'язати матричне рівняння ![]()
Рішення. Позначимо:
Тоді матричне рівняння запишеться як: A·X = B.
Визначник матриці А дорівнює detA=0
Оскільки A вироджена матриця (визначник дорівнює 0), отже рівняння рішення немає.
Приклад №3. Завдання. Знайти рішення матричного рівняння
Рішення. Позначимо:
Тоді матричне рівняння запишеться як: X·A = B.
Визначник матриці А дорівнює detA=-60
Оскільки A невироджена матриця, існує зворотна матриця A -1 . Помножимо праворуч обидві частини рівняння на A -1: X·A·A -1 = B·A -1 , звідки знаходимо, що X = B·A -1
Знайдемо зворотну матрицю A-1.
Транспонована матриця A T: 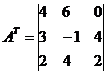
Зворотна матриця A-1: 
Матрицю X шукаємо за формулою: X = B · A -1 
Відповідь: > 
За допомогою матричного онлайн калькулятора ви можете скласти, віднімати, помножити, транспонуватиматриці, обчислити зворотнуматрицю, псевдозворотнуматрицю, рангматриці, визначникматриці, m-норму та l-норму матриці, звести матрицю до ступеня, помножити матрицю на числозробити скелетне розкладанняматриці, видалити з матриці лінійно залежні рядкиабо лінійно залежні стовпці, проводити виняток Гауса, розв'язати матричне рівняння AX=B, зробити LU розкладання матриці,обчислити ядро (нуль простір) матрицізробити ортогоналізацію Грамма-Шмідта та ортонормалізацію Грамма-Шмідта.
Матричний онлайн калькулятор працює не лише з десятковими числами, а й із дробами. Для введення дробу потрібно у вихідні матриці та вводити числа у вигляді aабо a/b, де aі bцілі чи десяткові числа ( bпозитивне число). Наприклад, 12/67, -67.78/7.54, 327.6, -565.
Кнопка у верхньому лівому куті матриці відкриває меню (Рис.1) для перетворення вихідної матриці (створення одиничної матриці, нульової матриці або очищати вміст осередків).

При обчислення порожній осередок сприймається як нуль.
Для операцій із однією матрицею (тобто. транспонування, зворотне, псевдооборотное, скелетне розкладання тощо.) спочатку вибирається конкретна матриця з допомогою радіокнопки .
Кнопки Fn1, Fn2 та Fn3 перемикають різні групи функцій.
Натискаючи на обчислених матрицях відкривається меню (Рис.2), що дозволяє записати дану матрицю у вихідні матриці і , а також перетворити на місці елементи матриці у звичайний дріб, змішаний дріб або десяткове число.
Обчислення суми, різниці, твори матриць онлайн
суму, різницю або добуток матриць. Для обчислення суми або різниці матриць, необхідно, щоб вони були однакової розмірності, а для обчислення добутку матриць, кількість стовпців першої матриці має дорівнювати кількості рядків другої матриці.
Для обчислення суми, різниці чи добутку матриць:
Обчислення зворотної матриці онлайн
Матричним онлайн калькулятором можна обчислити зворотну матрицю. Для того, щоб існувала зворотна матриця, вихідна матриця має бути невиродженою квадратною матрицею.
Для обчислення зворотної матриці:
Для детального обчислення зворотної матриці за кроками використовуйте цей калькулятор для обчислення зворотної матриці . Теорію обчислення зворотної матриці дивіться.
Обчислення визначника матриці онлайн
Матричним онлайн калькулятором можна обчислити визначник матриці. Для того, щоб існував визначник матриці, вихідна матриця має бути невиродженою квадратною матрицею.
Для обчислення визначника матриці:
Для детального обчислення визначника матриці за кроками використовуйте цей калькулятор для обчислення визначника матриці . Теорію обчислення визначника матриці дивіться.
Обчислення рангу матриці онлайн
Матричним онлайн калькулятором можна обчислити ранг матриці.
Для обчислення рангу матриці:
Для детального обчислення рангу матриці за кроками використовуйте цей калькулятор для обчислення рангу матриці . Теорію обчислення рангу матриці дивіться.
Обчислення псевдозворотної матриці онлайн
Матричним онлайн калькулятором можна обчислити псевдозворотну матрицю. Псевдозворотна до цієї матриці завжди існує.
Для обчислення псевдозворотної матриці:
Видалення лінійно залежних рядків або стовпців матриці онлайн
Матричним онлайн калькулятор дозволяє видалити з матриці лінійно залежні рядки чи стовпці, тобто. створити матрицю повного рангу.
Для видалення лінійно залежних рядків або стовпців матриці:
Скелетне розкладання матриці онлайн
Для проведення скелетного розкладання матриці онлайн
Розв'язання матричного рівняння або системи лінійних рівнянь AX=B онлайн
Матричним онлайн калькулятором можна вирішити матричне рівняння AX=B по відношенню до матриці X. В окремому випадку, якщо матриця B є вектор-стовпцем, то X буде рішенням системи лінійних рівнянь AX=B.
Для розв'язання матричного рівняння:
Врахуйте, що матриці повинні мати однакову кількість рядків.
Виключення Гауса або приведення матриці до трикутного (ступінчастого) виду онлайн
Матричний онлайн калькулятор проводить виняток Гауса як для квадратних матриць, так і прямокутних матриць будь-якого рангу. Спочатку проводиться стандартний спосіб Гаусса. Якщо якомусь етапі провідний елемент дорівнює нулю, то вибирається інший варіант виключення Гауса з вибором найбільшого провідного елемента в стовпці.
Для виключення Гауса або приведення матриці до трикутного вигляду
LU-розкладання або LUP-розкладання матриці онлайн
Даний матричний калькулятор дозволяє проводити LU-розкладання матриці (A=LU) або LUP-розкладання матриці (PA=LU) , де L нижня трикутна матриця, U-верхня трикутна (трапецієподібна) матриця, P-матриця перестановок. Спочатку програма проводить LU розкладання, тобто. таке розкладання, у якому P=E, де E-одинична матриця (тобто. PA=EA=A). Якщо це неможливо, то проводиться LUP-розкладання. Матриця A може бути квадратною, так і прямокутною матрицею будь-якого рангу.
Для LU(LUP)-розкладання:
Побудова ядра (нуль-простору) матриці онлайн
За допомогою матричного калькулятора можна побудувати нуль-простір (ядро) матриці.
Для побудови нуль-простору (ядра) матриці.
>Всім привіт! Чи існує формула, за якою з матриці можна прибрати масштабування, не знаючи коефіцієнтів масштабування?
Відразу згадали полярне розкладання. Що, матриця M представляється у вигляді O * P. Де O ортогональна, а P позитивно визначена, симетрична - тобто матриця стиснення або розтягування. Ось матрицю O ми візьмемо.
Постає питання. А якщо розкладати M з іншого боку, то отримаємо P'*O'. Розкладання в іншому порядку, з іншими апріорі матричками. Чому б не взяти O'? Я мучився хвилин п'ять запитанням, поки не згадав, як ставив студентам незалік із цього приводу. Матриця O' насправді збігається з матрицею O. Якщо ви нещодавно закінчили університет або ще навчаєтесь – можете навіть спробувати довести цей факт.
Отже, полярне розкладання:
Для знаходження позитивного квадратного кореня з матриці у позитивній науці пропонується порахувати власні числа. Для кожного власного числа знайти власне підземний простір, потім акуратно виготовити власне квадратний корінь з оператора.
Я як уявив, що вийде для матриці, близької до одиничної, аж здригнувся. Все помре на неточностях флоату, ранги у матриць з'їдуть – повний колапс обіцяє бути.
А чому б благородним донам не спробувати ітерації, які божественні, як відомо?
Ось, корінь із числа шукається методом Ньютона. Послідовність a_(i+1) = 0.5*(a_i + x/a_i); гордо сходить до квадратного кореня з x. Для проби взяв чиюсь бібліотечку про mat3x3 та наклепав матричний аналог.
Прямий аналог методу Ньютона спритно сходиться за 3-4 ітерації, тести проходять як легкий вітерець. Виходить полярне розкладання для матриць, працездатність алгоритму очевидна з елементарної спектральної теорії операторів. Очевидна після півгодини скрипу мозком.
Отже, полярне розкладання ми виявили. Питання – навіщо? І тут я змушений перейти до основного поінту своєї доповіді. Вчення – зло. Час, який ви витратили на згадку про спектральну теорію операторів, успішно витрачено марно.
Розкладання Scale Shear Rotate шукається на один раз. Застосовуємо процес ортогоналізації та ортонормалізації до матриці. Стовпцями. Отримуємо чудову матрицю. І чим результат буде гіршим? Та нічим!
Побачив пост з кодом на паскалі, який і вважає це саме Scale Shear Rotate розкладання, і раптово зрозумів, що у мене немає аргументів за полярне розкладання. Що вимагає хрін знає який обчислювальної техніки.
Звичайно, є дрібні заперечення, майже причіпки. Наприклад, що tangent space простіше вважати ортонормальним. Обчислювально простіше. Зазвичай вважають dPosition/du нормаль, а третій вектор беруть перпендикулярним до цієї пари. Зрозуміло, що метод несиметричний щодо текстурних координат, яка їх перша, яка друга – зовсім незрозуміло. Начебто правильно застосувати полярне розкладання до матриці локального перетворення.
Може, ви помітите різницю між “правильним” полярним розкладанням і “неправильним” процесом ортогоналізації по стовпцях. Скоріше не помітите. І точно картинка не стане кращою.
P.S. А ось ще анімації зберігати у Scale Shear Rotate дуже круто. Три вектори, один кватерніон. Shear майже завжди 0, Scale майже завжди 1, константні треки можна викинути. А там де неконстантні треки - як-нитка вичавити за рахунок спеціалізації шаблону. Або ще чогось.
1)
Розглянемо спочатку дійсні матриці. Припустимо, що з матриці $%A$% вилучається корінь, тобто. Існує матриця $%B$% така, що $%B \cdot B=A$%. Припустимо, що матриця $%B$% може бути приведена до діагонального вигляду, тобто. існує матриця $%S$% така, що $%S^(-1)BS=B"$%, де $%B"$%- діагональна матриця. З рівностей $%B"B"=S^(-1)BSS^(-1)BS=S^(-1)BBS=S^(-1)AS$% випливає, що $%A"=S^ (-1)AS$% - теж діагональна матриця, тобто матриці $%A$% і $%B$% приводяться до діагонального вигляду одним і тим самим перетворенням Т.к. , то з наведених міркувань випливають такі висновки.
1.1)Якщо матриця $%A$% є симетричною позитивно визначеною матрицею, то з неї витягується корінь у вигляді дійсної матриці.
1.2) Алгоритм обчислення кореня з такої матриці наступний: розв'язати завдання на власні значення, витягти з власних значень коріння, скласти з них діагональну матрицю, застосувати до неї перетворення, зворотне до перетворення, що переводить матрицю $%A$% до діагонального виду.
1.3) Кількість різних матриць $ % B $ % дорівнює $ % 2 ^ n $ %, т.к. для кожного власного значення є 2 значення кореня – позитивне та негативне.
2) Для комплексної матриці міркування залишаться чинним, якщо замінити симетричність на унітарність. Вимога позитивної визначеності у своїй, звісно, зніметься.
3)
Рішення для загального випадку.Припустимо, що перетворення $%S$% наводить матрицю $%B$% не до діагонального, а до верхнього трикутного вигляду, тобто. матриця $%B"$% є верхньою трикутною. Таке перетворення існує для будь-якої квадратної матриці. Легко переконатися, що матриця $%A"$% при цьому теж вийде верхньої трикутної, причому діагональні елементи матриці $%A"$% будуть квадратами відповідних діагональних елементів матриці $%B"$%. Це дозволяє знайти всі діагональні елементи матриці $%B"$% вилученням кореня з діагональних елементів матриці $%A"$%, а потім по ланцюжку знайти і всі інші елементи матриці $%B"$%. Звідси виходять такі висновки.
3.1) З будь-якої комплексної матриці витягується корінь, у загальному випадку такого коріння $%2^n$%, але серед них можуть бути збігаються (кратні).
3.2) Алгоритм обчислення коренів наступний: перетворити матрицю $%A$% до верхнього трикутного вигляду, знайти матрицю $%B"$% за сформульованим алгоритмом і зробити зворотне перетворення.
3.3) Необхідною та достатньою умовою речовинності коренів з речовинної матриці є не негативність діагональних елементів після перетворення матриці до трикутного вигляду. Не негативність детермінанта є умовою необхідною, але недостатньою.
Додаток 1 (відповідь на коментар). Ви мали на увазі "до трикутного вигляду". Взагалі, у пп. 1, 2 все абсолютно чітко, а над п.3 потрібно, мабуть, ще подумати. Річ у тім, що метод Гаусса може зводитися до перетворення $%S^(-1)AS$%, але в цьому грунтується доказ. Тобто. доказ застосовується тільки до тих матриць, які приводяться до трикутного вигляду перетворенням $% S ^ (-1) AS $ %.
Додаток 2. Схоже, в п.3 в цілому все правильно, тільки потрібно використовувати перетворення матриці $%A$% до Жорданової форми - для цього перетворення завжди є матриця, що виходить з вирішення завдання на власні значення. Проблема в тому, що квадрат Жорданової матриці не є матрицею Жорданової (хоча є трикутною і навіть дводіагональною). Суворе обґрунтування алгоритму вимагає доказу наступної теореми: "Якщо $%A"=B"^2$% і $%A"$%-Жорданова матриця, то $%B"$%-трикутна матриця". Твердження здається вірним, але як довести – поки не знаю.
