Teorem. Fonksiyona izin ver x=φ(t) bir noktada sürekli A ve fonksiyon y=f(x) bir noktada sürekli b=φ(a). Daha sonra karmaşık fonksiyon y=f[φ(t)]=F(t) bir noktada sürekli A.

İzin vermek x=φ(t) Ve y=f(x)- birçok değere sahip en basit temel işlevler (X) işlevler x=φ(t) fonksiyonun kapsamı y=f(x). Bildiğimiz gibi temel fonksiyonlar verilen tanım kümesinin her noktasında süreklidir. Bu nedenle önceki teoreme göre karmaşık fonksiyon y=f(φ(t)) yani iki temel fonksiyonun süperpozisyonu süreklidir. Örneğin bir fonksiyon herhangi bir noktada süreklidir x ≠ 0 iki temel fonksiyonun karmaşık bir fonksiyonu olarak x=t -1 Ve y=sinx. Ayrıca işlev y=ln sin x aralıkların herhangi bir noktasında sürekli (2kπ,(2k+1)π), k ∈ Z (günah x>0).

Tanım. y = f(x) fonksiyonu x0 noktasında ve onun bazı komşuluklarında tanımlansın. y = f(x) fonksiyonu çağrılır x0 noktasında sürekli, Eğer:

1. var
2. Bu limit fonksiyonun x0 noktasındaki değerine eşittir:

Limit tanımlanırken f(x)'in x0 noktasında tanımlanamayacağı, bu noktada tanımlı olması durumunda f(x0) değerinin limitin belirlenmesine hiçbir şekilde katılmayacağı vurgulandı. Sürekliliği belirlerken f(x0)'ın var olması esastır ve bu değerin lim f(x)'e eşit olması gerekir.

Tanım. y = f(x) fonksiyonu x0 noktasında ve onun bazı komşuluklarında tanımlansın. Tüm ε>0 için, x0 noktasının δ-komşuluğundaki tüm x'ler için pozitif bir δ sayısı varsa, f(x) fonksiyonuna x0 noktasında sürekli denir (yani |x-x0|
Burada limit değerinin f(x0)'a eşit olması gerektiği dikkate alınır, bu nedenle limit tanımıyla karşılaştırıldığında 0 komşuluğunun delinme durumu ortadan kaldırılır.
Artımlar açısından bir tanım daha (bir öncekine eşdeğer) verelim. Δх = x - x0 olarak gösterelim; bu değere argümanın artışı adını vereceğiz. x->x0 olduğundan Δx->0 olur, yani Δx - b.m. (sonsuz) miktar. Δу = f(x)-f(x0) olarak gösterelim, |Δу| olduğundan bu değere fonksiyonun artışı adını vereceğiz. (yeterince küçük |Δх| için) rastgele bir ε>0 sayısından küçük olmalıdır, bu durumda Δу- aynı zamanda b.m'dir. bu nedenle değer

Tanım. y = f(x) fonksiyonu x0 noktasında ve onun bazı komşuluklarında tanımlansın. f(x) fonksiyonu çağrılır x0 noktasında sürekli, eğer argümandaki sonsuz küçük bir artış, fonksiyondaki sonsuz küçük bir artışa karşılık geliyorsa.

Tanım. x0 noktasında sürekli olmayan f(x) fonksiyonu, süreksiz denir Bu noktada.

Tanım. Bir f(x) fonksiyonu, bir X kümesinin her noktasında sürekli ise bu fonksiyona sürekli denir.

Bir toplamın, çarpımın ve bölümün sürekliliği üzerine teorem

Sürekli bir fonksiyonun işareti altında limite geçiş teoremi

Sürekli fonksiyonların süperpozisyonunun sürekliliğine ilişkin teorem

f(x) fonksiyonu bir aralıkta tanımlı olsun ve bu aralıkta monoton olsun. O halde f(x) bu doğru parçası üzerinde yalnızca birinci türden süreksizlik noktalarına sahip olabilir.

Ara değer teoremi. f(x) fonksiyonu bir doğru parçası üzerinde sürekliyse ve a ve b iki noktasında (a, b'den küçüktür) eşit olmayan değerler alıyorsa A = f(a) ≠ B = f(b), o zaman herhangi bir sayı için C A ile B arasında, fonksiyonun değerinin C'ye eşit olduğu bir c ∈ noktası vardır: f(c) = C.

Sürekli bir fonksiyonun bir aralıkta sınırlılığı üzerine teorem. Bir f(x) fonksiyonu bir aralıkta sürekli ise bu aralıkta sınırlıdır.

Minimum ve maksimum değerlere ulaşma teoremi. f(x) fonksiyonu bir aralıkta sürekli ise bu aralıkta alt ve üst sınırlarına ulaşır.

Ters fonksiyonun sürekliliğine ilişkin teorem. y=f(x) fonksiyonu sürekli ve [a,b] aralığında kesin olarak artan (azalan) olsun. Daha sonra segment üzerinde, yine monoton olarak artan (azalan) ve sürekli olan bir ters fonksiyon x = g(y) vardır.

Fonksiyonun sürekliliği. Kırılma noktaları.

Boğa yürürken yürüyor, sallanıyor, iç çekiyor:
- Ah, tahta bitiyor, şimdi düşeceğim!

Bu derste bir fonksiyonun sürekliliği kavramını, süreksizlik noktalarının sınıflandırılmasını ve yaygın bir pratik problemi inceleyeceğiz. fonksiyonların süreklilik çalışmaları. Pek çok kişi konunun adından itibaren sezgisel olarak neyin tartışılacağını tahmin ediyor ve materyalin oldukça basit olduğunu düşünüyor. Bu doğru. Ancak ihmal nedeniyle en sık cezalandırılan şey basit görevler ve bunları çözmeye yönelik yüzeysel bir yaklaşımdır. Bu nedenle yazıyı çok dikkatli incelemenizi, tüm incelikleri ve teknikleri yakalamanızı tavsiye ederim.

Neyi bilmeniz ve yapabilmeniz gerekiyor? Pek değil. Dersi iyi öğrenmek için ne olduğunu anlamalısınız bir fonksiyonun limiti. Hazırlık düzeyi düşük okuyucular için makaleyi kavramak yeterlidir. Fonksiyon sınırları. Çözüm örnekleri ve kılavuzdaki limitin geometrik anlamına bakın Temel fonksiyonların grafikleri ve özellikleri. Ayrıca kendinizi tanımanız da tavsiye edilir. grafiklerin geometrik dönüşümleriçünkü çoğu durumda pratik bir çizim yapmayı içerir. Beklentiler herkes için iyimser ve dolu bir su ısıtıcısı bile önümüzdeki bir veya iki saat içinde bu görevin üstesinden gelebilecek!

Fonksiyonun sürekliliği. Kırılma noktaları ve sınıflandırılması

Fonksiyonun sürekliliği kavramı

Tüm sayı doğrusunda sürekli olan bir fonksiyonu ele alalım:

Veya daha kısa ve öz bir şekilde ifade etmek gerekirse fonksiyonumuz (gerçel sayılar kümesi) üzerinde süreklidir.

Sürekliliğin “darkafalı” kriteri nedir? Açıkçası, sürekli bir fonksiyonun grafiği, kalemi kağıttan kaldırmadan çizilebilir.

Bu durumda iki basit kavramı açıkça birbirinden ayırmak gerekir: bir fonksiyonun alanı Ve fonksiyonun sürekliliği. Genel olarak bu aynı şey değil. Örneğin:

Bu fonksiyon sayı doğrusunun tamamında tanımlanır. herkes“X”in anlamının kendi “y” anlamı vardır. Özellikle eğer , o zaman . Diğer noktanın noktalama işaretli olduğuna dikkat edin, çünkü bir işlevin tanımı gereği, argümanın değeri şuna karşılık gelmelidir: tek şey fonksiyon değeri. Böylece, tanım alanı fonksiyonumuz: .

Fakat bu fonksiyon sürekli açık değildir!Şu aşamada acı çektiği çok açık açıklık. Terim aynı zamanda oldukça anlaşılır ve görseldir; aslında burada kalemin kağıttan koparılması gerekecektir. Biraz sonra kesme noktalarının sınıflandırılmasına bakacağız.

Bir fonksiyonun bir noktada ve bir aralıkta sürekliliği

Belirli bir matematik probleminde, bir fonksiyonun bir noktadaki sürekliliğinden, bir fonksiyonun bir aralıkta sürekliliğinden, bir yarım aralıkta ya da bir fonksiyonun bir doğru parçası üzerindeki sürekliliğinden söz edebiliriz. Yani, “sadece süreklilik” yoktur– fonksiyon BİR YERDE sürekli olabilir. Ve diğer her şeyin temel “yapı taşı” fonksiyonun sürekliliği bu noktada .

Matematiksel analiz teorisi, bir fonksiyonun bir noktadaki sürekliliğinin tanımını “delta” ve “epsilon” komşuluklarını kullanarak verir, ancak pratikte kullanımda olan ve bizim dikkat edeceğimiz farklı bir tanım vardır.

Öncelikle hatırlayalım tek taraflı sınırlarİlk derste hayatımıza girenler fonksiyon grafikleri hakkında. Gündelik bir durumu düşünün:

Ekseni noktaya yaklaştırırsak sol(kırmızı ok), o zaman “oyunların” karşılık gelen değerleri eksen boyunca noktaya (kızıl ok) doğru ilerleyecektir. Matematiksel olarak bu gerçek şu şekilde sabitlenir: sol limit:

Girişe dikkat edin ("x solda ka'ya eğilimlidir" yazıyor). “Katkı” “eksi sıfır”ı simgeliyor Bu aslında sayıya sol taraftan yaklaştığımız anlamına geliyor.

Benzer şekilde “ka” noktasına yaklaşırsanız Sağ(mavi ok), o zaman “oyunlar” aynı değere gelecektir ancak yeşil ok boyunca ve sağ limit aşağıdaki gibi biçimlendirilecektir:

"Katkı maddesi" sembolize eder ve girişte şöyle yazıyor: "x sağdaki ka'ya eğilimlidir."

Tek taraflı limitler sonlu ve eşitse(bizim durumumuzda olduğu gibi): , o zaman GENEL bir sınır var diyeceğiz. Çok basit, genel sınır bizim “olağan”ımızdır bir fonksiyonun limiti, sonlu bir sayıya eşittir.

Fonksiyon şurada tanımlanmamışsa (grafik dalındaki siyah noktayı çıkarın), yukarıdaki hesaplamaların geçerli kalacağını unutmayın. Daha önce birkaç kez belirtildiği gibi, özellikle makalede sonsuz küçük fonksiyonlar üzerinde, ifadeler "x" anlamına gelir sonsuz yakın noktaya yaklaşırken ÖNEMLİ DEĞİL fonksiyonun kendisinin belirli bir noktada tanımlanıp tanımlanmadığı. Fonksiyon analiz edildiğinde bir sonraki paragrafta iyi bir örnek bulunacaktır.

Tanım: Bir fonksiyonun belirli bir noktadaki limiti fonksiyonun o noktadaki değerine eşitse fonksiyon bir noktada süreklidir: .

Tanım aşağıdaki terimlerle detaylandırılmıştır:

1) Fonksiyonun noktada tanımlı olması yani değerin mevcut olması gerekmektedir.

2) Fonksiyonun genel bir limiti olmalıdır. Yukarıda belirtildiği gibi bu, tek taraflı limitlerin varlığını ve eşitliğini ima eder: .

3) Belirli bir noktadaki fonksiyonun limiti, fonksiyonun bu noktadaki değerine eşit olmalıdır: .

İhlal edilirse en az birÜç koşulun gerçekleşmesi halinde fonksiyon, noktasında süreklilik özelliğini kaybeder.

Bir fonksiyonun belirli bir aralıkta sürekliliği ustaca ve çok basit bir şekilde formüle edilmiştir: Bir fonksiyon, eğer verilen aralığın her noktasında sürekli ise, aralıkta da süreklidir.

Özellikle birçok fonksiyon sonsuz bir aralıkta, yani gerçek sayılar kümesinde süreklidir. Bu doğrusal bir fonksiyondur, polinomlar, üstel, sinüs, kosinüs vb. Ve genel olarak herhangi temel fonksiyon sürekli olarak tanım alanıörneğin logaritmik bir fonksiyon aralıkta süreklidir. Umarım şimdiye kadar temel fonksiyonların grafiklerinin nasıl göründüğüne dair oldukça iyi bir fikriniz vardır. Devamlılıkları hakkında daha detaylı bilgiyi Fichtenholtz isimli nazik bir adamdan alabilirsiniz.

Bir fonksiyonun bir segment üzerindeki sürekliliği ve yarım aralıkları ile her şey de zor değil ama bunu sınıfta konuşmak daha uygun bir segmentteki bir fonksiyonun minimum ve maksimum değerlerini bulma hakkında ama şimdilik endişelenmeyelim.

Kırılma noktalarının sınıflandırılması

Fonksiyonların büyüleyici yaşamı her türlü özel nokta açısından zengindir ve kırılma noktaları biyografilerinin sayfalarından yalnızca biridir.

Not : Her ihtimale karşı, temel bir nokta üzerinde duracağım: kırılma noktası her zaman tek nokta– “arka arkaya birkaç kırılma noktası” yoktur, yani “ara aralığı” diye bir şey yoktur.

Bu noktalar sırasıyla iki büyük gruba ayrılır: birinci türden kopmalar Ve ikinci türden kopmalar. Her boşluk türünün, şu anda inceleyeceğimiz kendine has karakteristik özellikleri vardır:

Birinci türden süreksizlik noktası

Bir noktada süreklilik koşulu ihlal edilirse ve tek taraflı sınırlar sonlu , o zaman denir Birinci türden süreksizlik noktası.

En iyimser durumla başlayalım. Dersin orijinal fikrine göre teoriyi “genel anlamda” anlatmak istedim ancak malzemenin gerçekliğini ortaya koymak için belirli karakterlerin olduğu seçeneğe karar verdim.

Ebedi Alev'in arka planında yeni evlilerin fotoğrafı gibi üzücü, ancak aşağıdaki çekim genel olarak kabul ediliyor. Fonksiyonun grafiğini çizimde gösterelim:


Bu fonksiyon nokta hariç tüm sayı doğrusunda süreklidir. Ve aslında payda sıfıra eşit olamaz. Ancak limitin anlamına uygun olarak şunları yapabiliriz: sonsuz yakın Hem soldan hem de sağdan "sıfıra" yaklaşın, yani tek taraflı sınırlar mevcuttur ve açıkça çakışmaktadır:
(Sürekliliğin 2 numaralı koşulu karşılanmıştır).

Ancak fonksiyon bu noktada tanımlı olmadığından sürekliliğin 1 numaralı koşulu ihlal edilmiş olur ve fonksiyon bu noktada süreksizliğe uğrar.

Bu tür bir mola (mevcut olanla) genel sınır) denir onarılabilir boşluk. Neden çıkarılabilir? Çünkü fonksiyon yeniden tanımla kırılma noktasında:

Tuhaf mı görünüyor? Belki. Ancak böyle bir fonksiyon gösterimi hiçbir şeyle çelişmez! Artık fark kapandı ve herkes mutlu:


Resmi bir kontrol yapalım:

2) – genel bir sınır vardır;
3)

Böylece, her üç koşul da sağlanır ve bir fonksiyonun bir noktadaki sürekliliğinin tanımıyla fonksiyon bir noktada süreklidir.

Bununla birlikte, matan'dan nefret edenler işlevi kötü bir şekilde tanımlayabilirler; örneğin :


Burada ilk iki süreklilik koşulunun karşılanması ilginçtir:
1) – fonksiyon belirli bir noktada tanımlıdır;
2) – genel bir sınır vardır.

Ancak üçüncü sınır geçilmemiştir: yani fonksiyonun noktadaki limiti. eşit değil Belirli bir fonksiyonun belirli bir noktadaki değeri.

Böylece bir noktada fonksiyon süreksizliğe maruz kalır.

İkinci, daha üzücü vaka denir birinci türden kopma bir atlama ile. Ve üzüntü tek taraflı sınırlamalarla çağrıştırılır sonlu ve farklı. Dersin ikinci çiziminde bir örnek gösterilmektedir. Böyle bir boşluk genellikle parçalı tanımlı fonksiyonlar makalede daha önce bahsedilenler grafik dönüşümleri hakkında.

Parçalı fonksiyonu düşünün ve çizimini tamamlayacağız. Bir grafik nasıl oluşturulur? Çok basit. Yarım aralıkta bir parabol parçası (yeşil), aralıkta - düz bir çizgi parçası (kırmızı) ve yarım aralıkta - düz bir çizgi (mavi) çiziyoruz.

Ayrıca eşitsizlik nedeniyle ikinci dereceden fonksiyon (yeşil nokta) için değer belirlenir ve eşitsizlik nedeniyle doğrusal fonksiyon (mavi nokta) için değer belirlenir:

En zor durumda, grafiğin her bir parçasının nokta nokta oluşturulmasına başvurmalısınız (ilk bölüme bakın). fonksiyonların grafikleri hakkında ders).

Şimdi sadece konuyla ilgileneceğiz. Devamlılık açısından inceleyelim:

2) Tek taraflı limitleri hesaplayalım.

Sol tarafta kırmızı bir çizgi segmentimiz var, dolayısıyla sol taraftaki limit şu şekildedir:

Sağda mavi düz çizgi ve sağdaki limit var:

Sonuç olarak aldık sonlu sayılar ve onlar eşit değil. Tek taraflı limitler olduğundan sonlu ve farklı: , o zaman fonksiyonumuz tolere eder birinci türden bir sıçrama ile süreksizlik.

Boşluğun ortadan kaldırılamaması mantıklıdır - önceki örnekte olduğu gibi, işlev gerçekte daha fazla tanımlanamaz ve "birbirine yapıştırılamaz".

İkinci türden süreksizlik noktaları

Genellikle diğer tüm yırtılma vakaları akıllıca bu kategoriye sınıflandırılır. Her şeyi listelemeyeceğim çünkü pratikte sorunların% 99'unda karşılaşacaksınız sonsuz boşluk– sol el veya sağ el kullanıldığında ve daha sıklıkla her iki sınır da sonsuzdur.

Ve elbette en belirgin resim sıfır noktasındaki hiperboldür. Burada her iki tek taraflı limit de sonsuzdur: dolayısıyla fonksiyon, noktasında ikinci türden bir süreksizliğe maruz kalır.

Yazılarımı mümkün olduğu kadar çeşitli içeriklerle doldurmaya çalışıyorum o yüzden gelin henüz görülmemiş bir fonksiyonun grafiğine bakalım:

standart şemaya göre:

1) Payda sıfıra gittiği için fonksiyon bu noktada tanımlı değildir.

Elbette fonksiyonun noktasında süreksizlik yaşadığı sonucunu hemen çıkarabiliriz, ancak genellikle koşulun gerektirdiği süreksizliğin niteliğini sınıflandırmak iyi olacaktır. Bunu yapmak için:

Size kayıt derken şunu kastettiğimizi hatırlatmama izin verin: sonsuz küçük negatif sayı ve girişin altında - sonsuz küçük pozitif sayı.

Tek taraflı limitler sonsuzdur, bu da fonksiyonun noktasında 2. türden bir süreksizliğin olduğu anlamına gelir. Y ekseni dikey asimptot grafik için.

Her iki tek taraflı sınırın da mevcut olması nadir değildir, ancak bunlardan yalnızca biri sonsuzdur, örneğin:

Bu fonksiyonun grafiğidir.

Süreklilik noktasını inceliyoruz:

1) Fonksiyon bu noktada tanımlanmamıştır.

2) Tek taraflı limitleri hesaplayalım:

Her ne kadar pek çok okuyucu her şeyi görmüş ve tahmin etmiş olsa da, dersin son iki örneğinde bu tür tek taraflı limitleri hesaplama yönteminden bahsedeceğiz.

Soldaki limit sonludur ve sıfıra eşittir ("noktanın kendisine gitmeyiz"), fakat sağdaki limit sonsuzdur ve grafiğin turuncu dalı, kendi noktasına sonsuz derecede yaklaşmaktadır. dikey asimptot, denklem tarafından verilmiştir (siyah noktalı çizgi).

Yani fonksiyon zarar görüyor ikinci tür süreksizlik noktada.

1. tür süreksizlikte fonksiyon süreksizlik noktasında tanımlanabilir. Örneğin parçalı bir fonksiyon için Koordinatların başlangıç ​​noktasına siyah, kalın bir nokta koymaktan çekinmeyin. Sağda bir hiperbolün dalı vardır ve sağdan limit sonsuzdur. Bu grafiğin neye benzediğine dair neredeyse herkesin bir fikri olduğunu düşünüyorum.

Herkesin sabırsızlıkla beklediği şey:

Bir fonksiyonun sürekliliği nasıl incelenir?

Bir noktadaki süreklilik için bir fonksiyonun incelenmesi, üç süreklilik koşulunun kontrol edilmesini içeren önceden belirlenmiş bir rutin şemaya göre gerçekleştirilir:

Örnek 1

İşlevi keşfedin

Çözüm:

1) Kapsam içindeki tek nokta, fonksiyonun tanımlanmadığı yerdir.

2) Tek taraflı limitleri hesaplayalım: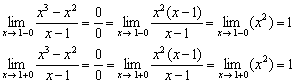

Tek taraflı limitler sonlu ve eşittir.

Böylece fonksiyon bu noktada çıkarılabilir bir süreksizliğe maruz kalır.

Bu fonksiyonun grafiği neye benziyor?

basitleştirmek isterim ve sıradan bir parabol elde edilmiş gibi görünüyor. ANCAK orijinal fonksiyon noktasında tanımlanmadığından aşağıdaki cümle gereklidir:

Çizimi yapalım:

Cevap: Fonksiyon, çıkarılabilir bir süreksizliğin olduğu nokta dışında tüm sayı doğrusunda süreklidir.

Fonksiyon iyi veya çok iyi olmayan bir şekilde daha ayrıntılı olarak tanımlanabilir, ancak duruma göre bu gerekli değildir.

Bunun çok uç bir örnek olduğunu mu söylüyorsunuz? Hiç de bile. Bu, pratikte onlarca kez yaşandı. Sitenin görevlerinin neredeyse tamamı gerçek bağımsız çalışma ve testlerden gelmektedir.

Favori modüllerimizden kurtulalım:

Örnek 2

İşlevi keşfedin süreklilik için. Varsa fonksiyon süreksizliklerinin doğasını belirleyin. Çizimi yürütün.

Çözüm: Bazı nedenlerden dolayı öğrenciler, karmaşık bir yanı olmamasına rağmen modül içeren işlevlerden korkuyor ve hoşlanmıyorlar. Zaten derste bu tür şeylere biraz değinmiştik. Grafiklerin geometrik dönüşümleri. Modül negatif olmadığından aşağıdaki şekilde genişletilir: , burada "alfa" bir ifadedir. Bu durumda fonksiyonumuzun parçalı olarak yazılması gerekir: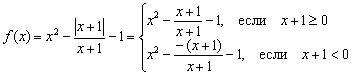

Ancak her iki parçanın kesirlerinin de azaltılması gerekir. Azaltma, önceki örnekte olduğu gibi, sonuçsuz gerçekleşmeyecektir. Payda sıfıra gittiği için orijinal fonksiyon bu noktada tanımlı değildir. Bu nedenle sistem ek olarak koşulu belirtmeli ve ilk eşitsizliği katı yapmalıdır:

Şimdi ÇOK FAYDALI bir karar tekniği hakkında: Taslak üzerinde işi bitirmeden önce (şartlar gerektirsin veya gerektirmesin) çizim yapmak avantajlıdır. Bu, öncelikle süreklilik noktalarını ve süreksizlik noktalarını anında görmenize yardımcı olacak ve ikinci olarak, tek taraflı limitleri bulurken sizi hatalardan %100 koruyacaktır.

Çizimi yapalım. Hesaplamalarımıza uygun olarak, noktanın soluna bir parabol parçası (mavi renk) ve sağa - bir parabol parçası (kırmızı renk) çizmek gerekirken, fonksiyon şu noktada tanımlanmamıştır: kendisini işaret eder:

Şüpheniz varsa birkaç x değeri alın ve bunları fonksiyona ekleyin (modülün olası eksi işaretini yok ettiğini unutmayın) ve grafiği kontrol edin.

Süreklilik fonksiyonunu analitik olarak inceleyelim:

1) Fonksiyon bu noktada tanımlı olmadığı için bu noktada sürekli olmadığını hemen söyleyebiliriz.

2) Süreksizliğin doğasını belirleyelim; bunun için tek taraflı limitleri hesaplayalım:

Tek taraflı limitler sonlu ve farklıdır; bu, fonksiyonun noktasındaki bir sıçramayla 1. türden bir süreksizliğe maruz kaldığı anlamına gelir. Limitleri bulurken kırılma noktasındaki fonksiyonun tanımlı olup olmamasının önemli olmadığını tekrar unutmayın.

Şimdi geriye kalan tek şey çizimi taslaktan aktarmak (sanki araştırma yardımıyla yapılmış gibi ;-)) ve görevi tamamlamak:

Cevap: fonksiyon, bir sıçrama ile birinci türden bir süreksizlik yaşadığı nokta dışında tüm sayı doğrusu üzerinde süreklidir.

Bazen süreksizlik sıçramasının ek göstergesine ihtiyaç duyarlar. Basitçe hesaplanır - sağ limitten sol limiti çıkarmanız gerekir: yani kırılma noktasında fonksiyonumuz 2 birim aşağıya sıçradı (eksi işaretinin bize söylediği gibi).

Örnek 3

İşlevi keşfedin süreklilik için. Varsa fonksiyon süreksizliklerinin doğasını belirleyin. Bir çizim yapın.

Bu kendi başınıza çözebileceğiniz bir örnek, dersin sonundaki örnek çözümdür.

İşlev üç bölümden oluştuğunda görevin en popüler ve yaygın versiyonuna geçelim:

Örnek 4

Bir fonksiyonu süreklilik açısından inceleyin ve fonksiyonun grafiğini çizin .

Çözüm: Fonksiyonun üç bölümünün de karşılık gelen aralıklarda sürekli olduğu açıktır, bu nedenle parçalar arasındaki yalnızca iki "birleşim" noktasını kontrol etmek kalır. Öncelikle bir taslak çizim yapalım; yazımın ilk bölümünde yapım tekniğini yeterince detaylı bir şekilde anlattım. Tekil noktalarımızı dikkatlice takip etmemiz gerekiyor: eşitsizlik nedeniyle değer düz çizgiye (yeşil nokta) ve eşitsizlik nedeniyle değer parabole (kırmızı nokta) aittir:


Prensip olarak her şey açık =) Geriye kalan tek şey kararı resmileştirmek. İki "ortak" noktanın her biri için standart olarak 3 süreklilik koşulunu kontrol ederiz:

BEN) Süreklilik noktasını inceliyoruz

1)

Tek taraflı limitler sonlu ve farklıdır; bu, fonksiyonun noktasındaki bir sıçramayla 1. türden bir süreksizliğe maruz kaldığı anlamına gelir.

Süreksizlik sıçramasını sağ ve sol limitler arasındaki fark olarak hesaplayalım:
yani grafik bir birim yukarı sarsıldı.

II) Süreklilik noktasını inceliyoruz

1) – fonksiyon belirli bir noktada tanımlanır.

2) Tek taraflı limitleri bulun:

– Tek taraflı limitler sonlu ve eşittir, yani genel bir limit vardır.

3) – Bir fonksiyonun bir noktadaki limiti, bu fonksiyonun belirli bir noktadaki değerine eşittir.

Son aşamada çizimi son versiyona aktarıyoruz, ardından son akoru koyuyoruz:

Cevap: fonksiyon, bir sıçrama ile birinci türden bir süreksizliğe maruz kaldığı nokta hariç, tüm sayı doğrusu üzerinde süreklidir.

Örnek 5

Bir fonksiyonu süreklilik açısından inceleyin ve grafiğini oluşturun .

Bu, dersin sonunda bağımsız çözüm, kısa çözüm ve problemin yaklaşık bir örneği için bir örnektir.

Bir noktada fonksiyonun sürekli olması gerektiği, diğer noktada ise süreksizliğin olması gerektiği izlenimine kapılabilirsiniz. Uygulamada bu her zaman böyle değildir. Kalan örnekleri ihmal etmemeye çalışın; birkaç ilginç ve önemli özellik olacaktır:

Örnek 6

Bir fonksiyon verildiğinde . Fonksiyonu noktalardaki süreklilik açısından inceleyin. Bir grafik oluşturun.

Çözüm: ve tekrar taslaktaki çizimi hemen yürütün:

Bu grafiğin özelliği parçalı fonksiyonun apsis ekseni denklemi ile verilmesidir. Burada bu alan yeşil renkle çizilmiştir, ancak bir defterde genellikle basit bir kalemle kalın harflerle vurgulanmıştır. Ve tabii ki koçlarımızı da unutmayın: değer teğet dalına (kırmızı nokta) ve değer de düz çizgiye aittir.

Çizimde her şey açıktır - fonksiyon tüm sayı doğrusu boyunca süreklidir, geriye kalan tek şey, 3-4 benzer örnekten sonra kelimenin tam anlamıyla tam otomasyona getirilen çözümü resmileştirmektir:

BEN) Süreklilik noktasını inceliyoruz

1) – fonksiyon belirli bir noktada tanımlanır.

2) Tek taraflı limitleri hesaplayalım:

yani genel bir limit var.

Her ihtimale karşı, size önemsiz bir gerçeği hatırlatmama izin verin: Bir sabitin limiti, sabitin kendisine eşittir. Bu durumda sıfırın limiti sıfırın kendisine eşittir (sol limit).

3) – Bir fonksiyonun bir noktadaki limiti, bu fonksiyonun belirli bir noktadaki değerine eşittir.

Dolayısıyla bir fonksiyonun bir noktadaki sürekliliğinin tanımına göre bir fonksiyon bir noktada süreklidir.

II) Süreklilik noktasını inceliyoruz

1) – fonksiyon belirli bir noktada tanımlanır.

2) Tek taraflı limitleri bulun:

Ve burada birin limiti birimin kendisine eşittir.

– genel bir sınır vardır.

3) – Bir fonksiyonun bir noktadaki limiti, bu fonksiyonun belirli bir noktadaki değerine eşittir.

Dolayısıyla bir fonksiyonun bir noktadaki sürekliliğinin tanımına göre bir fonksiyon bir noktada süreklidir.

Her zamanki gibi araştırma sonrasında çizimimizi son versiyona aktarıyoruz.

Cevap: Fonksiyon noktalarda süreklidir.

Lütfen, bu durumda bize süreklilik için tüm fonksiyonun incelenmesi hakkında hiçbir şey sorulmadığını ve bunun formüle edilmesinin iyi bir matematiksel form olarak kabul edildiğini unutmayın. kesin ve net sorulan sorunun cevabı. Bu arada, eğer koşullar bir grafik oluşturmanızı gerektirmiyorsa, o zaman onu oluşturmama hakkına sahipsiniz (ancak daha sonra öğretmen sizi bunu yapmaya zorlayabilir).

Sorunu kendi başınıza çözmek için küçük bir matematiksel "tekleme":

Örnek 7

Bir fonksiyon verildiğinde . Fonksiyonu noktalardaki süreklilik açısından inceleyin. Varsa kesme noktalarını sınıflandırın. Çizimi yürütün.

Tüm "kelimeleri" doğru "telaffuz etmeye" çalışın =) Ve grafiği daha kesin, doğru çizin, her yerde gereksiz olmayacak;-)

Hatırlayacağınız gibi çizimi taslak olarak hemen tamamlamanızı önermiştim ancak zaman zaman grafiğin neye benzediğini hemen anlayamadığınız örneklerle karşılaşıyorsunuz. Bu nedenle, bazı durumlarda önce tek taraflı limitleri bulmak ve ancak daha sonra çalışmaya dayalı olarak dalları tasvir etmek avantajlıdır. Son iki örnekte ayrıca bazı tek taraflı limitlerin hesaplanmasına yönelik bir teknik de öğreneceğiz:

Örnek 8

Fonksiyonu süreklilik açısından inceleyin ve şematik grafiğini oluşturun.

Çözüm: kötü noktalar açıktır: (üssün paydasını sıfıra indirir) ve (tüm kesrin paydasını sıfıra indirir). Bu fonksiyonun grafiğinin neye benzediği belli değil, bu da ilk önce biraz araştırma yapmanın daha iyi olacağı anlamına geliyor.

Tanım
Fonksiyon f (X) isminde x noktasında sürekli 0 bu noktanın komşuluğu ve eğer x'in limiti x'e doğru gidiyorsa 0 x'teki fonksiyon değerine eşit 0 :
.

Bir fonksiyonun limitinin Cauchy ve Heine tanımlarını kullanarak şunu verebiliriz: Bir fonksiyonun bir noktadaki sürekliliğine ilişkin genişletilmiş tanımlar .

Süreklilik kavramını şu şekilde formüle edebiliriz: artışlar açısından. Bunu yapmak için, x değişkeninin o noktadaki artışı adı verilen yeni bir değişken tanıtıyoruz.
.
O halde fonksiyon şu noktada süreklidir:
.
Yeni bir fonksiyon tanıtalım: Onu aradılar fonksiyon artışı
.

noktada.
Fonksiyon f (X) isminde O halde fonksiyon şu noktada süreklidir: 0 , eğer bu noktanın sağ taraftaki (sol taraftaki) bir komşuluğunda tanımlanmışsa ve x noktasındaki sağ (sol) limit ise 0 x'teki fonksiyon değerine eşit 0 :
.

Sürekli bir fonksiyonun sınırlılığı üzerine teorem
f fonksiyonu olsun (X) x noktasında süreklidir 0 . Sonra bir mahalle U var(x0)

, işlevin sınırlı olduğu.
Sürekli bir fonksiyonun işaretinin korunmasına ilişkin teorem
.
Fonksiyon bir noktada sürekli olsun.
Ve bu noktada pozitif (negatif) bir değere sahip olsun:

Daha sonra fonksiyonun pozitif (negatif) bir değere sahip olduğu noktanın bir komşuluğu vardır:
.
Sürekli fonksiyonların aritmetik özellikleri
Fonksiyonlar ve noktasında sürekli olsun.

O halde fonksiyonlar, ve noktasında süreklidir.
Eğer ise fonksiyon o noktada süreklidir.

Sol-sağ süreklilik özelliği

Karmaşık bir fonksiyonun sürekliliği

Bir fonksiyon bir noktada süreklidir ancak ve ancak sağda ve solda süreklidir.
Özelliklerin ispatları “Bir noktada sürekli olan fonksiyonların özellikleri” sayfasında verilmiştir.
Karmaşık bir fonksiyon için süreklilik teoremi

Fonksiyon bir noktada sürekli olsun.

Fonksiyonun bu noktada sürekli olmasına izin verin.
O halde karmaşık fonksiyon bu noktada süreklidir.
.
Karmaşık bir fonksiyonun limiti 0 Bir fonksiyonun sürekli fonksiyonunun limiti üzerine teorem
Fonksiyonun bir limiti olsun ve bu şuna eşit olsun:
İşte t noktası
.

sonlu veya sonsuz uzaklıkta olabilir: .
Fonksiyonun bu noktada sürekli olmasına izin verin.
O zaman karmaşık bir fonksiyonun bir limiti vardır ve şuna eşittir:
Karmaşık bir fonksiyonun sınırına ilişkin teorem
.

Fonksiyonun bir limiti olsun ve bir noktanın delinmiş mahallesini, bir noktanın delinmiş komşuluğuna eşleyin.

Fonksiyon bu komşuluk üzerinde tanımlansın ve üzerinde bir limit olsun.
İşte son veya sonsuz uzaklıktaki noktalar: . Mahalleler ve onlara karşılık gelen sınırlar iki taraflı veya tek taraflı olabilir. O halde karmaşık bir fonksiyonun bir limiti vardır ve bu şuna eşittir:
Kırılma noktaları
Kırılma noktasının belirlenmesi

Fonksiyonun noktanın bazı delinmiş komşuluklarında tanımlandığını varsayalım.
Nokta denir Birinci türden süreksizlik noktası fonksiyon kırılma noktası
.

iki koşuldan biri karşılanırsa:
1) 'de tanımlanmamış; 2) 'da tanımlıdır, ancak bu noktada değildir.
.

1. tür süreksizlik noktasının belirlenmesi
Nokta denir Nokta denir if bir kırılma noktasıdır ve solda ve sağda sonlu tek taraflı limitler vardır:
,
Fonksiyon atlamanın tanımı

Dolayısıyla çıkarılabilir süreksizlik noktası, fonksiyonun sıçramasının sıfıra eşit olduğu 1. tür süreksizlik noktasıdır.

2. tür süreksizlik noktasının belirlenmesi
Nokta denir ikinci türün süreksizlik noktası 1. türden bir süreksizlik noktası değilse.

Yani, en az bir tek taraflı limit yoksa veya bir noktada en az bir tek taraflı limit sonsuza eşittir.

Bir aralıkta sürekli olan fonksiyonların özellikleri
Bir aralıkta sürekli olan bir fonksiyonun tanımı

Bir fonksiyon, açık aralığın (at) tüm noktalarında ve sırasıyla a ve b noktalarında sürekli ise, bir (at) aralığında sürekli olarak adlandırılır.
Weierstrass'ın bir aralıkta sürekli olan bir fonksiyonun sınırlılığına ilişkin ilk teoremi

Bir fonksiyon bir aralıkta sürekli ise bu aralıkta sınırlıdır.
Maksimumun (minimum) ulaşılabilirliğinin belirlenmesi
Bir fonksiyon, eğer bir argüman varsa, kümedeki maksimum (minimum) değerine ulaşır.

herkes için.
Üst (alt) yüzün ulaşılabilirliğinin belirlenmesi
.

Bir fonksiyon, eğer bir argüman varsa, kümedeki üst (alt) sınırına ulaşır.
Weierstrass'ın sürekli bir fonksiyonun maksimum ve minimumuna ilişkin ikinci teoremi

Bir doğru parçası üzerinde sürekli olan bir fonksiyon, onun üzerinde üst ve alt sınırlarına ulaşır veya aynı şekilde, doğru parçası üzerinde maksimum ve minimum değerlerine ulaşır.
Bolzano-Cauchy ara değer teoremi
.

Fonksiyonun segment üzerinde sürekli olmasına izin verin.
Ve C'nin, segmentin uçlarındaki fonksiyonun değerleri arasında yer alan rastgele bir sayı olmasına izin verin: ve.
.

O zaman bir nokta var
Sonuç 1
Ve bu noktada pozitif (negatif) bir değere sahip olsun:

Fonksiyonun segment üzerinde sürekli olmasına izin verin.

Ve segmentin uçlarındaki fonksiyon değerlerinin farklı işaretlere sahip olmasına izin verin: veya .
Sonra fonksiyonun değerinin sıfıra eşit olduğu bir nokta vardır:
Bir fonksiyon, eğer bir argüman varsa, kümedeki maksimum (minimum) değerine ulaşır.
Sonuç 2 Fonksiyonun segment üzerinde sürekli olmasına izin verin. Ve öyle olsun.
.

Daha sonra fonksiyon, tüm değerlerin aralığını ve yalnızca bu değerlerden alır:
;
Ters fonksiyonlar
Bir fonksiyon, eğer bir argüman varsa, kümedeki maksimum (minimum) değerine ulaşır.

Ters fonksiyonun tanımı
Bir fonksiyonun X tanım alanına ve Y değerlerine sahip olmasına izin verin.

Ve şu özelliğe sahip olsun:
Doğrudan ve ters fonksiyonların grafikleri düz çizgiye göre simetriktir.

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teorem
Fonksiyonun segment üzerinde sürekli ve kesinlikle artan (azalan) olmasına izin verin.

Daha sonra ters fonksiyon tanımlanır ve kesinlikle artan (azalan) segment üzerinde süreklidir.

Artan bir fonksiyon için.
Azaltmak için - .

Bir aralıkta ters fonksiyonun varlığı ve sürekliliğine ilişkin teorem
Fonksiyonun açık sonlu veya sonsuz bir aralıkta sürekli ve kesinlikle artan (azalan) olmasına izin verin.

Daha sonra ters fonksiyon tanımlanır ve aralıkta süreklidir, bu kesinlikle artar (azalır).

Artan bir fonksiyon için.

Azaltmak için: .

Benzer şekilde ters fonksiyonun yarı aralıkta varlığı ve sürekliliğine ilişkin teoremi de formüle edebiliriz.

Temel fonksiyonların özellikleri ve sürekliliği Temel fonksiyonlar ve bunların tersi, tanım alanlarında süreklidir. Aşağıda karşılık gelen teoremlerin formülasyonlarını sunuyoruz ve kanıtlarına bağlantılar sağlıyoruz.Üstel fonksiyon > 0 Üstel fonksiyon f
,
(x) = balta
.

, a tabanlı
dizinin limiti
x'e yönelen rastgele bir rasyonel sayılar dizisi nerede: Teorem. Üstel Fonksiyonun Özellikleri
Üstel fonksiyon aşağıdaki özelliklere sahiptir:(S.0) 1 tanımlanmış, için, herkes için;
(S.1) bir ≠ için
birçok anlamı vardır; ;
(S.2) ;
kesinlikle artar, kesinlikle azalır, sabittir; ;
(S.3) ;
(S.3*) ;
(S.4) ;
(S.5)(S.6)
(S.7)(S.8)
Ve bu noktada pozitif (negatif) bir değere sahip olsun:

herkes için sürekli;

(S.9) ; Logaritma Logaritmik fonksiyon veya logaritma, y

= log a x
, a tabanlı a tabanlı üstel fonksiyonun tersidir. Teorem. Logaritmanın özellikleri
a tabanlı logaritmik fonksiyon, y = x'i günlüğe kaydet
, aşağıdaki özelliklere sahiptir: tanımlanmış, için, herkes için;
(L.1) argümanın pozitif değerleri için ve için tanımlanmış ve sürekli;
(L.2)(S.8)
(S.8)
(L.3) ;
kesinlikle artar, kesinlikle azalır;(S.8)
(L.4)(S.8)
(L.5)(S.8)
(L.6) Ve bu noktada pozitif (negatif) bir değere sahip olsun:

(L.7)

(L.8)
.
(L.9)

Üs ve doğal logaritma
Üstel fonksiyon ve logaritmanın tanımlarında kuvvetin tabanı veya logaritmanın tabanı olarak adlandırılan bir sabit ortaya çıkar. Matematiksel analizde, çoğu durumda, e sayısı temel olarak kullanılırsa daha basit hesaplamalar elde edilir:
"Doğal logaritma, ln x fonksiyonu"

Güç fonksiyonu

p üssüyle kuvvet fonksiyonu f fonksiyonu (x) = xp x noktasındaki değeri, p noktasındaki x tabanlı üstel fonksiyonun değerine eşittir.
Ayrıca, f (0) = 0 p = 0 p için > 0 .

Burada argümanın negatif olmayan değerleri için y = x p kuvvet fonksiyonunun özelliklerini ele alacağız.
Rasyonel rasyonellerde tek m için kuvvet fonksiyonu negatif x için de tanımlanır.

Bu durumda özellikleri çift veya tek kullanılarak elde edilebilir.
Bu durumlar “Güç fonksiyonu, özellikleri ve grafikleri” sayfasında ayrıntılı olarak tartışılmış ve gösterilmiştir.
Teorem. Güç fonksiyonunun özellikleri (x ≥ 0) p üssüne sahip bir kuvvet fonksiyonu, y = x p, aşağıdaki özelliklere sahiptir:
(C.1)
sette tanımlanmış ve sürekli

,

"de.
Trigonometrik fonksiyonlar Trigonometrik fonksiyonların sürekliliği üzerine teorem Trigonometrik fonksiyonlar: sinüs ( günah x), kosinüs ( çünkü x), teğet ( tg x

) ve kotanjant (
ctgx Ters trigonometrik fonksiyonların sürekliliğine ilişkin teorem Ters trigonometrik fonksiyonlar: arksinüs ( ark sin x), ark kosinüs ( arkcos x), arktanjant ( arktan x) ve ark teğet (

arkctg x
), tanım alanlarında süreklidir.
Kullanılan literatür:
O.I. Besov. Matematiksel analiz üzerine dersler. Bölüm 1. Moskova, 2004.