Büyük petrol ve gaz ansiklopedisi

Sözlü olarak cevap vereceğiz! Herhangi bir üçgen piramidin etrafında bir kürenin tanımlanabileceği doğru mu? Herhangi bir dörtgen piramidin etrafındaki bir küreyi tanımlamak mümkün müdür? Bir piramidin etrafındaki bir küreyi tanımlayabilmesi için hangi özelliklere sahip olması gerekir? Yan kenarı tabana dik olan bir kürenin içine bir piramit yazılmıştır. Bir kürenin merkezi nasıl bulunur? Düzenli bir piramidin yakınında bir küre tanımlanmaktadır. Merkezi piramidin elemanlarına göre nasıl konumlandırılmıştır?

Slayt 17 sunumdan "Geometri problemleri" 11. sınıf.

Sunumlu arşivin boyutu 1032 KB'dir.

Geometri 11. sınıf

diğer sunumların özeti

“Merkezi simetri kavramı” - Uzayın kendi üzerine haritalanması. Merkezi simetri. Şekil simetrik olarak adlandırılır. Merkezi simetri harekettir. Uzayın hareketi. M ve M1 noktalarına simetrik denir. Mülk. Hareketler. Uçağın hareketlerine aşina olduk. Görev. Merkezi simetri, dönmenin özel bir durumudur.

“Üçgenin alanını hesaplama sorunları” - Ivan Niven. Bir sorunu çözmek. Ders sloganı. Kişisel hedefler. Şeklin alanını bulun. Matematiksel dikte. Bir üçgenin alanını bulma yöntemleri. Bir ifade seçin. Beden eğitimi dakikası. Şeklin alanını hesaplayın. Şeklin alanı. İlerleme kontrol ediliyor. Kare.

“Sterometride görevler” - Köşeler arasındaki mesafenin karesini bulun. Görevler. Kurşun topun çapı. Topun hacmi ve parçaları. Çokyüzlünün açısını bulun. Piramidin hacmini bulun. A noktasının koordinatını bulun. Dairesel sektör. Silindirin hacmi V'yi bulun. Çokyüzlünün yüzey alanını bulun. Yamuğun alanını bulun. Çevre.

“Bir devrim cismin hacmini hesaplayın” - Küre. Silindir ve koni. Koni. Silindirler etrafımızdadır. Bir koninin hacmi V. Küp Koninin tanımı. Dönme cisimlerinin türleri. Top. Dönen cisimlerin hacimleri. Figür. Hacmi bulun. Silindirik kap. Silindirin tanımı. Yarıçaplar. Silindir. Bir koninin hacmi.

“Etrafımızda dönen cisimler” - Etrafımızda dönen cisimler. Endüstriyel ekipmanlar. Döndürme gövdelerini bulun. Orman koni ladin. İtalya'daki eğik kule. Uzayda. Melnikov'un evi. Koni. Yuvarlak kuleler. Yuvarlak Binanın Tarihi. Kozmik bedenler.

Çokyüzlü ve yuvarlak gövdelerin kombinasyonları

Küre ve top kavramları.

Küre uzaydaki tüm noktalardan oluşan bir kümeden oluşan bir şekildir; her birinin belirli bir O noktasına olan uzaklığı, belirli bir pozitif sayı r'ye eşittir. O noktasına denir merkez Küre ve bir noktayı küre üzerindeki herhangi bir noktaya bağlayan doğru parçası onun yarıçap. Bir kürenin tüm yarıçaplarının uzunluğu r'dir. r sayısına kürenin yarıçapı denir.

Küre, uzayda kendisine ait olmayan tüm noktaların kümesini iki alt kümeye böler: dahili Ve harici küreye göre alan. İç bölge, uzayda her birinin merkeze uzaklığı yarıçaptan küçük olan noktaları içerir ve dış bölge, her birinin merkeze uzaklığı yarıçaptan daha büyük olan noktaları içerir.

Top uzaydaki tüm noktalardan oluşan bir kümeden oluşan bir şekildir; her birinden belirli bir O noktasına olan mesafe, belirli bir pozitif sayıdan r daha büyük değildir. O noktasına denir merkez top ve r sayısı onun yarıçap. O merkezli, yarıçapı r olan bir küreye ne ad verilir? yüzey veya topun sınırı. Bir topun kendi yüzeyine ait olmayan tüm noktalarına topun iç noktaları veya topun içinde yatan noktalar denir. Dolayısıyla top, bir kürenin tüm noktalarının (topun yüzeyi) birleşmesinden ve bu küreye göre tüm iç noktaların kümesinden oluşan bir şekildir.

Topun yüzeyine teğet olan düzleme denir teğet düzlem baloya. Bir düzlem bir topa teğettir ancak ve ancak topun yüzeyinde bu noktaya çizilen yarıçapa dik bir noktadan geçerse. Ayrıca topun yüzeyindeki her noktadan topa teğet olan tek bir düzlemin geçtiğine dikkat edin.

Bir çokyüzlü etrafında çevrelenmiş bir küre.

Tanım. Küre denir çokyüzlünün etrafında tanımlanmış, eğer çokyüzlünün tüm köşeleri küre üzerinde yer alıyorsa.

Teorem 1.Herhangi bir üçgen piramidin etrafında bir küre tanımlanabilir.

Piramidin tabanının köşelerinden eşit uzaklıktaki noktalar kümesi, tabanın yakınındaki çevrelenmiş dairenin merkezinden çizilen bir diktir (bunun etrafında bir daire tanımlanabiliyorsa, belirli bir çokgenin köşelerinden eşit uzaklıktaki uzayda HMT mevcuttur). çokgendir ve bu çokgenin düzlemine çevrelenen dairenin merkezinden çizilen bir dik vardır. Çevrel dairenin merkezi, piramidin tabanının dik açıortaylarının kesişme noktasıdır.

Çevreleyen kürenin merkezini bulmak için, AD yan kenarının ortası olan M noktasından geçen bir düzlem çizin. Bu düzlem dikeyle (daha önce belirtilmişti) S noktasında kesişecektir. Yapısal olarak SA=SB=SC ve ayrıca ASD üçgeninin ikizkenar olması gerçeğinden (yine yapı itibariyle) SA=SD sonucu çıkar. Dolayısıyla piramidin tüm köşelerinden S noktasına olan mesafeler eşittir ve bu mesafe ABCD piramidinin yakınındaki çevrelenen kürenin yarıçapına eşittir (SA=SB=SC=SD=R).

Örnek 1 . Düzgün bir tetrahedronun çevrelediği kürenin yarıçapını bulun.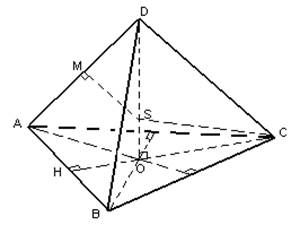

SOC üçgenini düşünün. Dik açılı O ile dikdörtgen olacaktır (yapısal olarak OD, piramidin yüksekliği olacaktır).

, çünkü O medyanların kesişme noktasıdır.

, burada DO piramidin yüksekliğidir.

Daha sonra Pisagor teoremine göre şu çıkar: veya

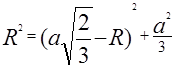
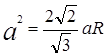
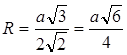
Cevap: Düzgün bir tetrahedronun çevrelediği kürenin yarıçapı şuna eşittir:

Teorem 2. Piramidin tabanı etrafında bir daire tanımlanabiliyorsa, piramidin etrafında bir küre de tanımlanabilir..

Zaten özel bir durumu değerlendirdik. Genel durumda kanıt benzerdir.

Teorem 3 . Eğik bir prizmanın yakınında bir küreyi tanımlamak imkansızdır; düz bir prizmanın yakınında bir küreyi tanımlayabilirsiniz; prizmanın tabanına yakınsa bir daireyi tanımlayabilirsiniz.

1) Öncelikle prizmanın eğik olduğu durumu ele alalım (örnek olarak üçgen prizmayı ele alalım). A, B ve C noktalarından eşit uzaklıktaki nokta, ABC üçgeninin düzlemine dik olan OS 1 düz çizgisi üzerinde olacaktır ve dikmenin tabanı, ABC üçgeninin kenarlarına çizilen orta dikmelerin kesişme noktasında olacaktır. .

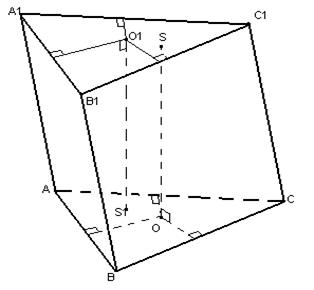
Benzer şekilde A 1, B 1, C 1 noktalarından eşit uzaklıktaki noktalar A 1 B 1 C 1 – O 1 S üçgeninin düzlemine dik üzerinde bulunur. Prizma eğik olduğundan OS 1 ve O 1 S çizgileri paralel olun ancak eşleşmeyin. Bu da ortak noktalarının olmayacağı anlamına gelir, dolayısıyla: prizmanın tüm köşelerine olan mesafenin aynı olacağı bir nokta yoktur, bu da eğimli bir prizma etrafında tanımlanan bir küre oluşturmanın imkansızlığına benzer.

2) Tabanına yakın bir yerde bir dairenin tanımlanabileceği düz bir prizma düşünün. O ve O 1 noktaları sırasıyla alt ve üst tabanlara yakın çevrelenmiş dairelerin merkezleridir. Prizma düz olduğundan, OO 1 düz çizgisi taban düzlemlerine dik olacaktır.

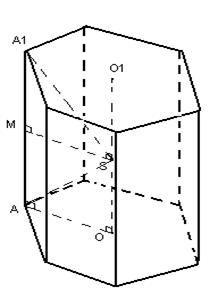
Daha sonra yan kaburgaların ortasından geçen düzlem, taban düzlemine paralel olacak ve OO 1'i S noktasında - OO 1'in ortasında kesecektir. O zaman prizmanın tüm köşelerinden S el arabasına kadar olan mesafe aynı olacaktır (yapısal olarak), bu nedenle S, normal prizma etrafında tanımlanan kürenin merkezidir.

Bu nedenle, eğimli bir prizmanın yakınında bir küreyi tanımlamanın imkansız olduğuna inanıyoruz, ancak düz bir prizmanın yakınında, tabanına yakın bir daire tanımlanabiliyorsa bu mümkündür.

Teorem 4. Kesik bir piramidin etrafında bir küre, ancak ve ancak tabanları etrafında daireler tanımlanabiliyorsa ve bu dairelerin merkezlerini birleştiren düz çizgi tabanların düzlemlerine dikse tanımlanabilir..

İlk koşul, çokgenlerin köşelerinden eşit uzaklıktaki tabanların HMT olan diklerinin var olacağı ve ikincisi ise çakıştıkları, dolayısıyla tüm köşelerden eşit uzaklıkta olacak bir nokta olacağı anlamına gelir. kesik piramit.

XV ŞEHİR ÖĞRENCİ AÇIK KONFERANSI

"XXI.Yüzyılın Aydınları"

Bölüm: MATEMATİK

Olimpiyatlarda ve Birleşik Devlet Sınavında açıklanan alan

Kiyaeva Anna Anatolevna

Orenburg – 2008

1.2 Tanımlanan kapsam

1.2.1 Temel özellikler ve tanımlar

1.2.2 Piramit kombinasyonu

1.2.3 Prizma ile kombinasyon

1.2.4 Silindirle kombinasyon

1.2.5 Koni ile kombinasyon

2 Olimpiyat görevlerine örnekler

2.1 Piramitli Olimpiyat görevlerine örnekler

2.2 Prizmalı Olimpiyat görevlerine örnekler

2.3 Silindirle Olimpiyat görevlerine örnekler

2.4 Koni ile Olimpiyat görevlerine örnekler

3.3 Silindirli Birleşik Devlet Sınavı görevlerine örnekler

3.4 Konili Birleşik Devlet Sınavı görevlerine örnekler

giriiş

Bu çalışma, yatılı lisenin web sitesinde okul çocukları için bir matematik sayfası oluşturma projesi kapsamında yürütülmektedir ve “Matematiksel Yöntemler” bölümünde yayınlanacaktır.

Hedefçalışma - Olimpiyatlarda ve Birleşik Devlet Sınavında açıklanan küreyle geometrik problemleri çözme yöntemine adanmış bir referans kitabı oluşturmak.

Bu hedefe ulaşmak için aşağıdakileri çözmemiz gerekiyordu görevler :

1) açıklanan küre kavramına aşina olmak;

2) tarif edilen kürenin piramit, prizma, silindir ve koni ile kombinasyonlarının özelliklerini incelemek;

3) geometrik problemler arasından, tanımlanan bir kürenin varlığının koşulunu içerenleri seçin;

4) toplanan materyali analiz etmek, sistemleştirmek ve sınıflandırmak;

5) bağımsız çözüm için sorunların seçimini yapın;

6) Araştırma sonucunu özet halinde sunar.

Pratik önemi– hazırladığımız materyaller okul çocuklarını Olimpiyatlara, Birleşik Devlet Sınavına ve üniversitedeki sonraki çalışmalara hazırlamakta kullanılabilir.

1 Küre ve top

1.1 Küre ve top: temel kavramlar ve tanımlar

Küre belirli bir noktadan belirli bir mesafede bulunan uzaydaki tüm noktalardan oluşan bir yüzeydir.

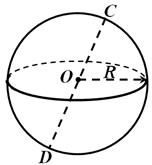
Bu noktaya denir kürenin merkezi(nokta HAKKINDAŞek. 1) ve bu mesafe kürenin yarıçapı. Kürenin merkezini herhangi bir noktasına bağlayan herhangi bir parçaya kürenin yarıçapı da denir. Bir küre üzerindeki iki noktayı birleştiren ve merkezinden geçen doğru parçasına ne ad verilir? küre çapı(bölüm DCŞek. 1). Çapının etrafında yarım daire döndürülerek bir küre elde edilebileceğini unutmayın.

Top küreyle sınırlanan cisimlere denir. Kürenin merkezi, yarıçapı ve çapına da denir. merkez , yarıçap Ve top çapı. Açıkçası, yarıçaplı bir top R merkezli HAKKINDA noktadan itibaren uzayda bulunan tüm noktaları içerir HAKKINDA aşmayan bir mesafede R(nokta dahil HAKKINDA) ve diğer noktaları içermez. Top yarım dairenin çapı etrafında dönüş şekli olarak da adlandırılır. Top segmenti- topun bir kısmı bir uçak tarafından ondan kesildi. Bir topun düzleme göre her bölümü bir dairedir. Bu dairenin merkezi, topun merkezinden kesme düzlemine çizilen dikmenin tabanıdır. Topun merkezinden geçen uçağa denir çap düzlemi. Bir topun çap düzlemine göre kesitine ne ad verilir? büyük daire ve kürenin kesiti büyük daire. Top sektörü – dairesel sektörü sınırlayan yarıçaplardan birini içeren düz bir çizgi etrafında 90°'den küçük bir açıyla dairesel bir sektörün döndürülmesiyle elde edilen geometrik bir cisim. Küresel sektör, küresel bir parça ve ortak tabanlı bir koniden oluşur.

Bir kürenin yüzey alanı:

S = 4π R 2 ,

Nerede R– topun yarıçapı, S- kürenin alanı.

Küre hacmi

Nerede V– topun hacmi

Top sektörü hacmi

V – küresel segmentin hacmi.

Segment yüzey alanı

- segment yüksekliği, segmental yüzey alanı

Segment tabanı yarıçapı

, - segment taban yarıçapı, - segment yüksekliği, 0<H < 2R .

Bir top bölümünün küresel yüzey alanı

- küresel segmentin küresel yüzeyinin alanı.

Uzayda bir top ve bir düzlem için üç durum mümkündür:

1) Topun merkezinden düzleme olan uzaklık topun yarıçapından büyükse, top ve düzlemin ortak noktaları yoktur.

2) Topun merkezinden düzleme olan mesafe topun yarıçapına eşitse, bu durumda düzlemin top ve onu sınırlayan küre ile yalnızca bir ortak noktası vardır.

3) Topun merkezinden düzleme olan uzaklık topun yarıçapından küçükse topun düzlemle kesişimi bir dairedir. Bu dairenin merkezi, topun merkezinin belirli bir düzleme izdüşümüdür. Düzlemin küre ile kesişimi, belirtilen dairenin çevresidir.

1.2 Tanımlanan küre

1.2.1 Tanımlar ve özellikler

Küre denir çokyüzlünün etrafında tanımlanmış(ve çokyüzlü küreye dahil), eğer çokyüzlünün tüm köşeleri küre üzerinde yer alıyorsa.

Tanımlanan kürenin tanımından iki gerçek çıkmaktadır:

1) bir kürenin içine yazılmış bir çokyüzlünün tüm köşeleri belirli bir noktadan (çevrelenen kürenin merkezinden) eşit uzaklıktadır;

2) bir küre içine yazılan bir çokyüzlünün her yüzü, belirli bir daireye, tam olarak kürenin kesitinde yüz düzlemi tarafından elde edilen daireye yazılmış bir çokgendir; bu durumda, yüzlerin düzleminde çevrelenen kürenin merkezinden indirilen dikmelerin tabanı, yüzlerin etrafında çevrelenen dairelerin merkezleridir.

Teorem 1 . Bir çokyüzlünün etrafında bir küre ancak ve ancak aşağıdaki koşullardan herhangi birinin karşılanması durumunda tanımlanabilir:

a) bir çokyüzlünün herhangi bir yüzünün etrafında bir daire tanımlanabilir ve çokyüzlünün yüzleri etrafında tanımlanan dairelerin eksenleri bir noktada kesişir;

b) çokyüzlünün kenarlarına dik olan ve orta noktalarından geçen düzlemler bir noktada kesişir;

c) Çokyüzlünün tüm köşelerinden eşit uzaklıkta tek bir nokta vardır.

Kanıt.

Gereklilik.Çokyüzlünün etrafında bir küre tanımlansın. a) koşulunun sağlandığını kanıtlayalım. Gerçekten de, bir çokyüzlünün belirli bir yüzünün düzlemi bir daire boyunca bir küreyle kesiştiğinden, küreye ait yüzün köşeleri ve yüzün düzlemi bunların kesişme çizgisine - daireye - aittir. Kürenin merkezi belirli bir yüzün tüm köşelerine eşit uzaklıkta olduğundan, yüzü çevreleyen dairenin merkezinden çizilen bu yüze dik bir noktada yer alır.

Yeterlilik. a) koşulu sağlansın. Bir çokyüzlü etrafında bir kürenin tanımlanabileceğini kanıtlayalım. Aslında yüzlerin etrafını saran dairelerin merkezlerinden çizilen yüzlere dik olanların ortak noktası çokyüzlünün tüm köşelerine eşit uzaklıkta olduğundan, çokyüzlünün etrafında merkezi bu noktada olan bir küre tanımlanır.

Bu durumda a) koşulu, b) ve c) koşullarına eşdeğerdir.

Eğer bir küre bir çokyüzlü etrafında çevrelenmişse, o zaman: a) kürenin merkezinden herhangi bir yüze bırakılan dikmenin tabanı, bu yüzün etrafında çevrelenen bir dairenin merkezidir (bir piramidin yüksekliğinin tabanı gibi) yan kenarlar - kürenin merkezinden belirli bir yüzün köşelerine çizilen yarıçapları); b) bir çokyüzlünün çevrelediği bir kürenin merkezi, çokyüzlünün içinde, yüzeyinde (bir yüzün etrafında çevrelenmiş bir dairenin merkezinde, özellikle bazı kenarların ortasında), çokyüzlünün dışında yerleştirilebilir.

1.2.2 Sınırlandırılmış küre ve piramit

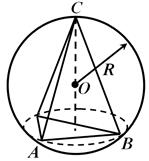
Teorem 2 . Bir piramidin etrafında bir küre ancak ve ancak tabanı etrafında bir daire tanımlanabiliyorsa tanımlanabilir.

Kanıt. Piramidin tabanı etrafında bir daire tanımlansın. Daha sonra bu daire ve bu dairenin düzleminin dışındaki bir nokta - piramidin tepesi - piramidin etrafını saracak tek bir küreyi tanımlar. Ve geri döndüm. Bir piramidin etrafında bir küre çevrelenmişse, o zaman kürenin piramidin taban düzlemine göre kesiti, tabanın etrafında çevrelenmiş bir daire olacaktır.

Sonuç 1. Herhangi bir tetrahedronun etrafında bir küre tanımlanabilir.

Sonuç 2. Herhangi bir normal piramidin yakınında, merkezi piramidin yüksekliğinde veya uzantısında bulunan bir küre tanımlanabilir.

Piramidin yakınında tanımlanan kürenin merkezi şu şekilde olabilir:

· piramidin tepesi, taban düzleminin bir tarafında olacak şekilde - piramidin içinde, yan yüz düzleminde (bu yüzün etrafında açıklanan dairenin merkezinde), piramidin dışında;

· taban düzleminde - tabanın yakınında tanımlanan bir dairenin merkezinde;

· Piramidin tepesi, taban düzleminin karşıt taraflarında olacak şekilde.

Teorem 3 . Piramidin yan kenarları taban düzlemine eşit derecede eğimliyse piramidin etrafında bir küre tanımlanabilir.

Kanıt. Yan kaburgalar piramidin taban düzlemine eşit eğimli olduğundan, piramidin tabanına yakın bir daire, ardından piramidin yakınında bir küre tanımlanabilir.

Bu teorem farklı şekilde formüle edilebilir: Eğer bir piramidin yan kenarları eşitse, o zaman piramidin etrafında bir küre tanımlanabilir.

Converse teoremi doğru değil

Teorem 4. Bir piramidin yakınında bir top tanımlanıyorsa, merkezi, piramidin kenarlarının bu kenarlara dik olan orta noktalarından çizilen tüm düzlemlerin kesişme noktasıdır.

Kanıt. Aslında, bir piramidin bir kenara bitişik iki köşesine eşit uzaklıktaki herhangi bir nokta, piramidin bu kenarına ortasından dik olarak çizilen bir düzlemde yer alır. Bu nedenle, piramidin tüm köşelerinden eşit uzaklıkta olan çevrelenmiş topun merkezi, bu tür düzlemlerin her birinde bulunmalıdır; tüm bu düzlemlerin kesişme noktasıdır. Bir çizim yaparken, okul çocukları genellikle verilen mekansal konfigürasyonu yeterince iyi hayal etmeden ve özellikle bu merkezin konumu hakkında herhangi bir mantık yürütmeden, tarif edilen topun merkezini rastgele yerleştirirler. Bu durumda kural olarak merkez piramidin içine yerleştirilir. Bu arada, açıklanan topun merkezi piramidin içinde, dışında veya yüzeyinde bulunabilir (piramidin spesifik türüne bağlı olarak).

Teorem 5 . Kesik bir piramidin etrafında bir küre ancak ve ancak aşağıdaki koşullardan herhangi birinin karşılanması durumunda tanımlanabilir:

A) merkezlerinin çizgisi düzlemlerine dik olan piramidin tabanlarının yakınında daireler tanımlanmaktadır;

B) piramidin tüm yan kenarları, tabanlardan birinin düzlemine eşit derecede eğimlidir;

C) piramidin tüm yan kenarları birbirine eşittir;

D) piramidin tüm yan yüzleri eşkenar yamuktur.

Kanıt. Belirli bir kesik piramidin tabanlarına yakın dairelerin tanımlanabildiğini ve bu dairelerin düzlemlerinin merkezlerinin çizgisine dik olduğunu varsayalım. Daha sonra bilindiği gibi bu iki daire, bu piramidin etrafında tanımlanacak olan tek bir küreyi tanımlar.

Bunun tersine, belirli bir kesik piramidin etrafında bir kürenin tanımlandığını varsayalım. Daha sonra piramidin tabanlarının düzlemlerine göre kürenin bölümleri, tabanların etrafında açıklanan daireler olacaktır. Sonraki. Piramidin tabanlarının düzlemlerine dik olan ve kürenin merkezinden geçen düz bir çizgi, tabanların çevresinde tanımlanan dairelerin merkezlerinden geçecektir.

Durum A) koşullara eşdeğerdir B), C), D).

Sonuçlar. Herhangi bir düzenli kesik piramidin etrafında bir küre tanımlanabilir.

1.2.3 Sınırlandırılmış küre ve prizma

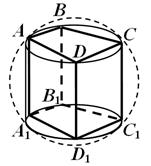
Teorem 6. Bir prizmanın etrafında bir küre, ancak ve ancak prizmanın düz olması ve tabanının etrafında bir dairenin tanımlanması durumunda tanımlanabilir.

Kanıt.

Gereklilik. Bir prizma bir kürenin içine yazılmışsa, o zaman yüzlerinin her biri bir daireye yazılır - bu yüzün düzlemine göre kürenin bir bölümü. Bu, prizmanın tabanına yakın bir dairenin tanımlanabileceği ve prizmanın tüm yan yüzlerinin dairelere - dikdörtgenlere - yazılan paralelkenarlara benzediği ve dolayısıyla prizmanın düz olduğu anlamına gelir.

Yeterlilik. Prizmanın düz olmasına ve tabanının etrafında bir daire çizilmesine izin verin. Daha sonra düzlemleri merkezlerinin çizgisine dik olan prizmanın tabanları etrafında çevrelenen daireler, prizmanın etrafında çevrelenecek tek bir küreyi tanımlar.

Sonuçlar:

a) herhangi bir düzenli prizmanın etrafında bir küre tanımlanabilir;

b) herhangi bir dik üçgen prizmanın etrafında bir küre tanımlanabilir;

c) herhangi bir dikdörtgen paralelyüzün etrafında bir küre tanımlanabilir;

Prizma etrafında çevrelenen kürenin merkezi, prizmanın tabanlarının düzlemlerinden eşit uzaklıkta olup prizmanın içinde, yan yüzünde (yüz çevresinde tanımlanan dairenin merkezinde), prizmanın dışında yer alabilir.

1.2.4 Sınırlandırılmış küre ve silindir

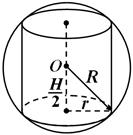
Küre denir silindir hakkında anlatılanlar silindirin tabanlarının daireleri üzerinde duruyorsa (Şek. 4). Her zaman bir silindirin etrafındaki küreyi tanımlayabilirsiniz.

1.2.5 Sınırlandırılmış küre ve koni

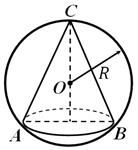
Küre denir koninin etrafında tanımlanmış, eğer koninin tabanının tepe noktası ve dairesi onun üzerinde yer alıyorsa (Şekil 5). Bir koninin etrafındaki küreyi tanımlamak her zaman mümkündür; yarıçapı, koninin eksenel bölümü etrafında açıklanan dairenin yarıçapına eşittir. Kesik koniye denir yazılı tabanları topun yüzeyinin bölümleri ise bir topun içine.

2 Olimpiyat görevlerine örnekler

2.1 Piramitli Olimpiyat görevlerine örnekler

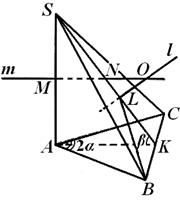
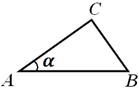
Örnek 1. Üçgen bir piramitte S ABC kenarı BC eşittir a, AB=AC, kenar S Ve ABC piramidinin tabanına dik olan kenardaki dihedral açı S A eşittir 2α , ve BC kenarında eşittir β (Şekil 6) . Çevreleyen kürenin yarıçapını bulun.

Çözüm. Bir piramit düşünün S ABC, sorun bildiriminde tartışılan şey. Kenardan beri S.A. taban düzlemine dik, daha sonra

VA S = CAS= 90° ve dolayısıyla açı SEN tam olarak kenardaki dihedral açının doğrusal açısıdır S.A.. Böylece piramidin tabanında açısı 2 olan bir ikizkenar üçgen bulunur. α üstte ve piramidin yüksekliği kenarla çakışıyor S A.

Yan kaburgaların çıkıntılarından beri S.B. Ve S İLE taban düzleminde eşittir, o zaman bu kenarların kendisi eşittir. Bu nedenle kenar İÇİNDE S İLE- bir ikizkenar üçgen ve yüksekliği tepe noktasından alçaltılmış S, ortasına düşüyor İLE kaburga Güneş.Üç dik teoremine göre AK- üçgenin yüksekliği SEN. Buradan açıkça görülüyor ki açı S CA- kenardaki dihedral açının doğrusal açısı güneş, yani

S CA = β .

Sınırlandırılmış topun merkezi çizginin kesişme noktasında bulunur ben, düzleme dik İÇİNDE S İLE ve üçgenin çevrelediği dairenin merkezinden geçerek İÇİNDE S İLE, kenarın ortasından geçen bir düzlem ile A S ona dik. Dümdüz ben bir uçakta yatıyor A S İLE: aslında uçak İÇİNDE S İLE düz bir çizgiden geçer güneş, düzleme dik A S İLE yani uçaklar İÇİNDE S İLE Ve A S İLE dik; aynı zamanda düz ben düzleme dik İÇİNDE S İLE ve bu düzlemlerin kesişme çizgisinden geçer, böylece düzlemde yer alır A S İLE .

Yani topun merkezi düzlemde yatıyor A S İLE. Bu uçağı özel bir çizime alalım. Top merkezi HAKKINDA daha sonra çizginin kesişme noktasında yer alacak ben ve düz M, dik A S ve ortasından geçiyor. Ancak genel olarak konuşursak üç olasılık ortaya çıkabilir: doğrudan ben Ve Tüçgenin içinde veya dışında kesişir A S İLE veya onun tarafındaysa tüm bu olasılıkları dikkate almamız gerekecek (bkz. Şekil 7, 8, 9). Aşağıda hesaplamalar sırasında bunlardan ikisinin gerçekte uygulanmadığını göstereceğiz. Yarıçapla ilgileniyoruz R sınırlı top, yani noktadan uzaklık HAKKINDA- diklerin kesişme noktaları T Ve ben açının kenarlarına İLE S A- asıl noktaya S, bu açının köşeleri. Öncelikle bulalım SL- gerekli mesafenin yan tarafa yansıtılması SK.üçgen Kaş. Çünkü bir üçgende AK B(Şekil 6) bacağını biliyoruz VK=

A ve açı KAV = α, O AK= A ctg α .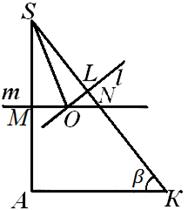

SK. =

Çünkü L- üçgen hakkında anlatılan merkez İÇİNDE S İLE daireler, ardından L.S. = L İÇİNDE, a çünkü üçgenden VK L bunu bulduk ( S İLE- SL ) 2 +HF 2 =B L 2 , yani

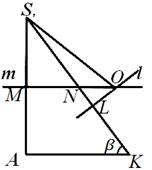
Segmentin hesaplamalarına dikkat çeken SL hiçbir şekilde merkezin konumuna bağlı değildi HAKKINDA açıklanan top, Şek. 2'ye dönelim. 7, 8, 9. ile gösterelim Nçizginin kesişme noktası M yan ile S İLE. Düz olduğu açık ben Ve T kesişmek dıştanüçgen CA S , Eğer SN <SL(Şekil 8); eğer S N> SL , sonra işaret et HAKKINDA bu üçgenin içinde yer alır (Şekil 7); nihayet eğer SN = SL , sonra işaret et HAKKINDA yan tarafta yatıyor S İLE bu üçgen (Şekil 9). Gelin bu hükümlerden hangisinin gerçekte gerçekleştiğini öğrenelim.

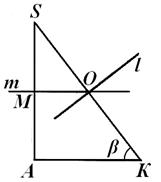
Çünkü MN CA S , O SN =

S İLE. Segmentlerin uzunluklarının karşılaştırılması SN Ve SL bunu herhangi biri için kolayca kanıtlayabiliriz a, α Ve

(geometrik değerlendirmelerden şu sonuç çıkıyor A> 0,0°<

< 90° ve 0°< β < 90°). Следовательно, каковы бы ни были размеры A , α Ve β piramitler S ABC, merkez HAKKINDA sınırlı bir top her zaman piramidin dışında bulunur. Bu da düzlemde çıkardığımız düz konfigürasyon anlamına gelir. CA S yalnızca Şekil 8'de gösterilen forma sahip olabilir; Şekil 2'de gösterilen yerler 7 ve 9 aslında gerçekleşemez. Şek. 8, bunu kolayca gösterebiliriz: β ve bu nedenle L.O. = Hollanda tg β = (SL -S N) tg β. Burada yukarıda elde edilen ifadeleri yerine koyarsak SL Ve S N, bariz hesaplamalardan sonra şunu elde ederiz:

L Ö =

A tg α günah β .

Son olarak bir dik üçgenden HAKKINDA L.S. buluruz

= .

Görebildiğimiz gibi, problemdeki hesaplamaların basit olduğu ortaya çıktı - çözümün asıl zorluğu, çevrelenen kürenin merkezinin konumunu belirleyen akıl yürütmede yatmaktadır.

Cevap: R =

Örnek 2. Tepe noktasında düz bir açıya sahip  düzgün bir üçgen piramit, R yarıçaplı bir topun içine yazılmıştır. Piramidin hacmini ve belirtilen piramidin etrafında açıklanan koninin yan yüzeyini bulun .

Çözüm. Piramidin tabanının bir tarafı olsun A, bu piramidin etrafında tanımlanan koninin tabanının yarıçapı şuna eşittir: R, Daha sonra

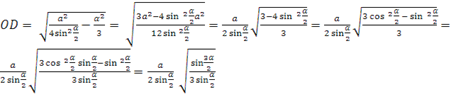(Şekil 10). Piramidin yüzleri ikizkenar üçgenlerdir. Daha sonra Bilmiyorum– yükseklik, ortanca ve açıortay  ABD. Bir dik üçgenden ADK sahibiz . Bir dik üçgenden piramidin yüksekliğini bulun AOD : ,

DM– topun çapı. Daha sonra topun çaptan geçen bölümünde DM ve dönem A, bir dik üçgen elde ederiz AMD. Bir dik üçgendeki metrik ilişkilerden elimizdeki

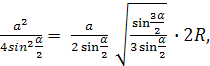Neresi

Daha sonra aşağıdaki formülü kullanarak tabanın alanını buluruz:

Ve formülden

Piramidin hacmini bulun: .

Kenar reklam tanımı gereği, sınırlı bir koni onun generatrisidir. Daha sonra aşağıdaki formülü kullanarak çevrelenmiş koninin yan yüzeyini buluruz. S kenar =  R ben :

Cevap:

;

Örnek 3. Piramidin tabanında kenarı a olan bir kare bulunur. Piramidin yüksekliği tabanın kenarlarından birinin ortasından geçer ve şuna eşittir:

. Piramidin çevrelediği kürenin yarıçapını bulun.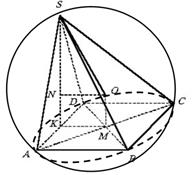

Çözüm. Bu sorunu çözerken yapılan tipik bir hata, açıklanan kürenin merkezinin kenarda olduğunun ifade edilmesidir. SBC(Şekil 11). Gerçekte noktanın konumu HAKKINDA kenara bağlı değil SBC.

Noktaların eşit uzaklığı nedeniyle HAKKINDAüstlerden S,A,B,C,Dşu şekildedir OABCD- düzenli dörtgen piramit. Bu nedenle uçurumun eşiğine ABCD nokta HAKKINDA bir noktaya kadar öngörülüyor M– köşegenlerin kesişme noktası. Üçgen A.S.D. ikizkenar, ardından piramidin yüksekliği SK.üçgenin medyanıdır A.S.D. ,

. Bir dik üçgenden S.A.K. bulacağız S.A. :

Bu nedenle üçgen S.A.D.– eşkenar ve OASD- düzenli üçgen piramit. Sonra işaret et HAKKINDA eşiğine kadar öngörülüyor S.A.D.üçgenin merkezine S.A.D.. Buradan

Bir üçgenden OĞUL gerekli yarıçapı bulun BU YÜZDEN,

Cevap:

Örnek 4. Yarıçaplı bir top için R alt tabanın düzleminin topun merkezinden geçtiği ve yan kenarın taban düzlemi ile 60 derecelik bir açı yaptığı düzenli bir altıgen kesik piramit yazılmıştır.

. Piramidin hacmini belirleyin.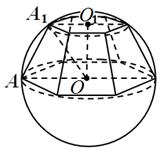

Çözüm.Şarta göre,

OAA 1 = 60 (Şekil 12); Araç, HAKKINDA 1 OA 1 =30 ve A 1 HAKKINDA 1 = A 1 Ö = ,O.O. 1 = .

S alt taban = 6

, S tepe temel = daha düşük temel .

Sonunda elde ettik

Cevap:

2.2 Prizmalı Olimpiyat görevlerine örnekler

Örnek 1. Hacmi eşit olan bir topun içine V , bir dik üçgen prizma yazılıdır. Prizmanın tabanı dar açılı bir dik üçgendir

ve en büyük yan yüzü karedir. Prizmanın hacmini bulun.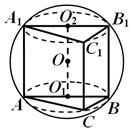

Çözüm.Öncelikle topun merkezinin prizmaya göre konumunu belirliyoruz. Topun, prizmanın tabanlarının düzlemlerine göre bölümleri, bu tabanların yazılı olduğu dairelerdir (Şekil 13) ve prizmanın tabanları eşit olduğundan, kesitlerin daireleri de eşit ve eşit uzaklıkta olur. topun merkezi. Merkezlerin her biri HAKKINDA 1 ve HAKKINDA 2, karşılık gelen hipotenüsün ortasına denk gelir.

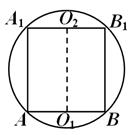
Bir topun düzlem kesitlerinin özelliklerinden, topun merkezinden çizilen dikmenin olduğu bilinmektedir. HAKKINDA kesit çemberinin düzlemi bu çemberin merkezinden geçer. Buradan, HAKKINDA 1 HAKKINDA

uçak ABC. Dümdüz HAKKINDA 1 HAKKINDA ayrıca geçer O 2 ve düzleme dik Böylece topun merkezi, segmentin ortasındaki yüzeyde yer alır. O 1 O. Prizmanın tüm yan yüzleri dikdörtgendir ve yüz - bunların en büyüğü (çünkü AB- bir üçgenin hipotenüsü A Güneş). Bu yüz geleneksel olarak bir karedir. Topun yüz düzlemine göre kesiti topun büyük bir dairesidir, dolayısıyla Şekil 2'de gösterilen dairenin yarıçapı da budur. 14, topun yarıçapına eşit R . Prizmanın yüksekliğine dikkat edin AA 1 = A 4 = . Şimdi geriye kalan tek şey tabanın alanını bulmak:

S A B İLE =

. (Şek. 15)

sahibiz AC = AB

, Araç,

S A B İLE =

Şimdi şunu anlıyoruz:

Vödül.

Şarta göre,

R 3 = V ,

Neresi R 3 =

,buradan,

Vödül.

Cevap: Vödül.

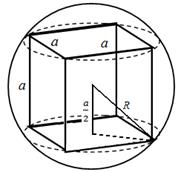
Örnek 2. Kürenin yüzeyi ve hacminin sırasıyla yazılı küpün yüzeyi ve hacmine oranını bulun

Çözüm. Topun yarıçapı şöyle olsun R , küpün kenarı eşittir A;

Daha sonra R 2 -

, Neresi a= .

Sırasıyla küre ve küpün hacimlerini ve yüzeylerini şu şekilde gösterelim: V 1 , V 2 , Ve S 1 , S 2 .

, V 2 = = , S 1 =4, S 2 = 6A 2 =8R 2 , V 2 = , S 1 S 2 = .

Cevap: V 1

V 2 = , S 1 S 2 = .

2.3 Silindirle Olimpiyat görevlerine örnekler

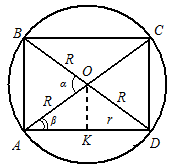
Örnek. Silindirin eksenel bölümünün köşegenleri arasındaki daha küçük açının şuna eşit olduğu biliniyorsa, kürenin hacminin, bu kürenin içine yazılan dik dairesel silindirin hacmine oranını bulun.

ve tabanın çapı silindirin yüksekliğinden daha büyüktür (Şek. 18).

Çözüm. Kürenin hacmini biliyoruz

ve silindirin hacmini formülü kullanarak buluyoruz, ancak bu nedenle

İzin vermek ABCD- silindirin eksenel bölümü (bkz. Şekil 18). Tabanın çapı silindirin yüksekliğinden büyük olduğundan

- köşe AOB. Bir üçgenden ASG bundan silindirin yüksekliği anlaşılmaktadır

Silindir tabanı yarıçapı

. .

Görünüşe göre

Bulunan verileri silindirin hacmi formülüne koyalım:

;

Böylece,

Hadi bir ilişki bulalım

Cevap:

2.4 Olimpiyat görevlerine örnekler koni

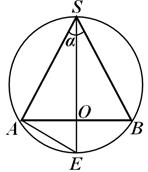
Örnek 1. Yarıçaplı bir top için R dairesel bir koni yazılmıştır; eksenel bölümdeki koninin genatrisleri arasındaki açı α'ya eşittir. Koninin tabanının yarıçapını oluşturan yüksekliği bulun.

Çözüm. Topun koninin ekseninden geçen bölümü topun büyük çemberidir;

AB S(Şekil 19), burada A İÇİNDE- koninin tabanının çapı. Koninin yüksekliğine (ekseni) devam edelim BU YÜZDEN noktada büyük daireyle kesişene kadar e ve düşün e S A:

bu üçgende

S.E. = 2R ,

S AE = 90° Ve A S e= .

A S = 2R

Şimdi

A İşletim Sistemi buluruz

A HAKKINDA = R = 2R

, BU YÜZDEN = h= 2R

Cevap : yani= 2R

A S = 2R , A HAKKINDA =.

Örnek 2. Koninin yüksekliğinin, etrafını saran topun yarıçapına oranı şuna eşittir: k . Bu cisimlerin hacimlerinin oranını bulun. Ne olduğunu öğren k görev mantıklı.

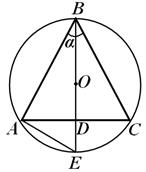
Çözüm. Koninin eksenel bölümünü ele alalım (Şekil 20). İzin vermek H- koninin yüksekliği, R- bir koninin etrafında çevrelenmiş bir kürenin yarıçapı. Daha sonra koşula göre,

=k yani H = kR .

Yarıçapı ifade edelim R koninin tabanı içinden R; akorları göz önünde bulundurarak klima Ve OLMAK,şunu elde ederiz:

İÇİNDE D

D e = A D D İLE(Çünkü AD=DC ,
– dikdörtgen, reklam – yükseklik dik açının tepe noktasından düştü).

(buradan, k < 2).

V w =

; V k ==

Böylece,

, (0'da< k < 2).

Cevap:

, (0'da< k < 2).

Örnek 3. Kesik bir konide alt ve üst tabanların yarıçapları sırasıyla eşittir R 1 Ve R 2 ve koninin generatrisi alt tabanın düzlemine α açısıyla eğimlidir (Şekil 21). Verilen kesik koninin içine yazıldığı kürenin yarıçapını bulun.

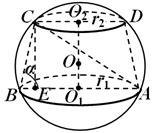
Çözüm. Topun kesik koninin ekseninden geçen bölümünde, içine bir yamuğun yazıldığı geniş bir top dairesi elde edilir. ABC D. düşünelim

A güneş, bu aynı zamanda topun büyük dairesinde de yazılıdır. Bu üçgenin açısı biliniyor İLE B.A. = α . Sinüs teoremi sayesinde, klima = 2R. Böylece belirlemek için R bulman yeterli AC. Konudan ayrılalım İLE dik GD Açık AB. Açıkça,

AE= R 1 + R 2 ,BE = R 1 - R 2,a CE = ( R 1 - R 2 )

Bu nedenle Pisagor teoremine göre

= = = nereden R =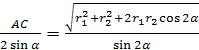

Cevap: R

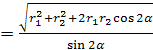3 Birleşik Devlet Sınavı görevlerine örnekler

3.1 Piramitli Birleşik Devlet Sınavı görevlerine örnekler

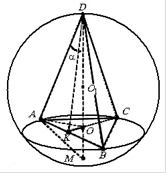
Örnek 1. Segment P N , 8'e eşit olan kürenin çapıdır. M noktaları, L Piramidin hacmi P olacak şekilde kürenin üzerinde uzanın N M L en büyüğü (Şek. 22). K üçgeninin alanını bulun L T, burada K ve T PM kenarlarının orta noktalarıdır ve N M sırasıyla.

Çözüm.İzin vermek HAKKINDA kürenin merkezidir ve R- yarıçapı. O zamandan beri R N = 2R= 8 ve noktalar M Ve L kürenin üzerine yat, o zaman VEYA = Ç L = Ç N = ÖM = R = 4. Kürenin düzlemlere göre bölümleri R LN Ve RM N- daire yarıçapı R = 4, üçgenler hakkında anlatıldı R LN Ve RM N , Ve

RM N = R LN= 90°, çapa bağlı olarak yazılı açılar olarak R N .

İzin vermek N- üstten indirilen piramidin yüksekliği M, A H- üçgenin yüksekliği R LN , yan tarafa tutuldu R N . noktadan beri M kürenin ve düzlemin üzerinde yatıyor R LN kürenin merkezini içerir, o zaman N

R , Ve N = R , Eğer MO R Hollanda . Aynı şekilde, noktadan itibaren L kürenin üzerinde yatıyor, o zaman H R , Ve H = R , Eğer L HAKKINDA R N .

Dolayısıyla piramidin hacmi için R N M L sahibiz

, .

Yani piramit R N M Lüçgenler ise en büyük hacme sahiptir R LN Ve RM N ortak hipotenüslü dikdörtgen, ikizkenar R N, karşılıklı dik düzlemlerde uzanır. Üçgenlerden beri L HAKKINDA N , L VEYA, L OM, ROM, N OM iki ayak üzerinde eşittirler, sonra üçgenler L M N Ve L Bay yan ile doğru

Hollanda =P L = AÇIK

Bundan şu sonuç çıkıyor: medyanlar L İLE Ve L T bu üçgenler eşittir ve

L İLE =

= 2.

Üçgen İLE L T ikizkenar ve yüksekliği LD dik ikizkenar üçgenin medyanıdır L OM. Buradan

LD =

= 2.

BT- üçgenin orta çizgisi RM N ve bu nedenle BT = 0,5R N =R . Bu nedenle bölge S İLE L T =

BT LD = 4.

Cevap: 4

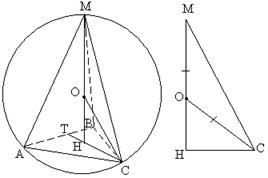
Örnek 2. Düzenli bir üçgen piramitte tabanın kenarı 5'tir ve yan kaburgalar tabana 60 derecelik bir açıyla eğimlidir. O. Piramidin çevrelediği kürenin yarıçapını bulun.

Çözüm.İzin vermek ABCM belirtilen piramit (bkz. Şekil 23) Piramit düzenli olduğu için açıklanan kürenin merkezi piramidin yüksekliğinde yer alır.

Piramidin yüksekliğinin tabanı üçgenin merkezidir ABC, yani medyanların kesişme noktası. Daha sonra:

ST =

CH= = = .

Şimdi üçgeni düşünün MNS.İşte köşe MSN yan kenar arasındaki açı olarak 60°'ye eşittir MS ve temel ABC. Köşe NMS 30'a eşit

. MO=İşletim Sistemi yarıçaplar gibi. Yani bu bir üçgen MOS ikizkenar. Bildiğiniz gibi ikizkenar üçgende taban açıları eşittir. Buradan, OSM = Zorunlu sağlık sigortası = 30, OSN = MSN - MCO = 60 - 30= 30.

Bir dik üçgenden OSN hipotenüsü tanımlayalım İşletim Sistemi dik üçgende trigonometrik fonksiyonların ilişkisini kullanarak:

Cevap: OC =

3.2 Prizma ile KULLANIM görevlerine örnekler

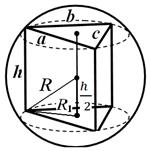
Örnek 1. Prizmanın tabanı kenarları olan bir üçgendir A , B , C . Prizma yüksekliği H (Şekil 25). Çevreleyen kürenin yarıçapını bulun.

Çözüm. Prizmanın etrafı bir küreyle çevrelendiğinden prizma düzdür ve yan kenarı yüksekliğine eşittir. Prizmanın tabanı çevresinde açıklanan dairenin yarıçapı formülle hesaplanır.

Cevap:

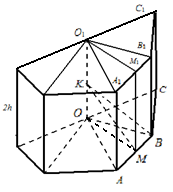
Örnek 2. Top yarıçapı R . Bir topun içine yüksekliği 2 olan düzgün bir n-gonal prizma yazılmıştır. H (Şekil 26). Prizmanın tabanının kenarını bulun.

Çözüm.İzin vermek İLE– çevrelenen kürenin merkezi. Sahibiz: K.B. = R , TAMAM = H. İzin vermek OM

AB, Daha sonra

O.B. =

(üçgenden Tamam).

Bir üçgenden OMB buluruz

A = 2M.B. = 2O.B.

Bu yüzden, A =

Cevap: A =

3.3 Silindirli Birleşik Devlet Sınavı görevlerine örnekler

Örnek 1. Dairesel bir silindirin yüksekliği taban yarıçapından 10 kat daha fazladır ve toplam yüzey alanı 144'tür.

. Çevreleyen kürenin yarıçapını bulun.

Çözüm. Sınırlandırılmış kürenin yarıçapı

(Şek. 27).

Silindir yüzey alanı

, 144,

Bu ifadeyi sadeleştirelim:

İkinci dereceden bir denklem elde ederiz

Bu denklemin köklerini bulalım

, negatif olduğundan uygun değildir. Yükseklik

Çevreleyen kürenin yarıçapını bulalım:

Cevap:

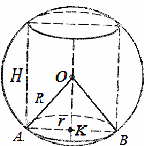
Örnek 2. Bir topun içine düz dairesel bir silindir yazılmıştır (Şek. 28). Kürenin yarıçapının silindirin taban yarıçapına oranının, kürenin yüzeyinin oranının yarısı kadar olduğu biliniyorsa, kürenin hacmi silindirin hacminden kaç kat daha büyüktür? Silindirin yan yüzeyine küre.

Çözüm. Bir kürenin hacminin yazılı bir silindirin hacmine oranı

Koşullu olarak biliniyor ki

; –

eşkenar

Kürenin ve yazılı silindirin hacimlerinin oranını bulalım

Cevap: 16:9.

3.4 Konili Birleşik Devlet Sınavı görevlerine örnekler

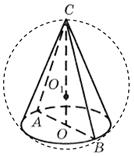
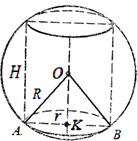
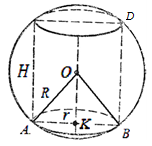
Örnek 1. Koninin tabanının çapı 6 m'dir, generatrix taban düzlemine 60° açıyla eğimlidir (Şekil 29). Koninin çevrelediği kürenin alanını bulun.

TAKSİ koninin generatrisi ile tabanının alanı arasındaki açıya eşittir. Bu yüzden CAB= 60° ve ikizkenar üçgen ABC- doğru. Şunu takip ediyor

CA = AB = BC= 6 m.

Koninin çevrelediği kürenin merkezinin konumunu bulalım. Böyle bir kürenin tanımı gereği, koninin tabanının çevresi çevrelenen kürenin bir kesitidir ve koninin tepe noktası bu kürenin üzerinde yer alır. Herhangi bir bölümünün merkezinden geçen kürenin çapının özelliğine göre düz çizgi CO koninin taban düzlemine ve dolayısıyla merkeze dik HAKKINDA 1 çevrelenmiş küre düz bir çizgi üzerinde yer alır CO.Şu kadar ki, merkez HAKKINDA Bir koni etrafında çevrelenen bir kürenin Şekil 1'i, eksenel bölümü etrafında çevrelenen bir dairenin merkezidir.

Bir dik üçgende

ABC R = O 1 C =

(M)

Kürenin alanını bulalım:

(m2).

Cevap: 48

m2.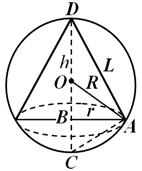

Örnek 2. Yarıçaplı bir top için R = 6 cm yüksekliğinde yazılı koni H (Şek. 30). Koninin hacmini ve yan yüzeyini argümanın bir fonksiyonu olarak ifade edin H .

Çözüm. Sahibiz:

Nerede R - taban yarıçapı, L- bir koni oluşturmak.

bunu göz önünde bulundurarak R = VA – dik açının tepe noktasından hipotenüse indirilen yükseklik, elimizde: ve . Veya R 2 ve

, .

Şimdi şunu anlıyoruz:

, .

Cevap:

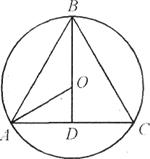
Örnek 3. Topun içine, generatrisi tabanın çapına eşit olan bir koni yazılmıştır (Şekil 31). Koninin yüzeyinin topun yüzeyine oranını bulun.

Çözüm. Topun merkezinden geçecek koninin eksenel bölümünü çizelim. Koninin tabanının çapı generatrise eşit olduğundan, kesitte bir daire içine yazılmış normal bir üçgen elde ederiz (Şekil 31). Topun yarıçapı eşit olsun R : Daha sonra

AB =R

, A D =

Koninin toplam yüzeyini şu şekilde gösterelim: S 1 ve topun yüzeyi S 2. Sahibiz

Neresi S 1: S 2 = 9:16.

Cevap: S 1: S 2 = 9:16.

Çözüm

Araştırma sırasında, Birleşik Devlet Sınavında açıklanan alanla ilgili sorunların okul çocuklarına oldukça sık sunulduğunu, dolayısıyla bu tür sorunları çözme yeteneğinin sınavları başarıyla geçmede çok önemli bir rol oynadığını öğrendik. Ayrıca, tanımlanan alanla ilgili problemlere genellikle çeşitli düzeylerdeki matematik olimpiyatlarında rastlanır. Çalışmamızda konuyla ilgili örnekler verilmiştir. Bu aşamada kendimizi, etrafı çevrelenmiş bir küre ile piramit, prizma, silindir ve koninin birleşimini içeren problemleri düşünmekle sınırladık. Bağımsız çalışma için seçilmiş görevler. Çalışmayı yürütme sürecinde şu yöntemleri kullandık: bilimsel ve popüler bilim literatürüyle çalışmak, internette bilgi toplamak, analiz etmek, sistemleştirmek, sınıflandırmak ve bilgisayarda işlemek. Sonuçlar şu anda özet biçiminde sunulmaktadır. Gelecekte çalışmanın yeni görevlerle desteklenmesi planlanıyor.

Referanslar

1. Abramovich M.I., Starodubtsev M.T. Matematik (geometri ve trigonometrik fonksiyonlar). Üniversitelerin hazırlık bölümleri için ders kitabı - M: Yüksekokul, 1976. - 304 s.

2. Voitovich F.S. Geometrik cisimlerin kombinasyonları: (yazılı ve çevreli toplar): Öğrenciler için kitap. – Minsk: Narodnaya Asveta, 1992. – 160 s.

3. Govorov V.M., Dybov P.T., Miroshin N.V. Ve diğerleri Matematikteki rekabet problemlerinin listesi (metodolojik talimatlar ve çözümlerle birlikte): ders kitabı. – ikinci baskı – M: Nauka, 1986. – 384 s.

4. Denishcheva L.O., Bezrukova G.K., Boychenko E.M. ve diğerleri Birleşik devlet sınavı, matematik, kontrol ölçüm materyalleri - M: Eğitim 2005. - 80 s.

5. Denishcheva L.O., Glazkov Yu.A., Krasnyanskaya K.A. ve diğerleri. Matematik. Öğrencileri hazırlamak için eğitim ve öğretim materyalleri / FIPI - M: Intellect-Center, 2008. - 240 s.

6. Dorofeev G.V., Potapov K.M., Rozov N.Kh. Üniversitelere girenler için matematik üzerine bir el kitabı - M: Nauka 1972. - 528 s.

7. Egerev V.K., Zaitsev V.V., Kordemsky B.A. ve diğerleri. Üniversitelere başvuran adaylar için çözümleri ile matematikte 2500 problem: - M: LLC Yayınevi "ONICS 21. yüzyıl": LLC Yayınevi "Dünya ve Eğitim", 2002. - 912 s.

8. Zvavich L.I., Ryazanovsky A.R. Tablolarda geometri - M: Bustard 2007. - 128 s.

9. Klimin S.V., Strunkina T.V., Panteleeva E.I. ve diğerleri Birleşik devlet sınavı, test görevleri - M: Eğitim 2002. - 24 s.

10. Modenov V.P., Dorofeev G.V., Novoselov S.I. ve diğerleri Matematik üzerine bir el kitabı - M: Moskova Üniversitesi Yayınevi, 1972. - 404 s.

11. Shuvalova E.Z., Kaplun V.I. Geometri: üniversitelerin hazırlık bölümleri için ders kitabı - M: Yüksekokul, 1980. - 265 s.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

Başvuru. Bağımsız çözüm için görevler

1. Piramidin içinde FABC kenarlar ABF Ve ABC dik, B.F. :F.A. = 15:11. Düz bir çizgi arasındaki açının tanjantı M.Ö. ve uçak ABF 5'e eşittir. Nokta M kenarda seçildi M.Ö. Bu yüzden B M :M C = 4:11. Nokta T düz bir çizgi üzerinde yatıyor F.A. ve noktalardan eşit uzaklıkta M Ve İÇİNDE. Bir piramidin çevrelediği bir kürenin merkezi FABC , kenarda yatıyor AB bu kürenin alanı 36

. Piramidin hacmini bulun ASMT. (Cevap: 6)

2. Piramidin tabanı FABCD bir dikdörtgendir ABCD . Uçak A.F.C. düzleme dik ABC , açının tanjantı FAC eşittir

, doğru arasındaki açının tanjantı M.Ö. ve uçak A.F.C. eşittir. Nokta M kenarda yatıyor M.Ö. , sanal makine =M.Ö. . Nokta L düz bir çizgi üzerinde yatıyor F.A. ve noktalardan eşit uzaklıkta M Ve C . Piramidin hacmi L İÇİNDE D M 72'ye eşittir. Piramidin çevrelediği kürenin merkezi FABCD , tabanının düzleminde yer alır. Bu kürenin yarıçapını bulun. (Cevap: 5)

3. Normal piramidin yakınında FABC merkezi taban düzleminde yer alan bir küreyi tanımlar ABC piramitler. Nokta M kenarda yatıyor AB Bu yüzden A M :M B=1:3. Nokta T düz bir çizgi üzerinde yatıyor F.A. ve noktadan eşit uzaklıkta M Ve İÇİNDE. Piramidin hacmi TVSM eşittir

. Piramidin çevrelediği kürenin yarıçapını bulun FABC . (Cevap: )

4. Segment AB– kürenin çapı. Puanlar İLE, D ABCD en iyisi. Çizgiler arasındaki açının kosinüsünü bulun SANTİMETRE Ve AB, Eğer M– kaburganın ortası BD . (Cevap:

)

5. Segment R N , 8'e eşit olan kürenin çapıdır. Nokta M, L Piramidin hacmi öyle olacak şekilde kürenin üzerinde uzanın R N M L en iyisi. Üçgenin alanını bulun KLT , Nerede k Ve T – kaburgaların ortası RM Ve N M sırasıyla. (Cevap: 4

)

6. Yarıçapı 6 olan bir küre verilmiştir. Kürenin düzleme göre kesiti çapı olan bir dairedir. BT. Kesit düzlemi kürenin merkezinden 5 mesafede kaldırılır. R küre üzerinde seçilir ve nokta L RK L T en iyisi. Düz çizgi arasındaki açıyı bulun LM ve uçak PTK , Eğer M yaprak orta damarı RK. (Cevap: 30

)

7. Merkez aracılığıyla HAKKINDA F küre üzerinde seçilir ve noktalar A , B , C , D – FABCD en iyisi. Puanlar M, T, L – kaburgaların ortası Facebook , CD Ve reklam sırasıyla. Bir üçgenin alanı MLT 64'e eşit

. Kürenin yarıçapını bulun. (Cevap: 2)

8. Merkez aracılığıyla HAKKINDA bu küreden bir bölüm yapılmıştır. Nokta F küre üzerinde seçilir ve noktalar A , B , C , D – piramidin hacmini sağlayacak şekilde kesit daire üzerinde sırayla FABCD en iyisi. Doğru arasındaki açının sinüsünü bulun AM ve uçak B.F.D. . (Cevap:

)

9. Yarıçapı 10 olan bir küre verilmiştir. Bu kürenin düzlemsel kısmı çapı 10 olan bir dairedir. AB. Kesit düzlemi kürenin merkezinden 8 mesafede kaldırılır. D küre üzerinde seçilir ve nokta İLE- piramidin hacmini sağlayacak şekilde kesit çevresi üzerinde ABC D en iyisi. Yüzün alanını bulun AKD .(Cevap: 27

)

10. Piramidin tabanı bir dikdörtgendir. Düzlem düzleme diktir ABC, doğru arasındaki açının tanjantı Güneş ve uçak FAC 2'ye eşittir. Nokta M kenarda yatıyor Güneş Ve OG =

Nokta L düz bir çizgi üzerinde yatıyor F.A. ve noktalardan eşit uzaklıkta M Ve İLE. Bir piramidin çevrelediği bir kürenin merkezi F.A. İÇİNDE CD, piramidin taban düzleminde yer alır, bu kürenin yarıçapı 4'tür. Piramidin hacmini bulun L.A. MS. (Cevap: 48)

11. Yarıçapı 2 olan bir topun içine

ABCA 1 İÇİNDE 1 İLE 1. Dümdüz klima 1 Düzlemli formlar ABB (Cevap: 288)

12. Bir kürenin içine düzgün bir üçgen prizma yazılmıştır ABCA 1 İÇİNDE 1 İLE 1, hacmi 4,5'tir. Dümdüz VA Düzlemli 1 form VSS 1 korner45

. Kürenin yüzey alanını bulun. (Cevap: 11)

13. Yarıçaplı bir topun içine

düzenli bir üçgen prizma yazılıdır ABCA 1 İÇİNDE 1 İLE 1. Dümdüz AB Düzlemli 1 form ACC 1 açı 45. Prizmanın hacmini bulun. (Cevap: 36)

14. Yarıçapı bilerek düzgün üçgen prizmanın kenarlarını hesaplayın R sınırlı küre ve eğim açısı α bu topun yarıçapı prizmanın tepe noktasına, bu tepe noktasını içeren yan yüze çizilir. (Cevap: 2

)

15. Yarıçaplı bir top için R sağ dairesel bir koni yazılıdır. Yüksekliği ise koninin yan yüzeyini bulun H . (Cevap:

)

16. Bir kürenin içine bir koni yazılmıştır. Koninin eksenel kesit alanı eşittir S. Yüksekliği ile jeneratör arasındaki açı eşittir α . Kürenin hacmini bulun. (Cevap:

)

17. Yarıçapın uzunluğunu bilerek koninin yan yüzeyini belirleyin R etrafındaki küre ve açı α, altında koninin generatrisi topun merkezinden görülebilir. (Cevap:

)

18. Koninin eksenel bölümünün tepesindeki açı eşitse, bir topun içine yazılan bir dik koninin toplam yüzey alanının bu topun yüzey alanına oranını bulun. α Ve

. (Cevap:

)

19. Bir topun içine, yüksekliği topun merkezine ortalama ve ekstrem oranda bölünecek şekilde bir koni yazılmıştır. Koninin eksenel bölümünün tepe noktasındaki açıyı bulun. Kürenin hacminin koninin hacminden kaç kat daha büyük olduğunu belirleyin. (Cevap:

; 4 kez )

Örnek 2.Düzenli bir üçgen piramitte tabanın kenarı 5'tir ve yan kaburgalar tabana 60 derecelik bir açıyla eğimlidir. O. Piramidin çevrelediği kürenin yarıçapını bulun.

Çözüm.İzin vermek ABCM belirtilen piramit (bkz. Şekil 23) Piramit düzenli olduğu için açıklanan kürenin merkezi piramidin yüksekliğinde yer alır.

Piramidin yüksekliğinin tabanı üçgenin merkezidir ABC, yani medyanların kesişme noktası. Daha sonra:

CH= ST = CH= = = .

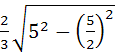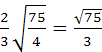Şimdi üçgeni düşünün MNS.İşte köşe MSN yan kenar arasındaki açı olarak 60°'ye eşittir MS ve temel ABC. Köşe NMS eşittir 30. MO=İşletim Sistemi yarıçaplar gibi. Yani bu bir üçgen MOS ikizkenar. Bildiğiniz gibi ikizkenar üçgende taban açıları eşittir. Buradan,

OSM = Zorunlu sağlık sigortası = 30, OSN = MSN - MCO = 60 - 30= 30.

Bir dik üçgenden OSN hipotenüsü tanımlayalım İşletim Sistemi dik üçgende trigonometrik fonksiyonların ilişkisini kullanarak:

İşletim Sistemi= = .

Cevap: OC= .

3.2 Prizma ile KULLANIM görevlerine örnekler

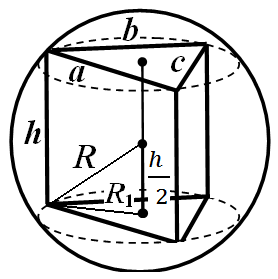
Örnek 1.Prizmanın tabanı kenarları olan bir üçgendirA, B, C. Prizma yüksekliğiH(Şekil 25). Çevreleyen kürenin yarıçapını bulun.

Cevap:

Örnek 2.Top yarıçapıR. Bir topun içine yüksekliği 2 olan düzgün bir n-gonal prizma yazılmıştır.H(Şekil 26). Prizmanın tabanının kenarını bulun.

Çözüm.İzin vermek İLE– çevrelenen kürenin merkezi. Sahibiz: K.B.= R, TAMAM= H. İzin vermek OMAB, Daha sonra

O.B.=

(üçgenden Tamam).

Bir üçgenden OMB buluruz

A= 2M.B.= 2O.B..

Bu yüzden, A= .

Cevap: A= .

3.3 Silindirli Birleşik Devlet Sınavı görevlerine örnekler

Örnek 1.Dairesel bir silindirin yüksekliği taban yarıçapından 10 kat daha fazladır ve toplam yüzey alanı 144'tür.. Çevreleyen kürenin yarıçapını bulun.

Çözüm. Sınırlandırılmış kürenin yarıçapı

Silindir yüzey alanı

Bu ifadeyi sadeleştirelim:

İkinci dereceden bir denklem elde ederiz

Bu denklemin köklerini bulalım

Kök negatif olduğu için uygun değildir. Yükseklik

Çevreleyen kürenin yarıçapını bulalım:

Cevap: .

Örnek 2.Bir topun içine düz dairesel bir silindir yazılmıştır (Şek. 28). Kürenin yarıçapının silindirin taban yarıçapına oranının, kürenin yüzeyinin oranının yarısı kadar olduğu biliniyorsa, kürenin hacmi silindirin hacminden kaç kat daha büyüktür? Silindirin yan yüzeyine küre.

Çözüm. Bir kürenin hacminin yazılı bir silindirin hacmine oranı

Koşullu olarak biliniyor ki

eşkenar

Kürenin ve yazılı silindirin hacimlerinin oranını bulalım

Cevap: 16:9.

3.4 Konili Birleşik Devlet Sınavı görevlerine örnekler

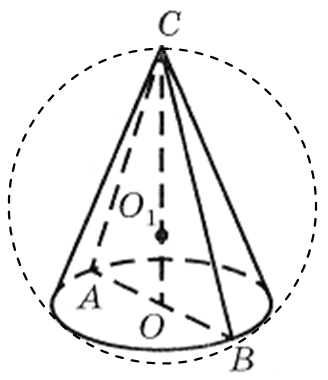
Örnek 1.Koninin tabanının çapı 6 m'dir, generatrix taban düzlemine 60° açıyla eğimlidir (Şekil 29). Koninin çevrelediği kürenin alanını bulun.

Çözüm.İzin vermek İLE - koninin üst kısmı HAKKINDA - tabanının merkezi, DIA- koninin eksenel bölümü. Koninin generatriksi taban düzlemine 60° açıyla eğimli olduğundan ve CO koninin yüksekliği, ardından düz çizgi AB- doğrudan projeksiyon SA koninin tabanının düzlemine. Buradan, TAKSİ koninin generatrisi ile tabanının alanı arasındaki açıya eşittir. Bu yüzden CAB= 60° ve ikizkenar üçgen ABC- doğru. Şunu takip ediyor

CA = AB = BC= 6m.

Koninin çevrelediği kürenin merkezinin konumunu bulalım. Böyle bir kürenin tanımı gereği, koninin tabanının çevresi çevrelenen kürenin bir kesitidir ve koninin tepe noktası bu kürenin üzerinde yer alır. Herhangi bir bölümünün merkezinden geçen kürenin çapının özelliğine göre düz çizgi CO koninin taban düzlemine ve dolayısıyla merkeze dik HAKKINDA Sınırlandırılmış kürenin 1 tanesi düz bir çizgi üzerinde yer almaktadır CO.Şu kadar ki, merkez HAKKINDA 1 Bir koni etrafında çevrelenen bir küre, eksenel kesiti etrafında çevrelenen bir dairenin merkezidir.

Bir dik üçgende

ABCR= O 1 C= (M)

Örnek 3.Topun içine, generatrisi tabanın çapına eşit olan bir koni yazılmıştır (Şekil 31). Koninin yüzeyinin topun yüzeyine oranını bulun.

AB= R , AD =

Koninin toplam yüzeyini şu şekilde gösterelim: S 1 ve topun yüzeyi S 2. Sahibiz

Neresi S 1: S 2 = 9:16.

Cevap:S 1: S 2 = 9:16.

Çözüm

Referanslar

Abramovich M.I., Starodubtsev M.T. Matematik (geometri ve trigonometrik fonksiyonlar). Üniversitelerin hazırlık bölümleri için ders kitabı - M: Yüksekokul, 1976. - 304 s.

Voitovich F.S.

Geometrik cisimlerin kombinasyonları: (yazılı ve çevrelenmiş küreler): Öğrenciler için kitap.

– Minsk: Narodnaya Asveta, 1992. – 160 s.

Govorov V.M., Dybov P.T., Miroshin N.V. Ve diğerleri Matematikteki rekabet problemlerinin listesi (metodolojik talimatlar ve çözümlerle birlikte): ders kitabı.

– ikinci baskı – M: Nauka, 1986. – 384 s.

Egerev V.K., Zaitsev V.V., Kordemsky B.A. ve diğerleri. Üniversitelere başvuran adaylar için çözümleri ile matematikte 2500 problem: - M: LLC Yayınevi "ONICS 21. yüzyıl": LLC Yayınevi "Dünya ve Eğitim", 2002. - 912 s.

Zvavich L.I., Ryazanovsky A.R. Tablolarda geometri - M: Bustard 2007. - 128 s.

Klimin S.V., Strunkina T.V., Panteleeva E.I. ve diğerleri Birleşik devlet sınavı, test görevleri - M: Eğitim 2002. - 24 s.

Modenov V.P., Dorofeev G.V., Novoselov S.I. ve diğerleri Matematik üzerine bir el kitabı - M: Moskova Üniversitesi Yayınevi, 1972. - 404 s.

Shuvalova E.Z., Kaplun V.I. Geometri: üniversitelerin hazırlık bölümleri için ders kitabı - M: Yüksekokul, 1980. - 265 s.

http :// kuantum. ayna1. mccme. ru/ pdf/2000/06/ kv0600 çözüm. pdf

http :// ru. Vikipedi. kuruluş/ wiki/% D0%9 F% D0% OLMAK% D1%80% D1%82% D0% B0% D0% BB:% D0%9 D% D0% B0% D1%83% D0% B.A.% D0% B0

rgp . nm. ru/ geometri/ praktika11/ zadaça119. HTML

Başvuru. Bağımsız çözüm için görevler

“Çokyüzlüler, silindir, koni ve topla ilgili farklı problemler” konusu 11. sınıf geometri dersinin en zor konularından biridir. Geometrik problemleri çözmeden önce genellikle problem çözerken atıfta bulunulan teorinin ilgili bölümlerini incelerler. S. Atanasyan ve diğerlerinin bu konuyla ilgili ders kitabında (s. 138) yalnızca bir küre etrafında tanımlanan çokyüzlü, küre içine yazılan çokyüzlü, çokyüzlüye yazılan küre ve bir küre etrafında tanımlanan bir kürenin tanımları bulunabilir. çokyüzlü. Bu ders kitabı için metodolojik öneriler (bkz. S.M. Sahakyan ve V.F. Butuzov'un "Studying Geometry in Grades 10-11" kitabı, s. 159), 629-646 numaralı problemleri çözerken hangi cisim kombinasyonlarının dikkate alındığını söylüyor ve dikkat çekiyor "Belirli bir problemi çözerken, öncelikle öğrencilerin durumda belirtilen cisimlerin göreceli konumlarını iyi anlamalarını sağlamak gerekir." 638(a) ve 640 numaralı problemlerin çözümü aşağıdadır.

Yukarıdakilerin tümü ve öğrenciler için en zor problemlerin topun diğer cisimlerle birleşimi olduğu göz önüne alındığında, ilgili teorik ilkelerin sistematize edilmesi ve öğrencilere aktarılması gerekmektedir.

Tanımlar.

1. Bir topun bir çokyüzlü içine yazılı olduğu söylenir ve eğer topun yüzeyi çokyüzlünün tüm yüzlerine temas ediyorsa, bir çokyüzlünün topun etrafında çevrelendiği söylenir.

2. Topun yüzeyi çokyüzlünün tüm köşelerinden geçiyorsa, bir çokyüzlü etrafında çevrelenmiş bir top ve bir topun içine yazılmış bir çokyüzlü denir.

3. Bir topun, bir silindirin içine yazılı olduğu söylenir, kesik koni (koni) ve bir silindirin, kesik koninin (koni), eğer topun yüzeyi tabanlara (taban) ve tüm silindirin generatrikleri, kesik koni (koni).

(Bu tanımdan, bir topun büyük dairesinin bu cisimlerin herhangi bir eksenel bölümüne yazılabileceği sonucu çıkar).

4. Taban daireleri (taban dairesi ve tepe noktası) topun yüzeyine aitse, topun bir silindir, kesik bir koni (koni) etrafında çevrelendiği söylenir.

(Bu tanımdan, bu gövdelerin herhangi bir eksenel bölümünün etrafında topun daha büyük bir dairesinin dairesinin tanımlanabileceği sonucu çıkar).

Topun merkezinin konumu hakkında genel notlar.

1. Bir çokyüzlünün içine yazılmış bir topun merkezi, çokyüzlünün tüm dihedral açılarının açıortay düzlemlerinin kesişme noktasında bulunur. Sadece polihedronun içinde bulunur.

2. Bir çokyüzlünün çevrelediği bir topun merkezi, çokyüzlünün tüm kenarlarına dik olan ve orta noktalarından geçen düzlemlerin kesişme noktasında yer alır. Çokyüzlünün içine, yüzeyine veya dışına yerleştirilebilir.

Küre ve prizmanın birleşimi.

1. Düz bir prizmanın içine yazılmış bir top.

Teorem 1. Düz bir prizmaya bir küre yazılabilir, ancak ve ancak prizmanın tabanına bir daire çizilebilirse ve prizmanın yüksekliği bu dairenin çapına eşitse.

Sonuç 1. Dik prizma içine yazılmış bir kürenin merkezi, tabana yazılı dairenin merkezinden geçen prizmanın yüksekliğinin orta noktasında yer alır.

Sonuç 2.Özellikle bir top düz çizgilerle yazılabilir: H = 2r koşulu altında üçgen, düzenli, dörtgen (tabanın karşıt kenarlarının toplamı birbirine eşittir), burada H topun yüksekliğidir. prizma, r tabanda yazılı dairenin yarıçapıdır.

2. Bir prizma etrafında çevrelenmiş bir küre.

Teorem 2. Bir prizmanın etrafında bir küre, ancak ve ancak prizmanın düz olması ve tabanının etrafında bir dairenin tanımlanması durumunda tanımlanabilir.

Sonuç 1. Düz bir prizmanın çevresine çevrelenmiş bir kürenin merkezi, tabanın çevresine çevrelenmiş bir çemberin merkezinden çizilen prizmanın yüksekliğinin orta noktasında yer alır.

Sonuç 2.Özellikle bir top şu şekilde tanımlanabilir: sağ üçgen prizmanın yakınında, düzenli prizmanın yakınında, dikdörtgen paralel yüzlünün yakınında, tabanın zıt açılarının toplamının 180 dereceye eşit olduğu sağ dörtgen prizmanın yakınında.

L.S. Atanasyan'ın ders kitabından top ve prizma kombinasyonu için 632, 633, 634, 637(a), 639(a,b) numaralı problemler önerilebilir.

Bir topun bir piramit ile birleşimi.

1. Bir piramidin yakınında tanımlanan bir top.

Teorem 3. Bir topun bir piramidin etrafında tanımlanması ancak ve ancak tabanının etrafında bir daire tanımlanabiliyorsa mümkündür.

Sonuç 1. Bir piramidin çevrelediği bir kürenin merkezi, bu tabanın çevrelediği bir dairenin merkezinden geçen, piramidin tabanına dik bir düz çizgi ile piramidin ortasından çizilen herhangi bir yan kenara dik bir düzlemin kesiştiği noktada yer alır. bu kenar.

Sonuç 2. Piramidin yan kenarları birbirine eşitse (veya taban düzlemine eşit derecede eğimliyse), bu durumda böyle bir piramidin etrafında bir top tanımlanabilir. Bu durumda bu topun merkezi, piramidin kesişme noktasında yer alır. piramidin yüksekliği (veya uzantısı), yan kenarın simetri ekseni, yan kenar ve yükseklik düzleminde yer alır.

Sonuç 3.Özellikle bir top şu şekilde tanımlanabilir: üçgen bir piramidin yakınında, düzenli bir piramidin yakınında, karşıt açıların toplamı 180 derece olan dörtgen bir piramidin yakınında.

2. Piramidin içine yazılmış bir top.

Teorem 4. Piramidin yan yüzleri tabana eşit eğimliyse, böyle bir piramidin içine bir top yazılabilir.

Sonuç 1. Yan yüzleri tabana eşit eğimli olan bir piramitte yazılı bir topun merkezi, piramidin yüksekliğinin, piramidin tabanındaki herhangi bir dihedral açının doğrusal açısının açıortayı ile kesişme noktasında yer alır. piramidin tepesinden çizilen yan yüzün yüksekliğidir.

Sonuç 2. Bir topu normal bir piramite sığdırabilirsiniz.

L.S. Atanasyan'ın ders kitabından topun piramit ile birleşimi için 635, 637(b), 638, 639(c), 640, 641 numaralı problemler önerilebilir.

Bir topun kesik bir piramit ile birleşimi.

1. Düzgün kesik bir piramit etrafında çevrelenmiş bir top.

Teorem 5. Herhangi bir düzenli kesik piramidin etrafında bir küre tanımlanabilir. (Bu koşul yeterlidir ancak gerekli değildir)

2. Düzenli kesik piramit içine yazılmış bir top.

Teorem 6. Bir top, ancak ve ancak piramidin özünün tabanların özlerinin toplamına eşit olması durumunda düzenli bir kesik piramite yazılabilir.

L.S. Atanasyan’ın ders kitabında (No. 636) topun kesik piramitle birleştirilmesinde tek bir sorun vardır.

Topun yuvarlak gövdelerle birleşimi.

Teorem 7. Bir top, bir silindirin, kesik bir koninin (düz dairesel) veya bir koninin etrafında tanımlanabilir.

Teorem 8. Bir top (düz dairesel) bir silindirin içine ancak ve ancak silindirin eşkenar olması durumunda yazılabilir.

Teorem 9. Herhangi bir koniye (düz dairesel) bir top yerleştirebilirsiniz.

Teorem 10. Bir top, kesik bir koniye (düz dairesel) ancak ve ancak onun generatrix'i tabanların yarıçaplarının toplamına eşitse yazılabilir.

L.S. Atanasyan'ın ders kitabından topun yuvarlak gövdelerle birleşimi için 642, 643, 644, 645, 646 numaralı problemler önerilebilir.

Bu konuyla ilgili materyali daha başarılı bir şekilde incelemek için derslere sözlü görevlerin dahil edilmesi gerekmektedir:

1. Küpün kenarı a'ya eşittir. Küpün içine yazılan ve etrafı çevrelenen topların yarıçaplarını bulun. (r = a/2, R = a3).

2. Aşağıdakilerin etrafındaki bir küreyi (topu) tanımlamak mümkün müdür: a) bir küp; b) dikdörtgen paralel yüzlü; c) tabanında bir dikdörtgen bulunan eğimli bir paralel boru; d) düz paralel yüzlü; e) eğimli bir paralel yüzlü mü? (a) evet; B: Evet; c) hayır; d) hayır; hayır)

3. Herhangi bir üçgen piramidin etrafında bir kürenin tanımlanabileceği doğru mudur? (Evet)

4. Herhangi bir dörtgen piramidin etrafındaki küreyi tanımlamak mümkün müdür? (Hayır, herhangi bir dörtgen piramidin yakınında değil)

5. Bir piramidin etrafındaki küreyi tanımlayabilmesi için hangi özelliklere sahip olması gerekir? (Tabanında, çevresinde bir dairenin tanımlanabileceği bir çokgen bulunmalıdır)

6. Yan kenarı tabana dik olan bir kürenin içine bir piramit yazılmıştır. Bir kürenin merkezi nasıl bulunur? (Kürenin merkezi, uzaydaki iki geometrik noktanın kesişme noktasıdır. Birincisi, piramidin taban düzlemine, etrafını çevreleyen bir dairenin merkezinden çizilen bir diktir. İkincisi bir düzlemdir. belirli bir yan kenara dik ve ortasından çizilen)

7. Tabanında yamuk bulunan bir prizmanın etrafındaki küreyi hangi koşullar altında tanımlayabilirsiniz? (Etrafında bir daire tanımlanabilmesi için öncelikle prizmanın düz olması, ikinci olarak yamuğun ikizkenar olması gerekir)

8. Bir prizmanın çevresinde bir kürenin tanımlanabilmesi için hangi koşulları sağlaması gerekir? (Prizma düz olmalı ve tabanı, çevresinde bir dairenin tanımlanabileceği bir çokgen olmalıdır)

9. Merkezi prizmanın dışında bulunan üçgen prizmanın etrafında bir küre tanımlanmaktadır. Prizmanın tabanı hangi üçgendir? (Geniş üçgen)

10. Eğik bir prizmanın etrafındaki küreyi tanımlamak mümkün müdür? (Hayır, yapamazsınız)

11. Bir dik üçgen prizma etrafında çevrelenen bir kürenin merkezi hangi koşullar altında prizmanın yan yüzlerinden birinde yer alır? (Taban bir dik üçgendir)

12. Piramidin tabanı ikizkenar bir yamuktur. Piramidin tepesinin taban düzlemine dik izdüşümü yamuğun dışında bulunan bir noktadır. Böyle bir yamuğun etrafında bir küre tanımlamak mümkün müdür? (Evet, yapabilirsiniz. Piramidin tepesinin dik çıkıntısının tabanının dışında yer alması önemli değil. Piramidin tabanında bir ikizkenar yamuk - çevresinde bir dairenin olabileceği bir çokgen bulunması önemlidir. açıklanan)

13. Düzenli bir piramidin yakınında bir küre tanımlanmaktadır. Merkezi piramidin elemanlarına göre nasıl konumlandırılmıştır? (Kürenin merkezi, taban düzlemine merkezinden geçen dik bir çizgi üzerindedir)

14. Dik üçgen prizma etrafında tanımlanan kürenin merkezi hangi koşullar altında bulunur: a) prizmanın içinde; b) prizmanın dışında mı? (Prizmanın tabanında: a) dar bir üçgen; b) geniş üçgen)

15. Kenarları 1 dm, 2 dm ve 2 dm olan dikdörtgen bir paralelyüzün etrafında bir küre tanımlanmaktadır. Kürenin yarıçapını hesaplayın. (1,5 dm)

16. Bir küre hangi kesik koniye sığabilir? (Eksenel bölümüne daire yazılabilen kesik bir konide. Koninin eksenel bölümü ikizkenar yamuktur, tabanlarının toplamı yan kenarlarının toplamına eşit olmalıdır. Başka bir deyişle, koninin tabanlarının yarıçaplarının toplamı jeneratöre eşit olmalıdır)

17. Kesik bir koninin içine bir küre yazılmıştır. Koninin generatrisi kürenin merkezinden hangi açıda görülebilir? (90 derece)

18. Düz bir prizmanın içine bir küre sığabilmesi için hangi özelliğe sahip olması gerekir? (Birincisi, düz bir prizmanın tabanında içine bir dairenin yazılabileceği bir çokgen bulunmalıdır ve ikinci olarak prizmanın yüksekliği tabana yazılan dairenin çapına eşit olmalıdır)

19. Küreye sığmayan piramit örneği verir misiniz? (Örneğin, tabanında bir dikdörtgen veya paralelkenar bulunan dörtgen bir piramit)

20. Düz bir prizmanın tabanında bir eşkenar dörtgen vardır. Bu prizmaya bir küre sığdırmak mümkün mü? (Hayır, bu imkansızdır, çünkü genel olarak bir eşkenar dörtgen etrafındaki daireyi tanımlamak imkansızdır)

21. Bir küre hangi koşullar altında dik üçgen prizmanın içine yazılabilir? (Prizmanın yüksekliği tabanda yazılı dairenin yarıçapının iki katı ise)

22. Hangi koşullar altında düzgün dörtgen şeklinde kesik bir piramitin içine bir küre yazılabilir? (Belirli bir piramidin kesiti, tabanın kendisine dik tarafının ortasından geçen bir düzlem ise, içine bir dairenin yazılabileceği ikizkenar yamuktur)

23. Üçgen şeklinde kesik bir piramidin içine bir küre yazılmıştır. Piramidin hangi noktası kürenin merkezidir? (Bu piramidin içine yazılan kürenin merkezi, piramidin yan yüzlerinin oluşturduğu iki taraflı üç açı düzleminin tabanla kesiştiği noktadadır)

24. Bir silindirin etrafındaki küreyi (sağdaki dairesel) tanımlamak mümkün müdür? (Evet, yapabilirsin)

25. Bir koninin etrafındaki bir küreyi, kesik bir koniyi (düz dairesel) tanımlamak mümkün müdür? (Evet, her iki durumda da yapabilirsiniz)

26. Herhangi bir silindirin içine küre yazılabilir mi? Bir silindirin içine bir küre sığabilmesi için hangi özelliklere sahip olması gerekir? (Hayır, her zaman değil: silindirin eksenel bölümü kare olmalıdır)

27. Herhangi bir koninin içine küre yazılabilir mi? Bir koninin içine yazılmış bir kürenin merkezinin konumu nasıl belirlenir? (Evet, kesinlikle. Yazılı kürenin merkezi, koninin yüksekliği ile generatrisin taban düzlemine eğim açısının açıortayının kesiştiği noktadadır)

Yazar, "Çokyüzlü, silindir, koni ve topla ilgili farklı problemler" konulu üç planlama dersinden iki dersin bir topu diğer cisimlerle birleştirme problemlerini çözmeye ayırmanın tavsiye edildiğine inanıyor. Derste sürenin yetersiz olması nedeniyle yukarıda verilen teoremlerin ispatlanması önerilmez. Bunun için yeterli beceriye sahip öğrencileri, ispatın dersini veya planını belirterek (öğretmenin takdirine bağlı olarak) ispat etmeye davet edebilirsiniz.