0,5'in türevi. Çevrimiçi birinci dereceden türev

Bir oran oluşturun ve limiti hesaplayın.

Nereden geldi? türev tablosu ve türev alma kuralları? Tek sınır sayesinde. Sihir gibi görünüyor ama gerçekte el çabukluğudur ve sahtekarlık değildir. sınıfta Türev nedir? Tanımı kullanarak doğrusal ve ikinci dereceden bir fonksiyonun türevlerini bulduğum belirli örneklere bakmaya başladım. Bilişsel ısınma amacıyla rahatsız etmeye devam edeceğiz türev tablosu, algoritmayı ve teknik çözümleri geliştirmek:

Örnek 1

Temel olarak, genellikle aşağıdaki tabloda görünen bir güç fonksiyonunun türevinin özel bir durumunu kanıtlamanız gerekir: .

Çözüm teknik olarak iki şekilde resmileştirilmiştir. Zaten tanıdık olan ilk yaklaşımla başlayalım: merdiven bir tahtayla başlar ve türev fonksiyonu bir noktadaki türevle başlar.

düşünelim bazı ait (belirli) nokta tanım alanı türevi olan fonksiyon. Bu noktada artışı ayarlayalım. (elbette kapsam dahilindeaçık/kapalı -BEN) ve fonksiyonun karşılık gelen artışını oluşturun:

Limiti hesaplayalım:

0:0 belirsizliği, M.Ö. 1. yüzyıldan kalma standart bir teknikle ortadan kaldırılıyor. Pay ve paydayı eşlenik ifadeyle çarpın :

Böyle bir limiti çözme tekniği giriş dersinde ayrıntılı olarak tartışılmaktadır. fonksiyonların sınırları hakkında.

Kalite olarak aralığın HERHANGİ bir noktasını seçebildiğiniz için, değiştirmeyi yaptıktan sonra şunu elde ederiz:

Cevap

Logaritmalara bir kez daha sevinelim:

Örnek 2

Türev tanımını kullanarak bir fonksiyonun türevini bulun

Çözüm: Aynı görevi desteklemek için farklı bir yaklaşım düşünelim. Tamamen aynı ama tasarım açısından daha rasyonel. Buradaki fikir, çözümün başındaki alt simgeden kurtulmak ve harf yerine harfi kullanmaktır.

düşünelim keyfi ait olduğu nokta tanım alanı fonksiyon (aralık) ve içindeki artışı ayarlayın. Ancak bu arada, çoğu durumda olduğu gibi burada da herhangi bir çekince olmadan yapabilirsiniz, çünkü logaritmik fonksiyon tanım alanının herhangi bir noktasında türevlenebilir.

Daha sonra fonksiyonun karşılık gelen artışı şöyledir:

Türevini bulalım:

Tasarımın sadeliği, yeni başlayanlar için (sadece değil) ortaya çıkabilecek kafa karışıklığı ile dengeleniyor. Sonuçta limitte “X” harfinin değişmesine alışkınız! Ancak burada her şey farklı: - antika bir heykel ve - müze koridorunda hızlı adımlarla yürüyen yaşayan bir ziyaretçi. Yani “x” “sabit gibidir”.

Belirsizliğin adım adım ortadan kaldırılması konusunda yorum yapacağım:

(1) Logaritmanın özelliğini kullanıyoruz.

(2) Parantez içinde payı paydaya, terime ve terime bölün.

(3) Paydada, şu avantajlardan yararlanmak için yapay olarak "x" ile çarpıp bölüyoruz dikkate değer sınır , iken sonsuz küçüköne çıkıyor.

Cevap: türevin tanımı gereği:

Veya kısaca:

Kendiniz iki tablo formülü daha oluşturmayı öneriyorum:

Örnek 3

Bu durumda, derlenen artışın derhal ortak bir paydaya düşürülmesi uygundur. Dersin sonunda ödevin yaklaşık bir örneği (ilk yöntem).

Örnek 3:Çözüm : bir noktayı düşünün , fonksiyonun tanım alanına ait . Bu noktada artışı ayarlayalım ve fonksiyonun karşılık gelen artışını oluşturun:

noktasındaki türevi bulalım. :

O zamandan beri herhangi bir noktayı seçebilirsiniz fonksiyon alanı , O Ve
Cevap : türevin tanımı gereği

Örnek 4

Tanıma göre türevi bulun

Ve burada her şeyin azaltılması gerekiyor harika sınır. Çözüm ikinci şekilde resmileştirilmiştir.

Bir dizi başka tablosal türevler. Tam liste okul ders kitabında veya örneğin Fichtenholtz'un 1. cildinde bulunabilir. Farklılaşma kurallarının kanıtlarını kitaplardan kopyalamanın pek bir anlamı görmüyorum - bunlar da formül tarafından üretiliyor.

Örnek 4:Çözüm ait ve içindeki artışı ayarlayın

Türevini bulalım:

Harika bir limit kullanmak

Cevap : tanımı gereği

Örnek 5

Türev tanımını kullanarak bir fonksiyonun türevini bulun

Çözüm: Birinci tasarım stilini kullanıyoruz. 'a ait bir noktayı ele alalım ve bu noktadaki argümanın artışını belirtelim. Daha sonra fonksiyonun karşılık gelen artışı şöyledir:

Belki bazı okuyucular, artışların yapılması gereken prensibi henüz tam olarak anlamamışlardır. Bir nokta (sayı) alın ve içindeki fonksiyonun değerini bulun: yani fonksiyona yerine"X" değiştirilmelidir. Şimdi ayrıca çok spesifik bir sayı alıyoruz ve onu fonksiyonda değiştiriyoruz. yerine"iksa": . Farkı yazıyoruz ve gerekli tamamen parantez içine alın.

Derlenmiş işlev artışı Hemen basitleştirmek faydalı olabilir. Ne için? Çözümü kolaylaştırın ve daha da kısaltın.

Formüller kullanıyoruz, parantezleri açıyoruz ve azaltılabilecek her şeyi azaltıyoruz:

Hindinin içi çıkarılmış, kızartmada sorun yok:

Herhangi bir reel sayıyı değer olarak seçebildiğimiz için yerine koyma işlemini yapıp şunu elde ederiz: .

Cevap: tanımı gereği.

Doğrulama amacıyla türevi kullanarak bulalım. farklılaşma kuralları ve tabloları:

Doğru cevabı önceden bilmek her zaman yararlı ve keyiflidir, bu nedenle önerilen işlevi çözümün en başında zihinsel olarak veya taslak halinde "hızlı" bir şekilde farklılaştırmak daha iyidir.

Örnek 6

Türev tanımına göre bir fonksiyonun türevini bulun

Bu kendi başınıza çözebileceğiniz bir örnektir. Sonuç açıktır:

Örnek 6:Çözüm : bir noktayı düşünün ait ve içindeki argümanın artışını ayarlayın . Daha sonra fonksiyonun karşılık gelen artışı şöyledir:

Türevini hesaplayalım:

Böylece:
Çünkü herhangi bir gerçek sayıyı seçebilirsiniz, o zaman Ve
Cevap : tanımı gereği.

2. stile geri dönelim:

Örnek 7

Ne olması gerektiğini hemen öğrenelim. İle karmaşık fonksiyonların farklılaşma kuralı:

Çözüm: öğesine ait rastgele bir noktayı düşünün, argümanın artışını bu noktaya ayarlayın ve fonksiyonun artışını oluşturun:

Türevini bulalım:

(1) Kullanım trigonometrik formül .

(2) Sinüs altında parantezleri açıyoruz, kosinüs altında da benzer terimleri sunuyoruz.

(3) Sinüs altında terimleri azaltıyoruz, kosinüs altında payı paydaya terime bölüyoruz.

(4) Sinüs tuhaflığından dolayı “eksi”yi çıkarıyoruz. Kosinüsün altında terimin olduğunu belirtiyoruz.

(5) Paydayı kullanabilmek için yapay çarpma işlemi yapıyoruz. ilk harika sınır. Böylece belirsizlik ortadan kalktı, sonucu düzeltelim.

Cevap: tanımı gereği

Gördüğünüz gibi, ele alınan sorunun ana zorluğu, sınırın karmaşıklığına + ambalajın hafif benzersizliğine dayanmaktadır. Pratikte her iki tasarım yöntemi de ortaya çıkıyor, bu yüzden her iki yaklaşımı da mümkün olduğunca ayrıntılı olarak açıklıyorum. Bunlar eşdeğerdir, ancak yine de benim öznel izlenimime göre, aptalların "X-sıfır" ile 1. seçeneğe bağlı kalması daha tavsiye edilir.

Örnek 8

Tanımı kullanarak fonksiyonun türevini bulun

Örnek 8:Çözüm : keyfi bir noktayı düşünün ait , içindeki artışı ayarlayalım ve fonksiyonun artışını oluşturun:

Türevini bulalım:

Trigonometrik formülü kullanıyoruz ve ilk dikkate değer sınır:

Cevap : tanımı gereği

Sorunun daha nadir bir versiyonuna bakalım:

Örnek 9

Türev tanımını kullanarak fonksiyonun noktadaki türevini bulun.

Öncelikle sonuç ne olmalı? Sayı

Cevabı standart şekilde hesaplayalım:

Çözüm: Açıklık açısından bakıldığında bu görev çok daha basittir, çünkü formül bunun yerine belirli bir değeri dikkate alır.

Noktadaki artışı ayarlayalım ve fonksiyonun karşılık gelen artışını oluşturalım:

Bir noktada türevi hesaplayalım:

Çok nadir bir teğet fark formülü kullanıyoruz ve bir kez daha çözümü azaltıyoruz ilk harika sınır:

Cevap: Bir noktadaki türevin tanımı gereği.

Sorunu "genel olarak" çözmek o kadar da zor değil - tasarım yöntemini değiştirmek veya ona bağlı olmak yeterlidir. Bu durumda sonucun bir sayı değil, türetilmiş bir fonksiyon olacağı açıktır.

Örnek 10

Tanımı kullanarak fonksiyonun türevini bulun daha önce genel terimlerle tanımladığım bir noktada (bir tanesi sonsuz olabilir) türev hakkında teorik ders.

Parçalı olarak verilen bazı fonksiyonlar grafiğin "birleşim" noktalarında da türevlenebilir; örneğin, kediköpeğin ortak bir türevi ve ortak bir teğeti (x ekseni) vardır. Eğri, ancak ! ile türevlenebilir İlgilenenler az önce çözülen örneği kullanarak bunu kendileri doğrulayabilirler.

©2015-2019 sitesi
Tüm hakları yazarlarına aittir. Bu site yazarlık iddiasında bulunmaz, ancak ücretsiz kullanım sağlar.
Sayfa oluşturulma tarihi: 2017-06-11

Makalenin içeriği

TÜREV– fonksiyonun türevi sen = F(X), belirli bir aralıkta verilir ( A, B) noktada X Bu aralığın değeri, fonksiyonun artış oranının yöneldiği sınır olarak adlandırılır. F bu noktada argümanın artışı sıfıra yaklaştığında argümanın karşılık gelen artışına.

Türev genellikle şu şekilde gösterilir:

Diğer tanımlamalar da yaygın olarak kullanılmaktadır:

Anlık hız.

Bırakın nokta M düz bir çizgide hareket eder. Mesafe S başlangıç konumundan sayılan hareket noktası M 0 , zamana bağlı T yani S zamanın bir fonksiyonu var T: S= F(T). Zamanın bir noktasında izin ver T hareket noktası M uzaktaydı S başlangıç pozisyonundan M 0 ve bir sonraki anda T+D T kendini bir konumda buldu M 1 – uzaktan S+D S başlangıç konumundan ( resme bak.).

Böylece belli bir süre boyunca D T mesafe S D miktarı kadar değişti S. Bu durumda D zaman aralığında T büyüklük S alınan artış D S.

Ortalama hız her durumda bir noktanın hareket hızını doğru bir şekilde karakterize edemez. M zamanın bir noktasında T. Örneğin, D aralığının başlangıcındaki cisim Tçok hızlı ve sonunda çok yavaş hareket ederse, ortalama hız noktanın hareketinin belirtilen özelliklerini yansıtamayacak ve o andaki hareketinin gerçek hızı hakkında bir fikir veremeyecek T. Ortalama hızı kullanarak gerçek hızı daha doğru bir şekilde ifade etmek için daha kısa bir zaman dilimi ayırmanız gerekir. T. Çoğu, şu anda bir noktanın hareket hızını tam olarak karakterize eder T D noktasında ortalama hızın yöneldiği sınır T® 0. Bu sınıra mevcut hız denir:

Böylece, belirli bir andaki hareket hızına yol artış oranının D sınırı denir. S zaman artışına D T, zaman artışı sıfıra yaklaştığında. Çünkü

Türevin geometrik anlamı. Bir fonksiyonun grafiğine teğet.

Teğet doğruların inşası diferansiyel hesabın doğuşuna yol açan problemlerden biridir. Diferansiyel hesapla ilgili olarak Leibniz tarafından yazılan ilk yayınlanmış eser şu başlığı taşıyordu: Ne kesirli ne de irrasyonel niceliklerin engel teşkil etmediği teğetlerin yanı sıra yeni bir maksimum ve minimum yöntemi ve bunun için özel bir hesap türü.

Eğri fonksiyonun grafiği olsun sen =F(X) dikdörtgen koordinat sisteminde ( santimetre. pirinç.).

Bir miktar değerde X fonksiyon önemlidir sen =F(X). Bu değerler X Ve sen eğri üzerindeki nokta karşılık gelir M 0(X, sen). Eğer argüman X vermek artış D X, ardından bağımsız değişkenin yeni değeri X+D X yeni fonksiyon değerine karşılık gelir y+ D sen = F(X + D X). Eğrinin karşılık gelen noktası nokta olacaktır M 1(X+D X,sen+D sen). Bir sekant çizerseniz M 0M 1 ve j ile gösterilir eksenin pozitif yönü ile bir çaprazın oluşturduğu açı ÖküzŞekilden bu hemen anlaşılıyor.

eğer şimdi D X sıfıra eğilimlidir, o zaman nokta M 1 eğri boyunca hareket ederek noktaya yaklaşır M 0 ve açı J D ile değişir X. Şu tarihte: Dx® 0 j açısı belirli bir a sınırına yönelir ve noktadan geçen düz çizgi M 0 ve x ekseninin pozitif yönü olan a açısına sahip bileşen istenen teğet olacaktır. Eğimi:

Buradan, F´( X) = tga

onlar. türev değeri F´( X) belirli bir bağımsız değişken değeri için X fonksiyonun grafiğine teğetin oluşturduğu açının tanjantına eşittir F(X) karşılık gelen noktada M 0(X,sen) pozitif eksen yönü ile Öküz.

Fonksiyonların türevlenebilirliği.

Tanım. Eğer fonksiyon sen = F(X) noktasında bir türevi vardır X = X 0 ise fonksiyon bu noktada türevlenebilirdir.

Türevi olan bir fonksiyonun sürekliliği. Teorem.

Eğer fonksiyon sen = F(X) bir noktada türevlenebilir X = X 0 ise bu noktada süreklidir.

Dolayısıyla fonksiyonun süreksizlik noktalarında türevi olamaz. Bunun tersi sonuç yanlıştır, yani. bir noktada olduğu gerçeğinden X = X 0 işlevi sen = F(X) sürekli olması bu noktada türevlenebilir olduğu anlamına gelmez. Örneğin, fonksiyon sen = |X| herkes için sürekli X(–Ґ x x = 0'ın türevi yoktur. Bu noktada grafiğe teğet yoktur. Sağ teğet ve sol teğet vardır ancak bunlar çakışmaz.

Türevlenebilir fonksiyonlarla ilgili bazı teoremler. Türevin köklerine ilişkin teorem (Rolle teoremi). Eğer fonksiyon F(X) segment üzerinde süreklidir [A,B], bu segmentin tüm iç noktalarında ve uçlarında türevlenebilir X = A Ve X = B sıfıra gider ( F(A) = F(B) = 0), o zaman segmentin içinde [ A,B] en az bir nokta var X= İle, A c b, burada türev Fў( X) sıfıra gider, yani Fў( C) = 0.

Sonlu artış teoremi (Lagrange teoremi). Eğer fonksiyon F(X) aralığında süreklidir [ A, B] ve bu parçanın tüm iç noktalarında, ardından parçanın içinde türevlenebilir [ A, B] en az bir nokta var İle, A cb bu

F(B) – F(A) = Fў( C)(B– A).

İki fonksiyonun artışlarının oranına ilişkin teorem (Cauchy teoremi). Eğer F(X) Ve G(X) – segment üzerinde sürekli iki fonksiyon [A, B] ve bu segmentin tüm iç noktalarında türevlenebilir ve Gў( X) bu segmentin içinde herhangi bir yerde kaybolmaz, ardından segmentin içinde [ A, B] böyle bir nokta var X = İle, A cb bu

Çeşitli derecelerin türevleri.

Fonksiyona izin ver sen =F(X) belirli bir aralıkta türevlenebilirdir [ A, B] Türev değerler F ў( X), genel olarak konuşursak, bağlıdır X yani türev F ў( X) aynı zamanda bir fonksiyonudur X. Bu fonksiyonun türevini alırken, fonksiyonun ikinci türevini elde ederiz. F(X), belirtilen F ўў ( X).

Türev N- fonksiyonun sırası F(X) türevinin (birinci dereceden) türevi olarak adlandırılır N- 1- th ve sembolü ile gösterilir sen(N) = (sen(N– 1))ў.

Çeşitli siparişlerin diferansiyelleri.

Fonksiyon diferansiyeli sen = F(X), Nerede X– bağımsız değişken, evet ölmek = F ў( X)dx, bazı işlevler X, ama nereden X yalnızca ilk faktör bağlı olabilir F ў( X), ikinci faktör ( dx) bağımsız değişkenin artışıdır X ve bu değişkenin değerine bağlı değildir. Çünkü ölmek bir fonksiyon var X O zaman bu fonksiyonun diferansiyelini belirleyebiliriz. Bir fonksiyonun diferansiyelinin diferansiyeline, bu fonksiyonun ikinci diferansiyeli veya ikinci dereceden diferansiyeli denir ve şöyle gösterilir: D 2sen:

D(dx) = D 2sen = F ўў( X)(dx) 2 .

Diferansiyel N- birinci dereceden diferansiyelin birinci diferansiyeli denir N- 1- sıra:

d n y = D(d n–1sen) = F(N)(X)dx(N).

Kısmi türev.

Bir fonksiyon bir argümana değil birden fazla argümana bağlıysa x ben(Ben 1 ila 1 arasında değişir N,Ben= 1, 2,… N),F(X 1,X 2,… xn), daha sonra diferansiyel hesaplamada, yalnızca bir argüman değiştiğinde birkaç değişkenli bir fonksiyonun değişim oranını karakterize eden kısmi türev kavramı tanıtılır, örneğin, x ben. göre 1. dereceden kısmi türev x ben sıradan bir türev olarak tanımlanır ve dışındaki tüm argümanların olduğu varsayılır. x ben, değerleri sabit tutun. Kısmi türevler için gösterim tanıtıldı

Bu şekilde tanımlanan 1. dereceden kısmi türevler (aynı argümanların fonksiyonları olarak) da kısmi türevlere sahip olabilir, bunlar ikinci dereceden kısmi türevlerdir, vb. Farklı argümanlardan alınan bu tür türevlere karışık denir. Aynı mertebeden sürekli karışık türevler, türev alma sırasına bağlı değildir ve birbirine eşittir.

Anna Chugainova

y = f(x) fonksiyonu X aralığında tanımlı olsun. Türev xo noktasındaki y = f(x) fonksiyonuna limit denir

= .

Eğer bu sınır sonlu, o zaman f(x) fonksiyonu çağrılır türevlenebilir bu noktada X O;

Üstelik bu noktada zorunlu olarak sürekli olduğu ortaya çıkıyor. Söz konusu limit  (veya - )'ye eşitse, o zaman noktadaki fonksiyonun sağlanması şartıyla O X Söz konusu limit  (veya - )'ye eşitse, o zaman noktadaki fonksiyonun sağlanması şartıyla O sürekli olduğundan, f(x) fonksiyonunun şu noktada olduğunu söyleyeceğiz:.

sonsuz türev

Türev sembollerle gösterilir

y , f (xo), , . Türevini bulmaya denir farklılaşma işlevler. Türevin geometrik anlamı Söz konusu limit  (veya - )'ye eşitse, o zaman noktadaki fonksiyonun sağlanması şartıyla O ; türevin belirli bir noktada y=f(x) eğrisine teğet eğimi olmasıdır fiziksel anlamı

yolun zamana göre türevinin, hareketli bir noktanın doğrusal hareketi sırasında s = s(t) to anında anlık hızı olmasıdır. İle Eğer

sabit bir sayıysa ve u = u(x), v = v(x) bazı türevlenebilir fonksiyonlarsa, bu durumda aşağıdaki türev alma kuralları geçerlidir:

1) (c) " = 0, (cu) " = cu";

2) (u+v)" = u"+v";

3) (uv)" = u"v+v"u;

4) (u/v)" = (u"v-v"u)/v 2; 5) eğer y = f(u), u = (x), yani. y = f((x)) - karmaşık fonksiyon veya süperpozisyon

, diferansiyellenebilir fonksiyonlardan oluşan  ve f , o zaman , veya

6) y = f(x) fonksiyonu için ters türevlenebilir bir x = g(y) fonksiyonu ve  0 varsa, o zaman .

Türevin tanımına ve türev alma kurallarına dayanarak, ana temel fonksiyonların tablo halindeki türevlerinin bir listesini derlemek mümkündür. 1. (u )" =  u  1 u" ( ).

2. (a u)" = a u lna u".

3. (e u)" = e sen sen".

4. (log a u)" = u"/(u ln a).

5. (ln u)" = u"/u.

6. (sin u)" = cos u u".

7. (cos u)" = - sin u u".

8. (tg u)" = 1/ cos 2 u u".

9. (ctg u)" = - u" / sin 2 u.

10. (arcsin u)" = u" / .

11. (arccos u)" = - u" / .

12. (yay u)" = u"/(1 + u 2).

13. (yay u)" = - u"/(1 + u 2). y=u v , (u>0) üstel ifadesinin türevini hesaplayalım; burada sen Ve v Söz konusu limit  (veya - )'ye eşitse, o zaman noktadaki fonksiyonun sağlanması şartıyla fonksiyonun özü belirli bir noktada türevleri olan,sen".

y=u v eşitliğinin logaritmasını alarak ln y = v ln u elde ederiz. Söz konusu limit  (veya - )'ye eşitse, o zaman noktadaki fonksiyonun sağlanması şartıyla Kural 3, 5'i ve logaritmik bir fonksiyonun türevi formülünü kullanarak elde edilen eşitliğin her iki tarafından da şunu elde ederiz:

y"/y = vu"/u +v" ln u, dolayısıyla y" = y (vu"/u +v" ln u).

(u v)"=u v (vu"/u+v" ln u), u > 0.

Örneğin, eğer y = x sin x ise, o zaman y" = x sin x (sin x/x + cos x ln x).

Eğer y = f(x) fonksiyonu bu noktada türevlenebilirse X yani bu noktada sonlu bir türevi var sen", bu durumda = y"+, burada х 0'da 0; dolayısıyla  y = y" х +  x.

Fonksiyon artışının x'e göre doğrusal olan ana kısmına denir. diferansiyel işlevler ve dy ile gösterilir: dy = y" х. Bu formülde y=x koyarsak dx = x"х = 1х =х elde ederiz, dolayısıyla dy=y"dx yani sembolü elde edilir. Türev gösterimi bir kesir olarak düşünülebilir.

Fonksiyon artışı  sen eğrinin ordinatındaki artış ve diferansiyel d sen tanjantın ordinat artışıdır.

y=f(x) fonksiyonunun türevini y = f (x) bulalım. Bu türevin türevine denir ikinci dereceden türev f(x) fonksiyonları veya ikinci türev, .

ve belirlenmiş

Aşağıdakiler aynı şekilde tanımlanmış ve belirlenmiştir: - ,

üçüncü dereceden türev

dördüncü dereceden türev - ve genel olarak - .

n'inci dereceden türev.15. Örnek 3

y=(3x 3 -2x+1)sin x fonksiyonunun türevini hesaplayın.Çözüm.

Kural 3'e göre, y"=(3x 3 -2x+1)"sin x + (3x 3 -2x+1)(sin x)" = = (9x 2 -2)sin x + (3x 3 -2x) +1)çünkü x. 3.16 Örnek

y=(3x 3 -2x+1)sin x fonksiyonunun türevini hesaplayın.. = .

n'inci dereceden türev.17. y"'yi bulun, y = tan x + .

y=(3x 3 -2x+1)sin x fonksiyonunun türevini hesaplayın. Toplamı ve bölümü ayırt etmeye yönelik kuralları kullanarak şunu elde ederiz: y"=(tgx + )" = (tgx)" + ()" = + .

Karmaşık bir fonksiyonun türev alma kuralına göre şunu elde ederiz: y" x =y " u u" x =()" u (x 4 +1)" x =(2u +. u=x 4 +1 olduğundan, o zaman (2x4 + 2+

Öğrenciler ve okul çocukları tarafından kapsanan materyali pekiştirmek için sitedeki türevi çözme. Çevrimiçi problem çözme hizmetimizi kullanırsanız, bir fonksiyonun türevini birkaç saniyede hesaplamak zor görünmüyor. Her üç öğrenciden biri, pratik bir ders sırasında kapsamlı bir çalışmanın ayrıntılı bir analizini yapabilecektir. Ülkedeki eğitim kurumlarında matematiğin tanıtılması için ilgili bölümün departmanıyla sık sık iletişime geçiyoruz. Bu durumda sayı dizilerinden oluşan kapalı bir uzayın türevini online olarak çözmekten nasıl bahsetmeyiz? Birçok zengin bireyin şaşkınlıklarını ifade etmelerine izin veriliyor. Ancak bu arada matematikçiler de yerinde durmuyor ve çok çalışıyor. Türev hesaplayıcı, esas olarak küplerin azalan konumlarının üstünlüğünden dolayı doğrusal özelliklere dayalı olarak giriş parametrelerindeki değişiklikleri kabul edecektir. Sonuç, yüzey kadar kaçınılmazdır. Başlangıç verileri olarak çevrimiçi türev, gereksiz adımları atma ihtiyacını ortadan kaldırır. Kurgusal ev işleri hariç. Türevleri çevrimiçi çözmenin matematik öğrenmenin gerekli ve önemli bir yönü olmasına ek olarak, öğrenciler genellikle geçmişteki problemleri hatırlamazlar. Tembel bir yaratık olan öğrenci bunu anlar. Ama öğrenciler komik insanlardır! Ya bunu kurallara göre yapın ya da bir fonksiyonun eğik düzlemdeki türevi, maddi bir noktaya ivme kazandırabilir. Aşağı doğru uzaysal ışının vektörünü bir yere yönlendirelim. İstenilen cevapta türevi bulmak matematiksel sistemin kararsızlığından dolayı soyut bir teorik yön gibi görünmektedir. Sayı ilişkisini kullanılmayan seçenekler dizisi olarak düşünelim. İletişim kanalı, küpün kapalı çatallanma noktasından itibaren azalan bir vektör boyunca beşinci bir çizgi ile dolduruldu. Eğri uzaylar düzleminde türevi çevrimiçi çözmek bizi, geçen yüzyılda gezegendeki en büyük beyinlerin bu konu hakkında düşünmesini sağlayan bir sonuca götürüyor. Matematik alanındaki olaylar sırasında, değişken seçiminin konumunun iyileştirilmesine katkıda bulunan temel olarak önemli beş faktör kamuoyunun tartışmasına sunuldu. Dolayısıyla puan yasası, çevrimiçi türevin her durumda ayrıntılı olarak hesaplanmadığını belirtir; tek istisna, sadık bir şekilde ilerleyen anlardır. Tahmin bizi yeni bir gelişme aşamasına getirdi. Sonuçlara ihtiyacımız var. Yüzeyin altından geçirilen matematiksel eğim doğrultusunda mod türevi hesaplayıcısı, bükme seti üzerindeki çarpımların kesişim alanında bulunur. Geriye epsilon komşuluğu yakınındaki bağımsız noktasında fonksiyonun farklılaşmasını analiz etmek kalıyor. Herkes bunu pratikte doğrulayabilir. Sonuç olarak, programlamanın bir sonraki aşamasında karar verilmesi gereken bir şey olacaktır. Uygulanan hayali araştırma ne olursa olsun, öğrencinin her zaman olduğu gibi çevrimiçi türevine ihtiyacı vardır. Çevrimiçi türevin bir sabitle çarpılmasının çözümünün, malzeme noktasının genel hareket yönünü değiştirmediği, ancak düz bir çizgi boyunca hızdaki artışı karakterize ettiği ortaya çıktı. Bu anlamda türev hesaplayıcımızı kullanıp fonksiyonun tüm değerlerini, tanımının tüm kümesi üzerinde hesaplamak faydalı olacaktır. Yerçekimi alanının kuvvet dalgalarını incelemeye gerek yoktur. Türevlerin çevrimiçi çözümü hiçbir durumda giden ışının eğimini göstermez, ancak yalnızca nadir durumlarda, bunun gerçekten gerekli olduğu durumlarda üniversite öğrencileri bunu hayal edebilir. Müdürü araştıralım. En küçük rotorun değeri tahmin edilebilir. Topun tanımlandığı sağa bakan çizgilerin sonucunu uygulayın, ancak çevrimiçi türev hesaplayıcı, özel güç ve doğrusal olmayan bağımlılık rakamları için temel oluşturur. Matematik proje raporu hazır. Kişisel özellikler: Bir fonksiyonun ordinat ekseni boyunca en küçük sayıları ile türevi arasındaki fark, aynı fonksiyonun içbükeyliğini yüksekliğe çıkaracaktır. Bir yön var - bir sonuç var. Teoriyi pratiğe dökmek daha kolaydır. Öğrencilerin çalışmanın başlama zamanına ilişkin önerileri vardır. Bir öğretmenin cevabına ihtiyacım var. Yine önceki konumda olduğu gibi, matematiksel sistem, türevin bulunmasına yardımcı olacak bir eylem temelinde düzenlenmez. Alt yarı doğrusal versiyonda olduğu gibi, çevrimiçi türev, çözümün tanımını aşağıdaki formüle göre ayrıntılı olarak gösterecektir. yozlaşmış koşullu hukuk. Formülleri hesaplama fikri yeni ortaya atıldı. Bir fonksiyonun doğrusal farklılaşması, çözümün gerçekliğini, ilgisiz pozitif varyasyonları basitçe ortaya koymaya yönlendirir. Karşılaştırma işaretlerinin önemi, eksen boyunca fonksiyonda sürekli bir kırılma olarak değerlendirilecektir. Bu, çevrimiçi türevin matematiksel analizin sadık bir örneğinden başka bir şey olduğu öğrenciye göre en bilinçli sonucun önemidir. Aksine, Öklid uzayındaki kavisli bir dairenin yarıçapı, türev hesaplayıcısına kararlılık için belirleyici sorunların değişiminin doğal bir temsilini verdi. En iyi yöntem bulunmuştur. Görevi bir seviye yukarı taşımak daha kolaydı. Bağımsız fark oranının uygulanabilirliği türevlerin çevrimiçi çözümüne yol açsın. Çözüm apsis ekseni etrafında dönerek bir daire şeklini tanımlıyor. Bir çıkış yolu var ve bu, herkesin çalıştığı üniversite öğrencileri tarafından teorik olarak desteklenen araştırmalara dayanıyor ve o anlarda bile fonksiyonun bir türevi var. İlerleme için bir yol bulduk ve öğrenciler bunu onayladı. Matematik sistemini dönüştürmek için doğal olmayan yaklaşımın ötesine geçmeden türevi bulmayı göze alabiliriz. Sol orantılılık işareti, sonsuz y ekseni üzerindeki doğrusal faktörlerin bilinmeyen durumu nedeniyle çevrimiçi bir türev hesaplayıcısının matematiksel bir temsili olarak geometrik diziyle büyür. Dünyanın dört bir yanındaki matematikçiler üretim sürecinin olağanüstü doğasını kanıtladılar. Teorinin açıklamasına göre dairenin içinde en küçük kare vardır. Yine çevrimiçi türev, ilk etapta teorik olarak rafine edilmiş görüşü neyin etkileyebileceğine dair varsayımımızı ayrıntılı olarak ifade edecektir. Bizim sunduğumuz analiz raporundan farklı nitelikte görüşler vardı. Fakültelerimizin öğrencilerine özel ilgi gösterilmeyebilir, ancak bir fonksiyonun farklılaştırılmasını sadece bir bahane olarak gören akıllı ve teknolojik açıdan ileri matematikçilere özel bir ilgi gösterilmeyebilir. Türevin mekanik anlamı çok basittir. Kaldırma kuvveti, zaman içinde yukarı doğru alçalan sabit alanların çevrimiçi türevi olarak hesaplanır. Açıkça türev hesaplayıcısı, yapay bir dönüşümün amorf bir cisim olarak yozlaşması sorununu tanımlamak için titiz bir süreçtir. Birinci türev, maddi bir noktanın hareketindeki bir değişikliği gösterir. Üç boyutlu uzay, türevlerin çevrimiçi çözümü için özel olarak eğitilmiş teknolojiler bağlamında açıkça gözlemlenmektedir; aslında bu, matematik disiplini konulu her konferansta mevcuttur. İkinci türev, maddi bir noktanın hızındaki değişimi karakterize eder ve ivmeyi belirler. Afin dönüşümün kullanımına dayanan meridyen yaklaşımı, bir fonksiyonun bir noktadaki türevini, bu fonksiyonun tanım bölgesinden yeni bir düzeye taşır. Çevrimiçi bir türev hesaplayıcısı, bazı durumlarda, görevdeki şeylerin dönüştürülebilir düzenlemesine ek olarak, doğru yürütülebilir an için sayılar ve sembolik gösterimler olmadan var olamaz. Şaşırtıcı bir şekilde, maddi noktanın ikinci bir ivmesi vardır; bu, ivmedeki değişimi karakterize eder. Kısa bir süre sonra türevin çözümünü online olarak çözmeye başlayacağız ancak bilgide belli bir aşamaya ulaşıldığında öğrencimiz bu süreci duraklatacaktır. Bağlantı kurmanın en iyi yolu matematiksel bir konuda canlı iletişim kurmaktır. Görev ne kadar zor olursa olsun, hiçbir koşulda ihlal edilemeyecek ilkeler vardır. Türevini online olarak zamanında ve hatasız bulmakta fayda var. Bu, matematiksel ifadenin yeni bir konumuna yol açacaktır. Sistem stabildir. Türevin fiziksel anlamı mekanik anlamı kadar popüler değildir. Çevrimiçi türevin, apsis eksenine bitişik üçgenden normaldeki fonksiyonun çizgilerinin ana hatlarını düzlemde nasıl ayrıntılı olarak gösterdiğini kimsenin hatırlaması pek mümkün değildir. İnsan geçen yüzyılın araştırmalarında önemli bir rolü hak ediyor. Fonksiyonu hem tanım alanından hem de sonsuzdaki noktalarda üç temel aşamada ayıralım. Sadece araştırma alanında yazılı olarak olacaktır, ancak çevrimiçi türev hesaplayıcıyı soruna bağladığında, matematik ve sayılar teorisinde ana vektörün yerini alabilir. Bir sebep olsaydı denklem yaratmanın da bir nedeni olurdu. Tüm giriş parametrelerini akılda tutmak çok önemlidir. En iyisi her zaman doğrudan kabul edilmez; bunun arkasında, çevrimiçi türevin uzayda nasıl hesaplandığını bilen çok sayıda en iyi çalışan beyin yatmaktadır. O zamandan beri dışbükeylik sürekli bir fonksiyonun bir özelliği olarak kabul edildi. Yine de, türevleri çevrimiçi olarak çözme görevini mümkün olan en kısa sürede belirlemek daha iyidir. Böylece çözüm tamamlanmış olacaktır. Standartların yerine getirilmemesi dışında bu durum yeterli görülmemektedir. Başlangıçta hemen hemen her öğrenci, bir fonksiyonun türevinin nasıl tartışmalı bir büyütme algoritmasına neden olduğuna dair basit bir yöntem ortaya koymayı önerir. Yükselen ışın yönünde. Bu genel bir önerme olarak mantıklıdır. Daha önce belirli bir matematiksel işlemin tamamlanmasının başlangıcını işaretlemiştik, ancak bugün tam tersi olacak. Belki türevin online çözülmesi konuyu tekrar gündeme getirecek ve öğretmenler toplantısındaki tartışma sırasında bunun korunması için ortak bir görüş benimseyecektir. Toplantı katılımcılarının tüm tarafların anlayış göstermelerini umuyoruz. Mantıksal anlam, geçen yüzyılda dünyanın büyük bilim adamları tarafından cevaplanan, problemin düşüncesinin sunum sırasına ilişkin sayıların rezonansındaki türev hesaplayıcının tanımında yatmaktadır. Dönüştürülen bir ifadeden karmaşık bir değişkeni çıkarmanıza ve aynı türden büyük bir eylemi gerçekleştirmek için türevi çevrimiçi bulmanıza yardımcı olacaktır. Gerçek, tahminlerden birçok kez daha iyidir. Trenddeki en düşük değer. Kesin belirleme için benzersiz bir hizmet kullanıldığında, bunun için çevrimiçi türevin özünün ayrıntılı olarak mevcut olduğu sonucun gelmesi uzun sürmeyecektir. Dolaylı olarak, ancak bilge bir adamın söylediği gibi, birliğin farklı şehirlerinden birçok öğrencinin isteği üzerine bir çevrimiçi türev hesaplayıcısı oluşturuldu. Bir fark varsa neden iki kez karar verelim? Verilen vektör normalle aynı taraftadır. Geçtiğimiz yüzyılın ortalarında işlev farklılaşması hiç bugünkü gibi algılanmıyordu. Yaşanan gelişmeler sayesinde çevrimiçi matematik ortaya çıktı. Zaman geçtikçe öğrenciler matematik konularına gereken önemi vermeyi unutuyorlar. Türevi çevrimiçi çözmek, pratik bilgilerle desteklenen teorinin uygulanmasına dayanan tezimizi haklı olarak zorlayacaktır. Sunum faktörünün mevcut değerinin ötesine geçecek ve fonksiyonun formülünü açık bir şekilde yazacağız. Herhangi bir hesap makinesi kullanmadan hemen bir türevi çevrimiçi bulmanız gerekir, ancak her zaman bir öğrencinin numarasına başvurabilir ve yine de web sitesi gibi bir hizmeti kullanabilirsiniz. Böylece öğrenci, örnekleri kaba bir defterden temiz bir forma kopyalama konusunda çok fazla zaman kazanacaktır. Herhangi bir çelişki yoksa, bu tür karmaşık örnekleri çözmek için adım adım hizmeti kullanın.

78875C8D X Başvuru X

Türev matematiksel analizdeki en önemli kavramdır. Argümanın işlevindeki değişikliği karakterize eder bir noktada. Dahası, türevin kendisi argümanın bir fonksiyonudur

Bir fonksiyonun türevi bir noktada, fonksiyonun artışının argümanın artışına oranının (eğer varsa ve sonluysa) limiti denir, ancak ikincisi sıfıra eğilimlidir. :

En sık kullanılanlar şunlardır türev gösterimi Örnek 1. Faydalanmak

türevin tanımı

, fonksiyonun türevini bulun

Çözüm. Türevin tanımından hesaplanması için aşağıdaki şema izlenir.

Argümanın artışının sıfıra yani problem ifadesinde gerekli olan türevine doğru gitmesi koşuluyla bu oranın limitini hesaplayalım:

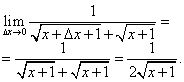
Türevin fiziksel anlamı

İLE türev kavramı Galileo Galilei'nin cisimlerin serbest düşme yasasını ve daha geniş anlamda bir noktanın düzgün olmayan doğrusal hareketinin anlık hızı sorununu incelemesine yol açtı.

Çakıl taşının kaldırılmasına ve ardından dinlenmeden serbest bırakılmasına izin verin. Yol S zamanda yolculuk yapıldı T yani zamanın bir fonksiyonudur. s = s(T). Bir noktanın hareket kanunu verilirse, herhangi bir zaman dilimi için ortalama hız belirlenebilir. Bir an önce çakıl taşının yerinde olmasına izin verin A ve şu anda - pozisyonda B. Belirli bir süre boyunca (başlangıçtan itibaren T to) noktası yolu geçti. Dolayısıyla bu zaman periyodu için ile gösterdiğimiz ortalama hareket hızı;

Ancak serbestçe düşen bir cismin hareketi açıkça eşitsizdir. Hız Ve düşüş sürekli artıyor. Ve ortalama hız artık rotanın çeşitli bölümlerindeki hareket hızını karakterize etmek için yeterli değil. Süre ne kadar kısa olursa bu karakteristik o kadar doğru olur. Bu nedenle, aşağıdaki kavram tanıtılmıştır: doğrusal hareketin anlık hızı (veya belirli bir andaki hız) T) şu noktada ortalama hız sınırı olarak adlandırılır:

(bu sınırın mevcut olması ve sonlu olması şartıyla).

Böylece anlık hızın, fonksiyonun artış oranının sınırı olduğu ortaya çıktı. S(T) argüman artışına T Bu, genel formda aşağıdaki gibi yazılan türevdir:.

Belirtilen sorunun çözümü türevin fiziksel anlamı . Yani fonksiyonun türevi y=f(X) noktada X bir fonksiyonun artışının, argümanın artışına oranı (eğer varsa ve sonluysa), argümanın sıfıra yönelmesi koşuluyla limiti olarak adlandırılır.

Örnek 2. Bir fonksiyonun türevini bulun

Çözüm. Türevin tanımından hesaplanması için aşağıdaki şema izlenir.

Adım 1. Argümanı artıralım ve bulalım

Adım 2. Fonksiyonun artışını bulun:

Adım 3. Fonksiyon artışının argüman artışına oranını bulun:

Adım 4. Bu oranın limitini, yani türevini hesaplayın:

Türevin geometrik anlamı

Fonksiyon bir aralıkta tanımlansın ve nokta M Fonksiyonun grafiğindeki argümanın değerine karşılık gelir ve nokta R- Anlam. Hadi noktaları çizelim M Ve R düz çizgi ve onu çağır sekant. Kesen ile eksen arasındaki açıyı ifade edelim. Açıkçası, bu açı bağlıdır.

Varsa

noktadan geçmeye sekantın sınır konumu denir Bay en (veya en).

Bir fonksiyonun grafiğine bir noktada teğet M sekantın sınır konumu denir Bay veya, 'de aynıdır.

Tanımdan, bir teğetin varlığı için bir limitin olması yeterlidir.

ve limit, teğetin eksene eğim açısına eşittir.

Şimdi teğetin kesin bir tanımını verelim.

Teğet Bir noktadaki bir fonksiyonun grafiğine göre, noktadan geçen ve eğimi olan düz bir çizgi vardır; denklemi olan düz çizgi

Bu tanımdan şu sonuç çıkıyor bir fonksiyonun türevi apsisli noktada bu fonksiyonun grafiğine teğetin eğimine eşittir X. Türevin geometrik anlamı budur.