7.1. Çapraz çarpımın tanımı
Aynı düzlemde olmayan üç a, b ve c vektörleri belirtilen sıraya göre alınırsa, üçüncü vektör c'nin ucundan birinci vektör a'dan ikinci vektör b'ye en kısa dönüş görülüyorsa sağ yönlü bir üçlü oluşturur. saat yönünün tersine olacak ve saat yönünde ise sol üçlü olacak (bkz. Şekil 16).
A vektörü ile b vektörünün vektör çarpımına c vektörü denir ve bu:
1. a ve b vektörlerine dik, yani c ^ a ve c ^ B ;
2. a ve vektörleri üzerine inşa edilmiş bir paralelkenarın alanına sayısal olarak eşit bir uzunluğa sahiptirB yanlarda olduğu gibi (bkz. Şekil 17), yani.
3. a, b ve c vektörleri sağ yönlü bir üçlü oluşturur.


Çapraz çarpım a x b veya [a,b] ile gösterilir. Vektör çarpımının tanımından doğrudan takip ettiğim birim vektörler arasındaki aşağıdaki ilişkiler, J Ve k
(bkz. Şekil 18):
ben x j = k, j x k = ben, k x ben = j.Örneğin şunu kanıtlayalım:
ben xj =k. ^ 1) k ^ ben, k
J ; 2) |k |=1, fakat | ben xj
| = |i | Ve|J | günah(90°)=1;
3) i, j ve vektörleri
sağ üçlü oluşturur (bkz. Şekil 16).
7.2. Çapraz çarpımın özellikleri = -(1. Faktörleri yeniden düzenlerken vektör çarpımı işaret değiştirir, yani.).
ve xb =(b xa) (bkz. Şekil 19).

a xb ve b xa vektörleri eşdoğrusaldır, aynı modüllere sahiptir (paralelkenarın alanı değişmeden kalır), ancak zıt yönlüdürler (karşıt yönelimli a, b, a xb ve a, b, b xa üçlüleri). Yani balta b xa B 2. Vektör çarpımı, skaler faktöre göre birleştirme özelliğine sahiptir, yani. l (a xb) = (la) x b = a x (l b). B l>0 olsun. Vektör l(a xb), a ve b vektörlerine diktir. vektör ( balta ben balta a)x balta b xa B aynı zamanda a ve vektörlerine de diktir
(vektörler a, balta ancak aynı düzlemde yer alır). Bu, vektörlerin balta(bir xb) ve ( balta<0.
doğrusal. Yönlerinin örtüştüğü açıktır. Aynı uzunluğa sahipler: B Bu yüzden<=>(birxb)=

bir xb. Benzer şekilde kanıtlanmıştır
3. Sıfır olmayan iki vektör a ve
(ancak ve ancak vektör çarpımları sıfır vektörüne eşitse eşdoğrusaldırlar, yani a ||b ve xb =0. BÖzellikle, i *i =j *j =k *k =0 .
4. Vektör çarpımı dağıtım özelliğine sahiptir:
7.3. Çapraz çarpımı koordinat cinsinden ifade etme
i vektörlerinin çapraz çarpım tablosunu kullanacağız, Vektör çarpımının tanımından doğrudan takip ettiğim birim vektörler arasındaki aşağıdaki ilişkiler, ve k:

birinci vektörden ikinciye olan en kısa yolun yönü okun yönü ile çakışıyorsa, çarpım üçüncü vektöre eşittir; çakışmıyorsa üçüncü vektör eksi işaretiyle alınır.
İki vektör a =a x i +a y verilsin Vektör çarpımının tanımından doğrudan takip ettiğim birim vektörler arasındaki aşağıdaki ilişkiler,+az Ve ve b =bx Ben+b y Vektör çarpımının tanımından doğrudan takip ettiğim birim vektörler arasındaki aşağıdaki ilişkiler,+bz Ve. Bu vektörlerin vektör çarpımını polinomlarla çarparak (vektör çarpımının özelliklerine göre) bulalım:

![]()
Ortaya çıkan formül daha da kısaca yazılabilir:

Eşitliğin (7.1) sağ tarafı, üçüncü dereceden determinantın birinci satırın elemanları açısından genişletilmesine karşılık geldiğinden, eşitliğin (7.2) hatırlanması kolaydır.
7.4. Çapraz çarpımın bazı uygulamaları
Vektörlerin eşdoğrusallığının kurulması

Paralelkenarın ve üçgenin alanını bulma
Vektörlerin vektör çarpımının tanımına göre A ve B |bir xb | =|bir | * |b |sin g, yani S çiftleri = |a x b |. Ve dolayısıyla DS =1/2|a x b |.
Bir noktaya göre kuvvet momentinin belirlenmesi
A noktasına bir kuvvet uygulansın F =AB bırak gitsin HAKKINDA- uzayda bir nokta (bkz. Şekil 20).

Fizikten biliniyor ki kuvvet anı F noktaya göre HAKKINDA vektör denir M, hangi noktadan geçer HAKKINDA Ve:
1) noktalardan geçen düzleme dik O, A, B;
2) sayısal olarak kol başına kuvvetin çarpımına eşittir
3) OA ve A B vektörleriyle bir dik üçlü oluşturur.
Bu nedenle M = OA x F.
Doğrusal dönüş hızını bulma
Hız v Açısal hızla dönen katı bir cismin M noktası w sabit bir eksen etrafında, Euler formülü ile belirlenir v =w xr, burada r =OM, burada O eksenin sabit bir noktasıdır (bkz. Şekil 21).

Vektör çarpımı kavramını vermeden önce, üç boyutlu uzayda sıralı bir a →, b →, c → vektör üçlüsünün yönelimi sorununa dönelim.
Başlangıç olarak, bir noktadan itibaren a → , b → , c → vektörlerini bir kenara bırakalım. a → , b → , c → üçlüsünün yönelimi, c → vektörünün yönüne bağlı olarak sağa veya sola olabilir. a → , b → , c → üçlüsünün türü, a → vektöründen b → c → vektörünün ucundan itibaren en kısa dönüşün yapıldığı yönden belirlenecektir.
En kısa dönüş saat yönünün tersine yapılırsa, a → , b → , c → vektörlerinin üçlüsü denir Sağ, saat yönünde ise – sol.
Daha sonra, doğrusal olmayan iki a → ve b → vektörünü alın. Daha sonra A noktasından A B → = a → ve A C → = b → vektörlerini çizelim. Hem A B → hem de A C →'ye aynı anda dik olan bir AD → = c → vektörü oluşturalım. Böylece, AD → = c → vektörünün kendisini oluştururken, bunu iki şekilde yapabiliriz, ona bir yön veya ters yön verebiliriz (resme bakın).

a → , b → , c → vektörlerinin sıralı üçlüsü, öğrendiğimiz gibi, vektörün yönüne bağlı olarak sağ veya sol olabilir.
Yukarıdakilerden bir vektör çarpımının tanımını tanıtabiliriz. Bu tanım, üç boyutlu uzayın dikdörtgen koordinat sisteminde tanımlanan iki vektör için verilmiştir.
Tanım 1
İki vektörün vektör çarpımı a → ve b → üç boyutlu uzayın dikdörtgen koordinat sisteminde tanımlanan böyle bir vektörü şöyle adlandıracağız:
- a → ve b → vektörleri eşdoğrusal ise sıfır olacaktır;
- hem a vektörüne hem de b vektörüne dik olacaktır, yani. ∠ a → c → = ∠ b → c → = π 2 ;
- uzunluğu şu formülle belirlenir: c → = a → · b → · sin ∠ a → , b → ;
- a → , b → , c → vektörlerinin üçlüsü verilen koordinat sistemiyle aynı yönelime sahiptir.
a → ve b → vektörlerinin vektör çarpımı aşağıdaki gösterime sahiptir: a → × b →.
Vektör çarpımının koordinatları
Herhangi bir vektörün koordinat sisteminde belirli koordinatları olduğundan, vektör çarpımının ikinci bir tanımını sunabiliriz; bu, vektörlerin verilen koordinatlarını kullanarak koordinatlarını bulmamızı sağlayacaktır.
Tanım 2
Üç boyutlu uzayın dikdörtgen koordinat sisteminde iki vektörün vektör çarpımı a → = (a x ; a y ; a z) ve b → = (b x ; b y ; b z) bir vektör olarak adlandırılır c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , burada i → , j → , k → koordinat vektörleridir.
Vektör çarpımı üçüncü dereceden bir kare matrisin determinantı olarak temsil edilebilir; burada ilk satır i → , j → , k → vektör vektörlerini içerir, ikinci satır a → vektörünün koordinatlarını içerir ve üçüncü satır belirli bir dikdörtgen koordinat sisteminde b → vektörünün koordinatlarını içerir, bu matrisin determinantı şu şekilde görünür: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Bu determinantı ilk satırın elemanlarına genişleterek eşitliği elde ederiz: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · ben → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y b z - a z b y) ben → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Çapraz çarpımın özellikleri
Koordinatlardaki vektör çarpımının c → = a → × b → = i → j → k → a x a y a z b x b y b z matrisinin determinantı olarak temsil edildiği bilinmektedir. matris determinantının özellikleri aşağıdakiler görüntülenir bir vektör ürününün özellikleri:
- antideğişme a → × b → = - b → × a → ;
- dağılım a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → veya a → × b (1) → + b (2) → = a → × b (1) → + bir → × b (2) → ;
- ilişkilendirilebilirlik λ a → × b → = λ a → × b → veya a → × (λ b →) = λ a → × b →, burada λ isteğe bağlı bir gerçek sayıdır.
Bu özelliklerin basit kanıtları vardır.
Örnek olarak, bir vektör çarpımının anti-değişme özelliğini kanıtlayabiliriz.
Antideğişmenin kanıtı
Tanım gereği, a → × b → = i → j → k → a x a y a z b x b y b z ve b → × a → = i → j → k → b x b y b z a x a y a z. Ve eğer matrisin iki satırı değiştirilirse, matrisin determinantının değeri ters yönde değişmelidir, bu nedenle, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , bu da vektör çarpımının ters-değişmeli olduğunu kanıtlar.
Vektör çarpımı - örnekler ve çözümler
Çoğu durumda üç tür sorun vardır.
Birinci tür problemlerde genellikle iki vektörün uzunlukları ve aralarındaki açı verilir ve vektör çarpımının uzunluğunu bulmanız gerekir. Bu durumda aşağıdaki formülü kullanın c → = a → · b → · sin ∠ a → , b → .
örnek 1
a → = 3, b → = 5, ∠ a →, b → = π 4'ü biliyorsanız, a → ve b → vektörlerinin vektör çarpımının uzunluğunu bulun.
Çözüm
a → ve b → vektörlerinin vektör çarpımının uzunluğunu belirleyerek bu sorunu çözeriz: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2.
Cevap: 15 2 2 .
İkinci tip problemlerin vektörlerin koordinatları, vektör çarpımı, uzunluğu vb. ile bağlantısı vardır. Verilen vektörlerin bilinen koordinatları üzerinden arama yapılır bir → = (a x; a y; a z) Ve b → = (b x ; b y ; b z) .
Bu tür bir problem için birçok görev seçeneğini çözebilirsiniz. Örneğin, a → ve b → vektörlerinin koordinatları belirtilemez, ancak bunların formun koordinat vektörlerine açılımları belirtilebilir. b → = b x · ben → + b y · j → + b z · k → ve c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → veya a → ve b → vektörleri başlangıç koordinatlarıyla belirtilebilir ve bitiş noktaları.
Aşağıdaki örnekleri göz önünde bulundurun.
Örnek 2
Dikdörtgen koordinat sisteminde iki vektör verilir: a → = (2; 1; - 3), b → = (0; - 1; 1). Çapraz çarpımlarını bulun.
Çözüm
İkinci tanıma göre, verilen koordinatlardaki iki vektörün vektör çarpımını buluruz: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · ben → + ((- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 ben → - 2 j → - 2 k → .
Vektör çarpımını matrisin determinantı üzerinden yazarsak, bu örneğin çözümü şu şekilde görünür: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 ben → - 2 j → - 2 k → .
Cevap: a → × b → = - 2 ben → - 2 j → - 2 k → .
Örnek 3
i → - j → ve i → + j → + k → vektörlerinin vektör çarpımının uzunluğunu bulun; burada i →, j →, k → dikdörtgen Kartezyen koordinat sisteminin birim vektörleridir.
Çözüm
İlk olarak, belirli bir dikdörtgen koordinat sisteminde belirli bir i → - j → × i → + j → + k → vektör çarpımının koordinatlarını bulalım.
i → - j → ve i → + j → + k → vektörlerinin sırasıyla (1; - 1; 0) ve (1; 1; 1) koordinatlarına sahip olduğu bilinmektedir. Matrisin determinantını kullanarak vektör çarpımının uzunluğunu bulalım, o zaman i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Bu nedenle, i → - j → × i → + j → + k → vektör çarpımı verilen koordinat sisteminde (- 1 ; - 1 ; 2) koordinatlara sahiptir.
Vektör çarpımının uzunluğunu şu formülü kullanarak buluruz (bir vektörün uzunluğunu bulma bölümüne bakın): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Cevap: ben → - j → × ben → + j → + k → = 6 . .
Örnek 4
Dikdörtgen Kartezyen koordinat sisteminde A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) üç noktasının koordinatları verilmektedir. A B → ve A C →'ye aynı anda dik olan bir vektör bulun.
Çözüm
A B → ve A C → vektörleri sırasıyla (- 1 ; 2 ; 2) ve (0 ; 4 ; 1) koordinatlarına sahiptir. A B → ve AC → vektörlerinin vektör çarpımını bulduktan sonra, bunun tanımı gereği hem A B → hem de AC →'ye dik bir vektör olduğu, yani sorunumuza bir çözüm olduğu açıktır. Bunu bulalım A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Cevap: - 6 ben → + j → - 4 k → . - dik vektörlerden biri.
Üçüncü tip problemler, vektörlerin vektör çarpımının özelliklerinin kullanılmasına odaklanmıştır. Bunu uyguladıktan sonra verilen soruna bir çözüm elde edeceğiz.
Örnek 5
a → ve b → vektörleri diktir ve uzunlukları sırasıyla 3 ve 4'tür. 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → vektör çarpımının uzunluğunu bulun + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Çözüm
Bir vektör çarpımının dağılma özelliği ile 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 yazabiliriz. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
İlişkilendirilebilirlik özelliğiyle, son ifadedeki vektör çarpımlarının işaretinden sayısal katsayıları alıyoruz: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
a → × a → ve b → × b → vektör çarpımları 0'a eşittir, çünkü a → × a → = a → · a → · sin 0 = 0 ve b → × b → = b → · b → · sin 0 = 0, sonra 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
Vektör çarpımının antideğişme özelliğinden şu sonuç çıkar: - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Vektör çarpımının özelliklerini kullanarak 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → eşitliğini elde ederiz.
Koşul gereği, a → ve b → vektörleri diktir, yani aralarındaki açı π 2'ye eşittir. Şimdi geriye kalan tek şey, bulunan değerleri uygun formüllerde değiştirmektir: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · günah (a → , b →) = 5 · 3 · 4 · günah π 2 = 60 .
Cevap: 3 a → - b → × a → - 2 b → = 60.
Tanım gereği vektörlerin vektör çarpımının uzunluğu şuna eşittir: a → × b → = a → · b → · sin ∠ a → , b → . Zaten bilindiği için (okul kursundan), bir üçgenin alanının, iki kenarının uzunluğunun çarpımının yarısına, bu kenarlar arasındaki açının sinüsüne eşit olduğu bilinmektedir. Sonuç olarak, vektör ürününün uzunluğu paralelkenarın alanına eşittir - çift üçgen, yani bir noktadan sinüs ile ortaya konulan a → ve b → vektörleri biçimindeki kenarların çarpımı aralarındaki açı sin ∠ a →, b →.
Bu bir vektör çarpımının geometrik anlamıdır.

Vektör çarpımının fiziksel anlamı
Fiziğin dallarından biri olan mekanikte vektör çarpımı sayesinde bir kuvvetin uzaydaki bir noktaya göre momenti belirlenebilmektedir.
Tanım 3
A noktasına göre B noktasına F → kuvveti uygulandığında, aşağıdaki A B → × F → vektör çarpımını anlayacağız.
Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.
Vektörler arasındaki açı
İki vektörün vektör çarpımı kavramını tanıtabilmemiz için öncelikle bu vektörler arasındaki açı gibi bir kavramı anlamamız gerekir.
Bize iki $\overline(α)$ ve $\overline(β)$ vektörü verilsin. Uzayda bir $O$ noktası alalım ve buradan $\overline(α)=\overline(OA)$ ve $\overline(β)=\overline(OB)$ vektörlerini çizelim, sonra $AOB$ açısını çizelim bu vektörler arasındaki açı olarak adlandırılacaktır (Şekil 1).
Gösterim: $∠(\overline(α),\overline(β))$
Vektörlerin vektör çarpımı kavramı ve bulma formülü
Tanım 1
İki vektörün vektör çarpımı, verilen her iki vektöre dik bir vektördür ve uzunluğu, bu vektörlerin uzunluklarının bu vektörler arasındaki açının sinüsü ile çarpımına eşit olacaktır ve ayrıca bu vektörün iki başlangıç noktası vardır: Kartezyen koordinat sistemiyle aynı yönelim.
Gösterim: $\overline(α)х\overline(β)$.
Matematiksel olarak şöyle görünür:
- $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin∠(\overline(α),\overline(β))$
- $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
- $(\overline(α)х\overline(β),\overline(α),\overline(β))$ ve $(\overline(i),\overline(j),\overline(k))$ aynı yönelimli (Şekil 2)
Açıkçası, iki durumda vektörlerin dış çarpımı sıfır vektörüne eşit olacaktır:
- Bir veya her iki vektörün uzunluğu sıfır ise.
- Bu vektörler arasındaki açı $180^\circ$ veya $0^\circ$'a eşitse (çünkü bu durumda sinüs sıfırdır).
Vektörlerin çapraz çarpımının nasıl bulunduğunu açıkça görmek için aşağıdaki çözüm örneklerini göz önünde bulundurun.
örnek 1
$\overline(α)=(0,4,0)$ ve $\overline(β) koordinatlarına sahip vektörlerin vektör çarpımının sonucu olacak $\overline(δ)$ vektörünün uzunluğunu bulun. =(3,0,0 )$.
Çözüm.
Bu vektörleri Kartezyen koordinat uzayında gösterelim (Şekil 3):
Şekil 3. Kartezyen koordinat uzayındaki vektörler. Avtor24 - öğrenci çalışmalarının çevrimiçi değişimi
Bu vektörlerin sırasıyla $Ox$ ve $Oy$ eksenlerinde yer aldığını görüyoruz. Bu nedenle aralarındaki açı $90^\circ$ olacaktır. Bu vektörlerin uzunluklarını bulalım:
$|\overline(α)|=\sqrt(0+16+0)=4$
$|\overline(β)|=\sqrt(9+0+0)=3$
Daha sonra Tanım 1'e göre $|\overline(δ)|$ modülünü elde ederiz.
$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$
Cevap: 12$.
Vektör koordinatlarından çapraz çarpımın hesaplanması
Tanım 1, iki vektörün vektör çarpımını bulmaya yönelik bir yöntemi hemen ima eder. Bir vektörün değerinin yanı sıra bir yönü de olduğundan, onu yalnızca skaler bir büyüklük kullanarak bulmak imkansızdır. Ama bunun yanında koordinatları kullanarak bize verilen vektörleri bulmanın da bir yolu var.
Bize sırasıyla $(α_1,α_2,α_3)$ ve $(β_1,β_2,β_3)$ koordinatlarına sahip $\overline(α)$ ve $\overline(β)$ vektörleri verilsin. Daha sonra çapraz çarpımın vektörü (yani koordinatları) aşağıdaki formül kullanılarak bulunabilir:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$
Aksi takdirde determinantı genişleterek aşağıdaki koordinatları elde ederiz
$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Örnek 2
$(0,3,3)$ ve $(-1,2,6)$ koordinatlarına sahip $\overline(α)$ ve $\overline(β)$ eşdoğrusal vektörlerinin vektör çarpımının vektörünü bulun.
Çözüm.
Yukarıda verilen formülü kullanalım. Aldık
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\overline(i)-(0+3)\overline(j)+(0+3)\overline(k)=12\overline(i)-3\overline(j)+3\overline(k) )=(12,-3,3)$
Cevap: $(12,-3,3)$.
Vektörlerin vektör çarpımının özellikleri
Rastgele karışık üç vektör $\overline(α)$, $\overline(β)$ ve $\overline(γ)$ ile $r∈R$ için aşağıdaki özellikler geçerlidir:
Örnek 3
Köşeleri $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ ve $(3,8,0) koordinatlarına sahip olan paralelkenarın alanını bulun $.
Çözüm.
Öncelikle bu paralelkenarı koordinat uzayında gösterelim (Şekil 5):
Şekil 5. Koordinat uzayında paralelkenar. Avtor24 - öğrenci çalışmalarının çevrimiçi değişimi
Bu paralelkenarın iki tarafının $\overline(α)=(3,0,0)$ ve $\overline(β)=(0,8,0)$ koordinatlarına sahip eşdoğrusal vektörler kullanılarak oluşturulduğunu görüyoruz. Dördüncü özelliği kullanarak şunu elde ederiz:
$S=|\overline(α)х\overline(β)|$
$\overline(α)х\overline(β)$ vektörünü bulalım:
$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$
Buradan
$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$
Açıkçası, bir vektör çarpımı durumunda, vektörlerin alınma sırası da önemlidir,
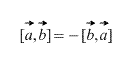
Ayrıca doğrudan tanımdan, herhangi bir k (sayı) skaler faktörü için aşağıdakilerin doğru olduğu sonucu çıkar:
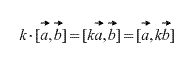
Doğrusal vektörlerin çapraz çarpımı sıfır vektörüne eşittir. Ayrıca, iki vektörün çapraz çarpımı ancak ve ancak aynı doğrultuda olmaları durumunda sıfırdır. (Bunlardan birinin sıfır vektör olması durumunda, sıfır vektörünün tanım gereği herhangi bir vektörle eşdoğrusal olduğunu unutmamak gerekir).

Vektör çarpımı dağılma özelliği, yani

Vektör çarpımının vektörlerin koordinatları aracılığıyla ifade edilmesi.
İki vektör verilsin

(Bir vektörün koordinatları, başlangıç ve bitiş koordinatlarından nasıl bulunur - Vektörlerin nokta çarpımı makalesine bakın, nokta çarpımın alternatif tanımı veya koordinatlarıyla belirtilen iki vektörün nokta çarpımının hesaplanması maddesi.)

Neden bir vektör ürününe ihtiyacınız var?
Çapraz çarpımı kullanmanın birçok yolu vardır, örneğin yukarıda yazıldığı gibi, iki vektörün çapraz çarpımını hesaplayarak bunların eşdoğrusal olup olmadıklarını öğrenebilirsiniz.

Veya bu vektörlerden oluşturulan paralelkenarın alanını hesaplamanın bir yolu olarak kullanılabilir. Tanıma göre, ortaya çıkan vektörün uzunluğu verilen paralelkenarın alanıdır.
Elektrik ve manyetizma alanında da çok sayıda uygulama vardır.Çevrimiçi vektör ürün hesaplayıcısı.
Bu hesap makinesini kullanarak iki vektörün skaler çarpımını bulmak için, ilk vektörün koordinatlarını sırasıyla ilk satıra, ikinci vektörün koordinatlarını ikinci satıra girmeniz gerekir. Vektörlerin koordinatları başlangıç ve bitiş koordinatlarından hesaplanabilir (makaleye bakın) Vektörlerin nokta çarpımı, öğe Nokta çarpımın alternatif bir tanımı veya koordinatlarıyla verilen iki vektörün nokta çarpımının hesaplanması.)
vektör çizimleriüç boyutlu Öklid uzayındaki vektörler üzerinde "vektör çarpımı" ikili işleminin sonucu olan, iki faktörden oluşturulan bir düzleme dik bir sözde vektördür. Vektör çarpımı değişme ve birleşme özelliklerine sahip değildir (anti-değişmelidir) ve vektörlerin skaler çarpımından farklı olarak bir vektördür. Birçok mühendislik ve fizik uygulamasında yaygın olarak kullanılır. Örneğin açısal momentum ve Lorentz kuvveti matematiksel olarak vektörel çarpım olarak yazılır. Çapraz çarpım, vektörlerin dikliğini "ölçmek" için kullanışlıdır - iki vektörün çapraz çarpımının modülü, bunlar dikse modüllerinin çarpımına eşittir ve vektörler paralel veya antiparalelse sıfıra düşer.
Vektör çarpımı farklı şekillerde tanımlanabilir ve teorik olarak herhangi bir n boyutlu uzayda n-1 vektörün çarpımı hesaplanabilir, böylece hepsine dik tek bir vektör elde edilebilir. Ancak çarpım, vektör sonuçları olan önemsiz ikili ürünlerle sınırlıysa, o zaman geleneksel vektör çarpımı yalnızca üç boyutlu ve yedi boyutlu uzaylarda tanımlanır. Bir vektör çarpımının sonucu, tıpkı bir skaler çarpım gibi, Öklid uzayının metriğine bağlıdır.
Üç boyutlu dikdörtgen koordinat sistemindeki koordinatlardan skaler çarpım vektörlerini hesaplama formülünden farklı olarak çapraz çarpım formülü, dikdörtgen koordinat sisteminin yönüne veya başka bir deyişle "kiralliğine" bağlıdır.
Tanım:
R3 uzayındaki a vektörü ile b vektörünün vektör çarpımı, aşağıdaki gereksinimleri karşılayan bir c vektörüdür:
c vektörünün uzunluğu, a ve b vektörlerinin uzunlukları ile aralarındaki φ açısının sinüsünün çarpımına eşittir:
|c|=|a||b|sin φ;
c vektörü a ve b vektörlerinin her birine diktir;
c vektörü, abc vektörlerinin üçlüsü sağ yönlü olacak şekilde yönlendirilir;
R7 uzayı durumunda, a, b, c vektörlerinin üçlüsünün ilişkilendirilebilirliği gereklidir.
Tanım:
c===a × b

Pirinç. 1. Paralelkenarın alanı vektör çarpımının modülüne eşittir
Çapraz çarpımın geometrik özellikleri:
Sıfırdan farklı iki vektörün doğrusallığı için gerekli ve yeterli koşul, bunların vektör çarpımının sıfıra eşit olmasıdır.
Çapraz Ürün Modülü alan eşittir S Ortak bir kökene indirgenmiş vektörler üzerine oluşturulmuş paralelkenar A Ve B(bkz. Şekil 1).
Eğer e- vektörlere dik birim vektör A Ve B ve üç tane olacak şekilde seçildi a,b,e- doğru ve Süzerlerine inşa edilen paralelkenarın alanı (ortak bir kökene indirgenmiş), o zaman vektör çarpımının formülü geçerlidir:
=S e
İncir. 2. Vektör ve vektörlerin skaler çarpımı kullanılarak bir paralelyüzün hacmi; noktalı çizgiler c vektörünün a × b'ye ve a vektörünün b × c'ye izdüşümlerini gösterir; ilk adım skaler çarpımları bulmaktır
Eğer C- bazı vektörler, π
- bu vektörü içeren herhangi bir düzlem, e- düzlemde yer alan birim vektör π
ve dik c,g- düzleme dik birim vektör π
ve vektörlerin üçlüsü olacak şekilde yönlendirildi ekg doğru, o zaman uçakta yatan herkes için π
vektör A formül doğrudur:
=Pr e a |c|g
burada Pr ea e vektörünün a'ya izdüşümüdür.
|c|-c vektörünün modülü
Vektör ve skaler çarpımları kullanırken, ortak bir kökene indirgenmiş vektörler üzerine kurulu bir paralelyüzün hacmini hesaplayabilirsiniz. a, b Ve C. Üç vektörün böyle bir çarpımına karışık denir.
V=|a (b×c)|
Şekil bu hacmin iki şekilde bulunabileceğini göstermektedir: "skaler" ve "vektör" çarpımları değiştirilse bile geometrik sonuç korunur:
V=a×b c=a b×c
Çapraz çarpımın büyüklüğü, orijinal vektörler arasındaki açının sinüsüne bağlıdır, dolayısıyla çapraz çarpım, vektörlerin "diklik" derecesi olarak algılanabilir, tıpkı skaler çarpımın "paralellik derecesi" olarak görülebilmesi gibi. ”. İki birim vektörün vektör çarpımı, orijinal vektörler dik ise 1'e (birim vektör), vektörler paralel veya antiparalel ise 0'a (sıfır vektör) eşittir.
Çapraz çarpımın Kartezyen koordinatlarda ifadesi
İki vektör ise A Ve B dikdörtgen Kartezyen koordinatlarıyla tanımlanır veya daha kesin olarak ortonormal temelde temsil edilir
a=(a x ,a y ,az)
b=(b x ,b y ,bz)
ve koordinat sistemi sağ el ise, bunların vektör çarpımı şu şekildedir:
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
Bu formülü hatırlamak için:
ben =∑ε ijk a j b k
Nerede ε ijk- Levi-Civita'nın sembolü.
