Bu makalede, birçok geometri problemini basit aritmetiğe indirgemenizi sağlayacak bir "sihirli değnek"i tartışmaya başlayacağız. Bu "çubuk", özellikle mekansal figürler, bölümler vb. oluşturma konusunda emin olmadığınız durumlarda hayatınızı çok daha kolaylaştırabilir. Bütün bunlar, belirli bir hayal gücü ve pratik beceriler gerektirir. Burada ele almaya başlayacağımız yöntem, her türlü geometrik yapı ve akıl yürütmeden neredeyse tamamen soyutlanmanıza olanak sağlayacaktır. Yöntem denir "koordinat yöntemi". Bu yazıda aşağıdaki soruları ele alacağız:
- Koordinat uçağı
- Düzlemdeki noktalar ve vektörler
- İki noktadan bir vektör oluşturma
- Vektör uzunluğu (iki nokta arasındaki mesafe)
- Segmentin ortasının koordinatları
- Vektörlerin nokta çarpımı
- İki vektör arasındaki açı
Koordinat yöntemine neden böyle denildiğini zaten tahmin ettiğinizi düşünüyorum. Doğru, geometrik nesnelerle değil, onların sayısal özellikleriyle (koordinatlarıyla) çalıştığı için bu ismi almıştır. Geometriden cebire geçmemizi sağlayan dönüşümün kendisi de bir koordinat sisteminin tanıtılmasından ibarettir. Orijinal şekil düzse koordinatlar iki boyutludur, şekil üç boyutluysa koordinatlar üç boyutludur. Bu yazıda sadece iki boyutlu durumu ele alacağız. Ve makalenin asıl amacı size koordinat yönteminin bazı temel tekniklerini nasıl kullanacağınızı öğretmektir (bazen Birleşik Devlet Sınavının B Bölümünde planimetri ile ilgili problemleri çözerken faydalı oldukları ortaya çıkar). Bu konuyla ilgili sonraki iki bölüm, C2 problemlerini (stereometri problemi) çözme yöntemlerinin tartışılmasına ayrılmıştır.
Koordinat yöntemini tartışmaya nereden başlamak mantıklı olur? Muhtemelen koordinat sistemi kavramından. Onunla ilk karşılaştığınız zamanı hatırlayın. Bana öyle geliyor ki 7. sınıfta örneğin doğrusal bir fonksiyonun varlığını öğrenmiştiniz. Bunu nokta nokta inşa ettiğinizi hatırlatmama izin verin. Hatırlıyor musun? Rastgele bir sayı seçtiniz, bunu formülde yerine koydunuz ve bu şekilde hesapladınız. Örneğin, eğer, o zaman, eğer, o zaman vb. Sonunda ne elde ettiniz? Ve koordinatları olan puanlar aldınız: ve. Daha sonra bir “çapraz” (koordinat sistemi) çizdiniz, üzerinde bir ölçek seçtiniz (birim segment olarak kaç hücreye sahip olacağınız) ve elde ettiğiniz noktaları üzerinde işaretleyerek bunları düz bir çizgiyle birleştirdiniz; çizgi fonksiyonun grafiğidir.
Burada size biraz daha ayrıntılı olarak anlatılması gereken birkaç nokta var:
1. Kolaylık olması açısından tek bir segment seçersiniz, böylece her şey çizime güzel ve kompakt bir şekilde sığar
2. Eksenin soldan sağa, eksenin aşağıdan yukarıya doğru gittiği kabul edilir.
3. Dik açılarda kesişirler ve kesiştikleri noktaya orijin denir. Bir harfle belirtilir.
4. Bir noktanın koordinatlarını yazarken, örneğin, parantez içinde solda noktanın eksen boyunca ve sağda eksen boyunca koordinatları vardır. Özellikle, bu şu anlama gelir:
5. Koordinat ekseninde herhangi bir noktayı belirtmek için koordinatlarını belirtmeniz gerekir (2 sayı)
6. Eksen üzerinde yer alan herhangi bir nokta için,
7. Eksen üzerinde yer alan herhangi bir nokta için,
8. Eksene x ekseni denir
9. Eksen y ekseni olarak adlandırılır
Şimdi bir sonraki adıma geçelim: iki noktayı işaretleyin. Bu iki noktayı bir doğru parçasıyla birleştirelim. Ve sanki noktadan noktaya bir doğru parçası çiziyormuşuz gibi oku koyacağız: yani parçamızın yönlendirilmesini sağlayacağız!

Başka bir yönlü segmentin ne dendiğini hatırlıyor musunuz? Doğru, buna vektör deniyor!
Yani noktayı noktaya bağlarsak, ve başlangıç A noktası olacak ve son B noktası olacak, sonra bir vektör elde ederiz. Bu inşaatı 8. sınıfta da yapmıştın, hatırladın mı?
Noktalar gibi vektörlerin de iki sayı ile gösterilebileceği ortaya çıktı: bu sayılara vektör koordinatları denir. Soru: Bir vektörün koordinatlarını bulmak için başlangıç ve bitiş koordinatlarını bilmemiz sizce yeterli midir? Görünüşe göre evet! Ve bu çok basit bir şekilde yapılır:
Böylece, bir vektörde nokta başlangıç ve nokta son olduğundan, vektör aşağıdaki koordinatlara sahiptir:
Örneğin, eğer öyleyse vektörün koordinatları
Şimdi bunun tersini yapalım, vektörün koordinatlarını bulalım. Bunun için neyi değiştirmemiz gerekiyor? Evet, başlangıcı ve bitişi değiştirmeniz gerekiyor: şimdi vektörün başlangıcı noktada olacak ve sonu da noktada olacak. Daha sonra:
Dikkatlice bakın, vektörler arasındaki fark nedir? Tek farkları koordinatlardaki işaretlerdir. Onlar birbirine zıttır. Bu gerçek genellikle şu şekilde yazılır:
Bazen, hangi noktanın vektörün başlangıcı ve hangisinin sonu olduğu özellikle belirtilmezse, vektörler iki büyük harfle değil, bir küçük harfle gösterilir, örneğin: , vb.
Şimdi biraz pratik kendiniz ve aşağıdaki vektörlerin koordinatlarını bulun:
Muayene:
Şimdi biraz daha zor bir problemi çözün:
Bir noktada başlangıcı olan bir vektörün co-or-di-na-you'su vardır. Abs-cis-su noktalarını bulun.
Yine de oldukça sıradan: Noktanın koordinatları olsun. Daha sonra
Sistemi vektör koordinatlarının ne olduğunun tanımına göre derledim. O halde noktanın koordinatları vardır. Apsisle ilgileniyoruz. Daha sonra
Cevap:
Vektörlerle başka neler yapabilirsiniz? Evet, hemen hemen her şey sıradan sayılarla aynıdır (bölemeyeceğiniz hariç, ancak iki şekilde çarpabilirsiniz; bunlardan birini biraz sonra burada tartışacağız)
- Vektörler birbirine eklenebilir
- Vektörler birbirinden çıkarılabilir
- Vektörler sıfırdan farklı bir sayıyla çarpılabilir (veya bölünebilir)
- Vektörler birbirleriyle çarpılabilir
Tüm bu işlemlerin çok net bir geometrik temsili vardır. Örneğin, toplama ve çıkarma için üçgen (veya paralelkenar) kuralı:



Bir vektör bir sayıyla çarpıldığında veya bölündüğünde uzar, daralır veya yön değiştirir:

Ancak burada koordinatlara ne olacağı sorusuyla ilgileneceğiz.
1. İki vektörü toplarken (çıkarırken), bunların koordinatlarını öğe öğe ekleriz (çıkarırız). Yani:
2. Bir vektörü bir sayıyla çarparken (bölerken), tüm koordinatları bu sayıyla çarpılır (bölülür):
Örneğin:
· Yüzyıldan bugüne eş-or-di-nat miktarını bulun.

Önce vektörlerin her birinin koordinatlarını bulalım. İkisi de aynı kökene sahiptir; başlangıç noktası. Bunların sonu farklıdır. Daha sonra, . Şimdi vektörün koordinatlarını hesaplayalım. O halde ortaya çıkan vektörün koordinatlarının toplamı eşittir.
Cevap:
Şimdi aşağıdaki sorunu kendiniz çözün:
· Vektör koordinatlarının toplamını bulun

Kontrol ediyoruz:
Şimdi şu problemi ele alalım: Koordinat düzleminde iki noktamız var. Aralarındaki mesafe nasıl bulunur? Birinci nokta ve ikincisi olsun. Aralarındaki mesafeyi ile gösterelim. Açıklık sağlamak için aşağıdaki çizimi yapalım:

Ne yaptım? Öncelikle noktaları birleştirdim ve ayrıca noktadan eksene paralel bir çizgi çizdim, noktadan da eksene paralel bir çizgi çizdim. Bir noktada kesişerek dikkat çekici bir şekil mi oluşturdular? Onun nesi bu kadar özel? Evet, sen ve ben dik üçgen hakkında neredeyse her şeyi biliyoruz. Elbette Pisagor teoremi. Gerekli bölüm bu üçgenin hipotenüsüdür ve bölümler bacaklardır. Noktanın koordinatları nelerdir? Evet, resimden bulmak kolaydır: Parçalar eksenlere paralel olduğundan ve sırasıyla uzunluklarını bulmak kolaydır: Parçaların uzunluklarını sırasıyla ile belirtirsek, o zaman
Şimdi Pisagor teoremini kullanalım. Bacakların uzunluklarını biliyoruz, hipotenüsü bulacağız:
Dolayısıyla iki nokta arasındaki mesafe, koordinatlardan olan farkların karelerinin toplamının köküdür. Veya - iki nokta arasındaki mesafe, onları bağlayan parçanın uzunluğudur. Noktalar arasındaki mesafenin yöne bağlı olmadığını görmek kolaydır. Daha sonra:
Buradan üç sonuç çıkarıyoruz:
İki nokta arasındaki mesafeyi hesaplama konusunda biraz pratik yapalım:
Örneğin, eğer ve arasındaki mesafe şuna eşitse:
Veya başka bir yoldan gidelim: vektörün koordinatlarını bulun
Ve vektörün uzunluğunu bulun:
Gördüğünüz gibi aynı şey!
Şimdi biraz kendiniz pratik yapın:
Görev: Belirtilen noktalar arasındaki mesafeyi bulun:
Kontrol ediyoruz:
Kulağa biraz farklı gelse de, aynı formülü kullanan birkaç problem daha var:
1. Göz kapağı uzunluğunun karesini bulun.

2. Göz kapağı uzunluğunun karesini bulun

Sanırım onlarla zorluk çekmeden başa çıktın? Kontrol ediyoruz:
1. Bu da dikkat içindir) Vektörlerin koordinatlarını daha önce bulmuştuk: . O halde vektörün koordinatları vardır. Uzunluğunun karesi şuna eşit olacaktır:
2. Vektörün koordinatlarını bulun
O zaman uzunluğunun karesi
Karmaşık bir şey yok, değil mi? Basit aritmetik, başka bir şey değil.
Aşağıdaki problemler açık bir şekilde sınıflandırılamaz; bunlar daha çok genel bilgi ve basit resimler çizme becerisiyle ilgilidir.
1. Noktayı apsis eksenine bağlayan kesimden itibaren açının sinüsünü bulun.
 Ve
Ve
Burada nasıl ilerleyeceğiz? Eksen ile arasındaki açının sinüsünü bulmamız gerekiyor. Sinüs'ü nerede arayabiliriz? Bu doğru, bir dik üçgende. Peki ne yapmamız gerekiyor? Bu üçgeni inşa edin!

Noktanın koordinatları ve olduğundan, segment eşittir ve segmenttir. Açının sinüsünü bulmamız gerekiyor. Sinüsün karşı kenarın hipotenüse oranı olduğunu hatırlatmama izin verin, o zaman
Bizim için yapacak ne kaldı? Hipotenüsü bulun. Bunu iki şekilde yapabilirsiniz: Pisagor teoremini kullanarak (bacaklar bilinir!) veya iki nokta arasındaki mesafe formülünü kullanarak (aslında ilk yöntemle aynı şeydir!). Ben ikinci yola gideceğim:
Cevap:
Bir sonraki görev size daha da kolay görünecek. Noktanın koordinatlarında.
Görev 2. Per-pen-di-ku-lyar'ın ab-ciss eksenine indirildiği noktadan itibaren. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.
Bir çizim yapalım:

Bir dikmenin tabanı x eksenini (ekseni) kestiği noktadır, benim için bu bir noktadır. Şekil koordinatlara sahip olduğunu göstermektedir: . Apsisle yani “x” bileşeniyle ilgileniyoruz. O eşittir.
Cevap: .
Görev 3.Önceki problemin koşullarında, noktadan koordinat eksenlerine olan mesafelerin toplamını bulun.
Bir noktadan eksenlere olan mesafenin ne olduğunu biliyorsanız, görev genellikle basittir. Bilirsin? Umarım, ama yine de hatırlatacağım:
Peki, hemen yukarıdaki çizimimde zaten böyle bir dik çizgi çizmiş miydim? Hangi eksendedir? Eksene. Peki uzunluğu ne kadardır? O eşittir. Şimdi eksene kendiniz dik bir çizgi çizin ve uzunluğunu bulun. Eşit olacak değil mi? O zaman toplamları eşittir.
Cevap: .
Görev 4. Görev 2 koşullarında, apsis eksenine göre noktaya simetrik bir noktanın koordinatını bulun.
Simetrinin ne olduğu sizin için sezgisel olarak açık sanırım? Birçok nesnede bulunur: birçok bina, masa, uçak, birçok geometrik şekil: top, silindir, kare, eşkenar dörtgen vb. Kabaca konuşursak, simetri şu şekilde anlaşılabilir: bir şekil iki (veya daha fazla) aynı yarıdan oluşur. Bu simetriye eksenel simetri denir. O halde eksen nedir? Bu tam olarak şeklin göreceli olarak eşit yarıya "kesilebileceği" çizgidir (bu resimde simetri ekseni düzdür):

Şimdi görevimize geri dönelim. Eksene göre simetrik olan bir nokta aradığımızı biliyoruz. O halde bu eksen simetri eksenidir. Bu, eksenin parçayı iki eşit parçaya keseceği bir noktayı işaretlememiz gerektiği anlamına gelir. Böyle bir noktayı kendiniz işaretlemeye çalışın. Şimdi benim çözümümle karşılaştırın:

Sizin için de aynı şekilde mi sonuçlandı? İyi! Bulunan noktanın koordinatıyla ilgileniyoruz. Eşittir
Cevap:
Şimdi söyleyin bana, birkaç saniye düşündükten sonra, ordinat eksenine göre A noktasına simetrik olan bir noktanın apsisi ne olur? Cevabınız nedir? Doğru cevap: .
Genel olarak kural şu şekilde yazılabilir:
Apsis eksenine göre bir noktaya simetrik bir noktanın koordinatları vardır:
Ordinat eksenine göre bir noktaya simetrik bir noktanın koordinatları vardır:
Eh, şimdi tamamen korkutucu görev: orijine göre noktaya simetrik olan bir noktanın koordinatlarını bulun. Önce kendin düşün, sonra çizimime bak!

Cevap:
Şimdi paralelkenar problemi:
Görev 5: Noktalar ver-shi-na-mi pa-ral-le-lo-gram-ma olarak görünür. Bu noktada or-di'yi bulun.

Bu sorunu iki şekilde çözebilirsiniz: mantık ve koordinat yöntemi. Önce koordinat yöntemini kullanacağım, sonra size bunu nasıl farklı şekilde çözebileceğinizi anlatacağım.
Noktanın apsisinin eşit olduğu oldukça açıktır. (noktadan apsis eksenine çizilen dik üzerinde yer alır). Ordinatı bulmamız gerekiyor. Şeklimizin paralelkenar olmasından yararlanalım, bu şu anlama geliyor. İki nokta arasındaki mesafe formülünü kullanarak doğru parçasının uzunluğunu bulalım:
Noktayı eksene bağlayan dikmeyi indiriyoruz. Kesişme noktasını harfle belirteceğim.

Segmentin uzunluğu eşittir. (bu noktayı tartıştığımız yerde sorunu kendiniz bulun), sonra Pisagor teoremini kullanarak parçanın uzunluğunu bulacağız:
Bir parçanın uzunluğu tam olarak ordinatıyla çakışır.
Cevap: .
Başka bir çözüm (Sadece bunu gösteren bir resim vereceğim)

Çözüm ilerlemesi:
1. Davranış
2. Noktanın ve uzunluğun koordinatlarını bulun
3. Bunu kanıtlayın.
Bir diğeri bölüm uzunluğu sorunu:
Noktalar üçgenlerin üstünde görünür. Orta çizgisinin paralel uzunluğunu bulun.

Bir üçgenin orta çizgisinin ne olduğunu hatırlıyor musunuz? O zaman bu görev sizin için temeldir. Hatırlamıyorsanız hatırlatayım: Üçgenin orta çizgisi, karşılıklı kenarların orta noktalarını birleştiren çizgidir. Tabana paralel ve yarısına eşittir.
Taban bir segmenttir. Uzunluğunu daha önce aramamız gerekiyordu, eşit. Daha sonra orta çizginin uzunluğu yarısı kadar büyük ve eşittir.
Cevap: .
Yorum Yap: Bu sorun, biraz sonra ele alacağımız başka bir şekilde çözülebilir.
Bu arada, işte size birkaç problem; onlarla pratik yapın, çok basitler ama koordinat yöntemini kullanmada daha iyi olmanıza yardımcı oluyorlar!
1. Noktalar tra-pe-yonların en üstünde görünür. Orta çizgisinin uzunluğunu bulun.

2. Noktalar ve görünümler ver-shi-na-mi pa-ral-le-lo-gram-ma. Bu noktada or-di'yi bulun.

3. Noktayı birleştirerek kesimden itibaren uzunluğu bulun ve

4. Koordinat düzleminde renkli şeklin arkasındaki alanı bulun.

5. Merkezi na-cha-le ko-or-di-nat'ta olan bir daire bu noktadan geçiyor. Onun yarıçapını bulun.

6. Çemberin-di-te ra-di-us'unu bulun, dik açı hakkında-san-noy-no-ka'yı tanımlayın, bir şeyin üst kısımlarının bir ko-veya -di-na-varlığı var, o kadar sorumlusunuz ki

Çözümler:
1. Bir yamuğun orta çizgisinin tabanlarının toplamının yarısına eşit olduğu bilinmektedir. Taban eşittir ve taban. Daha sonra
Cevap:
2. Bu problemi çözmenin en kolay yolu (paralelkenar kuralı) olduğunu not etmektir. Vektörlerin koordinatlarını hesaplamak zor değildir: . Vektörleri eklerken koordinatlar eklenir. Sonra koordinatları var. Vektörün orijini koordinatların olduğu nokta olduğundan nokta da bu koordinatlara sahiptir. Ordinatla ilgileniyoruz. O eşittir.
Cevap:
3. Hemen iki nokta arasındaki mesafe formülüne göre hareket ediyoruz:
Cevap:
4. Resme bakın ve gölgeli alanın hangi iki şeklin arasına sıkıştırıldığını söyleyin? İki kare arasına sıkıştırılmıştır. Daha sonra istenen şeklin alanı, büyük karenin alanından küçük olanın alanına eşittir. Küçük bir karenin kenarı noktaları birleştiren bir doğru parçası olup uzunluğu
O zaman küçük karenin alanı
Aynısını büyük bir kareyle yapıyoruz: kenarı noktaları birleştiren bir segmenttir ve uzunluğu eşittir
O halde büyük karenin alanı
İstenilen şeklin alanını aşağıdaki formülü kullanarak buluyoruz:
Cevap:
5. Bir dairenin merkezi orijine sahipse ve bir noktadan geçiyorsa, yarıçapı tam olarak parçanın uzunluğuna eşit olacaktır (bir çizim yapın ve bunun neden açık olduğunu anlayacaksınız). Bu parçanın uzunluğunu bulalım:
Cevap:
6. Bir dikdörtgenin çevrelediği dairenin yarıçapının, köşegeninin yarısına eşit olduğu bilinmektedir. İki köşegenden herhangi birinin uzunluğunu bulalım (sonuçta dikdörtgende bunlar eşittir!)
Cevap:
Peki her şeyin üstesinden geldin mi? Bunu anlamak çok zor olmadı değil mi? Burada tek bir kural var - görsel bir resim oluşturabilmek ve içindeki tüm verileri basitçe "okuyabilmek".
Çok az şeyimiz kaldı. Aslında tartışmak istediğim iki nokta daha var.
Bu basit sorunu çözmeye çalışalım. İki puan verelim. Doğru parçasının orta noktasının koordinatlarını bulun. Bu sorunun çözümü şu şekildedir: Nokta istenen orta olsun, o zaman koordinatları vardır:
Yani: parçanın ortasının koordinatları = parçanın uçlarının karşılık gelen koordinatlarının aritmetik ortalaması.
Bu kural çok basittir ve genellikle öğrenciler için zorluk yaratmaz. Hangi problemlerde ve nasıl kullanıldığını görelim:
1. Kesimden-di-te veya-di-na-tu se-re-di-ny'yi bulun, noktayı bağlayın ve

2. Puanlar dünyanın zirvesi gibi görünüyor. Dia-go-na-ley'in per-re-se-che-niya'sını bul.

3. Çemberin merkezini bulun, dikdörtgen-no-ka hakkında-san-noy'u tanımlayın, bir şeyin üstleri co-or-di-na-you-sorumlu bir şekilde-ama var.

Çözümler:
1. İlk sorun tam bir klasiktir. Segmentin ortasını belirlemek için hemen ilerliyoruz. Koordinatları var. Ordinat eşittir.
Cevap:
2. Bu dörtgenin bir paralelkenar (hatta bir eşkenar dörtgen) olduğunu görmek kolaydır. Kenar uzunluklarını hesaplayıp birbirleriyle karşılaştırarak bunu kendiniz kanıtlayabilirsiniz. Paralelkenarlar hakkında ne biliyorum? Köşegenleri kesişme noktasına göre ikiye bölünmüştür! Evet! Peki köşegenlerin kesişme noktası nedir? Bu herhangi bir köşegenin ortasıdır! Özellikle köşegeni seçeceğim. O zaman noktanın koordinatları vardır. Noktanın ordinatı eşittir.
Cevap:
3. Dikdörtgenin çevrelediği dairenin merkezi neyle çakışmaktadır? Köşegenlerinin kesişme noktasına denk gelir. Dikdörtgenin köşegenleri hakkında ne biliyorsunuz? Eşittirler ve kesişme noktası onları ikiye böler. Görev bir öncekine indirildi. Örneğin köşegeni ele alalım. O zaman çevrel çemberin merkezi ise orta noktadır. Koordinatları arıyorum: Apsis eşittir.
Cevap:
Şimdi kendi başınıza biraz pratik yapın, kendinizi test edebilmeniz için her sorunun yanıtını vereceğim.
1. Çemberin yarıçapını bulun, üçgen açıyı tanımlayın-no-ka, bir şeyin üst kısımlarında bir co-or-di -no misters var

2. Çemberin merkezini bulun-di-te veya-di-on-noy'u, üstleri koordinatlara sahip olan üçgen-no-ka hakkında tanımlayın
3. Ab-ciss eksenine karşılık gelecek şekilde merkezi bir noktada olan bir dairenin yarıçapı nasıl olmalıdır?

4. Eksenin yeniden ayrıldığı noktayı ve kesme noktasını bulun, noktayı birleştirin ve

Yanıtlar:
Her şey başarılı mıydı? Bunu gerçekten umuyorum! Şimdi - son itiş. Şimdi özellikle dikkatli olun. Şimdi açıklayacağım materyal yalnızca Kısım B'deki koordinat yöntemindeki basit problemlerle doğrudan ilgili değil, aynı zamanda Problem C2'nin her yerinde bulunuyor.
Hangi sözlerimi henüz tutmadım? Vektörler üzerinde hangi işlemleri tanıtmaya söz verdiğimi ve hangilerini sonuçta tanıttığımı hatırlıyor musunuz? Hiçbir şeyi unutmadığıma emin misin? Unutmuş olmak! Vektör çarpımının ne anlama geldiğini açıklamayı unuttum.
Bir vektörü bir vektörle çarpmanın iki yolu vardır. Seçilen yönteme bağlı olarak farklı nitelikteki nesneler elde edeceğiz:
Çapraz çarpım oldukça akıllıca yapılmıştır. Bir sonraki makalede bunun nasıl yapılacağını ve neden gerekli olduğunu tartışacağız. Ve bunda skaler çarpıma odaklanacağız.
Bunu hesaplamamıza izin veren iki yol var:
Tahmin ettiğiniz gibi sonuç aynı olmalı! O halde önce ilk yönteme bakalım:
Koordinatlar aracılığıyla nokta çarpımı
Bul: - skaler çarpım için genel kabul görmüş gösterim
Hesaplama formülü aşağıdaki gibidir:
Yani skaler çarpım = vektör koordinatlarının çarpımlarının toplamı!
Örnek:
Bul-di-te

Çözüm:
Her bir vektörün koordinatlarını bulalım:
Skaler çarpımı aşağıdaki formülü kullanarak hesaplıyoruz:
Cevap:
Bakın kesinlikle karmaşık bir şey yok!
Peki, şimdi kendiniz deneyin:
· Yüzyılların skaler bir pro-iz-ve-de-nie'sini bulun ve

Becerebildin mi? Belki küçük bir yakalama fark ettiniz? Hadi kontrol edelim:
Önceki problemde olduğu gibi vektör koordinatları! Cevap: .
Koordinat olana ek olarak, skaler çarpımı hesaplamanın başka bir yolu da vardır, yani vektörlerin uzunlukları ve aralarındaki açının kosinüsü aracılığıyla:
Ve vektörleri arasındaki açıyı belirtir.
Yani skaler çarpım, vektörlerin uzunlukları ile aralarındaki açının kosinüsünün çarpımına eşittir.
Madem ki çok daha basit olan birinci formüle sahibiz, en azından içinde kosinüs yok, bu ikinci formüle neden ihtiyacımız var? Ve birinci ve ikinci formüllerden vektörler arasındaki açıyı nasıl bulacağımızı çıkarabilmemiz için buna ihtiyaç var!
O zaman vektörün uzunluğunun formülünü hatırlayalım!
Daha sonra bu verileri skaler çarpım formülünde değiştirirsem şunu elde ederim:
Ama başka bir şekilde:
Peki sen ve ben ne elde ettik? Artık iki vektör arasındaki açıyı hesaplamamızı sağlayan bir formülümüz var! Bazen kısa olması açısından şu şekilde de yazılır:
Yani, vektörler arasındaki açıyı hesaplamak için kullanılan algoritma aşağıdaki gibidir:
- Koordinatlar aracılığıyla skaler çarpımı hesaplayın
- Vektörlerin uzunluklarını bulun ve çarpın
- 1. noktanın sonucunu 2. noktanın sonucuna bölün
Örneklerle pratik yapalım:
1. Göz kapakları ile arasındaki açıyı bulun. Cevabı grad-du-sah'ta verin.

2. Önceki problemin koşullarında vektörler arasındaki kosinüsü bulun
Haydi şunu yapalım: İlk sorunu çözmenize yardım edeceğim ve ikincisini kendiniz yapmaya çalışın! Kabul etmek? O zaman başlayalım!
1. Bu vektörler bizim eski dostlarımızdır. Skaler çarpımlarını zaten hesaplamıştık ve eşitti. Koordinatları: , . Sonra uzunluklarını buluyoruz:
Daha sonra vektörler arasındaki kosinüsü ararız:
Açının kosinüsü nedir? Burası köşe.
Cevap:
Şimdi ikinci sorunu kendiniz çözün ve sonra karşılaştırın! Çok kısa bir çözüm sunacağım:
2. Koordinatları vardır, koordinatları vardır.
Vektörler arasındaki açı olsun ve sonra
Cevap:
Sınav kağıdının B Bölümünde doğrudan vektörler ve koordinat yöntemiyle ilgili problemlerin oldukça nadir olduğunu belirtmek gerekir. Ancak C2 problemlerinin büyük çoğunluğu bir koordinat sistemi getirilerek kolayca çözülebilir. Dolayısıyla bu makaleyi, karmaşık sorunları çözmek için ihtiyaç duyacağımız oldukça akıllı yapılar yapacağımız temel olarak düşünebilirsiniz.
KOORDİNATLAR VE VEKTÖRLER. ORTALAMA SEVİYE
Sen ve ben koordinat yöntemini incelemeye devam ediyoruz. Son bölümde aşağıdakileri yapmanıza olanak tanıyan bir dizi önemli formül türettik:
- Vektör koordinatlarını bulun
- Bir vektörün uzunluğunu bulun (alternatif olarak: iki nokta arasındaki mesafe)
- Vektörleri ekleyin ve çıkarın. Bunları gerçek sayıyla çarpın
- Bir segmentin orta noktasını bulun
- Vektörlerin nokta çarpımını hesaplayın
- Vektörler arasındaki açıyı bulun
Elbette koordinat yönteminin tamamı bu 6 noktaya sığmıyor. Üniversitede aşina olacağınız analitik geometri gibi bir bilimin temelini oluşturur. Sorunları tek bir eyalette çözmenize olanak sağlayacak bir temel oluşturmak istiyorum. sınav. Bölüm B'deki görevleri hallettik. Şimdi tamamen yeni bir seviyeye geçme zamanı! Bu makale, koordinat yöntemine geçmenin mantıklı olacağı C2 problemlerini çözmeye yönelik bir yönteme ayrılacaktır. Bu makullük problemde neyin bulunması gerektiği ve hangi rakamın verildiği ile belirlenir. Dolayısıyla sorular şu şekildeyse koordinat yöntemini kullanırdım:
- İki düzlem arasındaki açıyı bulun
- Düz bir çizgi ile bir düzlem arasındaki açıyı bulun
- İki düz çizgi arasındaki açıyı bulun
- Bir noktadan bir düzleme olan mesafeyi bulun
- Bir noktadan bir çizgiye olan mesafeyi bulun
- Düz bir çizgiden bir düzleme olan mesafeyi bulun
- İki çizgi arasındaki mesafeyi bulun
Problem cümlesinde verilen şekil bir dönel cisim ise (top, silindir, koni...)
Koordinat yöntemi için uygun rakamlar şunlardır:
- Dikdörtgen paralel yüzlü
- Piramit (üçgen, dörtgen, altıgen)
Ayrıca deneyimlerime göre için koordinat yöntemini kullanmak uygun değildir.:
- Kesit alanlarını bulma
- Vücut hacimlerinin hesaplanması
Ancak şunu hemen belirtmek gerekir ki koordinat yöntemi için üç "olumsuz" durum pratikte oldukça nadirdir. Çoğu görevde kurtarıcınız olabilir, özellikle de üç boyutlu yapılar konusunda pek iyi değilseniz (ki bu bazen oldukça karmaşık olabilir).
Yukarıda listelediğim tüm rakamlar nelerdir? Artık örneğin bir kare, bir üçgen, bir daire gibi düz değiller, hacimlidirler! Buna göre iki boyutlu değil, üç boyutlu bir koordinat sistemini düşünmemiz gerekiyor. Oluşturulması oldukça kolaydır: apsis ve ordinat eksenine ek olarak başka bir eksen, uygulama ekseni tanıtacağız. Şekil şematik olarak göreceli konumlarını göstermektedir:

Hepsi birbirine diktir ve koordinatların orijini diyeceğimiz bir noktada kesişirler. Daha önce olduğu gibi, apsis eksenini, ordinat eksenini ve tanıtılan uygulama eksenini - göstereceğiz.
Daha önce düzlemdeki her nokta iki sayıyla (apsis ve koordinat) tanımlanıyorsa, uzaydaki her nokta zaten üç sayıyla (apsis, ordinat ve aplike) tanımlanıyordu. Örneğin:

Buna göre bir noktanın apsisi eşittir, ordinatı dır ve uygulaması dır.
Bazen bir noktanın apsisine, bir noktanın apsis eksenine izdüşümü, ordinat - bir noktanın ordinat eksenine izdüşümü ve uygulama - bir noktanın uygulama eksenine izdüşümü de denir. Buna göre bir nokta verilirse koordinatları olan bir nokta:
bir noktanın düzleme izdüşümüne denir
bir noktanın düzleme izdüşümüne denir
Doğal olarak şu soru ortaya çıkıyor: İki boyutlu durum için türetilen tüm formüller uzayda geçerli midir? Cevap evet, adil ve aynı görünüme sahipler. Küçük bir detay için. Sanırım hangisi olduğunu zaten tahmin ettiniz. Tüm formüllerde uygulama ekseninden sorumlu bir terim daha eklememiz gerekecek. Yani.
1. Eğer iki puan verilirse: , o zaman:
- Vektör koordinatları:
- İki nokta arasındaki mesafe (veya vektör uzunluğu)
- Segmentin orta noktasının koordinatları vardır
2. Eğer iki vektör verilirse: ve, o zaman:
- Bunların skaler çarpımı şuna eşittir:
- Vektörler arasındaki açının kosinüsü şuna eşittir:
Ancak uzay o kadar basit değil. Anladığınız gibi, bir koordinat daha eklemek, bu alanda "yaşayan" figürlerin yelpazesine önemli bir çeşitlilik katıyor. Ve daha fazla anlatım için, kabaca konuşursak, düz çizginin bazı "genellemelerini" tanıtmam gerekecek. Bu “genelleme” bir düzlem olacaktır. Uçak hakkında ne biliyorsun? Uçak nedir sorusunu cevaplamaya çalışın. Bunu söylemek çok zor. Ancak hepimiz sezgisel olarak bunun neye benzediğini hayal ederiz:

Kabaca söylemek gerekirse, bu uzaya sıkışmış bir tür sonsuz "çarşaftır". “Sonsuzluk”, düzlemin her yöne uzandığı, yani alanının sonsuza eşit olduğu anlaşılmalıdır. Ancak bu “uygulamalı” açıklama, uçağın yapısı hakkında en ufak bir fikir vermiyor. Ve bizimle ilgilenecek olan odur.
Geometrinin temel aksiyomlarından birini hatırlayalım:
- Düz bir çizgi, düzlem üzerinde iki farklı noktadan geçer ve yalnızca bir tanesi:

Veya uzaydaki analogu:

Elbette, bir çizginin denklemini verilen iki noktadan nasıl çıkaracağınızı hatırlıyorsunuz; bu hiç de zor değil: eğer ilk noktanın koordinatları varsa: ve ikincisi, o zaman çizginin denklemi aşağıdaki gibi olacaktır:
Bunu 7. sınıfta almıştın. Uzayda bir çizginin denklemi şuna benzer: Bize koordinatları olan iki nokta verilse: o zaman bunlardan geçen çizginin denklemi şu şekilde olur:
Örneğin bir çizgi noktalardan geçer:
Bu nasıl anlaşılmalıdır? Bu şu şekilde anlaşılmalıdır: Koordinatları aşağıdaki sistemi sağlıyorsa, bir nokta bir çizgi üzerinde yer alır:
Bir doğrunun denklemiyle pek ilgilenmeyeceğiz ama bir doğrunun yön vektörü gibi çok önemli bir kavrama dikkat etmemiz gerekiyor. - belirli bir çizgi üzerinde veya ona paralel olan sıfırdan farklı herhangi bir vektör.

Örneğin, her iki vektör de bir düz çizginin yön vektörleridir. Bir doğru üzerinde uzanan bir nokta ve onun yön vektörü olsun. O zaman doğrunun denklemi aşağıdaki biçimde yazılabilir:
Bir kez daha söylüyorum, düz çizgi denklemiyle pek ilgilenmeyeceğim ama yön vektörünün ne olduğunu hatırlamanıza gerçekten ihtiyacım var! Tekrar: bu, bir doğru üzerinde veya ona paralel uzanan sıfırdan farklı HERHANGİ bir vektördür.
Geri çekilmek verilen üç noktaya dayalı bir düzlemin denklemi artık o kadar önemsiz değil ve bu konu genellikle lise derslerinde ele alınmıyor. Ama boşuna! Karmaşık sorunları çözmek için koordinat yöntemine başvurduğumuzda bu teknik hayati önem taşır. Ancak yeni bir şeyler öğrenmeye hevesli olduğunuzu varsayıyorum? Üstelik, genellikle analitik geometri derslerinde çalışılan bir tekniğin nasıl kullanılacağını zaten bildiğiniz ortaya çıktığında, üniversitedeki öğretmeninizi etkileyebileceksiniz. Öyleyse başlayalım.
Bir düzlemin denklemi, bir düzlem üzerindeki düz bir çizginin denkleminden çok farklı değildir, yani şu şekildedir:
bazı sayılar (tümü sıfıra eşit değildir), ancak değişkenler, örneğin: vb. Gördüğünüz gibi bir düzlemin denklemi düz bir çizginin denkleminden (doğrusal fonksiyon) çok farklı değildir. Ancak sen ve ben ne tartıştık hatırlıyor musun? Aynı doğru üzerinde yer almayan üç noktamız varsa, o zaman düzlemin denkleminin bunlardan benzersiz bir şekilde yeniden oluşturulabileceğini söyledik. Ama nasıl? Size bunu açıklamaya çalışacağım.
Düzlemin denklemi şu olduğundan:
Ve noktalar bu düzleme aitse, her noktanın koordinatlarını düzlem denkleminde yerine koyarken doğru kimliği elde etmeliyiz:
Bu nedenle bilinmeyen üç denklemin çözülmesi gerekiyor! İkilem! Ancak bunu her zaman varsayabilirsiniz (bunu yapmak için bölmeniz gerekir). Böylece üç bilinmeyenli üç denklem elde ederiz:
Ancak böyle bir sistemi çözmeyeceğiz, ondan çıkan gizemli ifadeyi yazacağız:
Verilen üç noktadan geçen bir düzlemin denklemi
\[\sol| (\begin(array)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(array)) \right| = 0\]
Durmak! Bu nedir? Çok sıradışı bir modül! Ancak karşınızda gördüğünüz nesnenin modülle hiçbir ilgisi yoktur. Bu nesneye üçüncü dereceden determinant denir. Artık düzlemde koordinat yöntemiyle uğraştığınızda aynı determinantlarla çok sık karşılaşacaksınız. Üçüncü dereceden determinant nedir? İşin tuhafı, bu sadece bir sayı. Belirleyiciyle hangi belirli sayıyı karşılaştıracağımızı anlamak için kalır.
Önce üçüncü dereceden determinantı daha genel bir biçimde yazalım:
Bazı numaralar nerede? Ayrıca ilk indeks ile satır numarasını, indeks ile de sütun numarasını kastediyoruz. Örneğin bu sayının ikinci satır ile üçüncü sütunun kesişiminde olduğu anlamına gelir. Şu soruyu soralım: Böyle bir determinantı tam olarak nasıl hesaplayacağız? Yani, onunla hangi spesifik sayıyı karşılaştıracağız? Üçüncü dereceden determinant için buluşsal (görsel) bir üçgen kuralı vardır, şuna benzer:

- Ana köşegenin elemanlarının çarpımı (sol üst köşeden sağ alta kadar) ana köşegene “dik” olan birinci üçgeni oluşturan elemanların çarpımı Ana köşegene “dik” olan ikinci üçgeni oluşturan elemanların çarpımı ana diyagonal
- İkincil köşegenin elemanlarının çarpımı (sağ üst köşeden sol alta kadar) ikincil köşegene “dik” olan birinci üçgeni oluşturan elemanların çarpımı İkinci köşegene “dik” olan ikinci üçgeni oluşturan elemanların çarpımı ikincil diyagonal
- Daha sonra determinant, adımda elde edilen değerler arasındaki farka eşittir ve
Bütün bunları rakamlarla yazarsak aşağıdaki ifadeyi elde ederiz:
Bununla birlikte, bu formdaki hesaplama yöntemini hatırlamanıza gerek yoktur; sadece üçgenleri kafanızda tutmanız ve neyin neye ekleneceği ve daha sonra neyin neyden çıkarılacağı fikrini aklınızda tutmanız yeterlidir).
Üçgen yöntemini bir örnekle açıklayalım:
1. Belirleyiciyi hesaplayın:
Ne eklediğimizi ve ne çıkardığımızı bulalım:
Artı ile gelen terimler:
Bu ana köşegendir: elemanların çarpımı eşittir
İlk üçgen, "ana köşegene dik: elemanların çarpımı eşittir"
İkinci üçgen, "ana köşegene dik: elemanların çarpımı eşittir"
Üç sayıyı toplayın:
Eksi ile gelen terimler
Bu bir yan köşegendir: elemanların çarpımı eşittir
İlk üçgen, “ikincil köşegenlere dik: elemanların çarpımı eşittir
İkinci üçgen, “ikincil köşegenlere dik: elemanların çarpımı eşittir
Üç sayıyı toplayın:
Geriye kalan tek şey “artı” terimlerin toplamını “eksi” terimlerin toplamından çıkarmaktır:
Böylece,
Gördüğünüz gibi üçüncü dereceden determinantların hesaplanmasında karmaşık veya doğaüstü hiçbir şey yoktur. Üçgenleri hatırlamak ve aritmetik hatalar yapmamak önemlidir. Şimdi bunu kendiniz hesaplamaya çalışın:
Kontrol ediyoruz:
- Ana köşegene dik olan ilk üçgen:
- Ana köşegene dik ikinci üçgen:
- Artı ile terimlerin toplamı:
- İkincil köşegene dik olan ilk üçgen:
- Yan köşegenlere dik olan ikinci üçgen:
- Eksili terimlerin toplamı:
- Artı olan terimlerin toplamı eksi eksi olan terimlerin toplamı:
İşte birkaç belirleyici daha: değerlerini kendiniz hesaplayın ve cevaplarla karşılaştırın:
Yanıtlar:
Peki her şey çakıştı mı? Harika, o zaman devam edebilirsiniz! Zorluklar varsa, tavsiyem şu: İnternette determinantı çevrimiçi hesaplamak için birçok program var. İhtiyacınız olan tek şey, kendi determinantınızı bulmak, onu kendiniz hesaplamak ve ardından bunu programın hesapladığıyla karşılaştırmaktır. Ve sonuçlar çakışmaya başlayana kadar böyle devam eder. Bu anın gelmesinin uzun sürmeyeceğinden eminim!
Şimdi verilen üç noktadan geçen bir düzlemin denkleminden bahsederken yazdığım determinant konusuna geri dönelim:
İhtiyacınız olan tek şey, değerini doğrudan hesaplamak (üçgen yöntemini kullanarak) ve sonucu sıfıra ayarlamaktır. Doğal olarak bunlar değişken olduğundan onlara bağlı bazı ifadeler elde edersiniz. Aynı düz çizgi üzerinde yer almayan üç noktadan geçen bir düzlemin denklemi olacak olan bu ifadedir!
Bunu basit bir örnekle açıklayalım:
1. Noktalardan geçen bir düzlemin denklemini oluşturun
Bu üç nokta için bir determinant derliyoruz:
Basitleştirelim:
Şimdi bunu doğrudan üçgen kuralını kullanarak hesaplıyoruz:
\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ sağ| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]
Böylece noktalardan geçen düzlemin denklemi şu şekildedir:
Şimdi bir sorunu kendiniz çözmeye çalışın, sonra tartışacağız:
2. Noktalardan geçen düzlemin denklemini bulun
Şimdi çözümü tartışalım:
Bir determinant oluşturalım:
Ve değerini hesaplayın:
O halde düzlemin denklemi şu şekildedir:
Veya azaltarak şunu elde ederiz:
Şimdi kendi kendini kontrol etmek için iki görev:
- Üç noktadan geçen bir düzlemin denklemini oluşturun:
Yanıtlar:
Her şey çakıştı mı? Yine, bazı zorluklar varsa, o zaman tavsiyem şu: kafanızdan üç nokta alın (yüksek olasılıkla aynı düz çizgide uzanmayacaklardır), bunlara dayalı bir uçak yapın. Daha sonra kendinizi çevrimiçi olarak kontrol edersiniz. Örneğin sitede:
Ancak determinantların yardımıyla sadece düzlemin denklemini oluşturmayacağız. Hatırlayın, size vektörler için sadece nokta çarpımının tanımlanmadığını söylemiştim. Karışık çarpımın yanı sıra vektör çarpımı da vardır. Ve eğer iki vektörün skaler çarpımı bir sayı ise, o zaman iki vektörün vektör çarpımı bir vektör olacak ve bu vektör verilenlere dik olacaktır:

Üstelik modülü ve vektörleri üzerine kurulu bir paralelkenarın alanına eşit olacaktır. Bir noktadan bir çizgiye olan mesafeyi hesaplamak için bu vektöre ihtiyacımız olacak. Vektörlerin vektör çarpımını ve koordinatları verilmişse nasıl hesaplayabiliriz? Üçüncü dereceden determinant yine yardımımıza koşuyor. Ancak vektör çarpımını hesaplamak için kullanılan algoritmaya geçmeden önce küçük bir açıklama yapmam gerekiyor.
Bu arasöz temel vektörlerle ilgilidir.
Şekilde şematik olarak gösterilmiştir:

Neden bunlara temel denildiğini düşünüyorsunuz? Gerçek şu ki :
Veya resimde:

Bu formülün geçerliliği açıktır çünkü:
vektör çizimleri
Artık çapraz çarpımı tanıtmaya başlayabilirim:
İki vektörün vektör çarpımı bir vektördür ve aşağıdaki kurala göre hesaplanır:
Şimdi çapraz çarpımın hesaplanmasına ilişkin bazı örnekler verelim:
Örnek 1: Vektörlerin çapraz çarpımını bulun:
Çözüm: Bir determinant oluşturuyorum:
Ve bunu hesaplıyorum:
Şimdi temel vektörler üzerinden yazdıktan sonra olağan vektör gösterimine döneceğim:
Böylece:
Şimdi dene.
Hazır? Kontrol ediyoruz:
Ve geleneksel olarak iki kontrol için görevler:
- Aşağıdaki vektörlerin vektör çarpımını bulun:
- Aşağıdaki vektörlerin vektör çarpımını bulun:
Yanıtlar:
Üç vektörün karışık çarpımı
İhtiyacım olan son yapı üç vektörün karışık çarpımıdır. Skaler gibi bir sayıdır. Bunu hesaplamanın iki yolu vardır. - bir determinant yoluyla, - bir karma çarpım aracılığıyla.
Yani bize üç vektör verilsin:
Daha sonra ile gösterilen üç vektörün karışık çarpımı şu şekilde hesaplanabilir:
1. - yani karışık çarpım bir vektörün skaler çarpımı ile diğer iki vektörün vektör çarpımıdır
Örneğin, üç vektörün karışık çarpımı şöyledir:
Vektör çarpımını kullanarak bunu kendiniz hesaplamaya çalışın ve sonuçların eşleştiğinden emin olun!
Ve yine bağımsız çözümler için iki örnek:
Yanıtlar:
Koordinat sisteminin seçilmesi
Artık karmaşık stereometrik geometri problemlerini çözmek için gerekli tüm bilgi temeline sahibiz. Ancak bunları çözmek için doğrudan örneklere ve algoritmalara geçmeden önce şu soru üzerinde durmanın faydalı olacağına inanıyorum: Tam olarak nasıl belirli bir şekil için bir koordinat sistemi seçin. Sonuçta, hesaplamaların ne kadar hantal olacağını nihai olarak belirleyecek olan, koordinat sisteminin göreceli konumunun ve uzaydaki şeklin seçimidir.
Bu bölümde aşağıdaki rakamları dikkate aldığımızı hatırlatmama izin verin:
- Dikdörtgen paralel yüzlü
- Düz prizma (üçgen, altıgen...)
- Piramit (üçgen, dörtgen)
- Tetrahedron (üçgen piramit ile aynı)
Dikdörtgen paralel yüzlü veya küp için size aşağıdaki yapıyı öneririm:

Yani figürü “köşeye” yerleştireceğim. Küp ve paralel yüzlü çok iyi figürlerdir. Onlar için köşelerinin koordinatlarını her zaman kolayca bulabilirsiniz. Örneğin, eğer (şekilde gösterildiği gibi)

bu durumda köşelerin koordinatları aşağıdaki gibidir:
Tabii ki, bunu hatırlamanıza gerek yok, ancak bir küp veya dikdörtgen paralel borunun en iyi nasıl yerleştirileceğini hatırlamanız tavsiye edilir.
Düz prizma
Prizma daha zararlı bir figürdür. Uzayda farklı şekillerde konumlandırılabilir. Ancak aşağıdaki seçenek bana en kabul edilebilir görünüyor:
Üçgen prizma:

Yani üçgenin kenarlarından birini tamamen eksenin üzerine yerleştiriyoruz ve köşelerden biri koordinatların orijini ile çakışıyor.
Altıgen prizma:

Yani köşelerden biri orijine denk gelir ve kenarlardan biri eksen üzerinde yer alır.
Dörtgen ve altıgen piramit:

Durum bir küpe benzer: Tabanın iki tarafını koordinat eksenleriyle hizalıyoruz ve köşelerden birini koordinatların kökeniyle hizalıyoruz. Tek hafif zorluk noktanın koordinatlarını hesaplamak olacaktır.
Altıgen bir piramit için - altıgen prizmayla aynı. Ana görev yine tepe noktasının koordinatlarını bulmak olacaktır.

Tetrahedron (üçgen piramit)

Durum üçgen prizma için verdiğim duruma çok benziyor: bir köşe orijine denk geliyor, bir taraf koordinat ekseninde yatıyor.
Artık sen ve ben nihayet sorunları çözmeye başlamaya yaklaştık. Makalenin en başında söylediklerimden şu sonucu çıkarabilirsiniz: C2 problemlerinin çoğu 2 kategoriye ayrılır: açı problemleri ve mesafe problemleri. Öncelikle açı bulma problemlerine bakacağız. Bunlar sırasıyla aşağıdaki kategorilere ayrılır (karmaşıklık arttıkça):
Açı bulma problemleri
- İki düz çizgi arasındaki açıyı bulma
- İki düzlem arasındaki açıyı bulma
Bu problemlere sırasıyla bakalım: İki düz çizgi arasındaki açıyı bularak başlayalım. Peki, unutma, sen ve ben daha önce benzer örnekleri çözmemiş miydik? Hatırlıyor musunuz, buna benzer bir şeyimiz vardı zaten... İki vektör arasındaki açıyı arıyorduk. Hatırlatayım, eğer iki vektör verilirse ve aralarındaki açı bağıntıdan bulunursa:
Şimdi amacımız iki düz çizgi arasındaki açıyı bulmak. “Düz resme” bakalım:

İki düz çizgi kesiştiğinde kaç açı elde ettik? Sadece birkaç şey. Doğru, bunlardan sadece ikisi eşit değil, diğerleri ise onlara dikey (ve dolayısıyla onlarla çakışıyor). Peki iki düz çizgi arasındaki açıyı hangi açı olarak düşünmeliyiz: veya? Burada kural şudur: iki düz çizgi arasındaki açı her zaman dereceden fazla değildir. Yani iki açıdan her zaman derece ölçüsü en küçük olan açıyı seçeceğiz. Yani bu resimde iki düz çizgi arasındaki açı eşittir. Kurnaz matematikçiler, her seferinde iki açıdan en küçüğünü bulma zahmetine girmemek için bir modül kullanmayı önerdiler. Böylece iki düz çizgi arasındaki açı aşağıdaki formülle belirlenir:
Dikkatli bir okuyucu olarak sizin şu soruyu sormanız gerekirdi: Bir açının kosinüsünü hesaplamak için ihtiyaç duyduğumuz bu sayıları tam olarak nereden alıyoruz? Cevap: Bunları doğruların yön vektörlerinden alacağız! Böylece iki düz çizgi arasındaki açıyı bulma algoritması aşağıdaki gibidir:
- Formül 1'i uyguluyoruz.
Veya daha ayrıntılı olarak:
- İlk düz çizginin yön vektörünün koordinatlarını arıyoruz
- İkinci düz çizginin yön vektörünün koordinatlarını arıyoruz
- Skaler çarpımlarının modülünü hesaplıyoruz
- İlk vektörün uzunluğunu arıyoruz
- İkinci vektörün uzunluğunu arıyoruz
- 4. noktanın sonuçlarını 5. noktanın sonuçlarıyla çarpın
- 3. noktanın sonucunu 6. noktanın sonucuna bölüyoruz. Doğrular arasındaki açının kosinüsünü alıyoruz
- Bu sonuç açıyı doğru bir şekilde hesaplamamıza izin veriyorsa, onu ararız.
- Aksi takdirde ark kosinüs yoluyla yazarız
Evet şimdi sıra sorunlara geçiyor: İlk ikisinin çözümünü detaylı olarak göstereceğim, diğerinin çözümünü kısa bir şekilde sunacağım, son iki sorunun ise sadece cevaplarını vereceğim; onlar için tüm hesaplamaları kendiniz yapmalısınız.
Görevler:
1. Sağ tet-ra-ed-re'de, tet-ra-ed-ra'nın yüksekliği ile orta taraf arasındaki açıyı bulun.
2. Sağdaki altı köşeli pi-ra-mi-de'de yüz os-no-va-niya eşittir ve yan kenarlar eşittir, ve çizgileri arasındaki açıyı bulun.
3. Sağdaki dört kömürlü pi-ra-mi-dy'nin tüm kenarlarının uzunlukları birbirine eşittir. Düz çizgiler arasındaki açıyı bulun ve eğer kesimden itibaren - verilen pi-ra-mi-dy ile iseniz, nokta bo-co-ikinci kaburga üzerinde se-re-di-dir
4. Küpün kenarında düz çizgiler arasındaki açıyı bulacak bir nokta vardır.
5. Nokta - küpün kenarlarında Düz çizgiler arasındaki açıyı bulun.
Görevleri bu sıraya göre düzenlemem tesadüf değil. Henüz koordinat yöntemini kullanmaya başlamamış olsanız da, ben en “sorunlu” rakamları kendim analiz edeceğim ve en basit küple uğraşmayı size bırakacağım! Yavaş yavaş tüm rakamlarla nasıl çalışılacağını öğrenmeniz gerekecek; Konudan konuya görevlerin karmaşıklığını artıracağım.
Sorunları çözmeye başlayalım:
1. Bir tetrahedron çizin ve daha önce önerdiğim gibi koordinat sistemine yerleştirin. Tetrahedron düzgün olduğundan, tüm yüzleri (taban dahil) düzgün üçgenlerdir. Kenarın uzunluğu verilmediğine göre bunu eşit alabilirim. Sanırım açının aslında tetrahedronumuzun ne kadar "gerildiğine" bağlı olmayacağını anladınız mı? Ayrıca tetrahedrondaki yüksekliği ve ortancayı da çizeceğim. Yol boyunca tabanını çizeceğim (bizim için de faydalı olacak).

ile arasındaki açıyı bulmam gerekiyor. Biz ne biliyoruz? Sadece noktanın koordinatını biliyoruz. Bu, noktaların koordinatlarını bulmamız gerektiği anlamına gelir. Şimdi şöyle düşünüyoruz: Bir nokta, üçgenin yüksekliklerinin (veya açıortaylarının veya kenarortaylarının) kesişme noktasıdır. Ve bir nokta yükseltilmiş bir noktadır. Nokta segmentin ortasıdır. O zaman nihayet şunu bulmamız gerekiyor: noktaların koordinatları: .
En basit şeyle başlayalım: noktanın koordinatları. Şekle bakın: Bir noktanın uygulamasının sıfıra eşit olduğu açıktır (nokta düzlem üzerindedir). Ordinatı eşittir (ortanca olduğu için). Apsislerini bulmak daha zordur. Ancak bu Pisagor teoremine dayanarak kolaylıkla yapılabilir: Bir üçgen düşünün. Hipotenüsü eşittir ve bacaklarından biri eşittir O halde:
Sonunda elimizde: .
Şimdi noktanın koordinatlarını bulalım. Uygulamasının yine sıfıra eşit olduğu ve koordinatının noktanınkiyle aynı olduğu açıktır. Apsisini bulalım. Bunu hatırlarsanız, bu oldukça önemsiz bir şekilde yapılır. Bir eşkenar üçgenin kesişme noktasına göre yükseklikleri orantılı olarak bölünür, üstten sayıyorum. Çünkü: , o zaman parçanın uzunluğuna eşit olan noktanın gerekli apsisi şuna eşittir: . Buna göre noktanın koordinatları şöyledir:
Noktanın koordinatlarını bulalım. Apsis ve koordinatının noktanın apsis ve koordinatıyla örtüştüğü açıktır. Ve uygulama, segmentin uzunluğuna eşittir. - bu üçgenin bacaklarından biri. Bir üçgenin hipotenüsü bir segmenttir - bir bacak. Kalın harflerle işaretlediğim nedenlerle aranıyor:
Nokta segmentin ortasıdır. O zaman parçanın orta noktasının koordinatlarının formülünü hatırlamamız gerekiyor:
İşte bu kadar, şimdi yön vektörlerinin koordinatlarını arayabiliriz:
Her şey hazır: tüm verileri formüle yerleştiriyoruz:
Böylece,
Cevap:
Bu tür "korkutucu" yanıtlardan korkmamalısınız: C2 sorunları için bu yaygın bir uygulamadır. Bu bölümdeki “güzel” cevaba şaşırmayı tercih ederim. Ayrıca, fark ettiğiniz gibi, Pisagor teoremi ve eşkenar üçgenin yükseklik özelliği dışında pratikte hiçbir şeye başvurmadım. Yani stereometrik problemi çözmek için minimum düzeyde stereometri kullandım. Bundaki kazanç oldukça hantal hesaplamalarla kısmen “söndürülmüştür”. Ama oldukça algoritmikler!
2. Koordinat sistemi ve tabanıyla birlikte düzenli bir altıgen piramidi tasvir edelim:

Çizgiler arasındaki açıyı bulmamız gerekiyor. Böylece görevimiz noktaların koordinatlarını bulmaktır: . Küçük bir çizim kullanarak son üçünün koordinatlarını bulacağız ve noktanın koordinatı üzerinden tepe noktasının koordinatını bulacağız. Yapılacak çok iş var ama başlamamız gerekiyor!
a) Koordinat: Uygulama ve ordinatının sıfıra eşit olduğu açıktır. Apsis'i bulalım. Bunu yapmak için bir dik üçgen düşünün. Ne yazık ki, burada sadece eşit olan hipotenüsü biliyoruz. Bacağını bulmaya çalışacağız (çünkü bacağın iki katı uzunluğunun bize noktanın apsisini vereceği açıktır). Onu nasıl arayabiliriz? Piramidin tabanında nasıl bir figür olduğunu hatırlayalım mı? Bu normal bir altıgen. Bu ne anlama geliyor? Bu, tüm kenarların ve tüm açıların eşit olduğu anlamına gelir. Böyle bir açı bulmamız gerekiyor. Herhangi bir fikir? Pek çok fikir var ama bir formül var:
Düzenli bir n-gon'un açılarının toplamı .
Böylece düzgün altıgenin açılarının toplamı dereceye eşittir. O halde açıların her biri şuna eşittir:
Fotoğrafa tekrar bakalım. Doğru parçasının açınınortay olduğu açıktır. O halde açı dereceye eşittir. Daha sonra:
O zaman nereden.
Böylece koordinatları vardır
b) Artık noktanın koordinatını kolaylıkla bulabiliriz: .
c) Noktanın koordinatlarını bulun. Apsisleri segmentin uzunluğuna denk geldiğinden eşittir. Ordinatı bulmak da çok zor değil: Noktaları birleştirirsek ve çizginin kesişme noktasını örneğin olarak belirlersek. (basit inşaatı kendiniz yapın). O halde B noktasının ordinatı, parçaların uzunluklarının toplamına eşittir. Şimdi üçgene tekrar bakalım. Daha sonra
O zamandan bu yana noktanın koordinatları var
d) Şimdi noktanın koordinatlarını bulalım. Dikdörtgeni düşünün ve şunu kanıtlayın: Böylece noktanın koordinatları:
e) Tepe noktasının koordinatlarını bulmak kalır. Apsis ve koordinatının noktanın apsis ve koordinatıyla örtüştüğü açıktır. Uygulamayı bulalım. O zamandan beri. Bir dik üçgen düşünün. Sorunun durumuna göre bir yan kenar. Bu benim üçgenimin hipotenüsü. O halde piramidin yüksekliği bir bacaktır.
O zaman noktanın koordinatları vardır:
İşte bu kadar, ilgimi çeken tüm noktaların koordinatları elimde. Düz çizgilerin yönlendirici vektörlerinin koordinatlarını arıyorum:
Bu vektörler arasındaki açıyı arıyoruz:
Cevap:
Yine, bu problemi çözerken, düzenli bir n-gon'un açılarının toplamı formülü ve ayrıca bir dik üçgenin kosinüs ve sinüs tanımı dışında herhangi bir karmaşık teknik kullanmadım.
3. Piramidin kenarlarının uzunlukları yine bize verilmediğinden, bunları bire eşit kabul edeceğim. Böylece, sadece yan kenarlar değil, TÜM kenarlar birbirine eşit olduğundan, piramidin tabanında ve bende bir kare vardır ve yan yüzler normal üçgenlerdir. Problem metninde verilen tüm verileri not ederek böyle bir piramidi ve tabanını bir düzlem üzerine çizelim:

ile arasındaki açıyı arıyoruz. Noktaların koordinatlarını araştırırken çok kısa hesaplamalar yapacağım. Bunları “deşifre etmeniz” gerekecek:
b) - segmentin ortası. Koordinatları:
c) Pisagor teoremini kullanarak bir üçgende doğru parçasının uzunluğunu bulacağım. Bunu bir üçgende Pisagor teoremini kullanarak bulabilirim.
Koordinatlar:
d) - segmentin ortası. Koordinatları
e) Vektör koordinatları
f) Vektör koordinatları
g) Açının aranması:
Küp en basit şekildir. Eminim bunu kendi başınıza çözeceksiniz. 4. ve 5. sorunun cevapları aşağıdaki gibidir:
Düz bir çizgi ile bir düzlem arasındaki açıyı bulma
Basit bulmacaların zamanı bitti! Şimdi örnekler daha da karmaşık olacak. Düz bir çizgi ile düzlem arasındaki açıyı bulmak için şu şekilde ilerleyeceğiz:
- Üç noktayı kullanarak düzlemin denklemini oluşturuyoruz
,
üçüncü dereceden bir determinant kullanarak. - İki nokta kullanarak düz çizginin yönlendirici vektörünün koordinatlarını ararız:
- Düz bir çizgi ile bir düzlem arasındaki açıyı hesaplamak için formülü uygularız:
Gördüğünüz gibi bu formül, iki düz çizgi arasındaki açıları bulmak için kullandığımız formüle çok benziyor. Sağ taraftaki yapı tamamen aynıdır ve solda artık daha önce olduğu gibi kosinüsü değil sinüsü arıyoruz. Buna kötü bir eylem daha eklendi: Düzlemin denklemini aramak.
Ertelemeyelim çözüm örnekleri:
1. Ana-ama-va-ni-em doğrudan prizma-biz sizin-fakir-ren-üçgeninin-takma adı ile eşitiz-ve-o prizma-biz eşitiz. Düz çizgi ile düzlem arasındaki açıyı bulun
2. Batıdan dikdörtgen bir par-ral-le-le-pi-pe-de'de Düz çizgi ile düzlem arasındaki açıyı bulun
3. Altı köşeli bir sağ prizmada tüm kenarlar eşittir. Düz çizgi ile düzlem arasındaki açıyı bulun.
4. Bilinen kaburgaların os-no-va-ni-em'i ile sağ üçgen pi-ra-mi-de'de Bir köşe bulun, ob-ra-zo-van -taban olarak düz ve düz, griden geçen kaburga ve
5. Tepe noktası olan dik dörtgensel pi-ra-mi-dy'nin tüm kenarlarının uzunlukları birbirine eşittir. Nokta pi-ra-mi-dy'nin kenarı tarafındaysa, düz çizgi ile düzlem arasındaki açıyı bulun.
Yine ilk iki problemi detaylı, üçüncüyü kısaca çözeceğim ve son ikisini kendi başınıza çözmenize bırakacağım. Ayrıca, üçgen ve dörtgen piramitlerle zaten uğraşmak zorundaydınız, ancak henüz prizmalarla uğraşmadınız.
Çözümler:
1. Bir prizmayı ve tabanını tasvir edelim. Bunu koordinat sistemiyle birleştirelim ve problem ifadesinde verilen tüm verileri not edelim:

Oranlara uymadığım için özür dilerim, ancak sorunu çözmek için bu aslında o kadar da önemli değil. Uçak, prizmamın basitçe "arka duvarı"dır. Böyle bir düzlemin denkleminin şu şekilde olduğunu basitçe tahmin etmek yeterlidir:
Ancak bu doğrudan gösterilebilir:
Bu düzlemde rastgele üç nokta seçelim: örneğin .
Düzlemin denklemini oluşturalım:
Kendiniz için egzersiz yapın: Bu determinantı kendiniz hesaplayın. Başardın mı? O zaman düzlemin denklemi şöyle görünür:
Ya da sadece
Böylece,
Örneği çözmek için düz çizginin yön vektörünün koordinatlarını bulmam gerekiyor. Nokta koordinatların orijini ile çakıştığı için vektörün koordinatları noktanın koordinatlarıyla çakışacaktır. Bunu yapmak için önce noktanın koordinatlarını buluyoruz.
Bunu yapmak için bir üçgen düşünün. Tepe noktasından yüksekliği (medyan ve açıortay olarak da bilinir) çizelim. Çünkü noktanın ordinatı eşittir. Bu noktanın apsisini bulmak için doğru parçasının uzunluğunu hesaplamamız gerekir. Pisagor teoremine göre elimizde:
O zaman noktanın koordinatları vardır:
Nokta "yükseltilmiş" bir noktadır:
O zaman vektör koordinatları şöyledir:
Cevap:
Gördüğünüz gibi, bu tür sorunları çözerken temelde zor olan hiçbir şey yoktur. Aslında prizma gibi bir şeklin “düzlüğü” ile süreç biraz daha basitleştirilmiştir. Şimdi bir sonraki örneğe geçelim:
2. Bir paralel uçlu çizin, içine bir düzlem ve düz bir çizgi çizin ve ayrıca alt tabanını ayrı ayrı çizin:

İlk önce düzlemin denklemini buluyoruz: İçinde bulunan üç noktanın koordinatları:
(ilk iki koordinat net bir şekilde elde edilmiştir ve son koordinatı noktadan itibaren resimden rahatlıkla bulabilirsiniz). Daha sonra düzlemin denklemini oluştururuz:
Hesaplıyoruz:
Kılavuz vektörün koordinatlarını arıyoruz: Koordinatlarının noktanın koordinatlarıyla örtüştüğü açık değil mi? Koordinatlar nasıl bulunur? Bunlar, uygulanan eksen boyunca birer yükseltilmiş noktanın koordinatlarıdır! . Sonra istenen açıyı ararız:
Cevap:
3. Düzenli bir altıgen piramit çizin ve ardından içine bir düzlem ve düz bir çizgi çizin.

Burada bir düzlem çizmek bile sorunlu, bu sorunu çözmekten bahsetmiyorum bile, ancak koordinat yöntemi umursamıyor! Çok yönlülüğü ana avantajıdır!
Uçak üç noktadan geçer: . Koordinatlarını arıyoruz:
1). Son iki noktanın koordinatlarını kendiniz bulun. Bunun için altıgen piramit problemini çözmeniz gerekecek!
2) Düzlemin denklemini oluşturuyoruz:
Vektörün koordinatlarını arıyoruz: . (Üçgen piramit problemine tekrar bakın!)
3) Bir açı arıyorum:
Cevap:
Gördüğünüz gibi bu görevlerde doğaüstü derecede zor olan hiçbir şey yok. Sadece köklere çok dikkat etmeniz gerekiyor. Sadece son iki sorunun cevabını vereceğim:
Gördüğünüz gibi problemleri çözme tekniği her yerde aynıdır: Asıl görev, köşelerin koordinatlarını bulmak ve bunları belirli formüllerde değiştirmektir. Açıları hesaplamak için hâlâ bir sınıf problem daha ele almamız gerekiyor:
İki düzlem arasındaki açıların hesaplanması
Çözüm algoritması şu şekilde olacaktır:
- Üç noktayı kullanarak ilk düzlemin denklemini ararız:
- Diğer üç noktayı kullanarak ikinci düzlemin denklemini ararız:
- Formülü uyguluyoruz:
Gördüğünüz gibi formül, düz çizgiler arasındaki ve düz çizgi ile düzlem arasındaki açıları aradığımız önceki iki formüle çok benziyor. Bu yüzden bunu hatırlamanız zor olmayacak. Görevlerin analizine geçelim:
1. Sağ üçgen prizmanın tabanının kenarı eşittir ve yan yüzün köşegeni eşittir. Düzlem ile prizmanın eksen düzlemi arasındaki açıyı bulun.
2. Tüm kenarları eşit olan sağdaki dört köşeli pi-ra-mi-de'de, kalem-di-ku- noktasından geçen düzlem ile düzlem kemiği arasındaki açının sinüsünü bulun. lyar-ama düz.
3. Normal bir dört köşeli prizmada tabanın kenarları eşittir ve yan kenarlar eşittir. Benden-che-on'un kenarında bir nokta var ki. Düzlemler arasındaki açıyı bulun ve
4. Bir dik dörtgen prizmada tabanın kenarları eşit ve yan kenarlar eşittir. Bu noktadan itibaren kenarda bir nokta var ve böylece düzlemler arasındaki açıyı bulun.
5. Bir küpte düzlemler ile düzlemler arasındaki açının kosinüsünü bulun.
Sorun çözümleri:
1. Düzenli (tabanda bir eşkenar üçgen) üçgen prizma çiziyorum ve problem ifadesinde görünen düzlemleri bunun üzerine işaretliyorum:

İki düzlemin denklemlerini bulmamız gerekiyor: Tabanın denklemi önemsizdir: karşılık gelen determinantı üç noktayı kullanarak oluşturabilirsiniz, ancak denklemi hemen oluşturacağım:
Şimdi denklemi bulalım Noktanın koordinatları vardır Nokta - Üçgenin ortancası ve yüksekliği olduğundan, üçgende Pisagor teoremi kullanılarak kolayca bulunur. O zaman noktanın koordinatları vardır: Noktanın uygulamasını bulalım. Bunu yapmak için bir dik üçgen düşünün.
Daha sonra aşağıdaki koordinatları elde ederiz: Düzlemin denklemini oluştururuz.
Düzlemler arasındaki açıyı hesaplıyoruz:
Cevap:
2. Çizim yapmak:
En zor şey, noktadan dik olarak geçen bunun ne tür gizemli bir düzlem olduğunu anlamaktır. Peki, asıl mesele şu ki, bu nedir? Önemli olan dikkat! Aslında çizgi diktir. Düz çizgi aynı zamanda diktir. O halde bu iki doğrunun içinden geçen düzlem, doğruya dik olacak ve bu arada, noktadan geçecektir. Bu düzlem aynı zamanda piramidin tepesinden de geçer. Sonra istenen uçak - Ve uçak zaten bize verildi. Noktaların koordinatlarını arıyoruz.
Noktanın koordinatını noktadan geçerek buluyoruz. Küçük resimden noktanın koordinatlarının şu şekilde olacağı sonucunu çıkarmak kolaydır: Piramidin tepesinin koordinatlarını bulmak için şimdi ne bulunacak? Ayrıca yüksekliğini de hesaplamanız gerekir. Bu, aynı Pisagor teoremi kullanılarak yapılır: önce bunu kanıtlayın (önemsiz olarak tabanda bir kare oluşturan küçük üçgenlerden). Koşullu olarak elimizde:
Artık her şey hazır: köşe koordinatları:
Düzlemin denklemini oluşturuyoruz:
Belirleyicileri hesaplama konusunda zaten uzmansınız. Zorluk yaşamadan şunları alacaksınız:
Veya aksi takdirde (her iki tarafı da ikinin köküyle çarparsak)
Şimdi düzlemin denklemini bulalım:
(Düzlem denklemini nasıl elde ettiğimizi unutmadınız değil mi? Bu eksi birin nereden geldiğini anlamıyorsanız, o zaman düzlem denkleminin tanımına geri dönün! Her zaman ondan önce ortaya çıktı. uçağım kökene aitti!)
Belirleyiciyi hesaplıyoruz:
(Düzlemin denkleminin noktalardan geçen doğrunun denklemiyle örtüştüğünü fark etmişsinizdir! Nedenini bir düşünün!)
Şimdi açıyı hesaplayalım:
Sinüs bulmamız gerekiyor:
Cevap:
3. Zor soru: Sizce dikdörtgen prizma nedir? Bu sadece iyi bildiğiniz bir paralelyüzlü! Hemen bir çizim yapalım! Tabanı ayrı ayrı tasvir etmenize bile gerek yok; burada çok az faydası var:

Daha önce belirttiğimiz gibi düzlem bir denklem biçiminde yazılmıştır:
Şimdi bir uçak oluşturalım
Hemen düzlemin denklemini yaratıyoruz:
Bir açı arıyorum:
Şimdi son iki sorunun cevapları:
Artık biraz ara vermenin zamanı geldi çünkü sen ve ben harikayız ve harika bir iş çıkardık!
Koordinatlar ve vektörler. İleri düzey
Bu yazıda sizinle koordinat yöntemi kullanılarak çözülebilecek başka bir problem sınıfını tartışacağız: mesafe hesaplama problemleri. Yani aşağıdaki durumları ele alacağız:
- Kesişen çizgiler arasındaki mesafenin hesaplanması.
Bu görevleri artan zorluk derecesine göre sıraladım. Bulmak en kolayı gibi görünüyor noktadan düzleme uzaklık ve en zor şey bulmaktır geçiş çizgileri arasındaki mesafe. Tabii ki hiçbir şey imkansız değildir! Ertelemeyelim ve hemen birinci sınıf sorunları ele almaya başlayalım:
Bir noktadan bir düzleme olan mesafenin hesaplanması
Bu sorunu çözmek için neye ihtiyacımız var?
1. Nokta koordinatları
Dolayısıyla gerekli tüm verileri alır almaz formülü uyguluyoruz:
Son bölümde tartıştığım problemlerden bir düzlemin denklemini nasıl oluşturduğumuzu zaten biliyor olmalısınız. Hemen görevlere geçelim. Şema şu şekildedir: 1, 2 - Karar vermenize yardımcı oluyorum ve biraz ayrıntılı olarak 3, 4 - yalnızca cevap, çözümü kendiniz gerçekleştiriyorsunuz ve karşılaştırıyorsunuz. Hadi başlayalım!
Görevler:
1. Bir küp verildi. Küpün kenar uzunlukları eşittir. Se-re-di-na'dan kesimden düzleme olan mesafeyi bulun
2. Sağdaki dört kömür pi-ra-mi-evet verildiğinde, tarafın tarafı tabana eşittir. Noktadan kenarlarda - se-re-di-olan düzleme olan mesafeyi bulun.
3. Os-no-va-ni-em ile sağ üçgen pi-ra-mi-de'de, yan kenar eşittir ve os-no-vania'daki yüz-ro-eşittir. Üstten düzleme olan mesafeyi bulun.
4. Bir sağ altıgen prizmada tüm kenarlar eşittir. Bir noktadan bir düzleme olan mesafeyi bulun.
Çözümler:
1. Tek kenarlı bir küp çizin, bir doğru parçası ve bir düzlem oluşturun, parçanın ortasını bir harfle belirtin
 .
.
Öncelikle kolay olanla başlayalım: noktanın koordinatlarını bulun. O zamandan beri (segmentin ortasının koordinatlarını hatırlayın!)
Şimdi üç noktayı kullanarak düzlemin denklemini oluşturuyoruz
\[\sol| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]
Artık mesafeyi bulmaya başlayabilirim:
2. Tüm verileri işaretlediğimiz bir çizimle yeniden başlıyoruz!
Bir piramit için tabanını ayrı ayrı çizmek faydalı olacaktır.

Pençesiyle tavuk gibi çizim yapmam bile bu sorunu kolaylıkla çözmemize engel olmayacak!
Artık bir noktanın koordinatlarını bulmak çok kolay
Noktanın koordinatları olduğundan,
2. a noktasının koordinatları doğru parçasının ortası olduğuna göre, o zaman
Düzlemdeki iki noktanın daha koordinatlarını sorunsuz bir şekilde bulabiliriz. Düzlem için bir denklem oluşturup onu basitleştiriyoruz:
\[\sol| (\left| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 )(2))\end(array)) \right|) \right| = 0\]
Noktanın koordinatları: olduğundan mesafeyi hesaplarız:
Cevap (çok nadir!):
Peki anladın mı? Bana öyle geliyor ki burada her şey bir önceki bölümde incelediğimiz örneklerdeki kadar teknik. Bu yüzden eminim ki eğer bu materyale hakimseniz geri kalan iki problemi çözmeniz sizin için zor olmayacaktır. Size sadece cevapları vereceğim:
Düz bir çizgiden bir düzleme olan mesafenin hesaplanması
Aslında burada yeni bir şey yok. Düz bir çizgi ve bir düzlem birbirine göre nasıl konumlandırılabilir? Tek bir olasılıkları var: kesişmek ya da düz bir çizginin düzleme paralel olması. Sizce bir düz çizgi ile bu doğrunun kesiştiği düzlem arasındaki mesafe nedir? Bana öyle geliyor ki burada böyle bir mesafenin sıfıra eşit olduğu açık. İlginç olmayan bir durum.

İkinci durum daha yanıltıcıdır: burada mesafe zaten sıfır değildir. Ancak doğru düzleme paralel olduğundan, doğrunun her noktası bu düzleme eşit uzaklıktadır:

Böylece:
Bu, görevimin bir öncekine indirgendiği anlamına geliyor: Düz bir çizgi üzerindeki herhangi bir noktanın koordinatlarını arıyoruz, düzlemin denklemini arıyoruz ve noktadan düzleme olan mesafeyi hesaplıyoruz. Aslında Birleşik Devlet Sınavında bu tür görevler oldukça nadirdir. Yalnızca bir sorun bulmayı başardım ve içindeki veriler öyleydi ki koordinat yöntemi buna pek uygulanamadı!
Şimdi başka, çok daha önemli bir sorun sınıfına geçelim:
Bir noktanın bir çizgiye olan mesafesini hesaplama
Neye ihtiyacımız var?
1. Mesafeyi aradığımız noktanın koordinatları:
2. Bir doğru üzerindeki herhangi bir noktanın koordinatları
3. Düz çizginin yönlendirici vektörünün koordinatları
Hangi formülü kullanıyoruz?
Bu kesrin paydasının ne anlama geldiği sizin için açık olmalıdır: bu, düz çizginin yönlendirici vektörünün uzunluğudur. Bu çok zor bir paydır! İfadesi, vektörlerin vektör çarpımının modülünü (uzunluğunu) ifade eder ve vektör çarpımının nasıl hesaplanacağını çalışmanın önceki bölümünde inceledik. Bilgilerinizi tazeleyin, artık buna çok ihtiyacımız olacak!
Böylece, problem çözme algoritması aşağıdaki gibi olacaktır:
1. Mesafeyi aradığımız noktanın koordinatlarını arıyoruz:
2. Mesafeyi aradığımız doğru üzerindeki herhangi bir noktanın koordinatlarını arıyoruz:
3. Bir vektör oluşturun
4. Düz bir çizginin yönlendirici vektörünü oluşturun
5. Vektör çarpımını hesaplayın
6. Ortaya çıkan vektörün uzunluğunu ararız:
7. Mesafeyi hesaplayın:
Yapacak çok işimiz var ve örnekler oldukça karmaşık olacak! O halde şimdi tüm dikkatinizi odaklayın!
1. Tepesi olan dik üçgen bir pi-ra-mi-da verilmiştir. Pi-ra-mi-dy temelinde yüz-ro-eşittir, sen eşitsin. Gri kenardan, ve noktalarının gri kenarlar olduğu düz çizgiye ve veterinere olan mesafeyi bulun.
2. Kaburgaların uzunlukları ve düz açılı par-ral-le-le-pi-pe-da buna göre eşittir ve üstten düz çizgiye olan mesafeyi bulun
3. Bir sağ altıgen prizmada tüm kenarlar eşittir; bir noktadan düz bir çizgiye olan mesafeyi bulun
Çözümler:
1. Tüm verileri işaretlediğimiz düzgün bir çizim yapıyoruz:

Yapacak çok işimiz var! Öncelikle neyi arayacağımızı ve hangi sırayla araştıracağımızı kelimelerle anlatmak isterim:
1. Noktaların koordinatları ve
2. Nokta koordinatları
3. Noktaların koordinatları ve
4. Vektörlerin koordinatları ve
5. Çapraz çarpımları
6. Vektör uzunluğu
7. Vektör çarpımının uzunluğu
8. Uzaklık
Neyse, önümüzde çok işimiz var! Hadi kolları sıvamış olarak işe başlayalım!
1. Piramidin yüksekliğinin koordinatlarını bulmak için noktanın koordinatlarını bilmemiz gerekir. Uygulaması sıfırdır ve ordinatı apsisine eşit olduğundan parçanın yüksekliğine eşittir. bir eşkenar üçgen, buradan itibaren tepe noktasından sayılarak orana bölünür. Sonunda koordinatları aldık:
Nokta koordinatları
2. - segmentin ortası
3. - segmentin ortası
Segmentin orta noktası
4. Koordinatlar
Vektör koordinatları
5. Vektör çarpımını hesaplayın:

6. Vektör uzunluğu: Değiştirmenin en kolay yolu, parçanın üçgenin orta çizgisi olması, yani tabanın yarısına eşit olmasıdır. Bu yüzden.
7. Vektör çarpımının uzunluğunu hesaplayın:
8. Son olarak mesafeyi buluyoruz:
İşte bu! Size dürüstçe söyleyeyim: Bu sorunu geleneksel yöntemlerle (inşaat yoluyla) çözmek çok daha hızlı olacaktır. Ama burada her şeyi hazır bir algoritmaya indirgedim! Çözüm algoritmasının sizin için açık olduğunu düşünüyorum? Bu nedenle geri kalan iki sorunu kendiniz çözmenizi isteyeceğim. Cevapları karşılaştıralım mı?
Tekrar ediyorum: Bu sorunları koordinat yöntemine başvurmak yerine inşaatlarla çözmek daha kolaydır (daha hızlıdır). Bu çözüm yöntemini yalnızca size "hiçbir şey inşa etmeyi bitirmemenize" olanak tanıyan evrensel bir yöntem göstermek için gösterdim.
Son olarak, son sınıftaki sorunları ele alalım:
Kesişen çizgiler arasındaki mesafenin hesaplanması
Burada problem çözme algoritması öncekine benzer olacaktır. Neyimiz var:
3. Birinci ve ikinci çizginin noktalarını birleştiren herhangi bir vektör:
Çizgiler arasındaki mesafeyi nasıl buluruz?
Formül aşağıdaki gibidir:
Pay, karışık çarpımın modülüdür (bunu önceki bölümde tanıtmıştık) ve payda, önceki formülde olduğu gibi (düz çizgilerin yön vektörlerinin vektör çarpımının modülü, aralarındaki mesafe) arıyoruz).
sana şunu hatırlatacağım

Daha sonra mesafe formülü şu şekilde yeniden yazılabilir::
Bu bir determinantın bir determinantla bölünmesidir! Gerçi dürüst olmak gerekirse burada şaka yapacak vaktim yok! Bu formül aslında oldukça hantaldır ve oldukça karmaşık hesaplamalara yol açmaktadır. Senin yerinde olsaydım, buna yalnızca son çare olarak başvururdum!
Yukarıdaki yöntemi kullanarak birkaç sorunu çözmeye çalışalım:
1. Tüm kenarları eşit olan bir dik üçgen prizmada, düz çizgiler arasındaki mesafeyi bulun.
2. Bir dik üçgen prizma verildiğinde, tabanın tüm kenarları gövde kaburgasından geçen kesite eşittir ve se-re-di-well kaburgalar bir karedir. Düz çizgiler arasındaki mesafeyi bulun ve
Birincisine ben karar veririm ve buna göre ikincisine sen karar verirsin!
1. Bir prizma çiziyorum ve düz çizgiler çiziyorum ve

C noktasının koordinatları: o halde
Nokta koordinatları
Vektör koordinatları
Nokta koordinatları
Vektör koordinatları
Vektör koordinatları
\[\left((B,\overrightarrow (A(A_1)) \overrightarrow (B(C_1)) ) \right) = \left| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(array))\\(\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(array))\end(array)) \right| = \frac((\sqrt 3 ))(2)\]
Vektörler arasındaki vektör çarpımını hesaplıyoruz ve
\[\overrightarrow (A(A_1)) \cdot \overrightarrow (B(C_1)) = \left| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(array)\end(array) \right| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]
Şimdi uzunluğunu hesaplıyoruz:
Cevap:
Şimdi ikinci görevi dikkatlice tamamlamaya çalışın. Bunun cevabı şu olacaktır: .
Koordinatlar ve vektörler. Kısa açıklama ve temel formüller
Bir vektör yönlendirilmiş bir bölümdür. - vektörün başlangıcı, - vektörün sonu.
Bir vektör veya ile gösterilir.
Mutlak değer vektör - vektörü temsil eden parçanın uzunluğu. Olarak belirtildi.
Vektör koordinatları:
,
\displaystyle a vektörünün uçları nerede?
Vektörlerin toplamı: .
Vektörlerin çarpımı:
Vektörlerin nokta çarpımı:
Vektörlerin skaler çarpımı, mutlak değerlerinin çarpımına ve aralarındaki açının kosinüsüne eşittir:
KALAN 2/3 MAKALELER SADECE SİZ AKILLI ÖĞRENCİLERE SUNULMUŞTUR!
YouClever öğrencisi olun,
“Ayda bir fincan kahve” fiyatına Birleşik Devlet Sınavına veya Matematikte Birleşik Devlet Sınavına hazırlanın,
Ayrıca "YouClever" ders kitabına, "100gia" hazırlık programına (çalışma kitabı), sınırsız deneme Birleşik Devlet Sınavı ve Birleşik Devlet Sınavı, çözüm analizi ile 6000 problem ve diğer YouClever ve 100gia hizmetlerine sınırsız erişim elde edin.
Bir vektör, sayısal değeri ve yönü ile karakterize edilen bir niceliktir. Başka bir deyişle, bir vektör yönlendirilmiş bir bölümdür. Konum vektör AB uzayda başlangıç noktasının koordinatları ile verilir vektör A ve bitiş noktaları vektör B. Orta noktanın koordinatlarının nasıl belirleneceğine bakalım vektör.
Talimatlar
Öncelikle başlangıç ve bitiş tanımlarını tanımlayalım. vektör. Vektör AB olarak yazılırsa A noktası başlangıç noktasıdır. vektör ve B noktası sondur. Ve tam tersi, çünkü vektör BA noktası B başlangıçtır vektör ve A noktası sondur. Bize orijin koordinatlarına sahip bir AB vektörü verilsin vektör A = (a1, a2, a3) ve son vektör B = (b1, b2, b3). Daha sonra koordinatlar vektör AB şu şekilde olacaktır: AB = (b1 – a1, b2 – a2, b3 – a3), yani. uç koordinattan vektör karşılık gelen orijin koordinatını çıkarmak gerekir vektör. Uzunluk vektör AB (veya modülü), koordinatlarının karelerinin toplamının karekökü olarak hesaplanır: |AB| = ?((b1 – a1)^2 + (b2 – a2)^2 + (b3 – a3)^2).
Ortadaki noktanın koordinatlarını bulun vektör. O = (o1, o2, o3) harfiyle gösterelim. Ortanın koordinatları bulunur vektör aşağıdaki formüllere göre normal bir parçanın ortasının koordinatlarıyla aynıdır: o1 = (a1 + b1)/2, o2 = (a2 + b2)/2, o3 = (a3 + b3)/2. Koordinatları bulalım vektör AO: AO = (o1 – a1, o2 – a2, o3 – a3) = ((b1 – a1)/2, (b2 – a2)/2, (b3 – a3)/2).
Bir örneğe bakalım. AB vektörü orijinin koordinatlarıyla verilsin vektör A = (1, 3, 5) ve sonu vektör B = (3, 5, 7). Daha sonra koordinatlar vektör AB, AB = (3 – 1, 5 – 3, 7 – 5) = (2, 2, 2) şeklinde yazılabilir. Modülü bulalım vektör AB: |AB| = ?(4 + 4 + 4) = 2 * ?3. Belirtilen uzunluk değeri vektör ortadaki koordinatların doğruluğunu daha da doğrulamamıza yardımcı olacak vektör. Daha sonra O noktasının koordinatlarını buluyoruz: O = ((1 + 3)/2, (3 + 5)/2, (5 + 7)/2) = (2, 4, 6). Daha sonra koordinatlar vektör AO, AO = (2 – 1, 4 – 3, 6 – 5) = (1, 1, 1) şeklinde hesaplanır.
Hadi kontrol edelim. Uzunluk vektör AO = ?(1 + 1 + 1) = ?3. Orijinalin uzunluğunu hatırlayın vektör 2 * ?3'e eşittir, yani. yarım vektör gerçekten orijinalin uzunluğunun yarısına eşit vektör. Şimdi koordinatları hesaplayalım vektör OB: OB = (3 – 2, 5 – 4, 7 – 6) = (1, 1, 1). AO ve OB vektörlerinin toplamını bulalım: AO + OB = (1 + 1, 1 + 1, 1 + 1) = (2, 2, 2) = AB. Bu nedenle ortanın koordinatları vektör doğru bulunmuştur.
Yararlı tavsiye
Vektörün ortasının koordinatlarını hesapladıktan sonra, en azından en basit kontrolü yaptığınızdan emin olun - vektörün uzunluğunu hesaplayın ve bunu verilen vektörün uzunluğuyla karşılaştırın.
Aşağıdaki makale, bir doğru parçasının uç noktalarının koordinatları başlangıç verisi olarak mevcutsa, o doğru parçasının ortasının koordinatlarını bulma konusunu ele alacaktır. Ancak konuyu incelemeye başlamadan önce birkaç tanım sunalım.
Tanım 1
Çizgi segmenti– bir parçanın uçları adı verilen, iki rastgele noktayı birleştiren düz bir çizgi. Örnek olarak bunlar A ve B noktaları ve buna göre A B doğru parçası olsun.
A B doğru parçası A ve B noktalarından her iki yönde de devam ederse A B düz bir çizgisi elde ederiz. O zaman A B parçası, A ve B noktalarıyla sınırlanan, sonuçta ortaya çıkan düz çizginin bir parçasıdır. A B doğru parçası, uçları olan A ve B noktalarını ve aradaki noktaları birleştirir. Örneğin, A ve B noktaları arasında bulunan herhangi bir K noktasını alırsak, K noktasının A B doğru parçası üzerinde bulunduğunu söyleyebiliriz.
Tanım 2
Bölüm uzunluğu– belirli bir ölçekte bir parçanın uçları arasındaki mesafe (birim uzunlukta bir parça). A B doğru parçasının uzunluğunu şu şekilde gösterelim: A B .
Tanım 3
Segmentin orta noktası– Bir doğru parçası üzerinde bulunan ve uçlarından eşit uzaklıkta olan bir nokta. A B doğru parçasının ortası C noktası ile gösterilirse eşitlik doğru olacaktır: A C = C B
Başlangıç verileri: Ox koordinat çizgisi ve üzerinde çakışmayan noktalar: A ve B. Bu noktalar gerçek sayılara karşılık gelir x A ve xB. C noktası A B segmentinin ortasıdır: koordinatı belirlemek gerekir x C.
C noktası A B doğru parçasının orta noktası olduğundan eşitlik doğru olacaktır: | AC | = | CB | . Noktalar arasındaki mesafe, koordinatlarındaki farkın modülü ile belirlenir, yani.
| AC | = | CB | ⇔ x C - x A = x B - x C
O zaman iki eşitlik mümkündür: x C - x A = x B - x C ve x C - x A = - (x B - x C)
İlk eşitlikten C noktasının koordinatları için formülü türetiyoruz: x C = x A + x B 2 (bölümün uçlarının koordinatlarının toplamının yarısı).
İkinci eşitlikten şunu elde ederiz: x A = x B, bu imkansızdır çünkü kaynak verilerde çakışmayan noktalar. Böylece, A B segmentinin ortasının koordinatlarını A (x A) uçları ile belirlemek için formül ve B(xB):
Ortaya çıkan formül, bir düzlemdeki veya uzaydaki bir segmentin ortasının koordinatlarını belirlemek için temel olacaktır.
Başlangıç verileri: O xy düzlemindeki dikdörtgen koordinat sistemi, verilen A x A, y A ve B x B, y B koordinatlarına sahip, çakışmayan iki keyfi nokta. C noktası A B doğru parçasının ortasıdır. C noktası için x C ve y C koordinatlarını belirlemek gerekir.
A ve B noktalarının çakışmadığı ve aynı koordinat çizgisi üzerinde veya eksenlerden birine dik bir çizgi üzerinde bulunmadığı durumu analiz için ele alalım. A x , Ay ; B x, B y ve C x, C y - A, B ve C noktalarının koordinat eksenleri üzerindeki projeksiyonları (düz çizgiler O x ve O y).

Yapıya göre A Ax, B Bx, C Cx doğruları paraleldir; çizgiler de birbirine paraleldir. Bununla birlikte Thales teoremine göre A C = C B eşitliğinden şu eşitlikler çıkar: A x C x = C x B x ve A y C y = C y B y ve bunlar da C x noktasının şu olduğunu gösterir: A x B x bölümünün ortası ve C y, A y B y bölümünün ortasıdır. Daha önce elde edilen formüle dayanarak şunu elde ederiz:
x C = x A + x B 2 ve y C = y A + y B 2
A ve B noktalarının aynı koordinat çizgisi üzerinde veya eksenlerden birine dik bir çizgi üzerinde olması durumunda aynı formüller kullanılabilir. Bu vakanın ayrıntılı bir analizini yapmayacağız; bunu yalnızca grafiksel olarak ele alacağız:


Yukarıdakilerin hepsini özetlersek, uçların koordinatları ile düzlemde A B segmentinin ortasının koordinatları bir (x Bir , y Bir) Ve B(xB, yB) olarak tanımlanır:
(x A + x B 2 , y A + y B 2)
Başlangıç verileri: O x y z koordinat sistemi ve verilen A (x A, y A, z A) ve B (x B, y B, z B) koordinatlarına sahip iki rastgele nokta. A B doğru parçasının ortası olan C noktasının koordinatlarını belirlemek gerekir.
A x , A y , A z ; B x , B y , B z ve C x , C y , C z - koordinat sisteminin eksenleri üzerindeki tüm belirli noktaların projeksiyonları.
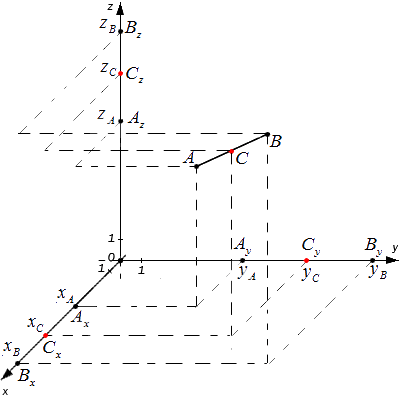
Thales teoremine göre aşağıdaki eşitlikler doğrudur: A x C x = C x B x , A y C y = C y B y , A z Cz = C z B z
Bu nedenle, C x , C y , C z noktaları sırasıyla A x B x , A y B y , A z B z doğru parçalarının orta noktalarıdır. Daha sonra, Uzaydaki bir parçanın ortasının koordinatlarını belirlemek için aşağıdaki formüller doğrudur:
x C = x A + x B 2, y c = y A + y B 2, z c = z A + Z B 2
Ortaya çıkan formüller, A ve B noktalarının koordinat çizgilerinden birinde yer aldığı durumlarda da uygulanabilir; eksenlerden birine dik olan düz bir çizgi üzerinde; bir koordinat düzleminde veya koordinat düzlemlerinden birine dik bir düzlemde.
Bir parçanın ortasının koordinatlarının, uçlarının yarıçap vektörlerinin koordinatları aracılığıyla belirlenmesi
Bir parçanın ortasının koordinatlarını bulma formülü, vektörlerin cebirsel yorumuna göre de türetilebilir.
Giriş verileri: dikdörtgen Kartezyen koordinat sistemi O x y, verilen A (x A, y A) ve B (x B, x B) koordinatlarına sahip noktalar. C noktası A B doğru parçasının ortasıdır.
Vektörler üzerindeki eylemlerin geometrik tanımına göre aşağıdaki eşitlik doğru olacaktır: O C → = 1 2 · O A → + O B → . Bu durumda C noktası, O A → ve O B → vektörleri temel alınarak oluşturulan bir paralelkenarın köşegenlerinin kesişme noktasıdır, yani. köşegenlerin orta noktası. Noktanın yarıçap vektörünün koordinatları noktanın koordinatlarına eşitse eşitlikler doğrudur: O A → = (x A, y A), O B → = (x B) , y B). Koordinatlardaki vektörler üzerinde bazı işlemler yapalım ve şunu elde edelim:
Ö C → = 1 2 · Ö A → + Ö B → = x A + x B 2 , y A + y B 2
Bu nedenle C noktasının koordinatları vardır:
x A + x B 2 , y A + y B 2
Benzer şekilde, uzaydaki bir parçanın ortasının koordinatlarını bulmak için bir formül belirlenir:
C (x A + x B 2, y A + y B 2, z A + z B 2)
Bir parçanın orta noktasının koordinatlarını bulmayla ilgili problem çözme örnekleri
Yukarıda elde edilen formüllerin kullanımını içeren problemler arasında, doğrudan sorunun doğru parçasının ortasının koordinatlarını hesaplamak olduğu ve bu soruya verilen koşulları getirmeyi içeren problemler vardır: "medyan" terimi. sıklıkla kullanılır, amaç bir parçanın uçlarından birinin koordinatlarını bulmaktır ve simetri sorunları da yaygındır, bu konuyu inceledikten sonra çözümü de genel olarak zorluk yaratmamalıdır. Tipik örneklere bakalım.
örnek 1
İlk veri: düzlemde - verilen A (- 7, 3) ve B (2, 4) koordinatlarına sahip noktalar. A B doğru parçasının orta noktasının koordinatlarını bulmak gerekir.
Çözüm
A B doğru parçasının ortasını C noktasıyla gösterelim. Koordinatları, segmentin uçlarının koordinatlarının toplamının yarısı kadar belirlenecektir, yani. A ve B noktaları.
x C = x A + x B 2 = - 7 + 2 2 = - 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Cevap: A B - 5 2, 7 2 segmentinin ortasının koordinatları.
Örnek 2
İlk veri: A B C üçgeninin koordinatları bilinmektedir: A (- 1, 0), B (3, 2), C (9, - 8). Ortanca A M'nin uzunluğunu bulmak gerekir.
Çözüm
- Problemin koşullarına göre AM ortancadır, yani M, B C doğru parçasının orta noktasıdır. Öncelikle B C doğru parçasının ortasının koordinatlarını bulalım. M puanı:
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + (- 8) 2 = - 3
- Artık medyanın her iki ucunun (A ve M noktaları) koordinatlarını bildiğimize göre, noktalar arasındaki mesafeyi belirlemek ve medyan A M'nin uzunluğunu hesaplamak için formülü kullanabiliriz:
AM = (6 - (- 1)) 2 + (- 3 - 0) 2 = 58
Cevap: 58
Örnek 3
İlk veri:üç boyutlu uzayın dikdörtgen koordinat sisteminde paralel yüzlü bir A B C D A 1 B 1 C 1 D 1 verilmiştir. C 1 noktasının koordinatları verilmiş (1, 1, 0) ve B D 1 köşegeninin orta noktası olan ve M (4, 2, - 4) koordinatlarına sahip olan M noktası da tanımlanmıştır. A noktasının koordinatlarını hesaplamak gerekir.
Çözüm
Paralel borunun köşegenleri, tüm köşegenlerin orta noktası olan bir noktada kesişir. Bu ifadeye dayanarak problemin koşullarından bilinen M noktasının A C 1 doğru parçasının orta noktası olduğunu aklımızda tutabiliriz. Uzaydaki bir parçanın ortasının koordinatlarını bulma formülüne dayanarak A noktasının koordinatlarını buluyoruz: x M = x A + x C 1 2 ⇒ x A = 2 x M - x C 1 = 2 4 - 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 y M - y C 1 = 2 2 - 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 z M - z C 1 = 2 · (- 4) - 0 = - 8
Cevap: A noktasının koordinatları (7, 3, - 8).
Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.
Sonunda bu kapsamlı ve uzun zamandır beklenen konuya kavuştum. analitik geometri. Öncelikle yüksek matematiğin bu bölümü hakkında biraz bilgi verelim... Artık sayısız teorem, bunların kanıtları, çizimleri vb. içeren bir okul geometri dersini hatırlıyorsunuzdur. Öğrencilerin önemli bir kısmı için sevilmeyen ve çoğunlukla anlaşılması güç bir konu olan ne saklanmalı? Garip bir şekilde analitik geometri daha ilginç ve erişilebilir görünebilir. “Analitik” sıfatı ne anlama geliyor? Hemen aklıma iki klişe matematik tabiri geliyor: “grafiksel çözüm yöntemi” ve “analitik çözüm yöntemi.” Grafik yöntemi elbette grafiklerin ve çizimlerin yapımıyla ilişkilidir. Analitik veya yöntem sorunları çözmeyi içerir daha çok cebirsel işlemler yoluyla. Bu bağlamda, analitik geometrinin hemen hemen tüm problemlerini çözmeye yönelik algoritma basit ve şeffaftır; çoğu zaman gerekli formülleri dikkatlice uygulamak yeterlidir - ve cevap hazır! Hayır elbette çizim olmadan bunu yapamayacağız, ayrıca malzemenin daha iyi anlaşılması için gereksiz yere alıntı yapmaya çalışacağım.
Yeni açılan geometri dersleri teorik olarak tamamlanmış gibi görünmüyor; pratik problemlerin çözümüne odaklanıyor. Derslerime yalnızca benim bakış açıma göre pratik açıdan önemli olan şeyleri dahil edeceğim. Herhangi bir alt bölüm hakkında daha kapsamlı yardıma ihtiyacınız varsa, aşağıdaki oldukça erişilebilir literatürü öneririm:
1) Şaka değil, birkaç neslin aşina olduğu bir şey: Geometri üzerine okul ders kitabı, yazarlar - L.S. Atanasyan ve Şirketi. Bu okul soyunma odası askısı zaten 20 (!) yeniden basımdan geçti ve bu elbette sınır değil.
2) 2 ciltte geometri. Yazarlar L.S. Atanasyan, Bazylev V.T.. Bu lise için edebiyat, ihtiyacın olacak ilk cilt. Nadiren karşılaşılan görevler görüş alanımdan çıkabilir ve öğreticinin çok değerli yardımı olacaktır.
Her iki kitap da çevrimiçi olarak ücretsiz olarak indirilebilir. Ayrıca sayfada bulabileceğiniz hazır çözümlerle arşivimi kullanabilirsiniz. Yüksek matematikteki örnekleri indirin.
Araçlar arasında yine kendi gelişimimi öneriyorum - yazılım paketi Analitik geometride hayatı büyük ölçüde kolaylaştıracak ve çok zaman kazandıracak.
Okuyucunun temel geometrik kavram ve şekillere aşina olduğu varsayılmaktadır: nokta, doğru, düzlem, üçgen, paralelkenar, paralelyüz, küp vb. Bazı teoremleri, en azından Pisagor teoremini hatırlamanız tavsiye edilir, tekrarlayıcılara merhaba)
Şimdi sırasıyla ele alacağız: vektör kavramı, vektörlerle eylemler, vektör koordinatları. Devamını okumanızı tavsiye ederim en önemli makale Vektörlerin nokta çarpımı, ve ayrıca Vektör ve vektörlerin karışık çarpımı. Yerel bir görev - bu bağlamda bir segmentin bölünmesi - de gereksiz olmayacaktır. Yukarıdaki bilgilere dayanarak ustalaşabilirsiniz. düzlemdeki bir doğrunun denklemiİle en basit çözüm örnekleri, izin verecek geometri problemlerini çözmeyi öğrenin. Aşağıdaki makaleler de faydalıdır: Uzayda bir düzlemin denklemi, Uzayda bir çizginin denklemleri, Düz bir çizgi ve düzlemde temel problemler, analitik geometrinin diğer bölümleri. Doğal olarak yol boyunca standart görevler dikkate alınacaktır.
Vektör kavramı. Ücretsiz vektör
Öncelikle bir vektörün okuldaki tanımını tekrarlayalım. Vektör isminde yönlendirilmiş başlangıcı ve bitişinin belirtildiği bir bölüm:
Bu durumda parçanın başı nokta, parçanın sonu ise noktadır. Vektörün kendisi ile gösterilir. Yönçok önemli, eğer oku parçanın diğer ucuna hareket ettirirseniz bir vektör elde edersiniz ve bu zaten tamamen farklı vektör. Vektör kavramını fiziksel bir bedenin hareketiyle özdeşleştirmek uygundur: Kabul etmelisiniz ki bir enstitünün kapısından girmek veya bir enstitünün kapısından çıkmak tamamen farklı şeylerdir.
Bir düzlemin veya uzayın bireysel noktalarını sözde olarak düşünmek uygundur. sıfır vektör. Böyle bir vektör için son ve başlangıç çakışır.
!!! Not: Burada ve ayrıca vektörlerin aynı düzlemde bulunduğunu veya uzayda yer aldıklarını varsayabilirsiniz - sunulan malzemenin özü hem düzlem hem de uzay için geçerlidir.
Tanımlar: Birçoğu, adında ok bulunmayan çubuğu hemen fark etti ve üstte de bir ok olduğunu söyledi! Doğru, bunu bir okla yazabilirsiniz: , ancak bu da mümkündür gelecekte kullanacağım giriş. Neden? Görünüşe göre bu alışkanlık pratik nedenlerden dolayı gelişti; okuldaki ve üniversitedeki atıcılarımın çok farklı boyutlarda ve tüylü olduğu ortaya çıktı. Eğitim literatüründe bazen çivi yazısıyla hiç uğraşmazlar, ancak harfleri kalın harflerle vurgularlar: , böylece bunun bir vektör olduğunu ima ederler.
Bu stilistikti ve şimdi vektör yazmanın yolları hakkında:
1) Vektörler iki büyük Latin harfiyle yazılabilir:
ve benzeri. Bu durumda ilk harf mutlaka vektörün başlangıç noktasını, ikinci harf ise vektörün bitiş noktasını belirtir.
2) Vektörler ayrıca küçük Latin harfleriyle de yazılır:
Özellikle, vektörümüz kısa olması açısından küçük bir Latin harfiyle yeniden tasarlanabilir.
Uzunluk veya modül sıfır olmayan bir vektöre parçanın uzunluğu denir. Sıfır vektörünün uzunluğu sıfırdır. Mantıklı.
Vektörün uzunluğu modül işaretiyle gösterilir: ,
Biraz sonra bir vektörün uzunluğunu nasıl bulacağımızı öğreneceğiz (ya da kime bağlı olarak tekrarlayacağız).
Bu, tüm okul çocuklarının aşina olduğu, vektörler hakkında temel bilgilerdi. Analitik geometride, sözde Ücretsiz vektör.
Basitçe söylemek gerekirse - vektör herhangi bir noktadan çizilebilir:
Bu tür vektörleri eşit olarak adlandırmaya alışkınız (eşit vektörlerin tanımı aşağıda verilecektir), ancak tamamen matematiksel açıdan bakıldığında bunlar AYNI VEKTÖR veya Ücretsiz vektör. Neden ücretsiz? Çünkü problemleri çözerken, şu veya bu "okul" vektörünü ihtiyacınız olan uçağın veya uzayın HERHANGİ bir noktasına "bağlayabilirsiniz". Bu çok harika bir özellik! Rasgele uzunlukta ve yönde yönlendirilmiş bir parça hayal edin; sonsuz sayıda "klonlanabilir" ve uzayın herhangi bir noktasında, aslında HER YERDE mevcuttur. Şöyle bir öğrenci söylüyor: Her hoca vektöre önem verir. Sonuçta, bu sadece esprili bir kafiye değil, her şey neredeyse doğru - oraya yönlendirilmiş bir bölüm de eklenebilir. Ama sevinmek için acele etmeyin, çoğu zaman acı çekenler öğrencilerin kendisidir =)
Bu yüzden, Ücretsiz vektör- Bu bir demet aynı yönlendirilmiş bölümler. Paragrafın başında verilen bir vektörün okul tanımı: "Yönlendirilmiş bir parçaya vektör denir..." özel belirli bir kümeden alınan ve düzlem veya uzaydaki belirli bir noktaya bağlanan yönlendirilmiş bir bölüm.
Fizik açısından bakıldığında serbest vektör kavramının genel olarak yanlış olduğu ve uygulama noktasının önemli olduğu unutulmamalıdır. Aslında, benim aptal örneğimi geliştirmeye yetecek kadar aynı kuvvetin buruna veya alnına doğrudan darbesi farklı sonuçlara yol açar. Fakat, özgür olmayan vektörler ayrıca vyshmat sürecinde de bulunur (oraya gitmeyin :)).
Vektörlerle yapılan eylemler. Vektörlerin doğrusallığı
Bir okul geometri kursu, vektörlerle birlikte bir dizi eylemi ve kuralı kapsar: Üçgen kuralına göre toplama, paralelkenar kuralına göre toplama, vektör farkı kuralı, bir vektörün bir sayı ile çarpılması, vektörlerin skaler çarpımı vb. Başlangıç noktası olarak analitik geometri problemlerinin çözümüyle özellikle ilgili olan iki kuralı tekrarlayalım.
Üçgen kuralını kullanarak vektörleri ekleme kuralı
Sıfır olmayan iki rastgele vektörü düşünün ve: 
Bu vektörlerin toplamını bulmanız gerekiyor. Tüm vektörlerin serbest kabul edilmesi nedeniyle, vektörü bir kenara koyacağız. son vektör: 
Vektörlerin toplamı vektördür. Kuralın daha iyi anlaşılması için, buna fiziksel bir anlam verilmesi tavsiye edilir: Bir cismin önce vektör boyunca, sonra da vektör boyunca ilerlemesine izin verin. O halde vektörlerin toplamı, başlangıcı kalkış noktasında ve sonu varış noktasında olmak üzere ortaya çıkan yolun vektörüdür. Herhangi bir sayıda vektörün toplamı için benzer bir kural formüle edilmiştir. Dedikleri gibi, vücut, toplamın ortaya çıkan vektörü boyunca bir zikzak boyunca veya belki de otopilotta çok eğilerek yoluna gidebilir.
Bu arada, eğer vektör ertelenirse başladı vektör, o zaman eşdeğerini elde ederiz paralelkenar kuralı vektörlerin eklenmesi.
İlk olarak vektörlerin eşdoğrusallığı hakkında. İki vektör denir doğrusal, eğer aynı doğru üzerinde veya paralel doğrular üzerinde yer alıyorlarsa. Kabaca söylemek gerekirse paralel vektörlerden bahsediyoruz. Ancak bunlarla ilgili olarak her zaman “doğrusal” sıfatı kullanılır.
İki eşdoğrusal vektör düşünün. Bu vektörlerin okları aynı yöne yönlendirilirse, bu tür vektörlere denir. ortak yönetmen. Oklar farklı yönleri gösteriyorsa vektörler zıt yönler.
Tanımlar: Vektörlerin doğrusallığı olağan paralellik sembolüyle yazılır: , detaylandırma mümkündür: (vektörler birlikte yönlendirilir) veya (vektörler zıt yönlendirilir).
İş bir sayı üzerindeki sıfır olmayan bir vektör, uzunluğu eşit olan bir vektördür ve ve vektörleri, ile birlikte ve zıt olarak yönlendirilir.
Bir vektörü bir sayıyla çarpma kuralını bir resim yardımıyla anlamak daha kolaydır: 
Daha ayrıntılı olarak bakalım:
1 yön. Çarpan negatifse, vektör yön değiştirir tam tersine.
2) Uzunluk. Çarpan veya içinde yer alıyorsa, vektörün uzunluğu azalır. Yani vektörün uzunluğu, vektörün uzunluğunun yarısı kadardır. Çarpan modülü birden büyükse vektörün uzunluğu artışlar zamanında.
3) Lütfen şunu unutmayın tüm vektörler eşdoğrusaldır, bir vektör diğeri aracılığıyla ifade edilirken, örneğin . Bunun tersi de doğrudur: Eğer bir vektör bir diğeri aracılığıyla ifade edilebiliyorsa, bu tür vektörler zorunlu olarak eşdoğrusaldır. Böylece: bir vektörü bir sayıyla çarparsak eşdoğrusal hale geliriz(orijinaline göre) vektör.
4) Vektörler birlikte yönlendirilir. Vektörler ve ayrıca birlikte yönlendirilirler. Birinci grubun herhangi bir vektörü, ikinci grubun herhangi bir vektörüne göre zıt yönlüdür.
Hangi vektörler eşittir?
İki vektör aynı yöndeyse ve aynı uzunluğa sahipse eşittir. Eş yönlülüğün, vektörlerin eşdoğrusallığını ima ettiğini unutmayın. Eğer şöyle dersek tanım hatalı (gereksiz) olacaktır: "İki vektör eğer aynı doğru üzerindeyse, eş yönlüyse ve aynı uzunluğa sahipse eşittir."
Serbest vektör kavramı açısından bakıldığında, önceki paragrafta tartışıldığı gibi eşit vektörler aynı vektördür.
Düzlemde ve uzayda vektör koordinatları
İlk nokta düzlemdeki vektörleri dikkate almaktır. Kartezyen dikdörtgen koordinat sistemini gösterelim ve koordinatların başlangıç noktasından başlayarak grafiğini çizelim. Bekar vektörler ve:

Vektörler ve dikey. Ortogonal = Dik. Terimlere yavaş yavaş alışmanızı öneririm: paralellik ve diklik yerine sırasıyla kelimeleri kullanıyoruz eşdoğrusallık Ve diklik.
Tanım: Vektörlerin ortogonalliği olağan diklik sembolüyle yazılır, örneğin: .
Göz önünde bulundurulan vektörlere denir koordinat vektörleri veya ort. Bu vektörler temel yüzeyde. Çoğu kişi için temelin ne olduğu sezgisel olarak açıktır; daha ayrıntılı bilgi makalede bulunabilir; Vektörlerin doğrusal (bağımsız) bağımlılığı. Vektörlerin temeli Basit bir deyişle, koordinatların temeli ve kökeni tüm sistemi tanımlar - bu, üzerinde tam ve zengin bir geometrik yaşamın kaynadığı bir tür temeldir.
Bazen inşa edilmiş temel denir ortonormal düzlemin temeli: "orto" - koordinat vektörleri dik olduğundan, "normalleştirilmiş" sıfatı birim anlamına gelir, yani. temel vektörlerin uzunlukları bire eşittir.
Tanım: temel genellikle parantez içinde yazılır; kesin sırayla temel vektörler listelenir, örneğin: . Koordinat vektörleri yasaktır yeniden düzenleyin.
Herhangi düzlem vektör tek yol olarak ifade edilen: ![]() , Nerede - sayılar bunlara denir vektör koordinatları bu temelde. Ve ifadenin kendisi
, Nerede - sayılar bunlara denir vektör koordinatları bu temelde. Ve ifadenin kendisi ![]() isminde vektör ayrışmasıtemelde .
isminde vektör ayrışmasıtemelde .
Servis edilen akşam yemeği:

Alfabenin ilk harfiyle başlayalım: . Çizim, bir vektörü tabana ayrıştırırken az önce tartışılanların kullanıldığını açıkça göstermektedir:
1) bir vektörü bir sayıyla çarpma kuralı: ve;
2) Üçgen kuralına göre vektörlerin toplanması: .
Şimdi düzlemdeki herhangi bir noktadan vektörü zihinsel olarak çizin. Çürümesinin “amansızca onu takip edeceği” çok açık. İşte, vektörün özgürlüğü - vektör "her şeyi kendisiyle birlikte taşır." Bu özellik elbette her vektör için geçerlidir. Temel (serbest) vektörlerin başlangıç noktasından itibaren çizilmesine gerek olmaması komiktir; örneğin biri sol altta, diğeri sağ üstte çizilebilir ve hiçbir şey değişmez! Doğru, bunu yapmanıza gerek yok, çünkü öğretmen de özgünlük gösterecek ve beklenmedik bir yerde size bir "kredi" çekecektir.
Vektörler, bir vektörü bir sayıyla çarpma kuralını tam olarak gösterir; vektör, temel vektörle eş yönlüdür, vektör, temel vektörün tersi yöndedir. Bu vektörler için koordinatlardan biri sıfıra eşitse bunu şu şekilde titizlikle yazabilirsiniz:
Ve bu arada temel vektörler şöyle: (aslında kendileri aracılığıyla ifade ediliyorlar).
Ve sonunda: , . Bu arada, vektör çıkarma nedir ve neden çıkarma kuralından bahsetmedim? Lineer cebirde bir yerde, nerede olduğunu hatırlamıyorum, çıkarmanın toplamanın özel bir durumu olduğunu belirtmiştim. Böylece “de” ve “e” vektörlerinin açılımları kolaylıkla toplam olarak yazılabilir: , ![]() . Bu durumlarda üçgen kuralına göre vektörlerin eski güzel toplamının ne kadar net çalıştığını görmek için çizimi takip edin.
. Bu durumlarda üçgen kuralına göre vektörlerin eski güzel toplamının ne kadar net çalıştığını görmek için çizimi takip edin.
Formun dikkate alınan ayrıştırması ![]() bazen vektör ayrıştırması denir ort sisteminde(yani birim vektörlerden oluşan bir sistemde). Ancak bir vektör yazmanın tek yolu bu değildir; aşağıdaki seçenek yaygındır:
bazen vektör ayrıştırması denir ort sisteminde(yani birim vektörlerden oluşan bir sistemde). Ancak bir vektör yazmanın tek yolu bu değildir; aşağıdaki seçenek yaygındır:
Veya eşittir işaretiyle:
Temel vektörlerin kendisi şu şekilde yazılır: ve
Yani vektörün koordinatları parantez içinde gösterilmiştir. Pratik problemlerde her üç gösterim seçeneği de kullanılır.
Konuşup konuşmamak konusunda kararsızdım ama yine de söyleyeyim: vektör koordinatları yeniden düzenlenemez. Kesinlikle ilk sırada birim vektöre karşılık gelen koordinatı yazıyoruz, kesinlikle ikinci sırada birim vektöre karşılık gelen koordinatı yazıyoruz. Aslında ve iki farklı vektördür.
Uçağın koordinatlarını bulduk. Şimdi üç boyutlu uzaydaki vektörlere bakalım, burada hemen hemen her şey aynı! Sadece bir koordinat daha ekleyecek. Üç boyutlu çizimler yapmak zordur, bu yüzden kendimi bir vektörle sınırlayacağım ve basitlik açısından onu orijinden ayıracağım: 
Herhangi 3 boyutlu uzay vektörü tek yol ortonormal bir temele göre genişletin: ![]() , bu temelde vektörün (sayı) koordinatları nerededir.
, bu temelde vektörün (sayı) koordinatları nerededir.
Resimden örnek: ![]() . Burada vektör kurallarının nasıl çalıştığını görelim. Öncelikle vektörü şu sayıyla çarpın: (kırmızı ok), (yeşil ok) ve (ahududu oku). İkinci olarak, burada birkaç, bu durumda üç vektörün eklenmesine ilişkin bir örnek verilmiştir: . Toplam vektör başlangıç noktasından (vektörün başlangıcı) başlar ve son varış noktasında (vektörün sonu) biter.
. Burada vektör kurallarının nasıl çalıştığını görelim. Öncelikle vektörü şu sayıyla çarpın: (kırmızı ok), (yeşil ok) ve (ahududu oku). İkinci olarak, burada birkaç, bu durumda üç vektörün eklenmesine ilişkin bir örnek verilmiştir: . Toplam vektör başlangıç noktasından (vektörün başlangıcı) başlar ve son varış noktasında (vektörün sonu) biter.
Üç boyutlu uzayın tüm vektörleri de doğal olarak özgürdür; vektörü zihinsel olarak başka herhangi bir noktadan ayırmaya çalışın ve onun ayrışmasının "onunla kalacağını" anlayacaksınız.
Düz kasaya benzer, yazıya ek olarak ![]() parantezli versiyonlar yaygın olarak kullanılmaktadır: ya .
parantezli versiyonlar yaygın olarak kullanılmaktadır: ya .
Genişletmede bir (veya iki) koordinat vektörü eksikse, onların yerine sıfırlar konur. Örnekler:
vektör (titizlikle ![]() ) - Hadi yaz ;
) - Hadi yaz ;
vektör (titizlikle ![]() ) - Hadi yaz ;
) - Hadi yaz ;
vektör (titizlikle ![]() ) - Hadi yaz .
) - Hadi yaz .
Temel vektörler şu şekilde yazılır:
Belki de analitik geometri problemlerini çözmek için gereken minimum teorik bilginin tamamı budur. Çok fazla terim ve tanım olabilir o yüzden çaydanlık yapanların bu bilgileri tekrar okuyup anlamalarını öneririm. Ve herhangi bir okuyucunun, materyali daha iyi özümsemesi için zaman zaman temel derse başvurması yararlı olacaktır. Eşdoğrusallık, ortogonallik, ortonormal temel, vektör ayrıştırması - bunlar ve diğer kavramlar gelecekte sıklıkla kullanılacaktır. Tüm teoremleri dikkatlice (ve kanıt olmadan) şifrelediğim için sitedeki materyallerin geometri üzerine teorik testi veya kolokyumu geçmek için yeterli olmadığını - bilimsel sunum tarzının zararına, ancak anlayışınıza bir artı - not ediyorum. konu. Detaylı teorik bilgi almak için lütfen Profesör Atanasyan'ın önünde eğilin.
Ve pratik kısma geçiyoruz:
Analitik geometrinin en basit problemleri.
Koordinatlardaki vektörlerle yapılan işlemler
Tamamen otomatik olarak değerlendirilecek görevlerin ve formüllerin nasıl çözüleceğini öğrenmeniz önemle tavsiye edilir. ezberlemek, bunu bilerek hatırlamanıza bile gerek yok, kendileri hatırlayacaklardır =) Bu çok önemlidir, çünkü analitik geometrinin diğer problemleri en basit temel örneklere dayanmaktadır ve piyon yemeye fazladan zaman harcamak can sıkıcı olacaktır. . Gömleğinizin üst düğmelerini iliklemenize gerek yok; okuldan aşina olduğunuz birçok şey var.
Materyalin sunumu hem uçak hem de uzay açısından paralel bir seyir izleyecek. Çünkü tüm formülleri... kendiniz göreceksiniz.
İki noktadan bir vektör nasıl bulunur?
Düzlemin iki noktası verilirse, vektör aşağıdaki koordinatlara sahiptir: ![]()
Uzayda iki nokta verilirse, vektör aşağıdaki koordinatlara sahiptir:
Yani, vektörün sonunun koordinatlarından karşılık gelen koordinatları çıkarmanız gerekir vektörün başlangıcı.
Egzersiz yapmak: Aynı noktalar için vektörün koordinatlarını bulma formüllerini yazın. Dersin sonunda formüller.
örnek 1
Düzlemin iki noktası verildiğinde ve . Vektör koordinatlarını bulun
Çözüm: ilgili formüle göre:
Alternatif olarak aşağıdaki giriş kullanılabilir:
Buna estetik karar verecek:
Şahsen ben kaydın ilk versiyonuna alışkınım.
Cevap:
Koşula göre, bir çizim oluşturmak gerekli değildi (ki bu analitik geometri problemleri için tipiktir), ancak kuklalar için bazı noktaları açıklığa kavuşturmak için tembel olmayacağım: 
Kesinlikle anlamalısın nokta koordinatları ve vektör koordinatları arasındaki fark:
Nokta koordinatları– bunlar dikdörtgen koordinat sistemindeki sıradan koordinatlardır. Sanırım herkes 5-6. sınıftan itibaren koordinat düzleminde noktaların nasıl çizileceğini biliyor. Her noktanın düzlemde kesin bir yeri vardır ve hiçbir yere taşınamazlar.
Vektörün koordinatları– bu, bu durumda onun temele göre genişlemesidir. Herhangi bir vektör serbesttir, dolayısıyla istenirse veya gerekliyse, onu düzlemdeki başka bir noktadan kolayca uzaklaştırabiliriz (karışıklığı önlemek için onu yeniden tasarlayabiliriz, örneğin ile). İlginçtir ki vektörler için eksen veya dikdörtgen koordinat sistemi oluşturmanıza gerek yoktur; sadece bir tabana, bu durumda düzlemin ortonormal tabanına ihtiyacınız vardır.
Noktaların koordinatları ile vektörlerin koordinatlarının kayıtları benzer görünmektedir: , ve koordinatların anlamı kesinlikle farklı ve bu farkın çok iyi farkında olmalısınız. Bu fark elbette uzay için de geçerli.
Bayanlar ve baylar, ellerimizi dolduralım:
Örnek 2
a) Puan ve verilir. Vektörleri bulun ve .
b) Puan verilir ![]() Ve . Vektörleri bulun ve .
Ve . Vektörleri bulun ve .
c) Puan ve verilir. Vektörleri bulun ve .
d) Puan verilir. Vektörleri bulun ![]() .
.
Belki bu yeterlidir. Bunlar kendi başınıza karar vermeniz için örneklerdir, ihmal etmemeye çalışın, işe yarayacaktır ;-). Çizim yapmaya gerek yoktur. Dersin sonunda çözümler ve cevaplar.
Analitik geometri problemlerini çözerken önemli olan nedir? Ustaca yapılan “iki artı iki eşittir sıfır” hatasını yapmamak için SON DERECE DİKKATLİ olmak önemlidir. Bir yerde hata yaptıysam hemen özür dilerim =)
Bir segmentin uzunluğu nasıl bulunur?
Uzunluk, daha önce belirtildiği gibi modül işaretiyle gösterilir.
Düzlemin iki noktası verilirse ve o zaman parçanın uzunluğu formül kullanılarak hesaplanabilir.
Uzayda iki nokta verilirse, parçanın uzunluğu formül kullanılarak hesaplanabilir.
Not: Karşılık gelen koordinatlar değiştirilirse formüller doğru kalacaktır: ve , ancak ilk seçenek daha standarttır
Örnek 3
Çözüm: ilgili formüle göre:
Cevap: ![]()
Netlik sağlamak için bir çizim yapacağım 
Çizgi segmenti - bu bir vektör değil ve tabii ki onu hiçbir yere taşıyamazsınız. Ayrıca ölçekli çizim yaparsanız: 1 birim. = 1 cm (iki dizüstü bilgisayar hücresi), o zaman ortaya çıkan cevap, parçanın uzunluğu doğrudan ölçülerek normal bir cetvelle kontrol edilebilir.
Evet çözüm kısa ama burada açıklığa kavuşturmak istediğim birkaç önemli nokta daha var:
Öncelikle cevaba boyutu koyuyoruz: “birimler”. Koşul ne olduğunu söylemiyor; milimetre, santimetre, metre veya kilometre. Bu nedenle, matematiksel olarak doğru bir çözüm, genel formülasyon olacaktır: "birimler" - "birimler" olarak kısaltılır.
İkinci olarak, yalnızca ele alınan görev için yararlı olmayan okul materyalini tekrarlayalım:
dikkat et önemli teknik – çarpanı kökün altından kaldırmak. Hesaplamalar sonucunda bir sonuç elde ediyoruz ve iyi bir matematik stili, faktörün (mümkünse) kökün altından çıkarılmasını içerir. Daha ayrıntılı olarak süreç şöyle görünür: ![]() . Elbette cevabı olduğu gibi bırakmak bir hata olmayacaktır - ancak bu kesinlikle bir eksiklik ve öğretmen açısından saçma sapan bir argüman olacaktır.
. Elbette cevabı olduğu gibi bırakmak bir hata olmayacaktır - ancak bu kesinlikle bir eksiklik ve öğretmen açısından saçma sapan bir argüman olacaktır.
İşte diğer yaygın durumlar: 
Genellikle kök oldukça büyük bir sayı üretir; örneğin . Bu gibi durumlarda ne yapmalı? Hesap makinesini kullanarak sayının 4'e bölünebilir olup olmadığını kontrol ederiz: . Evet, tamamen bölünmüştü, dolayısıyla: ![]() . Ya da belki sayı tekrar 4'e bölünebilir? . Böylece:
. Ya da belki sayı tekrar 4'e bölünebilir? . Böylece: ![]() . Sayının son rakamı tek olduğundan üçüncü kez 4'e bölmek elbette işe yaramayacaktır. Dokuza bölmeye çalışalım: . Sonuç olarak:
. Sayının son rakamı tek olduğundan üçüncü kez 4'e bölmek elbette işe yaramayacaktır. Dokuza bölmeye çalışalım: . Sonuç olarak:
Hazır.
Çözüm: kökün altında bir bütün olarak çıkarılamayan bir sayı alırsak, o zaman faktörü kökün altından kaldırmaya çalışırız - bir hesap makinesi kullanarak sayının şu şekilde bölünebilir olup olmadığını kontrol ederiz: 4, 9, 16, 25, 36, 49 vb.
Çeşitli problemleri çözerken sıklıkla köklerle karşılaşılır; öğretmenin yorumlarına göre çözümlerinizi sonuçlandırırken daha düşük not almaktan ve gereksiz sorunlardan kaçınmak için her zaman faktörleri kökün altından çıkarmaya çalışın.
Köklerin karesini almayı ve diğer kuvvetleri de tekrarlayalım: 
Genel biçimde kuvvetlerle çalışmanın kuralları bir okul cebir ders kitabında bulunabilir, ancak verilen örneklerden her şeyin veya neredeyse her şeyin zaten açık olduğunu düşünüyorum.
Uzayda bir segmentle bağımsız çözüm görevi:
Örnek 4
Puanlar ve verilir. Segmentin uzunluğunu bulun.
Çözüm ve cevap dersin sonundadır.
Bir vektörün uzunluğu nasıl bulunur?
Bir düzlem vektörü verilirse uzunluğu formülle hesaplanır.
Bir uzay vektörü verilirse uzunluğu formülle hesaplanır. ![]() .
.
Bu formüller (bir parçanın uzunluğuna ilişkin formüllerin yanı sıra) iyi bilinen Pisagor teoremi kullanılarak kolayca türetilir.
