Talimatlar
Yan yüzün bir üçgeninde, özdeyiş (f) yüksekliktir, bu nedenle, yan kenarın (b) bilinen uzunluğu ve onunla özdeyişin indirildiği kenar arasındaki açı (γ) ile, şunları yapabilirsiniz: Üçgenin yüksekliğini hesaplamak için iyi bilinen formülü kullanın. Verilen kenar uzunluğunu bilinen açının sinüsüyle çarpın: f = b*sin(γ). Bu formül herhangi bir (düzenli veya düzensiz) şekle sahip piramitlere uygulanabilir.
Düzenli bir üçgen piramidin üç özünün (f) her birini hesaplamak için yalnızca bir parametreyi bilmek yeterlidir - kenarın uzunluğu (a). Bu, böyle bir piramidin yüzlerinin aynı büyüklükte eşkenar üçgenler şeklinde olmasıyla açıklanmaktadır. Her birinin yüksekliğini bulmak için kenar uzunluğunun çarpımının yarısını ve üçün karekökünü hesaplayın: f = a*√3/2.
Piramidin yan yüzünün alan(lar)ı biliniyorsa, buna ek olarak bu yüzün hacimsel şeklin tabanı ile ortak kenarının uzunluğunun (a) bilinmesi yeterlidir. Bu durumda alan ile kenar uzunluğu arasındaki oranı iki katına çıkararak özdeyişin uzunluğunu (f) bulun: f = 2*s/a.
Piramidin toplam yüzey alanını (S) ve tabanının çevresini (p) bilerek, aynı zamanda hesaplayabiliriz. özlü söz(f), ancak yalnızca normal bir çokyüzlü için. Yüzey alanını ikiye katlayın ve sonucu çevreye bölün: f = 2*S/p. Bu durumda tabanın şekli önemli değil.
Koşullar, yan yüzün kenarının (b) uzunluğunu ve düzgün bir düzlemin iki bitişik yan kenarının oluşturduğu açının (a) değerini veriyorsa, tabanın (n) köşe veya kenar sayısının bilinmesi gerekir. piramit. Bu başlangıç koşulları altında hesaplayın özlü söz(f) tabanın kenar sayısının bilinen bir açının sinüsü ve kenar kenarının kare uzunluğunun çarpımı ve ardından elde edilen değerin ikiye bölünmesi: f = n*sin(α)*b²/2.
Dörtgen tabanlı düzenli bir piramitte, çokyüzlünün yüksekliğini (H) ve taban kenarının uzunluğunu (a) kullanarak kısa adın uzunluğunu (f) bulabilirsiniz. Yüksekliğin karesi ile kenar uzunluğunun karesinin çeyreğinin toplamının karekökünü alın: f = √(H²+a²/4).
Apothem - düzenli bir piramit şeklinde çizilen yan yüzün zirvesinden yüksekliği. Hem düzenli bir piramitte hem de kesik bir piramitte bulunabilir. Her iki durumu da ele alalım
Talimatlar
Doğru piramit
İçinde tüm yan kenarlar eşittir, yan yüzler ikizkenar eşit üçgenlerdir ve taban normal bir çokgendir. Çünkü Normal bir piramidin tüm özleri eşittir, o zaman herhangi bir üçgende bir tane bulmak yeterlidir. Üçgenler ikizkenardır ve özdeyiş yüksekliktir. Bir ikizkenar üçgende tepe noktasından tabana çizilen yükseklik kenarortay ve açıortaydır. Medyan bir kenarı ikiye böler ve açıortay bir açıyı iki eşit açıya böler. Yükseklik üstten tabana çizilen bir diktir.
Bir ikizkenar üçgenin tüm kenarlarının bilindiğini ve tabanı iki eşit parçaya bölen bir kenarortay çizildiğini varsayalım. Çünkü Medyan yüksekliktir, o zaman diktir, yani. Medyan ile taban arasındaki açı 90 derecedir. Yani bunun bir dik üçgen olduğu ortaya çıkıyor. Yan taraf hipotenüs, tabanın yarısı ve yükseklik (ortanca) bacaklardır. Pisagor teoremi şunu belirtir: Hipotenüsün karesi, bacakların karelerinin toplamına eşittir. Bu şekilde yüksekliği bulabilirsiniz.
Tabanın karşısındaki açı bilinsin. Ve kenarlardan biri (ya yan ya da taban). Yukarıdan tabana çizilen açıortay yüksekliktir. Bu nedenle yine bir dik üçgen elde ederiz. Açı ve kenarlardan biri bilinmektedir. Sinüs, kosinüs ve tanjant kullanarak yüksekliği bulabilirsiniz. Sinüs karşı bacağın hipotenüse oranıdır, bacak bitişik bacağın hipotenüse oranıdır, teğet sinüsün kosinüse veya karşı bacağın komşuya oranıdır. Bilinen kenarları yerine koyarak yüksekliği hesaplayın.
Düzenli bir piramidin yan yüzeyinin alanı, tabanın çevresi ile apothemin çarpımının yarısına eşittir.
- özlü söz- normal bir piramidin tepe noktasından çizilen yan yüzünün yüksekliği (ayrıca kısa çizgi, normal çokgenin ortasından yanlarından birine indirilen dik uzunluğun uzunluğudur);
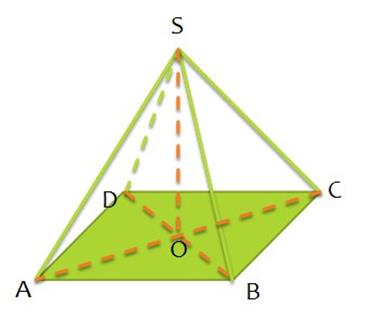
- yan yüzler (ASB, BSC, CSD, DSA) - tepe noktasında buluşan üçgenler;
- yan kaburgalar ( GİBİ , B.S. , CS , D.S. ) - yan yüzlerin ortak kenarları;
- piramidin tepesi (t.S) - yan kaburgaları birleştiren ve taban düzleminde yer almayan bir nokta;
- yükseklik ( BU YÜZDEN ) - piramidin tepesinden tabanının düzlemine çizilen dikey bir bölüm (böyle bir bölümün uçları piramidin tepesi ve dikin tabanı olacaktır);
- piramidin çapraz bölümü- piramidin üst kısmından ve tabanın köşegeninden geçen bir bölümü;
- temel (ABCD) - piramidin tepe noktasına ait olmayan bir çokgen.
Piramidin özellikleri.
1. Tüm yan kenarlar aynı boyutta olduğunda:
- piramidin tabanına yakın bir daire tanımlamak kolaydır ve piramidin tepesi bu dairenin merkezine yansıtılacaktır;
- yan kaburgalar taban düzlemi ile eşit açılar oluşturur;
- Üstelik bunun tersi de doğrudur; Yan kaburgalar taban düzlemi ile eşit açı oluşturduğunda veya piramidin tabanı etrafında bir daire tanımlanabildiğinde ve piramidin tepesi bu dairenin merkezine doğru yansıtıldığında, bu tüm yan kenarların olduğu anlamına gelir. piramidin boyutları aynı.
2. Yan yüzler taban düzlemine aynı değerde bir eğim açısına sahip olduğunda:
- piramidin tabanına yakın bir daire tanımlamak kolaydır ve piramidin tepesi bu dairenin merkezine yansıtılacaktır;
- yan yüzlerin yükseklikleri eşit uzunluktadır;
- yan yüzeyin alanı, tabanın çevresinin ve yan yüzün yüksekliğinin ½ çarpımına eşittir.
3. Piramidin tabanında çevresinde bir dairenin tanımlanabileceği bir çokgen varsa, bir piramidin etrafında bir küre tanımlanabilir (gerekli ve yeterli bir koşul). Kürenin merkezi, piramidin kendilerine dik kenarlarının ortasından geçen düzlemlerin kesişme noktası olacaktır. Bu teoremden, bir kürenin hem herhangi bir üçgenin hem de herhangi bir düzenli piramidin etrafında tanımlanabileceği sonucuna varıyoruz.
4. Piramidin iç dihedral açılarının açıortay düzlemleri 1. noktada kesişiyorsa (gerekli ve yeterli koşul) bir piramite küre yazılabilir. Bu nokta kürenin merkezi olacak.
En basit piramit.
Açı sayısına bağlı olarak piramidin tabanı üçgen, dörtgen vb. şeklinde ayrılır.
Bir piramit olacak üçgensel, dörtgen, vb., piramidin tabanı bir üçgen, bir dörtgen vb. olduğunda. Üçgen bir piramit bir tetrahedrondur - bir tetrahedron. Dörtgen - beşgen vb.
Piramit. Kesilmiş piramit
Piramit yüzlerinden biri çokgen olan bir çokyüzlüdür ( temel ) ve diğer tüm yüzler ortak bir köşe noktasına sahip üçgenlerdir ( yan yüzler ) (Şek. 15). Piramit denir doğru tabanı düzenli bir çokgen ise ve piramidin tepesi tabanın ortasına doğru çıkıntı yapıyorsa (Şekil 16). Tüm kenarları eşit olan üçgen piramit denir dörtyüzlü .
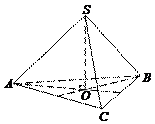
Yan kaburga Bir piramidin yan yüzünün tabana ait olmayan tarafı Yükseklik piramit, tepesinden taban düzlemine kadar olan mesafedir. Düzenli bir piramidin tüm yan kenarları birbirine eşittir, tüm yan yüzler eşit ikizkenar üçgenlerdir. Düzgün bir piramidin tepe noktasından çizilen yan yüzünün yüksekliğine ne denir? özlü söz . Çapraz bölüm Aynı yüze ait olmayan iki yan kenardan geçen düzleme piramidin kesiti denir.
Yan yüzey alanı piramit tüm yan yüzlerin alanlarının toplamıdır. Toplam yüzey alanı tüm yan yüzlerin ve tabanın alanlarının toplamına denir.
Teoremler
1. Bir piramitte tüm yan kenarlar taban düzlemine eşit olarak eğimliyse, piramidin tepesi tabanın yakınında çevrelenen dairenin merkezine yansıtılır.
2. Bir piramidin tüm yan kenarları eşit uzunluklara sahipse, piramidin tepesi, tabanın yakınında çevrelenen bir dairenin merkezine yansıtılır.
3. Bir piramidin tüm yüzleri taban düzlemine eşit derecede eğimliyse, piramidin tepesi tabanda yazılı bir dairenin merkezine yansıtılır.
Rastgele bir piramidin hacmini hesaplamak için doğru formül şöyledir:
Nerede V- hacim;
S tabanı– üs alanı;
H– piramidin yüksekliği.
Düzenli bir piramit için aşağıdaki formüller doğrudur:
![]()
Nerede P– taban çevresi;
ha bir– özlü söz;
H- yükseklik;
S dolu
S tarafı
S tabanı– üs alanı;
V– düzenli bir piramidin hacmi.
Kesilmiş piramit piramidin taban ile piramidin tabanına paralel bir kesme düzlemi arasında kalan kısmına denir (Şekil 17). Düzenli kesik piramit Düzenli bir piramidin taban ile piramidin tabanına paralel kesme düzlemi arasında kalan kısmına denir.
Gerekçeler kesik piramit - benzer çokgenler. Yan yüzler – yamuklar. Yükseklik Kesik bir piramidin tabanları arasındaki mesafedir. Diyagonal kesik bir piramit, aynı yüzde yer almayan köşelerini birleştiren bir bölümdür. Çapraz bölüm kesik piramidin aynı yüze ait olmayan iki yan kenardan geçen bir düzlemle kesitidir.
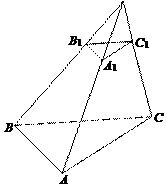
Kesik bir piramit için aşağıdaki formüller geçerlidir:
![]() (4)
(4)
Nerede S 1 , S 2 – üst ve alt tabanların alanları;
S dolu- toplam yüzey alanı;
S tarafı– yan yüzey alanı;
H- yükseklik;
V– kesik bir piramidin hacmi.
Düzenli bir kesik piramit için formül doğrudur:
![]()
Nerede P 1 , P 2 – tabanların çevreleri;
ha bir– düzenli kesik piramidin özeti.
Örnek 1. Düzenli bir üçgen piramitte tabandaki dihedral açı 60°'dir. Yan kenarın eğim açısının taban düzlemine teğetini bulun.
Çözüm. Bir çizim yapalım (Şek. 18).
 |
Piramit düzenlidir, yani tabanda bir eşkenar üçgen vardır ve tüm yan yüzler eşit ikizkenar üçgenlerdir. Tabandaki dihedral açı, piramidin yan yüzünün taban düzlemine eğim açısıdır. Doğrusal açı açıdır A iki dik arasında: vb. Piramidin tepesi üçgenin merkezine (çevrel dairenin merkezi ve üçgenin yazılı dairesi) yansıtılır. ABC). Yan kenarın eğim açısı (örneğin S.B.) kenarın kendisi ile taban düzlemine izdüşümü arasındaki açıdır. Kaburga için S.B. bu açı açı olacak SBD. Teğeti bulmak için bacakları bilmeniz gerekir BU YÜZDEN Ve O.B.. Segmentin uzunluğuna izin verin BD 3'e eşittir A. Nokta HAKKINDAçizgi segmenti BD parçalara ayrılmıştır: ve Bulduğumuz yerden BU YÜZDEN: ![]() Şunu buluyoruz:
Şunu buluyoruz: 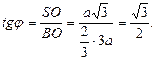
Cevap:
Örnek 2. Tabanlarının köşegenleri cm ve cm'ye eşit ve yüksekliği 4 cm ise düzgün kesik dörtgen piramidin hacmini bulun.
Çözüm. Kesik bir piramidin hacmini bulmak için formül (4)'ü kullanırız. Tabanların alanını bulmak için taban karelerinin köşegenlerini bilerek kenarlarını bulmanız gerekir. Tabanların kenarları sırasıyla 2 cm ve 8 cm'ye eşittir. Bu, tabanların alanları anlamına gelir ve tüm verileri formülde yerine koyarak kesik piramidin hacmini hesaplarız:
Cevap: 112 cm3.
Örnek 3. Tabanlarının kenarları 10 cm ve 4 cm, piramidin yüksekliği 2 cm olan düzgün üçgen kesik piramidin yan yüzünün alanını bulun.
Çözüm. Bir çizim yapalım (Şek. 19).
Bu piramidin yan yüzü ikizkenar yamuktur. Bir yamuğun alanını hesaplamak için tabanını ve yüksekliğini bilmeniz gerekir. Tabanlar duruma göre verilir, sadece yüksekliği bilinmez. Onu nereden bulacağız A 1 e bir noktadan dik A 1 alt taban düzleminde, A 1 D– itibaren dik A başına 1 AC. A 1 e= 2 cm, çünkü bu piramidin yüksekliğidir. Bulmak AlmanyaÜstten görünümü gösteren ek bir çizim yapalım (Şek. 20). Nokta HAKKINDA– üst ve alt tabanların merkezlerinin projeksiyonu. o zamandan beri (bkz. Şekil 20) ve Öte yandan TAMAM– dairenin içine yazılan yarıçap ve ![]() OM– yazılı dairenin yarıçapı.
OM– yazılı dairenin yarıçapı.
giriiş
Stereometrik şekilleri incelemeye başladığımızda “Piramit” konusuna değinmiştik. Bu konuyu beğendik çünkü piramit mimaride çok sık kullanılıyor. Gelecekteki mimarlık mesleğimiz de bu figürden ilham aldığı için bizi mükemmel projelere itebileceğini düşünüyoruz.
Mimari yapıların sağlamlığı en önemli özelliğidir. Gücü, öncelikle oluşturuldukları malzemelerle ve ikinci olarak tasarım çözümlerinin özellikleriyle ilişkilendirdiğimizde, bir yapının gücünün doğrudan onun için temel olan geometrik şekille ilişkili olduğu ortaya çıkıyor.
Yani ilgili mimari formun modeli sayılabilecek geometrik bir figürden bahsediyoruz. Geometrik şeklin aynı zamanda mimari yapının sağlamlığını da belirlediği ortaya çıktı.
Antik çağlardan beri Mısır piramitleri en dayanıklı mimari yapılar olarak kabul edildi. Bildiğiniz gibi düzenli dörtgen piramitler şeklindedirler.
Geniş taban alanı nedeniyle en büyük stabiliteyi sağlayan bu geometrik şekildir. Öte yandan piramit şekli yerden yükseklik arttıkça kütlenin azalmasını sağlar. Piramidi istikrarlı ve dolayısıyla yerçekimi koşulları altında güçlü kılan bu iki özelliktir.
Projenin amacı: Piramitler hakkında yeni şeyler öğrenin, bilginizi derinleştirin ve pratik uygulamayı bulun.
Bu hedefe ulaşmak için aşağıdaki görevleri çözmek gerekiyordu:
· Piramit hakkında tarihsel bilgileri öğrenin
· Piramidi geometrik bir şekil olarak düşünün
· Yaşamda ve mimaride uygulama bulun
· Dünyanın farklı yerlerinde bulunan piramitler arasındaki benzerlikleri ve farklılıkları bulun
Teorik kısım
Tarihi bilgi
Piramit geometrisi Eski Mısır ve Babil'de başladı, ancak Antik Yunanistan'da aktif olarak geliştirildi. Piramidin hacmini ilk belirleyen Demokritos'tu ve Knidoslu Eudoxus bunu kanıtladı. Antik Yunan matematikçi Öklid, "Elementler" kitabının XII. cildinde piramit hakkındaki bilgileri sistematik hale getirdi ve aynı zamanda piramidin ilk tanımını da türetti: bir düzlemden bir noktaya yakınlaşan düzlemlerle sınırlanan katı bir şekil.
Mısır firavunlarının mezarları. Bunların en büyüğü - El Giza'daki Keops, Kefren ve Mikerin piramitleri - eski zamanlarda Dünyanın Yedi Harikasından biri olarak kabul ediliyordu. Yunanlıların ve Romalıların, kralların eşi benzeri görülmemiş gururunun ve tüm Mısır halkını anlamsız inşaatlara mahkum eden zulmün bir anıtını zaten gördükleri piramidin inşası, en önemli kült eylemiydi ve görünüşe göre, ülkenin ve hükümdarının mistik kimliği. Ülke nüfusu yılın tarım işlerinden uzak olan kısmında türbenin inşasında çalıştı. Bir dizi metin, kralların (daha sonraki bir zamanda da olsa) mezarlarının ve onu inşa edenlerin inşasına gösterdikleri ilgi ve özene tanıklık etmektedir. Piramidin kendisine verilen özel kült onurları da biliniyor.
Temel konseptler
Piramit tabanı çokgen olan ve geri kalan yüzleri ortak bir tepe noktasına sahip olan üçgenlere çokyüzlü denir.
Özlem- düzenli bir piramidin tepe noktasından çizilen yan yüzünün yüksekliği;
Yan yüzler- bir tepe noktasında buluşan üçgenler;
Yan kaburgalar- yan yüzlerin ortak kenarları;
Piramidin tepesi- yan kaburgaları birleştiren ve taban düzleminde uzanmayan bir nokta;
Yükseklik- piramidin tepesinden tabanının düzlemine çizilen dikey bir bölüm (bu bölümün uçları piramidin tepesi ve dikin tabanıdır);
Bir piramidin çapraz bölümü- piramidin tabanın üstünden ve köşegeninden geçen bölümü;
Temel- piramidin tepe noktasına ait olmayan bir çokgen.
Düzenli bir piramidin temel özellikleri
Yan kenarlar, yan yüzler ve özler sırasıyla eşittir.
Tabandaki dihedral açılar eşittir.
Yan kenarlardaki dihedral açılar eşittir.
Her yükseklik noktası tabanın tüm köşelerine eşit uzaklıktadır.
Her yükseklik noktası tüm yan yüzlerden eşit uzaklıktadır.
Temel piramit formülleri
Piramidin yanal ve toplam yüzeyinin alanı.
Bir piramidin yan yüzeyinin alanı (tam ve kesik), tüm yan yüzlerinin alanlarının toplamıdır, toplam yüzey alanı ise tüm yüzlerinin alanlarının toplamıdır.
Teorem: Düzenli bir piramidin yan yüzeyinin alanı, tabanın çevresi ile piramidin özdeyişinin çarpımının yarısına eşittir.
![]()
P- taban çevresi;
H- özlü söz.
Kesik bir piramidin yan ve tam yüzeylerinin alanı.
![]()
sayfa 1, P 2 - taban çevreleri;
H- özlü söz.
![]()
R- düzenli bir kesik piramidin toplam yüzey alanı;
S tarafı- düzenli bir kesik piramidin yan yüzeyinin alanı;
S 1 + S 2- üs alanı
Piramidin hacmi
Biçim hacim ula her türlü piramitler için kullanılır.
H- piramidin yüksekliği.
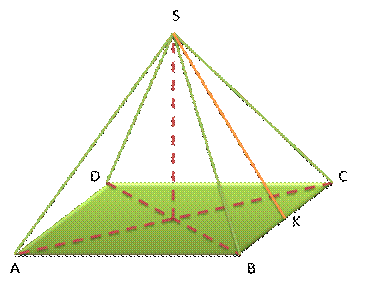
Piramit köşeleri
Piramidin yan yüzü ile tabanının oluşturduğu açılara piramidin tabanındaki dihedral açılar denir.
İki dik açı bir dihedral açı oluşturur.
Bu açıyı belirlemek için sıklıkla üç dik teoremi kullanmanız gerekir..
Yan kenarın oluşturduğu açılara ve taban düzlemine izdüşümüne denir. yan kenar ile taban düzlemi arasındaki açılar.
İki yan kenarın oluşturduğu açıya denir piramidin yan kenarındaki dihedral açı.
Piramidin bir yüzünün iki yan kenarının oluşturduğu açıya denir. piramidin tepesindeki açı.
Piramit bölümleri
Bir piramidin yüzeyi bir çokyüzlünün yüzeyidir. Yüzlerinin her biri bir düzlemdir, dolayısıyla bir piramidin kesme düzlemi tarafından tanımlanan bölümü, ayrı düz çizgilerden oluşan kesikli bir çizgidir.
Çapraz bölüm
Piramidin aynı yüz üzerinde yer almayan iki yan kenarından geçen düzlemin kesitine ne ad verilir? çapraz bölüm piramitler.
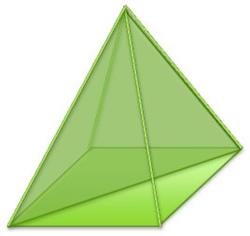
Paralel bölümler
Teorem:
Piramit tabana paralel bir düzlemle kesişiyorsa, piramidin yan kenarları ve yükseklikleri bu düzlem tarafından orantılı parçalara bölünür;
6. Yüksekliğin her noktası tabanın tüm köşelerinden eşit uzaklıkta
7. her yükseklik noktası tüm yan kenarlardan eşit uzaklıkta
Kesilmiş piramit- piramidin tabanı ile tabana paralel bir kesme düzlemi arasında kalan kısmı.
Kesik piramidin tabanına ve ona karşılık gelen kısmına ne ad verilir? kesik piramidin tabanları.
Bir tabanın herhangi bir noktasından diğerinin düzlemine çizilen dikmeye ne ad verilir? kesik bir piramidin yüksekliği.
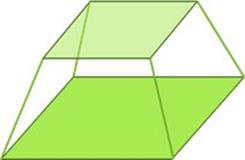
Görevler
1 numara. Düzgün dörtgen piramitte O noktası tabanın merkezidir, SO=8 cm, BD=30 cm SA yan kenarını bulun.
Problem çözme
1 numara. Düzenli bir piramitte tüm yüzler ve kenarlar eşittir.
OSB'yi düşünün: OSB dikdörtgen bir dikdörtgendir çünkü.
SB2 =SO2 +OB2
SB 2 =64+225=289
Mimarlıkta piramit
Bir piramit, kenarların bir noktada birleştiği sıradan, düzenli bir geometrik piramit biçiminde anıtsal bir yapıdır. İşlevsel amaçlarına göre, eski çağlardaki piramitler mezar veya kült ibadet yerleriydi. Bir piramidin tabanı üçgen, dörtgen veya keyfi sayıda köşeye sahip bir çokgen şeklinde olabilir, ancak en yaygın versiyon dörtgen tabandır.
Antik Dünyanın farklı kültürleri tarafından, çoğunlukla tapınak veya anıt olarak inşa edilmiş çok sayıda piramit vardır. Büyük piramitler Mısır piramitlerini içerir.
Dünyanın her yerinde piramit şeklindeki mimari yapıları görebilirsiniz. Piramit binaları eski zamanları anımsatıyor ve çok güzel görünüyor.
Mısır piramitleri, “Dünyanın Yedi Harikasından” biri olan Keops Piramidi de dahil olmak üzere Eski Mısır'ın en büyük mimari anıtlarıdır. Ayaktan tepeye kadar 137,3 metreye ulaşan yüksekliği, tepeyi kaybetmeden önce 146,7 metreydi.

Slovakya'nın başkentinde ters bir piramidi andıran radyo istasyonu binası 1983 yılında inşa edilmiştir. Ofisler ve hizmet binalarının yanı sıra hacmin içinde Slovakya'nın en büyük organlarından birine sahip oldukça geniş bir konser salonu bulunmaktadır.

“Bir piramit gibi sessiz, değişmeyen ve heybetli” olan Louvre, dünyanın en büyük müzesi olmadan önce yüzyıllar boyunca pek çok değişikliğe uğramıştır. 1190 yılında Philip Augustus tarafından inşa edilen ve kısa süre sonra kraliyet ikametgahı haline gelen bir kale olarak doğmuştur. 1793 yılında saray müze haline getirildi. Koleksiyonlar vasiyet veya satın alma yoluyla zenginleşiyor.

