Tanım: Sayısal bir fonksiyon, belirli bir kümedeki her x sayısını tek bir y sayısıyla ilişkilendiren bir yazışmadır.

Tanım:

burada x bağımsız değişkendir (argüman), y ise bağımlı değişkendir (fonksiyon). X'in değerleri kümesine fonksiyonun tanım kümesi denir (D(f) ile gösterilir). Y'nin değerleri kümesine fonksiyonun değer aralığı denir (E(f) ile gösterilir). Bir fonksiyonun grafiği, koordinatları (x, f(x)) olan düzlemdeki noktaların kümesidir.

Bir işlevi belirtme yöntemleri.

1. analitik yöntem (matematiksel bir formül kullanarak);
2. tablo yöntemi (bir tablo kullanarak);
3. betimleyici yöntem (sözlü açıklamayı kullanarak);
4. grafiksel yöntem (bir grafik kullanarak).

Fonksiyonun temel özellikleri.

1. Çift ve tek

Bir fonksiyon çağrılsa bile
– fonksiyonun tanım bölgesi sıfıra göre simetriktir
f(-x) = f(x)

Çift fonksiyonun grafiği eksene göre simetriktir 0 yıl

Bir fonksiyona tek ise denir
– fonksiyonun tanım bölgesi sıfıra göre simetriktir
– tanım alanındaki herhangi bir x için f(-x) = –f(x)

Tek bir fonksiyonun grafiği orijine göre simetriktir.

2. Frekans

Bir f(x) fonksiyonu, tanım tanım kümesinden herhangi bir x için ise periyotlu periyodik olarak adlandırılır. f(x) = f(x+T) = f(x-T) .

Periyodik bir fonksiyonun grafiği sınırsız tekrarlanan özdeş parçalardan oluşur.

3. Monotonluk (artan, azalan)

f(x) fonksiyonu, eğer bu kümeden herhangi bir x 1 ve x 2 için, x 1 olacak şekilde P kümesi üzerinde artıyorsa

f(x) fonksiyonu P kümesinde bu kümeden herhangi bir x 1 ve x 2 için x 1 f(x 2) olacak şekilde azalır.

4. Aşırılıklar

Xmax'ın herhangi bir komşuluğundaki tüm x'ler için f(x) f(Xmax) eşitsizliği karşılanıyorsa, Xmax noktasına f(x) fonksiyonunun maksimum noktası denir.

Y max =f(X max) değerine bu fonksiyonun maksimumu denir.

X max – maksimum nokta
Maksimum - maksimumda

X min'in herhangi bir komşuluğundaki tüm x'ler için f(x) f(X min) eşitsizliği karşılanıyorsa, X min noktasına f(x) fonksiyonunun minimum noktası denir.

Y min =f(X min) değerine bu fonksiyonun minimumu denir.

X dk – minimum nokta
Y dk – minimum

X min, X max – ekstrem noktalar
Y min , Y max – ekstrema.

5. Fonksiyonun sıfırları

Bir y = f(x) fonksiyonunun sıfırı, fonksiyonun sıfır olduğu x argümanının değeridir: f(x) = 0.

X 1, X 2, X 3 – y = f(x) fonksiyonunun sıfırları.

"Bir fonksiyonun temel özellikleri" konusundaki görevler ve testler

• Fonksiyon Özellikleri - Sayısal fonksiyonlar 9. sınıf

  Dersler: 2 Ödevler: 11 Testler: 1

• Logaritmanın özellikleri - Üstel ve logaritmik fonksiyonlar 11. sınıf

  Dersler: 2 Ödevler: 14 Testler: 1

• Karekök fonksiyonu, özellikleri ve grafiği - Karekök fonksiyonu. Karekök 8. sınıfın özellikleri

  Dersler: 1 Ödevler: 9 Testler: 1

• Güç fonksiyonları, özellikleri ve grafikleri - Dereceler ve kökler. Güç fonksiyonları 11. sınıf

  Dersler: 4 Ödevler: 14 Testler: 1

• Fonksiyonlar - Matematikte Birleşik Devlet Sınavının gözden geçirilmesi için önemli konular

  Görevler: 24

Bu konuyu inceledikten sonra, çeşitli fonksiyonların tanım tanım kümesini bulabilmeli, bir fonksiyonun monotonluk aralıklarını grafikler kullanarak belirleyebilmeli ve fonksiyonları düzgünlük ve teklik açısından inceleyebilmelisiniz. Aşağıdaki örnekleri kullanarak benzer problemleri çözmeyi düşünelim.

Örnekler.

1. Fonksiyonun tanım tanım kümesini bulun.

Çözüm: fonksiyonun tanım alanı koşuldan bulunur

Fonksiyonlar ve özellikleri

Fonksiyon matematiksel kavramların en önemlilerinden biridir.İşlev X değişkeninin her değerinin, y değişkeninin tek bir değerine karşılık geldiği, y değişkeninin x değişkenine böyle bir bağımlılığını çağırırlar.

Değişken X isminde bağımsız değişken veya argüman. Değişken en isminde bağımlı değişken. Bunu da söylüyorlary değişkeni x değişkeninin bir fonksiyonudur. Bağımlı değişkenin değerlerine denirfonksiyon değerleri.

Değişkenin bağımlılığı iseen değişkendenX bir fonksiyon ise kısaca şu şekilde yazılabilir:sen= F( X ). (Okumak:en eşittirF itibarenX .) SembolF( X) argümanın değerine karşılık gelen fonksiyonun değerini belirtirX .

Bağımsız değişken formunun tüm değerleribir fonksiyonun alanı . Bağımlı değişkenin oluşturduğu tüm değerlerfonksiyon aralığı .

Bir fonksiyon bir formülle belirtilmişse ve tanım alanı belirtilmemişse, fonksiyonun tanım alanı, formülün anlamlı olduğu argümanın tüm değerlerinden oluştuğu kabul edilir.

Bir işlevi belirtme yöntemleri:

1.analitik yöntem (işlev matematiksel bir formül kullanılarak belirtilir;

2. tablo yöntemi (işlev bir tablo kullanılarak belirtilir)

3.açıklayıcı yöntem (işlev sözlü açıklamayla belirtilir)

4. grafiksel yöntem (işlev bir grafik kullanılarak belirtilir).

Fonksiyon grafiği Apsisleri argümanın değerlerine eşit olan koordinat düzleminin tüm noktalarının ve koordinatların kümesini adlandırın - karşılık gelen fonksiyon değerleri.

FONKSİYONLARIN TEMEL ÖZELLİKLERİ

1. Fonksiyon sıfırları

Bir fonksiyonun sıfırı, fonksiyonun değerinin sıfıra eşit olduğu argümanın değeridir.

2. Bir fonksiyonun sabit işaretinin aralıkları

Bir fonksiyonun sabit işaret aralıkları, fonksiyon değerlerinin yalnızca pozitif veya yalnızca negatif olduğu argüman değerleri kümesidir.

3. Arttırma (azaltma) fonksiyonu.

Artan Belirli bir aralıkta, bir fonksiyon, bu aralıktaki argümanın daha büyük bir değerinin, fonksiyonun daha büyük bir değerine karşılık geldiği bir fonksiyondur.

İşlev y = F ( X ) isminde artan aralıkta (A; B ), eğer herhangi biri için X 1 Ve X 2 bu aralıktan öyle kiX 1 < X 2 , eşitsizlik doğrudurF ( X 1 )< F ( X 2 ).

Azalan Belirli bir aralıkta, bir fonksiyon, bu aralıktaki argümanın daha büyük bir değerinin, fonksiyonun daha küçük bir değerine karşılık geldiği bir fonksiyondur.

İşlev en = F ( X ) isminde azalan aralıkta (A; B ) , eğer herhangi biri için X 1 Ve X 2 bu aralıktan öyle ki X 1 < X 2 , eşitsizlik doğrudurF ( X 1 )> F ( X 2 ).

4. Çift (tek) işlevi

Eşit işlev - Tanım alanı orijine göre simetrik olan ve herhangi bir fonksiyon içinX tanım alanından eşitlikF (- X ) = F ( X ) . Çift fonksiyonun grafiği ordinat etrafında simetriktir.

Örneğin, y = x 2 - eşit işlev.

Tek fonksiyon- Tanım alanı orijine göre simetrik olan ve herhangi bir fonksiyon için X tanım alanından eşitlik doğrudur F (- X ) = - F (X ). Tek bir fonksiyonun grafiği orijine göre simetriktir.

Örneğin: y = x 3 - tek işlev .

Genel formun bir fonksiyonu çift veya tek değildir (y = x 2 +x ).

Bazı fonksiyonların özellikleri ve grafikleri

1. Doğrusal fonksiyon formun bir fonksiyonu denir , Nerede k Ve B – sayılar.

Doğrusal bir fonksiyonun tanım alanı bir kümedirR gerçek sayılar.

Doğrusal bir fonksiyonun grafiğien = kx + B ( k ≠ 0), (0;) noktasından geçen düz bir çizgidir;B ) ve çizgiye paralelen = kx .

Düz, eksene paralel değilAh, doğrusal bir fonksiyonun grafiğidir.

Doğrusal bir fonksiyonun özellikleri.

1. Ne zaman k > 0 işlevi en = kx + B

2. Ne zaman k < 0 işlevi y = kx + B tanım alanında azalma.

sen = kx + B ( k ≠ 0 ) sayı doğrusunun tamamıdır, yani birçokR gerçek sayılar.

Şu tarihte: k = 0 fonksiyon değeri setiy = kx + B bir sayıdan oluşurB .

3. Ne zaman B = 0 ve k = 0 fonksiyon ne çift ne de tektir.

Şu tarihte: k = 0 doğrusal fonksiyon formuna sahiptiry = B ve B ≠ 0 eşit.

Şu tarihte: k = 0 ve B = 0 doğrusal fonksiyon formuna sahiptiry = 0 ve hem çift hem de tektir.

Doğrusal bir fonksiyonun grafiğiy = B (0;) noktasından geçen düz bir çizgidir; B ) ve eksene paralelAh. Ne zaman olduğunu unutmayın B = 0 fonksiyon grafiğiy = B eksenle çakışmak Ah .

5. Ne zaman k > 0 bizde buna sahibiz en> 0 ise ve en< 0 ise. Şu tarihte: k < 0 elimizde y > 0 ise ve< 0, если .

2. İşlev sen = X 2

Rgerçek sayılar.

Bir değişken vermekX fonksiyonun etki alanından çeşitli değerler ve karşılık gelen değerlerin hesaplanmasıen formüle göre sen = X 2 , fonksiyonun grafiğini gösteriyoruz.

Bir fonksiyonun grafiği sen = X 2 isminde parabol.

y = x fonksiyonunun özellikleri 2 .

1. Eğer X= 0 ise y = 0, yani Parabolün koordinat eksenleri (0; 0) ile ortak bir noktası vardır - koordinatların kökeni.

2. Eğer x ≠ 0 , O en > 0, yani parabolün orijin hariç tüm noktaları x ekseninin üzerinde yer alır.

3. Fonksiyon değerlerinin ayarlanmasıen = X 2 yayılma fonksiyonuen = X 2 azalır.

X

3.Fonksiyon

Bu fonksiyonun etki alanı yayılma fonksiyonudursen = | X | azalır.

7. Fonksiyon en küçük değerini o noktada alırX, BT 0'a eşittir. En büyük değer yoktur.

6. İşlev

İşlev kapsamı: .

Fonksiyon aralığı: .

Grafik bir abartıdır.

1. Fonksiyon sıfırları.

y ≠ 0, sıfır yok.

2. İşaretlerin değişmezlik aralıkları,

Eğer k > 0, o zaman en> 0'da X > 0; en < 0 при X < О.

Eğer k < 0, то en < 0 при X > 0; en> 0'da X < 0.

3. Artma ve azalma aralıkları.

Eğer k > 0 ise fonksiyon şu şekilde azalır: .

Eğer k < 0, то функция возрастает при .

4. Çift (tek) işlevi.

Fonksiyon tuhaf.

Kare üç terimli

Formun denklemi balta 2 + bx + C = 0, burada A , B Ve İle - bazı sayılar vea≠ 0, çağrıldı kare.

İkinci dereceden bir denklemdebalta 2 + bx + C = 0 katsayısı A isminde ilk katsayı B - ikinci katsayılar, - ücretsiz üye.

İkinci dereceden bir denklemin köklerinin formülü şöyledir:

.

İfade denir ayrımcı ikinci dereceden denklem ve ile gösterilirD .

Eğer D = 0 ise denklemi sağlayan tek bir sayı vardır balta 2 + bx + C = 0. Bununla birlikte, bu durumda ikinci dereceden denklemin iki eşit gerçek kökü olduğunu ve sayının kendisinin olduğunu söyleme konusunda anlaştık. isminde çift ​​kök.

Eğer D < 0, то квадратное уравнение не имеет действительных корней.

Eğer D > 0 ise ikinci dereceden denklemin iki farklı gerçek kökü vardır.

İkinci dereceden bir denklem verilsinbalta 2 + bx + C = 0. Çünkü a≠ 0, sonra bu denklemin her iki tarafını da bölerekA, denklemi elde ederiz . İnanmak Ve , denkleme varıyoruz , burada birinci katsayı 1'e eşittir. Bu denklem denirverildi.

Yukarıdaki ikinci dereceden denklemin köklerinin formülü şöyledir:

.

Formun denklemleri

A X 2 + bx = 0, balta 2 + s = 0, A X 2 = 0

denir tamamlanmamış ikinci dereceden denklemler. Eksik ikinci dereceden denklemler, denklemin sol tarafının çarpanlara ayrılmasıyla çözülür.

Vieta'nın teoremi .

İkinci dereceden bir denklemin köklerinin toplamı, ikinci katsayının ters işaretle alınan birinciye oranına eşittir ve köklerin çarpımı, serbest terimin birinci katsayıya oranıdır, yani.

Converse teoremi.

Herhangi iki sayının toplamı iseX 1 Ve X 2 eşit ve çarpımları eşittir, o zaman bu sayılar ikinci dereceden denklemin kökleridirAh 2 + B x + c = 0.

Formun işlevi Ah 2 + B x + c isminde kare üç terimli. Bu fonksiyonun kökleri karşılık gelen ikinci dereceden denklemin kökleridir.Ah 2 + B x + c = 0.

İkinci dereceden bir trinomiyalin diskriminantı sıfırdan büyükse, bu trinom şu şekilde temsil edilebilir:

Ah 2 + B x + c = a(x-x 1 )(x-x 2 )

Nerede X 1 Ve X 2 - trinomialin kökleri

Eğer ikinci dereceden bir trinomiyalin diskriminantı sıfır ise, bu trinom şu şekilde temsil edilebilir:

Ah 2 + B x + c = a(x-x 1 ) 2

Nerede X 1 - üç terimlinin kökü.

Örneğin, 3x 2 - 12x + 12 = 3(x - 2) 2 .

Formun denklemi Ah 4 + B X 2 + s= 0 denir iki kareli. Formülü kullanarak değişken değiştirmeyi kullanmaX 2 = sen ikinci dereceden bir denkleme indirgenirA sen 2 + ile + ç = 0.

İkinci dereceden fonksiyon

İkinci dereceden fonksiyon formundaki bir formülle yazılabilen bir fonksiyondursen = balta 2 + bx + C , Nerede X – bağımsız değişken,A , B Ve C – bazı sayılar veA ≠ 0.

Fonksiyonun özellikleri ve grafiğinin türü esas olarak katsayı değerlerine göre belirlenir.A ve ayrımcı.

İkinci dereceden bir fonksiyonun özellikleri

Kapsam:R;

Değer aralığı:

en A > 0 [- D/(4 A); ∞)

en A < 0 (-∞; - D/(4 A)];

Çift, tek:

en B = 0 çift fonksiyon

en B ≠ 0 fonksiyonu ne çift ne de tektir

en D> 0 iki sıfır: ,

en D= 0 bir sıfır:

en D < 0 нулей нет

İmza tutarlılığı aralıkları:

a > 0 ise, D> 0 ise

a > 0 ise, D= 0 ise

e a > 0 ise, D < 0, то

eğer bir< 0, D> 0 ise

eğer bir< 0, D= 0 ise

eğer bir< 0, D < 0, то

- Monotonluk aralıkları

> 0 için

bir< 0

İkinci dereceden bir fonksiyonun grafiğiparabol – düz bir çizgiye göre simetrik bir eğri , parabolün tepe noktasından geçerek (parabolün tepe noktası, parabolün simetri ekseni ile kesişme noktasıdır).

İkinci dereceden bir fonksiyonun grafiğini çizmek için şunlara ihtiyacınız vardır:

1) parabolün tepe noktasının koordinatlarını bulun ve bunu koordinat düzleminde işaretleyin;

2) parabole ait birkaç nokta daha oluşturun;

3) işaretli noktaları düzgün bir çizgiyle birleştirin.

Parabolün tepe noktasının koordinatları aşağıdaki formüllerle belirlenir:

; .

Fonksiyon grafiklerini dönüştürme

1. Esneme grafiklery = x 2 eksen boyuncaen V|bir| kez (saatte|bir| < 1, 1/'nin sıkıştırılmış halidir|bir| bir kere).

Eğer ve< 0, произвести, кроме того, зеркальное отражение графика отно­сительно оси X (parabolün dalları aşağıya doğru yönlendirilecektir).

Sonuç: bir fonksiyonun grafiğiy = ah 2 .

2. Paralel aktarım fonksiyon grafikleriy = ah 2 eksen boyuncaX Açık| M | (ne zaman sağa

M > 0 ve sola doğruT< 0).

Sonuç: fonksiyon grafiğiy = a(x - t) 2 .

3. Paralel aktarım fonksiyon grafikleri eksen boyuncaen Açık| N | (yukarıdap> 0 ve aşağıN< 0).

Sonuç: fonksiyon grafiğiy = a(x - t) 2 + s.

İkinci dereceden eşitsizlikler

Form eşitsizlikleriAh 2 + B x + c > 0 veAh 2 + bx + c< 0, neredeX - değişken,A , B Veİle - bazı sayılar vea≠ 0'a tek değişkenli ikinci dereceden eşitsizlikler denir.

Bir değişkendeki ikinci derece eşitsizliği çözmek, karşılık gelen ikinci dereceden fonksiyonun pozitif veya negatif değerler aldığı aralıkları bulmak olarak düşünülebilir.

Formdaki eşitsizlikleri çözmek içinAh 2 + bx + c > 0 veAh 2 + bx + c< 0 aşağıdaki gibi ilerleyin:

1) İkinci dereceden trinomiyalin diskriminantını bulun ve trinomiyalin köklerinin olup olmadığını öğrenin;

2) Üç terimlinin kökleri varsa, bunları eksende işaretleyinX ve işaretli noktalar aracılığıyla şematik olarak dalları yukarıya doğru yönlendirilen bir parabol çizilir.A > 0 veya aşağı olduğundaA< 0; Üç terimlinin kökleri yoksa, üst yarı düzlemde bulunan bir parabolü şematik olarak tasvir edin.A > 0 veya daha düşükA < 0;

3) eksende bulunurX parabolün noktalarının eksenin üzerinde bulunduğu aralıklarX (eşitsizlik çözülürseAh 2 + bx + c > 0) veya eksenin altındaX (eşitsizlik çözülürseAh 2 + bx + c < 0).

Örnek:

Eşitsizliği çözelim .

İşlevi düşünün

Grafiği, dalları aşağı doğru yönlendirilmiş bir paraboldür (çünkü ).

Grafiğin eksene göre nasıl yerleştirildiğini öğrenelimX. Bunun denklemini çözelim . Bunu anlıyoruzx = 4. Denklemin tek kökü vardır. Bu, parabolün eksene dokunduğu anlamına gelirX.

Bir parabolü şematik olarak tasvir ederek, fonksiyonun herhangi bir değer için negatif değerler aldığını görüyoruz.X, 4 hariç.

Cevap şu şekilde yazılabilir:X - 4'e eşit olmayan herhangi bir sayı.

Aralık yöntemini kullanarak eşitsizlikleri çözme

çözüm diyagramı

1. Sıfırları bulun eşitsizliğin sol tarafında fonksiyon görür.

2. Sıfırların sayı eksenindeki konumunu işaretleyin ve çokluklarını belirleyin (Eğerk Ben çift ​​ise sıfır çift katlıdır, eğerk Ben tuhaf tuhaftır).

3. Fonksiyonun işaretlerini bulun sıfırlar arasındaki aralıklarda, en sağdaki aralıktan başlayarak: bu aralıkta eşitsizliğin sol tarafındaki fonksiyon her zaman pozitiftir Verilen eşitsizlik biçimi için. Bir fonksiyonun sıfırından sağdan sola bir aralıktan bitişik aralığa geçerken aşağıdakiler dikkate alınmalıdır:

sıfır tek ise çokluk, fonksiyonun işareti değişir,

sıfır çift ise çokluk durumunda fonksiyonun işareti korunur.

4. Cevabı yazın.

Örnek:

(x + 6) (x + 1) (X - 4) < 0.

Fonksiyon sıfırları bulundu. Bunlar eşittir:X 1 = -6; X 2 = -1; X 3 = 4.

Fonksiyonun sıfırlarını koordinat doğrusu üzerinde işaretleyelim.F ( X ) = (x + 6) (x + 1) (X - 4).

Bu fonksiyonun işaretlerini (-∞; -6), (-6; -1), (-1; 4) ve aralıklarının her birinde bulalım.

Eşitsizliğin çözüm kümesinin (-∞; -6) ve (-1; 4) aralıklarının birleşimi olduğu şekilden açıkça görülmektedir.

Cevap: (-∞ ; -6) ve (-1; 4).

Eşitsizlikleri çözmek için dikkate alınan yönteme deniraralık yöntemi.

Bir fonksiyonun tanım alanı ve değer aralığı.İlköğretim matematikte fonksiyonlar yalnızca gerçek sayılar kümesinde incelenir. R.Bu, işlev argümanının yalnızca işlevin tanımlandığı gerçek değerleri alabileceği anlamına gelir; aynı zamanda yalnızca gerçek değerleri kabul eder. Birçok X tüm geçerli geçerli argüman değerleri X, bunun için fonksiyon sen= F(X)tanımlanmış, çağrılmış fonksiyonun alanı. Birçok e tüm gerçek değerler sen fonksiyonun kabul ettiği şeye denir fonksiyon aralığı. Artık fonksiyonun daha kesin bir tanımını verebiliriz: kural(yasası) X ve Y kümeleri arasındaki yazışmalar, buna göre kümedeki her öğe içinX, Y kümesinden fonksiyon adı verilen bir ve yalnızca bir öğe bulabilir.

Bu tanımdan, bir fonksiyonun aşağıdaki durumlarda tanımlanmış olduğu sonucu çıkar:

Fonksiyonun alanı belirtildi X ;

İşlev aralığı belirtildi e ;

Yazışma kuralı (yasası) bilinmektedir ve öyle ki her biri için

Bir bağımsız değişken değeri için yalnızca bir işlev değeri bulunabilir.

Fonksiyonun benzersizliğine ilişkin bu gereklilik zorunludur.

Monoton fonksiyon. Argümanın herhangi iki değeri için ise X 1 ve X koşulun 2'si X 2 > X 1 takip F(X 2) > F(X 1), ardından fonksiyon F(X) denir artan; eğer herhangi biri için X 1 ve X koşulun 2'si X 2 > X 1 takip F(X 2) < F(X 1), ardından fonksiyon F(X) denir azalan. Yalnızca artan veya yalnızca azalan fonksiyona denir monoton.

Sınırlı ve sınırsız işlevler. Fonksiyon çağrılır sınırlı eğer böyle pozitif bir sayı varsa M ne | F(X) | M tüm değerler için X. Eğer böyle bir sayı yoksa fonksiyon sınırsız.

ÖRNEKLER.

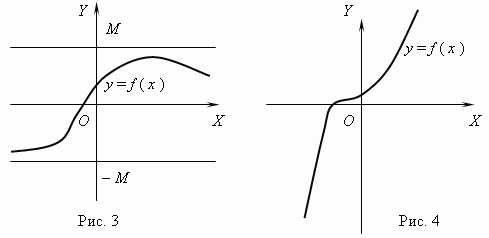
Şekil 3'te gösterilen fonksiyon sınırlıdır ancak monoton değildir. Şekil 4'teki fonksiyon ise bunun tam tersidir, monotondur ancak sınırsızdır. (Bunu açıklayın lütfen!).

Sürekli ve süreksiz fonksiyonlar.İşlev sen = F (X) denir sürekli bu noktadaX = A, Eğer:

1) fonksiyon ne zaman tanımlanır? X = A, yani F (A) var;

2) mevcut sonlu limit limiti F (X) ;

X→A

(bkz. İşlev Sınırları)

3) F (A) = lim F (X) .

X→A

Bu koşullardan en az biri karşılanmazsa fonksiyon çağrılır. patlayıcı bu noktada X = A.

Eğer fonksiyon sürekli ise herkes tanım alanının noktaları, o zaman denir sürekli fonksiyon.

Çift ve tek fonksiyonlar. Eğer için herhangi X F(- X) = F (X), sonra fonksiyon çağrılır eşit;eğer meydana gelirse: F(- X) = - F (X), sonra fonksiyon çağrılır garip. Çift fonksiyonun grafiği Y eksenine göre simetrik(Şekil 5), tek bir fonksiyonun grafiği Simkökene göre metrik(Şekil 6).

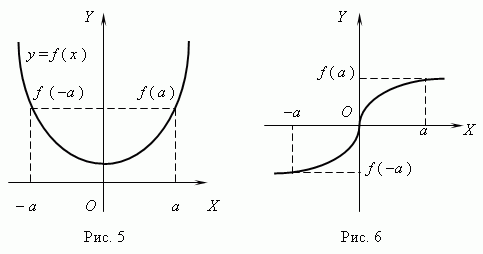
Periyodik fonksiyon.İşlev F (X) - periyodik eğer böyle bir şey varsa sıfır olmayan sayı T Ne için herhangi X fonksiyonun tanım alanından aşağıdakiler geçerlidir: F (X + T) = F (X). Bu en az numara aranır fonksiyonun süresi. Tüm trigonometrik fonksiyonlar periyodiktir.

Örnek 1. Bu günahı ispatla X 2 periyodu vardır.

Çözüm: Günahı biliyoruz ( x+ 2N) = günah X, Nerede N= 0, ± 1, ± 2, …

Bu nedenle ekleme 2 N sinüs argümanına değil

Anlamını değiştirir. bunun başka numarası var mı

Aynı mülk mü?

Diyelim ki P- böyle bir sayı, yani eşitlik:

Günah( x+P) = günah X,

Her değer için geçerlidir X. Ama sonra var

Yer ve zaman X= / 2, yani

Günah(/2 + P) = günah / 2 = 1.

Ancak indirgeme formülüne göre günah ( / 2 + P) = çünkü P. Daha sonra

Son iki eşitlikten şu sonuç çıkıyor çünkü P= 1, ancak biz

Bunun ancak şu durumlarda doğru olduğunu biliyoruz: P = 2N. En küçüğünden bu yana

2'den sıfır olmayan bir sayı N 2 ise bu sayı

Ve bir adet günahı var X. Benzer şekilde kanıtlanabilir ki 2 itibaren N yani bu periyot günah 2 X.

Fonksiyon sıfırları. Fonksiyonun 0'a eşit olduğu argüman değeri denir sıfır (kök) işlevi. Bir fonksiyonun birden fazla sıfırı olabilir. Örneğin; sen = X (X + 1) (X-3) üç sıfıra sahiptir: X= 0, X= -1, X= 3. Geometrik olarak boş işlev - bu, fonksiyon grafiğinin eksenle kesişme noktasının apsisidir X .

Şekil 7 sıfırlı bir fonksiyonun grafiğini göstermektedir: X= A, X = B Ve X= C.

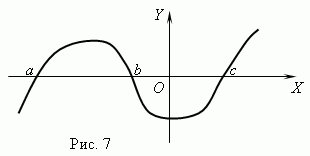
Asimptot. Bir fonksiyonun grafiği orijinden uzaklaşırken belirli bir doğruya süresiz olarak yaklaşıyorsa bu doğruya denir. asimptot.

Gizliliğinizin korunması bizim için önemlidir. Bu nedenle bilgilerinizi nasıl kullandığımızı ve sakladığımızı açıklayan bir Gizlilik Politikası geliştirdik. Lütfen gizlilik uygulamalarımızı inceleyin ve herhangi bir sorunuz varsa bize bildirin.

Kişisel bilgilerin toplanması ve kullanılması

Kişisel bilgiler, belirli bir kişiyi tanımlamak veya onunla iletişim kurmak için kullanılabilecek verileri ifade eder.

Bizimle iletişime geçtiğinizde istediğiniz zaman kişisel bilgilerinizi vermeniz istenebilir.

Aşağıda toplayabileceğimiz kişisel bilgi türlerine ve bu bilgileri nasıl kullanabileceğimize dair bazı örnekler verilmiştir.

Hangi kişisel bilgileri topluyoruz:

• Siteye bir başvuru gönderdiğinizde adınız, telefon numaranız, e-posta adresiniz vb. dahil olmak üzere çeşitli bilgiler toplayabiliriz.

Kişisel bilgilerinizi nasıl kullanıyoruz:

• Topladığımız kişisel bilgiler, benzersiz teklifler, promosyonlar, diğer etkinlikler ve gelecek etkinlikler konusunda sizinle iletişim kurmamıza olanak tanır.
• Zaman zaman kişisel bilgilerinizi önemli bildirimler ve iletişimler göndermek için kullanabiliriz.
• Kişisel bilgileri, sunduğumuz hizmetleri geliştirmek ve size hizmetlerimizle ilgili tavsiyeler sunmak amacıyla denetimler, veri analizi ve çeşitli araştırmalar yapmak gibi şirket içi amaçlarla da kullanabiliriz.
• Bir ödül çekilişine, yarışmaya veya benzer bir promosyona katılırsanız, sağladığınız bilgileri bu tür programları yönetmek için kullanabiliriz.

Bilgilerin üçüncü şahıslara açıklanması

Sizden aldığımız bilgileri üçüncü şahıslara açıklamıyoruz.

İstisnalar:

• Gerekirse - yasaya, adli prosedüre uygun olarak, yasal işlemlerde ve/veya kamunun talepleri veya Rusya Federasyonu'ndaki devlet kurumlarının talepleri temelinde - kişisel bilgilerinizi ifşa etmek. Ayrıca, bu tür bir açıklamanın güvenlik, kanun yaptırımı veya diğer kamu önemi amaçları açısından gerekli veya uygun olduğunu tespit etmemiz halinde, hakkınızdaki bilgileri de açıklayabiliriz.
• Yeniden yapılanma, birleşme veya satış durumunda topladığımız kişisel bilgileri ilgili halef üçüncü tarafa aktarabiliriz.

Kişisel bilgilerin korunması

Kişisel bilgilerinizi kayıp, hırsızlık ve kötüye kullanımın yanı sıra yetkisiz erişime, ifşa edilmeye, değiştirilmeye ve imhaya karşı korumak için idari, teknik ve fiziksel önlemler alıyoruz.

Şirket düzeyinde gizliliğinize saygı duymak

Kişisel bilgilerinizin güvende olduğundan emin olmak için gizlilik ve güvenlik standartlarını çalışanlarımıza aktarıyor ve gizlilik uygulamalarını sıkı bir şekilde uyguluyoruz.

Bu öğretim materyali yalnızca referans amaçlıdır ve çok çeşitli konularla ilgilidir. Makale, temel temel fonksiyonların grafiklerine genel bir bakış sağlar ve en önemli konuyu ele alır: bir grafiğin doğru ve HIZLI bir şekilde nasıl oluşturulacağı. Temel temel fonksiyonların grafikleri hakkında bilgi sahibi olmadan yüksek matematik çalışması sırasında zor olacaktır, bu nedenle parabol, hiperbol, sinüs, kosinüs vb. grafiklerinin neye benzediğini hatırlamak ve bazılarını hatırlamak çok önemlidir. fonksiyonların anlamları. Ayrıca ana fonksiyonların bazı özelliklerinden de bahsedeceğiz.

Materyallerin eksiksizliği ve bilimsel bütünlüğü iddiasında değilim; her şeyden önce uygulamaya - hangi şeylere - ağırlık verilecektir. Yüksek matematiğin herhangi bir konusunda kelimenin tam anlamıyla her adımda karşılaşılır. Aptallar için çizelgeler mi? Öyle söylenebilir.

Okuyuculardan gelen çok sayıda istek nedeniyle tıklanabilir içindekiler tablosu:

Ayrıca konuyla ilgili çok kısa bir özet var
– ALTI sayfayı inceleyerek 16 tür grafikte ustalaşın!

Cidden altı, ben bile şaşırdım. Bu özet geliştirilmiş grafikler içerir ve cüzi bir ücret karşılığında mevcuttur; demo sürümü görüntülenebilir. Grafiklerin her zaman elinizin altında olması için dosyayı yazdırmak uygundur. Projeyi desteklediğiniz için teşekkür ederiz!

Ve hemen başlayalım:

Koordinat eksenleri doğru şekilde nasıl oluşturulur?

Uygulamada testler neredeyse her zaman öğrenciler tarafından kare şeklinde dizilmiş ayrı defterlerde tamamlanır. Neden damalı işaretlere ihtiyacınız var? Sonuçta, çalışma prensip olarak A4 sayfalarda yapılabilir. Ve kafes sadece çizimlerin yüksek kaliteli ve doğru tasarımı için gereklidir.

Bir fonksiyon grafiğinin herhangi bir çizimi koordinat eksenleriyle başlar.

Çizimler iki boyutlu veya üç boyutlu olabilir.

İlk önce iki boyutlu durumu ele alalım Kartezyen dikdörtgen koordinat sistemi:

1) Koordinat eksenlerini çizin. Eksen denir x ekseni ve eksen y ekseni . Her zaman onları çizmeye çalışıyoruz düzgün ve çarpık değil. Okların da Papa Carlo'nun sakalına benzememesi gerekiyor.

2) Eksenleri büyük harflerle “X” ve “Y” ile imzalıyoruz. Eksenleri etiketlemeyi unutmayın.

3) Ölçeği eksenler boyunca ayarlayın: bir sıfır ve iki bir çiz. Çizim yaparken en kullanışlı ve en sık kullanılan ölçek şudur: 1 birim = 2 hücre (soldaki çizim) - mümkünse ona sadık kalın. Ancak zaman zaman çizimin defter sayfasına sığmadığı durumlar olur - o zaman ölçeği azaltırız: 1 birim = 1 hücre (sağdaki çizim). Nadiren de olsa çizimin ölçeğinin daha da küçültülmesi (veya arttırılması) gerekebilir.

“Makineli tüfeğe” GEREK YOKTUR…-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Koordinat düzlemi Descartes için bir anıt olmadığı gibi, öğrenci de bir güvercin değildir. biz koyduk sıfır Ve eksenler boyunca iki birim. Bazen yerine birimler, diğer değerleri "işaretlemek" uygundur, örneğin apsis ekseninde "iki" ve ordinat ekseninde "üç" - ve bu sistem (0, 2 ve 3) aynı zamanda koordinat ızgarasını benzersiz bir şekilde tanımlayacaktır.

Çizimi oluşturmadan ÖNCE çizimin tahmini boyutlarını tahmin etmek daha iyidir. Yani, örneğin, eğer görev köşeleri olan bir üçgen çizmeyi gerektiriyorsa , , , o zaman popüler 1 birim = 2 hücre ölçeğinin işe yaramayacağı tamamen açıktır. Neden? Gelin şu noktaya bakalım - burada on beş santimetre aşağıyı ölçmeniz gerekecek ve açıkçası çizim bir defter sayfasına sığmayacak (veya zar zor sığacak). Bu nedenle hemen daha küçük bir ölçek seçiyoruz: 1 birim = 1 hücre.

Bu arada, yaklaşık santimetre ve dizüstü bilgisayar hücreleri. 30 defter hücresinin 15 santimetre içerdiği doğru mu? Eğlenmek için not defterinizde 15 santimetreyi bir cetvelle ölçün. SSCB'de bu doğru olabilir... Aynı santimetreyi yatay ve dikey olarak ölçerseniz sonuçların (hücrelerdeki) farklı olacağını belirtmek ilginçtir! Açıkçası, modern defterler kareli değil dikdörtgen şeklindedir. Bu saçma görünebilir, ancak bu gibi durumlarda örneğin pusula ile bir daire çizmek çok sakıncalıdır. Dürüst olmak gerekirse, böyle anlarda yerli otomobil endüstrisi, düşen uçaklar veya patlayan enerji santralleri bir yana, üretimde hack çalışmaları için kamplara gönderilen Stalin Yoldaş'ın doğruluğunu düşünmeye başlıyorsunuz.

Kaliteden bahsetmişken ya da kırtasiye konusunda kısa bir tavsiye. Bugün satışta olan dizüstü bilgisayarların çoğu, en azından tam bir saçmalık. Sadece jel kalemlerden değil, tükenmez kalemlerden de ıslanmaları nedeniyle! Kağıt üzerinde tasarruf ediyorlar. Testleri tamamlamak için, daha pahalı olmasına rağmen Arkhangelsk Kağıt Hamuru ve Kağıt Fabrikası'ndan (18 sayfa, kare) veya "Pyaterochka" defterlerini kullanmanızı öneririm. Bir jel kalem seçmeniz önerilir; en ucuz Çin jel dolumu bile, kağıdı lekeleyen veya yırtan tükenmez kalemden çok daha iyidir. Hatırlayabildiğim tek "rekabetçi" tükenmez kalem Erich Krause'dur. İster dolu ister neredeyse boş olsun, net, güzel ve tutarlı bir şekilde yazıyor.

Ek olarak: Makalede analitik geometri gözüyle dikdörtgen koordinat sisteminin görünümü ele alınmaktadır. Vektörlerin doğrusal (bağımsız) bağımlılığı. Vektörlerin temeli, koordinat çeyrekleri hakkında detaylı bilgiyi dersin ikinci paragrafında bulabilirsiniz. Doğrusal eşitsizlikler.

3D kasa

Burada da hemen hemen aynı.

1) Koordinat eksenlerini çizin. Standart: eksen uygulaması – yukarıya doğru, eksen – sağa doğru, eksen – aşağıya sola doğru kesinlikle 45 derecelik bir açıyla.

2) Eksenleri etiketleyin.

3) Ölçeği eksenler boyunca ayarlayın. Eksen boyunca ölçek, diğer eksenler boyunca olan ölçekten iki kat daha küçüktür. Ayrıca sağdaki çizimde eksen boyunca standart olmayan bir "çentik" kullandığımı da unutmayın. (bu olasılık yukarıda zaten belirtilmiştir). Benim açımdan bu daha doğru, daha hızlı ve estetik açıdan daha hoş - mikroskop altında hücrenin ortasını aramaya ve koordinatların kökenine yakın bir birimi "şekillendirmeye" gerek yok.

3 boyutlu çizim yaparken yine ölçeğe öncelik verin
1 birim = 2 hücre (soldaki çizim).

Bütün bu kurallar ne için? Kurallar çiğnenmek içindir. Şimdi yapacağım şey bu. Gerçek şu ki, makalenin sonraki çizimleri benim tarafımdan Excel'de yapılacak ve koordinat eksenleri, doğru tasarım açısından yanlış görünecektir. Tüm grafikleri elle çizebilirim, ancak Excel bunları daha doğru çizme konusunda isteksiz olduğundan bunları çizmek aslında korkutucu.

Temel fonksiyonların grafikleri ve temel özellikleri

Denklemde doğrusal bir fonksiyon verilmektedir. Doğrusal fonksiyonların grafiği doğrudan. Düz bir çizgi çizebilmek için iki noktayı bilmek yeterlidir.

Örnek 1

Fonksiyonun grafiğini oluşturun. İki nokta bulalım. Noktalardan biri olarak sıfırı seçmek avantajlıdır.

Eğer öyleyse

Başka bir noktayı ele alalım, örneğin 1.

Eğer öyleyse

Görevleri tamamlarken noktaların koordinatları genellikle bir tabloda özetlenir:

Ve değerlerin kendisi sözlü olarak veya bir taslakta, bir hesap makinesinde hesaplanır.

İki nokta bulundu, çizimi yapalım:

Çizim hazırlarken mutlaka grafikleri imzalarız.

Doğrusal bir fonksiyonun özel durumlarını hatırlamak faydalı olacaktır:

İmzaları nasıl attığıma dikkat edin. imzalar çizimi incelerken tutarsızlıklara izin vermemelidir. Bu durumda, çizgilerin kesişme noktasının yanına veya grafiklerin sağ alt kısmına imza koymak son derece istenmeyen bir durumdu.

1) () formunun doğrusal bir fonksiyonuna doğru orantılılık denir. Örneğin, . Doğru orantılılık grafiği her zaman orijinden geçer. Böylece düz bir çizgi oluşturmak basitleştirilmiştir - yalnızca bir noktayı bulmak yeterlidir.

2) Formun bir denklemi eksene paralel bir düz çizgiyi belirtir, özellikle eksenin kendisi denklem tarafından verilir. Fonksiyonun grafiği herhangi bir nokta bulunmadan hemen çizilir. Yani giriş şu şekilde anlaşılmalıdır: "x'in herhangi bir değeri için y her zaman -4'e eşittir."

3) Formun bir denklemi eksene paralel bir düz çizgiyi belirtir, özellikle eksenin kendisi denklem tarafından verilir. Fonksiyonun grafiği de hemen çizilir. Giriş şu şekilde anlaşılmalıdır: "x, y'nin herhangi bir değeri için her zaman 1'e eşittir."

Bazıları soracak, neden 6. sınıfı hatırladınız?! Bu böyledir, belki de öyledir, ancak yıllar süren pratikte veya gibi bir grafik oluşturma görevi karşısında şaşkına dönen bir düzine öğrenciyle tanıştım.

Düz bir çizgi oluşturmak, çizim yaparken en yaygın eylemdir.

Düz çizgi analitik geometri dersinde ayrıntılı olarak tartışılmaktadır ve ilgilenenler bu makaleye başvurabilirler. Düzlemde düz bir çizginin denklemi.

İkinci dereceden, kübik bir fonksiyonun grafiği, bir polinomun grafiği

Parabol. İkinci dereceden bir fonksiyonun grafiği () bir parabolü temsil eder. Ünlü vakayı düşünün:

Fonksiyonun bazı özelliklerini hatırlayalım.

Yani denklemimizin çözümü: – parabolün tepe noktası bu noktadadır. Bunun neden böyle olduğunu türev hakkındaki teorik makaleden ve fonksiyonun ekstremumlarına ilişkin dersten öğrenebilirsiniz. Bu arada karşılık gelen “Y” değerini de hesaplayalım:

Böylece tepe noktası bu noktadadır

Şimdi parabolün simetrisini küstahça kullanarak başka noktalar buluyoruz. Şunu belirtmek gerekir ki, fonksiyon – bile değil ancak yine de hiç kimse parabolün simetrisini iptal etmedi.

Kalan puanların hangi sırayla bulunacağı final masasından anlaşılacaktır diye düşünüyorum:

Bu inşaat algoritması mecazi olarak Anfisa Chekhova ile "mekik" veya "ileri geri" ilkesi olarak adlandırılabilir.

Çizimi yapalım:

İncelenen grafiklerden bir başka faydalı özellik akla geliyor:

İkinci dereceden bir fonksiyon için () aşağıdakiler doğrudur:

Eğer öyleyse parabolün dalları yukarı doğru yönlendirilir.

Eğer öyleyse parabolün dalları aşağıya doğru yönlendirilir.

Eğri hakkında derinlemesine bilgi Hiperbol ve parabol dersinde elde edilebilir.

Fonksiyon tarafından kübik bir parabol verilmektedir. İşte okuldan tanıdık bir çizim:

Fonksiyonun ana özelliklerini listeleyelim

Bir fonksiyonun grafiği

Bir parabolün dallarından birini temsil eder. Çizimi yapalım:

Fonksiyonun ana özellikleri:

Bu durumda eksen dikey asimptot 'deki bir hiperbolün grafiği için.

Bir çizimi çizerken dikkatsizce grafiğin bir asimptotla kesişmesine izin verirseniz, bu BÜYÜK bir hata olur.

Ayrıca tek taraflı limitler bize hiperbolün yukarıdan sınırlı değil Ve aşağıdan sınırlı değil.

Fonksiyonu sonsuzda inceleyelim: yani eksen boyunca sola (veya sağa) sonsuza doğru hareket etmeye başlarsak, o zaman “oyunlar” düzenli bir adım olacaktır. sonsuz yakın sıfıra yaklaşır ve buna göre hiperbolün dalları sonsuz yakın eksene yaklaşın.

Yani eksen yatay asimptot Bir fonksiyonun grafiği için, eğer “x” artı veya eksi sonsuza eğilimliyse.

İşlev garip ve bu nedenle hiperbol orijine göre simetriktir. Bu gerçek çizimde açıkça görülmektedir, ayrıca analitik olarak da kolayca doğrulanabilir: .

() formundaki bir fonksiyonun grafiği, bir hiperbolün iki dalını temsil eder.

Eğer ise hiperbol birinci ve üçüncü koordinat çeyreğinde bulunur(yukarıdaki resme bakın).

Eğer ise hiperbol ikinci ve dördüncü koordinat çeyreğinde bulunur.

Belirtilen hiperbol yerleşim modelinin grafiklerin geometrik dönüşümleri açısından analiz edilmesi kolaydır.

Örnek 3

Hiperbolün sağ dalını oluşturun

Noktasal inşa yöntemini kullanıyoruz ve değerleri bir bütüne bölünebilecek şekilde seçmek avantajlıdır:

Çizimi yapalım:

Hiperbolün sol dalını oluşturmak zor olmayacak; fonksiyonun tuhaflığı burada yardımcı olacaktır. Kabaca söylemek gerekirse, nokta nokta yapım tablosunda her sayıya zihinsel olarak bir eksi ekliyoruz, karşılık gelen noktaları koyuyoruz ve ikinci dalı çiziyoruz.

Dikkate alınan çizgi hakkında ayrıntılı geometrik bilgi Hiperbol ve parabol makalesinde bulunabilir.

Üstel Fonksiyonun Grafiği

Bu bölümde hemen üstel fonksiyonu ele alacağım çünkü yüksek matematik problemlerinde vakaların %95'inde üstel ortaya çıkıyor.

Bunun irrasyonel bir sayı olduğunu hatırlatayım: Aslında törensiz yapacağım bir grafik oluştururken bu gerekecek. Üç nokta muhtemelen yeterlidir:

Şimdilik fonksiyonun grafiğini burada bırakalım, daha sonra buna daha fazla değinelim.

Fonksiyonun ana özellikleri:

Fonksiyon grafikleri vb. temelde aynı görünür.

İkinci durumun pratikte daha az sıklıkta yaşandığını söylemeliyim ama oluyor, bu yüzden bu yazıya dahil etmeyi gerekli gördüm.

Logaritmik bir fonksiyonun grafiği

Doğal logaritmalı bir fonksiyonu düşünün.
Nokta nokta bir çizim yapalım:

Logaritmanın ne olduğunu unuttuysanız lütfen okul ders kitaplarınıza bakın.

Fonksiyonun ana özellikleri:

Tanım alanı:

Değer aralığı: .

İşlev yukarıdan sınırlı değildir: Yavaş da olsa logaritmanın dalı sonsuza kadar gider.
Sağdaki fonksiyonun sıfıra yakın davranışını inceleyelim: . Yani eksen dikey asimptot “x” gibi bir fonksiyonun grafiği sağdan sıfıra doğru yönelir.

Logaritmanın tipik değerini bilmek ve hatırlamak zorunludur: .

Prensip olarak, tabana göre logaritmanın grafiği aynı görünür: , , (10 tabanına göre ondalık logaritma), vb. Üstelik taban ne kadar büyük olursa grafik o kadar düz olur.

Bu durumu dikkate almayacağız; en son ne zaman böyle bir temele dayalı bir grafik oluşturduğumu hatırlamıyorum. Ve logaritma, yüksek matematik problemlerinde çok nadir görülen bir misafir gibi görünüyor.

Bu paragrafın sonunda bir gerçek daha söyleyeceğim: Üstel fonksiyon ve logaritmik fonksiyon– bunlar karşılıklı olarak ters iki fonksiyondur. Logaritmanın grafiğine yakından bakarsanız, bunun aynı üs olduğunu, sadece biraz farklı konumda olduğunu görebilirsiniz.

Trigonometrik fonksiyonların grafikleri

Okulda trigonometrik işkence nerede başlar? Sağ. sinüsten

Fonksiyonun grafiğini çizelim

Bu çizgiye denir sinüzoid.

“Pi”nin irrasyonel bir sayı olduğunu ve trigonometride gözlerinizi kamaştırdığını hatırlatayım.

Fonksiyonun ana özellikleri:

Bu fonksiyon periyodik dönem ile. Bu ne anlama geliyor? Bölüme bakalım. Solunda ve sağında grafiğin tam olarak aynı parçası sonsuza kadar tekrarlanıyor.

Tanım alanı: yani her “x” değeri için bir sinüs değeri vardır.

Değer aralığı: . İşlev sınırlı: yani tüm "oyunlar" kesinlikle segmentte yer alıyor.
Bu olmuyor, daha doğrusu oluyor ama bu denklemlerin çözümü yok.