Wielka encyklopedia ropy i gazu

Odpowiemy ustnie! Czy prawdą jest, że wokół dowolnej piramidy trójkątnej można opisać kulę? Czy można opisać kulę wokół dowolnej czworokątnej piramidy? Jakie właściwości musi mieć piramida, aby opisać otaczającą ją kulę? Piramida jest wpisana w kulę, której boczna krawędź jest prostopadła do podstawy. Jak znaleźć środek kuli? Kula jest opisana w pobliżu regularnej piramidy. Jak położony jest jego środek względem elementów piramidy?

Slajd 17 z prezentacji „Zadania z geometrii” klasa 11. Rozmiar archiwum z prezentacją wynosi 1032 KB.

Geometria 11 klasa

podsumowanie innych prezentacji

„Koncepcja symetrii centralnej” – Mapowanie przestrzeni na samą siebie. Centralna symetria. Figurę nazywa się symetryczną. Centralna symetria to ruch. Ruch przestrzeni. Punkty M i M1 nazywane są symetrycznymi. Nieruchomość. Ruchy. Zapoznaliśmy się z ruchami samolotu. Zadanie. Symetria centralna jest szczególnym przypadkiem rotacji.

„Problemy z obliczaniem pola trójkąta” – Ivan Niven. Rozwiązanie jednego problemu. Motto lekcji. Osobiste cele. Znajdź obszar figury. Dyktando matematyczne. Metody znajdowania pola trójkąta. Wybierz oświadczenie. Minuta wychowania fizycznego. Oblicz pole figury. Obszar figury. Sprawdzanie postępu. Kwadrat.

„Zadania w stereometrii” - Znajdź kwadrat odległości między wierzchołkami. Zadania. Średnica kulki ołowianej. Objętość piłki i jej części. Znajdź kąt wielościanu. Znajdź objętość piramidy. Znajdź współrzędną punktu A. Sektor kołowy. Znajdź objętość V cylindra. Znajdź pole powierzchni wielościanu. Znajdź obszar trapezu. Obwód.

„Oblicz objętość ciała wirującego” - Kula. Cylinder i stożek. Stożek. Cylindry są wszędzie wokół nas. Objętość V stożka. Sześcian Definicja stożek. Rodzaje ciał wirujących. Piłka. Tomy organów obrotowych. Postać. Znajdź głośność. Naczynie cylindryczne. Definicja cylindra. Promienie. Cylinder. Objętość stożka.

„Objętości i powierzchnie ciał obrotowych” – Proponowanie i testowanie hipotez. Podsumuj wiedzę. Objętości i powierzchnie ciał obrotowych. Wskaż kształt geometryczny. Formułowanie problemu. Problem. Przykłady z zajęć praktycznych. Dlaczego zbiornik termometru nagrzewa się szybciej? Czajniczek w kształcie kuli ma najmniejszą powierzchnię. Wolumeny.

„Ciała wirujące wokół nas” - Ciała wirujące wokół nas. Sprzęt przemysłowy. Znajdź ciała obrotowe. Świerk szyszkowy leśny. Krzywa Wieża we Włoszech. W przestrzeni kosmicznej. Dom Mielnikowa. Stożek. Okrągłe wieże. Historia okrągłego budynku. Ciała kosmiczne.

Kombinacje wielościanów i ciał okrągłych

Pojęcia kuli i kuli.

Kula jest figurą składającą się ze zbioru wszystkich punktów w przestrzeni, z których każdy ma odległość do danego punktu O jest równa danej liczbie dodatniej r. Punkt O nazywa się Centrum kula, a odcinek łączący punkt z dowolnym punktem kuli jest jej promień. Wszystkie promienie kuli mają długość r. Liczba r nazywana jest promieniem kuli.

Kula dzieli zbiór wszystkich punktów w przestrzeni, które do niej nie należą, na dwa podzbiory: wewnętrzny I zewnętrzny pole względem kuli. Obszar wewnętrzny obejmuje te punkty w przestrzeni, z których każdy znajduje się w odległości mniejszej niż promień, a obszar zewnętrzny obejmuje te punkty, których odległość do środka jest większa niż promień.

Piłka jest figurą składającą się ze zbioru wszystkich punktów w przestrzeni, z których każdy odległość do danego punktu O nie jest większa niż dana liczba dodatnia r. Punkt O nazywa się Centrum kula, a liczba r jest jej promień. Nazywa się kulę o środku O i promieniu r powierzchnia lub granicę piłki. Wszystkie punkty piłki, które nie należą do jej powierzchni, nazywane są punktami wewnętrznymi piłki lub punktami leżącymi wewnątrz piłki. Zatem kula jest figurą składającą się z sumy wszystkich punktów kuli (powierzchni kuli) oraz zbioru wszystkich punktów wewnętrznych względem tej kuli.

Nazywa się płaszczyznę styczną do powierzchni kuli płaszczyzna styczna na piłkę. Płaszczyzna jest styczna do piłki wtedy i tylko wtedy, gdy przechodzi przez punkt na powierzchni kuli prostopadły do promienia poprowadzonego do tego punktu. Należy także zauważyć, że przez każdy punkt na powierzchni kuli przechodzi jedna i tylko jedna płaszczyzna styczna do piłki.

Kula opisana na wielościanie.

Definicja. Kula nazywa się opisane wokół wielościanu, jeśli wszystkie wierzchołki wielościanu leżą na kuli.

Twierdzenie 1.Kulę można opisać wokół dowolnej trójkątnej piramidy.

Zbiór punktów w jednakowej odległości od wierzchołków podstawy ostrosłupa to prostopadła poprowadzona ze środka opisanego okręgu w pobliżu podstawy (GMT w przestrzeni równoodległej od wierzchołków danego wielokąta istnieje, jeśli można opisać okrąg wokół tego wielokąta i istnieje prostopadła poprowadzona do płaszczyzny tego wielokąta przez środek opisanego okręgu). Środek okręgu opisanego jest punktem przecięcia dwusiecznych podstawy ostrosłupa.

Aby znaleźć środek opisanej kuli, narysuj płaszczyznę przechodzącą przez punkt M - środek bocznej krawędzi AD. Płaszczyzna ta przecina wskazaną wcześniej prostopadłą w punkcie S. Z konstrukcji SA=SB=SC, a także z faktu, że trójkąt ASD jest równoramienny (również konstrukcyjnie) wynika, że SA=SD. Zatem odległości od wszystkich wierzchołków piramidy do punktu S są równe i odległość ta jest równa promieniowi kuli opisanej w pobliżu piramidy ABCD (SA=SB=SC=SD=R).

Przykład 1 . Znajdź promień kuli opisanej na czworościanie foremnym.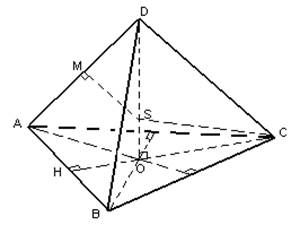

Rozważmy trójkąt SOC. Będzie prostokątny z kątem prostym O (z konstrukcji OD będzie wysokością piramidy).

, ponieważ O jest punktem przecięcia środkowych.

, gdzie DO jest wysokością piramidy.

Zatem z twierdzenia Pitagorasa wynika, że Lub

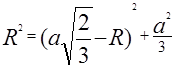
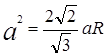
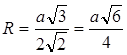
Odpowiedź: Promień kuli opisanej na czworościanie foremnym jest równy

Twierdzenie 2. Jeśli wokół podstawy piramidy można opisać okrąg, to wokół piramidy można opisać kulę.

Rozważaliśmy już szczególny przypadek. W ogólnym przypadku dowód jest podobny.

Twierdzenie 3 . Nie da się opisać kuli w pobliżu nachylonego pryzmatu; w pobliżu prostego pryzmatu można opisać kulę, jeśli w pobliżu podstawy pryzmatu można opisać okrąg.

1) Rozważmy najpierw przypadek, gdy pryzmat jest nachylony (weźmy jako przykład pryzmat trójkątny). Punkt w jednakowej odległości od punktów A, B i C będzie leżał na prostej OS 1, która jest prostopadła do płaszczyzny trójkąta ABC, a podstawa tej prostopadłej znajduje się w punkcie przecięcia dwusiecznych prostopadłych poprowadzonych do boków trójkąta ABC .

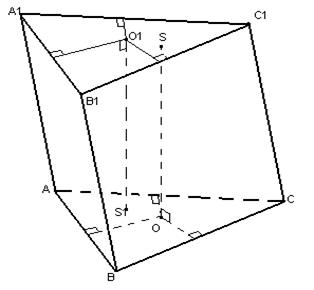
Podobnie punkty w jednakowej odległości od punktów A 1, B 1, C 1 leżą prostopadle do płaszczyzny trójkąta A 1 B 1 C 1 – O 1 S. Ponieważ pryzmat jest nachylony, linie OS 1 i O 1 S będą być równoległe, ale nie pasujące. A to oznacza, że nie będą miały punktów wspólnych, zatem: nie ma takiego punktu, aby odległość do wszystkich wierzchołków pryzmatu była taka sama, co jest podobne do niemożności zbudowania kuli opisanej wokół nachylonego pryzmatu.

2) Rozważmy prosty pryzmat, w pobliżu którego podstawy można opisać okrąg. Punkty O i O 1 są środkami opisanych okręgów odpowiednio w pobliżu dolnej i górnej podstawy. Ponieważ pryzmat jest prosty, linia prosta OO 1 będzie prostopadła do płaszczyzn podstawy.

Następnie płaszczyzna przechodząca przez środek bocznych żeber będzie równoległa do płaszczyzny podstawy i przetnie OO 1 w punkcie S - środek OO 1. Wtedy odległość wszystkich wierzchołków pryzmatu do taczki S będzie taka sama (konstrukcyjnie), zatem S jest środkiem kuli opisanej wokół graniastosłupa foremnego.

Jesteśmy więc przekonani, że nie da się opisać kuli w pobliżu nachylonego pryzmatu, ale w pobliżu prostego pryzmatu jest to możliwe, jeśli można opisać okrąg w pobliżu jego podstawy.

Twierdzenie 4. Kulę można opisać wokół ostrosłupa ściętego wtedy i tylko wtedy, gdy wokół jej podstaw można opisać okręgi, a linia prosta łącząca środki tych okręgów jest prostopadła do płaszczyzn podstaw.

Pierwszy warunek oznacza, że będą istniały prostopadłe, czyli HMT, podstaw w jednakowej odległości od wierzchołków wielokątów, a drugi, że będą one zbieżne, zatem powstanie punkt, który będzie jednakowo oddalony od wszystkich wierzchołków wielokąta ścięta piramida.

XV MIASTA OTWARTA KONFERENCJA STUDENTÓW

„INTELEKTUALNI XXI WIEKU”

Sekcja: MATEMATYKA

Opisany obszar na olimpiadach i jednolitym egzaminie państwowym

Kiyaeva Anna Anatolevna

Orenburg – 2008

1.2 Opisany zakres

1.2.1 Podstawowe właściwości i definicje

1.2.2 Kombinacja piramidy

1.2.3 Połączenie z pryzmatem

1.2.4 Połączenie z butlą

1.2.5 Połączenie ze stożkiem

2 Przykłady zadań olimpijskich

2.1 Przykłady zadań olimpijskich z piramidą

2.2 Przykłady zadań olimpijskich z pryzmatem

2.3 Przykłady zadań olimpijskich z cylindrem

2.4 Przykłady zadań olimpijskich ze stożkiem

3.3 Przykłady zadań egzaminu Unified State Exam z cylindrem

3.4 Przykłady zadań egzaminu Unified State Exam ze stożkiem

Wstęp

Praca ta jest realizowana w ramach projektu utworzenia strony matematycznej dla uczniów na stronie internetowej internatu i zostanie zamieszczona w dziale „Metody matematyczne”.

Cel praca - stworzenie podręcznika poświęconego metodzie rozwiązywania problemów geometrycznych z opisaną kulą na olimpiadach i egzaminie jednolitym.

Aby osiągnąć ten cel, musieliśmy rozwiązać następujące problemy zadania :

1) zapoznać się z koncepcją opisywanej sfery;

2) zbadać cechy kombinacji opisywanej kuli z piramidą, pryzmatem, cylindrem i stożkiem;

3) spośród problemów geometrycznych wybrać te, które zawierają warunek istnienia opisanej kuli;

4) analizować, systematyzować i klasyfikować zebrany materiał;

5) dokonać wyboru problemów do samodzielnego rozwiązania;

6) przedstawić wyniki badań w formie streszczenia.

Praktyczne znaczenie– przygotowane przez nas materiały można wykorzystać w przygotowaniu uczniów do olimpiad, jednolitego egzaminu państwowego i późniejszych studiów na uczelni.

1 Kula i piłka

1.1 Kula i kula: podstawowe pojęcia i definicje

Kula to powierzchnia składająca się ze wszystkich punktów w przestrzeni znajdujących się w danej odległości od danego punktu.

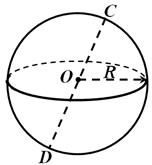
Ten punkt nazywa się środek kuli(kropka O na ryc. 1) i tę odległość promień kuli. Dowolny odcinek łączący środek i dowolny punkt kuli nazywany jest także promieniem kuli. Odcinek łączący dwa punkty kuli i przechodzący przez jej środek nazywa się średnica kuli(odcinek DC na ryc. 1). Należy pamiętać, że kulę można uzyskać, obracając półkole wokół jej średnicy.

Piłka nazywa się ciałem ograniczonym kulą. Nazywa się także środkiem, promieniem i średnicą kuli Centrum , promień I średnica kuli. Oczywiście kula o promieniu R wyśrodkowany przy O zawiera wszystkie punkty w przestrzeni, które znajdują się od punktu O w odległości nie przekraczającej R(w tym pkt O) i nie zawiera innych punktów. Piłka zwana także figurą obrotu półkola wokół jego średnicy. Odcinek kulkowy- część piłki odcięta od niej przez jakiś samolot. Każdy przekrój kuli przez płaszczyznę jest okręgiem. Środek tego okręgu jest podstawą prostopadłej poprowadzonej ze środka kuli na płaszczyznę cięcia. Nazywa się płaszczyznę przechodzącą przez środek kuli płaszczyzna średnicowa. Nazywa się przekrój kuli przez płaszczyznę średnicy duże koło, a przekrój kuli wynosi duże koło. Sektor piłek – bryła geometryczna uzyskana poprzez obrót wycinka kołowego o kąt mniejszy niż 90° wokół linii prostej zawierającej jeden z promieni ograniczających wycinek kołowy. Sektor kulisty składa się z odcinka kuli i stożka o wspólnej podstawie.

Pole powierzchni kuli:

S = 4π R 2 ,

Gdzie R– promień kuli, S- powierzchnia kuli.

Objętość kuli

Gdzie V– objętość piłki

Objętość sektora piłki

V – objętość odcinka kuli.

Powierzchnia segmentowa

- wysokość segmentu, powierzchnia segmentu

Promień podstawy segmentu

, - promień podstawy segmentu, - wysokość segmentu, 0<H < 2R .

Sferyczna powierzchnia segmentu kuli

- obszar powierzchni sferycznej segmentu kulistego.

W przestrzeni dla kuli i samolotu możliwe są trzy przypadki:

1) Jeżeli odległość środka kuli od płaszczyzny jest większa niż promień kuli, to kula i płaszczyzna nie mają wspólnych punktów.

2) Jeżeli odległość środka kuli od płaszczyzny jest równa promieniowi kuli, to płaszczyzna ma tylko jeden punkt wspólny z piłką i ograniczającą ją kulą.

3) Jeżeli odległość środka kuli od płaszczyzny jest mniejsza niż promień kuli, to przecięcie kuli z płaszczyzną jest okręgiem. Środek tego okręgu jest rzutem środka kuli na daną płaszczyznę. Przecięcie płaszczyzny z kulą jest obwodem określonego okręgu.

1.2 Opisana kula

1.2.1 Definicje i właściwości

Kula nazywa się opisane wokół wielościanu(a wielościan jest zawarte w kuli), jeśli wszystkie wierzchołki wielościanu leżą na kuli.

Z definicji opisywanej sfery wynikają dwa fakty:

1) wszystkie wierzchołki wielościanu wpisanego w kulę są w jednakowej odległości od pewnego punktu (od środka opisanej kuli);

2) każda ściana wielościanu wpisanego w kulę jest wielokątem wpisanym w pewien okrąg, właśnie w okrąg, który w przekroju kuli uzyskuje się przez płaszczyznę ściany; w tym przypadku podstawą prostopadłych obniżonych ze środka opisanej kuli na płaszczyźnie ścian są środki okręgów opisanych na ścianach.

Twierdzenie 1 . Kulę można opisać wokół wielościanu wtedy i tylko wtedy, gdy spełniony jest którykolwiek z poniższych warunków:

a) wokół dowolnej ściany wielościanu można opisać okrąg, a osie okręgów opisanych wokół ścian wielościanu przecinają się w jednym punkcie;

b) płaszczyzny prostopadłe do krawędzi wielościanu i przechodzące przez ich środki przecinają się w jednym punkcie;

c) istnieje jeden punkt w jednakowej odległości od wszystkich wierzchołków wielościanu.

Dowód.

Konieczność. Opiszmy kulę wokół wielościanu. Udowodnimy, że warunek a) jest spełniony. Rzeczywiście, skoro płaszczyzna danej ściany wielościanu przecina kulę po okręgu, to wierzchołki ściany należącej do kuli i płaszczyzna ściany należą do linii ich przecięcia - koła. Ponieważ środek kuli jest w równej odległości od wszystkich wierzchołków danej ściany, leży ona na prostopadłej do tej ściany poprowadzonej przez środek okręgu opisanego na tej ścianie.

Adekwatność. Niech warunek a) będzie spełniony. Udowodnimy, że wokół wielościanu można opisać kulę. W rzeczywistości, ponieważ wspólny punkt prostopadłych ścian poprowadzonych przez środki okręgów opisanych na ścianach jest w równej odległości od wszystkich wierzchołków wielościanu, wokół wielościanu opisano kulę ze środkiem w tym punkcie.

Warunek a) w tym przypadku jest równoważny warunkom b) ic).

Jeżeli kulę opisano na wielościanie, to: a) podstawa prostopadłej rzuconej ze środka kuli na dowolną ścianę jest środkiem okręgu opisanego na tej ścianie (podobnie jak podstawa wysokości piramidy o równych krawędzie boczne – promienie kuli poprowadzone od jej środka do wierzchołków danej ściany); b) środek kuli opisanej na wielościanie może znajdować się wewnątrz wielościanu, na jego powierzchni (w środku okręgu opisanego na ścianie, w szczególności pośrodku jakiejś krawędzi), na zewnątrz wielościanu.

1.2.2 Opisana kula i piramida

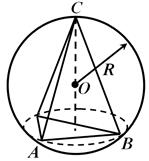
Twierdzenie 2 . Kulę można opisać wokół piramidy wtedy i tylko wtedy, gdy można opisać okrąg wokół jej podstawy.

Dowód. Niech zostanie opisany okrąg wokół podstawy piramidy. Wtedy ten okrąg i punkt poza płaszczyzną tego okręgu – wierzchołek piramidy – definiują pojedynczą kulę, która będzie opisana wokół piramidy. I z powrotem. Jeżeli wokół piramidy opisano kulę, to przekrój kuli przez płaszczyznę podstawy piramidy jest okręgiem opisanym na podstawie.

Wniosek 1. Kulę można opisać wokół dowolnego czworościanu.

Konsekwencja 2. Wokół każdej regularnej piramidy można opisać kulę, której środek leży na wysokości piramidy lub na jej przedłużeniu.

Środek kuli opisanej w pobliżu piramidy może być:

· wierzchołkiem piramidy po jednej stronie płaszczyzny jej podstawy – wewnątrz piramidy, w płaszczyźnie ściany bocznej (w środku okręgu opisanego wokół tej ściany), na zewnątrz piramidy;

· w płaszczyźnie podstawy – w środku okręgu opisanego w pobliżu podstawy;

· ze szczytem piramidy po przeciwnych stronach płaszczyzny jej podstawy.

Twierdzenie 3 . Jeśli boczne krawędzie piramidy są równo nachylone do płaszczyzny jej podstawy, wówczas wokół piramidy można opisać kulę.

Dowód. Ponieważ boczne krawędzie są równo nachylone do płaszczyzny podstawy piramidy, można opisać okrąg w pobliżu podstawy piramidy, a następnie w pobliżu piramidy można opisać kulę.

Twierdzenie to można sformułować inaczej: jeśli piramida ma równe krawędzie boczne, to wokół piramidy można opisać kulę.

Twierdzenie odwrotne nie prawda

Twierdzenie 4. Jeżeli kulę opisujemy w pobliżu piramidy, to jej środkiem jest punkt przecięcia wszystkich płaszczyzn pociągniętych przez środki krawędzi piramidy prostopadłe do tych krawędzi.

Dowód. W rzeczywistości każdy punkt w równej odległości od dwóch wierzchołków piramidy przylegających do jednej krawędzi leży w płaszczyźnie poprowadzonej prostopadle do tej krawędzi piramidy przez jej środek. Zatem środek opisanej kuli, znajdujący się w równej odległości od wszystkich wierzchołków piramidy, musi znajdować się w każdej z takich płaszczyzn, tj. jest to punkt przecięcia wszystkich tych płaszczyzn. Podczas rysowania uczniowie często umieszczają środek opisywanej kuli losowo, nie wyobrażając sobie dostatecznie zadanej konfiguracji przestrzennej, a zwłaszcza nie przeprowadzając żadnego rozumowania na temat położenia tego środka. W tym przypadku z reguły środek umieszcza się wewnątrz piramidy. Tymczasem środek opisywanej kuli może leżeć wewnątrz, na zewnątrz lub na powierzchni piramidy (w zależności od konkretnego typu piramidy).

Twierdzenie 5 . Kulę można opisać wokół ściętej piramidy wtedy i tylko wtedy, gdy spełniony jest którykolwiek z poniższych warunków:

A) w pobliżu podstaw piramidy opisano koła, których linia środków jest prostopadła do ich płaszczyzn;

B) wszystkie boczne krawędzie piramidy są jednakowo nachylone do płaszczyzny jednej z podstaw;

C) wszystkie boczne krawędzie piramidy są sobie równe;

D) wszystkie boczne ściany piramidy są trapezami równobocznymi.

Dowód. Załóżmy, że w pobliżu podstaw danej ściętej piramidy można opisać okręgi, a płaszczyzny tych okręgów są prostopadłe do linii ich środków. Wtedy, jak wiadomo, takie dwa okręgi wyznaczają jedną kulę, która będzie opisana wokół tej piramidy.

Załóżmy przeciwnie, że wokół danej ściętej piramidy opisano kulę. Wtedy przekroje kuli przy płaszczyznach podstaw piramidy będą okręgami opisanymi wokół podstaw. Dalej. Linia prosta prostopadła do płaszczyzn podstaw piramidy i przechodząca przez środek kuli przejdzie przez środki okręgów opisanych wokół podstaw.

Stan A) jest równoważne warunkom B), C), D).

Konsekwencja. Kulę można opisać wokół dowolnej regularnej ściętej piramidy.

1.2.3 Opisana kula i pryzmat

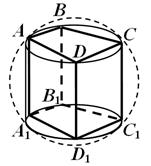
Twierdzenie 6. Kulę można opisać wokół pryzmatu wtedy i tylko wtedy, gdy pryzmat jest prosty, a wokół jego podstawy można opisać okrąg.

Dowód.

Konieczność. Jeśli w kulę wpisano pryzmat, to każdą z jego ścian wpisano w okrąg - wycinek kuli przez płaszczyznę tej ściany. Oznacza to, że w pobliżu podstawy pryzmatu można opisać okrąg, a wszystkie boczne ściany pryzmatu są jak równoległoboki wpisane w okręgi - prostokąty i dlatego pryzmat jest prosty.

Adekwatność. Niech pryzmat będzie prosty i okrąg opisany wokół jego podstawy. Następnie okręgi opisane wokół podstaw graniastosłupa, których płaszczyzny są prostopadłe do linii ich środków, wyznaczają pojedynczą kulę, która będzie opisana wokół pryzmatu.

Konsekwencje:

a) kulę można opisać wokół dowolnego graniastosłupa foremnego;

b) kulę można opisać wokół dowolnego prostopadłościanu trójkątnego;

c) kulę można opisać wokół dowolnego prostokątnego równoległościanu;

Środek kuli opisanej na pryzmacie jest w jednakowej odległości od płaszczyzn podstaw graniastosłupa i może znajdować się wewnątrz pryzmatu, na jego bocznej ścianie (w środku okręgu opisanego na ścianie), na zewnątrz pryzmatu.

1.2.4 Opisana kula i walec

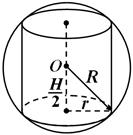
Kula nazywa się opisane na temat cylindra, jeśli leżą na nim koła podstaw walca (ryc. 4). Zawsze możesz opisać kulę wokół cylindra.

1.2.5 Opisana kula i stożek

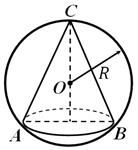
Kula nazywa się opisane wokół stożka, jeżeli leży na nim wierzchołek i okrąg podstawy stożka (ryc. 5). Zawsze można opisać kulę wokół stożka; jego promień jest równy promieniowi okręgu opisanego wokół osiowego przekroju stożka. Nazywa się stożek ścięty wpisany w kulę, jeśli jej podstawy stanowią wycinki powierzchni kuli.

2 Przykłady zadań olimpijskich

2.1 Przykłady zadań olimpijskich z piramidą

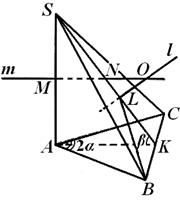
Przykład 1. W trójkątnej piramidzie S Krawędź ABC BC jest równa krawędzi a, AB=AC S I prostopadle do podstawy piramidy ABC, kąt dwuścienny na krawędzi S A jest równe 2α , i na krawędzi BC jest równe β (ryc. 6) . Znajdź promień opisanej kuli.

Rozwiązanie. Rozważmy piramidę S ABC, co jest omówione w opisie problemu. Od krawędzi SA prostopadle do płaszczyzny podstawy, zatem

VA S = CAS= 90°, a zatem i kąt TY jest dokładnie kątem liniowym kąta dwuściennego na krawędzi SA. Zatem u podstawy piramidy leży trójkąt równoramienny o kącie 2 α u góry, a wysokość piramidy pokrywa się z krawędzią S A.

Od występów bocznych żeber S.B. I S Z na płaszczyźnie podstawy są równe, to same krawędzie są równe. Dlatego krawędź W S Z- trójkąt równoramienny i jego wysokość obniżona od wierzchołka S, wpada w środek DOżeberka Słońce. Z twierdzenia o trzech prostopadłych AK- wysokość trójkąta TY. Z tego jasno wynika, że kąt S Kalifornia- kąt liniowy kąta dwuściennego na krawędzi słońce, tj.

S Kalifornia = β .

Środek opisanej kuli leży na przecięciu linii l, prostopadle do płaszczyzny W S Z i przechodząc przez środek okręgu opisanego na trójkącie W S Z, z płaszczyzną przechodzącą przez środek krawędzi A S prostopadle do niego. Prosty l leży w samolocie A S DO: właściwie samolot W S Z przechodzi przez linię prostą słońce, prostopadle do płaszczyzny A S DO, czyli samoloty W S Z I A S DO prostopadły; jednocześnie prosto l prostopadle do płaszczyzny W S Z i przechodzi przez linię przecięcia tych płaszczyzn, tak że leży na płaszczyźnie A S DO .

Zatem środek kuli leży w płaszczyźnie A S DO. Weźmy ten samolot na specjalny rysunek. Centrum piłki O będzie wówczas znajdować się na przecięciu prostej l i proste M, prostopadły do A S i przechodząc przez jego środek. Ale ogólnie rzecz biorąc, mogą pojawić się trzy możliwości: bezpośrednia l I T przecinają się wewnątrz lub na zewnątrz trójkąta A S DO lub po jego stronie i będziemy musieli rozważyć wszystkie te możliwości (patrz ryc. 7, 8, 9). Poniżej w trakcie obliczeń wykażemy, że dwa z nich faktycznie nie są realizowane. Nas interesuje promień R kula ograniczona, tj. odległość od punktu O- punkty przecięcia prostopadłych T I l do boków kąta DO S A- do momentu S, wierzchołki tego kąta. Przede wszystkim znajdźmy SL- rzut wymaganej odległości na bok SK trójkąt KAS. Ponieważ w trójkącie AK B(ryc. 6) znamy nogę VK=

A i kąt KAV = α, To AK= A ctg α .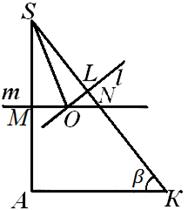

SK =

Ponieważ L- środek opisany wokół trójkąta W S Z kręgi, zatem L.S. = L W, a ponieważ z trójkąta VC L znaleźliśmy to ( S DO- SL ) 2 +HF 2 =B L 2 , tj.

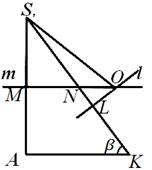
Należy zauważyć, że obliczenia segmentu SL nie zależało w żaden sposób od lokalizacji ośrodka O opisaną piłkę, wróćmy do rys. 7, 8, 9. Oznaczmy przez N punkt przecięcia linii M z boku S DO. To jasne, że prosto l I T przecinać poza trójkąt Kalifornia S , Jeśli SN <SL(ryc. 8); Jeśli S N> SL , następnie wskaż O leży wewnątrz tego trójkąta (ryc. 7); wreszcie, jeśli SN = SL , następnie wskaż O leży na boku S DO tego trójkąta (ryc. 9). Przekonajmy się, który z tych zapisów rzeczywiście ma miejsce.

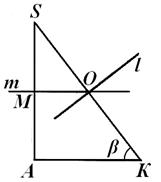
Ponieważ MN Kalifornia S , To SN =

S DO. Porównywanie długości odcinków SN I SL, możemy to łatwo udowodnić dla każdego a, α I

(z rozważań geometrycznych wynika, że A> 0,0°<

< 90° i 0°< β < 90°). Следовательно, каковы бы ни были размеры A , α I β piramidy S ABC, Centrum O ograniczona kula zawsze leży na zewnątrz piramidy. To z kolei oznacza, że płaską konfigurację zajęliśmy w samolocie Kalifornia S może mieć jedynie formę przedstawioną na rys. 8; miejsca pokazane na rys. 7 i 9 nie mogą faktycznie mieć miejsca. Patrząc na rys. 8, możemy łatwo pokazać, że = β , i dlatego LO = Holandia tg β = (SL -S N) tg β. Zastępując tutaj wyrażenia uzyskane powyżej dla SL I S N, po oczywistych obliczeniach otrzymujemy:

L O =

A tg α grzech β .

Na koniec z trójkąta prostokątnego O L.S. znaleźliśmy

= .

Jak widać obliczenia w zadaniu okazały się proste – główna trudność rozwiązania polega na rozumowaniu ustalającym położenie środka opisanej kuli.

Odpowiedź: R =

Przykład 2. Regularna trójkątna piramida z kątem płaskim  na wierzchołku jest wpisana w kulę o promieniu R. Znajdź objętość piramidy, a także powierzchnię boczną stożka opisanego wokół wskazanej piramidy .

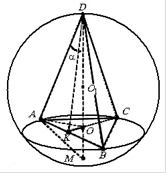
Rozwiązanie. Niech będzie bok podstawy piramidy A, promień podstawy stożka opisanego wokół tej piramidy jest równy R, Następnie

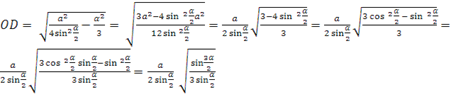(ryc. 10). Ściany piramidy są trójkątami równoramiennymi. Następnie DK– wysokość, mediana i dwusieczna  ABD. Z trójkąta prostokątnego ADK mamy . Znajdź wysokość ostrosłupa w trójkącie prostokątnym AOD : ,

DM– średnica kuli. Następnie w przekroju kuli przechodzącym przez średnicę DM i okres A, otrzymujemy trójkąt prostokątny AMD. Z relacji metrycznych w trójkącie prostokątnym mamy

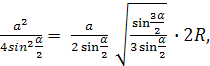Gdzie

Następnie znajdujemy obszar podstawy za pomocą wzoru:

I ze wzoru

znajdź objętość piramidy: .

Krawędź OGŁOSZENIE z definicji stożek ograniczony jest jego tworzącą. Następnie znajdujemy powierzchnię boczną opisanego stożka, korzystając ze wzoru S bok =  R l :

Odpowiedź:

;

Przykład 3. U podstawy piramidy leży kwadrat o boku a. Wysokość piramidy przechodzi przez środek jednej z krawędzi podstawy i jest równa

. Znajdź promień kuli opisanej wokół piramidy.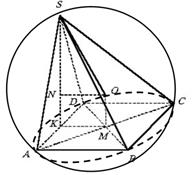

Rozwiązanie. Typowym błędem przy rozwiązywaniu tego zadania jest stwierdzenie, że środek opisywanej kuli znajduje się na krawędzi SBC(ryc. 11). W rzeczywistości położenie punktu O nie podłączony do krawędzi SBC.

Ze względu na równą odległość punktu O ze szczytów S, A, B, C, D wynika z tego OABCD- regularna czworokątna piramida. Dlatego do krawędzi ABCD kropka O rzutowane do pewnego momentu M– punkt przecięcia przekątnych. Trójkąt A.S.D. równoramienny, a następnie wysokość piramidy SK jest środkową trójkąta A.S.D. ,

. Z trójkąta prostokątnego S.A.K. znajdziemy SA :

Dlatego trójkąt SMUTNY.– równoboczny i OASD- regularna trójkątna piramida. Następnie wskaż O wyrzucony na skraj SMUTNY. do środka trójkąta SMUTNY.. Stąd

Z trójkąta SYN znajdź wymagany promień WIĘC,

Odpowiedź:

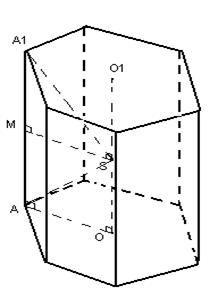
Przykład 4. Do kuli o promieniu R wpisano regularną sześciokątną ostrosłup ścięty, w który płaszczyzna dolnej podstawy przechodzi przez środek kuli, a krawędź boczna tworzy z płaszczyzną podstawy kąt 60°

. Wyznacz objętość piramidy.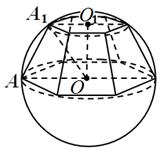

Rozwiązanie. Według warunku,

OAA 1 = 60 (ryc. 12); Oznacza, O 1 OA 1 = 30 i A 1 O 1 = A 1 O = ,OO 1 = .

S dolna podstawa = 6

, S szczyt podstawowy = niższy podstawowy .

Wreszcie dostajemy

Odpowiedź:

2.2 Przykłady zadań olimpijskich z pryzmatem

Przykład 1. W kulę, której objętość jest równa V , wpisano pryzmat prostokątny prostokątny. Podstawą pryzmatu jest trójkąt prostokątny o kącie ostrym

, a jego największa ściana boczna jest kwadratem. Znajdź objętość pryzmatu.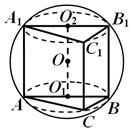

Rozwiązanie. Najpierw określamy położenie środka kuli względem pryzmatu. Przekroje kuli przy płaszczyznach podstaw pryzmatu są okręgami, w które wpisane są te podstawy (ryc. 13), a ponieważ podstawy pryzmatu są równe, okręgi przekrojów są równe i jednakowo odległe od środek piłki. Każdy z ośrodków O 1 i O 2 pokrywa się ze środkiem odpowiedniej przeciwprostokątnej.

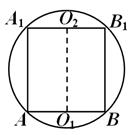
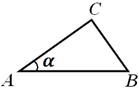
Z własności przekrojów kuli przez płaszczyznę wiadomo, że prostopadła poprowadzona jest ze środka kuli O płaszczyzna okręgu przekroju poprzecznego przechodzi przez środek tego okręgu. Stąd, O 1 O

samolot ABC. Prosty O 1 O również przechodzi O 2 i prostopadle do płaszczyzny, zatem środek kuli leży na ścianie pośrodku segmentu O 1 O. Wszystkie boczne ściany pryzmatu są prostokątami, a ściana - największy z nich (od AB- przeciwprostokątna trójkąta A Słońce). Ta twarz jest umownie kwadratowa. Przekrój kuli przez płaszczyznę ściany jest dużym kołem kuli, stąd promień okręgu pokazany na ryc. 14, równy promieniowi kuli R . Zwróć uwagę na wysokość pryzmatu AA 1 = A 4 = . Teraz pozostaje tylko znaleźć obszar podstawy:

S A B Z =

. Od (ryc. 15)

mamy AC = AB

, Oznacza,

S A B Z =

Teraz otrzymujemy:

V nagroda.

Według warunku,

R 3 = V ,

Gdzie R 3 =

,stąd,

V nagroda.

Odpowiedź: V nagroda.

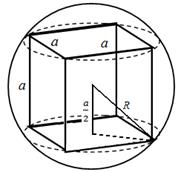
Przykład 2. Znajdź stosunek odpowiednio powierzchni i objętości kuli do powierzchni i objętości wpisanego sześcianu

Rozwiązanie. Niech promień kuli będzie R , krawędź sześcianu jest równa A;

Następnie R 2 -

, Gdzie a= .

Oznaczmy odpowiednio objętości i powierzchnie kuli i sześcianu przez V 1 , V 2 , I S 1 , S 2 .

, V 2 = = , S 1 =4, S 2 = 6A 2 =8R 2 , V 2 = , S 1 S 2 = .

Odpowiedź: V 1

V 2 = , S 1 S 2 = .

2.3 Przykłady zadań olimpijskich z cylindrem

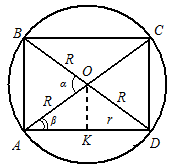
Przykład. Znajdź stosunek objętości kuli do objętości prawego walca kołowego wpisanego w tę kulę, jeśli wiadomo, że mniejszy kąt między przekątnymi przekroju osiowego walca jest równy

a średnica podstawy jest większa niż wysokość cylindra (ryc. 18).

Rozwiązanie. Znamy objętość kuli

i znajdujemy objętość cylindra za pomocą wzoru, ale dlatego

Pozwalać ABCD- przekrój osiowy cylindra (patrz rys. 18). Ponieważ średnica podstawy jest większa niż wysokość cylindra, wówczas

- narożnik AOB. Z trójkąta ABW wynika z tego wysokość cylindra

Promień podstawy cylindra

. .

Okazało się, że

Podstawmy znalezione dane do wzoru na objętość walca:

;

Zatem,

Znajdźmy związek

Odpowiedź:

2.4 Przykłady zadań olimpijskich z stożek

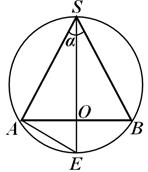
Przykład 1. Do kuli o promieniu R wpisany jest okrągły stożek; kąt między tworzącymi stożka w przekroju osiowym jest równy α. Znajdź wysokość tworzącą promień podstawy stożka.

Rozwiązanie. Przekrój kuli przechodzący przez oś stożka to okrąg wielki kuli, w którym

AB S(ryc. 19), gdzie A W- średnica podstawy stożka. Kontynuujmy wysokość (oś) stożka WIĘC aż przetnie w tym punkcie okrąg wielki mi i rozważ mi S A:

w tym trójkącie

SE = 2R ,

S AE = 90° I A S E= .

A S = 2R

Teraz od

A system operacyjny znaleźliśmy

A O = R = 2R

, WIĘC = h= 2R

Odpowiedź : TAK= 2R

A S = 2R , A O =.

Przykład 2. Stosunek wysokości stożka do promienia kuli opisanej wokół niego jest równy k . Znajdź stosunek objętości tych ciał. Dowiedz się przy czym k zadanie ma sens.

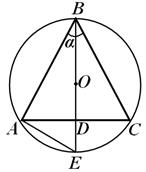
Rozwiązanie. Rozważmy przekrój osiowy stożka (ryc. 20). Pozwalać H- wysokość stożka, R- promień kuli opisanej na stożku. Następnie, pod warunkiem,

=k, tj. H = kR .

Wyraźmy promień R podstawa stożka R; biorąc pod uwagę akordy AC I BYĆ, otrzymujemy:

W D

D mi = A D D Z(ponieważ AD=DC ,
– prostokątne, OGŁOSZENIE – wysokość obniżona z wierzchołka kąta prostego).

(stąd, k < 2).

V w =

; V k ==

Zatem,

, (o godzinie 0< k < 2).

Odpowiedź:

, (o godzinie 0< k < 2).

Przykład 3. W ściętym stożku promienie dolnej i górnej podstawy są odpowiednio równe R 1 I R 2 , a tworząca stożka jest nachylona do płaszczyzny dolnej podstawy pod kątem α (ryc. 21). Znajdź promień kuli, w którą wpisany jest dany stożek ścięty.

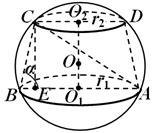
Rozwiązanie. W przekroju kuli przechodzącym przez oś ściętego stożka uzyskuje się duży okrąg kuli, w który wpisany jest trapez ABC D. Rozważmy

A słońce, który jest również wpisany w okrąg wielki kuli. Znany jest kąt w tym trójkącie Z licencjat = α . Na mocy twierdzenia sinusoidalnego AC = 2R. Zatem do ustalenia R wystarczy znaleźć AC. Odejdźmy od tematu Z prostopadły SE NA AB. Oczywiście,

AE= R 1 + R 2 ,BYĆ = R 1 - R 2, za CE = ( R 1 - R 2 )

Dlatego zgodnie z twierdzeniem Pitagorasa

= = = skąd R =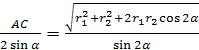

Odpowiedź: R

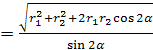3 Przykłady zadań z ujednoliconego egzaminu państwowego

3.1 Przykłady zadań egzaminu Unified State Exam z piramidą

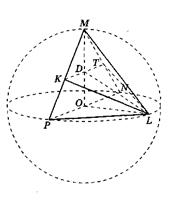
Przykład 1. Odcinek P N , równa 8, jest średnicą kuli. Punkty M, L połóż się na kuli tak, aby objętość piramidy wynosiła P N M L największy (ryc. 22). Znajdź obszar trójkąta K L T, gdzie K i T są środkami krawędzi PM i N M odpowiednio.

Rozwiązanie. Pozwalać O jest środkiem kuli, oraz R- jego promień. Ponieważ R N = 2R= 8 i kropki M I L więc połóż się na kuli LUB = O L = O N = OM = R = 4. Przekroje kuli według płaszczyzn R LN I RM N- promień okręgu R = 4, opisano o trójkątach R LN I RM N , I

RM N = R LN= 90°, jako kąty wpisane oparte na średnicy R N .

Pozwalać N- wysokość piramidy obniżonej od góry M, A H- wysokość trójkąta R LN , trzymany z boku R N . Od tego momentu M leży na kuli i na płaszczyźnie R LN zawiera zatem środek kuli N

R , I N = R , Jeśli MO R Holandia . Podobnie od momentu L leży zatem na kuli H R , I H = R , Jeśli L O R N .

Stąd objętość piramidy R N M L mamy

, .

Zatem piramida R N M L ma największą objętość, jeśli trójkąty R LN I RM N prostokątne, równoramienne ze wspólną przeciwprostokątną R N, leżące w wzajemnie prostopadłych płaszczyznach. Od trójkątów L O N , L LUB, L OM, ROM, N OM są równe na dwóch nogach, następnie trójkąty L M N I L PAN poprawne z boku

Holandia =P L = NA

Wynika z tego, że mediany L DO I L T te trójkąty są równe i

L DO =

= 2.

Trójkąt DO L T równoramienny i jego wysokość LD jest medianą prawego trójkąta równoramiennego L OM. Stąd

LD =

= 2.

CT- środkowa linia trójkąta RM N i dlatego CT = 0,5R N =R . Dlatego obszar S DO L T =

CT LD = 4.

Odpowiedź: 4

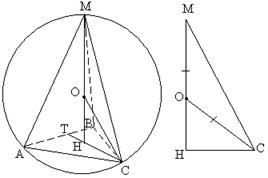
Przykład 2. W regularnej trójkątnej piramidzie bok podstawy wynosi 5, a boczne żebra są nachylone do podstawy pod kątem 60 O. Znajdź promień kuli opisanej wokół piramidy.

Rozwiązanie. Pozwalać ABCM wskazana piramida (patrz ryc. 23) Środek opisywanej kuli leży na wysokości piramidy, ponieważ piramida jest regularna.

Podstawą wysokości ostrosłupa jest środek trójkąta ABC, czyli punkt przecięcia środkowych. Następnie:

ST =

CH= = = .

Rozważmy teraz trójkąt MNS. Oto róg MSN równy 60°, jako kąt pomiędzy krawędzią boczną SM i podstawa ABC. Narożnik NMS równa 30

. MO=system operacyjny jak promienie. Zatem jest to trójkąt MOS równoramienny. Jak wiadomo, w trójkącie równoramiennym kąty przy podstawie są równe. Stąd, OSM = Obowiązkowe ubezpieczenie zdrowotne = 30, OSN = MSN - MKO = 60 - 30= 30.

Z trójkąta prostokątnego OSN zdefiniujmy przeciwprostokątną system operacyjny korzystając ze związku funkcji trygonometrycznych w trójkącie prostokątnym:

Odpowiedź: OC =

3.2 Przykłady zadań USE z pryzmatem

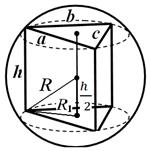
Przykład 1. Podstawą pryzmatu jest trójkąt o bokach A , B , C . Wysokość pryzmatu H (Rysunek 25). Znajdź promień opisanej kuli.

Rozwiązanie. Ponieważ wokół pryzmatu opisano kulę, pryzmat jest prosty, a jego boczna krawędź jest równa jego wysokości. Promień okręgu opisanego wokół podstawy pryzmatu oblicza się ze wzoru

Odpowiedź:

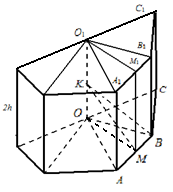
Przykład 2. Promień kuli R . Regularny n-kątny pryzmat o wysokości 2 jest wpisany w kulę. H (Rysunek 26). Znajdź bok podstawy pryzmatu.

Rozwiązanie. Pozwalać DO– środek opisanej kuli. Mamy: K.B. = R , OK = H. Pozwalać OM

AB, Następnie

O.B. =

(z trójkąta OK).

Z trójkąta OMB znaleźliśmy

A = 2M.B. = 2O.B.

Więc, A =

Odpowiedź: A =

3.3 Przykłady zadań egzaminu Unified State Exam z cylindrem

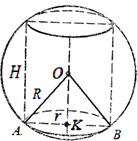
Przykład 1. Wysokość okrągłego walca jest o 10 większa od promienia podstawy, a jego całkowita powierzchnia wynosi 144

. Znajdź promień opisanej kuli.

Rozwiązanie. Promień opisanej kuli

(ryc. 27).

Powierzchnia cylindra

, 144,

Uprośćmy to wyrażenie:

Otrzymujemy równanie kwadratowe

Znajdźmy pierwiastki tego równania

, nie jest odpowiedni, ponieważ jest negatywny. Wysokość

Znajdźmy promień opisanej kuli:

Odpowiedź:

Przykład 2. W kulę wpisany jest prosty okrągły walec (ryc. 28). Ile razy objętość kuli jest większa od objętości walca, jeśli wiadomo, że stosunek promienia kuli do promienia podstawy walca jest o połowę mniejszy niż stosunek powierzchni walca? kulę do bocznej powierzchni cylindra.

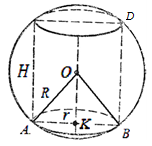
Rozwiązanie. Stosunek objętości kuli do objętości wpisanego walca

Z warunku wiadomo, że

; –

równoboczny

Znajdźmy stosunek objętości kuli i walca wpisanego

Odpowiedź: 16:9.

3.4 Przykłady zadań egzaminu Unified State Exam ze stożkiem

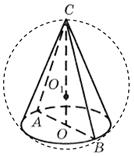
Przykład 1. Średnica podstawy stożka wynosi 6 m, tworząca jest nachylona do płaszczyzny podstawy pod kątem 60° (ryc. 29). Znajdź obszar kuli opisany na stożku.

TAKSÓWKA równy kątowi między tworzącą stożka a polem jego podstawy. Dlatego CAB= 60° i trójkąt równoramienny ABC - prawidłowy. Wynika, że

CA = AB = BC= 6m.

Znajdźmy położenie środka kuli opisanej na stożku. Z definicji takiej kuli obwód podstawy stożka jest wycinkiem opisanej kuli i wierzchołek stożka leży na tej kuli. Zgodnie z właściwością średnicy kuli przechodzącej przez środek dowolnego jej odcinka, linia prosta WSPÓŁ prostopadle do płaszczyzny podstawy stożka, a zatem do środka O 1 z opisanej kuli leży na linii prostej WSPÓŁ. Wynika z tego, że centrum O 1 kuli opisanej na stożku jest środkiem okręgu opisanego na jej przekroju osiowym.

W trójkącie prostokątnym

ABC R = O 1 C =

(M)

Znajdźmy obszar kuli:

(m2).

Odpowiedź: 48

m 2.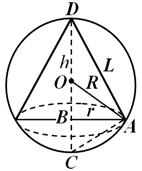

Przykład 2. Do kuli o promieniu R = Wpisany stożek o wysokości 6 cm H (ryc. 30). Wyraź objętość i powierzchnię boczną stożka jako funkcję argumentu H .

Rozwiązanie. Mamy:

Gdzie R - promień podstawy, L- tworząc stożek.

biorąc pod uwagę, że R = VA – wysokość obniżona od wierzchołka kąta prostego do przeciwprostokątnej, mamy: i . Lub R 2 i

, .

Teraz otrzymujemy:

, .

Odpowiedź:

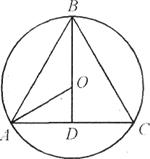
Przykład 3. W kulę wpisany jest stożek, którego tworząca jest równa średnicy podstawy (ryc. 31). Znajdź stosunek powierzchni stożka do powierzchni kuli.

Rozwiązanie. Przedstawmy przekrój osiowy stożka, który przejdzie przez środek kuli. Ponieważ średnica podstawy stożka jest równa tworzącej, w przekroju otrzymujemy trójkąt foremny wpisany w okrąg (ryc. 31). Niech promień kuli będzie równy R : Następnie

AB =R

, A D =

Oznaczmy całkowitą powierzchnię stożka przez S 1, a powierzchnia piłki przechodzi S 2. Mamy

Gdzie S 1: S 2 = 9:16.

Odpowiedź: S 1: S 2 = 9:16.

Wniosek

W trakcie badań odkryliśmy, że problemy z opisywanego obszaru dość często stawiane są uczniom na egzaminie Unified State Exam, dlatego umiejętność rozwiązywania tego typu problemów odgrywa bardzo ważną rolę w pomyślnym zdaniu egzaminów. Również problemy z opisywanym obszarem często spotykane są na olimpiadach matematycznych na różnych poziomach. Odpowiednie przykłady podano w naszej pracy. Na tym etapie ograniczyliśmy się do rozważenia problemów związanych z połączeniem opisanej kuli z piramidą, pryzmatem, cylindrem i stożkiem. Wybrane zadania do samodzielnej pracy. W trakcie realizacji pracy zastosowaliśmy następujące metody: pracę z literaturą naukową i popularnonaukową, gromadzenie informacji w Internecie, analizę, systematyzację, klasyfikację i przetwarzanie na komputerze. Wyniki prezentowane są obecnie w formie abstrakcyjnej. W przyszłości planowane jest uzupełnienie pracy o nowe zadania.

Bibliografia

1. Abramowicz M.I., Starodubtsev M.T. Matematyka (geometria i funkcje trygonometryczne). Podręcznik dla wydziałów przygotowawczych uniwersytetów - M: Szkoła Wyższa, 1976. - 304 s.

2. Wojtowicz F.S. Kombinacje ciał geometrycznych: (kula wpisana i ograniczona): Książka dla studentów. – Mińsk: Narodnaja Aswieta, 1992. – 160 s.

3. Govorov V.M., Dybov P.T., Miroshin N.V. I inne Lista problemów konkurencyjnych w matematyce (wraz z instrukcjami metodologicznymi i rozwiązaniami): podręcznik. – wydanie drugie – M: Nauka, 1986. – 384 s.

4. Denishcheva L.O., Bezrukova G.K., Boychenko E.M. i inne Jednolity egzamin państwowy, matematyka, kontrola materiałów pomiarowych - M: Edukacja 2005. - 80 s.

5. Denishcheva L.O., Glazkov Yu.A., Krasnyanskaya K.A. i inne.Ujednolicony egzamin państwowy. Matematyka. Materiały edukacyjno-szkoleniowe do przygotowania uczniów / FIPI - M: Intellect-Center, 2008. - 240 s.

6. Dorofeev G.V., Potapov K.M., Rozov N.Kh. Podręcznik matematyki dla rozpoczynających naukę na uniwersytetach - M: Nauka 1972. - 528 s.

7. Egerev V.K., Zaitsev V.V., Kordemsky B.A. i inne 2500 problemów z matematyki wraz z rozwiązaniami dla osób rozpoczynających naukę na uniwersytetach: - M: Wydawnictwo LLC „ONICS 21st century”: Wydawnictwo LLC „Świat i edukacja”, 2002. - 912 s.

8. Zvavich L.I., Ryazanovsky A.R. Geometria w tablicach - M: Drop 2007. - 128 s.

9. Klimin S.V., Strunkina T.V., Panteleeva E.I. i inne.Ujednolicony egzamin państwowy, zadania testowe - M: Edukacja 2002. - 24 s.

10. Modenov V.P., Dorofeev G.V., Novoselov S.I. i inne Podręcznik matematyki - M: Wydawnictwo Uniwersytetu Moskiewskiego, 1972. - 404 s.

11. Shuvalova E.Z., Kaplun V.I. Geometria: podręcznik dla wydziałów przygotowawczych uniwersytetów - M: Szkoła Wyższa, 1980. - 265 s.

12. http://kvant.mirror1.mccme.ru/pdf/2000/06/kv0600solut.pdf

13. http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D1%80%D1%82%D0%B0%D0%BB:%D0%9D%D0%B0%D1% 83%D0%BA%D0%B0

14. http://rgp.nm.ru/geometriia/praktika11/zadatcha119.html

Aplikacja. Zadania do samodzielnego rozwiązania

1. W piramidzie FABC krawędzie ABF I ABC prostopadły, B.F. :FA. = 15:11. Tangens kąta między prostą PNE. i samolot ABF równa się 5. Punkt M wybrane na krawędzi PNE. Więc B M :M C = 4:11. Kropka T leży na linii prostej FA. i w równej odległości od punktów M I W.Środek kuli opisanej na piramidzie FABC , leży na krawędzi AB, pole tej kuli wynosi 36

. Znajdź objętość piramidy ASMT. (Odpowiedź: 6)

2. Podstawa piramidy FABCD jest prostokątem ABCD . Samolot AFC prostopadle do płaszczyzny ABC , tangens kąta FAK równa się

, tangens kąta między prostą PNE. i samolot AFC równy . Kropka M leży na krawędzi PNE. , VM =PNE. . Kropka L leży na linii prostej FA. i w równej odległości od punktów M I C . Objętość piramidy L W D M wynosi 72. Środek kuli opisanej na piramidzie FABCD , leży na płaszczyźnie swojej podstawy. Znajdź promień tej kuli. (Odpowiedź: 5)

3. W pobliżu zwykłej piramidy FABC opisuje kulę, której środek leży w płaszczyźnie podstawy ABC piramidy. Kropka M leży na krawędzi AB Więc A M :M B=1:3. Kropka T leży na linii prostej FA. i w równej odległości od punktu M I W. Objętość piramidy TVSM równa się

. Znajdź promień kuli opisanej przez piramidę FABC . (Odpowiedź: )

4. Odcinek AB– średnica kuli. Zwrotnica Z, D ABCD największy. Znajdź cosinus kąta między liniami CM I AB, Jeśli M– środek żebra BD . (Odpowiedź:

)

5. Odcinek R N , równa 8, jest średnicą kuli. Kropka M, L połóż się na kuli tak, aby objętość piramidy R N M L największy. Znajdź obszar trójkąta KLT , Gdzie K I T – środek żeber RM I N M odpowiednio. (Odpowiedź: 4

)

6. Dana jest kula o promieniu 6. Przekrój kuli w płaszczyźnie to okrąg o średnicy CT. Płaszczyzna przekroju jest usuwana ze środka kuli w odległości 5. punktu R jest wybrany na kuli i punkt L RK L T największy. Znajdź kąt pomiędzy linią prostą L.M. i samolot PTK , Jeśli Mżyłka RK. (Odpowiedź: 30

)

7. Przez centrum O F jest wybrany na kuli i punktach A , B , C , D – FABCD największy. Zwrotnica M, T, L – środek żeber pełne wyżywienie , płyta CD I OGŁOSZENIE odpowiednio. Pole trójkąta MLT równa 64

. Znajdź promień kuli. (Odpowiedź: 2)

8. Przez centrum O z tej kuli wykonany jest przekrój. Kropka F jest wybrany na kuli i punktach A , B , C , D – kolejno na okręgu przekroju poprzecznego, tak aby objętość piramidy FABCD największy. Znajdź sinus kąta między prostą JESTEM i samolot B.F.D. . (Odpowiedź:

)

9. Dana jest kula o promieniu 10. Płaskim przekrojem tej kuli jest okrąg o średnicy AB. Płaszczyzna przekroju jest usuwana ze środka kuli w odległości 8. punktu D jest wybrany na kuli i punkt Z– na obwodzie przekroju tak, aby uzyskać objętość piramidy ABC D największy. Znajdź obszar twarzy ACD .(Odpowiedź: 27

)

10. Podstawą piramidy jest prostokąt. Płaszczyzna jest prostopadła do płaszczyzny ABC, tangens kąta między prostą Słońce i samolot FAK równa się 2. Punkt M leży na krawędzi Słońce I SN =

Kropka L leży na linii prostej FA. i w równej odległości od punktów M I Z. Środek kuli opisanej na piramidzie FA. W płyta CD, leży w płaszczyźnie podstawy piramidy, promień tej kuli wynosi 4. Znajdź objętość piramidy LA. SM. (Odpowiedź: 48)

11. W kulę o promieniu 2

ABCA 1 W 1 Z 1. Prosty AC 1 Formy z płaszczyzną WĄTEK (Odpowiedź: 288)

12. W kulę wpisano regularny trójkątny pryzmat ABCA 1 W 1 Z 1, którego objętość wynosi 4,5. Prosty VA 1 formy z płaszczyzną VSS 1 róg45

. Znajdź pole powierzchni kuli. (Odpowiedź: 11)

13. W kulę o promieniu

wpisany jest regularny trójkątny pryzmat ABCA 1 W 1 Z 1. Prosty AB 1 formy z płaszczyzną AKC 1 kąt 45. Znajdź objętość pryzmatu. (Odpowiedź: 36)

14. Oblicz krawędzie regularnego trójkątnego pryzmatu, znając promień R ograniczona kula i kąt nachylenia α promień tej kuli pociągnięty do wierzchołka pryzmatu, do ściany bocznej zawierającej ten wierzchołek. (Odpowiedź: 2

)

15. Do kuli o promieniu R wpisano prawy stożek okrągły. Znajdź powierzchnię boczną stożka, jeśli jego wysokość wynosi H . (Odpowiedź:

)

16. W kulę wpisano stożek. Osiowe pole przekroju stożka jest równe S. Kąt między jego wysokością a generatorem jest równy α . Znajdź objętość kuli. (Odpowiedź:

)

17. Wyznacz powierzchnię boczną stożka, znając długość promienia R kula ograniczona wokół niej i kąt α, pod którym ze środka kuli widoczna jest tworząca stożka. (Odpowiedź:

)

18. Znajdź stosunek całkowitej powierzchni prawego stożka wpisanego w kulę do pola powierzchni tej kuli, jeśli kąt przy wierzchołku przekroju osiowego stożka jest równy α I

. (Odpowiedź:

)

19. W kulę wpisano stożek w taki sposób, że jego wysokość jest podzielona przez środek kuli w stosunku średnim i skrajnym. Znajdź kąt na wierzchołku osiowego przekroju stożka. Oblicz, ile razy objętość kuli jest większa od objętości stożka. (Odpowiedź:

; 4 razy )

Przykład 2.W regularnej trójkątnej piramidzie bok podstawy wynosi 5, a boczne żebra są nachylone do podstawy pod kątem 60 O. Znajdź promień kuli opisanej wokół piramidy.

Rozwiązanie. Pozwalać ABCM wskazana piramida (patrz ryc. 23) Środek opisywanej kuli leży na wysokości piramidy, ponieważ piramida jest regularna.

Podstawą wysokości ostrosłupa jest środek trójkąta ABC, czyli punkt przecięcia środkowych. Następnie:

CH= ST = CH= = = .

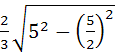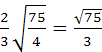Rozważmy teraz trójkąt MNS. Oto róg MSN równy 60°, jako kąt pomiędzy krawędzią boczną SM i podstawa ABC. Narożnik NMS równa się 30. MO=system operacyjny jak promienie. Zatem jest to trójkąt MOS równoramienny. Jak wiadomo, w trójkącie równoramiennym kąty przy podstawie są równe. Stąd,

OSM = Obowiązkowe ubezpieczenie zdrowotne = 30, OSN = MSN - MKO = 60 - 30= 30.

Z trójkąta prostokątnego OSN zdefiniujmy przeciwprostokątną system operacyjny korzystając ze związku funkcji trygonometrycznych w trójkącie prostokątnym:

system operacyjny= = .

Odpowiedź: OC= .

3.2 Przykłady zadań USE z pryzmatem

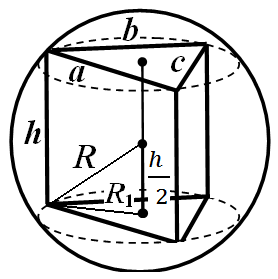
Przykład 1.Podstawą pryzmatu jest trójkąt o bokachA, B, C. Wysokość pryzmatuH(Rysunek 25). Znajdź promień opisanej kuli.

Odpowiedź:

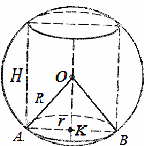
Przykład 2.Promień kuliR. Regularny n-kątny pryzmat o wysokości 2 jest wpisany w kulę.H(Rysunek 26). Znajdź bok podstawy pryzmatu.

Rozwiązanie. Pozwalać DO– środek opisanej kuli. Mamy: K.B.= R, OK= H. Pozwalać OMAB, Następnie

O.B.=

(z trójkąta OK).

Z trójkąta OMB znaleźliśmy

A= 2M.B.= 2O.B..

Więc, A= .

Odpowiedź: A= .

3.3 Przykłady zadań egzaminu Unified State Exam z cylindrem

Przykład 1.Wysokość okrągłego walca jest o 10 większa od promienia podstawy, a jego całkowita powierzchnia wynosi 144. Znajdź promień opisanej kuli.

Rozwiązanie. Promień opisanej kuli

Powierzchnia cylindra

Uprośćmy to wyrażenie:

Otrzymujemy równanie kwadratowe

Znajdźmy pierwiastki tego równania

Korzeń nie jest odpowiedni, ponieważ jest ujemny. Wysokość

Znajdźmy promień opisanej kuli:

Odpowiedź: .

Przykład 2.W kulę wpisany jest prosty okrągły walec (ryc. 28). Ile razy objętość kuli jest większa od objętości walca, jeśli wiadomo, że stosunek promienia kuli do promienia podstawy walca jest o połowę mniejszy niż stosunek powierzchni walca? kulę do bocznej powierzchni cylindra.

Rozwiązanie. Stosunek objętości kuli do objętości wpisanego walca

Z warunku wiadomo, że

równoboczny

Znajdźmy stosunek objętości kuli i walca wpisanego

Odpowiedź: 16:9.

3.4 Przykłady zadań egzaminu Unified State Exam ze stożkiem

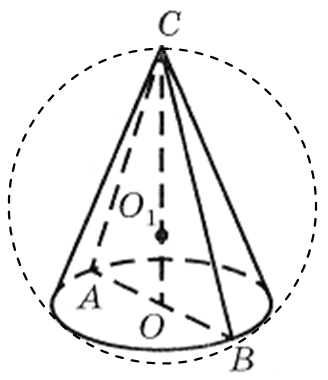
Przykład 1.Średnica podstawy stożka wynosi 6 m, tworząca jest nachylona do płaszczyzny podstawy pod kątem 60° (ryc. 29). Znajdź obszar kuli opisany na stożku.

Rozwiązanie. Pozwalać Z - wierzchołek stożka O -środek podstawy, ŚREDNICA - przekrój osiowy stożka. Ponieważ tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 60°, a WSPÓŁ jest wysokością stożka, a następnie linią prostą AB- projekcja bezpośrednia SA na płaszczyznę podstawy stożka. Stąd, TAKSÓWKA równy kątowi między tworzącą stożka a polem jego podstawy. Dlatego CAB= 60° i trójkąt równoramienny ABC - prawidłowy. Wynika, że

CA = AB = BC= 6 m.

Znajdźmy położenie środka kuli opisanej na stożku. Z definicji takiej kuli obwód podstawy stożka jest wycinkiem opisanej kuli i wierzchołek stożka leży na tej kuli. Zgodnie z właściwością średnicy kuli przechodzącej przez środek dowolnego jej odcinka, linia prosta WSPÓŁ prostopadle do płaszczyzny podstawy stożka, a zatem do środka O 1 z opisanej kuli leży na linii prostej WSPÓŁ. Wynika z tego, że centrum O 1 kula opisana na stożku jest środkiem okręgu opisanego na jego przekroju osiowym.

W trójkącie prostokątnym

ABCR= O 1 C= (M)

Przykład 3.W kulę wpisany jest stożek, którego tworząca jest równa średnicy podstawy (ryc. 31). Znajdź stosunek powierzchni stożka do powierzchni kuli.

AB= R , AD =

Oznaczmy całkowitą powierzchnię stożka przez S 1, a powierzchnia piłki przechodzi S 2. Mamy

Gdzie S 1: S 2 = 9:16.

Odpowiedź:S 1: S 2 = 9:16.

Wniosek

Bibliografia

Abramowicz M.I., Starodubtsev M.T. Matematyka (geometria i funkcje trygonometryczne). Podręcznik dla wydziałów przygotowawczych uniwersytetów - M: Szkoła Wyższa, 1976. - 304 s.

Wojtowicz F.S. Kombinacje ciał geometrycznych: (kula wpisana i ograniczona): Książka dla studentów. – Mińsk: Narodnaja Aswieta, 1992. – 160 s.

Govorov V.M., Dybov P.T., Miroshin N.V. I inne Lista problemów konkurencyjnych w matematyce (wraz z instrukcjami metodologicznymi i rozwiązaniami): podręcznik. – wydanie drugie – M: Nauka, 1986. – 384 s.

Denishcheva L.O., Bezrukova G.K., Boychenko E.M. i inne Jednolity egzamin państwowy, matematyka, kontrola materiałów pomiarowych - M: Edukacja 2005. - 80 s.

Denishcheva L.O., Glazkov Yu.A., Krasnyanskaya K.A. i inne.Ujednolicony egzamin państwowy. Matematyka. Materiały edukacyjno-szkoleniowe do przygotowania uczniów / FIPI - M: Intellect-Center, 2008. - 240 s.

Dorofeev G.V., Potapov K.M., Rozov N.Kh. Podręcznik matematyki dla rozpoczynających naukę na uniwersytetach - M: Nauka 1972. - 528 s.

Egerev V.K., Zaitsev V.V., Kordemsky B.A. i inne 2500 problemów z matematyki wraz z rozwiązaniami dla osób rozpoczynających naukę na uniwersytetach: - M: Wydawnictwo LLC „ONICS 21st century”: Wydawnictwo LLC „Świat i edukacja”, 2002. - 912 s.

Zvavich L.I., Ryazanovsky A.R. Geometria w tablicach - M: Drop 2007. - 128 s.

Klimin S.V., Strunkina T.V., Panteleeva E.I. i inne.Ujednolicony egzamin państwowy, zadania testowe - M: Edukacja 2002. - 24 s.

Modenov V.P., Dorofeev G.V., Novoselov S.I. i inne Podręcznik matematyki - M: Wydawnictwo Uniwersytetu Moskiewskiego, 1972. - 404 s.

Shuvalova E.Z., Kaplun V.I. Geometria: podręcznik dla wydziałów przygotowawczych uniwersytetów - M: Szkoła Wyższa, 1980. - 265 s.

http :// kwant. lustro1. mccme. ru/ pdf/2000/06/ kv0600 rozwiązanie. pdf

http :// ru. wikipedia. org/ wiki/% D0%9 F% D0% BYĆ% D1%80% D1%82% D0% B0% D0% nocleg ze śniadaniem:% D0%9 D% D0% B0% D1%83% D0% licencjat% D0% B0

rgp . nm. ru/ wymiary/ praktika11/ zadatcha119. HTML

Aplikacja. Zadania do samodzielnego rozwiązania

Temat „Różne problemy dotyczące wielościanów, walca, stożka i kuli” jest jednym z najtrudniejszych na kursie geometrii w klasie 11. Przed rozwiązaniem problemów geometrycznych zwykle studiują odpowiednie sekcje teorii, do których odwołuje się przy rozwiązywaniu problemów. W podręczniku S. Atanasyana i innych na ten temat (s. 138) można znaleźć jedynie definicje wielościanu opisanego wokół kuli, wielościanu wpisanego w kulę, kuli wpisanej w wielościan i kuli opisanej wokół kuli. wielościan. Zalecenia metodyczne do tego podręcznika (patrz książka „Studying Geometry in Grades 10–11” S.M. Sahakyana i V.F. Butuzova, s. 159) mówią, jakie kombinacje ciał są brane pod uwagę przy rozwiązywaniu problemów nr 629–646 , i zwraca się na to uwagę na fakt, że „rozwiązując konkretny problem, należy przede wszystkim upewnić się, że uczniowie dobrze rozumieją względne położenie ciał wskazanych w warunku”. Poniżej znajduje się rozwiązanie zadań nr 638(a) i nr 640.

Biorąc pod uwagę wszystko powyższe oraz fakt, że najtrudniejszym dla uczniów problemem jest połączenie piłki z innymi ciałami, konieczne jest usystematyzowanie odpowiednich zasad teoretycznych i przekazanie ich studentom.

Definicje.

1. Kulę nazywa się wpisaną w wielościan, a wielościanem opisuje się wokół kuli, jeśli powierzchnia kuli dotyka wszystkich ścian wielościanu.

2. Kulę opisano na wielościanie, a wielościan wpisano w kulę, jeżeli powierzchnia kuli przechodzi przez wszystkie wierzchołki wielościanu.

3. Mówi się, że kula jest wpisana w cylinder, ścięty stożek (stożek), a walec, ścięty stożek (stożek) jest wpisany wokół kuli, jeśli powierzchnia kuli dotyka podstaw (podstawy) i wszystkie tworzące walca, stożek ścięty (stożek).

(Z tej definicji wynika, że okrąg wielki kuli można wpisać w dowolny przekrój osiowy tych ciał).

4. Mówi się, że kula jest opisana na walcu, ściętym stożku (stożku), jeżeli okręgi podstaw (okrąg podstawowy i wierzchołek) należą do powierzchni kuli.

(Z tej definicji wynika, że wokół dowolnego przekroju osiowego tych ciał można opisać okrąg większego okręgu kuli).

Ogólne uwagi dotyczące położenia środka kuli.

1. Środek kuli wpisanej w wielościan leży w punkcie przecięcia płaszczyzn dwusiecznych wszystkich kątów dwuściennych wielościanu. Znajduje się tylko wewnątrz wielościanu.

2. Środek kuli opisanej na wielościanie leży w punkcie przecięcia płaszczyzn prostopadłych do wszystkich krawędzi wielościanu i przechodzących przez ich środki. Może być umiejscowiony wewnątrz, na powierzchni lub na zewnątrz wielościanu.

Połączenie kuli i pryzmatu.

1. Kula wpisana w prosty pryzmat.

Twierdzenie 1. W pryzmat prosty można wpisać kulę wtedy i tylko wtedy, gdy w podstawę pryzmatu można wpisać okrąg, a wysokość graniastosłupa jest równa średnicy tego okręgu.

Wniosek 1.Środek kuli wpisanej w prawy pryzmat leży w środku wysokości pryzmatu przechodzącego przez środek okręgu wpisanego w podstawę.

Konsekwencja 2. W szczególności kulę można wpisać w linie proste: trójkątne, foremne, czworokątne (w których sumy przeciwległych boków podstawy są sobie równe) pod warunkiem H = 2r, gdzie H jest wysokością pryzmat, r jest promieniem okręgu wpisanego w podstawę.

2. Kula opisana na pryzmacie.

Twierdzenie 2. Kulę można opisać wokół pryzmatu wtedy i tylko wtedy, gdy pryzmat jest prosty, a wokół jego podstawy można opisać okrąg.

Wniosek 1. Środek kuli opisanej na prostym graniastosłupie leży w środku wysokości graniastosłupa poprowadzonej przez środek okręgu opisanego na podstawie.

Konsekwencja 2. W szczególności kulę można opisać: w pobliżu graniastosłupa prostokątnego, w pobliżu graniastosłupa foremnego, w pobliżu równoległościanu prostokątnego, w pobliżu graniastosłupa prawego czworokątnego, w którym suma przeciwległych kątów podstawy wynosi 180 stopni.

Z podręcznika L.S. Atanasyana można zaproponować zadania nr 632, 633, 634, 637(a), 639(a,b) dla kombinacji kuli i pryzmatu.

Połączenie piłki z piramidą.

1. Kula opisana w pobliżu piramidy.

Twierdzenie 3. Kulę można opisać wokół piramidy wtedy i tylko wtedy, gdy można opisać okrąg wokół jej podstawy.

Wniosek 1.Środek kuli opisanej na piramidzie leży w punkcie przecięcia prostej prostopadłej do podstawy piramidy przechodzącej przez środek okręgu opisanego na tej podstawie z płaszczyzną prostopadłą do dowolnej krawędzi bocznej poprowadzonej przez środek ostrosłupa tę krawędź.

Konsekwencja 2. Jeżeli boczne krawędzie ostrosłupa są sobie równe (lub jednakowo nachylone do płaszczyzny podstawy), to wokół takiej piramidy można opisać kulę, której środek leży w tym przypadku w punkcie przecięcia wysokość ostrosłupa (lub jego przedłużenia) z osią symetrii krawędzi bocznej leżącą w płaszczyźnie krawędzi bocznej i wysokością.

Konsekwencja 3. W szczególności kulę można opisać: w pobliżu piramidy trójkątnej, w pobliżu piramidy regularnej, w pobliżu piramidy czworokątnej, w której suma przeciwległych kątów wynosi 180 stopni.

2. Kula wpisana w piramidę.

Twierdzenie 4. Jeżeli boczne ściany piramidy są równo nachylone do podstawy, wówczas w taką piramidę można wpisać kulę.

Wniosek 1.Środek kuli wpisanej w ostrosłup, którego ściany boczne są równo nachylone do podstawy, leży w punkcie przecięcia wysokości ostrosłupa z dwusieczną kąta liniowego dowolnego kąta dwuściennego u podstawy ostrosłupa, bok z czego jest wysokość ściany bocznej narysowanej od szczytu piramidy.

Konsekwencja 2. Możesz zmieścić piłkę w zwykłej piramidzie.

Z podręcznika L.S. Atanasyana można zaproponować zadania nr 635, 637(b), 638, 639(c), 640, 641 dla połączenia piłki z piramidą.

Połączenie kuli ze ściętą piramidą.

1. Kula opisana na planie regularnej ściętej piramidy.

Twierdzenie 5. Kulę można opisać wokół dowolnej regularnej ściętej piramidy. (Warunek ten jest wystarczający, ale nie konieczny)

2. Kula wpisana w regularną ściętą piramidę.

Twierdzenie 6. W regularną ściętą piramidę można wpisać kulę wtedy i tylko wtedy, gdy apotem piramidy jest równy sumie apotemów podstaw.

Jest tylko jeden problem połączenia piłki ze ściętą piramidą w podręczniku L.S. Atanasyana (nr 636).

Połączenie kuli z okrągłymi korpusami.

Twierdzenie 7. Kulę można opisać wokół walca, stożka ściętego (prostego koła) lub stożka.

Twierdzenie 8. Kulę można wpisać w (prosty okrągły) cylinder wtedy i tylko wtedy, gdy walec jest równoboczny.

Twierdzenie 9. Kulkę można zmieścić w dowolnym stożku (prostym okrągłym).

Twierdzenie 10. W stożek ścięty (prosty okrągły) można wpisać kulę wtedy i tylko wtedy, gdy jej generator jest równy sumie promieni podstaw.

Z podręcznika L.S. Atanasyana można zaproponować zadania nr 642, 643, 644, 645, 646 dotyczące połączenia piłki z okrągłymi korpusami.

Aby skuteczniej przestudiować materiał na ten temat, konieczne jest uwzględnienie na lekcjach zadań ustnych:

1. Krawędź sześcianu jest równa a. Znajdź promienie kul: wpisanych w sześcian i opisanych wokół niego. (r = a/2, R = a3).

2. Czy można opisać kulę (kulę) wokół: a) sześcianu; b) prostokątny równoległościan; c) nachylony równoległościan z prostokątem u podstawy; d) prosty równoległościan; e) nachylony równoległościan? a) tak; b) tak; c) nie; d) nie; d) nie)

3. Czy prawdą jest, że wokół dowolnej piramidy trójkątnej można opisać kulę? (Tak)

4. Czy można opisać kulę wokół dowolnej czworokątnej piramidy? (Nie, nie w pobliżu żadnej czworokątnej piramidy)

5. Jakie właściwości musi mieć piramida, aby opisać otaczającą ją kulę? (U jego podstawy powinien znajdować się wielokąt, wokół którego można opisać okrąg)

6. Piramida jest wpisana w kulę, której boczna krawędź jest prostopadła do podstawy. Jak znaleźć środek kuli? (Środkiem kuli jest punkt przecięcia dwóch geometrycznych loci punktów w przestrzeni. Pierwszy to prostopadła poprowadzona do płaszczyzny podstawy piramidy, przez środek okręgu wokół niej opisanego. Druga to płaszczyzna prostopadle do danej krawędzi bocznej i poprowadzone przez jej środek)

7. W jakich warunkach można opisać kulę wokół pryzmatu, u podstawy którego znajduje się trapez? (Po pierwsze, pryzmat musi być prosty, a po drugie, trapez musi być równoramienny, aby można było wokół niego opisać okrąg)

8. Jakie warunki musi spełniać pryzmat, aby wokół niego można było opisać kulę? (pryzmat musi być prosty, a jego podstawą musi być wielokąt, wokół którego można opisać okrąg)

9. Wokół trójkątnego pryzmatu opisano kulę, której środek leży na zewnątrz pryzmatu. Który trójkąt jest podstawą pryzmatu? (Trójkąt rozwarty)

10. Czy można opisać kulę wokół nachylonego pryzmatu? (Nie, nie możesz)

11. W jakim warunku środek kuli opisanej na prostopadłościanie trójkątnym znajdzie się na jednej z bocznych ścian pryzmatu? (Podstawą jest trójkąt prostokątny)

12. Podstawą ostrosłupa jest trapez równoramienny.Rzut ortogonalny wierzchołka piramidy na płaszczyznę podstawy to punkt znajdujący się na zewnątrz trapezu. Czy można opisać kulę wokół takiego trapezu? (Tak, można. To, że rzut wierzchołka piramidy znajduje się poza jej podstawą, nie ma znaczenia. Ważne jest, aby u podstawy piramidy znajdował się trapez równoramienny – wielokąt, wokół którego można kreślić okrąg opisane)

13. W pobliżu regularnej piramidy opisano kulę. Jak położony jest jego środek względem elementów piramidy? (Środek kuli leży na prostopadłej poprowadzonej do płaszczyzny podstawy przez jej środek)

14. W jakim stanie środek kuli opisanej wokół graniastosłupa prostokątnego leży: a) wewnątrz pryzmatu; b) poza pryzmatem? (U podstawy pryzmatu: a) ostry trójkąt; b) trójkąt rozwarty)

15. Wokół prostokątnego równoległościanu opisano kulę, której krawędzie wynoszą 1 dm, 2 dm i 2 dm. Oblicz promień kuli. (1,5 dm)

16. W jakim ściętym stożku zmieści się kula? (W stożku ściętym, w którego przekrój osiowy można wpisać okrąg. Przekrój osiowy stożka jest trapezem równoramiennym, suma jego podstaw musi być równa sumie jego boków bocznych. Innymi słowy, suma promieni podstaw stożka musi być równa generatorowi)

17. W ścięty stożek wpisano kulę. Pod jakim kątem ze środka kuli widoczna jest tworząca stożka? (90 stopni)

18. Jaką właściwość musi mieć prostopadłościan, aby można było w niego wpisać kulę? (Po pierwsze, u podstawy prostego graniastosłupa musi znajdować się wielokąt, w który można wpisać okrąg, a po drugie, wysokość pryzmatu musi być równa średnicy okręgu wpisanego w podstawę)

19. Podaj przykład piramidy, w której nie mieści się kula? (Na przykład czworokątna piramida z prostokątem lub równoległobokiem u podstawy)

20. U podstawy prostego pryzmatu znajduje się romb. Czy da się zmieścić kulę w tym pryzmacie? (Nie, to niemożliwe, bo w ogóle nie da się opisać koła wokół rombu)

21. Pod jakim warunkiem w pryzmat trójkąta prostokątnego można wpisać kulę? (Jeśli wysokość pryzmatu jest dwukrotnie większa od promienia okręgu wpisanego w podstawę)

22. Pod jakim warunkiem kula może zostać wpisana w regularną czworokątną piramidę ściętą? (Jeśli przekrój danej piramidy jest płaszczyzną przechodzącą przez środek prostopadłego do niej boku podstawy, to jest to trapez równoramienny, w który można wpisać okrąg)

23. W trójkątną ściętą piramidę wpisano kulę. Który punkt piramidy jest środkiem kuli? (Środek kuli wpisanej w tę piramidę znajduje się na przecięciu trzech dwusiecznych płaszczyzn kątów utworzonych przez boczne ściany piramidy z podstawą)

24. Czy można opisać kulę wokół walca (prawy okrągły)? (Tak, możesz)

25. Czy można opisać kulę wokół stożka, stożka ściętego (prostego koła)? (Tak, możesz, w obu przypadkach)

26. Czy w dowolny cylinder można wpisać kulę? Jakie właściwości musi mieć walec, aby zmieściła się w nim kula? (Nie, nie za każdym razem: przekrój osiowy cylindra musi być kwadratowy)

27. Czy w dowolny stożek można wpisać kulę? Jak wyznaczyć położenie środka kuli wpisanej w stożek? (Tak, absolutnie. Środek wpisanej kuli znajduje się na przecięciu wysokości stożka i dwusiecznej kąta nachylenia tworzącej do płaszczyzny podstawy)

Autor uważa, że z trzech lekcji planowania na temat „Różne problemy dotyczące wielościanów, walca, stożka i kuli” wskazane jest poświęcenie dwóch lekcji na rozwiązywanie problemów związanych z łączeniem piłki z innymi ciałami. Nie zaleca się udowadniania powyższych twierdzeń ze względu na niewystarczającą ilość czasu na zajęciach. Możesz zaprosić uczniów, którzy mają do tego wystarczające umiejętności, aby to udowodnili, wskazując (według uznania prowadzącego) przebieg lub plan dowodu.