Układy równań są szeroko stosowane w sektorze gospodarczym do matematycznego modelowania różnych procesów. Na przykład przy rozwiązywaniu problemów związanych z zarządzaniem i planowaniem produkcji, tras logistycznych (problem transportu) lub rozmieszczenia sprzętu.
Układy równań wykorzystuje się nie tylko w matematyce, ale także w fizyce, chemii i biologii przy rozwiązywaniu problemów wyznaczania wielkości populacji.
Układ równań liniowych to dwa lub więcej równań z kilkoma zmiennymi, dla których konieczne jest znalezienie wspólnego rozwiązania. Taki ciąg liczb, dla którego wszystkie równania stają się prawdziwymi równościami lub dowodzą, że ciąg nie istnieje.
Równanie liniowe
Równania w postaci ax+by=c nazywane są liniowymi. Oznaczenia x, y to niewiadome, których wartość należy znaleźć, b, a to współczynniki zmiennych, c to wolny składnik równania.
Rozwiązanie równania poprzez jego wykreślenie będzie wyglądać jak linia prosta, której wszystkie punkty są rozwiązaniami wielomianu.
Rodzaje układów równań liniowych
Za najprostsze przykłady uważa się układy równań liniowych z dwiema zmiennymi X i Y.
F1(x, y) = 0 i F2(x, y) = 0, gdzie F1,2 to funkcje, a (x, y) to zmienne funkcyjne.
Rozwiązać układ równań - oznacza to znalezienie wartości (x, y), przy których układ zamienia się w prawdziwą równość lub ustalenie, że odpowiednie wartości x i y nie istnieją.
Para wartości (x, y), zapisana jako współrzędne punktu, nazywana jest rozwiązaniem układu równań liniowych.
Jeśli systemy mają jedno wspólne rozwiązanie lub nie ma żadnego rozwiązania, nazywa się je równoważnymi.
Jednorodne układy równań liniowych to układy, których prawa strona jest równa zeru. Jeżeli prawa część po znaku równości ma wartość lub jest wyrażona funkcją, to taki układ jest heterogeniczny.
Liczba zmiennych może być znacznie większa niż dwie, wówczas powinniśmy mówić o przykładzie układu równań liniowych z trzema lub większą liczbą zmiennych.
W obliczu systemów uczniowie zakładają, że liczba równań musi koniecznie pokrywać się z liczbą niewiadomych, ale tak nie jest. Liczba równań w układzie nie zależy od zmiennych; może ich być tyle, ile potrzeba.
Proste i złożone metody rozwiązywania układów równań
Nie ma ogólnej metody analitycznej rozwiązywania takich układów; wszystkie metody opierają się na rozwiązaniach numerycznych. Szkolny kurs matematyki szczegółowo opisuje takie metody jak permutacja, dodawanie algebraiczne, podstawienie, a także metody graficzne i macierzowe, rozwiązanie metodą Gaussa.
Głównym zadaniem nauczania metod rozwiązywania problemów jest nauczenie prawidłowej analizy systemu i znalezienia optymalnego algorytmu rozwiązania dla każdego przykładu. Najważniejsze nie jest zapamiętywanie systemu zasad i działań dla każdej metody, ale zrozumienie zasad stosowania konkretnej metody
Rozwiązywanie przykładów układów równań liniowych w programie nauczania ogólnego w klasie VII jest dość proste i szczegółowo wyjaśnione. W każdym podręczniku do matematyki tej sekcji poświęca się wystarczająco dużo uwagi. Rozwiązywanie przykładów układów równań liniowych metodą Gaussa i Cramera jest szerzej studiowane na pierwszych latach studiów wyższych.
Rozwiązywanie układów metodą podstawieniową
Działania metody podstawieniowej mają na celu wyrażenie wartości jednej zmiennej za pomocą drugiej. Wyrażenie podstawiamy do pozostałego równania, a następnie sprowadzamy do postaci z jedną zmienną. Czynność powtarza się w zależności od ilości niewiadomych w systemie
Podajmy rozwiązanie przykładowego układu równań liniowych klasy 7 metodą podstawieniową:
Jak widać na przykładzie zmienną x wyrażono poprzez F(X) = 7 + Y. Powstałe wyrażenie, podstawione w miejsce X do 2. równania układu, pozwoliło otrzymać w 2. równaniu jedną zmienną Y . Rozwiązanie tego przykładu jest łatwe i pozwala uzyskać wartość Y. Ostatnim krokiem jest sprawdzenie otrzymanych wartości.
Nie zawsze możliwe jest rozwiązanie przykładowego układu równań liniowych przez podstawienie. Równania mogą być złożone i wyrażenie zmiennej w kategoriach drugiej niewiadomej będzie zbyt kłopotliwe do dalszych obliczeń. Jeżeli w systemie są więcej niż 3 niewiadome, rozwiązywanie przez podstawienie również jest niewłaściwe.
Rozwiązanie przykładowego układu równań liniowych niejednorodnych:
Rozwiązanie wykorzystujące dodawanie algebraiczne
Szukając rozwiązań układów metodą dodawania, równania dodaje się termin po wyrazie i mnoży przez różne liczby. Ostatecznym celem operacji matematycznych jest równanie z jedną zmienną.
Stosowanie tej metody wymaga praktyki i obserwacji. Rozwiązywanie układu równań liniowych metodą dodawania, gdy występują 3 lub więcej zmiennych, nie jest łatwe. Dodawanie algebraiczne jest wygodne w użyciu, gdy równania zawierają ułamki zwykłe i dziesiętne.
Algorytm rozwiązania:
- Pomnóż obie strony równania przez określoną liczbę. W wyniku operacji arytmetycznej jeden ze współczynników zmiennej powinien przyjąć wartość 1.
- Dodaj wynikowe wyrażenie termin po terminie i znajdź jedną z niewiadomych.
- Podstaw uzyskaną wartość do drugiego równania układu, aby znaleźć pozostałą zmienną.
Metoda rozwiązania poprzez wprowadzenie nowej zmiennej
Nową zmienną można wprowadzić, jeśli układ wymaga znalezienia rozwiązania nie więcej niż dwóch równań; liczba niewiadomych również nie powinna być większa niż dwie.
Metodę tę stosuje się w celu uproszczenia jednego z równań poprzez wprowadzenie nowej zmiennej. Nowe równanie rozwiązuje się dla wprowadzonej niewiadomej, a otrzymaną wartość wykorzystuje się do wyznaczenia pierwotnej zmiennej.
Przykład pokazuje, że wprowadzając nową zmienną t, możliwe było sprowadzenie pierwszego równania układu do standardowego trójmianu kwadratowego. Wielomian można rozwiązać, znajdując dyskryminator.
Wartość dyskryminatora należy znaleźć ze znanego wzoru: D = b2 - 4*a*c, gdzie D jest pożądanym wyróżnikiem, b, a, c są współczynnikami wielomianu. W podanym przykładzie a=1, b=16, c=39, zatem D=100. Jeśli dyskryminator jest większy od zera, to są dwa rozwiązania: t = -b±√D / 2*a, jeśli dyskryminator jest mniejszy od zera, to jest jedno rozwiązanie: x = -b / 2*a.
Rozwiązanie dla powstałych układów można znaleźć metodą addycji.
Wizualna metoda rozwiązywania układów
Nadaje się do 3 układów równań. Metoda polega na konstruowaniu wykresów każdego równania wchodzącego w skład układu na osi współrzędnych. Współrzędne punktów przecięcia krzywych będą rozwiązaniem ogólnym układu.
Metoda graficzna ma wiele niuansów. Przyjrzyjmy się kilku przykładom rozwiązywania układów równań liniowych w sposób wizualny.
Jak widać na przykładzie, dla każdej prostej skonstruowano dwa punkty, arbitralnie wybrano wartości zmiennej x: 0 i 3. Na podstawie wartości x znaleziono wartości dla y: 3 i 0. Na wykresie zaznaczono punkty o współrzędnych (0, 3) i (3, 0) i połączono je linią.
Kroki należy powtórzyć dla drugiego równania. Punkt przecięcia prostych jest rozwiązaniem układu.
Poniższy przykład wymaga znalezienia graficznego rozwiązania układu równań liniowych: 0,5x-y+2=0 i 0,5x-y-1=0.
Jak widać na przykładzie układ nie ma rozwiązania, ponieważ wykresy są równoległe i nie przecinają się na całej długości.
Układy z przykładów 2 i 3 są podobne, ale po zbudowaniu staje się oczywiste, że ich rozwiązania są różne. Należy pamiętać, że nie zawsze można stwierdzić, czy układ ma rozwiązanie, czy nie, zawsze konieczne jest skonstruowanie grafu.
Macierz i jej odmiany
Macierze służą do zwięzłego pisania układu równań liniowych. Macierz to specjalny rodzaj tabeli wypełnionej liczbami. n*m ma n - wierszy i m - kolumn.
Macierz jest kwadratowa, gdy liczba kolumn i wierszy jest równa. Macierz-wektor jest macierzą jednokolumnową z nieskończenie możliwą liczbą wierszy. Macierz z jedynkami wzdłuż jednej z przekątnych i innymi elementami zerowymi nazywa się tożsamością.
Macierz odwrotna to macierz, przez którą pierwotna macierz zamienia się w macierz jednostkową; taka macierz istnieje tylko dla pierwotnej kwadratowej.
Zasady przekształcania układu równań w macierz
W odniesieniu do układów równań współczynniki i wyrazy wolne równań zapisuje się jako liczby macierzowe; jedno równanie odpowiada jednemu wierszowi macierzy.
Mówi się, że wiersz macierzy jest niezerowy, jeśli przynajmniej jeden element wiersza jest różny od zera. Dlatego jeśli w którymkolwiek z równań liczba zmiennych jest różna, wówczas w miejsce brakującej niewiadomej należy wpisać zero.
Kolumny macierzy muszą ściśle odpowiadać zmiennym. Oznacza to, że współczynniki zmiennej x można zapisać tylko w jednej kolumnie, np. w pierwszej, współczynnik nieznanej y - tylko w drugiej.
Podczas mnożenia macierzy wszystkie elementy macierzy są kolejno mnożone przez liczbę.
Opcje znajdowania macierzy odwrotnej
Wzór na znalezienie macierzy odwrotnej jest dość prosty: K -1 = 1 / |K|, gdzie K -1 jest macierzą odwrotną, a |K| jest wyznacznikiem macierzy. |K| nie może być równe zero, wówczas układ ma rozwiązanie.
Wyznacznik można łatwo obliczyć dla macierzy dwa na dwa; wystarczy pomnożyć elementy przekątne przez siebie. Dla opcji „trzy na trzy” istnieje wzór |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + za 3 b 2 do 1 . Możesz skorzystać ze wzoru lub pamiętać, że musisz wziąć po jednym elemencie z każdego wiersza i każdej kolumny, aby w pracy nie powtarzały się numery kolumn i rzędów elementów.
Rozwiązywanie przykładów układów równań liniowych metodą macierzową
Macierzowa metoda znajdowania rozwiązania pozwala na ograniczenie uciążliwych wpisów przy rozwiązywaniu układów z dużą liczbą zmiennych i równań.
W przykładzie a nm to współczynniki równań, macierz to wektor. x n to zmienne, a b n to terminy wolne.
Rozwiązywanie układów metodą Gaussa
W matematyce wyższej metodę Gaussa bada się łącznie z metodą Cramera, a proces znajdowania rozwiązań układów nazywa się metodą rozwiązań Gaussa-Cramera. Metody te służą do znajdowania zmiennych układów o dużej liczbie równań liniowych.
Metoda Gaussa jest bardzo podobna do rozwiązań metodą podstawienia i dodawania algebraicznego, ale jest bardziej systematyczna. Na zajęciach szkolnych stosuje się rozwiązanie metodą Gaussa dla układów 3 i 4 równań. Celem metody jest zredukowanie układu do postaci odwróconego trapezu. Za pomocą przekształceń algebraicznych i podstawień wartość jednej zmiennej znajduje się w jednym z równań układu. Drugie równanie jest wyrażeniem z 2 niewiadomymi, natomiast 3 i 4 z 3 i 4 zmiennymi.
Po doprowadzeniu układu do opisanej postaci dalsze rozwiązanie sprowadza się do sekwencyjnego podstawienia znanych zmiennych do równań układu.
W podręcznikach szkolnych dla klasy 7 przykład rozwiązania metodą Gaussa opisano w następujący sposób:
Jak widać na przykładzie, w kroku (3) otrzymano dwa równania: 3x 3 -2x 4 =11 i 3x 3 +2x 4 =7. Rozwiązanie któregokolwiek z równań pozwoli ci znaleźć jedną ze zmiennych x n.
Twierdzenie 5, o którym mowa w tekście, stwierdza, że jeśli jedno z równań układu zostanie zastąpione równaniem równoważnym, to powstały układ również będzie równoważny pierwotnemu.
Metoda Gaussa jest trudna do zrozumienia dla gimnazjalistów, ale jest jednym z najciekawszych sposobów rozwijania pomysłowości dzieci zapisanych do zaawansowanych programów nauczania na lekcjach matematyki i fizyki.
Aby ułatwić rejestrację, obliczenia zwykle wykonuje się w następujący sposób:
Współczynniki równań i wyrazy wolne zapisuje się w postaci macierzy, gdzie każdemu wierszowi macierzy odpowiada jedno z równań układu. oddziela lewą stronę równania od prawej. Cyfry rzymskie wskazują numery równań w układzie.
Najpierw zapisz macierz, z którą będziesz pracować, a następnie wszystkie czynności wykonane z jednym z wierszy. Otrzymaną macierz zapisuje się po znaku „strzałki” i kontynuuje niezbędne działania algebraiczne aż do uzyskania wyniku.
Wynikiem powinna być macierz, w której jedna z przekątnych jest równa 1, a wszystkie pozostałe współczynniki są równe zeru, to znaczy macierz jest zredukowana do postaci jednostkowej. Nie możemy zapomnieć o wykonaniu obliczeń z liczbami po obu stronach równania.
Ta metoda rejestrowania jest mniej uciążliwa i pozwala nie rozpraszać się wypisywaniem wielu niewiadomych.
Swobodne korzystanie z dowolnej metody rozwiązania będzie wymagało ostrożności i pewnego doświadczenia. Nie wszystkie metody mają charakter stosowany. Niektóre metody znajdowania rozwiązań są bardziej preferowane w określonym obszarze działalności człowieka, inne istnieją w celach edukacyjnych.
Metoda Gaussa rozwiązywania układów liniowych równań algebraicznych polega na sekwencyjnym eliminowaniu niewiadomych za pomocą przekształceń elementarnych i sprowadzaniu ich do równania górnego trójkąta (schodkowego lub trapezowego). Następnie rozwiązują układ od końca do początku, podstawiając znalezione rozwiązania.
Rozważmy przykłady rozwiązywania układów równań liniowych metodą Gaussa, wykorzystując jako odniesienie zbiór problemów V.P. Dubovika, I.I. "Wyższa matematyka".
-------------
Rozwiązać układ liniowych równań algebraicznych.
1) Przekształćmy pierwotny system do postaci stopniowej. Aby to zrobić, od drugiego równania odejmujemy pierwsze pomnożone przez 3, a od czwartego odejmujemy pierwsze pomnożone przez 4.
W rezultacie mamy trzecie równanie. Podstawiamy otrzymaną wartość do pierwotnego równania, aby znaleźć
Otrzymane wartości podstawiamy do pierwszego równania
Rozwiązaniem układu trzech równań liniowych będą następujące wartości zmiennych
2) Mamy układ trzech równań z czterema niewiadomymi. W takich przypadkach jedna zmienna może być wolna, a reszta będzie przez nią wyrażona. Sprowadźmy system do postaci krokowej. Aby to zrobić, odejmij pierwsze od drugiego i trzeciego równania
Z dwóch ostatnich równań otrzymujemy identyczne rozwiązania
Po podstawieniu do pierwszego równania otrzymujemy
To równanie wiąże trzy zmienne. Zatem dowolną ze zmiennych można wyrazić w kategoriach pozostałych dwóch
Otrzymujemy więc następujące rozwiązanie
3) Mamy rzadki układ równań liniowych piątego rzędu z pięcioma niewiadomymi. Sprowadźmy to do postaci krokowej. Z drugiego równania odejmujemy pierwsze i zapisujemy je w formie dogodnej do analizy
Z drugiego równania dowiadujemy się, że . Podstawiamy wartości do wszystkich niższych równań i przenosimy je poza znak równości. Zamieńmy także drugie i trzecie równanie
Równanie czwarte i piąte są równoważne. Wyraźmy jedną ze zmiennych za pomocą drugiej
Podstawiamy wynikową wartość do drugiego równania i znajdujemy
Z pierwszego równania ustalamy
Rozwiązanie układu równań jest następujące
Przy obliczaniu układów liniowych równań algebraicznych metodą Gaussa konieczne jest sprowadzenie układu równań liniowych do postaci krokowej. Aby to zrobić, wygodnie jest zapisywać zmienne pod zmiennymi, ponieważ w ostatnim przykładzie przyspieszy to rozwiązanie. Reszta zależy od matrycy do rozwiązania i Twoich umiejętności.
Układ m równań liniowych z n niewiadomymi zwany systemem formy
Gdzie ij I b ja (I=1,…,M; B=1,…,N) to kilka znanych liczb, i x 1 ,…,x rz- nieznany. W wyznaczaniu współczynników ij pierwszy indeks I oznacza numer równania, a drugi J– liczba niewiadomych, przy której stoi ten współczynnik.
Współczynniki niewiadomych zapiszemy w postaci macierzy 
, który nazwiemy macierz układu.
Liczby po prawej stronie równań to b 1 ,…,b m są nazywane wolni członkowie.
Całość N liczby do 1 ,…,c n zwany decyzja danego układu, jeżeli każde równanie układu staje się równością po podstawieniu do niego liczb do 1 ,…,c n zamiast odpowiednich niewiadomych x 1 ,…,x rz.
Naszym zadaniem będzie znalezienie rozwiązań dla systemu. W takim przypadku mogą zaistnieć trzy sytuacje:
Układ równań liniowych, który ma co najmniej jedno rozwiązanie nazywa się wspólny. W przeciwnym razie, tj. jeśli system nie ma rozwiązań, nazywa się go nie wspólne.
Zastanówmy się, jak znaleźć rozwiązania dla systemu.
METODA MATRYCOWA ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH
Macierze umożliwiają krótkie zapisanie układu równań liniowych. Niech będzie dany układ 3 równań z trzema niewiadomymi:
Rozważmy macierz systemu 
i macierze kolumny nieznanych i wolnych terminów 
Znajdźmy pracę
te. w wyniku iloczynu otrzymujemy lewe strony równań tego układu. Następnie korzystając z definicji równości macierzy układ ten można zapisać w postaci
lub krócej A∙X=B.
Oto macierze A I B są znane, oraz macierz X nieznany. Trzeba go znaleźć, bo... jego elementy są rozwiązaniem tego systemu. To równanie nazywa się równanie macierzowe.
Niech wyznacznik macierzy będzie różny od zera | A| ≠ 0. Następnie równanie macierzowe rozwiązuje się w następujący sposób. Pomnóż obie strony równania po lewej stronie przez macierz A-1, odwrotność macierzy A: . Ponieważ A -1 A = E I mi∙X = X, wówczas otrzymujemy rozwiązanie równania macierzowego w postaci X = A -1 B .
Należy zauważyć, że ponieważ macierz odwrotną można znaleźć tylko dla macierzy kwadratowych, metoda macierzowa może rozwiązać tylko te układy, w których liczba równań pokrywa się z liczbą niewiadomych. Jednakże macierzowy zapis układu jest możliwy również w przypadku, gdy liczba równań nie jest równa liczbie niewiadomych, wówczas macierz A nie będzie kwadratowy i dlatego nie da się znaleźć rozwiązania układu w postaci X = A -1 B.
Przykłady. Rozwiązywać układy równań.
REGUŁA CRAMERA
Rozważmy układ 3 równań liniowych z trzema niewiadomymi:
Wyznacznik trzeciego rzędu odpowiadający macierzy układu, tj. złożony ze współczynników niewiadomych,
zwany wyznacznik systemu.
Skomponujmy jeszcze trzy wyznaczniki w następujący sposób: zamień kolejno 1, 2 i 3 kolumny w wyznaczniku D na kolumnę wolnych terminów
Następnie możemy udowodnić następujący wynik.
Twierdzenie (reguła Cramera). Jeżeli wyznacznik układu Δ ≠ 0, to rozpatrywany układ ma jedno i tylko jedno rozwiązanie, a
Dowód. Rozważmy więc układ trzech równań z trzema niewiadomymi. Pomnóżmy pierwsze równanie układu przez dopełnienie algebraiczne 11 element 11, 2 równanie – włączone 21 i 3. – dalej 31:
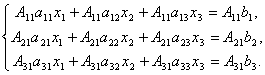
Dodajmy te równania:
Przyjrzyjmy się każdemu z nawiasów i prawej stronie tego równania. Według twierdzenia o rozwinięciu wyznacznika w elementach pierwszej kolumny
Podobnie można wykazać, że i .
Wreszcie łatwo to zauważyć 
Otrzymujemy zatem równość: .
Stąd, .
Równości i wyprowadza się w podobny sposób, z czego wynika stwierdzenie twierdzenia.
Zauważamy zatem, że jeśli wyznacznik układu Δ ≠ 0, to układ ma rozwiązanie jednoznaczne i odwrotnie. Jeżeli wyznacznik układu jest równy zeru, to układ albo ma nieskończoną liczbę rozwiązań, albo nie ma żadnych rozwiązań, tj. niekompatybilny.
Przykłady. Rozwiązać układ równań
METODA GAUssa
Omówione wcześniej metody można stosować do rozwiązywania tylko tych układów, w których liczba równań pokrywa się z liczbą niewiadomych, a wyznacznik układu musi być różny od zera. Metoda Gaussa jest bardziej uniwersalna i odpowiednia dla układów o dowolnej liczbie równań. Polega ona na konsekwentnym eliminowaniu niewiadomych z równań układu.
Rozważmy ponownie układ trzech równań z trzema niewiadomymi:
.
Pierwsze równanie pozostawimy bez zmian, a z drugiego i trzeciego wykluczymy terminy zawierające x 1. Aby to zrobić, podziel drugie równanie przez A 21 i pomnóż przez – A 11, a następnie dodaj go do pierwszego równania. Podobnie dzielimy trzecie równanie przez A 31 i pomnóż przez – A 11, a następnie dodaj go do pierwszego. W efekcie oryginalny system przyjmie postać:
Teraz z ostatniego równania eliminujemy termin zawierający x 2. Aby to zrobić, podziel trzecie równanie przez, pomnóż przez drugie i dodaj z drugim. Wtedy będziemy mieli układ równań:
Stąd z ostatniego równania łatwo jest znaleźć x 3, to z drugiego równania x 2 i wreszcie, od 1-go - x 1.
W przypadku stosowania metody Gaussa równania można w razie potrzeby zamienić.
Często zamiast pisać nowy układ równań ograniczają się do napisania rozszerzonej macierzy układu:
a następnie doprowadź go do postaci trójkątnej lub ukośnej za pomocą elementarnych przekształceń.
DO elementarne przemiany macierze obejmują następujące przekształcenia:
- przestawianie wierszy lub kolumn;
- mnożenie ciągu przez liczbę inną niż zero;
- dodanie innych linii do jednej linii.
Przykłady: Rozwiązywać układy równań metodą Gaussa.
Zatem układ ma nieskończoną liczbę rozwiązań.
5.1. Reguła CrameraPo ustaleniu podstawowych własności i metod obliczania wyznaczników macierzy dowolnego rzędu wróćmy do zadania głównego - rozwiązywania i badania układów równań pierwszego rzędu. Rozpocznijmy badanie tego zagadnienia od analizy głównego przypadku, gdy liczba równań pokrywa się z liczbą niewiadomych.
Pomnóżmy wszystkie wyrazy pierwszego równania układu (1) przez A 11 - dopełnienie algebraiczne elementu A 11 macierzy A, wszystkie wyrazy 2 równania układu (1) na A 21 - uzupełnienie algebraiczne elementu A 21 macierzy A wreszcie wszystkie wyrazy n-tego równania układu (1) na A n1 - uzupełnienie algebraiczne elementu A n1 macierzy A. Otrzymujemy wówczas układ
(1")
Dodajmy wszystkie równania układu termin po wyrazie, otrzymamy
(
A i1 A i1)x 1 +( A i2 A i1)x 2 +...+( A w A i1)x n =b i A i1
Zgodnie z twierdzeniem o dopełnieniach algebraicznych mamy
A i1 A i1 = det A A i2 A i1 =0,..........., A w A i1 =0
Dlatego powstałe równanie można przepisać w postaci 
Rozważ macierz
,
Otrzymane z macierzy A poprzez zastąpienie elementów pierwszej kolumny kolumną wolnych wyrazów równań układu. Rozwijając det B1 na elementy pierwszej kolumny, otrzymujemy det B 1 =b i A i1 , a zatem 
Podobnie mnożąc równania układu (1) przez Аі2 (u=1, 2, ... n) i dodając je otrzymujemy 
,
Robiąc to w przyszłości, otrzymamy układ równań
(2),
Gdzie macierz Bk otrzymuje się z A poprzez zastąpienie k-tej kolumny kolumną wolnych terminów. Oczywiście każde rozwiązanie układu (1) jest również rozwiązaniem układu (2).
(3)
Przypomnijmy, że wzory (3) otrzymano przy założeniu, że układ (1) ma rozwiązanie. Podstawiając bezpośrednio znalezione wartości X i do układu (1), można sprawdzić, czy są one rozwiązaniem układu (1), a zatem przy założeniu, że 
, układ (1) ma rozwiązanie i to w dodatku unikalne.
^ Twierdzenie (twierdzenie Cramera): jeśli wyznacznik macierzy głównej układu n równań pierwszego rzędu z n niewiadomymi jest różny od zera, to układ ma jednoznaczne rozwiązanie. W tym przypadku wartość każdej z niewiadomych jest równa części podziału wyznaczników dwóch macierzy: w mianowniku znajduje się wyznacznik macierzy głównej układu, a w liczniku wyznacznik uzyskanej macierzy z głównej macierzy systemu poprzez zastąpienie kolumny odpowiadającej wybranej niewiadomej kolumną wolnych terminów.
Z twierdzenia tego wynika, że jeżeli układ równań jest jednorodny, to znaczy wolne wyrazy we wszystkich równaniach układu są równe zeru i jeżeli wyznacznik macierzy głównej układu jest różny od zera, to układ ma tylko rozwiązanie zerowe. Rzeczywiście w tym przypadku macierze, których wyznaczniki znajdują się w liczniku wzorów (3), zawierają kolumnę zawierającą tylko zera, a zatem wszystkie liczby X i są równe zero. Z tego, co zostało udowodnione, wynika następujące twierdzenie:
^ Jeżeli układ n jednorodnych równań pierwszego rzędu z n niewiadomymi ma co najmniej jedno rozwiązanie niezerowe, to wyznacznik macierzy głównej układu jest równy zero. Rzeczywiście, gdyby ten wyznacznik nie był równy zeru, wówczas układ miałby tylko rozwiązanie zerowe, co jest sprzeczne z warunkiem.
W dalszej części udowodnimy, że równość wyznacznika układu do zera jest nie tylko obowiązkowym, koniecznym warunkiem istnienia niezerowego rozwiązania, ale także warunkiem wystarczającym istnienia takiego rozwiązania. Innymi słowy, jeśli wyznacznik układu równań jednorodnych jest równy zeru, to układ ma niezerowe rozwiązanie (i nieskończoną liczbę takich rozwiązań).
^ 5.2. Rozwiązywanie i badanie układów równań pierwszego rzędu metodą eliminacji całkowitej (metoda Gaussa).
Wzory Cramera pozwalają, stosując metodę obliczania wyznaczników, znaleźć wartości liczbowe rozwiązania układu równań w przypadku, gdy wyznacznik macierzy głównej układu jest różny od zera. Jednak praktyczne zastosowanie tych wzorów jest w wielu przypadkach skomplikowane. Przede wszystkim należy zaznaczyć, że aby znaleźć rozwiązania korzystając ze wzorów (3), konieczne jest obliczenie n+1 wyznaczników n-tego rzędu, co jest pracą dość pracochłonną, nawet przy zastosowaniu technik wskazanych w § 4. Ale najważniejsze jest to, że w przypadku, gdy współczynniki równania są podane w przybliżeniu (w rzeczywistych problemach prawie zawsze tak się dzieje), błąd w rozwiązaniu może być dość duży. Wyjaśnia to fakt, że wyrazy zawarte w każdym z wyznaczników, za pomocą których wyznaczane jest rozwiązanie układu, mogą być dość duże (pamiętajmy, że są iloczynem n czynników - różnych współczynników rozszerzonej macierzy układu ) i sam wyznacznik, który jest sumą algebraiczną, takie wyrazy mogą być małe. Nawet w przypadku, gdy współczynniki w układzie równań początkowych są dokładnie znane, ale same obliczenia przeprowadza się z uwzględnieniem tylko określonej liczby cyfr znaczących, z tych samych powodów możemy otrzymać dość duże błędy w wyniku. Dlatego w praktycznym rozwiązywaniu układów równań w większości przypadków nie stosuje się wzorów Cramera, ale inne metody obliczeniowe.
Na tym kursie omówimy metodę eliminacji całkowitej w zakresie rozwiązywania układów równań pierwszego rzędu także w przypadku, gdy liczba równań nie pokrywa się z liczbą niewiadomych. Ale zaczniemy prezentację tej metody od przypadku głównego: gdy liczba równań pokrywa się z liczbą niewiadomych.
Zatem ponownie otrzymamy układ n równań z n niewiadomymi:
(1)
Ponieważ co najmniej jeden ze współczynników A i1 jest różne od zera (w przeciwnym razie x1 w ogóle nie byłoby ujęte w układzie), a równania w układzie można zamieniać, to bez ograniczeń ogólności możemy założyć, że 
Podzielmy pierwsze równanie układu przez a11 i sprowadźmy je do postaci:
Mnożenie wszystkich wyrazów wynikowego równania przez ai1 i odejmowanie od і równaniu układu (1) otrzymujemy nowy układ
(2),
i=1, 2, ..., n; k=1, 2, ..., n
Ponieważ równania układu (2) otrzymujemy jako kombinacje liniowe równań układu (1), to każde rozwiązanie układu (1) jest również rozwiązaniem układu (2). Jednocześnie od
Wówczas równania układu (1) można otrzymać jako kombinację liniową równań układu (2). W konsekwencji każde rozwiązanie układu (2) jest również rozwiązaniem układu (1). Zatem systemy (1) i (2) są równoważne. (Kombinacja liniowa dwóch równań z 11 x 1 +c 12 x 2 +...+c 1n x n =d 1 i, z 21 x 1 +c 22 x 2 +...+c 2n x n =d 2 będzie nazwać równaniem 1 (c 11 x 1 +c 12 x 2 +...+c 1n x n) + 2 (c 21 x 1 +c 22 x 2 +...+c 2n x n)= 1 d 1 + 2 d 2, gdzie 1 i 2 to liczby)
Porównajmy teraz wyznaczniki D1 i D2 głównych macierzy układów (1) i (2). Pierwszy wiersz głównej macierzy układu (2) otrzymujemy z pierwszego wiersza głównej macierzy układu (1) dzieląc przez A jedenaście. Ta operacja odpowiada podzieleniu D1 przez a11. Pozostałe wiersze uzyskuje się poprzez odjęcie od odpowiednich wierszy macierzy głównej układu (1) wartości proporcjonalnych do pierwszego wiersza. Operacja ta nie zmienia wartości wyznacznika. Wynika z tego, że wyznacznik D2 macierzy głównej układu (2) jest równy 
. I dlatego 
, Jeśli 
i D2=0, jeśli D1=0. Na koniec zauważamy, że obliczenia przeprowadziliśmy tylko ze współczynnikami równań układu (1), więc nie ma potrzeby zapisywania samych równań. Wystarczy napisać tylko rozszerzoną macierz układu i przekształcić tylko elementy tej macierzy.
Przejście z jednej rozszerzonej macierzy do drugiej, czyli w istocie przejście z jednego układu równań do układu mu równoważnego, będziemy oznaczać symbolem 
Lub 
.
Następnie wykonane operacje można zapisać w następujący sposób:
Założymy najpierw, że wyznacznik D1 macierzy głównej układu (1) jest różny od zera. Następnie, jak stwierdzono powyżej, 
, a zatem w skrajnych przypadkach jedną z liczb 
(u=1, 2, ... , n) jest różne od zera, gdyż gdyby wszystkie były równe zeru, wyznacznik D2 macierzy głównej układu (2) również byłby równy zeru.
Ponieważ równania w układzie (2) można zamieniać, zatem bez ograniczeń możemy to założyć 
. Podzielmy drugie równanie układu (2) przez 
,
pomnóż otrzymaną linię przez (i=1, 3, 4, ... , n) i odejmij ją od i-tej linii.
Wtedy będziemy mieli
Układ równań odpowiadający macierzy B 3 jest równoważny układowi (2), a zatem układowi pierwotnemu (1). Wyznacznik D3 macierzy głównej tego układu jest niezerowy, ponieważ wyznacznik D2 jest niezerowy. Stąd w skrajnych przypadkach jedna z liczb 
(u=3, ... , n) jest różne od zera i można ponownie przeprowadzić te same operacje, co poprzednio. Kontynuując podobne rozważania, po n operacjach otrzymujemy macierz
Odpowiedni układ równań ma postać
(3),
Jedynym rozwiązaniem jest (4)
Ponieważ układ (3) jest równoważny układowi (1) i ma jednoznaczne rozwiązanie, to pierwotny układ (1) również ma jednoznaczne rozwiązanie, które wyznaczają wzory (4).
Przykład 1 . Rozwiąż system
Rozwiązanie
x1=1; x2=-1; x3=0; x4=2
Należy zauważyć, że jeśli układ jest jednorodny, czyli wszystkie liczby bi (u=1, 2, ..., n) są równe zeru, to wszystkie liczby są równe zeru 
Zatem układ (1) ma w tym przypadku tylko rozwiązanie zerowe.
Niech teraz wyznacznik D1 macierzy głównej układu (1) będzie równy zero. Wtedy nie da się już tego powiedzieć wśród liczb 
(u=m, m+1, ... , n) otrzymane po (m-1)-tym etapie przekształceń, będzie co najmniej jeden różny od zera. Co więcej, na pewnym etapie wszystkie te liczby na pewno staną się równe zeru (w przeciwnym razie mielibyśmy inny przypadek). W ten sposób otrzymamy macierz
Przestawmy m-tą kolumnę macierzy na miejsce n-tej i wszystkie następujące po m-tej kolumnie, z wyjątkiem kolumny wolnych wyrazów 
przesuńmy się o jedno miejsce w lewo (taka operacja oznacza oczywiście przestawienie niewiadomych w równaniach układu lub ich przenumerowanie, co oczywiście nie zmienia rozwiązania układu). W rezultacie otrzymujemy macierz
,
I=1, 2, ..., n;
k=m, m+1, ..., n.
Kontynuując te same przekształcenia co poprzednio, ostatecznie otrzymujemy macierz
(5)
Macierz (5) odpowiada układowi równań
(6),
w którym nieznane 
inny niż nieznany X і
w systemie (1) tylko poprzez numerację. Ponieważ układ (6) jest równoważny układowi (1), to wniosek o rozwiązaniu układu (1) jest równoznaczny z wnioskiem o rozwiązaniu układu (6).
Oczywiście, jeśli przynajmniej jedna z liczb 
(u=k+1, ... , n) nie jest równe zeru, to równania układu (6), a co za tym idzie, równania układu (1), są niezgodne. Jeśli wszystkie (i=k+1, ... , n) są równe zeru, to równania są spójne. Jednocześnie nieznany 
Można podawać dowolne wartości, a układ posiada następujące rozwiązania:
,
gdzie t1, t2, ... , te ( 
=n-k) dowolne
Aby ułatwić powrót do pierwotnego układu niewiadomych, warto zapisać oznaczenia odpowiednich niewiadomych nad kolumnami macierzy uzyskanymi podczas przekształceń. Zwracamy również uwagę, że jeśli pierwotny układ (1) jest jednorodny, to wszystkie liczby (u=1, 2, ..., n) są równe zeru. Dlatego też obowiązują następujące dwa stwierdzenia.
1. Układ równań jednorodnych pierwszego rzędu jest zawsze spójny.
2. Jeżeli wyznacznik układu równań jednorodnych pierwszego rzędu jest równy zero, to układ ma nieskończoną liczbę rozwiązań.
Przykład 2
Rozwiązanie
Układ równań odpowiadający otrzymanej macierzy ma postać:
Układ jest spójny, x4=t jest dowolny. Układ ma nieskończoną liczbę rozwiązań
gdzie t jest dowolną liczbą.
Należy zauważyć, że jeśli wolne terminy w równaniach byłyby inne niż te określone w warunku, system mógłby być niekompatybilny. Niech na przykład b4=1. Wtedy będzie przekształcona macierz układu
a ostatnie równanie układu będzie miało postać 0x1+0x2+0x3+0x4=1, co nie ma sensu.
Przykład 3.
Rozwiązanie.
Układ jest zgodny, x2=t jest dowolne; x1=1-t, x2=t, x3=-2, x4=1.
Analizowaną metodę można przenieść bez zmian na przypadek, gdy liczba niewiadomych nie pokrywa się z liczbą równań.
II. Przykłady rozwiązywania problemów
1,20. Rozwiąż system
Obliczmy wyznacznik układu
Ponieważ wyznacznik układu jest różny od zera, stosujemy regułę Cramera. Aby obliczyć wyznacznik detB1, zastępujemy kolumnę 
wyznacznik systemu za pomocą kolumny wolnych terminów 
. Mamy
Wyznacznik detB2 otrzymuje się przez zastąpienie kolumny 
wyznacznik systemu za pomocą kolumny wolnych terminów:
Zgodnie z regułą Cramera znajdujemy 
; 
Jedynym rozwiązaniem tego układu jest zbiór liczb (5;-4).
1.21. Znajdź rozwiązania systemowe
Wyznacznik współczynników układu innych niż zero:
deA= 
=2·3·(-5)+5·(-9) ·2+(-8) ·4·3-(-8) ·3·2-5·4·(-5)-2·3· (-9)=-140
Możemy zatem zastosować regułę Cramera
stąd znajdziemy 
; 
; 
Zbiór liczb (3, 2, 1) jest jedynym rozwiązaniem układu.
1,22. Rozwiąż system
/IVp+II-I-III/ ~
Łatwo zauważyć, że wyznacznik współczynników układu jest równy zeru, gdyż jego czwarty rząd składa się z zer. Ostatni wiersz rozszerzonej macierzy wskazuje, że system nie jest kompatybilny.
1,23. Rozwiąż system
Zapiszmy rozszerzoną macierz układu
/IIp. -2· I, IIIp. -I, IVp. -II-III/ ~
~
/divide ІІІр. w (-3), IVp. o (-3)/
~
/ІІІр. +2· ІІ/ ~
W wyniku wszystkich przekształceń ten układ równań liniowych został zredukowany do postaci trójkątnej.
Ma tylko jedno rozwiązanie.
x3=1 x4=-1 x2=-2 x1=2 ▲
Równania są zgodne, x4=t jest dowolne,
1,25. Znajdź rozwiązania systemowe
Układ jest spójny, x4=t jest dowolny,
1,26. Rozwiąż system
Układ jest kompatybilny, x4=t dowolny, x1=t, x2=-2t, x3=0, x4=t. ▲
^
§6 Rząd macierzy, twierdzenie o zgodności układów równań pierwszego rzędu
Aby zbadać wiele zagadnień związanych z rozwiązywaniem układów równań pierwszego rzędu, często wprowadza się to pojęcie ranga matrycy.
Definicja. Rząd macierzy jest najwyższym rzędem niezerowej wyznacznika podmacierzy kwadratowej uzyskanej z danej macierzy poprzez usunięcie niektórych wierszy i kolumn.
Rozważmy na przykład macierz
Usunięcie dowolnej liczby wierszy i kolumn uniemożliwia otrzymanie z danej macierzy macierzy kwadratowej rzędu wyższego niż 3. Dlatego jego ranga nie może być większa niż trzy. Ale skreślając jedną z kolumn, otrzymamy macierze kwadratowe, które mają dwa identyczne wiersze, a zatem ich wyznaczniki są równe zero. Zatem ranga oryginalnej macierzy jest mniejsza niż 3. Przekreślając np. 3. i 4. kolumnę oraz 3. rząd otrzymujemy macierz kwadratową 
, którego wyznacznik nie jest równy zero. Zatem wszystkie wyznaczniki podmacierzy trzeciego rzędu są równe zero, natomiast wśród wyznaczników macierzy drugiego rzędu znajduje się niezerowa jeden. Zatem ranga oryginalnej macierzy jest równa dwa.
Udowodnijmy twierdzenie: rząd macierzy nie zmienia się podczas operacji liniowych na jej wierszach.
Rzeczywiście, operacje liniowe na wierszach dowolnej macierzy prowadzą do tych samych operacji liniowych na wierszach dowolnej podmacierzy. Ale, jak wspomniano powyżej, podczas operacji liniowych na rzędach macierzy kwadratowych wyznaczniki tych macierzy uzyskuje się od siebie poprzez pomnożenie przez liczbę różną od zera. Zatem wyznacznik zerowy pozostaje zerowy, a wyznacznik niezerowy pozostaje niezerowy, to znaczy najwyższy rząd niezerowego wyznacznika podmacierzy nie może się zmienić. Oczywiście przestawienie kolumn nie wpływa na rząd macierzy, ponieważ takie przegrupowanie może wpłynąć jedynie na znak odpowiednich wyznaczników.
Z udowodnionego twierdzenia wynika, że przekształcone macierze rozpatrywane w poprzedniej sekcji mają tę samą rangę, co macierze pierwotne. Zatem rząd macierzy głównej układu równań pierwszego rzędu jest równy liczbie jedynek na głównej przekątnej przekształconej macierzy.
Udowodnimy teraz twierdzenie o zgodności układów równań pierwszego rzędu (twierdzenie Kroneckera-Capelliego): Aby układ równań pierwszego rzędu był zgodny, konieczne i wystarczające jest, aby stopień macierzy rozszerzonej pokrywał się z rangą macierzy głównej.
Niech rząd macierzy głównej układu będzie równy k. Jeśli rząd rozszerzonej macierzy układu również wynosi k, to oznacza to, że albo układ zawiera tylko k równań, albo wszystkie liczby 
(i= k+1, ... , k) w przekształconej macierzy są równe zeru (w przeciwnym razie rząd rozszerzonej macierzy przekształconej, a więc układu pierwotnego, wynosiłby k +1)
Niech rząd przekształconej (a więc pierwotnej) rozszerzonej macierzy układu będzie większy od k, czyli większy od liczby jedynek na głównej przekątnej przekształconej macierzy. Wówczas istnieje co najmniej jedna podmacierz rzędu (k+1), której wyznacznik nie jest równy zero. Taką podmacierz można otrzymać jedynie poprzez dodanie do macierzy jednostkowej rzędu k (która znajduje się w lewym górnym rogu przekształconej macierzy) jednego wiersza i kolumny, na którą składa się pierwszych k wolnych wyrazów równań układu przekształconego i dowolny wolny wyraz z następnych n-k równań. Aby wyznacznik określonej podmacierzy był niezerowy, ten ostatni dodany element, czyli liczba (i=k+1, ... , k), również musi być niezerowy. Ale, jak udowodniono wcześniej, w tym przypadku 
system jest niekompatybilny. Zatem system jest kompatybilny wtedy i tylko wtedy, gdy ranga macierzy głównej jest zgodna z rangą macierzy rozszerzonej.
II. Przykłady rozwiązywania problemów
1,39. Oblicz rząd macierzy za pomocą przekształceń elementarnych
Gdzie jest znak 
wskazuje, że połączone przez nią macierze powstają od siebie poprzez elementarne przekształcenia, a zatem mają tę samą rangę.
Rząd macierzy A wynosi 2, czyli r=2. ^
1,40. Korzystając z przekształceń elementarnych, oblicz rząd macierzy
r=3 , ponieważ wyznacznik macierzy trójkątnej z pierwszych trzech kolumn nie jest równy zero. ▲
Obliczanie rangi macierzy metodą kadrowania
Wybieramy w tej macierzy moll drugiego rzędu, który jest różny od zera. Następnie obliczamy nieletnie trzeciego rzędu, które otaczają (zawierają) wybraną, aż znajdziemy wśród nich niezerową. Następnie obliczamy niepełne molle czwartego rzędu, które tworzą niezerową mollę trzeciego rzędu, dopóki nie znajdziemy wśród nich niezerowej jedynki itd. Jeśli znajdziesz niezerową mollę r-tego rzędu, a wszystkie tworzące ją molle (r+1)-tego rzędu są równe zero lub już nie istnieją, to stopień macierzy jest równy r.
1,41. Oblicz rangę macierzy
∆ 
Przekreślone III. , od 2·ІІр. +Ja jestІІІр.
Wybierzmy np. 
Obliczmy nieletnie trzeciego rzędu, które to tworzą
moll trzeciego rzędu różny od zera.
Zawarta jest w wyznaczniku czwartego rzędu danej macierzy, który jest równy zero. Zatem r=3. ▲
1,42. Rozwiązywać układy równań
a) Tutaj r(A)=3, r(B)=3; kompatybilny z systemem, zdefiniowany.
Ponieważ 
,
następnie z pierwszych trzech systemów znajdujemy na przykład zgodnie ze wzorami Cramera
x1=-1, x2=0, x3=1
b) Tutaj r(A)=2, r(B)=2; system jest kompatybilny, ale nie zdefiniowany.
Wyznacznik 
oraz z dwóch pierwszych równań układu
gdzie niewiadomym x3 i x4 można podać dowolne wartości.
c) w tym przypadku r(A)=2, r(B)=3; i system jest niekompatybilny.
1,43. Stosując metodę Gaussa (sekwencyjna eliminacja niewiadomych) rozwiąż jednorodny układ równań:
i znaleźć jego podstawowy system rozwiązań.
Wypiszmy rozszerzoną macierz układu (w tym przypadku kolumny zerowej oczywiście nie można zapisać). Po wyraźnych przekształceniach będziemy mieli
oznacza to, że dany system jest równoważny następującemu:
Tutaj r=3, a trzy niewiadome można wyrazić za pomocą tej ostatniej, na przykład w ten sposób:
x 2 = -2x 3 -3x 4 -9x 5 = -2x 3 -12x 5
x 1 = -2x 2 -3x 3 -4x 4 -5x 5 =x 3 +15x 5
Układ podstawowy można otrzymać, jeśli niewiadomym wolnym x3, x5 przyjmie się wartość x3=1, x5=0 (wtedy x1=1, x2=-2, x4=0) i wartość x3=0, x5=1 ( wtedy x1=15, x2=-12, x4=1). Daje to podstawowy system rozwiązań:
mi 1 =(1, -2, 1, 0, 0), tj 2 =(15, -12, 0, 1, 1)
Stosując system podstawowy, rozwiązanie ogólne często zapisuje się jako liniową kombinację rozwiązań mi 1 ta mi 2, czyli:
1,44. Znajdź podstawowy układ rozwiązań układu równań liniowych i zapisz jego rozwiązanie ogólne
Odrzućmy trzecią linię. Układ został zredukowany do krokowego z niewiadomymi głównymi x1, x2 i niewiadomymi wolnymi x3, x4:
Z ostatniego równania 
. Od pierwszego 
Istnieją 2 wolne niewiadome. Dlatego wyznaczamy wyznacznik drugiego rzędu z elementami jednostkowymi przekątnej głównej i elementami zerowymi przekątnej wtórnej: 
.
Weźmy wektor mi 1 =
(
)
Wektory mi 1 i mi reprezentują podstawowy układ rozwiązań.
Teraz rozwiązanie ogólne można zapisać jako
Przypisywanie współczynników 
,
dowolne (dowolne) wartości liczbowe otrzymamy różne rozwiązania cząstkowe.
/odejmij IV od wszystkich linii/ 
Linie II, III, V, które są proporcjonalne do pierwszej linii, zostaną przekreślone. W powstałej macierzy przestawiamy kolumny I i II:
Ranga macierzy wynosi 2.
Główne niewiadome x2 i x1. Za darmo - x3, x4, x5. System wygląda teraz tak:
Przypisywanie sekwencyjne wartości do wolnych niewiadomych równych elementom kolumn wyznacznika
1) x3=1, x4=0, x5=0; 2) x3=0, x4=1, x5=0; 3) x3=0, x4=0, x5=1
1) x2=1, x1=1; 2) x2=1, x1=-2; 3) x2=-2, x1=1
czyli wektory C 1 = (1, 2, 1, 0, 0)
do 2 =(-2, 1, 0, 1, 0)
do 3 =(1, -2, 0, 0, 1)
stanowią podstawowy system rozwiązań. Ogólne rozwiązanie systemu pozostanie teraz.
Macierz współczynników
ma rangę r=2 (sprawdź).
Wybierzmy dla podstawowego molla 
Wtedy zredukowany układ ma postać:
Gdzie, licząc x3=c1, x4=c2, x5=c3, znajdujemy
Ogólne rozwiązanie układu
Z rozwiązania ogólnego znajdujemy podstawowy system rozwiązań
Korzystając z systemu podstawowego, można zapisać rozwiązanie ogólne
e=с1e1+с2e2+с3e3
^
§7 Podstawowe operacje na macierzach
W poprzednim akapicie powszechnie stosowano operacje liniowe na wierszach i kolumnach różnych macierzy. Jednak w niektórych zagadnieniach algebry liniowej konieczne jest rozważenie operacji na macierzach jak na pojedynczym obiekcie.
Badanie operacji na macierzach opiera się na koncepcji równości macierzy. Będziemy od tego kontynuować definicje: Mówi się, że dwie macierze tego samego wymiaru są równe, jeśli wszystkie odpowiadające im elementy są równe.
W konsekwencji macierze A i B o tym samym wymiarze nxm są równe wtedy i tylko wtedy, gdy Aik=Bik i=1, 2,... , n; k=1, 2,..., m. Jednocześnie jeszcze raz podkreślamy, że można porównywać tylko macierze tego samego wymiaru.
Suma dwóch macierzy A i B o tym samym wymiarze nxm jest macierzą C o tym samym wymiarze, taką że
(C) ik =(A) ik +(B) ik (1)
Dlatego dodając macierze (można dodawać tylko macierze tego samego wymiaru), należy dodać wszystkie odpowiadające im elementy.
Ponieważ dodawanie macierzy sprowadza się do dodawania liczb – elementów tych macierzy, oczywiście istnieje właściwość przemienności i asocjacji.
A+B=B+A; (A+B)+C=A+(B+C) (2)
Iloczynem macierzy A i liczby (lub liczby i macierzy A) jest macierz B taka, że
(B) ik =(A) ik (3),
to znaczy, mnożąc macierz przez liczbę (lub liczby przez macierz), wszystkie elementy macierzy należy pomnożyć przez tę liczbę. Przypomnijmy, że przy mnożeniu przez liczbę wyznacznika macierzy wystarczyło pomnożyć przez tę liczbę tylko elementy dowolnego wiersza (lub kolumny).
Łatwo sprawdzić, że przy mnożeniu macierzy przez liczbę zachodzi własność rozkładu:
(A+B)=A+B; (+)=A+B (4)
Zdefiniujmy teraz iloczyn dwóch macierzy. Niech będzie dana macierz A wymiaru nxm i macierz B wymiaru mxp.
Definicja. Iloczynem macierzy A o wymiarze nxm przez macierz B o wymiarze mxp jest macierz C o wymiarze nxp taka, że
(5),
innymi słowy, aby otrzymać element znajdujący się w i-tym wierszu i w k-tej kolumnie macierzy iloczynu, należy obliczyć sumę iloczynów elementów i-tego rzędu pierwszego czynnika i odpowiednie elementy k-tej kolumny drugiego czynnika. Zatem, aby móc dodać podaną sumę, liczba kolumn w pierwszej macierzy (czyli liczba elementów w każdym wierszu) musi być równa liczbie wierszy w drugiej (czyli liczbie elementów w każdej kolumnie).
Przykład 1.
Znajdź AB
Rozwiązanie. Macierz A ma wymiar 3x2, macierz B ma wymiar 2x2; iloczyn istnieje - jest to macierz 3x2.
Iloczyn macierzy nie ma własności przemiennej: AB, ogólnie rzecz biorąc, nie jest równe BA.
Po pierwsze, z faktu, że AB można obliczyć, wcale nie wynika, że BA ma sens. Przykładowo w omawianym przykładzie przestawianie czynników, czyli pomnożenie B przez A, jest niemożliwe, gdyż nie da się pomnożyć macierzy 2x2 przez macierz 3x2 - liczba kolumn pierwszej macierzy nie jest tu równa liczbę rzędów drugiego. Ale nawet jeśli produkt BA istnieje, to często 
. Spójrzmy na przykład.
Pozwalać 
. Następnie
Jednocześnie można udowodnić (zalecamy czytelnikowi przeprowadzenie takiego dowodu), że
(AB)C=A(BC) (6)
A(B+C)=AB+AC
(zwykle zakłada się, że wszystkie te dzieła mają sens).
Zgodnie z definicją iloczynu macierzowego zawsze można pomnożyć macierze kwadratowe tego samego rzędu i iloczyn będzie macierzą tego samego rzędu. Zauważmy bez dowodu jedną z własności iloczynu macierzy kwadratowych tego samego rzędu: wyznacznik iloczynu dwóch macierzy tego samego rzędu jest równy iloczynowi wyznaczników macierzy, które są mnożone.
Bardzo często musimy rozpatrywać iloczyn macierzy o wymiarze nxm przez macierz o wymiarze mx1, czyli macierz jednokolumnową. Oczywiście powinniśmy otrzymać w rezultacie macierz o wymiarze nx1, czyli także macierz jednokolumnową. Niech na przykład trzeba pomnożyć macierz
do matrixa 
W rezultacie otrzymujemy macierz 
, którego elementy oblicza się za pomocą wzorów:
Oznacza to jednak, że układ równań pierwszego rzędu omówiony w poprzednim akapicie można zapisać w bardzo wygodnej postaci macierzowej: AX=B.
Istotną rolę w różnych zastosowaniach algebry macierzy odgrywa macierz kwadratowa, w której wszystkie elementy przekątne (czyli elementy znajdujące się na głównej przekątnej) są równe 1, a wszystkie pozostałe elementy są równe zeru. Taka macierz nazywana jest macierzą tożsamości. Oczywiście wyznacznik macierzy tożsamości
= 1
Charakterystyczne są następujące właściwości macierzy jednostkowej: niech będzie dana macierz kwadratowa A rzędu n i macierz jednostkowa E tego samego rzędu. Wtedy AE=EA=A.
Naprawdę 
, Ale 
Dlatego w sumie 
tylko te składowe, dla których e=k są różne od zera. W konsekwencji (AE) ік =(A) ік, a zatem AE=A. Podobnie otrzymujemy dla produktu EA.
Przykłady rozwiązywania problemów
1,61. Znajdź iloczyn AB i BA dwóch macierzy
∆ Iloczyn AB nie istnieje, ponieważ liczba kolumn macierzy A nie jest równa liczbie wierszy macierzy B. Liczba kolumn macierzy B jest równa liczbie wierszy macierzy A. Zatem produkt BA istnieje:
1,62. Znajdź macierz 2A+5B jeśli
1. Metoda substytucyjna: z dowolnego równania układu wyrażamy jedną niewiadomą przez drugie i podstawiamy do drugiego równania układu.
Zadanie. Rozwiąż układ równań:
Rozwiązanie. Z pierwszego równania układu wyrażamy Na Poprzez X i podstawiamy go do drugiego równania układu. Weźmy system 
odpowiednik oryginału.
Po wprowadzeniu podobnych terminów system przyjmie postać:
Z drugiego równania znajdujemy: . Podstawiając tę wartość do równania Na = 2 - 2X, otrzymujemy Na= 3. Dlatego rozwiązaniem tego układu jest para liczb.
2. Metoda dodawania algebraicznego: Dodając dwa równania, otrzymasz równanie z jedną zmienną.
Zadanie. Rozwiąż równanie układu:
Rozwiązanie. Mnożąc obie strony drugiego równania przez 2, otrzymujemy układ 
odpowiednik oryginału. Dodając dwa równania tego układu, dochodzimy do układu 
Po wprowadzeniu podobnych terminów system ten przybierze postać: 
Z drugiego równania znajdujemy . Podstawiając tę wartość do równania 3 X + 4Na= 5, otrzymujemy 
, Gdzie . Dlatego rozwiązaniem tego układu jest para liczb.
3. Metoda wprowadzania nowych zmiennych: szukamy w systemie powtarzających się wyrażeń, które będziemy oznaczać nowymi zmiennymi, upraszczając w ten sposób wygląd systemu.
Zadanie. Rozwiąż układ równań:
Rozwiązanie. Zapiszmy ten system inaczej: 
Pozwalać x + y = ty, xy = w. Następnie otrzymujemy system
Rozwiążmy to metodą podstawieniową. Z pierwszego równania układu wyrażamy ty Poprzez w i podstawiamy go do drugiego równania układu. Weźmy system 
te. 
Z drugiego równania układu znajdujemy w 1 = 2, w 2 = 3.
Podstawiając te wartości do równania ty = 5 - w, otrzymujemy ty 1 = 3,
ty 2 = 2. Zatem mamy dwa systemy
Rozwiązując pierwszy układ, otrzymujemy dwie pary liczb (1; 2), (2; 1). Drugi układ nie ma rozwiązań.
Ćwiczenia do samodzielnej pracy
1. Rozwiązywać układy równań metodą podstawieniową.