Utsnitt av geometriske figurer har forskjellige former. Et parallellepipeds tverrsnitt er alltid et rektangel eller kvadrat. Den har en rekke parametere som kan finnes analytisk.
Bruksanvisning
Fire seksjoner kan trekkes gjennom parallellepipedet, som er firkanter eller rektangler. Totalt har den to diagonale og to tverrsnitt. Som regel har de forskjellige størrelser. Unntaket er kuben, som de er like for.
Før du konstruerer en del av et parallellepiped, få en ide om hva denne figuren representerer. Det er to typer parallellepipeder - vanlige og rektangulære. I et vanlig parallellepiped er ansiktene plassert i en viss vinkel til basen, mens de i en rektangulær er vinkelrett på den. Alle flater av en kuboid er rektangler eller firkanter. Det følger av dette at en kube er et spesialtilfelle av et rektangulært parallellepiped.
Enhver del av et parallellepiped har visse egenskaper. De viktigste er areal, omkrets og lengder på diagonaler. Hvis sidene av seksjonen eller noen av dens andre parametere er kjent fra problemforholdene, er dette nok til å finne omkretsen eller området. Diagonalene til seksjonene bestemmes også langs sidene. Den første av disse parameterne er det diagonale tverrsnittsarealet.
For å finne det diagonale tverrsnittsarealet, må du kjenne høyden og sidene til bunnen av parallellepipedet. Hvis lengden og bredden på bunnen av parallellepipedet er gitt, finn diagonalen ved å bruke Pythagoras teoremet:
d=?a^2+b^2.
Etter å ha funnet diagonalen og vite høyden på parallellepipedet, beregne tverrsnittsarealet til parallellepipedet:
S=d*h.
Omkretsen til diagonalseksjonen kan også beregnes fra to mengder - diagonalen til basen og høyden på parallellepipedet. I dette tilfellet, finn først to diagonaler (øvre og nedre baser) ved å bruke Pythagoras teorem, og legg dem deretter til med to ganger høyden.
Hvis du tegner et plan parallelt med kantene på parallellepipedet, kan du få et rektangulært snitt, hvis sider er en av sidene av bunnen av parallellepipedet og høyden. Finn området for denne delen som følger:
S=a*h.
Finn omkretsen til denne delen på lignende måte ved å bruke følgende formel:
p=2*(a+h).
Det siste tilfellet oppstår når seksjonen løper parallelt med de to basene til parallellepipedet. Da er arealet og omkretsen lik arealet og omkretsen til basene, dvs.:
S=a*b - tverrsnittsareal;
Portefølje av matematikklærer ved National Educational Institution Secondary School "LADA" Lisunova G.V.
Emne: "Konstruksjon av deler av et tetraeder og parallellepiped."
Punkt: geometri Klasse: 10 Pedagogiske teknologier som brukes: teknologi for prosjektbasert læring, informasjonsteknologi. Leksjonens tema: Konstruksjon av seksjoner av et tetraeder og parallellepiped Leksjonstype: en leksjon i å konsolidere og utvikle kunnskap. Arbeidsformer i timen: frontal, individuell Liste over brukte kilder og programvare og pedagogiske verktøy:L.S. Atanasyan. Geometri. 10-11 klassetrinn, - M: Utdanning, 2006.
V. N. Litvinenko. Oppgaver for utvikling av romlige konsepter. Bok for lærere. - M.: Utdanning, 1991.
G. Prokopenko. Metoder for å løse problemer ved å konstruere seksjoner av polyeder. Karakter 10. ChPGU, Chelyabinsk. Ukens undervisnings- og metodeavis "Matematikk" 31/2001.
A. Mordkovich. Seminar ni. Tema: Konstruksjon av seksjoner av polyedre (posisjonsproblemer). Ukentlig bilag til avisen «Første september». Matematikk. 3/94.
Multimedia interaktivt kurs "Åpen matematikk. Stereometri." Fysikon
"Levende geometri"
Test dine kunnskaper om teoretisk materiale om polyeder (tetraeder, parallellepiped).
Fortsett å utvikle evnen til å analysere en tegning, fremheve hovedelementene når du arbeider med en polyedermodell, skissere forløpet for å løse et problem, og forutse sluttresultatet.
Utvikle ferdigheter i å løse problemer som involverer konstruksjon av deler av polyeder.
Utvikle grafisk kultur og matematisk tale.
Å utvikle ferdigheter i bruk av datateknologi i geometritimer.
Pedagogisk:Utvikle elevenes kognitive interesse.
Å danne og utvikle romlig fantasi hos elever.
Pedagogisk:Fremme uavhengighet, nøyaktighet og hardt arbeid.
Utvikle evnen til å arbeide individuelt med en oppgave.
Dyrk viljen og utholdenheten for å oppnå endelige resultater.
Teknisk støtte:
Datamaskin med installerte programmer "Living Geometry", Power Point, multimediaprojektor.
Gi ut:Skjemakort med oppgaver for praktisk arbeid, blanke kort med svar for gjensidig testing, støtte - notater, presentasjon om emnet "Stereometriaksiomer, konsekvenser av dem", studentpresentasjon "Konstruksjon av deler av et parallellepiped", fargeblyanter.
Leksjonsstruktur.
| Hilsener. Organisering av tid. | ||
| Sette mål og mål for leksjonen. | ||
| Repetisjon av studert materiale ved bruk av presentasjon. | ||
| Oppdatering av grunnleggende kunnskap. | ||
| Praktisk arbeid med å bygge seksjoner. | ||
| Fagfellevurdering. | ||
| Hjemmelekser | ||
| Speilbilde. | ||
1) Hilsen. Organisering av tid.
2) Sette mål og mål for leksjonen.
Problemer med å konstruere seksjoner i polyedre inntar en fremtredende plass i løpet av stereometri. Deres rolle skyldes det faktum at løsning av denne typen problemer bidrar til assimilering av stereometriaksiomene, deres konsekvenser, utvikling av romlige konsepter og konstruktive ferdigheter. Evnen til å løse problemer som involverer konstruksjon av seksjoner er grunnlaget for å studere nesten alle emner i stereometrikurset. Når man løser mange stereometriske problemer, brukes plane seksjoner av polyedre. I tidligere leksjoner ble vi kjent med stereometriens aksiomer, følger fra aksiomene og teoremer om parallelliteten til rette linjer og plan i rommet. Vi så på algoritmer for å konstruere enkle deler av en kube, tetraeder og parallellepiped. Disse seksjonene ble som regel spesifisert av punkter plassert på kantene eller flatene til polyederet. I dag i leksjonen vil vi gjenta geometriske utsagn som lar oss formulere reglene for å konstruere seksjoner. Vi vil også lære å anvende denne kunnskapen når vi løser problemet med å konstruere en del av et tetraeder og et parallellepiped med et plan som går gjennom tre gitte punkter, slik at ikke tre av disse punktene ligger på samme side.
3) Repetisjon av studert materiale ved bruk av presentasjon.
La oss se på noen teorispørsmål.
- Hva er et skjæreplan? Hvordan kan du definere et skjæreplan? Hva er tverrsnittet til et tetraeder (parallellepipedum)? Hvilke polygoner fikk vi når vi konstruerte deler av tetraederet? Og hvilke polygoner kan vi få når vi konstruerer deler av et parallellepiped? La oss se på stereometriens aksiomer, deres konsekvenser og metoder for å definere et plan (presentasjon 1, lysbilde 1-10)
4) Oppdatering av grunnleggende kunnskap.
Elevpresentasjon "Konstruksjon av deler av et parallellepiped."
La oss nå huske algoritmen for å konstruere en tetraederseksjon ved å bruke eksemplet med to problemer (presentasjon 1, lysbilde 11-12). (konstruksjonen kommenteres trinn for trinn av lærer).- Alexey Pashchenko, ved hjelp av sin presentasjon, vil minne oss om algoritmer for å konstruere parallellepipediserte seksjoner (presentasjon 2, lysbilde 1-5) (eleven demonstrerer lysbilder og kommenterer konstruksjonsrekkefølgen)- Og nå, ved å bruke "Living Geometry"-programmet, vil vi "gjenopplive" rommet ved å bruke eksemplet med en del av en kube. Programmet lar deg rotere polyederet, som lar deg se tverrsnittet fra alle sider.
5) Praktisk arbeid med å bygge seksjoner etterfulgt av gjensidig verifisering.
Elevene får blanke kort for praktisk arbeid (vedlegg 1) Lavt belegg klasse (5 personer), et tilstrekkelig stort antall seter, samt påfølgende gjensidig verifisering gjør at arbeidet kan utføres i en variant. Skjemaene inneholder også flere ulike eksempler på å konstruere seksjoner. Hver elev har en påminnelse på pulten sin (Vedlegg 2). Praktisk arbeid består av 12 oppgaver med varierende vanskelighetsgrad. 5-7 riktig utførte oppgaver - score "3", 8-10 oppgaver - score "4", 11-12 oppgaver - score "5"
6) Gjensidig verifisering.
Elevene bytter ark med praktisk arbeid og får svarark for kontroll. (vedlegg 3) . Sjekk hverandres arbeid, merk riktig konstruerte seksjoner.
7) Lekser.
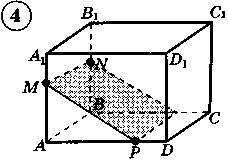
Som lekser vil jeg be deg løse problemer som ligner på oppgavene i praktisk arbeid, men om å konstruere deler av et tetraeder. Alle blir bedt om å fullføre 4 oppgaver (vedlegg 4) Oppgavene har tre vanskelighetsgrader.
8) Refleksjon.
Så, la oss oppsummere, hva lærte vi i klassen i dag? – Hvilke teoretiske prinsipper måtte vi ofte bruke? – Hvilke feil ble gjort ved problemløsning? Hvordan eliminerte du dem? – Hvem har måttet gå tilbake til en oppgave flere ganger? – Hvor i praktiske aktiviteter vil du finne dagens leksjon nyttig? På stadiet med aktivitetsrefleksjon analyserer elevene hvor og hvorfor feil ble gjort, hvordan de ble rettet, gjentar algoritmene som forårsaket vanskeligheter, og evaluerer aktivitetene deres i leksjonen.
9) Leksjonsoppsummering.
På slutten av leksjonen registrerer elevene ved hjelp av læreren graden av samsvar med det fastsatte målet og resultatene av aktiviteten. Karakterer gis.










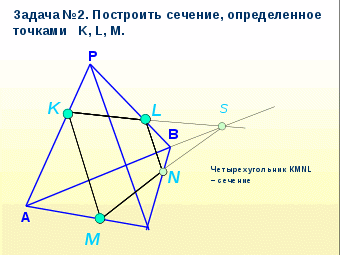





Praktisk arbeid med å konstruere deler av et parallellepiped. Vedlegg 1
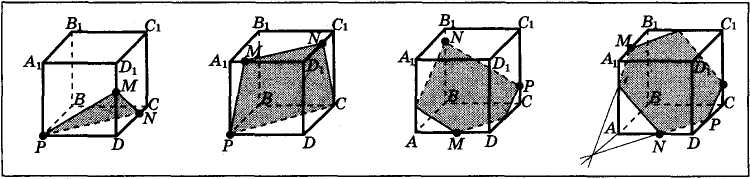



Vedlegg 2
Påminnelsesstøtte
- Axiom 1
. Gjennom tre punkter som ikke ligger på samme linje, passerer et fly gjennom, og bare ett. Axiom 2
. Hvis to punkter på en linje ligger i et plan, så ligger alle punktene på linjen i dette planet. Axiom 3
. Hvis to plan har et felles punkt, så har de en felles linje som alle de felles punktene til disse planene ligger på.
- Et fly passerer gjennom en rett linje og et punkt som ikke ligger på den, og bare ett plan på det. Et fly går gjennom to kryssende linjer, og bare én.




Vedlegg 3
Svar for praktisk arbeid.
|
|
|
|
|
|
|
|
Her er et geometriproblem om et rektangulært parallellepiped og et plan:
I det rektangulære parallellepipedet ABCDA1B1C1D1 er kantene AA1 = 6, AB = 6, AD = 3 røtter av 13 kjent Finn tverrsnittsarealet til parallellepipedet ved planet AMK, der punktene M og K deler kantene BB1 og. CC1 i forholdet 1:2, regnet fra rett linje BC.
For å løse dette problemet trenger du bare å forestille deg hva som er gitt oss i henhold til tilstanden og forstå hva som må finnes. Jeg anbefaler å dele tilstanden i deler og vurdere hver del separat. Nå skal jeg vise hvordan dette gjøres.
Leser helt fra begynnelsen: "I et rektangulært parallellepiped..."- det er nok. Og så har vi et rektangulært parallellepiped - en tredimensjonal geometrisk figur som er best tegnet på et stykke papir. Slik ser det rektangulære parallellepipedet ut på figuren. I det virkelige liv er det bare en vanlig skoeske.
"...kantene AA1 = 6, AB = 6, AD = 3 røtter av 13 er kjent." Nå kan vi merke lengden på disse kantene direkte i figuren. La oss se på bokstavene, jeg markerte disse tre kantene i blått.
Faktisk får vi dimensjonene til parallellepipedet. Og selv om lengden på ribbene i figuren ikke helt samsvarer med tilstanden, er det greit. Dette påvirker ikke algebraen til løsningen i det hele tatt. Vi bruker ikke tegning for å løse et problem grafisk. Vi trenger det bare for å forstå fremdriften i beslutningen. Identiske problemer for parallellepipeder av svært forskjellig størrelse vil ha samme løsning. Til slutt vil bare tallene være forskjellige.
Kan ikke forstå noe. Hvor kom M- og K-punktene fra? Etter disse ordene står det noe annet i problemstillingen. Derfor hopper vi over dette fragmentet og leser videre.
"...hvor punktene M og K deler kantene BB1 og CC1 i forholdet 1:2..." Ja, her kommer prikkene. Vi kan finne kantene i figuren, men hvordan skille dem "...i forholdet 1:2..."? Alt er veldig enkelt. La oss huske barnehagen. "Del segmentet i tre like deler og ta en del" er en veldig enkel oppgave som selv et barn kan håndtere. Og vi er allerede voksne. Hvordan vet du hvor mange deler du skal dele inn i? Uttrykk "Del i forhold 1:2" er ekvivalent med uttrykket "Del inn i 3 deler". Tross alt, 1+2=3. Lengden på alle vertikale kanter er 6 cm. En del vil være lik 6/3 = 2 cm. Vi må ta en del. Men hvilken? Nederst, topp eller midt? Vi leser videre problemformuleringen: "...regnet fra direkte sol". Hvorfor ble BC-kanten plutselig til en rett linje? Matematikere, som ekte kortslipere, elsker å erstatte noen konsepter med andre, og gjøre et enkelt problem til et ekte puslespill. Det er på grunn av slike gåter at mange hater matematikk. Rett linje BC faller sammen med kanten BC og de er plassert på den nedre bunnen av det rektangulære parallellepipedet, på bunnen av boksen. Derfor tar vi den nedre tredjedelen av de vertikale kantene. Vi markerer de nødvendige punktene i figuren.
Vi har analysert hele tilstanden til problemet til slutten, og nå er det på tide å gå tilbake til det manglende fragmentet: "Finn tverrsnittsarealet til parallellepipedet av planet AMK ...". Gjennom punktene M og K kan du tegne et helt hav av fly. Alle vil rotere på MK-segmentet, som en kebab på et spyd.
Vi er kun interessert i flyet som går gjennom punkt A. Det finnes bare ett slikt fly. Siden segmentet MK er parallelt med kanten BC, som igjen er parallelt med kanten AD, betyr det at planet vårt går gjennom denne kanten. I tverrsnitt får vi et rektangel ADMK, plassert i en vinkel til basen.
Vi må finne arealet til dette rektangelet (i figuren er det blått). Vi har en side, vi må finne lengden på den andre siden. Hvis du ser på den grønne trekanten, vil den andre siden av rektangelet vise seg å være hypotenusen til den rettvinklede trekanten ABM. Ved å bruke teoremet til Pythagoras kan vi enkelt finne lengden på denne hypotenusen. Som du kan se, er dette et to-trinns barnepuslespill.
Men jeg plages av vage tvil om at noen et sted er forvirret. Hvis vi for punktene M og K ikke tar en del fra kantene BB1 og CC1, men to deler, er lengden på hypotenusen lik to røtter av tretten. Ved beregning av tverrsnittsarealet kommer tallet tretten ut under roten og arealet er lik 78 centimeter i kvadrat. Det er tydelig at noen har tatt feil. Enten matematikere da de komponerte rebusen min, eller så dechiffrerte jeg ikke den elegante litteraturen til denne rebusen riktig. Du ser hva middelmådige forsøk på å fremstå smartere enn du egentlig er kan føre til. Dette gjelder både meg og matematikere. Forresten, hvis betingelsen hadde indikert forholdet 2:1, så hadde jeg løst dette problemet riktig og fått svar uten kvadratrot.
For skjæreplanet A1MK viser løsningen seg å være veldig vakker. Det samme Pythagoras teorem for den grønne trekanten, det samme området av rektangelet.
P.S. Du kan tegne bilder på papir. Jeg tegner bilder på datamaskinen for å vise dem til deg. Du kan også gjøre dette. Ta et blankt rektangulært parallellepipedum og mal det i henhold til betingelsene for oppgaven din. Da blir det mye lettere for deg å finne en løsning. Hvis du har en bærbar datamaskin og den overopphetes på grunn av din overdrevne innsats, vil en kjølepute hjelpe deg med å bli kvitt problemene. Dette stativet opererer fra selve den bærbare datamaskinen og er koblet til den via en USB-kontakt. Du trenger ikke ha med deg noen stikkontakter. Veldig praktisk og praktisk.