Enkle brøkregler. Subtrahere blandede fraksjoner

Brøkkalkulator designet for raskt å beregne operasjoner med brøker, vil det hjelpe deg enkelt å legge til, multiplisere, dele eller subtrahere brøker.

Moderne skolebarn begynner å studere brøker allerede i 5. klasse, og øvelser med dem blir mer kompliserte for hvert år. De matematiske termene og mengdene som vi lærer på skolen kan sjelden være nyttige for oss i voksenlivet. Imidlertid finnes brøker, i motsetning til logaritmer og potenser, ganske ofte i hverdagen (måling av avstander, veiing av varer osv.). Kalkulatoren vår er designet for raske operasjoner med brøker.

La oss først definere hva brøker er og hva de er. Brøker er forholdet mellom ett tall og et annet, det er et tall som består av et heltall av brøker av en enhet.

Typer brøker:

• Vanlig
• Desimal
• Blandet

Eksempel vanlige brøker:

Den øverste verdien er telleren, den nederste er nevneren. Bindestreken viser oss at det øverste tallet er delelig med det nederste tallet. I stedet for dette skriveformatet, når bindestreken er vannrett, kan du skrive annerledes. Du kan sette en skrå linje, for eksempel:

1/2, 3/7, 19/5, 32/8, 10/100, 4/1

Desimaler er den mest populære typen brøker. De består av en heltallsdel og en brøkdel, atskilt med komma.

Eksempel på desimalbrøker:

0,2 eller 6,71 eller 0,125

Består av et helt tall og en brøkdel. For å finne ut verdien av denne brøken, må du legge til hele tallet og brøken.

Eksempel på blandede fraksjoner:

Brøkkalkulatoren på nettstedet vårt er i stand til raskt å utføre alle matematiske operasjoner med brøker online:

• Addisjon
• Subtraksjon
• Multiplikasjon
• Inndeling

For å utføre beregningen må du skrive inn tall i feltene og velge en handling. For brøker må du fylle ut teller og nevner, det kan hende at hele tallet ikke skrives (hvis brøken er vanlig). Ikke glem å klikke på "lik"-knappen.

Det er praktisk at kalkulatoren umiddelbart gir prosessen for å løse et eksempel med brøker, og ikke bare et ferdig svar. Det er takket være den detaljerte løsningen at du kan bruke dette materialet til å løse skoleproblemer og for bedre å mestre materialet som dekkes.

Du må utføre eksempelberegningen:

Etter å ha lagt inn indikatorene i skjemafeltene, får vi:

For å lage din egen beregning, skriv inn dataene i skjemaet.

Brøkkalkulator

Skriv inn to brøker:

		+ - * :

Relaterte seksjoner.

Brøker er vanlige tall og kan også legges til og trekkes fra. Men fordi de har en nevner, krever de mer komplekse regler enn for heltall.

La oss vurdere det enkleste tilfellet, når det er to brøker med samme nevnere. Deretter:

For å legge til brøker med de samme nevnerne, må du legge til deres tellere og la nevneren være uendret.

For å trekke fra brøker med de samme nevnerne, må du trekke fra telleren til den andre fra telleren til den første brøken, og igjen la nevneren være uendret.

Innenfor hvert uttrykk er nevnerne til brøkene like. Som definisjon av å addere og subtrahere brøker får vi:

Som du kan se, er det ikke noe komplisert: vi legger bare til eller trekker fra tellerne og det er det.

Men selv i så enkle handlinger klarer folk å gjøre feil. Det som oftest glemmes er at nevneren ikke endres. For eksempel, når de legger dem til, begynner de også å legge seg sammen, og dette er grunnleggende feil.

Å bli kvitt den dårlige vanen med å legge til nevnere er ganske enkelt. Prøv det samme når du trekker fra. Som et resultat vil nevneren være null, og brøken vil (plutselig!) miste sin betydning.

Husk derfor en gang for alle: Når du legger til og trekker fra, endres ikke nevneren!

Mange gjør også feil når de legger til flere negative brøker. Det er forvirring med skiltene: hvor du skal sette et minus og hvor du skal sette et pluss.

Dette problemet er også veldig enkelt å løse. Det er nok å huske at minus før tegnet på en brøk alltid kan overføres til telleren - og omvendt. Og selvfølgelig, ikke glem to enkle regler:

1. Pluss for minus gir minus;
2. To negative gir en bekreftende.

La oss se på alt dette med spesifikke eksempler:

Oppgave. Finn betydningen av uttrykket:

I det første tilfellet er alt enkelt, men i det andre introduserer vi minuser i tellerne av brøkene:

Hva gjør du hvis nevnerne er forskjellige

Du kan ikke legge til brøker med forskjellige nevnere direkte. I det minste er denne metoden ukjent for meg. De opprinnelige brøkene kan imidlertid alltid skrives om slik at nevnerne blir de samme.

Det er mange måter å konvertere brøker på. Tre av dem er omtalt i leksjonen «Redusere brøker til en fellesnevner», så vi skal ikke dvele ved dem her. La oss se på noen eksempler:

Oppgave. Finn betydningen av uttrykket:

I det første tilfellet reduserer vi brøkene til en fellesnevner ved å bruke "på kryss og tvers"-metoden. I den andre vil vi se etter NOC. Merk at 6 = 2 · 3; 9 = 3 · 3. De siste faktorene i disse utvidelsene er like, og de første er relativt prime. Derfor er LCM(6, 9) = 2 3 3 = 18.

Hva gjør du hvis en brøk har en heltallsdel

Jeg kan glede deg: forskjellige nevnere i brøker er ikke det største onde. Mye flere feil oppstår når hele delen er uthevet i tilleggsbrøkene.

Selvfølgelig finnes det egne addisjons- og subtraksjonsalgoritmer for slike brøker, men de er ganske komplekse og krever lang studie. Bedre bruk det enkle diagrammet nedenfor:

1. Konverter alle brøker som inneholder en heltallsdel til uekte. Vi får normale termer (selv med ulike nevnere), som beregnes etter reglene omtalt ovenfor;
2. Beregn faktisk summen eller differansen av de resulterende brøkene. Som et resultat vil vi praktisk talt finne svaret;
3. Hvis dette er alt som var nødvendig i oppgaven, utfører vi den inverse transformasjonen, dvs. Vi blir kvitt en uekte brøk ved å fremheve hele delen.

Reglene for å flytte til uekte brøker og fremheve hele delen er beskrevet i detalj i leksjonen "Hva er en numerisk brøk". Hvis du ikke husker det, sørg for å gjenta det. Eksempler:

Oppgave. Finn betydningen av uttrykket:

Alt er enkelt her. Nevnerne i hvert uttrykk er like, så det gjenstår bare å konvertere alle brøker til uekte og telle. Vi har:

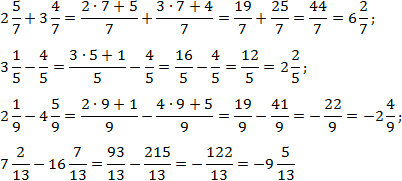
For å forenkle beregningene har jeg hoppet over noen åpenbare trinn i de siste eksemplene.

En liten merknad til de to siste eksemplene, der brøker med heltallsdelen uthevet trekkes fra. Minus før den andre brøken betyr at hele brøken trekkes fra, og ikke bare hele delen.

Les denne setningen på nytt, se på eksemplene – og tenk over det. Det er her nybegynnere gjør et stort antall feil. De elsker å gi slike problemer på tester. Du vil også møte dem flere ganger i testene til denne leksjonen, som vil bli publisert om kort tid.

Oppsummering: generell beregningsordning

Avslutningsvis vil jeg gi en generell algoritme som vil hjelpe deg å finne summen eller differansen av to eller flere brøker:

1. Hvis en eller flere brøker har en heltallsdel, konverter disse brøkene til uekte;
2. Bring alle brøkene til en fellesnevner på en hvilken som helst måte som er praktisk for deg (med mindre, selvfølgelig, forfatterne av oppgavene gjorde dette);
3. Legg til eller subtrahere de resulterende tallene i henhold til reglene for å addere og subtrahere brøker med like nevnere;
4. Hvis mulig, forkort resultatet. Hvis brøken er feil, velg hele delen.

Husk at det er bedre å markere hele delen helt på slutten av oppgaven, rett før du skriver ned svaret.

I det femte århundre f.Kr. formulerte den antikke greske filosofen Zeno av Elea sine berømte aporier, den mest kjente av disse er "Akilles og skilpadden". Slik høres det ut:

La oss si at Akilles løper ti ganger raskere enn skilpadden og er tusen skritt bak den. I løpet av tiden det tar Akilles å løpe denne distansen, vil skilpadden krype hundre skritt i samme retning. Når Akilles løper hundre skritt, kryper skilpadden ytterligere ti skritt, og så videre. Prosessen vil fortsette i det uendelige, Akilles vil aldri ta igjen skilpadden.

Dette resonnementet ble et logisk sjokk for alle påfølgende generasjoner. Aristoteles, Diogenes, Kant, Hegel, Hilbert... De betraktet alle Zenons aporia på en eller annen måte. Sjokket var så sterkt at " ... diskusjonene fortsetter den dag i dag, det vitenskapelige samfunnet har ennå ikke vært i stand til å komme til en felles mening om essensen av paradokser ... matematisk analyse, settteori, nye fysiske og filosofiske tilnærminger var involvert i studiet av problemet; ; ingen av dem ble en allment akseptert løsning på problemet..."[Wikipedia, "Zenos Aporia". Alle forstår at de blir lurt, men ingen forstår hva bedraget består av.

Fra et matematisk synspunkt demonstrerte Zeno i sin aporia tydelig overgangen fra kvantitet til . Denne overgangen innebærer bruk i stedet for permanente. Så vidt jeg forstår, har det matematiske apparatet for bruk av variable måleenheter enten ikke blitt utviklet ennå, eller det har ikke blitt brukt på Zenos aporia. Å bruke vår vanlige logikk fører oss inn i en felle. Vi, på grunn av treghet i tenkningen, bruker konstante tidsenheter på den gjensidige verdien. Fra et fysisk synspunkt ser dette ut som at tiden går ned til den stopper helt i det øyeblikket Akilles innhenter skilpadden. Hvis tiden stopper, kan ikke Akilles lenger løpe unna skilpadden.

Hvis vi snur vår vanlige logikk, faller alt på plass. Akilles løper med konstant hastighet. Hvert påfølgende segment av banen hans er ti ganger kortere enn den forrige. Følgelig er tiden brukt på å overvinne den ti ganger mindre enn den forrige. Hvis vi bruker begrepet "uendelighet" i denne situasjonen, vil det være riktig å si "Akilles vil ta igjen skilpadden uendelig raskt."

Hvordan unngå denne logiske fellen? Forbli i konstante tidsenheter og ikke bytt til gjensidige enheter. På Zenos språk ser det slik ut:

På tiden det tar Akilles å løpe tusen skritt, vil skilpadden krype hundre skritt i samme retning. I løpet av neste tidsintervall lik det første, vil Akilles løpe ytterligere tusen skritt, og skilpadden vil krype hundre skritt. Nå er Achilles åtte hundre skritt foran skilpadden.

Denne tilnærmingen beskriver virkeligheten tilstrekkelig uten noen logiske paradokser. Men dette er ikke en fullstendig løsning på problemet. Einsteins uttalelse om uimotståelig lyshastighet er veldig lik Zenos aporia "Akilles og skilpadden". Vi må fortsatt studere, tenke nytt og løse dette problemet. Og løsningen må søkes ikke i uendelig store antall, men i måleenheter.

En annen interessant aporia av Zeno forteller om en flygende pil:

En flygende pil er ubevegelig, siden den i hvert øyeblikk er i ro, og siden den er i ro i hvert øyeblikk av tiden, er den alltid i ro.

I denne aporiaen overvinnes det logiske paradokset veldig enkelt - det er nok til å klargjøre at i hvert øyeblikk er en flygende pil i ro på forskjellige punkter i rommet, som faktisk er bevegelse. Et annet poeng må bemerkes her. Fra ett fotografi av en bil på veien er det umulig å fastslå verken bevegelsen eller avstanden til den. For å finne ut om en bil beveger seg, trenger du to bilder tatt fra samme punkt på forskjellige tidspunkter, men du kan ikke bestemme avstanden fra dem. For å bestemme avstanden til en bil, trenger du to bilder tatt fra forskjellige punkter i rommet på ett tidspunkt, men fra dem kan du ikke bestemme bevegelsen (selvfølgelig trenger du fortsatt ytterligere data for beregninger, trigonometri vil hjelpe deg ). Det jeg vil trekke spesielt frem er at to punkter i tid og to punkter i rom er forskjellige ting som ikke bør forveksles, fordi de gir ulike muligheter for forskning.

onsdag 4. juli 2018

Forskjellene mellom sett og multisett er beskrevet veldig godt på Wikipedia. La oss se.

Som du kan se, "det kan ikke være to identiske elementer i et sett," men hvis det er identiske elementer i et sett, kalles et slikt sett et "multiset." Fornuftige vesener vil aldri forstå en slik absurd logikk. Dette er nivået av snakkende papegøyer og trente aper, som ikke har noen intelligens fra ordet "helt". Matematikere fungerer som vanlige trenere og forkynner for oss deres absurde ideer.

En gang i tiden var ingeniørene som bygde brua i en båt under brua mens de testet brua. Hvis broen kollapset, døde den middelmådige ingeniøren under ruinene av sin skapelse. Hvis broen tålte belastningen, bygde den dyktige ingeniøren andre broer.

Uansett hvordan matematikere gjemmer seg bak uttrykket "pass på, jeg er i huset", eller rettere sagt, "matematikk studerer abstrakte konsepter", er det en navlestreng som uløselig forbinder dem med virkeligheten. Denne navlestrengen er penger. La oss anvende matematisk settteori på matematikere selv.

Vi studerte matematikk veldig bra, og nå sitter vi i kassa og deler ut lønn. Så en matematiker kommer til oss for pengene sine. Vi teller ut hele beløpet til ham og legger det ut på bordet vårt i forskjellige hauger, der vi legger sedler av samme valør. Så tar vi en regning fra hver haug og gir matematikeren hans "matematiske sett med lønn." La oss forklare matematikeren at han vil motta de resterende regningene først når han beviser at et sett uten identiske elementer ikke er likt med et sett med identiske elementer. Det er her moroa begynner.

Først av alt vil logikken til varamedlemmene fungere: "Dette kan brukes på andre, men ikke på meg!" Da vil de begynne å forsikre oss om at sedler av samme valør har forskjellige seddelnummer, noe som betyr at de ikke kan betraktes som de samme elementene. Ok, la oss telle lønn i mynter - det er ingen tall på myntene. Her vil matematikeren begynne å febrilsk huske fysikk: forskjellige mynter har forskjellige mengder skitt, krystallstrukturen og arrangementet av atomer er unikt for hver mynt ...

Og nå har jeg det mest interessante spørsmålet: hvor er linjen utenfor hvilken elementene i et multisett blir til elementer i et sett og omvendt? En slik linje finnes ikke - alt bestemmes av sjamaner, vitenskapen er ikke engang i nærheten av å lyve her.

Se her. Vi velger fotballstadioner med samme feltareal. Arealene til feltene er de samme - noe som betyr at vi har et multisett. Men hvis vi ser på navnene på de samme stadionene, får vi mange, fordi navnene er forskjellige. Som du kan se, er det samme settet med elementer både et sett og et multisett. Hvilken er korrekt? Og her trekker matematikeren-sjaman-skarpisten frem et trumfess fra ermet og begynner å fortelle oss enten om et sett eller et multisett. Uansett vil han overbevise oss om at han har rett.

For å forstå hvordan moderne sjamaner opererer med settteori og knytter den til virkeligheten, er det nok å svare på ett spørsmål: hvordan skiller elementene i ett sett fra elementene i et annet sett? Jeg skal vise deg, uten noen "tenkbar som ikke en enkelt helhet" eller "ikke tenkelig som en enkelt helhet."

Søndag 18. mars 2018

Summen av sifrene til et tall er en dans av sjamaner med en tamburin, som ikke har noe med matematikk å gjøre. Ja, i matematikktimer blir vi lært å finne summen av sifrene til et tall og bruke det, men det er derfor de er sjamaner, for å lære etterkommerne deres ferdigheter og visdom, ellers vil sjamanene ganske enkelt dø ut.

Trenger du bevis? Åpne Wikipedia og prøv å finne siden «Summen av sifre i et tall». Hun finnes ikke. Det er ingen formel i matematikk som kan brukes til å finne summen av sifrene til et hvilket som helst tall. Tross alt er tall grafiske symboler som vi skriver tall med, og på matematikkspråket høres oppgaven slik ut: "Finn summen av grafiske symboler som representerer et hvilket som helst tall." Matematikere kan ikke løse dette problemet, men sjamaner kan gjøre det enkelt.

La oss finne ut hva og hvordan vi gjør for å finne summen av sifrene til et gitt tall. Så la oss få tallet 12345. Hva må gjøres for å finne summen av sifrene til dette tallet? La oss vurdere alle trinnene i rekkefølge.

1. Skriv ned tallet på et stykke papir. Hva har vi gjort? Vi har konvertert tallet til et grafisk tallsymbol. Dette er ikke en matematisk operasjon.

2. Vi kuttet ett resulterende bilde i flere bilder som inneholder individuelle tall. Å kutte et bilde er ikke en matematisk operasjon.

3. Konverter individuelle grafiske symboler til tall. Dette er ikke en matematisk operasjon.

4. Legg til de resulterende tallene. Nå er dette matematikk.

Summen av sifrene til tallet 12345 er 15. Dette er "skjære- og sykursene" som undervises av sjamaner som matematikere bruker. Men det er ikke alt.

Fra et matematisk synspunkt spiller det ingen rolle i hvilket tallsystem vi skriver et tall. Så i forskjellige tallsystemer vil summen av sifrene i samme tall være forskjellig. I matematikk er tallsystemet angitt som et abonnent til høyre for tallet. Med det store tallet 12345 vil jeg ikke lure hodet mitt, la oss vurdere tallet 26 fra artikkelen om. La oss skrive dette tallet i binære, oktale, desimale og heksadesimale tallsystemer. Vi vil ikke se på hvert trinn under et mikroskop, vi har allerede gjort det. La oss se på resultatet.

Som du kan se, i forskjellige tallsystemer er summen av sifrene til samme tall forskjellig. Dette resultatet har ingenting med matematikk å gjøre. Det er det samme som om du bestemte arealet til et rektangel i meter og centimeter, ville du få helt andre resultater.

Null ser likt ut i alle tallsystemer og har ingen tallsum. Dette er et annet argument for det faktum. Spørsmål til matematikere: hvordan er noe som ikke er et tall angitt i matematikk? Hva, for matematikere eksisterer ingenting bortsett fra tall? Jeg kan tillate dette for sjamaner, men ikke for forskere. Virkeligheten handler ikke bare om tall.

Resultatet som oppnås bør betraktes som bevis på at tallsystemer er måleenheter for tall. Vi kan tross alt ikke sammenligne tall med ulike måleenheter. Hvis de samme handlingene med forskjellige måleenheter av samme mengde fører til forskjellige resultater etter å ha sammenlignet dem, har dette ingenting med matematikk å gjøre.

Hva er ekte matematikk? Dette er når resultatet av en matematisk operasjon ikke er avhengig av størrelsen på tallet, måleenheten som brukes og hvem som utfører denne handlingen.

Skilt på døren Han åpner døren og sier:

Åh! Er ikke dette dametoalettet?
- Ung kvinne! Dette er et laboratorium for studiet av sjelenes indefiliske hellighet under deres oppstigning til himmelen! Halo på toppen og pil opp. Hvilket annet toalett?

Hunn... Haloen på toppen og pilen ned er hann.

Hvis et slikt designkunstverk blinker foran øynene dine flere ganger om dagen,

Da er det ikke overraskende at du plutselig finner et merkelig ikon i bilen din:

Personlig anstrenger jeg meg for å se minus fire grader hos en som bæser (ett bilde) (en sammensetning av flere bilder: et minustegn, tallet fire, en betegnelse på grader). Og jeg tror ikke denne jenta er en tosk som ikke kan fysikk. Hun har bare en sterk stereotyp av å oppfatte grafiske bilder. Og matematikere lærer oss dette hele tiden. Her er et eksempel.

1A er ikke "minus fire grader" eller "én a". Dette er "bajsende mann" eller tallet "tjueseks" i heksadesimal notasjon. De menneskene som hele tiden jobber i dette tallsystemet, oppfatter automatisk et tall og en bokstav som ett grafisk symbol.

Leksjonens innhold

Legge til brøker med like nevnere

Det er to typer addisjon av brøker:

1. Legge til brøker med like nevnere
2. Legge til brøker med forskjellige nevnere

La oss først lære addisjonen av brøker med like nevnere. Alt er enkelt her. For å legge til brøker med de samme nevnerne, må du legge til deres tellere og la nevneren være uendret. La oss for eksempel legge til brøkene og . Legg til tellerne og la nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi husker pizzaen, som er delt inn i fire deler. Legger du pizza til pizza, får du pizza:

Eksempel 2. Legg til brøker og .

Svaret viste seg å være en upassende brøkdel. Når slutten av oppgaven kommer, er det vanlig å kvitte seg med upassende brøker. For å bli kvitt en upassende brøkdel, må du velge hele delen av den. I vårt tilfelle er hele delen lett isolert - to delt på to er lik en:

Dette eksemplet kan lett forstås hvis vi husker om en pizza som er delt i to deler. Legger du til mer pizza i pizzaen, får du en hel pizza:

Eksempel 3. Legg til brøker og .

Igjen legger vi sammen tellerne og lar nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi husker pizzaen, som er delt inn i tre deler. Legger du til mer pizza i pizzaen får du pizza:

Eksempel 4. Finn verdien av et uttrykk

Dette eksemplet er løst på nøyaktig samme måte som de forrige. Tellerne må legges til og nevneren holdes uendret:

La oss prøve å skildre løsningen vår ved hjelp av en tegning. Legger du pizza til en pizza og legger til flere pizzaer, får du 1 hel pizza og flere pizzaer.

Som du kan se, er det ikke noe komplisert ved å legge til brøker med samme nevnere. Det er nok å forstå følgende regler:

1. For å legge til brøker med samme nevner, må du legge til deres tellere og la nevneren være uendret;

Legge til brøker med forskjellige nevnere

La oss nå lære hvordan du legger til brøker med forskjellige nevnere. Når man legger til brøker, må nevnerne til brøkene være de samme. Men de er ikke alltid like.

For eksempel kan brøker legges til fordi de har de samme nevnerne.

Men brøker kan ikke legges til med en gang, siden disse brøkene har forskjellige nevnere. I slike tilfeller må brøker reduseres til samme (felles)nevner.

Det er flere måter å redusere brøker til samme nevner. I dag skal vi se på bare en av dem, siden de andre metodene kan virke kompliserte for en nybegynner.

Essensen av denne metoden er at først LCM for nevnerne til begge brøkene søkes. LCM deles deretter med nevneren til den første brøken for å oppnå den første tilleggsfaktoren. De gjør det samme med den andre brøken - LCM deles på nevneren til den andre brøken og en andre tilleggsfaktor oppnås.

Tellerne og nevnerne til brøkene multipliseres deretter med tilleggsfaktorene deres. Som et resultat av disse handlingene blir brøker som hadde forskjellige nevnere til brøker som har samme nevner. Og vi vet allerede hvordan vi legger til slike brøker.

Eksempel 1. La oss legge til brøkene og

Først og fremst finner vi det minste felles multiplum av nevnerne til begge brøkene. Nevneren til den første brøken er tallet 3, og nevneren til den andre brøken er tallet 2. Minste felles multiplum av disse tallene er 6

LCM (2 og 3) = 6

La oss nå gå tilbake til brøker og . Del først LCM med nevneren til den første brøken og få den første tilleggsfaktoren. LCM er tallet 6, og nevneren til den første brøken er tallet 3. Del 6 med 3, vi får 2.

Det resulterende tallet 2 er den første tilleggsmultiplikatoren. Vi skriver det ned til den første brøken. For å gjøre dette, lag en liten skrå linje over brøken og skriv ned tilleggsfaktoren som finnes over den:

Vi gjør det samme med den andre brøken. Vi deler LCM med nevneren til den andre brøken og får den andre tilleggsfaktoren. LCM er tallet 6, og nevneren til den andre brøken er tallet 2. Del 6 med 2, vi får 3.

Det resulterende tallet 3 er den andre tilleggsmultiplikatoren. Vi skriver det ned til den andre brøken. Igjen lager vi en liten skrå linje over den andre brøken og skriver ned tilleggsfaktoren som finnes over den:

Nå har vi alt klart for tillegg. Det gjenstår å multiplisere tellerne og nevnerne til brøkene med deres tilleggsfaktorer:

Se nøye på hva vi har kommet til. Vi kom frem til at brøker som hadde forskjellige nevnere ble til brøker som hadde samme nevner. Og vi vet allerede hvordan vi legger til slike brøker. La oss ta dette eksemplet til slutten:

Dette fullfører eksemplet. Det viser seg å legge til.

La oss prøve å skildre løsningen vår ved hjelp av en tegning. Legger du pizza til en pizza, får du en hel pizza og ytterligere en sjettedel av en pizza:

Å redusere brøker til samme (felles)nevner kan også avbildes ved hjelp av et bilde. Ved å redusere brøkene og til en fellesnevner, fikk vi brøkene og . Disse to brøkene vil bli representert av de samme pizzastykkene. Den eneste forskjellen vil være at de denne gangen deles i like deler (redusert til samme nevner).

Den første tegningen representerer en brøk (fire stykker av seks), og den andre tegningen representerer en brøk (tre stykker av seks). Ved å legge til disse bitene får vi (syv av seks). Denne brøkdelen er upassende, så vi fremhevet hele delen av den. Som et resultat fikk vi (en hel pizza og en annen sjette pizza).

Vær oppmerksom på at vi har beskrevet dette eksemplet for mye detaljert. I utdanningsinstitusjoner er det ikke vanlig å skrive så detaljert. Du må raskt kunne finne LCM for både nevnerne og tilleggsfaktorene til dem, samt raskt multiplisere de funnet tilleggsfaktorene med tellerne og nevnerne dine. Hvis vi var på skolen, ville vi måtte skrive dette eksemplet som følger:

Men det er også en annen side ved mynten. Hvis du ikke tar detaljerte notater i de første stadiene av å studere matematikk, begynner slike spørsmål å dukke opp. "Hvor kommer det tallet fra?", "Hvorfor blir brøker plutselig til helt andre brøker? «.

For å gjøre det enklere å legge til brøker med forskjellige nevnere, kan du bruke følgende trinnvise instruksjoner:

1. Finn LCM for nevnerne til brøker;
2. Del LCM med nevneren for hver brøk og få en ekstra faktor for hver brøk;
3. Multipliser tellerne og nevnerne til brøker med tilleggsfaktorene deres;
4. Legg til brøker som har samme nevnere;
5. Hvis svaret viser seg å være en uekte brøk, velg hele delen;

Eksempel 2. Finn verdien av et uttrykk .

La oss bruke instruksjonene ovenfor.

Trinn 1. Finn LCM for nevnerne til brøkene

Finn LCM for nevnerne til begge brøkene. Nevnerne for brøker er tallene 2, 3 og 4

Trinn 2. Del LCM med nevneren for hver brøk og få en tilleggsfaktor for hver brøk

Del LCM med nevneren til den første brøken. LCM er tallet 12, og nevneren til den første brøken er tallet 2. Del 12 med 2, vi får 6. Vi fikk den første tilleggsfaktoren 6. Vi skriver den over den første brøken:

Nå deler vi LCM med nevneren til den andre brøken. LCM er tallet 12, og nevneren til den andre brøken er tallet 3. Del 12 med 3, vi får 4. Vi får den andre tilleggsfaktoren 4. Vi skriver den over den andre brøken:

Nå deler vi LCM med nevneren til den tredje brøken. LCM er tallet 12, og nevneren til den tredje brøken er tallet 4. Del 12 med 4, vi får 3. Vi får den tredje tilleggsfaktoren 3. Vi skriver den over den tredje brøken:

Trinn 3. Multipliser tellerne og nevnerne til brøkene med tilleggsfaktorene deres

Vi multipliserer tellerne og nevnerne med tilleggsfaktorene deres:

Trinn 4. Legg til brøker med samme nevnere

Vi kom frem til at brøker som hadde ulike nevnere ble til brøker som hadde samme (felles)nevnere. Alt som gjenstår er å legge til disse brøkene. Legg det til:

Addisjonen passet ikke på én linje, så vi flyttet det gjenværende uttrykket til neste linje. Dette er tillatt i matematikk. Når et uttrykk ikke passer på en linje, flyttes det til neste linje, og det er nødvendig å sette et likhetstegn (=) på slutten av den første linjen og i begynnelsen av den nye linjen. Likhetstegnet på den andre linjen indikerer at dette er en fortsettelse av uttrykket som var på den første linjen.

Trinn 5. Hvis svaret viser seg å være en uekte brøkdel, velg hele delen av det

Svaret vårt viste seg å være en upassende brøkdel. Vi må fremheve en hel del av det. Vi fremhever:

Vi fikk svar

Å trekke fra brøker med like nevnere

Det er to typer subtraksjon av brøker:

1. Å trekke fra brøker med like nevnere
2. Å trekke fra brøker med forskjellige nevnere

Først, la oss lære hvordan du trekker fra brøker med like nevnere. Alt er enkelt her. For å trekke en annen fra en brøk, må du trekke telleren til den andre brøken fra telleren til den første brøken, men la nevneren være den samme.

La oss for eksempel finne verdien av uttrykket . For å løse dette eksemplet må du trekke fra telleren til den andre brøken fra telleren til den første brøken, og la nevneren være uendret. La oss gjøre dette:

Dette eksemplet kan lett forstås hvis vi husker pizzaen, som er delt inn i fire deler. Hvis du kutter pizza fra en pizza, får du pizza:

Eksempel 2. Finn verdien av uttrykket.

Igjen, fra telleren til den første brøken, trekk fra telleren til den andre brøken, og la nevneren være uendret:

Dette eksemplet kan lett forstås hvis vi husker pizzaen, som er delt inn i tre deler. Hvis du kutter pizza fra en pizza, får du pizza:

Eksempel 3. Finn verdien av et uttrykk

Dette eksemplet er løst på nøyaktig samme måte som de forrige. Fra telleren til den første brøken må du trekke fra tellerne til de gjenværende brøkene:

Som du kan se, er det ikke noe komplisert ved å trekke fra brøker med de samme nevnerne. Det er nok å forstå følgende regler:

1. For å subtrahere en annen fra en brøk, må du trekke fra telleren til den andre brøken fra telleren til den første brøken, og la nevneren være uendret;
2. Hvis svaret viser seg å være en upassende brøkdel, må du markere hele delen av det.

Å trekke fra brøker med forskjellige nevnere

For eksempel kan du trekke en brøk fra en brøk fordi brøkene har samme nevnere. Men du kan ikke trekke en brøk fra en brøk, siden disse brøkene har forskjellige nevnere. I slike tilfeller må brøker reduseres til samme (felles)nevner.

Fellesnevneren er funnet ved å bruke samme prinsipp som vi brukte når vi adderte brøker med forskjellige nevnere. Først av alt, finn LCM for nevnerne til begge brøkene. Deretter divideres LCM med nevneren til den første brøken og den første tilleggsfaktoren oppnås, som er skrevet over den første brøken. På samme måte deles LCM med nevneren til den andre brøken og en andre tilleggsfaktor oppnås, som er skrevet over den andre brøken.

Brøkene multipliseres deretter med tilleggsfaktorene. Som et resultat av disse operasjonene konverteres brøker som hadde forskjellige nevnere til brøker som har samme nevner. Og vi vet allerede hvordan vi trekker fra slike brøker.

Eksempel 1. Finn betydningen av uttrykket:

Disse brøkene har forskjellige nevnere, så du må redusere dem til samme (felles) nevner.

Først finner vi LCM for nevnerne til begge brøkene. Nevneren til den første brøken er tallet 3, og nevneren til den andre brøken er tallet 4. Minste felles multiplum av disse tallene er 12

LCM (3 og 4) = 12

La oss nå gå tilbake til brøker og

La oss finne en tilleggsfaktor for den første brøken. For å gjøre dette, del LCM med nevneren til den første brøken. LCM er tallet 12, og nevneren til den første brøken er tallet 3. Del 12 med 3, vi får 4. Skriv en firer over den første brøken:

Vi gjør det samme med den andre brøken. Del LCM med nevneren til den andre brøken. LCM er tallet 12, og nevneren til den andre brøken er tallet 4. Del 12 med 4, vi får 3. Skriv en treer over den andre brøken:

Nå er vi klare for subtraksjon. Det gjenstår å multiplisere brøkene med deres tilleggsfaktorer:

Vi kom frem til at brøker som hadde forskjellige nevner ble til brøker som hadde samme nevner. Og vi vet allerede hvordan vi trekker fra slike brøker. La oss ta dette eksemplet til slutten:

Vi fikk svar

La oss prøve å skildre løsningen vår ved hjelp av en tegning. Hvis du kutter pizza fra en pizza, får du pizza

Dette er den detaljerte versjonen av løsningen. Hvis vi var på skolen, måtte vi løse dette eksempelet kortere. En slik løsning vil se slik ut:

Å redusere brøker til en fellesnevner kan også avbildes ved hjelp av et bilde. Ved å redusere disse brøkene til en fellesnevner, fikk vi brøkene og . Disse brøkene vil være representert av de samme pizzaskivene, men denne gangen deles de i like deler (redusert til samme nevner):

Det første bildet viser en brøk (åtte stykker av tolv), og det andre bildet viser en brøk (tre stykker av tolv). Ved å kutte tre stykker fra åtte stykker får vi fem stykker av tolv. Brøken beskriver disse fem stykkene.

Eksempel 2. Finn verdien av et uttrykk

Disse brøkene har forskjellige nevnere, så først må du redusere dem til samme (felles) nevner.

La oss finne LCM for nevnerne til disse brøkene.

Nevnerne til brøkene er tallene 10, 3 og 5. Minste felles multiplum av disse tallene er 30

LCM(10; 3; 5) = 30

Nå finner vi tilleggsfaktorer for hver brøk. For å gjøre dette, del LCM med nevneren for hver brøk.

La oss finne en tilleggsfaktor for den første brøken. LCM er tallet 30, og nevneren til den første brøken er tallet 10. Del 30 med 10, vi får den første tilleggsfaktoren 3. Vi skriver den over den første brøken:

Nå finner vi en tilleggsfaktor for den andre brøken. Del LCM med nevneren til den andre brøken. LCM er tallet 30, og nevneren til den andre brøken er tallet 3. Del 30 med 3, vi får den andre tilleggsfaktoren 10. Vi skriver den over den andre brøken:

Nå finner vi en tilleggsfaktor for den tredje brøken. Del LCM med nevneren til den tredje brøken. LCM er tallet 30, og nevneren til den tredje brøken er tallet 5. Del 30 med 5, vi får den tredje tilleggsfaktoren 6. Vi skriver den over den tredje brøken:

Nå er alt klart for subtraksjon. Det gjenstår å multiplisere brøkene med deres tilleggsfaktorer:

Vi kom frem til at brøker som hadde ulike nevnere ble til brøker som hadde samme (felles)nevnere. Og vi vet allerede hvordan vi trekker fra slike brøker. La oss avslutte dette eksemplet.

Fortsettelsen av eksemplet vil ikke passe på én linje, så vi flytter fortsettelsen til neste linje. Ikke glem likhetstegnet (=) på den nye linjen:

Svaret viste seg å være en vanlig brøk, og alt ser ut til å passe oss, men det er for tungvint og stygt. Vi bør gjøre det enklere. Hva kan bli gjort? Du kan forkorte denne brøken.

For å redusere en brøk, må du dele telleren og nevneren med (GCD) av tallene 20 og 30.

Så vi finner gcd av tallene 20 og 30:

Nå går vi tilbake til eksemplet vårt og deler telleren og nevneren av brøken med den funnet gcd, det vil si med 10

Vi fikk svar

Multiplisere en brøk med et tall

For å multiplisere en brøk med et tall, må du multiplisere telleren til den gitte brøken med det tallet og la nevneren være den samme.

Eksempel 1. Multipliser en brøk med tallet 1.

Multipliser telleren av brøken med tallet 1

Opptaket kan forstås som å ta halv 1 gang. For eksempel, hvis du tar pizza en gang, får du pizza

Fra multiplikasjonslovene vet vi at hvis multiplikaden og faktoren byttes, vil ikke produktet endres. Hvis uttrykket skrives som , vil produktet fortsatt være lik . Igjen fungerer regelen for å multiplisere et helt tall og en brøk:

Denne notasjonen kan forstås som å ta halvparten av en. For eksempel, hvis det er 1 hel pizza og vi tar halvparten av den, vil vi ha pizza:

Eksempel 2. Finn verdien av et uttrykk

Multipliser telleren av brøken med 4

Svaret var en uekte brøk. La oss fremheve hele delen av det:

Uttrykket kan forstås som å ta to kvarter 4 ganger. Tar du for eksempel 4 pizzaer, får du to hele pizzaer

Og hvis vi bytter ut multiplikanten og multiplikatoren, får vi uttrykket . Det vil også være lik 2. Dette uttrykket kan forstås som å ta to pizzaer fra fire hele pizzaer:

Multiplisere brøker

For å multiplisere brøker, må du multiplisere deres tellere og nevnere. Hvis svaret viser seg å være en upassende brøkdel, må du fremheve hele delen av det.

Eksempel 1. Finn verdien av uttrykket.

Vi fikk svar. Det er tilrådelig å redusere denne brøkdelen. Fraksjonen kan reduseres med 2. Da vil den endelige løsningen ha følgende form:

Uttrykket kan forstås som å ta en pizza fra en halv pizza. La oss si at vi har en halv pizza:

Hvordan ta to tredjedeler fra denne halvdelen? Først må du dele denne halvdelen i tre like deler:

Og ta to fra disse tre delene:

Vi lager pizza. Husk hvordan pizza ser ut når den er delt i tre deler:

Ett stykke av denne pizzaen og de to stykkene vi tok vil ha samme dimensjoner:

Vi snakker med andre ord om samme størrelse pizza. Derfor er verdien av uttrykket

Eksempel 2. Finn verdien av et uttrykk

Multipliser telleren til den første brøken med telleren til den andre brøken, og nevneren til den første brøken med nevneren til den andre brøken:

Svaret var en uekte brøk. La oss fremheve hele delen av det:

Eksempel 3. Finn verdien av et uttrykk

Multipliser telleren til den første brøken med telleren til den andre brøken, og nevneren til den første brøken med nevneren til den andre brøken:

Svaret viste seg å være en vanlig brøk, men det ville vært bra om det ble forkortet. For å redusere denne brøken må du dele telleren og nevneren til denne brøken med den største felles divisor (GCD) av tallene 105 og 450.

Så, la oss finne gcd av tallene 105 og 450:

Nå deler vi telleren og nevneren for svaret vårt med gcd som vi nå har funnet, det vil si med 15

Representerer et helt tall som en brøk

Ethvert heltall kan representeres som en brøk. For eksempel kan tallet 5 representeres som . Dette vil ikke endre betydningen av fem, siden uttrykket betyr "tallet fem delt på en", og dette er, som vi vet, lik fem:

Gjensidige tall

Nå skal vi bli kjent med et veldig interessant tema i matematikk. Det kalles "omvendte tall".

Definisjon. Tilbake til nummeren er et tall som multiplisert meden gir en.

La oss erstatte i denne definisjonen i stedet for variabelen en nummer 5 og prøv å lese definisjonen:

Tilbake til nummer 5 er et tall som multiplisert med 5 gir en.

Er det mulig å finne et tall som, multiplisert med 5, gir ett? Det viser seg at det er mulig. La oss forestille oss fem som en brøk:

Multipliser deretter denne brøken med seg selv, bare bytt om teller og nevner. Med andre ord, la oss multiplisere brøken med seg selv, bare opp ned:

Hva vil skje som følge av dette? Hvis vi fortsetter å løse dette eksemplet, får vi ett:

Dette betyr at inversen av tallet 5 er tallet , siden når du ganger 5 med får du en.

Den gjensidige av et tall kan også finnes for et hvilket som helst annet heltall.

Du kan også finne den gjensidige av en hvilken som helst annen brøk. For å gjøre dette, bare snu den.

Å dele en brøk på et tall

La oss si at vi har en halv pizza:

La oss dele det likt mellom to. Hvor mye pizza får hver person?

Det kan sees at etter å ha delt halvparten av pizzaen, ble det oppnådd to like stykker, som hver utgjør en pizza. Så alle får en pizza.

Deling av brøker gjøres ved å bruke resiproke. Gjensidige tall lar deg erstatte divisjon med multiplikasjon.

For å dele en brøk på et tall, må du multiplisere brøken med inversen av divisor.

Ved å bruke denne regelen vil vi skrive ned delingen av vår halvdel av pizzaen i to deler.

Så du må dele brøken med tallet 2. Her er utbyttet brøken og divisor er tallet 2.

For å dele en brøk med tallet 2, må du multiplisere denne brøken med den resiproke av divisor 2. Den resiproke av divisor 2 er brøken. Så du må gange med

For å legge til et helt tall til en brøk, er det nok å utføre en rekke handlinger, eller rettere sagt beregninger.

For eksempel har du 7 - et heltall du må legge det til brøken 1/2.

Vi går frem som følger:

• Vi ganger 7 med nevneren (2), vi får 14,
• legg til den øvre delen (1) til 14, du får 15,
• og erstatte nevneren.
• resultatet er 15/2.

På denne enkle måten kan du legge hele tall til brøker.

Og for å isolere et helt tall fra en brøk, må du dele telleren med nevneren, og resten - og det blir en brøk.

Operasjonen med å legge til et heltall til en riktig ordinær brøk er ikke komplisert og involverer noen ganger ganske enkelt dannelsen av en blandet brøk, der heltallsdelen er plassert til venstre for brøkdelen, for eksempel vil en slik brøk bli blandet:

Men oftere enn ikke, å legge et helt tall til en brøk resulterer i en uekte brøk der telleren er større enn nevneren. Denne operasjonen utføres som følger: hele tallet er representert som en uekte brøk med samme nevner som brøken som legges til, og deretter legges tellerne til begge brøkene ganske enkelt til. I et eksempel vil det se slik ut:

5+1/8 = 5*8/8+1/8 = 40/8+1/8 = 41/8

Jeg tror det er veldig enkelt.

For eksempel har vi brøken 1/4 (dette er det samme som 0,25, det vil si en fjerdedel av hele tallet).

Og til dette kvartalet kan du legge til et hvilket som helst heltall, for eksempel 3. Du får tre og en kvart:

3,25. Eller i brøk er det uttrykt slik: 3 1/4

Ved å bruke dette eksemplet kan du legge til alle brøker med alle heltall.

Du må heve et helt tall til en brøk med nevneren 10 (6/10). Deretter bringer du den eksisterende brøken til en fellesnevner på 10 (35=610). Vel, utfør operasjonen som med vanlige brøker 610+610=1210 for totalt 12.

Det er to måter å gjøre dette på.

1). En brøk kan konverteres til et helt tall og addisjon kan utføres. For eksempel er 1/2 0,5; 1/4 tilsvarer 0,25; 2/5 er 0,4 osv.

Ta heltall 5, som du må legge til brøken 4/5. La oss transformere brøken: 4/5 er 4 delt på 5 og vi får 0,8. Legger til 0,8 til 5 og vi får 5,8 eller 5 4/5.

2). Andre metode: 5 + 4/5 = 29/5 = 5 4/5.

Å legge til brøker er en enkel matematisk operasjon, for eksempel må du legge til heltall 3 og brøk 1/7. For å legge til disse to tallene må du ha samme nevner, så du må gange tre med syv og dele på det tallet, så får du 21/7+1/7, nevner en, legg til 21 og 1, du får svaret 22/ 7.

Bare ta og legg til et heltall til denne brøken La oss si at du trenger 6 + 1/2 = 6 1/2. Vel, hvis dette er en desimalbrøk, kan du gjøre det slik: 6+1,2=7,2.

For å legge til en brøk og et heltall, må du legge til brøken til heltallet og skrive dem ned som et komplekst tall, for eksempel når vi legger til en vanlig brøk med et heltall, får vi: 1/2 +3 = 3 1/ 2; når du legger til en desimalbrøk: 0,5 +3 =3,5.

En brøk i seg selv er ikke et helt tall, fordi dens mengde ikke når det, og derfor er det ikke nødvendig å konvertere hele tallet til denne brøken. Derfor forblir heltallet et heltall og demonstrerer den fulle verdien, og brøken legges til det, og viser hvor mye dette heltallet mangler før det neste hele punktet legges til.

Akademisk eksempel.

10 + 7/3 = 10 hele og 7/3.

Hvis det selvfølgelig er heltall, summeres de med heltall.

12 + 5 7/9 = 17 og 7/9.

Det avhenger av hvilket heltall og hvilken brøk.

Hvis begge begrepene er positive, skal denne brøken legges til hele tallet. Resultatet blir et blandet tall. Dessuten kan det være 2 tilfeller.

Sak 1.

• Brøken er riktig, dvs. telleren er mindre enn nevneren. Da vil det blandede antallet oppnådd etter oppgaven være svaret.

4/9 + 10 = 10 4/9 (ti komma fire niendedeler).



Tilfelle 2.

• Brøken er uekte, dvs. telleren er større enn nevneren. Da kreves det litt konvertering. En uekte brøk skal gjøres om til et blandet tall, med andre ord, hele delen skal skilles. Dette gjøres slik:



Etter dette må du legge til hele delen av den uriktige brøkdelen til hele tallet og legge til brøkdelen til den resulterende mengden. På samme måte legges en helhet til et blandet tall.

1) 11/4 + 5 = 2 3/4 + 5 = 7 3/4 (7 komma tre kvarter).

2) 5 1/2 + 6 = 11 1/2 (11 poeng én).

Hvis ett av begrepene eller begge negativ, så utfører vi addisjonen i henhold til reglene for å legge til tall med forskjellige eller identiske fortegn. Et helt tall er representert som forholdet mellom det tallet og 1, og deretter multipliseres både telleren og nevneren med et tall som er lik nevneren til brøken som hele tallet legges til.

3) 1/5 + (-2)= 1/5 + -2/1 = 1/5 + -10/5 = -9/5 = -1 4/5 (minus 1 poeng fire femtedeler).

4) -13/3 + (-4) = -13/3 + -4/1 = -13/3 + -12/3 = -25/3 = -8 1/3 (minus 8 poeng en tredjedel).

Kommentar.

Etter å ha blitt kjent med negative tall, når de studerer operasjoner med dem, bør elever i 6. klasse forstå at å legge til et positivt heltall til en negativ brøk er det samme som å trekke en brøk fra et naturlig tall. Denne handlingen er kjent for å utføres slik:



Faktisk, for å legge til en brøk og et heltall, trenger du ganske enkelt å konvertere det eksisterende heltall til en brøk, og å gjøre dette er like enkelt som å avskalle pærer. Du trenger bare å ta nevneren til en brøk (i eksemplet) og gjøre den til nevneren for et helt tall ved å multiplisere den med den nevneren og dele, her er et eksempel:

2+2/3 = 2*3/3+2/3 = 6/3+2/3 = 8/3