"Definisjonsdomene for en funksjon" - Definisjonsdomenet for en kvadratisk funksjon er et hvilket som helst reelt tall. En funksjon kalles logaritmisk hvis variabelverdien er under logaritmetegnet. Logaritmisk funksjon. En funksjon hvis variabel er i eksponenten kalles eksponentiell. Kvadratisk funksjon.
"Generelle egenskaper til funksjoner" - Generelle egenskaper til funksjoner. Finn definisjonsdomenet til funksjonen. Jevn funksjon. Om denne funksjonen er partall eller oddetall. Bruk grafen, bestem settet med verdier for funksjonen. Bruk grafen til å bestemme verdiene til X. Bruk grafen til å bestemme intervallene for reduksjon i funksjonen. Funksjon f(x) øker. Funksjonen y=f(x) er gitt.
"Økende og reduserende funksjon" - Økende og reduserende sinusfunksjon. La oss se på et annet eksempel. Intervallene for synkende cosinus er segmenter, n er et heltall. La for eksempel funksjonen f være jevn og økende på intervallet hvor b>a?0. Økende og redusere funksjoner. Økende og redusere cosinusfunksjon. Figuren nedenfor viser en graf for en funksjon definert på intervallet [-1;10].
"Anvendelse av kontinuitet" - Betydning av uttrykk. Geometrisk betydning av derivat. Intervall metode. Skriv en ligning for tangenten til grafen til funksjonen. Tangent til grafen til en funksjon. Grafen er nær en tangent. Formel. La oss beregne ved å bruke formelen. Tangenten til kurven i et gitt punkt M er grenseposisjonen til sekant NM. Hyperbel.
"Ekstrem funksjon" - Avhengighet av gasstrykk på temperatur. Leksjonsemne: «Tegn på økende og minkende funksjoner. Test. Endring i strømstyrke når kretsen åpnes. Undersøkelse av en funksjon til et ekstremum". Endring av vekselstrøm. Plan: Strømavhengighet av spenning. Avhengighet av gasstrykk på volum. Tema: «Tegn på økende og minkende funksjoner.
"Funksjoner og deres egenskaper" - Den uavhengige variabelen kalles et argument. Økende funksjon. Definisjon av en funksjon. Partall og odde funksjoner. Monotonicitet av funksjonen. Verdiene til den avhengige variabelen kalles funksjonens verdier. Alle verdier av den uavhengige variabelen danner definisjonsdomenet til funksjonen -D (f). 1. Funksjonsverdiene er positive.
Det er totalt 23 presentasjoner i temaet
Emne: Metoder for bruk av begrensede funksjoner.
Livet er bra på grunn av det som er i det
du kan gjøre matematikk.
(Leonard Euler)Mål: utvikling av ny ukonvensjonell tenkning, som med hell kan brukes på andre områder av menneskelig aktivitet (kybernetikk, datateknologi, økonomi, radiofysikk, kjemi, etc.).
Oppgaver: - opplæring i å vurdere den objektive og subjektive vanskeligheten til oppgaver og det rimelige valget av disse oppgavene i eksamen;
Å lage en "sparegrise" av ukonvensjonelle og uvanlige resonnementer.
I løpet av timene:
Org. øyeblikk. Studentene formulerer emnet for leksjonen ved å fullføre Unified State Exam-oppgavene del A og B og dechiffrere emnet i synkende rekkefølge etter svarene som mottas. (Krypter 12 kort nummerert fra -2 til 10 som antatte ord) (vedlegg 1 og 2)
begrensninger
2. Del elevene inn i 2 grupper, gi dem settet «Teori + 10 oppgaver» (vedlegg 3 og 4), be dem velge de oppgavene som kan gjennomføres for denne teoretiske delen, og begrunn valget.3. Vis fremdriften til disse oppgavene på tavlen av elevene: Noskova K., Dedevshin I., Veselov I.4. Del oppgavene fra kortet i 2 grupper for å løse dem, etterfulgt av selvtest ved hjelp av et ark med ferdige løsninger. (Vedlegg 5)5. Del ut til gruppene ark som beskriver nye ikke-standardiserte metoder for å løse likninger og ulikheter for valg av neste emne (som en hjemmeoppgave, finn problemer i Unified State Exam-samlingene som kan løses ved hjelp av denne metoden) (vedlegg 6)6. Elevrefleksjon (fyller ut tabellen) F.I. studentVedlegg 1.
Løs disse oppgavene og ordne svarene i synkende rekkefølge, samle emnet for leksjonen vår basert på svarene.
Finn abscissen til punktet i grafen til funksjonen y=3x 2 -7x+7, der tangenten til tangentvinkelen er lik -1.
Vedlegg 2.
9 2 0 7Studium av funksjoner ved bruk av deriverte. 10 5 1 -1 Metode for bruk av begrensede funksjoner. 4 -2 8 12Løse ulikheter grafisk.
3 11 6Løsninger av funksjonelle ligninger.
Studere
Vedlegg 3.
En av de effektive metodene for å løse likninger eller ulikheter er metoden basert på bruk av avgrensede funksjoner. De mest kjente begrensede funksjonene inkluderer for eksempel noen trigonometriske funksjoner; inverse trigonometriske funksjoner; funksjoner som inneholder modul, grad, rot med jevn grad og andre.
De vanligste ulikhetene er følgende:
│f(x) │≥
0, -1
≤
sinx ≤
1, -1
≤
cosx ≤
1, -
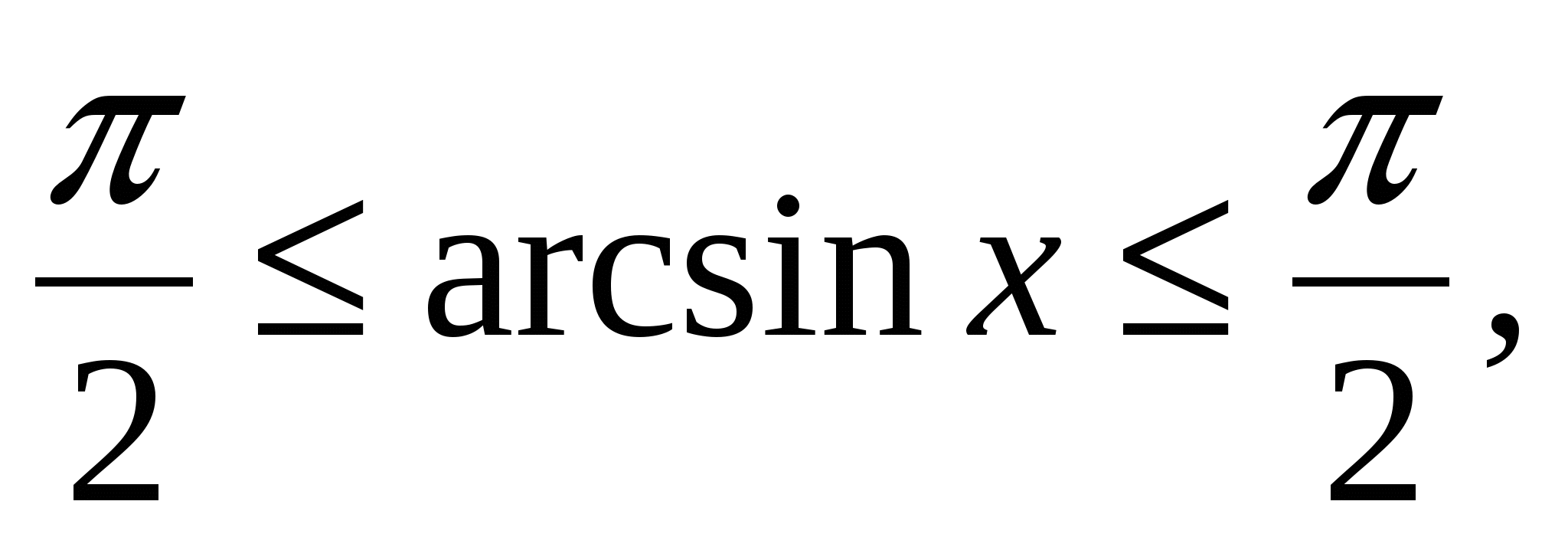
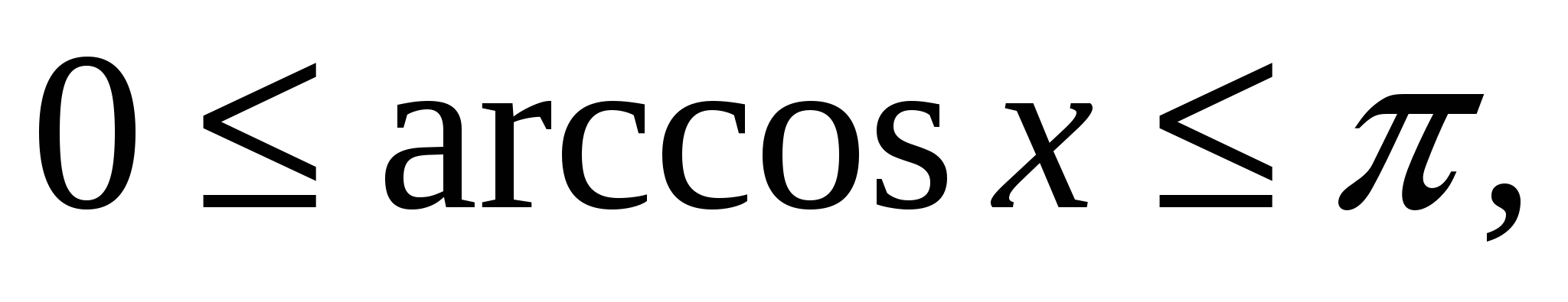 -
-

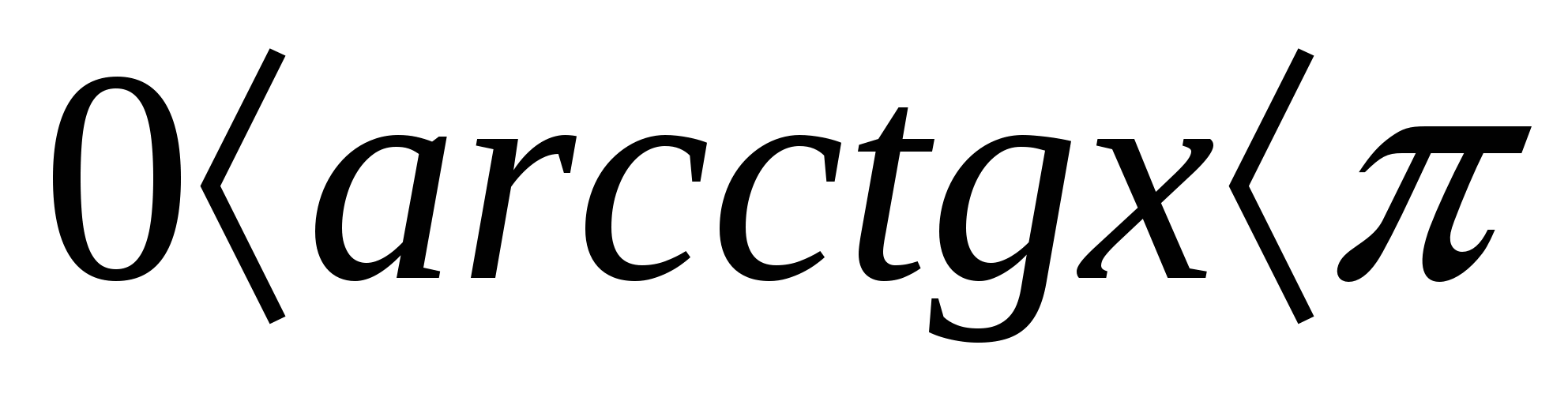 ,
en f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
,
en f ( x ) >0, (f(x) ±
g(x)) 2 n ≥
0,
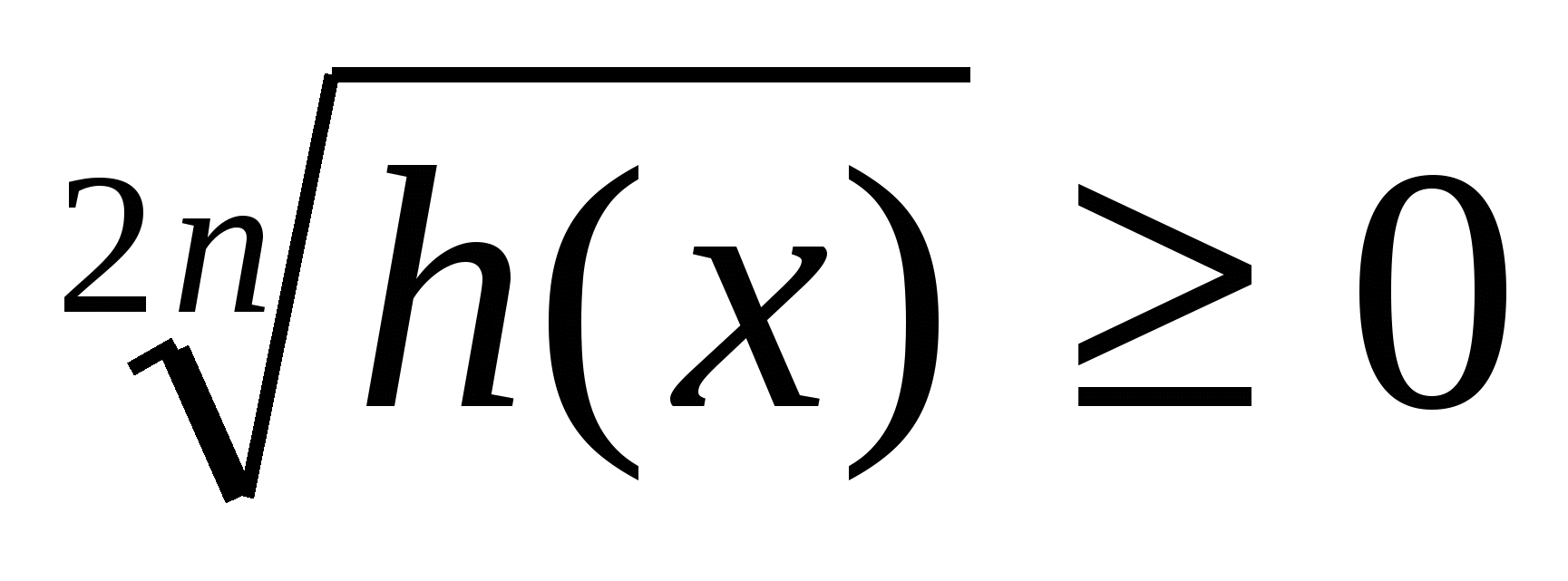 ,
en+
≥
2,
b+
≤
-2
og mange andre. Her n -naturlig tall, h(x) ≥
0,
en>0,
b
0.
,
en+
≥
2,
b+
≤
-2
og mange andre. Her n -naturlig tall, h(x) ≥
0,
en>0,
b
0.
I tillegg til de enkleste ulikhetene gitt ovenfor, er det også mer komplekse, spesielt trigonometriske ulikheter -,
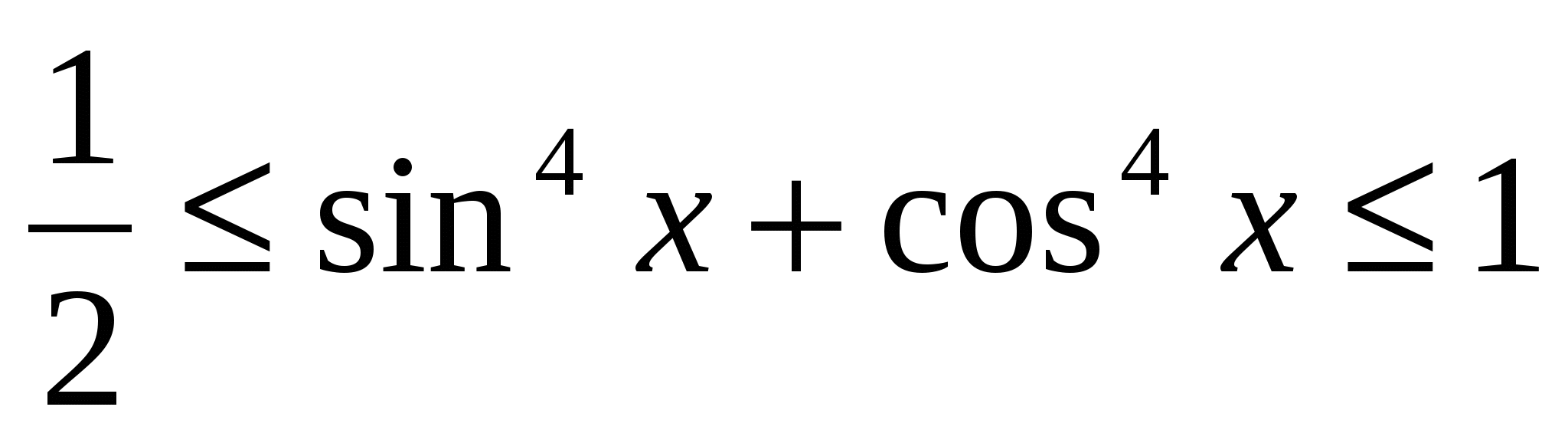 ,
,
og ulikheter med moduler av skjemaet 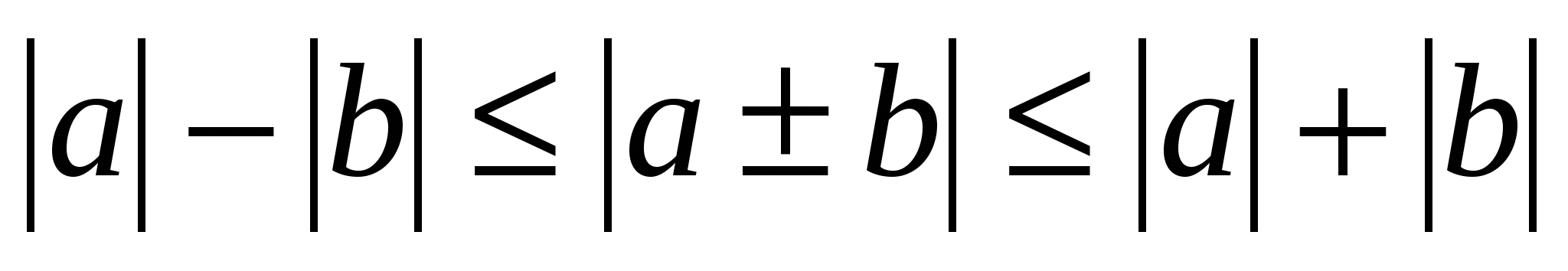 .
.
Eksempel 1.Løs ligningen: 
Løsning:
La oss velge et komplett kvadrat på høyre side av ligningen, dvs. . Det følger at 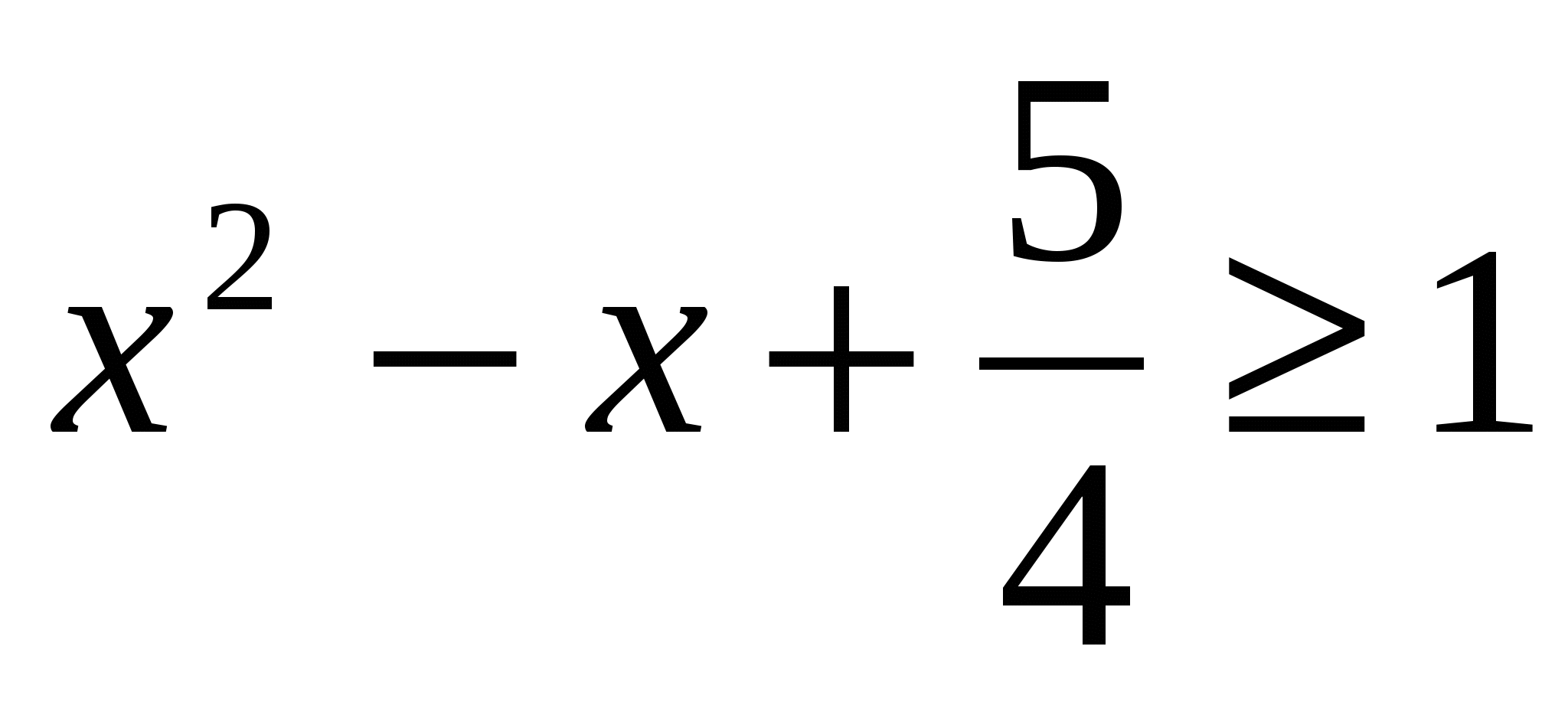 . Siden i dette tilfellet sinπ x ≤
1, så får vi et ligningssystem
. Siden i dette tilfellet sinπ x ≤
1, så får vi et ligningssystem 
Løser vi den andre ligningen i systemet, får vi at x=. Ved å substituere inn i den første ligningen sikrer vi at den funnet verdien av x er en løsning på systemet, og derfor er en løsning på den opprinnelige ligningen.
Svar: x=.
Eksempel 2.Løs ligningen: 
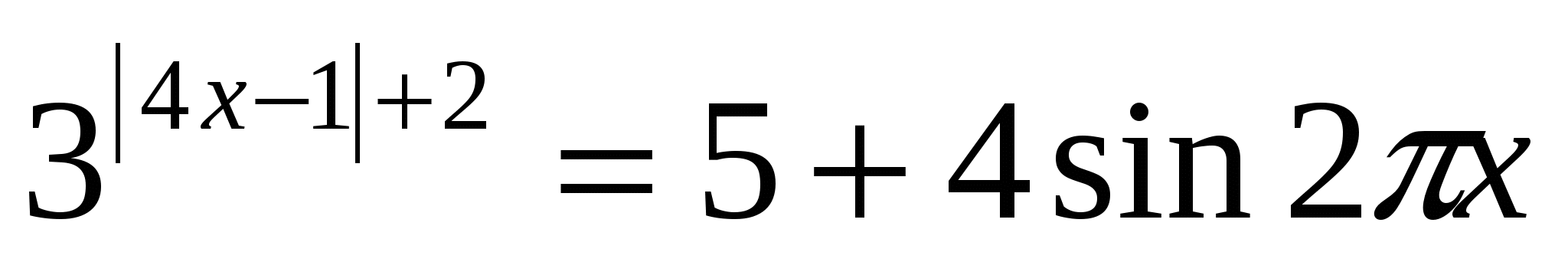
Løsning: siden Imidlertid sin2 π x ≤
1. Derfor, 5+4 sin2 π x ≤
9. Dermed får vi et ligningssystem: 
Herfra får vi et ligningssystem  , fra den første ligningen finner vi x=. La oss erstatte det i den andre ligningen i systemet og sørge for at x = er en løsning på systemet, og derfor er en løsning på den opprinnelige ligningen.
, fra den første ligningen finner vi x=. La oss erstatte det i den andre ligningen i systemet og sørge for at x = er en løsning på systemet, og derfor er en løsning på den opprinnelige ligningen.
Svar: x=
Vedlegg 4.
Fra den foreslåtte listen over oppgaver velger du de som kan løses ved hjelp av metoden med begrenset funksjon.
1. Løs ligningen x 2 -4 x=(2-cos  2. Finn antall heltallsløsninger til ulikheten x 2 ctg 2
2. Finn antall heltallsløsninger til ulikheten x 2 ctg 2 3. Løs ligningen
3. Løs ligningen 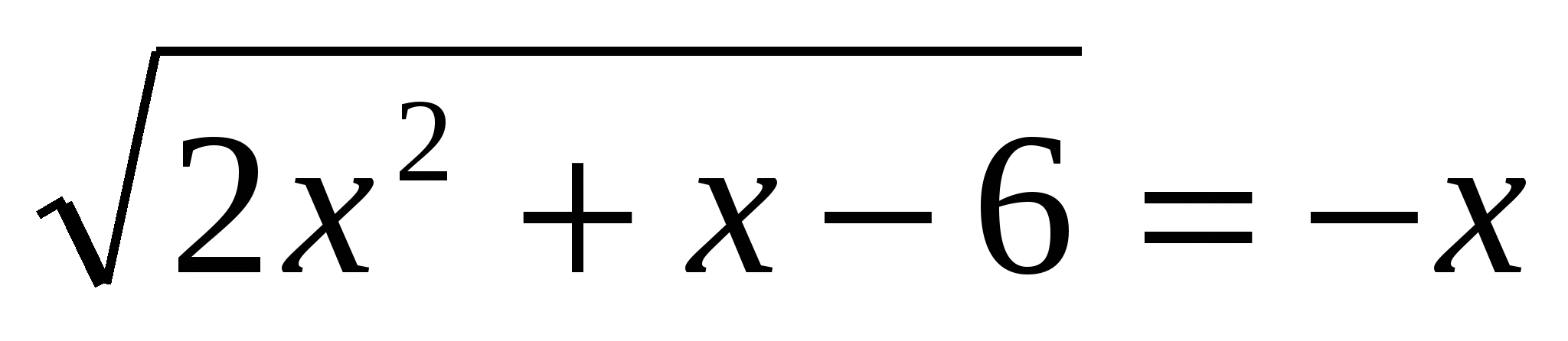 4. Løs ligning 3-(5. Finn antall heltallsløsninger til ulikheten 16s 2 ≥0 som tilfredsstiller betingelse 3 tg 2
4. Løs ligning 3-(5. Finn antall heltallsløsninger til ulikheten 16s 2 ≥0 som tilfredsstiller betingelse 3 tg 2  6. Løs ligningen
6. Løs ligningen  7. Løs ligningen -25x 2 +40x-23=( cos
7. Løs ligningen -25x 2 +40x-23=( cos 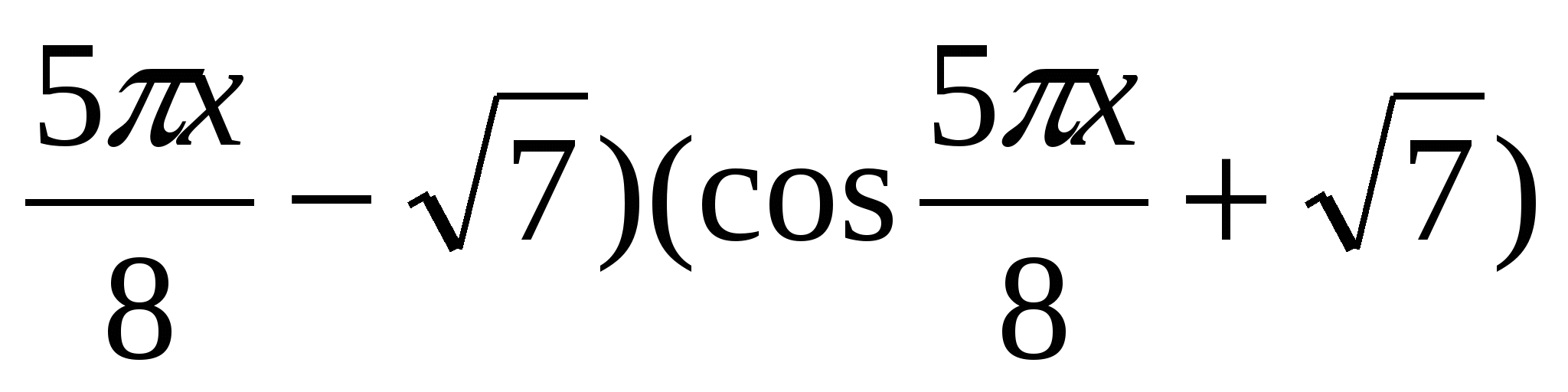 8. Finn produktet av røttene til ligningen x
8. Finn produktet av røttene til ligningen x  9. Løs ligningen
9. Løs ligningen  10. Løs ligning 3- cos 2
10. Løs ligning 3- cos 2 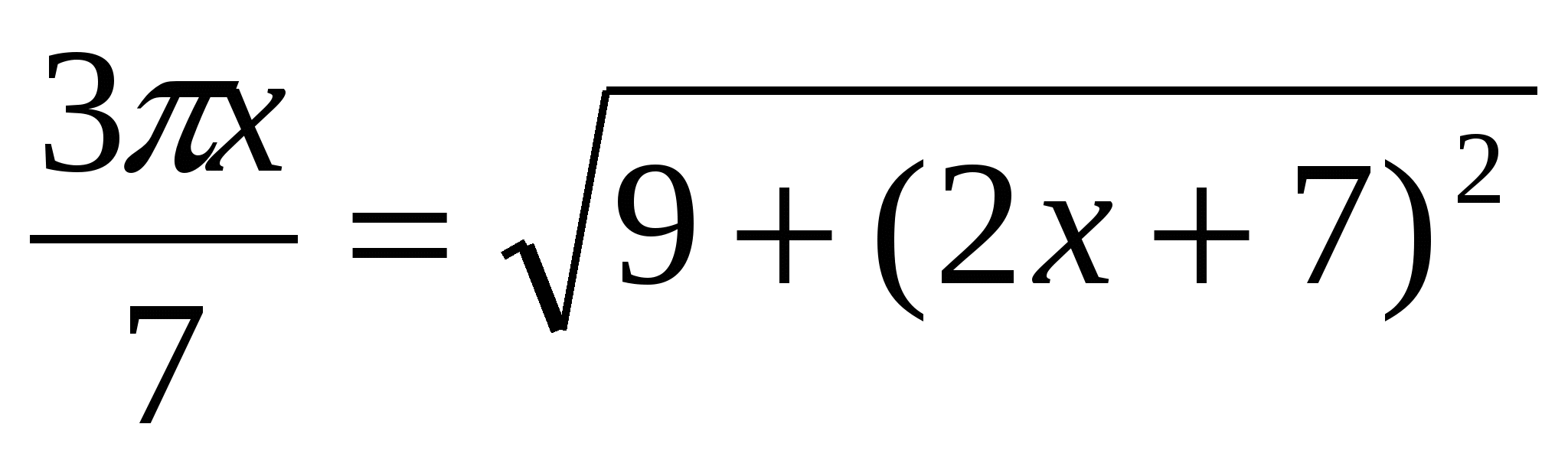
Selvtestark.
Vedlegg 5.
1. Løs ligningen
Løsning: fordi , da fordi og så
vi får et ligningssystem
løs den første ligningen, få x=, bytt denne verdien inn i den andre ligningen
2 . Løs ligningen 3-
cos 2 Løsning: fordi , da fordi og så
vi får et ligningssystem
løs den andre ligningen, få x=, bytt denne verdien inn i den første ligningen
dette betyr at x= er en løsning på den opprinnelige ligningen. Svar: x=
3. Finn antall heltallsløsninger til ulikheten x 2
+7х-8≤0, tilfredsstiller betingelsen ctg 2 Løsning: fordi og så for alle tillatte verdier av x vil vi finne nullene til kvadrattrinomialet, ved å bruke Vietas teorem vil vi løse ulikheten ved hjelp av intervallmetoden
At. vi vet det
heltallsverdier av x er tall eliminert Svar: 8 heltallsløsninger 4. Finn antall heltallsløsninger til ulikheten 16s 2 ≥0 som tilfredsstiller betingelse 3 tg 2 Løsning: fordi og deretter for alle tillatte verdier av x, finner vi nullpunktene til uttrykket, x = og x = Løs ulikheten ved å bruke intervallmetoden
At. vi vet det
heltallsverdier av x er tall eliminert Svar: 7 heltallsløsninger
Vedlegg 6.
Metode for å bruke monotoni av funksjoner. Når du løser en ligning som f(x)=g(x) i noen tilfeller er en effektiv metode som bruker monotoniteten til funksjonene y= f(x) og y= g(x) Hvis funksjonen y= f(x) er kontinuerlig og øker (minker) på segmentet en≤ x ≤ b, og funksjonen у= g(x) er kontinuerlig og avtar (øker) på samme segment, deretter ligningen f(x)=g(x) på segmentet en≤ x ≤ b kan ikke ha mer enn én rot, noe som betyr at det er nødvendig å enten prøve å finne den eneste roten av ligningen ved å velge, eller vise at en slik rot ikke eksisterer. Denne metoden er spesielt effektiv i tilfellet når begge sider av ligningen f(x) = g(x) er "ubeleilige" funksjoner for felles studier. Kommentar: Hvis funksjonen y= f(x) øker, og funksjonen y= g(x) reduseres for en≤ x ≤ b Og hvori f(a)>g(EN), da er røttene til ligningen blant en≤ x ≤ b Nei.
Eksempel: Løs ligningenLøsning: Utvalget av akseptable verdier av ligningen er x 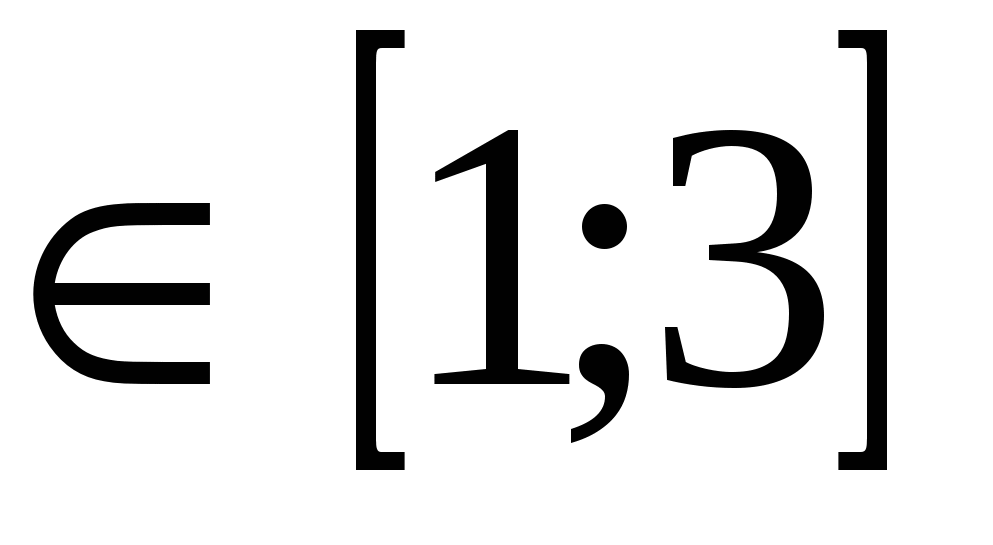 . Det er lett å se at i dette området øker venstre side av ligningen, og høyre side avtar, dvs. funksjonf(x)=
. Det er lett å se at i dette området øker venstre side av ligningen, og høyre side avtar, dvs. funksjonf(x)= øker, og funksjoneng(x)=
øker, og funksjoneng(x)= - minkende. I denne forbindelse kan den opprinnelige ligningen bare ha én rot (hvis noen). Ved seleksjon finner vi denne roten av ligningen x = 2.Svar: x=2
- minkende. I denne forbindelse kan den opprinnelige ligningen bare ha én rot (hvis noen). Ved seleksjon finner vi denne roten av ligningen x = 2.Svar: x=2
Metode for å løse funksjonelle ligninger.
Blant de vanskeligste problemene på Unified State Examination er problemer hvis løsning koker ned til vurdering av funksjonelle ligninger av formen f(f(….f(x)…))=x eller f(g(x))=f(h(x)), der f(x),g(x),h(x) er noen funksjoner og n≥ 2
Metoder for å løse disse funksjonelle ligningene er basert på anvendelsen av mange teoremer, la oss vurdere en av dem.
Teorem 1. Røttene til ligningen
f(x)=0 er røttene til ligningen f(f(….f(x)…))=x
Eksempel: Løs ligningen x= 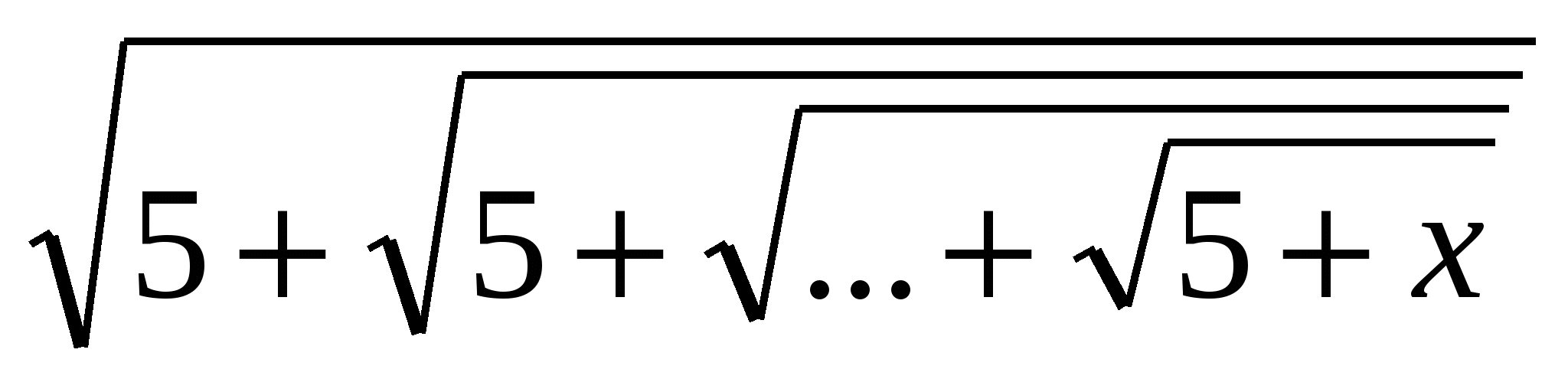 ,
hvor er kvadratroten tatt?nen gang ogn≥
1
Løsning: Fra problemforholdene følger det at x>
0. Laf(x)=
,
hvor er kvadratroten tatt?nen gang ogn≥
1
Løsning: Fra problemforholdene følger det at x>
0. Laf(x)=
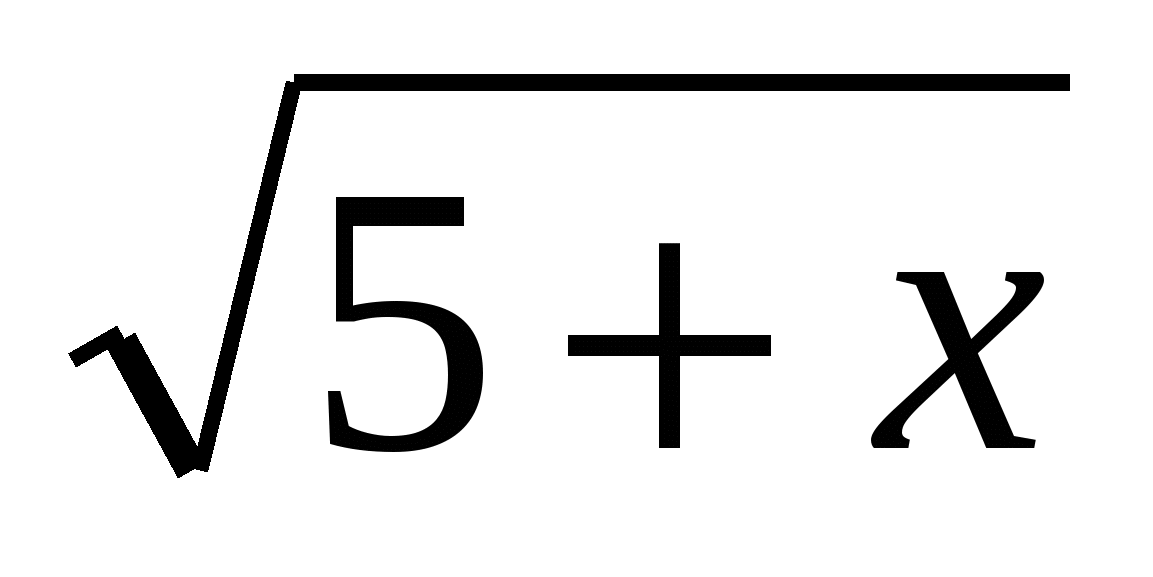 , så kan ligningen vår representeres som en funksjonell
f(
f(….
f(
x)…))=
x.
Siden ved x>
0 funksjonf(x)=
øker ogf(x)
>
0, så er ligningen x= ekvivalent med ligningenf(x)=
x, dvs.
=x, hvis positive løsning er x=
, så kan ligningen vår representeres som en funksjonell
f(
f(….
f(
x)…))=
x.
Siden ved x>
0 funksjonf(x)=
øker ogf(x)
>
0, så er ligningen x= ekvivalent med ligningenf(x)=
x, dvs.
=x, hvis positive løsning er x=  Svar: x=
Svar: x=
Galaeva Ekaterina, elev i 11. klasse ved MAOU Secondary School nr. 149 i Nizhny Novgorod
Arbeidet er både anvendt og forskning i naturen. For fullstendighets skyld ble følgende spørsmål vurdert:
– Hvordan gjenspeiles egenskapene til en funksjon når man løser likninger og ulikheter?
– Hvilke likninger og ulikheter løses ved å bestemme egenskapene til definisjonsdomenet, verdisettet, invariansen?
– Hva er løsningsalgoritmen?
– Vurderte oppgaver med parametere foreslått i KIM-materiell som forberedelse til Unified State-eksamenen.
I sitt arbeid undersøkte Ekaterina et bredt spekter av oppgaver og systematiserte dem i henhold til deres utseende.
Nedlasting:
Forhåndsvisning:
https://accounts.google.com
Lysbildetekster:
Løs ulikhet Løsning. Funksjonen f (x) = øker monotont på hele tallinjen, og funksjonen g (x) = avtar monotont på hele definisjonsdomenet. Derfor er ulikheten f (x) > g (x) tilfredsstilt hvis x >
Takk for din oppmerksomhet!
Forhåndsvisning:
For å bruke forhåndsvisninger av presentasjoner, opprett en Google-konto og logg på den: https://accounts.google.com
Lysbildetekster:
Anvendelse av egenskapene til en funksjon ved løsning av likninger og ulikheter Fullført arbeidet: Galaeva Ekaterina MBOU Secondary School nr. 149 i Moskovsky-distriktet Elever i klasse 11 “A” Vitenskapelig veileder: Fadeeva I. A. Matematikklærer
Hovedretninger: Studere egenskapene til en funksjon: monotonisitet, avgrensethet, definisjonsdomene og invarians Lær de grunnleggende utsagnene som oftest brukes når man løser likninger, ulikheter og systemer. Løse problemer fra CMM-materialer for å forberede Unified State-eksamenen
Monotonisitet En funksjon øker hvis en større verdi av argumentet tilsvarer en større verdi av funksjonen. En funksjon reduseres hvis en større verdi av argumentet tilsvarer en mindre verdi av funksjonen. f(x 1) f(x 2) x 1 x 2 f(x 1) f(x 2) x 1 x 2
Påstand 1. Hvis funksjonen y = f (x) er monoton, så har ligningen f (x) = c høyst én rot. x =2 f(x) = - monotont avtagende, noe som betyr at det ikke finnes andre løsninger. Svar: x =2
Påstand 2. Hvis funksjonen y = f (x) øker monotont, og funksjonen y = g (x) avtar monotont, så har ligningen f (x) = g (x) høyst én rot. 2 - x = log (x +11) + 1 g (x) = 2 - x er monotont avtagende, og funksjonen f (x) = log (x + 11) + 1 øker monotont på definisjonsdomenet, som betyr at ligningen f (x ) = g (x) har høyst én rot. Ved seleksjon bestemmer vi at x = -1. Utsagnet ovenfor rettferdiggjør det unike ved løsningen.
a) f (x) ≤ g (x) hvis og bare hvis x ϵ (- ∞ ; x 0 ); b) f (x) ≥ g (x) hvis og bare hvis x ϵ [x 0 ; +∞). Den visuelle betydningen av dette utsagnet er åpenbart Utsagn 3. Hvis funksjonen y = f (x) øker monotont på hele tallinjen, avtar funksjonen y = g (x) monotont på hele tallinjen og f (x 0) = g (x 0), da er følgende utsagn sanne:
Løs ulikhet Løsning. Funksjonen f (x) = øker monotont på hele tallinjen, og funksjonen g (x) = avtar monotont på hele definisjonsdomenet. Derfor er ulikheten f (x) > g (x) tilfredsstilt hvis x > 2. La oss legge til definisjonsdomenet til ulikheten. Dermed får vi systemet Svar: (2; 5).
Påstand 4. Hvis funksjonen y = f (x) øker monotont, så har likningene f (x) = x og f (f (x)) = x samme sett med røtter, uavhengig av antall innleiringer. Konsekvens. Hvis n er et naturlig tall, og funksjonen y = f (x) øker monotont, så har ligningene f (x) = x og n ganger samme sett med røtter.
Løs ligningen. Svar: Løsning. For x ≥1 er høyre side av ligningen ikke mindre enn 1, og venstre side er mindre enn 1. Derfor, hvis ligningen har røtter, så er noen av dem mindre enn 1. For x ≤0, høyre side av ligningen er ikke-positiv, og venstre side er positiv, på grunn av det faktum at . Dermed hører enhver rot av denne ligningen til intervallet (0; 1) Ved å multiplisere begge sider av denne ligningen med x og dele telleren og nevneren til venstre side med x, får vi).
Fra =. Ved å angi med t, hvor t 0, får vi ligningen = t. La oss vurdere en funksjon f (t)= 1+ som øker på sitt definisjonsdomene. Den resulterende ligningen kan skrives på formen f (f (f (f (t)))= t, og ved følge av påstand 4 har den samme sett med løsninger som ligningen f (t)= t, dvs. ligning 1 + = t, hvorfra. Den eneste positive roten til denne kvadratiske relative ligningen er. Dette betyr hvor, dvs. , eller. Svar:
Utsagn 1. Hvis maks f (x) = с og min g (x) = с, så har ligningen f (x) = g (x) samme sett med løsninger som systemet Boundedness Maksimalverdien til venstre side er 1 og minimumsverdien høyre side av 1, som betyr at løsningen til ligningen reduseres til ligningssystemet: , fra den andre ligningen finner vi en mulig kandidat x=0, og vi er overbevist om at det er en løsning til den første ligningen. Svar: x=1.
Løs ligningen Løsning. Siden sin3x≤1 og cos4x≤1, overstiger ikke venstre side av denne ligningen 7. Den kan være lik 7 hvis og bare hvis hvor k , n ϵ Z . Det gjenstår å fastslå om det er heltall k og n som sistnevnte system har løsninger for. Svar: Z
I problemer med ukjente x og parameter a, forstås definisjonsdomenet som settet av alle ordnede tallpar (x; a), som hver er slik at etter å ha erstattet de tilsvarende verdiene av x og a i alle relasjoner inkludert i problemet, vil de bli bestemt. Eksempel 1. Løs ulikhetsløsningen for hver verdi av parameter a. La oss finne definisjonsdomenet til denne ulikheten. Hvorfra det er klart at systemet ikke har noen løsninger. Dette betyr at definisjonsdomenet til ulikheten ikke inneholder noen tallpar x og a, og derfor har ulikheten ingen løsninger. Omfang svar:
Invarians, dvs. invariansen til en ligning eller ulikhet med hensyn til erstatning av en variabel med et eller annet algebraisk uttrykk for denne variabelen. Det enkleste eksemplet på invarians er paritet: hvis er en jevn funksjon, så er ligningen invariant under endringen av x og – x, siden = 0. Invarians
Finn røttene til ligningen. Løsning. Merk at paret er invariant under substitusjon. Substituting i likheten, får vi. Ved å multiplisere begge sider av denne likheten med 2 og trekke likhetsleddet for ledd fra den resulterende likheten, finner vi 3, hvorfra. Nå gjenstår det å løse ligningen, hvorfra røttene til ligningen er tall. Svar: .
Finn alle verdiene av a for hver av likningen har mer enn tre forskjellige løsninger. Løse problemer med parameteren Monotonicity-egenskap
|x|= positiv X= |x|= For at to røtter skal eksistere, må telleren være positiv. Derfor, Når røttene til den første og andre ligningen sammenfaller, som ikke oppfyller kravet til betingelsen: tilstedeværelsen av mer enn tre røtter. Svar: .
Finn alle verdiene av a for hver av likningen har to røtter. La oss transformere likningen til formen Og vurdere funksjonen f(x) = definert og kontinuerlig på hele tallinjen. Grafen til denne funksjonen er en brutt linje som består av rette og strålesegmenter, hvor hvert ledd er en del av en rett linje av formen y= kt+l. f(x)= For en hvilken som helst verdi overstiger ikke avsløringen av modulen til det første uttrykket k 8, derfor vil økningen og reduksjonen av funksjonen f(x) avhenge av avsløringen av den andre modulen. Ved x vil f(x) avta, og ved x vil den øke. Det vil si at ved x=3 vil funksjonen få størst verdi. For at en likning skal ha to røtter, er det nødvendig at f(3) Monotonicitetsegenskap
f(3)=12- |9-| 3+a || | 9-| 3+a || 9- | 3+a | - | 3+a | | 3+a | | 3+a | 3+a a Svar: a
Finn alle verdiene av parameteren a, for hver av dem gjelder ulikheten for en hvilken som helst reell verdi av x La oss skrive om ulikheten i skjemaet, introdusere en ny variabel t = og vurdere funksjonen f (t) =, definert. og kontinuerlig på hele tallinjen. Grafen til denne funksjonen er en brutt linje som består av linjesegmenter og stråler, hvor hver lenke er en del av en linje i formen, der
Siden, da t ϵ [-1; 1]. På grunn av den monotone reduksjonen av funksjonen y = f (t), er det nok å sjekke venstre kant av dette segmentet. Z. A er sann Dette betyr at det kun er mulig hvis tallene u og v har samme fortegn eller ett av dem er lik null. , = () () 0. Etter å ha faktorisert de kvadratiske trinomialene, får vi ulikheten (, hvorfra vi finner at a ϵ (-∞; -1] U (2) U [ 4; +∞). Svar: (- ∞; - 1] U (2) U )
