Areal av en trekant - formler og eksempler på problemløsning

Nedenfor er formler for å finne arealet av en vilkårlig trekant som er egnet for å finne arealet til en hvilken som helst trekant, uavhengig av dens egenskaper, vinkler eller størrelser. Formlene presenteres i form av et bilde, og forklaringer på deres anvendelse eller begrunnelse for deres korrekthet er også gitt her. En egen figur viser også samsvaret mellom bokstavsymbolene i formlene og de grafiske symbolene i tegningen.

Merk . Hvis trekanten har spesielle egenskaper (likebenet, rektangulær, likesidet), kan du bruke formlene gitt nedenfor, samt ytterligere spesialformler som bare er gyldige for trekanter med disse egenskapene:

• "Formel for arealet av en likesidet trekant"

Trekantarealformler

Forklaringer til formler:
a, b, c- lengdene på sidene i trekanten hvis areal vi ønsker å finne
r- radius av sirkelen innskrevet i trekanten
R- radius av sirkelen omskrevet rundt trekanten
h- høyden på trekanten senket til siden
s- halvomkretsen av en trekant, 1/2 summen av sidene (omkretsen)
α - vinkel motsatt side a av trekanten
β - vinkel motsatt side b av trekanten
γ - vinkel motsatt side c av trekanten
h en, h b , h c- høyden på trekanten senket til siden a, b, c

Vær oppmerksom på at de gitte notasjonene tilsvarer figuren ovenfor, slik at når du løser et reelt geometriproblem, vil det være visuelt lettere for deg å erstatte de riktige verdiene på de riktige stedene i formelen.

• Arealet av trekanten er halvparten av produktet av høyden på trekanten og lengden på siden som denne høyden senkes med(Formel 1). Riktigheten av denne formelen kan forstås logisk. Høyden senket til basen vil dele en vilkårlig trekant i to rektangulære. Hvis du bygger hver av dem inn i et rektangel med dimensjonene b og h, vil åpenbart arealet til disse trekantene være lik nøyaktig halvparten av rektangelets areal (Spr = bh)
• Arealet av trekanten er halvparten av produktet av de to sidene og sinusen til vinkelen mellom dem(Formel 2) (se et eksempel på å løse et problem ved å bruke denne formelen nedenfor). Til tross for at den virker annerledes enn den forrige, kan den lett forvandles til den. Hvis vi senker høyden fra vinkel B til side b, viser det seg at produktet av side a og sinus av vinkel γ, i henhold til egenskapene til sinus i en rettvinklet trekant, er lik høyden til trekanten vi tegnet , som gir oss den forrige formelen
• Arealet til en vilkårlig trekant kan bli funnet gjennom arbeid halvparten av radiusen til sirkelen som er innskrevet i den med summen av lengdene på alle sidene(Formel 3), enkelt sagt, du må multiplisere halvomkretsen av trekanten med radiusen til den innskrevne sirkelen (dette er lettere å huske)
• Arealet til en vilkårlig trekant kan bli funnet ved å dele produktet av alle sidene med 4 radier av sirkelen som er omskrevet rundt den (formel 4)
• Formel 5 er å finne arealet til en trekant gjennom lengdene på sidene og halvperimeteren (halvsummen av alle sidene)
• Herons formel(6) er en representasjon av samme formel uten å bruke begrepet semi-perimeter, bare gjennom lengdene på sidene
• Arealet til en vilkårlig trekant er lik produktet av kvadratet på siden av trekanten og sinusen til vinklene ved siden av denne siden delt på den doble sinusen til vinkelen motsatt denne siden (formel 7)
• Arealet til en vilkårlig trekant kan bli funnet som produktet av to kvadrater av sirkelen som er omskrevet rundt den av sinusene til hver av vinklene. (Formel 8)
• Hvis lengden på en side og verdiene til to tilstøtende vinkler er kjent, kan arealet av trekanten finnes som kvadratet på denne siden delt på den doble summen av cotangensene til disse vinklene (formel 9)
• Hvis bare lengden på hver av høydene til trekanten er kjent (formel 10), så er arealet av en slik trekant omvendt proporsjonal med lengdene på disse høydene, som i henhold til Herons formel
• Formel 11 lar deg beregne området til en trekant basert på koordinatene til dens toppunkter, som er spesifisert som (x;y) verdier for hver av toppunktene. Vær oppmerksom på at den resulterende verdien må tas modulo, siden koordinatene til individuelle (eller til og med alle) hjørner kan være i området med negative verdier

Merk. Følgende er eksempler på å løse geometriproblemer for å finne arealet til en trekant. Hvis du trenger å løse et geometriproblem som ikke ligner her, skriv om det i forumet. I løsninger, i stedet for "kvadratrot"-symbolet, kan funksjonen sqrt() brukes, der sqrt er kvadratrotsymbolet, og det radikale uttrykket er angitt i parentes.Noen ganger for enkle radikale uttrykk kan symbolet brukes √

Oppgave. Finn arealet gitt to sider og vinkelen mellom dem

Sidene i trekanten er 5 og 6 cm. Vinkelen mellom dem er 60 grader. Finn arealet av trekanten.

Løsning.

For å løse dette problemet bruker vi formel nummer to fra den teoretiske delen av leksjonen.
Arealet til en trekant kan finnes gjennom lengdene til to sider og sinusen til vinkelen mellom dem og vil være lik
S=1/2 ab sin γ

Siden vi har alle nødvendige data for løsningen (i henhold til formelen), kan vi bare erstatte verdiene fra problemforholdene i formelen:
S = 1/2 * 5 * 6 * synd 60

I tabellen over verdier for trigonometriske funksjoner vil vi finne og erstatte verdien av sinus 60 grader i uttrykket. Det vil være lik roten av tre ganger to.
S = 15 √3 / 2

Svar: 7,5 √3 (avhengig av lærerens krav, kan du sannsynligvis legge igjen 15 √3/2)

Oppgave. Finn arealet til en likesidet trekant

Finn arealet av en likesidet trekant med siden 3 cm.

Løsning .

Arealet av en trekant kan bli funnet ved å bruke Herons formel:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Siden a = b = c, har formelen for arealet av en likesidet trekant formen:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Svar: 9 √3 / 4.

Oppgave. Endring i areal ved endring av lengden på sidene

Hvor mange ganger vil arealet av trekanten øke hvis sidene økes med 4 ganger?

Løsning.

Siden dimensjonene til sidene i trekanten er ukjente for oss, vil vi for å løse problemet anta at lengdene på sidene er henholdsvis lik vilkårlige tall a, b, c. Deretter, for å svare på spørsmålet om problemet, vil vi finne arealet av den gitte trekanten, og så finner vi arealet av trekanten hvis sider er fire ganger større. Forholdet mellom arealene til disse trekantene vil gi oss svaret på problemet.

Nedenfor gir vi en tekstlig forklaring av løsningen på problemet trinn for trinn. Men helt til slutt presenteres den samme løsningen i en mer praktisk grafisk form. Interesserte kan umiddelbart gå ned på løsningene.

For å løse bruker vi Herons formel (se ovenfor i den teoretiske delen av leksjonen). Det ser slik ut:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(se første linje på bildet nedenfor)

Lengden på sidene i en vilkårlig trekant er spesifisert av variablene a, b, c.
Hvis sidene økes med 4 ganger, vil arealet til den nye trekanten c være:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(se andre linje i bildet nedenfor)

Som du kan se, er 4 en felles faktor som kan tas ut av parentes fra alle fire uttrykkene i henhold til de generelle reglene for matematikk.
Deretter

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - på tredje linje i bildet
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - fjerde linje

Kvadratroten av tallet 256 er perfekt trukket ut, så la oss ta den ut under roten
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(se femte linje på bildet nedenfor)

For å svare på spørsmålet som stilles i oppgaven, trenger vi bare å dele arealet til den resulterende trekanten med arealet til den opprinnelige.
La oss bestemme arealforholdene ved å dele uttrykkene med hverandre og redusere den resulterende brøken.

Konsept av område

Konseptet med arealet til enhver geometrisk figur, spesielt en trekant, vil være assosiert med en figur som en firkant. For enhetsarealet til en hvilken som helst geometrisk figur tar vi arealet til en firkant hvis side er lik en. For fullstendighetens skyld, la oss huske to grunnleggende egenskaper for konseptet med områder av geometriske figurer.

Eiendom 1: Hvis geometriske figurer er like, er deres arealer også like.

Eiendom 2: Enhver figur kan deles inn i flere figurer. Dessuten er arealet til den opprinnelige figuren lik summen av arealene til alle dens bestanddeler.

La oss se på et eksempel.

Eksempel 1

Tydeligvis er en av sidene av trekanten en diagonal av et rektangel, hvor den ene siden har en lengde på $5$ (siden det er $5$ celler), og den andre er $6$ (siden det er $6$ celler). Derfor vil arealet til denne trekanten være lik halvparten av et slikt rektangel. Arealet av rektangelet er

Da er arealet av trekanten lik

Svar: $15$.

Deretter vil vi vurdere flere metoder for å finne arealer av trekanter, nemlig å bruke høyden og basen, ved å bruke Herons formel og arealet til en likesidet trekant.

Hvordan finne arealet til en trekant ved hjelp av høyden og bunnen

Teorem 1

Arealet til en trekant kan finnes som halvparten av produktet av lengden på en side og høyden til den siden.

Matematisk ser det slik ut

$S=\frac(1)(2)αh$

der $a$ er lengden på siden, er $h$ høyden trukket til den.

Bevis.

Tenk på en trekant $ABC$ der $AC=α$. Høyden $BH$ er tegnet til denne siden, som er lik $h$. La oss bygge den opp til kvadratet $AXYC$ som i figur 2.

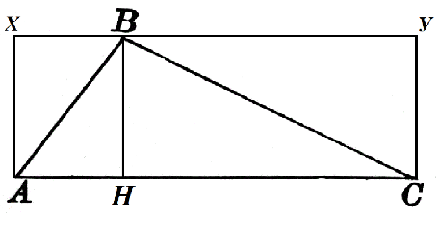
Arealet av rektangel $AXBH$ er $h\cdot AH$, og arealet av rektangel $HBYC$ er $h\cdot HC$. Deretter

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Derfor er det nødvendige arealet av trekanten, ved egenskap 2, lik

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

Teoremet er bevist.

Eksempel 2

Finn arealet av trekanten i figuren nedenfor hvis cellen har et areal lik én

Basen til denne trekanten er lik $9$ (siden $9$ er $9$ kvadrater). Høyden er også $9$. Så, ved teorem 1, får vi

$S=\frac(1)(2)\cdot 9\cdot 9=40,5$

Svar: $40,5$.

Herons formel

Teorem 2

Hvis vi får tre sider av en trekant $α$, $β$ og $γ$, kan arealet bli funnet som følger

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

her betyr $ρ$ halvperimeteren til denne trekanten.

Bevis.

Tenk på følgende figur:

Ved Pythagoras teorem får vi fra trekanten $ABH$

Fra trekanten $CBH$ har vi ifølge Pythagoras teorem

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

Fra disse to relasjonene oppnår vi likheten

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Siden $ρ=\frac(α+β+γ)(2)$, så er $α+β+γ=2ρ$, som betyr

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Ved teorem 1 får vi

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Skoleplanen legger opp til å lære barn geometri fra en tidlig alder. En av de mest grunnleggende kunnskapene på dette feltet er å finne området med forskjellige former. I denne artikkelen vil vi prøve å gi alle mulige måter å oppnå denne verdien på, fra de enkleste til de mest komplekse.

Grunnlaget

Den første formelen som barn lærer på skolen innebærer å finne arealet til en trekant gjennom lengden på høyden og bunnen. Høyde er et segment tegnet fra toppen av trekanten i rette vinkler til motsatt side, som vil være basen. Hvordan finne arealet av en trekant ved å bruke disse mengdene?

Hvis V er høyden og O er grunnflaten, er arealet S=V*O:2.

Et annet alternativ for å oppnå ønsket verdi krever at vi kjenner lengden på to sider, samt størrelsen på vinkelen mellom dem. Hvis vi har L og M - lengdene på sidene, og Q - vinkelen mellom dem, kan du få arealet ved å bruke formelen S=(L*M*sin(Q))/2.

Herons formel

I tillegg til alle de andre svarene på spørsmålet om hvordan man beregner arealet til en trekant, er det en formel som lar oss oppnå verdien vi trenger, bare vite lengdene på sidene. Det vil si at hvis vi kjenner lengdene på alle sider, trenger vi ikke tegne høyden og beregne lengden. Vi kan bruke den såkalte Herons formel.

Hvis M, N, L er lengdene på sidene, kan vi finne arealet av trekanten som følger. P=(M+N+L)/2, så er verdien vi trenger S 2 =P*(P-M)*(P-L)*(P-N). Til slutt er alt vi trenger å gjøre å beregne roten.

For en rettvinklet trekant er Herons formel litt forenklet. Hvis M, L er ben, så er S=(P-M)*(P-L).

Sirkler

En annen måte å finne arealet av en trekant på er å bruke insirkler og omskrevne sirkler. For å få verdien vi trenger ved å bruke en innskrevet sirkel, må vi kjenne radiusen. La oss betegne det "r". Deretter vil formelen som vi skal utføre beregninger med ha følgende form: S=r*P, hvor P er halvparten av summen av lengdene til alle sider.

I en rettvinklet trekant er denne formelen litt modifisert. Selvfølgelig kan du bruke den ovenfor, men det er bedre å bruke et annet uttrykk for beregninger. S=E*W, hvor E og W er lengdene på segmentene som hypotenusen er delt inn i med sirkelens tangenspunkt.

Når vi snakker om den omskrevne sirkelen, er det heller ikke vanskelig å finne arealet til trekanten. Ved å introdusere betegnelsen R som radiusen til den omskrevne sirkelen, kan du få følgende formel som er nødvendig for å beregne den nødvendige verdien: S= (M*N*L):(4*R). Der de tre første mengdene er sidene i trekanten.

Når vi snakker om en likesidet trekant, kan du gjennom en rekke enkle matematiske transformasjoner få litt modifiserte formler:

S=(3 1/2 *M2)/4;

S=(3*3 1/2 *R2)/4;

S=3*3 1/2 *r2.

I alle fall kan enhver formel som lar deg finne arealet til en trekant endres i samsvar med oppgavens data. Så alle skriftlige uttrykk er ikke absolutte. Når du løser problemer, reflekter for å finne den mest passende løsningen.

Koordinater

Når man studerer koordinatakser, blir oppgavene elevene står overfor mer komplekse. Men ikke så mye som å få panikk. For å finne arealet til en trekant fra koordinatene til toppunktene, kan du bruke den samme, men litt modifiserte Herons formel. For koordinater har den følgende form:

S=((x 2 -x 1) 2 *(y 2 - y 1) 2 * (z 2 -z 1) 2) 1/2.

Imidlertid forbyr ingen å bruke koordinater å beregne lengdene på sidene i en trekant og deretter, ved å bruke formlene skrevet ovenfor, å beregne arealet. For å konvertere koordinater til lengde, bruk følgende formel:

l=((x 2 -x 1) 2 +(y 2 - y 1) 2) 1/2.

Notater

Artikkelen brukte standardnotasjoner for mengder som brukes i de fleste oppgaver. I dette tilfellet betyr kraften "1/2" at du må trekke ut roten til hele uttrykket under parentesene.

Vær forsiktig når du velger en formel. Noen av dem mister sin relevans avhengig av startforholdene. For eksempel formelen omsirkel. Den er i stand til å beregne resultatet for deg i alle fall, men det kan være en situasjon der en trekant med de gitte parameterne kanskje ikke eksisterer i det hele tatt.

Sitter du hjemme og gjør lekser, så kan du bruke en nettbasert kalkulator. Mange nettsteder gir muligheten til å beregne ulike mengder ved hjelp av gitte parametere, og det spiller ingen rolle hvilke. Du kan ganske enkelt legge inn de første dataene i feltene, og datamaskinen (nettstedet) vil beregne resultatet for deg. På denne måten kan du unngå feil som er gjort på grunn av uforsiktighet.

Vi håper artikkelen vår svarte på alle spørsmålene dine angående beregning av arealet til en rekke trekanter, og du trenger ikke å lete etter ytterligere informasjon andre steder. Lykke til med studiene!

Trekanten er en figur kjent for alle. Og dette til tross for den rike variasjonen av dens former. Rektangulær, likesidet, akutt, likebenet, stump. Hver av dem er forskjellige på en eller annen måte. Men for alle må du finne ut arealet til en trekant.

Formler som er felles for alle trekanter som bruker lengdene på sider eller høyder

Betegnelsene som er vedtatt i dem: sider - a, b, c; høyder på de tilsvarende sidene på a, n in, n med.

1. Arealet av en trekant beregnes som produktet av ½, en side og høyden trukket fra den. S = ½ * a * n a. Formlene for de to andre sidene bør skrives på samme måte.

2. Herons formel, der semi-perimeteren vises (den er vanligvis betegnet med den lille bokstaven p, i motsetning til hele omkretsen). Halvperimeteren må beregnes som følger: legg sammen alle sidene og del dem på 2. Formelen for halvperimeteren er: p = (a+b+c) / 2. Deretter er likheten for arealet av ​​figuren ser slik ut: S = √ (p * (p - a) * ( р - в) * (р - с)).

3. Hvis du ikke vil bruke en semi-perimeter, vil en formel som bare inneholder lengdene på sidene være nyttig: S = ¼ * √ ((a + b + c) * (b + c - a ) * (a + c - c) * (a + b - c)). Den er litt lengre enn den forrige, men det vil hjelpe hvis du har glemt hvordan du finner halvperimeteren.

Generelle formler som involverer vinklene til en trekant

Notasjoner som kreves for å lese formlene: α, β, γ - vinkler. De ligger på motsatt side av henholdsvis a, b, c.

1. I følge det er halvparten av produktet av to sider og sinusen til vinkelen mellom dem lik arealet av trekanten. Det vil si: S = ½ a * b * sin γ. Formlene for de to andre tilfellene bør skrives på lignende måte.

2. Arealet av en trekant kan beregnes fra én side og tre kjente vinkler. S = (a 2 * sin β * sin γ) / (2 sin α).

3. Det er også en formel med én kjent side og to tilstøtende vinkler. Det ser slik ut: S = c 2 / (2 (ctg α + ctg β)).

De to siste formlene er ikke de enkleste. Det er ganske vanskelig å huske dem.

Generelle formler for situasjonen når radiene til innskrevne eller omskrevne sirkler er kjent

Ytterligere betegnelser: r, R - radier. Den første brukes for radiusen til den innskrevne sirkelen. Den andre er for den som er beskrevet.

1. Den første formelen som arealet til en trekant beregnes med, er relatert til halvperimeteren. S = r * r. En annen måte å skrive det på er: S = ½ r * (a + b + c).

2. I det andre tilfellet må du multiplisere alle sidene i trekanten og dele dem med firedoblet radiusen til den omskrevne sirkelen. I bokstavelig uttrykk ser det slik ut: S = (a * b * c) / (4R).

3. Den tredje situasjonen lar deg gjøre uten å kjenne sidene, men du trenger verdiene til alle tre vinklene. S = 2 R 2 * sin α * sin β * sin γ.

Spesialtilfelle: rettvinklet trekant

Dette er den enkleste situasjonen, siden bare lengden på begge bena er nødvendig. De er betegnet med de latinske bokstavene a og b. Arealet til en rettvinklet trekant er lik halvparten av arealet av rektangelet lagt til det.

Matematisk ser det slik ut: S = ½ a * b. Det er lettest å huske. Fordi det ser ut som formelen for arealet til et rektangel, vises bare en brøkdel, som indikerer halvparten.

Spesialtilfelle: likebenet trekant

Siden den har to like sider, ser noen formler for området noe forenklet ut. For eksempel har Herons formel, som beregner arealet av en likebenet trekant, følgende form:

S = ½ tommer √((a + ½ tommer)*(a - ½ tommer)).

Hvis du forvandler den, blir den kortere. I dette tilfellet er Herons formel for en likebenet trekant skrevet som følger:

S = ¼ i √(4 * a 2 - b 2).

Arealformelen ser noe enklere ut enn for en vilkårlig trekant hvis sidene og vinkelen mellom dem er kjent. S = ½ a 2 * sin β.

Spesialtilfelle: likesidet trekant

Vanligvis i problemer er siden om det kjent eller det kan bli funnet ut på en eller annen måte. Da er formelen for å finne arealet til en slik trekant som følger:

S = (a 2 √3) / 4.

Problemer med å finne området hvis trekanten er avbildet på rutete papir

Den enkleste situasjonen er når en rettvinklet trekant tegnes slik at bena sammenfaller med linjene på papiret. Da trenger du bare å telle antall celler som passer inn i bena. Multipliser dem deretter og del på to.

Når trekanten er spiss eller stump, må den tegnes til et rektangel. Da vil den resulterende figuren ha 3 trekanter. Den ene er den som er gitt i problemet. Og de to andre er hjelpe- og rektangulære. Arealene av de to siste må bestemmes ved hjelp av metoden beskrevet ovenfor. Beregn deretter arealet av rektangelet og trekk fra det de som er beregnet for hjelpeenhetene. Arealet av trekanten bestemmes.

Situasjonen der ingen av sidene i trekanten faller sammen med linjene på papiret, viser seg å være mye mer komplisert. Deretter må den skrives inn i et rektangel slik at toppunktene til den opprinnelige figuren ligger på sidene. I dette tilfellet vil det være tre hjelpetrekanter.

Eksempel på et problem som bruker Herons formel

Betingelse. Noen trekanter har kjente sider. De er lik 3, 5 og 6 cm Du må finne ut området.

Nå kan du beregne arealet av trekanten ved å bruke formelen ovenfor. Under kvadratroten er produktet av fire tall: 7, 4, 2 og 1. Det vil si at arealet er √(4 * 14) = 2 √(14).

Hvis større nøyaktighet ikke er nødvendig, kan du ta kvadratroten av 14. Det er lik 3,74. Da blir arealet 7,48.

Svar. S = 2 √14 cm 2 eller 7,48 cm 2.

Eksempeloppgave med rettvinklet trekant

Betingelse. Det ene beinet i en rettvinklet trekant er 31 cm større enn det andre. Du må finne ut lengden deres hvis arealet av trekanten er 180 cm 2.
Løsning. Vi må løse et system med to ligninger. Den første er relatert til areal. Den andre er med forholdet mellom bena, som er gitt i oppgaven.
180 = ½ a * b;

a = b + 31.
Først må verdien av "a" settes inn i den første ligningen. Det viser seg: 180 = ½ (in + 31) * in. Den har bare én ukjent mengde, så den er lett å løse. Etter å ha åpnet parentesen, oppnås den kvadratiske ligningen: 2 + 31 360 = 0. Dette gir to verdier for "in": 9 og - 40. Det andre tallet er ikke egnet som svar, siden lengden på siden av en trekant kan ikke være en negativ verdi.

Det gjenstår å beregne den andre etappen: legg til 31 til det resulterende tallet. Det viser seg 40. Dette er mengdene som søkes i oppgaven.

Svar. Trekantens ben er 9 og 40 cm.

Problem med å finne en side gjennom arealet, siden og vinkelen til en trekant

Betingelse. Arealet til en viss trekant er 60 cm 2. Det er nødvendig å beregne en av sidene hvis den andre siden er 15 cm og vinkelen mellom dem er 30º.

Løsning. Basert på den aksepterte notasjonen er ønsket side "a", den kjente siden er "b", den gitte vinkelen er "γ". Deretter kan arealformelen skrives om på følgende måte:

60 = ½ a * 15 * synd 30º. Her er sinusen på 30 grader 0,5.

Etter transformasjoner viser "a" seg å være lik 60 / (0,5 * 0,5 * 15). Altså 16.

Svar. Den nødvendige siden er 16 cm.

Oppgave om et kvadrat innskrevet i en rettvinklet trekant

Betingelse. Toppunktet til et kvadrat med en side på 24 cm faller sammen med den rette vinkelen på trekanten. De to andre ligger på sidene. Den tredje tilhører hypotenusen. Lengden på det ene bena er 42 cm. Hva er arealet av den rette trekanten?

Løsning. Tenk på to rette trekanter. Den første er den som er spesifisert i oppgaven. Den andre er basert på den kjente delen av den opprinnelige trekanten. De er like fordi de har en felles vinkel og er dannet av parallelle linjer.

Da er forholdet mellom bena deres like. Benene til den mindre trekanten er lik 24 cm (siden av kvadratet) og 18 cm (gitt ben 42 cm trekker siden av kvadratet 24 cm). De tilsvarende bena til en stor trekant er 42 cm og x cm Det er denne "x" som trengs for å beregne arealet av trekanten.

18/42 = 24/x, det vil si x = 24 * 42 / 18 = 56 (cm).

Da er arealet lik produktet av 56 og 42 delt på to, det vil si 1176 cm 2.

Svar. Det nødvendige arealet er 1176 cm 2.

En trekant er en geometrisk figur som består av tre rette linjer som kobles sammen på punkter som ikke ligger på samme rette linje. Forbindelsespunktene til linjene er hjørnene i trekanten, som er utpekt med latinske bokstaver (for eksempel A, B, C). De forbindende rette linjene i en trekant kalles segmenter, som også vanligvis er betegnet med latinske bokstaver. Følgende typer trekanter skilles ut:

• Rektangulært.
• Stumpet.
• Akutt kantete.
• Allsidig.
• Likesidet.
• Likebent.

Generelle formler for å beregne arealet av en trekant

Formel for arealet av en trekant basert på lengde og høyde

S= a*h/2,
der a er lengden på siden av trekanten hvis areal må finnes, h er lengden på høyden trukket til basen.

Herons formel

S=√р*(р-а)*(р-b)*(p-c),
hvor √ er kvadratroten, p er halvomkretsen av trekanten, a,b,c er lengden på hver side av trekanten. Halvomkretsen til en trekant kan beregnes ved å bruke formelen p=(a+b+c)/2.

Formel for arealet av en trekant basert på vinkelen og lengden på segmentet

S = (a*b*sin(α))/2,
hvor b,c er lengden på sidene i trekanten, sin(α) er sinusen til vinkelen mellom de to sidene.

Formel for arealet av en trekant gitt radiusen til den innskrevne sirkelen og tre sider

S=p*r,
der p er halvomkretsen til trekanten hvis areal må finnes, r er radiusen til sirkelen som er skrevet inn i denne trekanten.

Formel for arealet av en trekant basert på tre sider og radiusen til sirkelen som er omskrevet rundt den

S= (a*b*c)/4*R,
der a,b,c er lengden på hver side av trekanten, R er radiusen til sirkelen som er omskrevet rundt trekanten.

Formel for arealet av en trekant ved å bruke de kartesiske koordinatene til punktene

Kartesiske koordinater av punkter er koordinater i xOy-systemet, der x er abscissen, y er ordinaten. Det kartesiske koordinatsystemet xOy på et plan er de innbyrdes perpendikulære numeriske aksene Ox og Oy med felles origo i punktet O. Hvis koordinatene til punktene på dette planet er gitt på formen A(x1, y1), B(x2, y2 ) og C(x3, y3 ), så kan du beregne arealet av trekanten ved å bruke følgende formel, som er hentet fra vektorproduktet til to vektorer.
S = |(x1 – x3) (y2 – y3) – (x2 – x3) (y1 – y3)|/2,
hvor || står for modul.

Hvordan finne arealet av en rettvinklet trekant

En rettvinklet trekant er en trekant med én vinkel som måler 90 grader. En trekant kan bare ha én slik vinkel.

Formel for arealet av en rettvinklet trekant på to sider

S= a*b/2,
hvor a,b er lengden på beina. Ben er sidene ved siden av en rett vinkel.

Formel for arealet av en rettvinklet trekant basert på hypotenusen og den spisse vinkelen

S = a*b*sin(α)/ 2,
hvor a, b er trekantens ben, og sin(α) er sinusen til vinkelen der linjene a, b skjærer hverandre.

Formel for arealet av en rettvinklet trekant basert på siden og motsatt vinkel

S = a*b/2*tg(β),
hvor a, b er bena til trekanten, tan(β) er tangenten til vinkelen som bena a, b er forbundet med.

Hvordan beregne arealet av en likebenet trekant

En likebenet trekant er en som har to like sider. Disse sidene kalles sidene, og den andre siden er basen. For å beregne arealet av en likebenet trekant, kan du bruke en av følgende formler.

Grunnleggende formel for å beregne arealet av en likebenet trekant

S=h*c/2,
der c er trekantens grunnflate, h er høyden til trekanten senket til grunnflaten.

Formel for en likebenet trekant basert på side og base

S=(c/2)* √(a*a – c*c/4),
der c er basisen til trekanten, a er størrelsen på en av sidene i den likebenede trekanten.

Hvordan finne arealet til en likesidet trekant

En likesidet trekant er en trekant der alle sider er like. For å beregne arealet til en likesidet trekant, kan du bruke følgende formel:
S = (√3*a*a)/4,
hvor a er lengden på siden av den likesidede trekanten.

Ovennevnte formler lar deg beregne det nødvendige arealet av trekanten. Det er viktig å huske at for å beregne arealet av trekanter, må du vurdere typen trekant og tilgjengelige data som kan brukes til beregningen.