I praksis er det ofte nødvendig å beregne integraler av transcendentale funksjoner som inneholder trigonometriske funksjoner. Som en del av dette materialet vil vi beskrive hovedtypene av integrandfunksjoner og vise hvilke metoder som kan brukes for å integrere dem.

Integrering av sinus, cosinus, tangens og cotangens

La oss starte med metoder for å integrere de grunnleggende trigonometriske funksjonene - sin, cos, t g, c t g. Ved å bruke tabellen over antiderivater skriver vi umiddelbart at ∫ sin x d x = - cos x + C, og ∫ cos x d x = sin x + C.

For å beregne de ubestemte integralene til funksjonene t g og c t g, kan du bruke differensialtegnet:

∫ t g x d x = ∫ sin x cos x d x = d (cos x) = - sin x d x = = - ∫ d (cos x) cos x = - ln cos x + C ∫ c t g x d x = ∫ cos x sin x d x = d (sin x) = cos x d x = = ∫ d (sin x) sin x = ln sin x + C

Hvordan fikk vi formlene ∫ d x sin x = ln 1 - cos x sin x + C og ∫ d x cos x = ln 1 + sin x cos x + C, hentet fra tabellen over antiderivater? La oss forklare bare ett tilfelle, siden det andre vil være klart analogt.

Ved å bruke substitusjonsmetoden skriver vi:

∫ d x sin x = sin x = t ⇒ x = a r c sin y ⇒ d x = d t 1 - t 2 = d t t 1 - t 2

Her må vi integrere den irrasjonelle funksjonen. Vi bruker samme erstatningsmetode:

∫ d t t 1 - t 2 = 1 - t 2 = z 2 ⇒ t = 1 - z 2 ⇒ d t = - z d z 1 - z 2 = = ∫ - z d z z 1 - z 2 1 - z 2 = ∫ d z z 2 - 1 ∫ d z (z - 1) (z +) = = 1 2 ∫ d z z - 1 - 1 2 ∫ d z z + 1 = 1 2 ln z - 1 - 1 2 z + 1 + C = = 1 2 ln z - 1 z + 1 + C = ln z - 1 z + 1 + C

Nå gjør vi den omvendte substitusjonen z = 1 - t 2 og t = sin x:

∫ d x sin x = ∫ d t t 1 - t 2 = ln z - 1 z + 1 + C = = ln 1 - t 2 - 1 1 - t 2 + 1 + C = ln 1 - sin 2 x - 1 1 - sin 2 x + 1 + C = = ln cos x - 1 cos x + 1 + C = ln (cos x - 1) 2 sin 2 x + C = = ln cos x - 1 sin x + C

Vi vil separat analysere tilfeller med integraler som inneholder potenser av trigonometriske funksjoner, slik som ∫ sin n x d x, ∫ cos n x d x, ∫ d x sin n x, ∫ d x cos n x.

Du kan lese om hvordan du regner dem riktig ut i artikkelen om integrasjon ved hjelp av gjentaksformler. Hvis du vet hvordan disse formlene er utledet, kan du enkelt ta integraler som ∫ sin n x · cos m x d x med naturlig m og n.

Hvis vi har en kombinasjon av trigonometriske funksjoner med polynomer eller eksponentielle funksjoner, så må de integreres av deler. Vi anbefaler å lese en artikkel viet metoder for å finne integraler ∫ P n (x) · sin (a x) d x , ∫ P n (x) · cos (a x) d x , ∫ e a · x · sin (a x) d x , ∫ e a · x · cos (a x) d x .

De vanskeligste problemene er de der integranden inkluderer trigonometriske funksjoner med forskjellige argumenter. For å gjøre dette må du bruke grunnleggende trigonometriformler, så det er lurt å huske dem eller holde et notat av dem for hånden.

Eksempel 1

Finn settet med antideriverte av funksjonen y = sin (4 x) + 2 cos 2 (2 x) sin x · cos (3 x) + 2 cos 2 x 2 - 1 · sin (3 x) .

Løsning

La oss bruke formlene for å redusere graden og skrive at cos 2 x 2 = 1 + cos x 2, og cos 2 2 x = 1 + cos 4 x 2. Midler,

y = sin (4 x) + 2 cos 2 (2 x) sin x cos (3 x) + 2 cos 2 x 2 - 1 sin (3 x) = sin (4 x) + 2 1 + cos 4 x 2 sin x cos (3 x) + 2 1 + cos x 2 - 1 sin (3 x) = = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x)

I nevneren har vi formelen for sinus til summen. Da kan du skrive det slik:

y = sin (4 x) + cos (4 x) + 1 sin x cos (3 x) + cos x sin (3 x) = sin (4 x) + cos (4 x) + 1 sin (4 x ) = = 1 + cos (4 x) sin (4 x)

Vi fikk summen av 3 integraler.

∫ sin (4 x) + cos (4 x) + 1 sin x · cos (3 x) + cos x · sin (3 x) d x = = ∫ d x + cos (4 x) d x sin (4 x) + ∫ d x sin (4 x) = = x + 1 4 ln ∫ d (sin (4 x)) sin (4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) = = 1 4 ln sin ( 4 x) + 1 4 ln cos (4 x) - 1 sin (4 x) + C = x + 1 4 ln cos 4 x - 1 + C

I noen tilfeller kan trigonometriske funksjoner under integralet reduseres til rasjonelle brøkuttrykk ved bruk av standard substitusjonsmetode. La oss først ta formler som uttrykker sin, cos og t g gjennom tangenten til halvargumentet:

sin x = 2 t g x 2 1 + t g 2 x 2, sin x = 1 - t g 2 x 2 1 + t g 2 x 2, t g x = 2 t g x 2 1 - t g 2 x 2

Vi må også uttrykke differensialen d x i form av tangenten til halvvinkelen:

Siden d t g x 2 = t g x 2 "d x = d x 2 cos 2 x 2, så

d x = 2 cos 2 x 2 d t g x 2 = 2 d t g x 2 1 cos 2 x 2 = 2 d t g x 2 cos 2 x 2 + sin 2 x 2 cos 2 x 2 = 2 d t g x 2 1 + t g 2 x 2

Dermed er sin x = 2 z 1 + z 2, cos x 1 - z 2 1 + z 2, t g x 2 z 1 - z 2, d x = 2 d z 1 + z 2 ved z = t g x 2.

Eksempel 2

Finn det ubestemte integralet ∫ d x 2 sin x + cos x + 2 .

Løsning

Vi bruker metoden for standard trigonometrisk substitusjon.

2 sin x + cos x + 2 = 2 2 z 1 + z 2 + 1 - z 2 1 + z 2 = z 2 + 4 z + 3 1 + z 2 ⇒ d x 2 sin x + cos x + 2 = 2 d z 1 + z 2 z 2 + 4 z + 3 1 + z 2 = 2 d z z 2 + 4 z + 3

Vi får at ∫ d x 2 sin x + cos x + 2 = 2 d z z 2 + 4 z + 3 .

Nå kan vi utvide integranden til enkle brøker og få summen av to integraler:

∫ d x 2 sin x + cos x + 2 = 2 ∫ 2 d z z 2 + 4 z + 3 = 2 ∫ 1 2 1 z + 1 - 1 z + 3 d z = = ∫ d z z + 1 - ∫ C z + 3 = ln z + 1 - ln z + 3 + C = ln z + 1 z + 3 + C

∫ d x 2 sin x + cos x + 2 = ln z + 1 z + 3 + C = ln t g x 2 + 1 t g x 2 + 3 + C

Svar: ∫ d x 2 sin x + cos x + 2 = ln t g x 2 + 1 t g x 2 + 3 + C

Det er viktig å merke seg at de formlene som uttrykker funksjoner gjennom tangensen til et halvt argument ikke er identiteter, derfor er det resulterende uttrykket ln t g x 2 + 1 t g x 2 + 3 + C settet med antideriverte av funksjonen y = 1 2 sin x + cos x + 2 bare på definisjonsdomenet.

For å løse andre typer problemer kan du bruke grunnleggende integreringsmetoder.

Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter

Eksempler på løsninger av integraler etter deler vurderes i detalj, hvis integrand er produktet av et polynom med en eksponentiell (e til x-potensen) eller med en sinus (sin x) eller en cosinus (cos x).

Innhold

Se også: Metode for integrering etter deler
Tabell over ubestemte integraler
Metoder for å beregne ubestemte integraler
Grunnleggende elementære funksjoner og deres egenskaper

Formel for integrering etter deler

Når du løser eksempler i denne delen, brukes formelen for integrering etter deler:
;
.

Eksempler på integraler som inneholder produktet av et polynom og sin x, cos x eller e x

Her er eksempler på slike integraler:
, , .

For å integrere slike integraler er polynomet betegnet med u, og den resterende delen med v dx. Deretter bruker du formelen for integrering etter deler.

Nedenfor er en detaljert løsning på disse eksemplene.

Eksempler på løsning av integraler

Eksempel med eksponent, e i potensen av x

Bestem integralen:
.

La oss introdusere eksponenten under differensialtegnet:
e - x dx = - e - x d(-x) = - d(e - x).

La oss integrere med deler.

Her
.
Vi integrerer også den gjenværende integralen etter deler.
.
.
.
Endelig har vi:
.

Et eksempel på å definere et integral med sinus

Regn ut integralet:
.

La oss introdusere sinus under differensialtegnet:

La oss integrere med deler.

her u = x 2, v = cos(2 x+3), du = ( x 2 )′ dx

Vi integrerer også den gjenværende integralen etter deler. For å gjøre dette, introduser cosinus under differensialtegnet.


her u = x, v = sin(2 x+3), du = dx

Endelig har vi:

Eksempel på produktet av et polynom og cosinus

Regn ut integralet:
.

La oss introdusere cosinus under differensialtegnet:

La oss integrere med deler.

her u = x 2 + 3 x + 5, v = synd 2 x, du = ( x 2 + 3 x + 5 )′ dx

Integraler av trigonometriske funksjoner.
Eksempler på løsninger

I denne leksjonen skal vi se på integraler av trigonometriske funksjoner, det vil si at fyllingen av integralene vil være sinus, cosinus, tangenter og cotangens i ulike kombinasjoner. Alle eksempler vil bli analysert i detalj, tilgjengelig og forståelig selv for en tekanne.

For å lykkes med å studere integraler av trigonometriske funksjoner, må du ha god forståelse for de enkleste integralene, samt beherske noen integrasjonsteknikker. Du kan bli kjent med disse materialene i forelesninger Ubestemt integral. Eksempler på løsninger Og .

Og nå trenger vi: Tabell over integraler, Derivattabell Og Katalog over trigonometriske formler. Alle læremidler finner du på siden Matematiske formler og tabeller. Jeg anbefaler å skrive ut alt. Jeg fokuserer spesielt på trigonometriske formler, de skal være foran øynene dine– uten dette vil arbeidseffektiviteten reduseres merkbart.

Men først om hva integraler er i denne artikkelen Nei. Det er ingen integraler av formen, - cosinus, sinus, multiplisert med et eller annet polynom (sjeldnere noe med en tangent eller cotangens). Slike integraler er integrert av deler, og for å lære metoden, besøk leksjonen Integrasjon etter deler. Eksempler på løsninger Også her er det ingen integraler med "buer" - arctangent, arcsine, etc., de er også oftest integrert av deler.

Når du finner integraler av trigonometriske funksjoner, brukes en rekke metoder:

(4) Vi bruker tabellformelen , den eneste forskjellen er at i stedet for "X" har vi et komplekst uttrykk.

Eksempel 2

Eksempel 3

Finn det ubestemte integralet.

En klassiker av sjangeren for de som drukner i konkurransen. Som du sikkert har lagt merke til, i tabellen over integraler er det ingen integral av tangent og cotangens, men likevel kan slike integraler finnes.

(1) Vi bruker den trigonometriske formelen

(2) Vi bringer funksjonen under differensialtegnet.

(3) Vi bruker tabellintegralen .

Eksempel 4

Finn det ubestemte integralet.

Dette er et eksempel på en uavhengig løsning, den fullstendige løsningen og svaret er på slutten av leksjonen.

Eksempel 5

Finn det ubestemte integralet.

Gradene våre vil gradvis øke =).
Først løsningen:

(1) Vi bruker formelen

(2) Vi bruker den trigonometriske hovedidentiteten , hvorav det følger at .

(3) Del telleren med nevneren ledd for ledd.

(4) Vi bruker linearitetsegenskapen til det ubestemte integralet.

(5) Vi integrerer ved å bruke tabellen.

Eksempel 6

Finn det ubestemte integralet.

Dette er et eksempel på en uavhengig løsning, den fullstendige løsningen og svaret er på slutten av leksjonen.

Det er også integraler av tangenter og cotangenter, som er i høyere makter. Integralet til tangentkuben diskuteres i leksjonen Hvordan beregne arealet til en flat figur? Integraler av tangent (cotangens) til fjerde og femte potens kan fås på siden Komplekse integraler.

Redusere graden av integranden

Denne teknikken fungerer når integrand-funksjonene er fylt med sinus og cosinus til og med grader. For å redusere graden, bruk trigonometriske formler , og , og den siste formelen brukes ofte i motsatt retning: .

Eksempel 7

Finn det ubestemte integralet.

Løsning:

I prinsippet er det ikke noe nytt her, bortsett fra at vi brukte formelen (senker graden av integranden). Vær oppmerksom på at jeg har forkortet løsningen. Etter hvert som du får erfaring, kan integralen av finnes muntlig dette sparer tid og er ganske akseptabelt når du fullfører oppgaver. I dette tilfellet er det tilrådelig å ikke beskrive regelen , først tar vi verbalt integralet av 1, deretter av .

Eksempel 8

Finn det ubestemte integralet.

Dette er et eksempel på en uavhengig løsning, den fullstendige løsningen og svaret er på slutten av leksjonen.

Dette er den lovede gradøkningen:

Eksempel 9

Finn det ubestemte integralet.

Først løsningen, så kommentarene:

(1) Forbered integranden for å bruke formelen .

(2) Vi bruker faktisk formelen.

(3) Vi kvadrerer nevneren og tar konstanten ut av integrertegnet. Det kunne vært gjort litt annerledes, men etter min mening var det mer praktisk.

(4) Vi bruker formelen

(5) I tredje ledd reduserer vi igjen graden, men ved å bruke formelen .

(6) Vi presenterer lignende begreper (her delte jeg begrep for begrep og gjorde tillegget).

(7) Egentlig tar vi integralet, linearitetsregelen og metoden for å subsumere en funksjon under differensialtegnet utføres muntlig.

(8) Å kjemme svaret.

! I et ubestemt integral kan svaret ofte skrives på flere måter

I eksemplet som nettopp ble vurdert, kunne det endelige svaret vært skrevet annerledes - å åpne parentesene og til og med gjøre dette før du integrerer uttrykket, det vil si at følgende avslutning på eksemplet er ganske akseptabelt:

Det er ganske mulig at dette alternativet er enda mer praktisk, jeg forklarte det akkurat slik jeg er vant til å løse det selv). Her er et annet typisk eksempel for en uavhengig løsning:

Eksempel 10

Finn det ubestemte integralet.

Dette eksemplet kan løses på to måter, og du kan lykkes to helt forskjellige svar(mer presist vil de se helt annerledes ut, men fra et matematisk synspunkt vil de være likeverdige). Mest sannsynlig vil du ikke se den mest rasjonelle metoden og vil lide med åpningsparenteser og bruk av andre trigonometriske formler. Den mest effektive løsningen gis på slutten av leksjonen.

For å oppsummere avsnittet konkluderer vi: enhver integral av skjemaet , hvor og – til og med tall, løses ved å redusere graden av integranden.
I praksis kom jeg over integraler med 8 og 10 grader, og jeg måtte løse deres forferdelige rot ved å senke graden flere ganger, noe som resulterte i lange, lange svar.

Variabel erstatningsmetode

Som nevnt i artikkelen Variabel endringsmetode i ubestemt integral, hovedforutsetningen for å bruke erstatningsmetoden er det faktum at det i integranden er en viss funksjon og dens deriverte:
(funksjoner er ikke nødvendigvis i produktet)

Eksempel 11

Finn det ubestemte integralet.

Vi ser på tabellen med derivater og legger merke til formlene, , det vil si at i integranden vår er det en funksjon og dens deriverte. Imidlertid ser vi at under differensiering transformeres cosinus og sinus gjensidig til hverandre, og spørsmålet oppstår: hvordan utføre en endring av variabel og hva mener vi med sinus eller cosinus?! Spørsmålet kan løses ved vitenskapelig poking: hvis vi utfører erstatningen feil, vil det ikke komme noe godt ut av det.

En generell retningslinje: i lignende tilfeller må du angi funksjonen som er i nevneren.

Vi avbryter løsningen og gjør en erstatning

Alt er bra i nevneren, alt avhenger bare av , nå gjenstår det å finne ut hva det blir til.
For å gjøre dette finner vi differensialen:

Eller kort sagt:
Fra den resulterende likheten, ved å bruke proporsjonsregelen, uttrykker vi uttrykket vi trenger:

Så:

Nå er hele integranden vår avhengig av og vi kan fortsette å løse

Klar. La meg minne deg på at formålet med erstatningen er å forenkle integranden i dette tilfellet, alt kom ned til å integrere kraftfunksjonen i henhold til tabellen.

Det er ingen tilfeldighet at jeg beskrev dette eksempelet så detaljert at dette ble gjort med det formål å gjenta og forsterke leksjonsmateriellet Variabel endringsmetode i ubestemt integral.

Og nå to eksempler for din egen løsning:

Eksempel 12

Finn det ubestemte integralet.

Eksempel 13

Finn det ubestemte integralet.

Fullfør løsninger og svar på slutten av leksjonen.

Eksempel 14

Finn det ubestemte integralet.

Også her, i integranden, er det sinus og cosinus (en funksjon med en derivert), men i et produkt, og det oppstår et dilemma - hva mener vi med sinus eller cosinus?

Du kan prøve å utføre en erstatning ved å bruke vitenskapelig poking, og hvis ingenting fungerer, utpek det som en annen funksjon, men det er:

Generell retningslinje: du må angi funksjonen som billedlig talt er i en "ubehagelig posisjon".

Vi ser at i dette eksempelet «lider» elevkosinus av graden, og sinusen sitter fritt, av seg selv.

Derfor, la oss gjøre en erstatning:

Hvis noen fortsatt har problemer med algoritmen for å erstatte en variabel og finne differensialen, bør du gå tilbake til leksjonen Variabel endringsmetode i ubestemt integral.

Eksempel 15

Finn det ubestemte integralet.

La oss analysere integranden, hva skal betegnes med?
La oss huske retningslinjene våre:
1) Funksjonen er mest sannsynlig i nevneren;
2) Funksjonen er i en "ubeleilig posisjon".

Forresten, disse retningslinjene gjelder ikke bare for trigonometriske funksjoner.

Sinusen passer begge kriteriene (spesielt det andre), så en erstatning foreslår seg selv. I prinsippet kan utskiftingen allerede utføres, men først ville det være greit å finne ut hva man skal gjøre med? Først "kniper" vi av en cosinus:

Vi reserverer oss for vår "fremtidige" differensial

Og vi uttrykker det gjennom sinus ved å bruke den grunnleggende trigonometriske identiteten:

Nå her er erstatningen:

Generell regel: Hvis en av de trigonometriske funksjonene (sinus eller cosinus) i integranden er i merkelig grad, så må du "bite av" en funksjon fra den odde graden, og utpeke en annen funksjon bak den. Vi snakker kun om integraler der det er cosinus og sinus.

I det betraktede eksemplet hadde vi en cosinus med en oddetall potens, så vi plukket en cosinus fra potensen og utpekte den som en sinus.

Eksempel 16

Finn det ubestemte integralet.

Gradene tar av =).
Dette er et eksempel du kan løse på egen hånd. Full løsning og svar på slutten av timen.

Universell trigonometrisk substitusjon

Universell trigonometrisk substitusjon er et vanlig tilfelle av den variable erstatningsmetoden. Du kan prøve å bruke den når du "ikke vet hva du skal gjøre." Men faktisk er det noen retningslinjer for bruken. Typiske integraler der den universelle trigonometriske substitusjonen må brukes, er følgende integraler: , , , etc.

Eksempel 17

Finn det ubestemte integralet.

Den universelle trigonometriske substitusjonen i dette tilfellet implementeres på følgende måte. La oss erstatte: . Jeg bruker ikke bokstaven , men bokstaven , dette er ikke en slags regel, det er bare at igjen, jeg er vant til å løse ting på denne måten.

Her er det mer praktisk å finne differensialet for dette, fra likhet, uttrykker jeg:
Jeg fester en arctangent til begge deler:

Arctangens og tangens opphever hverandre:

Dermed:

I praksis trenger du ikke å beskrive det så detaljert, men bare bruk det ferdige resultatet:

! Uttrykket er bare gyldig hvis vi under sinus og cosinus bare har "X'er", for integralet (som vi skal snakke om senere) alt blir litt annerledes!

Ved utskifting blir sinus og cosinus til følgende brøker:
, , disse likhetene er basert på kjente trigonometriske formler: ,

Så det endelige designet kan se slik ut:

La oss utføre en universell trigonometrisk substitusjon:

Det vil også være problemer du kan løse på egen hånd, som du kan se svarene på.

Integranden kan konverteres fra produktet av trigonometriske funksjoner til summen

La oss vurdere integraler der integranden er produktet av sinus og cosinus av første grad av x multiplisert med forskjellige faktorer, det vil si integraler av formen

Bruk av kjente trigonometriske formler

(2)
(3)
(4)
man kan transformere hvert av produktene i integraler av formen (31) til en algebraisk sum og integrere i henhold til formlene

(5)

(6)

Eksempel 1. Finne

Løsning. I henhold til formel (2) kl

Eksempel 2. Finne integral av en trigonometrisk funksjon

Løsning. I henhold til formel (3) kl

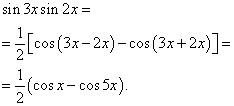
Eksempel 3. Finne integral av en trigonometrisk funksjon

Løsning. I henhold til formel (4) kl vi får følgende transformasjon av integranden:

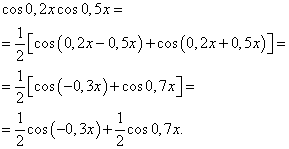
Ved å bruke formel (6), får vi

Integral av produktet av potensene sinus og cosinus av samme argument

La oss nå vurdere integraler av funksjoner som er produktet av potenser av sinus og cosinus av samme argument, dvs.

(7)

I spesielle tilfeller kan en av indikatorene ( m eller n) kan være null.

Ved integrering av slike funksjoner brukes det at en jevn potens av cosinus kan uttrykkes gjennom sinus, og differensialen til sinus er lik cos x dx(eller til og med sinusstyrke kan uttrykkes i form av cosinus, og differensialet til cosinus er lik - sin x dx ) .

To tilfeller bør skilles: 1) minst én av indikatorene m Og n merkelig; 2) begge indikatorene er jevne.

La det første tilfellet finne sted, nemlig indikatoren n = 2k+ 1 - merkelig. Da, gitt det

Integranden presenteres på en slik måte at en del av den er en funksjon av bare sinus, og den andre er differensialen til sinus. Bruker nå variabel erstatning t= synd x løsningen reduserer til å integrere polynomet mht t. Hvis bare graden m er rart, så gjør de det samme, og isolerer faktoren synd x, som uttrykker resten av integranden i form av cos x og tro t=cos x. Denne teknikken kan også brukes når integrere kvotientene til sinus og cosinus , Når minst én av indikatorene er merkelig . Hele poenget er det kvotienten av potensene sinus og cosinus er et spesielt tilfelle av deres produkt : Når en trigonometrisk funksjon er i nevneren til en integrand, er graden negativ. Men det er også tilfeller av partielle trigonometriske funksjoner, når deres krefter bare er jevne. Om dem - i neste avsnitt.

Hvis begge indikatorene m Og n– til og med da, ved å bruke trigonometriske formler

redusere eksponentene for sinus og cosinus, hvoretter et integral av samme type som ovenfor oppnås. Derfor bør integreringen videreføres etter samme ordning. Hvis en av partallseksponentene er negativ, det vil si at kvotienten av like potenser av sinus og cosinus vurderes, er dette opplegget ikke egnet . Deretter brukes en endring av variabel avhengig av hvordan integranden kan transformeres. En slik sak vil bli behandlet i neste avsnitt.

Eksempel 4. Finne integral av en trigonometrisk funksjon

Løsning. Cosinuseksponenten er merkelig. La oss derfor forestille oss

t= synd x(Deretter dt=cos x dx ). Så får vi

Tilbake til den gamle variabelen finner vi endelig

Eksempel 5. Finne integral av en trigonometrisk funksjon

.

Løsning. Cosinuseksponenten, som i forrige eksempel, er merkelig, men større. La oss forestille oss

og gjør en endring av variabel t= synd x(Deretter dt=cos x dx ). Så får vi

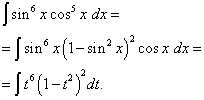
La oss åpne parentesene

og vi får

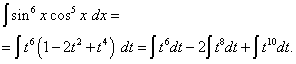
Gå tilbake til den gamle variabelen, vi får løsningen

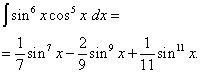
Eksempel 6. Finne integral av en trigonometrisk funksjon

Løsning. Eksponentene for sinus og cosinus er jevne. Derfor transformerer vi integrandfunksjonen som følger:

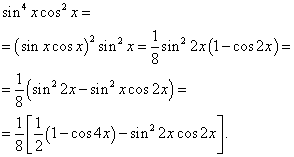
Så får vi

I det andre integralet gjør vi en endring av variabel, innstilling t= synd2 x. Deretter (1/2)dt= cos2 x dx . Derfor,

Endelig får vi

Bruke den variable erstatningsmetoden

Variabel erstatningsmetode ved integrering av trigonometriske funksjoner kan den brukes i tilfeller der integranden bare inneholder sinus eller bare cosinus, produktet av sinus og cosinus, der enten sinus eller cosinus er i første grad, tangent eller cotangens, samt kvotienten av til og med potenser av sinus og cosinus av ett og samme argument. I dette tilfellet er det mulig å utføre permutasjoner ikke bare synd x = t og synd x = t, men også tg x = t og ctg x = t .

Eksempel 8. Finne integral av en trigonometrisk funksjon

.

Løsning. La oss endre variabelen: , deretter . Den resulterende integranden kan enkelt integreres ved hjelp av tabellen over integraler:

.

Eksempel 9. Finne integral av en trigonometrisk funksjon

Løsning. La oss transformere tangenten til forholdet mellom sinus og cosinus:

La oss endre variabelen: , deretter . Den resulterende integranden er bordintegral med et minustegn:

.

Tilbake til den opprinnelige variabelen får vi til slutt:

.

Eksempel 10. Finne integral av en trigonometrisk funksjon

Løsning. La oss endre variabelen: , deretter .

La oss transformere integranden for å bruke den trigonometriske identiteten :

Vi endrer variabelen, ikke glem å sette et minustegn foran integralet (se ovenfor, hva er lik dt). Deretter faktoriserer vi integranden og integrerer ved å bruke tabellen:

Tilbake til den opprinnelige variabelen får vi til slutt:

.

Finn selv integralet til en trigonometrisk funksjon, og se så på løsningen

Universell trigonometrisk substitusjon

Universell trigonometrisk substitusjon kan brukes i tilfeller der integranden ikke faller inn under tilfellene omtalt i de foregående avsnittene. I utgangspunktet, når sinus eller cosinus (eller begge deler) er i nevneren til en brøk. Det er bevist at sinus og cosinus kan erstattes av et annet uttrykk som inneholder tangenten til halvparten av den opprinnelige vinkelen som følger:

Men merk at universell trigonometrisk substitusjon ofte innebærer ganske komplekse algebraiske transformasjoner, så den er best brukt når ingen annen metode vil fungere. La oss se på eksempler der, sammen med den universelle trigonometriske substitusjonen, substitusjon under differensialtegnet og metoden for ubestemte koeffisienter brukes.

Eksempel 12. Finne integral av en trigonometrisk funksjon

.

Løsning. Løsning. La oss dra nytte universell trigonometrisk substitusjon. Deretter
.

Vi ganger brøkene i telleren og nevneren med , og tar ut de to og plasserer det foran integrertegnet. Deretter

Tabell over antiderivater ("integraler"). Tabell over integraler. Tabellformede ubestemte integraler. (De enkleste integralene og integralene med en parameter). Formler for integrering etter deler. Newton-Leibniz formel.

Tabell over antiderivater ("integraler"). Tabellformede ubestemte integraler. (De enkleste integralene og integralene med en parameter).
Integral av en kraftfunksjon.	Integral av en kraftfunksjon.
Et integral som reduseres til integralet til en potensfunksjon hvis x drives under differensialtegnet.
	Integral av en eksponential, der a er et konstant tall.
Integral av en kompleks eksponentiell funksjon.	Integral av en eksponentiell funksjon.
Et integral lik den naturlige logaritmen.	Integral: "Lang logaritme".
	Integral: "Lang logaritme".
Integral: "Høy logaritme".	Et integral, der x i telleren er plassert under differensialtegnet (konstanten under tegnet kan enten legges til eller trekkes fra), er til syvende og sist lik et integral som er lik den naturlige logaritmen.
Integral: "Høy logaritme".
Cosinus integral.	Sinus integral.
Integral lik tangent.	Integral lik cotangens.
Integral lik både arcsine og arccosine
Et integral som er lik både arcsine og arccosine.	En integral som er lik både arctangens og arccotangent.
Integral lik cosecant.	Integral lik sekant.
Integral lik lysbue.	Integral lik arccosecant.
Integral lik lysbue.	Integral lik lysbue.
Integral lik hyperbolsk sinus.	Integral lik hyperbolsk cosinus.
Integral lik hyperbolsk sinus, der sinhx er hyperbolsk sinus i den engelske versjonen.	Integral lik hyperbolsk cosinus, der sinhx er hyperbolsk sinus i den engelske versjonen.
Integral lik den hyperbolske tangenten.	Integral lik den hyperbolske cotangensen.
Integral lik den hyperbolske sekanten.	Integral lik den hyperbolske cosekanten.

Formler for integrering etter deler. Integreringsregler.

Formler for integrering etter deler. Newton-Leibniz formel.
Integrering av et produkt (funksjon) med en konstant:
Integrering av summen av funksjoner:
ubestemte integraler:
Formel for integrering etter deler bestemte integraler:
Newton-Leibniz formel bestemte integraler:	Hvor F(a),F(b) er verdiene til antiderivatene på henholdsvis punktene b og a.

Tabell over derivater. Tabellformede derivater. Derivat av produktet. Avledet av kvotienten. Derivat av en kompleks funksjon.

Hvis x er en uavhengig variabel, da:

Tabell over derivater. Tabellderivater."tabellderivater" - ja, dessverre, det er akkurat slik de søkes etter på Internett
	Derivat av en potensfunksjon
	Derivert av eksponenten
Derivat av en kompleks eksponentiell funksjon	Derivert av eksponentiell funksjon
Derivert av en logaritmisk funksjon	Derivert av den naturlige logaritmen
	Derivert av den naturlige logaritmen til en funksjon
Derivert av sinus	Derivat av cosinus
Derivat av cosecant	Derivat av en sekant
Derivat av arcsine	Derivat av arc cosinus
Derivat av arcsine	Derivat av arc cosinus
Tangentderivat	Derivat av cotangens
Derivat av arctangens	Derivat av arc cotangens
Derivat av arctangens	Derivat av arc cotangens
Derivat av lysbue	Derivat av arccosecant
Derivat av lysbue	Derivat av arccosecant
Derivat av hyperbolsk sinus Derivat av hyperbolsk sinus i den engelske versjonen	Derivat av hyperbolsk cosinus Derivat av hyperbolsk cosinus i engelsk versjon
Derivat av hyperbolsk tangent	Derivat av hyperbolsk cotangens
Derivat av den hyperbolske sekanten	Derivat av den hyperbolske cosekanten

Regler for differensiering. Derivat av produktet. Avledet av kvotienten. Derivat av en kompleks funksjon.
Derivert av et produkt (funksjon) med en konstant:
Derivert av sum (funksjoner):
Avledet av produktet (funksjoner):
Derivert av kvotienten (av funksjoner):
Derivert av en kompleks funksjon:

Egenskaper til logaritmer. Grunnleggende formler for logaritmer. Desimal (lg) og naturlige logaritmer (ln).

Grunnleggende logaritmisk identitet
La oss vise hvordan enhver funksjon av formen a b kan gjøres eksponentiell. Siden en funksjon av formen e x kalles eksponentiell, da
Enhver funksjon av formen a b kan representeres som en potens av ti

Naturlig logaritme ln (logaritme til grunntall e = 2,718281828459045...) ln(e)=1; log(1)=0

Taylor-serien. Taylor-serien utvidelse av en funksjon.

Det viser seg at flertallet praktisk talt oppstått matematiske funksjoner kan representeres med hvilken som helst nøyaktighet i nærheten av et bestemt punkt i form av potensrekker som inneholder potenser av en variabel i økende rekkefølge. For eksempel, i nærheten av punktet x=1:

Ved bruk av serier kalt Taylors rader, blandede funksjoner som inneholder for eksempel algebraiske, trigonometriske og eksponentielle funksjoner kan uttrykkes som rene algebraiske funksjoner. Ved hjelp av serier kan du ofte raskt utføre differensiering og integrasjon.

Taylor-serien i nærheten av punkt a har formen:

1) , hvor f(x) er en funksjon som har deriverte av alle ordener ved x = a. R n - resten av leddet i Taylor-serien bestemmes av uttrykket

2)

Den k-te koeffisienten (ved x k) av serien bestemmes av formelen

3) Et spesielt tilfelle av Taylor-serien er Maclaurin (=McLaren)-serien (utvidelsen skjer rundt punktet a=0)

ved a=0

medlemmer av serien bestemmes av formelen

Vilkår for bruk av Taylor-serien.

1. For at funksjonen f(x) skal utvides til en Taylor-serie på intervallet (-R;R), er det nødvendig og tilstrekkelig at resten av leddet i Taylor (Maclaurin (=McLaren)) formel for dette funksjonen har en tendens til null som k →∞ på det spesifiserte intervallet (-R;R).

2. Det er nødvendig at det finnes deriverte for en gitt funksjon på punktet i nærheten av som vi skal konstruere Taylor-serien.

Egenskaper til Taylor-serien.

Hvis f er en analytisk funksjon, konvergerer dens Taylor-serie på et hvilket som helst punkt a i definisjonsdomenet til f til f i et eller annet nabolag til a.

Det er uendelig differensierbare funksjoner hvis Taylor-serie konvergerer, men som samtidig skiller seg fra funksjonen i et hvilket som helst nabolag til a. For eksempel:

Taylor-serier brukes i tilnærming (approksimasjon er en vitenskapelig metode som består i å erstatte noen objekter med andre, i en eller annen forstand nær de opprinnelige, men enklere) av en funksjon med polynomer. Spesielt linearisering ((fra lineær - lineær), en av metodene for omtrentlig representasjon av lukkede ikke-lineære systemer, der studiet av et ikke-lineært system erstattes av analysen av et lineært system, i en eller annen forstand tilsvarende det opprinnelige. .) ligninger oppstår ved å utvide til en Taylor-serie og kutte av alle ledd over første orden.

Dermed kan nesten enhver funksjon representeres som et polynom med en gitt nøyaktighet.

Eksempler på noen vanlige utvidelser av potensfunksjoner i Maclaurin-serien (=McLaren, Taylor i nærheten av punkt 0) og Taylor i nærheten av punkt 1. De første leddene for utvidelser av hovedfunksjonene i Taylor- og McLaren-serien.

Eksempler på noen vanlige utvidelser av potensfunksjoner i Maclaurin-serien (=McLaren, Taylor i nærheten av punkt 0)

Eksempler på noen vanlige utvidelser av Taylor-serien i nærheten av punkt 1