Dalam mekanik Newtonian klasik, saiz badan dan selang masa antara peristiwa dianggap sebagai nilai mutlak. Ini bermakna kita boleh bercakap tentang panjang badan tanpa menunjukkan sama ada badan ini dalam keadaan rehat atau bergerak. skala linear (panjang segmen) dan selang masa kekal tidak berubah apabila berpindah dari sistem rujukan pertama ke yang lain, i.e. tidak bergantung kepada pilihan sistem rujukan idea-idea ini mencerminkan konsep Newton tentang kemutlakan ruang dan masa.
2.Kinematik
Ini bahagian mekanik, kucing. Mereka mengkaji cara-cara menggambarkan pergerakan badan, tanpa berminat dengan punca-punca yang menimbulkan pergerakan ini.
3. Trajektori
Ini ialah garisan dalam ruang di mana zarah bergerak (lokasi geometri hujung vektor jejari zarah)
4. Bergerak
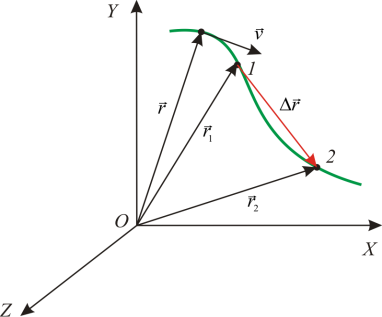
D r = r 2 – r 1 untuk suatu jangka masa D t ialah vektor yang dilukis dari kedudukan awal hingga akhir zarah (dari titik 1 betul-betul 2 ).
5. Vektor kelajuan purata< v>.
Vektor kelajuan purata< v> ialah vektor sama dengan nisbah sesaran zarah kepada masa D t yang mana ia dilakukan:
Vektor kelajuan purata < v> bertepatan dengan arah dengan vektor anjakan Dr.
6. Kelajuan segerav zarah (atau ringkasnya kelajuan) ialah vektor yang sama dengan terbitan vektor jejari r pada masa:
Kelajuan serta merta v diarahkan secara tangen ke trajektori dalam arah pergerakan zarah .SI:m/s
7. Pecutan dipanggil vektor sama dengan terbitan masa halaju v zarah:
8. Undang-undang pergerakan
dipanggil pergantungan masa koordinat zarah:
Terdapat hubungan mudah antara kaedah vektor dan koordinat untuk menerangkan gerakan. Mana-mana vektor boleh ditakrifkan melalui unjurannya pada paksi koordinat. Sebagai contoh, vektor jejari zarah:
di mana i, j, k– vektor unit paksi koordinat.
9. Kelajuan dengan kaedah koordinat untuk menerangkan gerakan
Kelajuan v, seperti mana-mana vektor, boleh diwakili melalui unjuran pada paksi DSC:
Mereka., kelajuanv zarah boleh diwakili dalam bentuk berikut: 
Dapat dilihat bahawa komponen halaju dinyatakan melalui fungsi x(t), y(t), z(t), adalah sama
10.Pecutan dengan kaedah koordinat menentukan gerakan Pecutan a, seperti mana-mana vektor, boleh diwakili melalui unjuran pada paksi DSC:
Mereka., kelajuanv zarah boleh diwakili dalam bentuk berikut
11.Laluans(atau D s) adalah sama dengan jarak yang diukur sepanjang trajektori dan dilalui oleh zarah semasa pergerakannya (panjang trajektori). Laluan ialah kuantiti skalar, bukan negatif dan tidak menurun.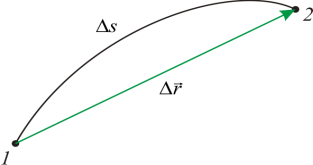 
12. Jumlah pecutan zarah
a boleh diwakili sebagai hasil tambah dua komponen berserenjang antara satu sama lain:
Modul pecutan penuh: 
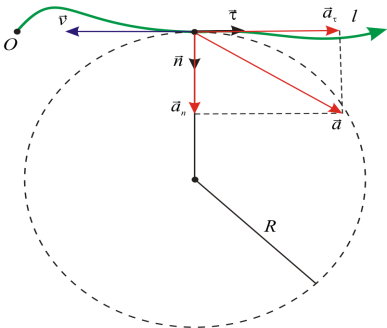
13.Pecutan tangen (tangensial).
vektor a t diarahkan secara tangen ke trajektori zarah; di mana a t v, jika pergerakan dipercepatkan; a t¯ v, jika pergerakannya perlahan. Pecutan tangen bagi zarah mencirikan perubahan dalam halaju modulo zarah (jika a t = 0, pergerakan adalah seragam).
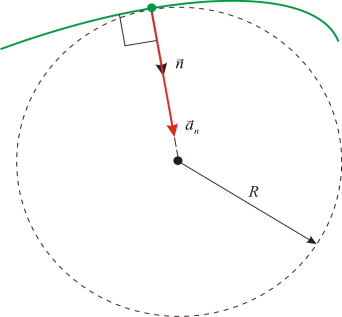
14.normal (centripetal)
pecutan
vektor a n sentiasa berserenjang dengan tangen kepada trajektori pergerakan, i.e. a n ^v Dan a n ^a t.
Pecutan normal mencirikan perubahan kelajuan dalam arah (untuk gerakan linear, apabila R = ¥, a n = 0)
15.Badan yang benar-benar tegar
dalam mekanik mereka memanggil jasad, semasa pergerakannya jarak antara mana-mana dua titiknya kekal tidak berubah. Oleh itu, badan pepejal tidak berubah bentuk di bawah pengaruh kuasa luar.
16. Bilangan darjah kebebasan badan ialah bilangan pembolehubah bebas (kuantiti) yang mesti ditetapkan untuk menentukan kedudukan jasad dalam ruang. Contoh. Bilangan darjah kebebasan titik material ialah 3 (tiga pembolehubah tidak bersandar (koordinat) x, y, z).
17.Halaju sudut badan
Biarkan badan berputar mengelilingi paksi Z, dicapai dalam tempoh yang singkat dt giliran asas dj.Halaju sudut badan dipanggil vektor
vektor w bertepatan dengan arah vektor dj, iaitu diarahkan sepanjang paksi putaran badan supaya ia membentuk skru kanan dengan arah putaran vektor w setiap paksi Z dan modulnya: 
Unit w
– radian sesaat
(rad/s)
Frasa halaju linear digunakan apabila mempertimbangkan gerakan lengkung badan dan ingin menekankan perbezaan antara kelajuan $v\ $ dan kelajuan jenayah $\omega $. Selalunya, perkataan linear ditinggalkan dan mereka hanya menyebut kelajuan.
Vektor kelajuan purata
Definisi
Nisbah pergerakan ($\Delta \overline(r)$) kepada tempoh masa semasa pergerakan ini berlaku dipanggil kelajuan purata($\left\langle \overline(v)\right\rangle $) pergerakan:
\[\left\langle \overline(v)\right\rangle =\frac(\Delta \overline(r))(\Delta t)\left(1\right),\]
di mana $\Delta \overline(r)$ ialah perubahan dalam vektor jejari titik bahan sepanjang masa $\Delta t$ (Rajah 1).
Vektor halaju purata $\left\langle \overline(v)\right\rangle $ mempunyai arah yang sama dengan vektor $\Delta \overline(r)$, sejak $\Delta t>0$. Panjang segmen yang menggambarkan vektor halaju purata (Rajah 1) tidak berkaitan dengan panjang vektor $\Delta \overline(r)$.
Kelajuan purata mencirikan kelajuan di mana titik bergerak. Ciri ini merujuk kepada tempoh masa tertentu.
Jika jasad bergerak di sepanjang lengkung, maka laluan ($\Delta s$) adalah lebih besar daripada modulus sesaran ($\Delta r$) untuk tempoh masa yang sama, kerana panjang lengkok sentiasa kurang daripada panjang daripada kord yang menguncupnya (Rajah 1). Laluan dan anjakan bertepatan apabila bergerak dalam garis lurus dalam satu arah. Kelajuan purata laluan ditakrifkan sebagai:
\[\left\langle v\right\rangle (\rm =)\frac(\Delta s)(\Delta t)\left(2\right).\]
Kelajuan purata mencirikan kelajuan pergerakan titik material dalam tempoh masa yang terhad
Kelajuan serta merta
Definisi
Dengan mengurangkan tempoh masa di mana pergerakan zarah dianggap ($\Delta t\kepada 0$), kami memperoleh ciri pergerakan titik pada masa tertentu. Nilainya sama dengan:
\[\overline(v)=(\mathop(\lim )_(\Delta t\to 0) \left\langle \overline(v)\right\rangle =\ )(\mathop(\lim )_(\ Delta t\to 0) \frac(\Delta \overline(r))(\Delta t)=\frac(d\overline(r))(dt)\left(3\right),\ )\]
dipanggil kelajuan serta merta atau hanya kelajuan.
Apabila mengira kelajuan menggunakan formula (3), adalah jelas bahawa penurunan dalam selang masa $\Delta t$ membawa kepada fakta bahawa pada akhirnya nilai kelajuan purata yang diperoleh seterusnya akan berbeza sedikit antara satu sama lain. Oleh itu, apabila mencari kelajuan serta-merta, mereka berhenti pada nilai akhir $\Delta t,\ $tetapi kecil, untuk dapat memperoleh ketepatan nilai kelajuan yang diperlukan.
Laluan ke had (3) mempunyai makna geometri. Vektor $\Delta \overline(r)$ diarahkan sepanjang kord yang menghubungkan dua titik trajektori ini membawa kepada fakta bahawa vektor ini mengambil kedudukan tangen kepada trajektori gerakan pada titik tertentu; . Ternyata vektor halaju diarahkan secara tangensial ke trajektori gerakan. Dalam gerakan rectilinear, vektor halaju diarahkan dalam garis lurus.
Kelajuan perjalanan ditentukan dengan cara yang sama:
Jika trajektori titik bahan adalah lengkung yang licin, maka semakin pendek lengkok, semakin dekat panjangnya dengan panjang kord. Dalam petikan kepada had pada $\ \Delta t\to 0$ kita boleh mengandaikan bahawa $\Delta s\to \Delta r$. Oleh itu,
Penambahan kelajuan
Halaju ialah kuantiti vektor. Jika titik material mengambil bahagian dalam beberapa pergerakan, maka kelajuannya didapati sebagai jumlah vektor bagi kelajuan setiap pergerakan:
\[\overline(v)=\sum\limits_i((\overline(v))_i\left(6\right).)\]
Dalam sesetengah kes, adalah mudah untuk memikirkan pergerakan kompleks sebagai superposisi beberapa pergerakan mudah. Kemudian kesamaan (6) boleh dianggap sebagai peraturan untuk menguraikan vektor halaju kepada komponen.
Kelajuan dan pecutan pergerakan
Apabila bergerak tidak sekata, titik material mempunyai pecutan ($\overline(a)$). Pecutan ialah terbitan pertama bagi kelajuan berkenaan dengan masa:
\[\overline(a)=\frac(d\overline(v))(dt)\left(7\right).\]
Daripada ungkapan (7) ia mengikuti bahawa mengetahui pecutan titik, kelajuan didapati sebagai:
\[\overline(v)=\int\limits^(t_2)_(t_1)(\overline(a)dt)\left(8\right).\]
Kelajuan sudut dan linear
Apabila bergerak dalam bulatan, bersama-sama dengan kelajuan pergerakan sepanjang trajektori ($v$ - kelajuan linear), halaju sudut ($\omega $) diperkenalkan, yang mencirikan kelajuan perubahan dalam sudut putaran $\varphi $:
\[\omega =\frac(d\varphi )(dt)\kiri(9\kanan).\]
Hubungan antara halaju linear dan sudut diberikan oleh ungkapan:
Contoh masalah dengan penyelesaian
Contoh 1
Senaman. Perubahan dalam vektor jejari yang menentukan kedudukan titik bahan diberikan oleh persamaan: $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline( j),$ dengan $\ overline(i)$ dan $\overline(j)$ ialah vektor unit paksi X dan Y (Rajah 2). Berapakah halaju serta-merta bagi titik pada masa $t=1$c?
Penyelesaian. Mari kita takrifkan kelajuan zarah sebagai:
\[\overline(v)=(\frac(d\overline(r))(dt) \left(1.1\right).\ )\]
Kami menggantikan ke dalam formula (1.1) persamaan untuk vektor jejari $\overline(r\ )\left(t\right)=t^4\overline(i)+3t^2\overline(j),$ kita dapat:
\[\overline(v)=\frac(d)(dt)\left(t^4\overline(i)+3t^2\overline(j)\right)=4t^3\overline(i)+6t \overline(j)\ \left(1.2\right).\]
Daripada persamaan (1.2) kita lihat bahawa:
\[\left\( \begin(array)(c) v_x=4t^3 \\ v_y=6t \end(array) \right.\left(1.3\right).\]
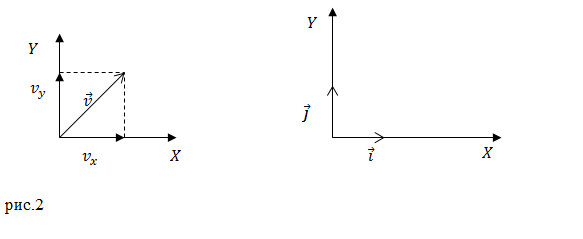
Mengikut teorem Pythagoras, kita dapati modul halaju sebagai:
Mari kita hitung kelajuan dengan menggantikan masa $t=1$c ke dalam formula yang terhasil:
Jawab.$v$=7.2 $\frac(m)(s)$
Contoh 2
Senaman. Titik material bergerak dalam garis lurus. Pecutan titik ini meningkat mengikut graf (Rajah 3). Berapakah kelajuan titik pada masa $t_1?$
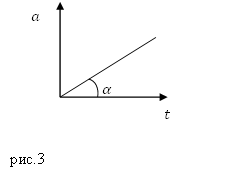
Penyelesaian. Dalam graf dalam Rajah 3, pecutan digambarkan sebagai garis lurus yang datang dari asal koordinat berdasarkan Rajah 3, kami menulis ungkapan analitik untuk pecutan sebagai:
di mana $k=tg\ \alfa $.
Kita dapati kelajuan titik sebagai:
Jawab.$v=\frac(tg\ \alfa \cdot t^2_1)(2)$
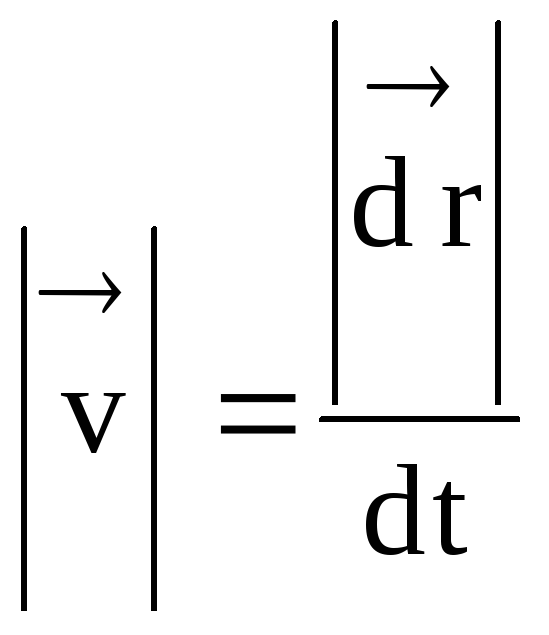
Mengurangkan selama-lamanya tempoh masa t semasa m.t bergerak dalam ruang dalam had apabila t 0, kita memperoleh kelajuan serta-merta, i.e.
Vektor halaju serta-merta adalah sama dengan had nisbah kenaikan vektor jejari m.t kepada tempoh masa semasa kenaikan ini berlaku, apabila t 0 atau sama dengan terbitan pertama bagi vektor jejari berkenaan dengan masa.
Vektor halaju serta-merta pada masa tertentu diarahkan secara tangen ke trajektori pada titik tertentu (Rajah 9).
Sesungguhnya, pada t 0, apabila titik M 2 menghampiri M 1, kord (sekan) 
, menghampiri panjang ruas lengkok s dan dalam had s = , dan sekan menjadi tangen. Ini jelas disahkan oleh eksperimen. Contohnya, percikan api apabila mengasah alat sentiasa diarahkan secara tangen ke roda pengisar. Oleh kerana kelajuan ialah kuantiti vektor, modulusnya
.
Dalam sesetengah jenis pemecut (contohnya, siklotron, dsb.), zarah bergerak berulang kali sepanjang trajektori tertutup tanpa berhenti. Akibatnya, pada mana-mana titik trajektori nilai mutlak vektor halaju serta-merta mesti berbeza daripada sifar. Kesimpulan ini disahkan bukan sahaja oleh persamaan (15), tetapi juga konsisten dengan konsep kelajuan skalar purata (formula 11). Jika dalam persamaan (11) kita pergi ke had pada t 0, maka kita perlu mempertimbangkan bahagian kecil laluan pada trajektori s yang tidak berbeza daripada modul vektor anjakan asas . Kemudian, berdasarkan persamaan (11), kita boleh mendapatkan nilai halaju skalar serta-merta 
bertepatan dengan magnitud vektor halaju serta-merta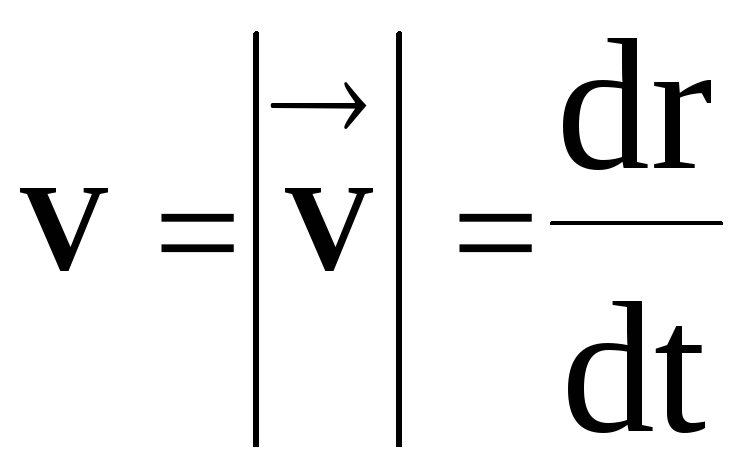 
,
kerana r = s untuk t 0.
Satu persamaan vektor halaju segera (15) boleh digantikan dengan sistem setara bagi tiga persamaan skalar, unjuran vektor halaju pada paksi koordinat
v x = dx/dt, v y = dy/dt, v z = dz/dt. (16)
Vektor halaju serta-merta berkaitan dengan unjurannya pada paksi koordinat oleh ungkapan
,
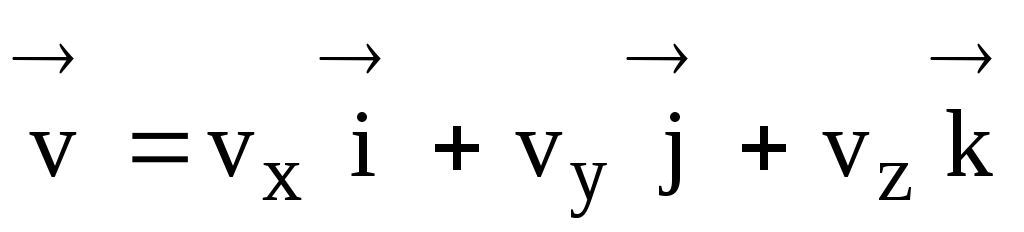(17)
di mana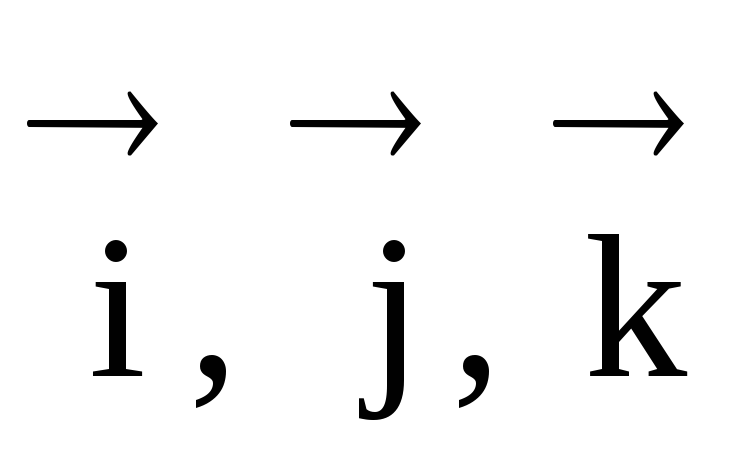 
– vektor unit diarahkan di sepanjang paksi X, Y, Z, masing-masing.
Modulo
.
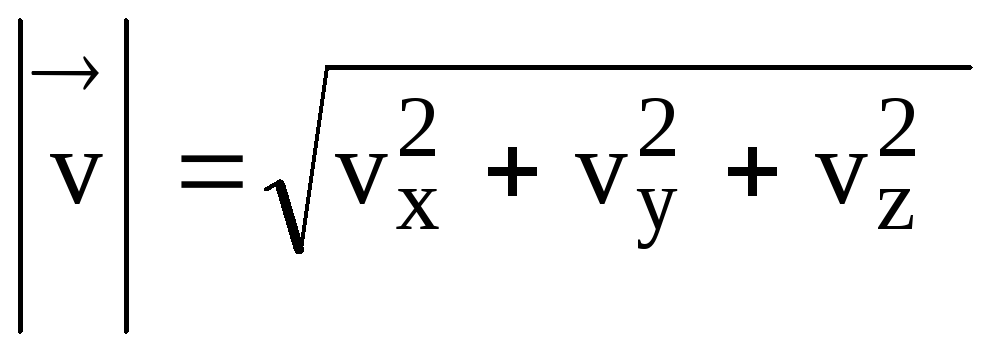(18)
Oleh itu, vektor halaju mencirikan kelajuan perubahan pergerakan dalam ruang dalam magnitud dan arah dari semasa ke semasa. Kelajuan adalah fungsi masa.
1.12. Purata pecutan
Apabila badan bergerak, kelajuan dalam kes umum boleh berubah dalam kedua-dua magnitud dan arah.
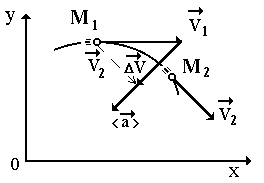
Biarkan m.t pada beberapa saat masa t 1 berada pada titik M 1 dan bergerak dengan laju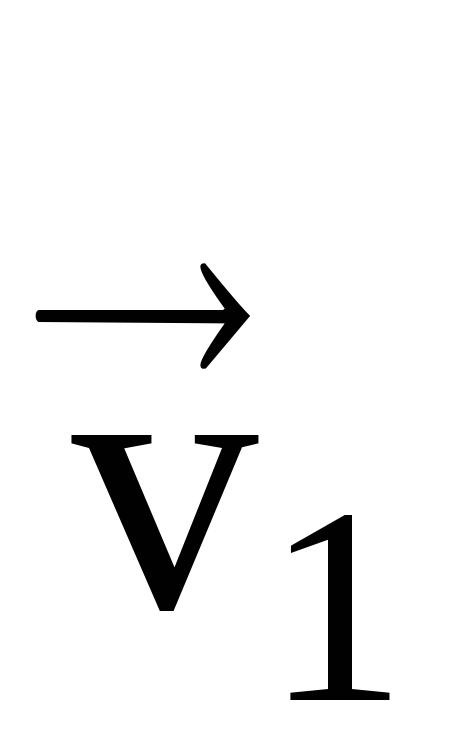 
, dan pada masa t 2 - pada titik M 2 - dengan kelajuan 
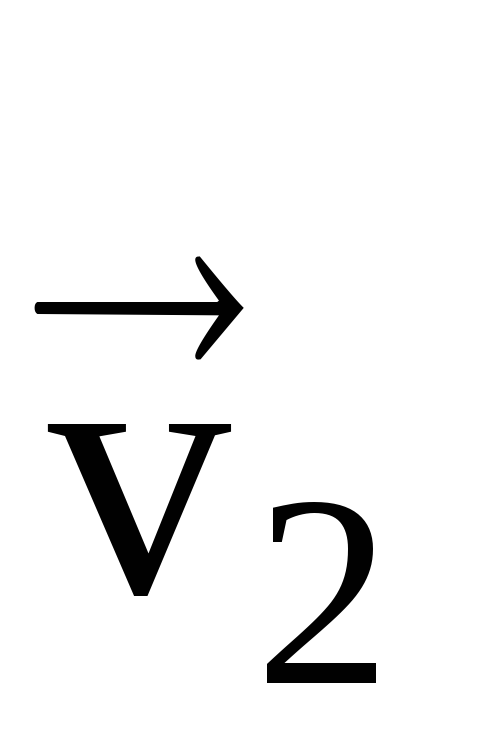(Gamb. 10).
Mari kita alihkan vektor 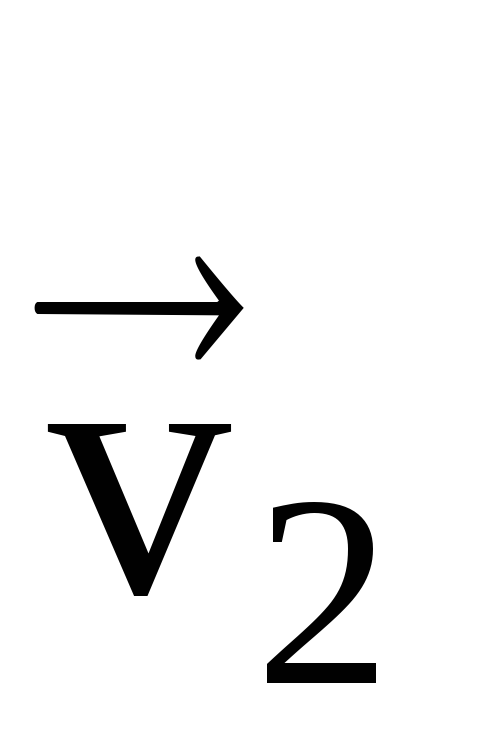selari dengan dirinya dengan titik M 1 supaya asal-usul vektor bertepat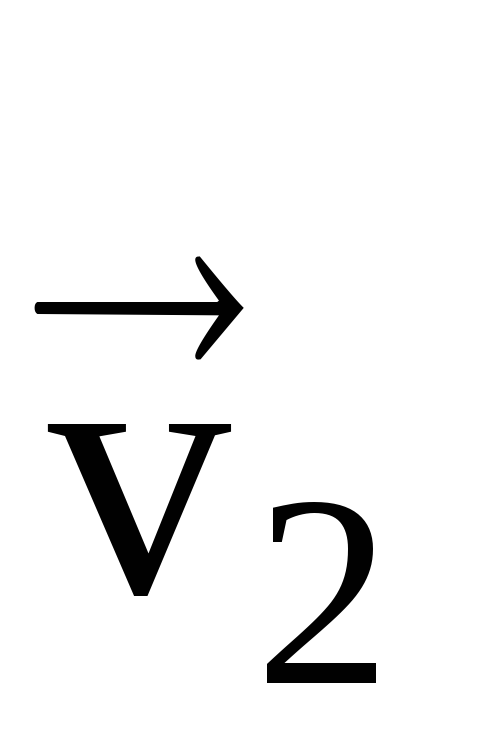an Dan .
Kemudian perbezaan vektor 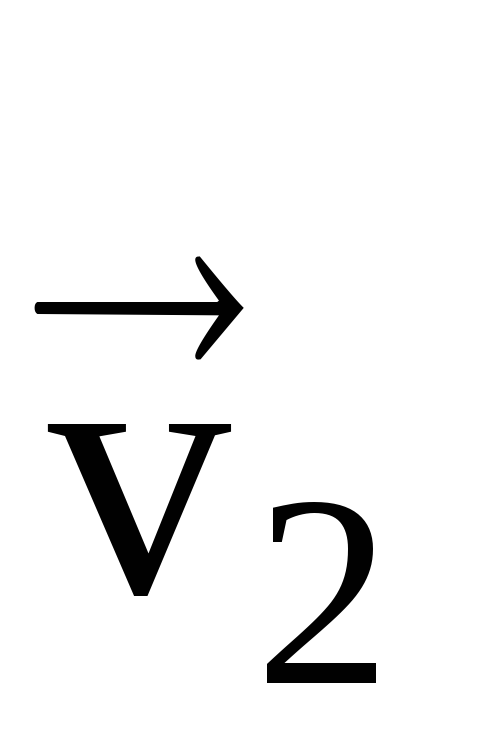Dan ialah vektor perubahan (kenaikan) kelajuan dalam tempoh masa t = t 2 – t 1, i.e.
.
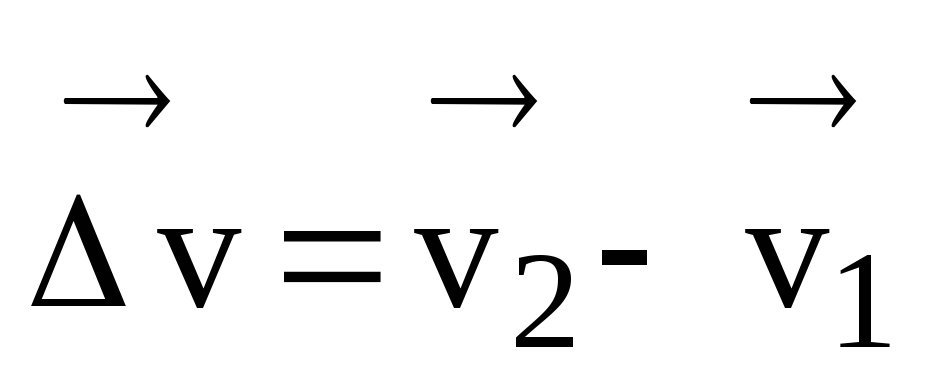(19)
Purata vektor pecutan adalah sama dengan nisbah vektor perubahan halaju kepada tempoh masa semasa perubahan ini berlaku.
Oleh itu,
.
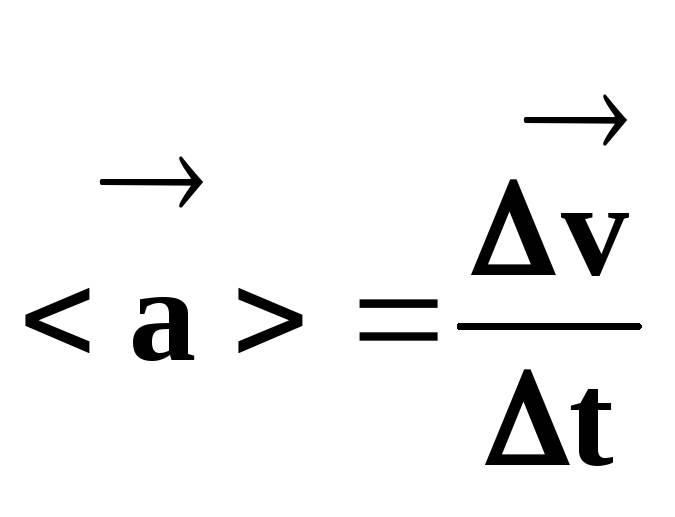(20)
Vektor pecutan purata bertepatan dengan arah vektor perubahan halaju dan diarahkan ke dalam kelengkungan trajektori.
Satu persamaan vektor (1.20) sepadan dengan sistem tiga persamaan skalar untuk unjuran vektor pecutan purata pada paksi koordinat
Modul vektor pecutan purata
.
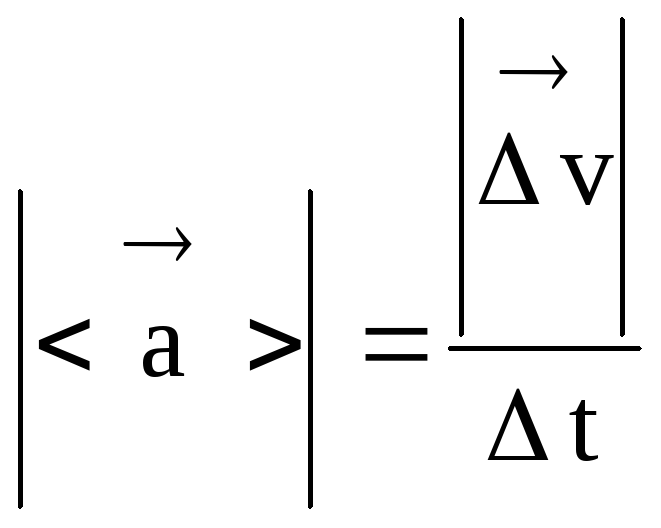(22)
Unit SI bagi pecutan ialah meter sesaat kuasa dua.
Jika magnitud halaju (atau magnitud vektor halaju) tidak berubah, pergerakan adalah seragam apabila magnitud halaju berubah, ia adalah tidak sekata.
pakaian seragam dipanggil pergerakan di mana jasad bergerak pada laluan yang sama pada mana-mana selang masa yang sama. Dalam kes ini, magnitud kelajuan kekal tidak berubah (dalam arah kelajuan boleh berubah jika pergerakan adalah lengkung).
Terus terang dipanggil pergerakan di mana trajektori adalah garis lurus. Dalam kes ini, arah kelajuan kekal tidak berubah (magnitud kelajuan boleh berubah jika pergerakan tidak seragam).
Pakaian seragam lurus dipanggil pergerakan yang seragam dan rectilinear. Dalam kes ini, kedua-dua magnitud dan arah kekal tidak berubah.
Dalam kes umum, apabila jasad bergerak, kedua-dua magnitud dan arah vektor halaju berubah. Untuk mencirikan seberapa cepat perubahan ini berlaku, kuantiti khas digunakan - pecutan.
Pecutan – ini adalah kuantiti yang sama dengan nisbah perubahan dalam kelajuan jasad kepada tempoh tempoh masa semasa perubahan kelajuan ini berlaku. Purata pecutan berdasarkan definisi ini ialah, m/s²:
Pecutan segera dipanggil kuantiti fizik sama dengan had di mana purata pecutan cenderung pada selang waktu∆t → 0, m/s²:
Memandangkan kelajuan boleh berubah dalam kedua-dua magnitud dan arah sepanjang trajektori, vektor pecutan mempunyai dua komponen.
Komponen vektor pecutan a, diarahkan sepanjang tangen ke trajektori pada titik tertentu, dipanggil pecutan tangen, yang mencirikan perubahan dalam vektor halaju dalam magnitud.
Komponen vektor pecutan a, diarahkan sepanjang normal ke tangen pada titik tertentu pada trajektori, dipanggil pecutan normal. Ia mencirikan perubahan arah vektor halaju dalam kes gerakan lengkung. Sememangnya, apabila jasad bergerak di sepanjang trajektori yang merupakan garis lurus, pecutan normal ialah sifar.
Pergerakan rectilinear dipanggil pembolehubah seragam jika, dalam mana-mana tempoh masa, kelajuan badan berubah dengan jumlah yang sama. Dalam kes ini hubungan
∆V/ ∆t adalah sama untuk sebarang selang masa. Oleh itu, magnitud dan arah pecutan kekal tidak berubah: a = const.
Untuk gerakan rectilinear, vektor pecutan diarahkan sepanjang garis gerakan. Jika arah pecutan bertepatan dengan arah vektor halaju, maka magnitud halaju akan meningkat. Dalam kes ini, pergerakan dipanggil seragam dipercepatkan. Jika arah pecutan adalah bertentangan dengan arah vektor halaju, maka magnitud halaju akan berkurangan. Dalam kes ini, pergerakan dipanggil perlahan secara seragam. Secara semula jadi terdapat pergerakan seragam dipercepatkan semula jadi - ini adalah jatuh bebas.
Jatuh bebas- dipanggil kejatuhan jasad jika satu-satunya daya yang bertindak ke atasnya ialah graviti. Eksperimen yang dijalankan oleh Galileo menunjukkan bahawa semasa jatuh bebas, semua jasad bergerak dengan pecutan graviti yang sama dan dilambangkan dengan huruf ĝ. Berhampiran permukaan bumi ĝ = 9.8 m/s². Pecutan jatuh bebas disebabkan oleh graviti dari Bumi dan diarahkan secara menegak ke bawah. Tegasnya, pergerakan sedemikian hanya boleh dilakukan dalam ruang hampa. Jatuh di udara boleh dianggap lebih kurang percuma.
Trajektori jasad jatuh bebas bergantung pada arah vektor halaju awal. Jika jasad dilemparkan secara menegak ke bawah, maka trajektori adalah segmen menegak, dan gerakan itu dipanggil pembolehubah seragam. Jika jasad dilemparkan secara menegak ke atas, maka trajektori terdiri daripada dua segmen menegak. Pertama, badan naik, bergerak sama perlahan. Pada titik pendakian maksimum, kelajuan menjadi sifar, selepas itu badan turun, bergerak secara seragam dipercepatkan.
Jika vektor halaju awal diarahkan pada sudut ke ufuk, maka pergerakan berlaku di sepanjang parabola. Beginilah cara bola yang dibaling, cakera, atlet yang melakukan lompat jauh, peluru terbang, dll.