Дефиниција: Нумеричка функција е кореспонденција што го поврзува секој број x од одредено множество со единечен број y.

Ознака:

каде што x е независна променлива (аргумент), y е зависна променлива (функција). Множеството вредности на x се нарекува домен на функцијата (означено D(f)). Множеството вредности на y се нарекува опсег на вредности на функцијата (означено E(f)). Графикот на функцијата е множество точки во рамнината со координати (x, f(x))

Методи за одредување функција.

1. аналитички метод (со користење на математичка формула);
2. табеларен метод (со користење на табела);
3. описен метод (со користење на вербален опис);
4. графички метод (со користење на график).

Основни својства на функцијата.

1. Парни и непарни

Функцијата се повикува дури и ако
– доменот на дефиниција на функцијата е симетричен околу нула
f(-x) = f(x)

Графикот на парна функција е симетричен во однос на оската 0 г

Функцијата се нарекува непарна ако
– доменот на дефиниција на функцијата е симетричен околу нула
– за кој било x од доменот на дефиниција f(-x) = –f(x)

Графикот на непарна функција е симетричен во однос на потеклото.

2. Фреквенција

Функцијата f(x) се нарекува периодична со период ако за кој било x од доменот на дефиниција f(x) = f(x+T) = f(x-T) .

Графикот на периодична функција се состои од неограничено повторување на идентични фрагменти.

3. Монотонија (зголемување, намалување)

Функцијата f(x) се зголемува на множеството P ако за кое било x 1 и x 2 од ова множество така што x 1

Функцијата f(x) се намалува на множеството P ако за кои било x 1 и x 2 од ова множество, така што x 1 f(x 2) .

4. Екстреми

Точката X max се нарекува максимална точка на функцијата f(x) ако за сите x од некое соседство на X max е исполнета неравенката f(x) f(X max).

Вредноста Y max =f(X max) се нарекува максимум на оваа функција.

X max – максимална точка
На максимум - максимум

Точката X min се нарекува минимална точка на функцијата f(x) ако за сите x од некое соседство на X min е исполнета неравенката f(x) f(X min).

Вредноста Y min =f(X min) се нарекува минимум на оваа функција.

X min – минимална точка
Y min – минимум

X min , X max – екстремни точки
Y min , Y max – екстремни.

5. Нули на функцијата

Нулата на функцијата y = f(x) е вредноста на аргументот x при кој функцијата станува нула: f(x) = 0.

X 1, X 2, X 3 – нули на функцијата y = f(x).

Задачи и тестови на тема „Основни својства на функцијата“

• Својства на функцијата - Нумерички функции 9-то одделение

  Лекции: 2 Задачи: 11 Тестови: 1

• Својства на логаритмите - Експоненцијални и логаритамски функции одделение 11

  Часови: 2 Задачи: 14 Тестови: 1

• Функција на квадратен корен, нејзините својства и графикон - Функција на квадратен корен. Својства на квадратен корен одделение 8

  Часови: 1 Задачи: 9 Тестови: 1

• Моќните функции, нивните својства и графикони - Степени и корени. Функции за напојување 11 степен

  Часови: 4 Задачи: 14 Тестови: 1

• Функции - Важни теми за прегледување на Единствениот државен испит по математика

  Задачи: 24

Откако ја проучувавте оваа тема, треба да бидете во можност да го пронајдете доменот на дефиниција на различни функции, да ги одредите интервалите на монотоност на функцијата користејќи графикони и да ги испитате функциите за рамномерност и непарност. Ајде да размислиме да решиме слични проблеми користејќи ги следните примери.

Примери.

1. Најдете го доменот на дефинирање на функцијата.

Решение:од условот се наоѓа доменот на дефинирање на функцијата

Функции и нивните својства

Функцијата е еден од најважните математички концепти.Функција Таквата зависност на променливата y ја нарекуваат од променливата x во која секоја вредност на променливата x одговара на една вредност на променливата y.

Променлива Xповикани независната променлива или аргумент.Променлива наповикани зависна променлива. Тоа го кажуваат и тиепроменливата y е функција на променливата x. Се нарекуваат вредностите на зависната променливафункционални вредности.

Ако зависноста на променливатана од променливаX е функција, тогаш може накратко да се напише на следниов начин:y= ѓ( x ). (Прочитајте:на еднаквиѓ одX .) Симболѓ( x) означете ја вредноста на функцијата што одговара на вредноста на аргументот еднаква наX .

Сите вредности на независната променлива формадомен на функција . Се формираат сите вредности што ги добива зависната променливаопсег на функции .

Ако функцијата е одредена со формула и нејзиниот домен на дефиниција не е наведен, тогаш доменот на дефиниција на функцијата се смета дека се состои од сите вредности на аргументот за кој формулата има смисла.

Методи за одредување функција:

1.аналитички метод (функцијата е наведена со помош на математичка формула;

2.табеларен метод (функцијата е одредена со помош на табела)

3.описен метод (функцијата се одредува со вербален опис)

4. графички метод (функцијата се одредува со помош на график).

График на функции наведете го множеството од сите точки на координатната рамнина, чии апсциси се еднакви на вредностите на аргументот и ординатите - соодветните функциски вредности.

ОСНОВНИ СВОЈСТВА НА ФУНКЦИИТЕ

1. Функција нули

Нула на функцијата е вредноста на аргументот при кој вредноста на функцијата е еднаква на нула.

2. Интервали на постојан знак на функција

Интервали на постојан знак на функција се збирови на вредности на аргументи на кои вредностите на функцијата се само позитивни или само негативни.

3. Зголемување (намалување) функција.

Зголемување во одреден интервал, функција е функција за која поголема вредност на аргументот од овој интервал одговара на поголема вредност на функцијата.

Функција y = ѓ ( x ) повикани се зголемува на интервалот (А; б ), ако за некој x 1 И x 2 од овој интервал така штоx 1 < x 2 , нееднаквоста е вистинаѓ ( x 1 )< ѓ ( x 2 ).

Опаѓачки во одреден интервал, функција е функција за која поголема вредност на аргументот од овој интервал одговара на помала вредност на функцијата.

Функција на = ѓ ( x ) повикани се намалувана интервалот (А; б ) , доколку има некој x 1 И x 2 од овој интервал така што x 1 < x 2 , нееднаквоста е вистинаѓ ( x 1 )> ѓ ( x 2 ).

4. Парна (непарна) функција

Дури и функција - функција чијшто домен на дефиниција е симетричен во однос на потеклото и за кој билоX од доменот на дефиниција еднаквостаѓ (- x ) = ѓ ( x ) . Графикот на парна функција е симетричен во однос на ординатата.

На пример, y = x 2 - дури и функција.

Непарна функција- функција чијшто домен на дефиниција е симетричен во однос на потеклото и за кој било Xод доменот на дефиниција еднаквоста е вистина ѓ (- x ) = - ѓ (x ). Графикот на непарна функција е симетричен во однос на потеклото.

На пример: y = x 3 - непарна функција .

Функцијата од општа форма не е парна или непарна (y = x 2 +x ).

Својства на некои функции и нивна графика

1. Линеарна функција наречена функција на формата , Каде к И б - бројки.

Доменот на дефиниција на линеарна функција е множествоР реални броеви.

График на линеарна функцијана = kx + б ( к ≠ 0) е права линија што минува низ точката (0;б ) и паралелно со праватана = kx .

Директно, не паралелно со оскатаОУ, е графикот на линеарна функција.

Својства на линеарна функција.

1. Кога к > 0 функција на = kx + б

2. Кога к < 0 функција y = kx + б се намалува во доменот на дефиниција.

y = kx + б ( к ≠ 0 ) е целата нумеричка права, т.е. еден купР реални броеви.

На к = 0 збир на вредности на функцииy = kx + б се состои од еден бројб .

3. Кога б = 0 и к = 0 функцијата не е ниту парна ниту непарна.

На к = 0 линеарна функција има формаy = б и во б ≠ 0 рамномерно е.

На к = 0 и б = 0 линеарна функција има формаy = 0 и е и парни и непарни.

График на линеарна функцијаy = б е права линија што минува низ точката (0; б ) и паралелно со оскатаО.Забележете дека кога б = 0 функционален графикy = б се совпаѓаат со оската О .

5. Кога к > 0 го имаме тоа на> 0, ако и на< 0 ако. На к < 0 имаме дека y > 0 акои во< 0, если .

2. Функција y = x 2

Рреални броеви.

Давање променливаX неколку вредности од доменот на функцијата и пресметување на соодветните вредностинаспоред формулата y = x 2 , го прикажуваме графикот на функцијата.

График на функција y = x 2 повикани парабола.

Својства на функцијата y = x 2 .

1. Ако X= 0, тогаш y = 0, т.е. Параболата има заедничка точка со координатните оски (0; 0) - потеклото на координатите.

2. Ако x ≠ 0 , Тоа на > 0, т.е. сите точки на параболата, освен потеклото, лежат над х-оската.

3. Збир на вредности на функциина = X 2 е функцијата на распонна = X 2 се намалува.

X

3.Функција

Доменот на оваа функција е функцијата spany = | x | се намалува.

7. Функцијата ја зема својата најмала вредност во точкатаX,тоа е еднакво на 0. Нема најголема вредност.

6. Функција

Опсег на функција: .

Опсег на функции: .

Графикот е хипербола.

1. Функција нули.

y ≠ 0, без нули.

2. Интервали на постојаност на знаците,

Ако к > 0, тогаш на> 0 во X > 0; на < 0 при X < О.

Ако к < 0, то на < 0 при X > 0; на> 0 во X < 0.

3. Интервали на зголемување и намалување.

Ако к > 0, тогаш функцијата се намалува како .

Ако к < 0, то функция возрастает при .

4. Парна (непарна) функција.

Функцијата е непарна.

Квадратен трином

Равенка на формата секира 2 + bx + в = 0, каде а , бИ Со - некои бројки иa≠ 0, повикан квадрат.

Во квадратна равенкасекира 2 + bx + в = 0 коефициент Аповикани првиот коефициент б - втори коефициенти, со - слободен член.

Формулата за корените на квадратната равенка е:

.

Изразот се нарекува дискриминаторски квадратна равенка и се означува соД .

Ако Д = 0, тогаш има само еден број што ја задоволува равенката секира 2 + bx + в = 0. Сепак, се согласивме да кажеме дека во овој случај квадратната равенка има два еднакви реални корени, а самиот број повикани двоен корен.

Ако Д < 0, то квадратное уравнение не имеет действительных корней.

Ако Д > 0, тогаш квадратната равенка има два различни реални корени.

Нека е дадена квадратна равенкасекира 2 + bx + в = 0. Бидејќи a≠ 0, а потоа се делат двете страни на оваа равенка соА, ја добиваме равенката . Верувајќи И , доаѓаме до равенката , во кој првиот коефициент е еднаков на 1. Таквата равенка се нарекувададена.

Формулата за корените на горната квадратна равенка е:

.

Равенки на формата

А x 2 + bx = 0, секира 2 + s = 0, А x 2 = 0

се нарекуваат нецелосни квадратни равенки. Нецелосните квадратни равенки се решаваат со факторинг на левата страна на равенката.

Теорема на Виета .

Збирот на корените на квадратната равенка е еднаков на односот на вториот коефициент со првиот, земен со спротивен знак, а производот на корените е односот на слободниот член со првиот коефициент, т.е.

Конверзна теорема.

Ако збирот на кои било два бројаX 1 И X 2 еднаква на , а нивниот производ е еднаков, тогаш овие броеви се корените на квадратната равенкаО 2 + б x + c = 0.

Функција на формата О 2 + б x + cповикани квадратен трином. Корените на оваа функција се корените на соодветната квадратна равенкаО 2 + б x + c = 0.

Ако дискриминантата на квадратен трином е поголема од нула, тогаш овој трином може да се претстави како:

О 2 + б x + c = a(x-x 1 ) (x-x 2 )

Каде X 1 И X 2 - корени на триномот

Ако дискриминантата на квадратен трином е нула, тогаш овој трином може да се претстави како:

О 2 + б x + c = a(x-x 1 ) 2

Каде X 1 - коренот на триномот.

На пример, 3x 2 - 12x + 12 = 3 (x - 2) 2 .

Равенка на формата О 4 + б X 2 + sсе нарекува = 0 биквадратски. Користење на замена на променлива со помош на формулатаX 2 = y се сведува на квадратна равенкаА y 2 + од страна на + c = 0.

Квадратна функција

Квадратна функција е функција која може да се запише со формула на форматаy = секира 2 + bx + в , Каде x - независната променлива,а , б И в – некои бројки иа ≠ 0.

Својствата на функцијата и видот на нејзиниот график се одредуваат главно од вредностите на коефициентота и дискриминаторски.

Својства на квадратна функција

Домен:Р;

Опсег на вредности:

на А > 0 [- Д/(4 а); ∞)

на А < 0 (-∞; - Д/(4 а)];

Пар, непарен:

на б = 0 парна функција

на б ≠ Функцијата 0 не е ниту парна ниту непарна

на Д> 0 две нули: ,

на Д= 0 една нула:

на Д < 0 нулей нет

Потпишувајте интервали на постојаност:

ако a > 0, Д> 0, тогаш

ако a > 0, Д= 0, тогаш

дако a > 0, Д < 0, то

ако< 0, Д> 0, тогаш

ако< 0, Д= 0, тогаш

ако< 0, Д < 0, то

- Интервали на монотонија

за > 0

на а< 0

Графикот на квадратна функција епарабола – крива симетрична за права линија , поминувајќи низ темето на параболата (темето на параболата е точка на пресек на параболата со оската на симетрија).

За да графирате квадратна функција, потребно е:

1) најдете ги координатите на темето на параболата и означете ја во координатната рамнина;

2) конструирај уште неколку точки кои припаѓаат на параболата;

3) поврзете ги означените точки со мазна линија.

Координатите на темето на параболата се одредуваат со формулите:

; .

Конвертирање на графикони на функции

1. Истегнување графички уметностиy = x 2 по оскатана В|а| пати (на|а| < 1 е компресија од 1/|а| еднаш).

Ако, и< 0, произвести, кроме того, зеркальное отражение графика отно­сительно оси X (гранките на параболата ќе бидат насочени надолу).

Резултат: график на функцијаy = ах 2 .

2. Паралелен трансфер функционална графикаy = ах 2 по оскатаX на| м | (надесно кога

м > 0 и лево когаТ< 0).

Резултат: графикон на функцијаy = a(x - t) 2 .

3. Паралелен трансфер функционална графика по оскатана на| n | (горе востр> 0 и надолу воП< 0).

Резултат: графикон на функцијаy = a(x - t) 2 + стр.

Квадратни нееднаквости

Неравенки на форматаО 2 + б x + c > 0 иО 2 + bx + c< 0, кадеX - променлива,а , б ИСо - некои бројки иa≠ 0 се нарекуваат неравенки од втор степен со една променлива.

Решавањето на неравенство од втор степен во една променлива може да се смета како пронаоѓање на интервалите во кои соодветната квадратна функција зема позитивни или негативни вредности.

Да се ​​решат неравенки на форматаО 2 + bx + c > 0 иО 2 + bx + c< 0 продолжи на следниов начин:

1) најдете го дискриминаторот на квадратниот трином и дознајте дали триномот има корени;

2) ако триномот има корени, тогаш означете ги на оскатаX а низ означените точки шематски се црта парабола чии гранки се насочени нагоре конА > 0 или надолу когаА< 0; ако триномот нема корени, тогаш шематски прикажете парабола сместена во горната полурамнина наА > 0 или пониско наА < 0;

3) пронајден на оскатаX интервали за кои точките на параболата се наоѓаат над оскатаX (ако се реши неравенствотоО 2 + bx + c > 0) или под оскатаX (ако се реши неравенствотоО 2 + bx + c < 0).

Пример:

Да ја решиме нееднаквоста .

Размислете за функцијата

Нејзиниот график е парабола, чии гранки се насочени надолу (пошто ).

Ајде да дознаеме како графикот се наоѓа во однос на оскатаX. Ајде да ја решиме равенката за ова . Го добиваме тоаx = 4. Равенката има еден корен. Ова значи дека параболата ја допира оскатаX.

Со шематски прикажување на параболата, откриваме дека функцијата зема негативни вредности за која билоX, освен 4.

Одговорот може да се напише вака:X - кој било број што не е еднаков на 4.

Решавање на неравенки со методот на интервал

дијаграм за решение

1. Најдете нули функција на левата страна на неравенката.

2. Означи ја положбата на нулите на бројната оска и определи ја нивната множина (Акок јас е парен, тогаш нулата е со парна множина акок јас чудно е чудно).

3. Најдете ги знаците на функцијата во интервалите помеѓу неговите нули, почнувајќи од најдесниот интервал: во овој интервал функцијата од левата страна на неравенката е секогаш позитивна за дадениот облик на неравенки. Кога се движите од десно кон лево низ нулата на функцијата од еден интервал во соседен, треба да се земе предвид:

ако нулата е непарна множина, знакот на функцијата се менува,

ако нулата е парна множина, знакот на функцијата е зачуван.

4. Запишете го одговорот.

Пример:

(x + 6) (x + 1) (X - 4) < 0.

Пронајдени се нули на функцијата. Тие се еднакви:X 1 = -6; X 2 = -1; X 3 = 4.

Да ги означиме нулите на функцијата на координатната линијаѓ ( x ) = (x + 6) (x + 1) (X - 4).

Да ги најдеме знаците на оваа функција во секој од интервалите (-∞; -6), (-6; -1), (-1; 4) и

Од сликата е јасно дека множеството решенија на неравенката е унија на интервалите (-∞; -6) и (-1; 4).

Одговор: (-∞ ; -6) и (-1; 4).

Разгледаниот метод за решавање на неравенки се нарекуваметод на интервал.

Доменот на дефиниција и опсегот на вредности на функцијата.Во елементарната математика, функциите се изучуваат само на множеството реални броеви РОва значи дека аргументот на функцијата може да ги земе само оние реални вредности за кои е дефинирана функцијата, т.е. прифаќа и само реални вредности. Еден куп Xсите валидни валидни вредности на аргументот x, за што функцијата y= ѓ(x)дефиниран, повикан домен на функцијата. Еден куп Yсите реални вредности y, која функцијата ја прифаќа, се нарекува опсег на функции. Сега можеме да дадеме попрецизна дефиниција на функцијата: правило(закон) на кореспонденција помеѓу множествата X и Y, според кој за секој елемент од множествотоX може да најде еден и само еден елемент од множеството Y, наречен функција.

Од оваа дефиниција произлегува дека функцијата се смета за дефинирана ако:

Доменот на функцијата е наведен X ;

Опсегот на функции е наведен Y ;

Познато е правилото (законот) на кореспонденција и такво што за секој

Може да се најде само една функционална вредност за вредност на аргументот.

Ова барање за уникатност на функцијата е задолжително.

Монотона функција.Ако за било кои две вредности на аргументот x 1 и x 2 од состојбата x 2 > x 1 следи ѓ(x 2) > ѓ(x 1), потоа функцијата ѓ(x) се нарекува се зголемува; ако за некој x 1 и x 2 од состојбата x 2 > x 1 следи ѓ(x 2) < ѓ(x 1), потоа функцијата ѓ(x) се нарекува се намалува. Се нарекува функција која само се зголемува или само се намалува монотоно.

Ограничени и неограничени функции.Функцијата се нарекува ограничен, ако има толку позитивен број Мшто | ѓ(x) | Мза сите вредности x.Ако таков број не постои, тогаш функцијата е неограничено.

ПРИМЕРИ.

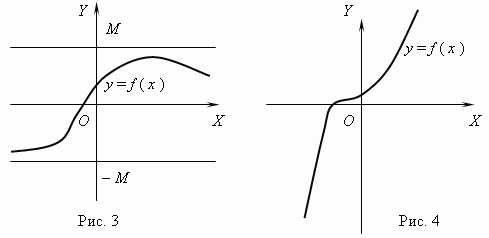
Функцијата прикажана на слика 3 е ограничена, но не и монотона. Функцијата на слика 4 е токму спротивна, монотона, но неограничена. (Објаснете го ова ве молам!).

Континуирани и дисконтинуирани функции.Функција y = ѓ (x) се нарекува континуирано во точкатаx = а, Ако:

1) функцијата е дефинирана кога x = а, т.е. ѓ (а) постои;

2) постои конечниограничување лим ѓ (x) ;

x→а

(види Ограничувања на функции)

3) ѓ (а) = лим ѓ (x) .

x→а

Ако барем еден од овие услови не е исполнет, тогаш функцијата се повикува експлозивво точката x = а.

Ако функцијата е континуирана за време на сите точки од неговиот домен на дефиниција, тогаш се нарекува континуирана функција.

Парни и непарни функции.Ако за било кој x ѓ(- x) = ѓ (x), тогаш се повикува функцијата дури;ако се појави: ѓ(- x) = - ѓ (x), тогаш се повикува функцијата чудно. График на парна функција симетрични во однос на оската Y(сл. 5), график на непарна функција Симметрика во однос на потеклото(сл. 6).

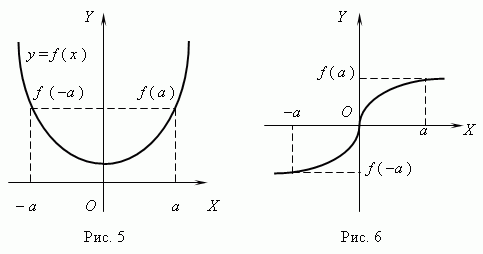
Периодична функција.Функција ѓ (x) - периодични, доколку постои такво нешто не-нулаброј Тза што било кој xод доменот на дефиниција на функцијата важи следново: ѓ (x + Т) = ѓ (x). Ова најмалкусе повикува бројот периодот на функцијата. Сите тригонометриски функции се периодични.

Пример 1. Докажи го тој грев xима период од 2.

Решение: Знаеме дека гревот ( x+ 2n) = грев x, Каде n= 0, ± 1, ± 2, ...

Затоа, додаток 2 nне на синус аргумент

Го менува своето значење. Дали има друг број со ова

Истиот имот?

Ајде да се преправаме дека П- таков број, т.е. еднаквост:

Грев ( x+ П) = грев x,

Важи за која било вредност x. Но, тогаш има

Место и време x= / 2, т.е.

Грев (/2 + П) = грев / 2 = 1.

Но, според формулата за намалување грев ( / 2 + П) = кос П. Потоа

Од последните две еднаквости следува дека кос П= 1, но ние

Знаеме дека тоа е точно само кога П = 2n. Уште од најмалите

Ненулта број од 2 nе 2, тогаш овој број

И има периоден грев x. На сличен начин може да се докаже дека 2од nе , значи ова е периодот грев 2 x.

Функција нули.Се повикува вредноста на аргументот при која функцијата е еднаква на 0 нула (корен) функција. Функцијата може да има повеќе нули.На пример, функцијата y = x (x + 1) (x-3) има три нули: x= 0, x= -1, x= 3. Геометриски нула функција - ова е апсциса на точката на пресек на функционалниот график со оската X .

Слика 7 покажува график на функција со нули: x= а, x = бИ x= в.

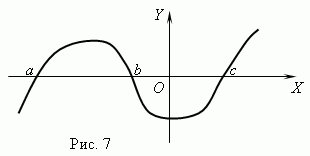
Асимптота.Ако графикот на функцијата неодредено се приближува до одредена линија додека се оддалечува од потеклото, тогаш оваа линија се нарекува асимптота.

Одржувањето на вашата приватност е важно за нас. Поради оваа причина, развивме Политика за приватност која опишува како ги користиме и складираме вашите информации. Ве молиме прегледајте ги нашите практики за приватност и кажете ни ако имате какви било прашања.

Собирање и користење на лични информации

Личните информации се однесуваат на податоци што може да се користат за идентификување или контактирање на одредена личност.

Може да биде побарано од вас да ги дадете вашите лични податоци во секое време кога ќе не контактирате.

Подолу се дадени неколку примери за типовите на лични информации што можеме да ги собираме и како можеме да ги користиме тие информации.

Кои лични податоци ги собираме:

• Кога поднесувате апликација на страницата, може да собереме различни информации, вклучувајќи го вашето име, телефонски број, адреса на е-пошта итн.

Како ги користиме вашите лични податоци:

• Личните информации што ги собираме ни овозможуваат да ве контактираме со уникатни понуди, промоции и други настани и претстојни настани.
• Од време на време, може да ги користиме вашите лични податоци за да испраќаме важни известувања и комуникации.
• Може да користиме и лични информации за внатрешни цели, како што се спроведување ревизии, анализа на податоци и разни истражувања со цел да ги подобриме услугите што ги обезбедуваме и да ви дадеме препораки во врска со нашите услуги.
• Ако учествувате во наградно извлекување, натпревар или слична промоција, ние може да ги користиме информациите што ги давате за администрирање на такви програми.

Откривање на информации на трети страни

Ние не ги откриваме информациите добиени од вас на трети страни.

Исклучоци:

• Доколку е потребно - во согласност со закон, судска процедура, во правни постапки и/или врз основа на јавни барања или барања од владини органи на територијата на Руската Федерација - да ги откриете вашите лични податоци. Ние, исто така, може да откриеме информации за вас ако утврдиме дека таквото откривање е неопходно или соодветно за безбедност, спроведување на законот или други цели од јавна важност.
• Во случај на реорганизација, спојување или продажба, можеме да ги пренесеме личните информации што ги собираме на соодветната трета страна наследник.

Заштита на лични информации

Преземаме мерки на претпазливост - вклучувајќи административни, технички и физички - за да ги заштитиме вашите лични информации од губење, кражба и злоупотреба, како и од неовластен пристап, откривање, менување и уништување.

Почитување на вашата приватност на ниво на компанија

За да се осигураме дека вашите лични информации се безбедни, ние ги пренесуваме стандардите за приватност и безбедност на нашите вработени и строго ги спроведуваме практиките за приватност.

Овој наставен материјал е само за референца и се однесува на широк спектар на теми. Статијата дава преглед на графиконите на основните елементарни функции и го разгледува најважното прашање - како правилно и БРЗО да се изгради графикон. Во текот на изучувањето на вишата математика без познавање на графиконите на основните елементарни функции ќе биде тешко, затоа е многу важно да се запамети како изгледаат графиконите на парабола, хипербола, синус, косинус и сл., а запомнете некои на значењата на функциите. Ќе зборуваме и за некои својства на главните функции.

Не тврдам комплетност и научна темелност на материјалите, акцентот ќе биде ставен, пред сè, на практиката - оние работи со кои се среќава буквално на секој чекор, во која било тема од вишата математика. Табели за кукли? Така може да се каже.

Поради многубројните барања на читателите табела со содржина што може да се кликне:

Во продолжение има ултракраток синопсис на темата
– совладајте 16 видови графикони со проучување на ШЕСТ страници!

Сериозно, шест, дури и јас бев изненаден. Ова резиме содржи подобрена графика и е достапно за номинална такса; може да се погледне демо верзија. Удобно е да се испечати датотеката така што графиконите се секогаш при рака. Ви благодариме за поддршката на проектот!

И да почнеме веднаш:

Како правилно да се конструираат координатни оски?

Во пракса, тестовите речиси секогаш ги пополнуваат учениците во посебни тетратки, наредени на квадрат. Зошто ви се потребни карирани ознаки? На крајот на краиштата, работата, во принцип, може да се направи на листови А4. А кафезот е неопходен само за висококвалитетен и прецизен дизајн на цртежи.

Секое цртање на функционален график започнува со координатни оски.

Цртежите можат да бидат дводимензионални или тридимензионални.

Ајде прво да го разгледаме дводимензионалниот случај Декартов правоаголен координатен систем:

1) Нацртајте координатни оски. Оската се нарекува x-оска , а оската е y-оска . Секогаш се трудиме да ги нацртаме уредно и не криво. Стрелките исто така не треба да личат на брадата на Папа Карло.

2) Ги потпишуваме оските со големи букви „X“ и „Y“. Не заборавајте да ги означите секирите.

3) Поставете ја скалата по оските: нацртајте нула и два. Кога правите цртеж, најзгодната и најчесто користена скала е: 1 единица = 2 ќелии (цртеж лево) - ако е можно, држете се до неа. Меѓутоа, одвреме-навреме се случува цртежот да не се вклопи на листот на тетратката - тогаш ја намалуваме скалата: 1 единица = 1 ќелија (цртеж од десната страна). Тоа е ретко, но се случува обемот на цртежот да се намали (или да се зголеми) уште повеќе

НЕМА ПОТРЕБА од „митралез“…-5, -4, -3, -1, 0, 1, 2, 3, 4, 5,….Зашто координатната рамнина не е споменик на Декарт, а ученикот не е гулаб. Ние ставивме нулаИ две единици долж оските. Понекогаш наместоединици, погодно е да се „означат“ други вредности, на пример, „два“ на оската на апсцисата и „три“ на оската на ординатите - и овој систем (0, 2 и 3) исто така уникатно ќе ја дефинира координатната мрежа.

Подобро е да се проценат проценетите димензии на цртежот ПРЕД да се конструира цртежот. Така, на пример, ако задачата бара цртање триаголник со темиња , , , тогаш е сосема јасно дека популарната скала од 1 единица = 2 ќелии нема да работи. Зошто? Ајде да ја погледнеме поентата - тука ќе треба да измерите петнаесет сантиметри надолу, и, очигледно, цртежот нема да се вклопи (или едвај се вклопува) на лист од тетратка. Затоа, веднаш избираме помала скала: 1 единица = 1 ќелија.

Патем, околу сантиметри и тетратки ќелии. Дали е вистина дека 30 ќелии за тетратки содржат 15 сантиметри? За забава измерете 15 сантиметри во тетратката со линијар. Во СССР ова можеби беше точно... Интересно е да се забележи дека ако ги измерите истите овие сантиметри хоризонтално и вертикално, резултатите (во ќелиите) ќе бидат различни! Строго кажано, модерните тетратки не се карирани, туку правоаголни. Ова може да изгледа бесмислено, но цртањето, на пример, круг со компас во такви ситуации е многу незгодно. Да бидам искрен, во такви моменти почнувате да размислувате за исправноста на другарот Сталин, кој беше испратен во кампови за хакерска работа во производството, а да не зборуваме за домашната автомобилска индустрија, паѓање авиони или експлозии на електрани.

Зборувајќи за квалитет, или кратка препорака за канцелариски материјал. Денес, повеќето од тетратките што се во продажба се, во најмала рака, целосна глупост. Од причина што се навлажнуваат, и тоа не само од гел пенкала, туку и од хемиско пенкала! Заштедуваат пари на хартија. За да ги завршите тестовите, препорачувам да користите тетратки од мелницата за пулпа и хартија Архангелск (18 листови, квадрат) или „Пјатерочка“, иако е поскапо. Препорачливо е да изберете гел пенкало; дури и најевтиниот кинески гел за полнење е многу подобар од хемиско пенкало, кое или ја размачка или кине хартијата. Единственото „конкурентно“ хемиско пенкало на кое можам да се сетам е Ерих Краузе. Таа пишува јасно, убаво и доследно – дали со полно јадро или со речиси празно.

дополнително: Визијата за правоаголен координатен систем низ очите на аналитичката геометрија е опфатена во статијата Линеарна (не) зависност на вектори. Основа на вектори, детални информации за координатни четвртини може да се најдат во вториот пасус од лекцијата Линеарни неравенки.

3D куќиште

Овде е скоро исто.

1) Нацртајте координатни оски. Стандард: оската се применуваат – насочена нагоре, оска – насочена надесно, оска – насочена надолу кон лево строгопод агол од 45 степени.

2) Обележете ги оските.

3) Поставете ја скалата долж оските. Скалата долж оската е два пати помала од скалата долж другите оски. Исто така, забележете дека во десниот цртеж користев нестандарден "засек" по должината на оската (оваа можност е веќе спомената погоре). Од моја гледна точка, ова е попрецизно, побрзо и естетски попријатно - нема потреба да се бара средината на клетката под микроскоп и да се „изваја“ единица блиску до потеклото на координатите.

Кога правите 3D цртеж, повторно, дајте приоритет на размерот
1 единица = 2 ќелии (цртеж лево).

За што се сите овие правила? Правилата се направени за да се прекршат. Тоа е она што ќе го направам сега. Факт е дека следните цртежи на статијата ќе бидат направени од мене во Excel, а координатните оски ќе изгледаат неточни од гледна точка на правилен дизајн. Би можел да ги нацртам сите графикони со рака, но всушност е страшно да ги нацртам бидејќи Excel не сака да ги нацрта многу попрецизно.

Графикони и основни својства на елементарните функции

Линеарна функција е дадена со равенката. Графикот на линеарни функции е директно. За да се изгради права линија, доволно е да се знаат две точки.

Пример 1

Конструирај график на функцијата. Ајде да најдеме две точки. Поволно е да се избере нула како една од точките.

Ако тогаш

Да земеме друга точка, на пример, 1.

Ако тогаш

При завршување на задачите, координатите на точките обично се сумираат во табела:

И самите вредности се пресметуваат усно или на нацрт, калкулатор.

Пронајдени се две точки, ајде да направиме цртеж:

Кога подготвуваме цртеж, секогаш ја потпишуваме графиката.

Би било корисно да се потсетиме на посебни случаи на линеарна функција:

Забележете како ги ставив потписите, потписите не треба да дозволуваат несогласувања при проучување на цртежот. Во овој случај, беше крајно непожелно да се стави потпис до точката на вкрстување на линиите или долу десно помеѓу графиконите.

1) Линеарна функција од формата () се нарекува директна пропорционалност. На пример,. Графикот на директна пропорционалност секогаш поминува низ потеклото. Така, конструирањето права линија е поедноставено - доволно е да се најде само една точка.

2) Равенката на формата одредува права линија паралелна на оската, особено, самата оска е дадена со равенката. Графикот на функцијата се исцртува веднаш, без да се најдат точки. Односно, записот треба да се разбере на следниов начин: „y е секогаш еднаков на –4, за која било вредност на x“.

3) Равенката на формата одредува права линија паралелна на оската, особено самата оска е дадена со равенката. Веднаш се исцртува и графикот на функцијата. Влезот треба да се разбере на следниов начин: „x е секогаш, за која било вредност на y, еднаква на 1“.

Некои ќе прашаат, зошто се сеќавате на 6-то одделение?! Така е, можеби е така, но со текот на годините на пракса запознав десетина студенти кои беа збунети од задачата да направат график како или.

Конструирањето права линија е најчестото дејство при изработка на цртежи.

Правата линија е детално дискутирана во текот на аналитичката геометрија, а заинтересираните можат да се повикаат на статијата Равенка на права линија на рамнина.

График на квадратна, кубна функција, график на полином

Парабола. График на квадратна функција () претставува парабола. Размислете за познатиот случај:

Да се ​​потсетиме на некои својства на функцијата.

Значи, решението на нашата равенка: – токму во оваа точка се наоѓа темето на параболата. Зошто е тоа така може да се дознае од теоретскиот напис за изводот и лекцијата за екстреми на функцијата. Во меѓувреме, да ја пресметаме соодветната вредност „Y“:

Така, темето е во точката

Сега наоѓаме други точки, додека дрско ја користиме симетријата на параболата. Треба да се напомене дека функцијата – не е дури, но, сепак, никој не ја откажал симетријата на параболата.

По кој редослед да се најдат преостанатите бодови, мислам дека ќе биде јасно од конечната табела:

Овој конструктивен алгоритам фигуративно може да се нарече „шатл“ или принцип „напред и назад“ со Анфиса Чехова.

Ајде да го направиме цртежот:

Од испитаните графикони, на ум ми доаѓа уште една корисна карактеристика:

За квадратна функција () точно е следново:

Ако , тогаш гранките на параболата се насочени нагоре.

Ако , тогаш гранките на параболата се насочени надолу.

Продлабочено знаење за кривата може да се добие на часот Хипербола и парабола.

Со функцијата е дадена кубна парабола. Еве еден цртеж познат од училиштето:

Да ги наведеме главните својства на функцијата

График на функција

Претставува една од гранките на параболата. Ајде да го направиме цртежот:

Главните својства на функцијата:

Во овој случај, оската е вертикална асимптота за графикот на хипербола кај .

Би било ГРУМА грешка ако при изготвувањето на цртежот безгрижно дозволите графикот да се вкрсти со асимптота.

Исто така, едностраните граници ни кажуваат дека хиперболата не е ограничен одозгораИ не е ограничен одоздола.

Да ја испитаме функцијата во бесконечност: , односно, ако почнеме да се движиме по оската лево (или десно) до бесконечност, тогаш „игрите“ ќе бидат во уреден чекор бескрајно блискупристап до нула, и, соодветно, гранките на хиперболата бескрајно блискусе приближи до оската.

Значи, оската е хоризонтална асимптота за графикот на функцијата, ако „x“ се стреми кон плус или минус бесконечност.

Функцијата е чудно, и, според тоа, хиперболата е симетрична во однос на потеклото. Овој факт е очигледен од цртежот, покрај тоа, лесно се проверува аналитички: .

Графикот на функција од формата () претставува две гранки на хипербола.

Ако , тогаш хиперболата се наоѓа во првата и третата координатна четвртина(види слика погоре).

Ако , тогаш хиперболата се наоѓа во втората и четвртата координатна четвртина.

Посочената шема на престој на хипербола е лесно да се анализира од гледна точка на геометриските трансформации на графиконите.

Пример 3

Конструирај ја десната гранка на хиперболата

Ние го користиме методот на градење по точка, и поволно е да се изберат вредностите така што тие се деливи со целина:

Ајде да го направиме цртежот:

Нема да биде тешко да се конструира левата гранка на хиперболата; тука ќе помогне необичноста на функцијата. Грубо кажано, во табелата за конструкција на точка, ментално додаваме минус на секој број, ги ставаме соодветните точки и ја цртаме втората гранка.

Детални геометриски информации за разгледуваната линија може да се најдат во статијата Хипербола и парабола.

График на експоненцијална функција

Во овој дел, веднаш ќе ја разгледам експоненцијалната функција, бидејќи во проблемите на вишата математика во 95% од случаите се појавува експоненцијалната.

Дозволете ми да ве потсетам дека ова е ирационален број: , ова ќе биде потребно при конструирање график, кој, всушност, ќе го изградам без церемонија. Три бода се веројатно доволни:

Ајде да го оставиме графикот на функцијата сам за сега, повеќе за него подоцна.

Главните својства на функцијата:

Графиконите на функции, итн., изгледаат фундаментално исто.

Морам да кажам дека вториот случај се случува поретко во пракса, но се случува, па затоа сметав дека е неопходно да го вклучам во оваа статија.

График на логаритамска функција

Размислете за функција со природен логаритам.
Ајде да направиме цртеж точка-по-точка:

Ако сте заборавиле што е логаритам, ве молиме погледнете ги вашите училишни учебници.

Главните својства на функцијата:

Домен:

Опсег на вредности: .

Функцијата не е ограничена одозгора: , иако бавно, но гранката на логаритмот оди до бесконечност.
Да го испитаме однесувањето на функцијата близу нула десно: . Значи, оската е вертикална асимптота за графикот на функција како „x“ се стреми кон нула од десно.

Императив е да се знае и да се запамети типичната вредност на логаритамот: .

Во принцип, графикот на логаритамот до основата изгледа исто: , , (децимален логаритам до основата 10) итн. Згора на тоа, колку е поголема основата, графикот ќе биде порамен.

Ние нема да го разгледаме случајот; не се сеќавам кога последен пат направив графикон со таква основа. А логаритамот се чини дека е многу редок гостин во проблемите од вишата математика.

На крајот од овој став ќе кажам уште еден факт: Експоненцијална функција и логаритамска функција– ова се две меѓусебно инверзни функции. Ако внимателно го погледнете графикот на логаритмот, можете да видите дека ова е истиот експонент, само што се наоѓа малку поинаку.

Графикони на тригонометриски функции

Каде започнува тригонометриското мачење на училиште? Во право. Од синус

Ајде да ја нацртаме функцијата

Оваа линија се нарекува синусоид.

Да те потсетам дека „пи“ е ирационален број: , а во тригонометријата ти ги заслепува очите.

Главните својства на функцијата:

Оваа функција е периодичнисо период . Што значи тоа? Да го погледнеме сегментот. Лево и десно од него, точно истото парче од графиконот се повторува бескрајно.

Домен: , односно за која било вредност на „x“ има синусна вредност.

Опсег на вредности: . Функцијата е ограничен: , односно, сите „игри“ се строго во сегментот .
Ова не се случува: или, поточно, се случува, но овие равенки немаат решение.