Лекција на тема: „Наоѓање екстремни точки на функции. Примери“
Дополнителни материјали
Почитувани корисници, не заборавајте да ги оставите вашите коментари, критики, желби! Сите материјали се проверени со антивирусна програма.
Прирачници и симулатори во онлајн продавницата Integral за одделение 10 од 1C
Решавање проблеми во геометријата. Интерактивни градежни задачи за 7-10 одделение
Софтверско опкружување „1C: Mathematical Constructor 6.1“
Што ќе проучуваме:
1. Вовед.
2. Минимални и максимални поени.
4. Како да се пресметаат екстремите?
5. Примери.
Вовед во Function Extrema
Момци, ајде да го погледнеме графикот на одредена функција:
Забележете дека однесувањето на нашата функција y=f (x) е во голема мера определено со две точки x1 и x2. Да го разгледаме подетално графикот на функцијата во и околу овие точки. До точка x2 функцијата се зголемува, во точката x2 има флексија, а веднаш по оваа точка функцијата се намалува до точка x1. Во точката x1 функцијата повторно се наведнува, а потоа повторно се зголемува. Засега точките x1 и x2 ќе ги нарекуваме точки на флексија. Ајде да нацртаме тангенти на овие точки:
Тангентите во нашите точки се паралелни со оската x, што значи дека наклонот на тангентата е нула. Ова значи дека изводот на нашата функција во овие точки е еднаков на нула.
Ајде да го погледнеме графикот на оваа функција:
Невозможно е да се нацртаат тангентни линии на точките x2 и x1. Тоа значи дека изводот не постои во овие точки. Сега да ги погледнеме повторно нашите точки на двата графикони. Точката x2 е точката во која функцијата ја достигнува својата најголема вредност во некој регион (близу точката x2). Точката x1 е точката во која функцијата ја достигнува својата најмала вредност во некој регион (близу точката x1).
Минимални и максимални поени
Дефиниција: Точката x= x0 се нарекува минимална точка на функцијата y=f(x) ако има соседство на точката x0 во која важи неравенството: f(x) ≥ f(x0).
Дефиниција: Точката x=x0 се нарекува максимална точка на функцијата y=f(x) ако има соседство на точката x0 во која важи неравенството: f(x) ≤ f(x0).
Момци, што е маало?
Дефиниција: Соседство на точка е збир на точки што ја содржат нашата точка и оние блиску до неа.
Ние можеме сами да го поставиме соседството. На пример, за точка x=2, можеме да дефинираме соседство во форма на точки 1 и 3.
Да се вратиме на нашите графикони, погледнете ја точката x2, таа е поголема од сите други точки од одредена населба, тогаш по дефиниција е максимална точка. Сега да ја погледнеме точката x1, таа е помала од сите други точки од одредена населба, тогаш по дефиниција е минимална точка.
Момци, да ја претставиме ознаката:
Y min - минимална точка,
y max - максимална точка.
Важно!Дечки, не мешајте ги максималните и минималните поени со најмалата и најголемата вредност на функцијата. Минималните и максималните вредности се бараат во целиот домен на дефинирање на дадена функција, а минималните и максималните поени се бараат во одредено соседство.
Екстреми на функцијата
За минимални и максимални поени постои заеднички термин - екстремни поени.
Extremum (лат. extremum – крајност) – максимална или минимална вредност на функција на дадено множество. Точката во која се достигнува екстремумот се нарекува екстремна точка.
Според тоа, ако се постигне минимум, екстремната точка се нарекува минимална точка, а ако се постигне максимум, се нарекува максимална точка.
Како да барате екстреми на функција?
Да се вратиме на нашите топ листи. Во нашите точки, изводот или исчезнува (на првиот график) или не постои (на вториот график).
Тогаш можеме да дадеме важна изјава: Ако функцијата y= f(x) има екстрем во точката x=x0, тогаш во оваа точка изводот на функцијата е или нула или не постои.
Се повикуваат точките во кои изводот е еднаков на нула стационарни.
Се повикуваат точките во кои не постои изводот на функцијата критички.
Како да се пресметаат екстремите?
Момци, да се вратиме на првиот графикон на функцијата:
Анализирајќи го овој график, рековме: до точката x2 функцијата се зголемува, во точката x2 се јавува флексија, а по оваа точка функцијата се намалува до точката x1. Во точката x1 функцијата повторно се наведнува, а потоа функцијата повторно се зголемува.
Врз основа на ваквото расудување, можеме да заклучиме дека функцијата во екстремните точки ја менува природата на монотоничноста и затоа дериватната функција го менува знакот. Потсетиме: ако функцијата се намалува, тогаш изводот е помал или еднаков на нула, а ако функцијата се зголемува, тогаш изводот е поголем или еднаков на нула.
Да го сумираме стекнатото знаење со следнава изјава:
Теорема: Доволен услов за екстрем: нека функцијата y=f(x) е континуирана на некој интервал X и има стационарна или критична точка x= x0 во интервалот. Потоа:
За да ги решите проблемите, запомнете ги овие правила: Ако се дефинираат знаците на деривати, тогаш:
Алгоритам за проучување на континуирана функција y= f(x) за монотоност и екстреми:
- Најдете го изводот на y'.
- Најдете стационарни точки (изводот е нула) и критични точки (изводот не постои).
- Обележете стационарни и критични точки на бројната права и определете ги знаците на изводот на добиените интервали.
- Врз основа на горенаведените изјави, извлечете заклучок за природата на екстремните точки.
Примери за наоѓање екстремни точки
1) Најди ги крајните точки на функцијата и определи ја нивната природа: y= 7+ 12*x - x 3
Решение: Нашата функција е континуирана, тогаш ќе го користиме нашиот алгоритам:
а) y"= 12 - 3x 2,
б) y"= 0, на x= ±2, 
Точката x= -2 е минималната точка на функцијата, точката x= 2 е максималната точка на функцијата.
Одговор: x= -2 е минималната точка на функцијата, x= 2 е максималната точка на функцијата.
2) Најдете ги екстремните точки на функцијата и определи ја нивната природа.
Решение: Нашата функција е континуирана. Ајде да го користиме нашиот алгоритам: А)
б) во точката x= 2 изводот не постои, бидејќи Не можете да делите со нула 
Домен на дефиниција на функцијата: , во овој момент нема екстрем, бидејќи соседството на точката не е дефинирано. Да ја најдеме вредноста на која изводот е еднаков на нула: 
в) Означи стационарни точки на бројната права и определи ги знаците на изводот: 
г) погледнете ја нашата фигура, која ги прикажува правилата за одредување на екстремите. Точката x= 3 е минималната точка на функцијата.
Одговор: x= 3 е минималната точка на функцијата.
3) Најдете ги екстремните точки на функцијата y= x - 2cos(x) и определи ја нивната природа, за -π ≤ x ≤ π.
Решение: Нашата функција е континуирана, ајде да го користиме нашиот алгоритам:
а) y"= 1 + 2sin(x),
б) најдете ги вредностите во кои изводот е еднаков на нула: 1 + 2sin(x)= 0, sin(x)= -1/2,
бидејќи -π ≤ x ≤ π, тогаш: x= -π/6, -5π/6,
в) означи стационарни точки на бројната права и определи ги знаците на изводот: 
г) погледнете ја нашата фигура, која ги прикажува правилата за одредување на екстремите.
Точката x= -5π/6 е максималната точка на функцијата.
Точката x= -π/6 е минималната точка на функцијата.
Одговор: x= -5π/6 е максималната точка на функцијата, x= -π/6 е минималната точка на функцијата.
4) Најдете ги екстремните точки на функцијата и определи ја нивната природа:
Решение: Нашата функција има дисконтинуитет само во една точка x= 0. Да го искористиме алгоритмот: А)
б) најдете ги вредностите во кои изводот е еднаков на нула: y"= 0 при x= ±2, в) означи стационарни точки на бројната права и определи ги знаците на изводот:
г) погледнете ја нашата фигура, која ги прикажува правилата за одредување на екстремите.
Точката x= -2 е минималната точка на функцијата.
Точката x= 2 е минималната точка на функцијата.
Во точката x= 0 функцијата не постои.
Одговор: x= ±2 - минимални точки на функцијата.
Проблеми кои треба да се решаваат самостојно
а) Најдете ги крајните точки на функцијата и определи ја нивната природа: y= 5x 3 - 15x - 5.б) Најдете ги екстремните точки на функцијата и определи ја нивната природа:
в) Најдете ги екстремните точки на функцијата и определи ја нивната природа: y= 2sin(x) - x за π ≤ x ≤ 3π. г) Најдете ги екстремните точки на функцијата и определи ја нивната природа:
Функции, воопшто не е неопходно да се знае за присуството на првиот и вториот деривати и да се разбере нивното физичко значење. Прво треба да го разберете следново:
- екстремите на функцијата ја максимизираат или, обратно, ја минимизираат вредноста на функцијата во произволно мало соседство;
- не треба да има дисконтинуитет на функцијата на екстремната точка.
И сега истото, само на едноставен јазик. Погледнете го врвот на хемиското пенкало. Ако пенкалото е поставено вертикално, со завршувањето на пишувањето, тогаш самата средина на топката ќе биде екстремот - највисоката точка. Во овој случај зборуваме за максимум. Сега, ако го свртите пенкалото со крајот на пишувањето надолу, тогаш во средината на топката веќе ќе има минимална функција. Користејќи ја фигурата дадена овде, можете да ги замислите наведените манипулации за канцелариски молив. Значи, екстремите на функцијата се секогаш критични точки: нејзиниот максимум или минимум. Соседниот дел од графиконот може да биде остар или мазен по желба, но мора да постои од двете страни, само во овој случај точката е екстрем. Ако графикот е присутен само на едната страна, оваа точка нема да биде екстрем дури и ако на едната страна се исполнети екстремните услови. Сега да ги проучиме екстремите на функцијата од научна гледна точка. За една точка да се смета за екстрем, потребно е и доволно:
- првиот извод бил нула или не постоел во точката;
- првиот дериват го промени својот знак во овој момент.
Условот се толкува малку поинаку од гледна точка на деривати од повисок ред: за функција која е диференцијабилна во точка, доволно е да постои извод од непарен ред што не е еднаков на нула, додека сите деривати од понизок ред мора да постојат и да биде еднаква на нула. Ова е наједноставното можно толкување на теоремите од учебниците, но за најобичните луѓе вреди да се објасни оваа точка со пример. Основата е обична парабола. Ајде да направиме резервација веднаш: на нултата точка има минимум. Само малку математика:
- прв дериват (X 2) | = 2X, за нултата точка 2X = 0;
- втор дериват (2X) | = 2, за нулта точка 2 = 2.
На овој едноставен начин, илустрирани се условите што ги одредуваат екстремите на функцијата и за деривати од прв и за повисок ред. Можеме да додадеме на ова дека вториот извод е токму истиот извод од непарен ред, а не еднаков на нула, што беше дискутирано веднаш погоре. Кога станува збор за екстреми на функција од две променливи, условите мора да бидат исполнети и за двата аргументи. Кога се случува генерализација, се користат парцијални деривати. Односно, за присуство на екстрем во точка, потребно е двата деривати од прв ред да бидат еднакви на нула, или барем еден од нив да не постои. За да се осигура дека присуството на екстремум е доволно, се проучува израз кој е разликата помеѓу производот на изводите од втор ред и квадратот на мешаниот извод од втор ред на функцијата. Ако овој израз е поголем од нула, тогаш постои екстрем, но ако е еднаков на нула, тогаш прашањето останува отворено и треба да се направат дополнителни истражувања.
Размислете за графикот на континуирана функција y=f(x)прикажан на сликата.
Вредност на функцијата во точка x 1 ќе биде поголема од вредностите на функциите на сите соседни точки и лево и десно од x 1 . Во овој случај велиме дека функцијата има во точката x 1 максимум. Во точката xФункцијата 3 очигледно има и максимум. Ако ја земеме предвид поентата x 2, тогаш вредноста на функцијата во неа е помала од сите соседни вредности. Во овој случај велиме дека функцијата има во точката x 2 минимум. Исто и за поентата x 4 .
Функција y=f(x)во точката x 0 има максимум, ако вредноста на функцијата во оваа точка е поголема од нејзините вредности во сите точки од одреден интервал што ја содржи точката x 0, т.е. ако постои такво соседство на точка x 0, што е за секого x≠x 0 , припаѓаат на ова соседство, нееднаквоста држи f(x)<f(x 0 ) .
Функција y=f(x)Тоа има минимумво точката x 0 , ако постои такво соседство на точка x 0 , тоа е за секого x≠x 0 што припаѓа на ова соседство, важи нееднаквоста f(x)>f(x 0.
Точките во кои функцијата го достигнува својот максимум и минимум се нарекуваат екстремни точки, а вредностите на функцијата во овие точки се нарекуваат екстреми на функцијата.
Да обрнеме внимание на фактот дека функцијата дефинирана на сегмент може да го достигне својот максимум и минимум само во точките содржани во сегментот што се разгледува.
Забележете дека ако функцијата има максимум во точка, тоа не значи дека во тој момент функцијата има најголема вредност во целиот домен на дефиниција. На сликата дискутирана погоре, функцијата во точката x 1 има максимум, иако има точки во кои вредностите на функцијата се поголеми отколку во точката x 1 . Особено, ѓ(x 1) < ѓ(x 4) т.е. минимумот на функцијата е поголем од максимумот. Од дефиницијата за максимум произлегува само дека ова е најголемата вредност на функцијата во точки доволно блиску до максималната точка.
Теорема 1. (неопходен услов за постоење на екстрем.)Ако диференцијабилната функција y=f(x)има во точката x=x 0 екстрем, тогаш неговиот дериват во овој момент станува нула.
Доказ. Нека, за дефинитивно, на точка xФункцијата 0 има максимум. Потоа, за доволно мали зголемувања Δ xние имаме f(x 0 + Δ x)
Премин во овие неравенки до границата на Δ x→ 0 и имајќи предвид дека изводот ѓ "(x 0) постои, и затоа границата лево не зависи од тоа како Δ x→ 0, добиваме: на Δ x → 0 – 0 ѓ"(x 0) ≥ 0 a на Δ x → 0 + 0 ѓ"(x 0) ≤ 0. Бидејќи ѓ"(x 0) дефинира број, тогаш овие две неравенки се компатибилни само ако ѓ"(x 0) = 0.
Докажаната теорема вели дека максималните и минималните точки можат да бидат само меѓу оние вредности на аргументот при кои изводот станува нула.
Го разгледавме случајот кога функцијата има извод во сите точки на одреден сегмент. Каква е состојбата во случаите кога изводот не постои? Ајде да погледнеме примери.
Примери.
- y=|x|.
Функцијата нема извод во точката x=0 (во овој момент графикот на функцијата нема дефинирана тангента), но во овој момент функцијата има минимум, бидејќи y(0)=0, и за сите x≠ 0y > 0.
- Нека x< x
0 . Потоа в< x
0 и f "(c)> 0.
Затоа f "(c) (x- x 0)<
0 и затоа
f(x) - f(x 0 )< 0, т.е. f(x)< f(x 0 ).
- Нека x > x 0 . Потоа c>x 0 и f" (в)< 0. Средства f "(c) (x- x 0)< 0. Затоа f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Најдете го доменот на функцијата f(x).
- Најдете го првиот извод на функцијата f" (x).
- Одредете ги критичните точки за ова:
- најдете ги вистинските корени на равенката f" (x)=0;
- најдете ги сите вредности xза кои дериватот f" (x)не постои.
- Определи го знакот на дериватот лево и десно од критичната точка. Бидејќи знакот на изводот останува константен помеѓу две критични точки, доволно е да се одреди знакот на изводот во една точка лево и една точка десно од критичната точка.
- Пресметајте ја вредноста на функцијата во екстремните точки.
- Најдете ги сите критични точки на функцијата во интервалот ( а, б) и пресметајте ги вредностите на функцијата во овие точки.
- Пресметајте ги вредностите на функцијата на краевите на сегментот кога x = a, x = b.
- Од сите добиени вредности изберете ја најголемата и најмалата.
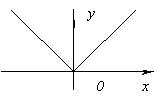
Функцијата нема извод на x=0, бидејќи оди до бесконечност во x=0. Но, во овој момент функцијата има максимум.
Функцијата нема извод на x=0, бидејќи 
на x→0. Во овој момент функцијата нема ниту максимум ниту минимум. Навистина, f(x)=0 и на x<0f(x)<0, а при x>0f(x)>0.
Така, од дадените примери и формулираната теорема е јасно дека функцијата може да има екстрем само во два случаи: 1) во точките каде што постои изводот и е еднаков на нула; 2) во точката каде што изводот не постои.
Меѓутоа, ако во одреден момент x 0 го знаеме тоа f" (x 0 ) =0, тогаш од ова не може да се заклучи дека во точката x 0 функцијата има екстрем.
На пример. 
.
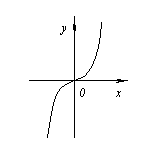
Но период x=0 не е екстремна точка, бидејќи лево од оваа точка вредностите на функцијата се наоѓаат под оската Вол, и горе десно.
Се повикуваат вредностите на аргументот од доменот на функцијата во која изводот на функцијата исчезнува или не постои критични точки.
Од сето горенаведено произлегува дека екстремните точки на функцијата се меѓу критичните точки и, сепак, не секоја критична точка е екстремна точка. Затоа, за да го пронајдете екстремот на функцијата, треба да ги најдете сите критични точки на функцијата, а потоа да ја испитате секоја од овие точки посебно за максимум и минимум. Следната теорема служи за оваа цел.
Теорема 2. (Доволен услов за постоење на екстрем.)Нека функцијата е континуирана на некој интервал кој ја содржи критичната точка x 0, и може да се разликува во сите точки од овој интервал (освен, можеби, самата точка x 0). Ако, при движење од лево кон десно низ оваа точка, дериватот го промени знакот од плус во минус, тогаш во точката x = xФункцијата 0 има максимум. Ако, при минување низ x 0 од лево кон десно, дериватот го менува знакот од минус во плус, тогаш функцијата има минимум во оваа точка.
Така, ако
Доказ. Прво да претпоставиме дека кога поминуваме низ x 0 дериватот го менува знакот од плус во минус, т.е. пред сите x, блиску до поентата x 0 f "(x)> 0 за x< x 0 , f" (x)< 0 за x> x 0 . Да ја примениме теоремата на Лагранж на разликата f(x) - f(x 0 ) = f "(c) (x- x 0), каде влежи помеѓу xИ x 0 .
Така, за сите вредности xдоволно блиску до x 0 f(x)< f(x 0 ) . И ова значи дека во точка xФункцијата 0 има максимум.
На сличен начин се докажува и вториот дел од минималната теорема.
Дозволете ни да го илустрираме значењето на оваа теорема на сликата. Нека f" (x 1 ) =0 и за било кој x,доволно блиску до x 1, нееднаквостите се задоволни
f" (x)< 0 во x< x 1 , f "(x)> 0 во x> x 1 .
Потоа лево од точката x 1 функцијата се зголемува и намалува десно, затоа, кога x = x 1 функција оди од зголемување во намалување, односно има максимум.
Слично на тоа, можеме да разгледаме точки x 2 и x 3 .
Сето горенаведено може шематски да се прикаже на сликата:
Правило за проучување на функцијата y=f(x) за екстрем
Примери. Истражете ги функциите за минимум и максимум.
МАКСИМАЛНИ И НАЈМАЛИ ВРЕДНОСТИ НА ФУНКЦИЈА НА Сегмент
Најголематавредноста на функцијата на интервал е најголемата од сите нејзини вредности на овој интервал и најмалото– најмалата од сите нејзини вредности.
Размислете за функцијата y=f(x)континуирано на сегментот [ а, б]. Како што е познато, таквата функција ги достигнува своите максимални и минимални вредности, или на границата на сегментот или внатре во неа. Ако најголемата или најмалата вредност на функцијата се постигне во внатрешна точка на сегментот, тогаш оваа вредност е максимумот или минимумот на функцијата, односно се постигнува во критичните точки.
Така, го добиваме следново правило за наоѓање најголеми и најмали вредности на функција на сегмент а, б] :
Екстреми на функцијата
Дефиниција 2
Точката $x_0$ се нарекува максимална точка на функцијата $f(x)$ ако има соседство на оваа точка така што за сите $x$ во ова соседство неравенката $f(x)\le f(x_0) $ држи.
Дефиниција 3
Точката $x_0$ се нарекува максимална точка на функцијата $f(x)$ ако има соседство на оваа точка така што за сите $x$ во ова соседство неравенката $f(x)\ge f(x_0) $ држи.
Концептот на екстрем на функција е тесно поврзан со концептот на критична точка на функцијата. Да ја претставиме неговата дефиниција.
Дефиниција 4
$x_0$ се нарекува критична точка на функцијата $f(x)$ ако:
1) $x_0$ - внатрешна точка на доменот на дефиниција;
2) $f"\left(x_0\right)=0$ или не постои.
За концептот на екстрем, можеме да формулираме теореми за доволни и неопходни услови за неговото постоење.
Теорема 2
Доволен услов за екстрем
Нека точката $x_0$ е критична за функцијата $y=f(x)$ и лежи во интервалот $(a,b)$. Нека на секој интервал $\left(a,x_0\right)\ и\ (x_0,b)$ постои дериватот $f"(x)$ и одржува константен знак. Тогаш:
1) Ако на интервалот $(a,x_0)$ дериватот е $f"\left(x\right)>0$, а на интервалот $(x_0,b)$ дериватот е $f"\left( x\десно)
2) Ако на интервалот $(a,x_0)$ дериватот $f"\left(x\right)0$, тогаш точката $x_0$ е минималната точка за оваа функција.
3) Ако и на интервалот $(a,x_0)$ и на интервалот $(x_0,b)$ дериватот $f"\left(x\right) >0$ или дериватот $f"\left(x \десно)
Оваа теорема е илустрирана на Слика 1.
Слика 1. Доволен услов за постоење на екстреми
Примери на крајности (сл. 2).
Слика 2. Примери на екстремни точки
Правило за проучување на функција за екстрем
2) Најдете го изводот $f"(x)$;
7) Извлечете заклучоци за присуството на максимум и минимум на секој интервал, користејќи теорема 2.
Зголемување и намалување на функции
Прво да ги воведеме дефинициите на функциите за зголемување и намалување.
Дефиниција 5
Функција $y=f(x)$ дефинирана на интервалот $X$ се вели дека се зголемува ако за која било точка $x_1,x_2\во X$ на $x_1
Дефиниција 6
Функцијата $y=f(x)$ дефинирана на интервалот $X$ се вели дека се намалува ако за која било точка $x_1,x_2\во X$ за $x_1f(x_2)$.
Проучување на функција за зголемување и намалување
Можете да ги проучувате функциите за зголемување и намалување користејќи го изводот.
За да ја испитате функцијата за интервали на зголемување и намалување, мора да го направите следново:
1) Најдете го доменот на дефиниција на функцијата $f(x)$;
2) Најдете го изводот $f"(x)$;
3) Најдете ги точките во кои важи еднаквоста $f"\left(x\right)=0$;
4) Најдете ги точките во кои $f"(x)$ не постои;
5) Означете ги на координатната права сите пронајдени точки и доменот на дефинирање на оваа функција;
6) Определи го знакот на изводот $f"(x)$ на секој добиен интервал;
7) Извлечете заклучок: во интервали каде $f"\left(x\right)0$ функцијата се зголемува.
Примери на проблеми за проучување на функции за зголемување, намалување и присуство на екстремни точки
Пример 1
Испитајте ја функцијата за зголемување и намалување и присуството на максимални и минимални точки: $f(x)=(2x)^3-15x^2+36x+1$
Бидејќи првите 6 точки се исти, ајде прво да ги спроведеме.
1) Домен на дефиниција - сите реални броеви;
2) $f"\лево(x\десно)=6x^2-30x+36$;
3) $f"\left(x\десно)=0$;
\ \ \
4) $f"(x)$ постои во сите точки од доменот на дефиниција;
5) Координатна линија:
Слика 3.
6) Одреди го знакот на изводот $f"(x)$ на секој интервал:
\ \}