ಅಡ್ಡ ಉತ್ಪನ್ನವು ಶೂನ್ಯಕ್ಕೆ ಏಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ? ಅಡ್ಡ ಉತ್ಪನ್ನ - ವ್ಯಾಖ್ಯಾನಗಳು, ಗುಣಲಕ್ಷಣಗಳು, ಸೂತ್ರಗಳು, ಉದಾಹರಣೆಗಳು ಮತ್ತು ಪರಿಹಾರಗಳು

7.1. ಅಡ್ಡ ಉತ್ಪನ್ನದ ವ್ಯಾಖ್ಯಾನ

ಮೂರು ನಾನ್-ಕೊಪ್ಲಾನರ್ ವೆಕ್ಟರ್‌ಗಳು a, b ಮತ್ತು c, ಸೂಚಿಸಲಾದ ಕ್ರಮದಲ್ಲಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ, ಮೂರನೇ ವೆಕ್ಟರ್ c ಯ ಅಂತ್ಯದಿಂದ ಮೊದಲ ವೆಕ್ಟರ್ a ನಿಂದ ಎರಡನೇ ವೆಕ್ಟರ್ b ಗೆ ಕಡಿಮೆ ತಿರುವು ಕಂಡುಬಂದರೆ ಬಲಗೈ ಟ್ರಿಪಲ್ ಅನ್ನು ರೂಪಿಸುತ್ತದೆ. ಅಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ಮತ್ತು ಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿದ್ದರೆ ಎಡಗೈ ತ್ರಿವಳಿ (ಚಿತ್ರ 16 ನೋಡಿ).

ವೆಕ್ಟರ್ ಎ ಮತ್ತು ವೆಕ್ಟರ್ ಬಿ ಯ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ವೆಕ್ಟರ್ ಸಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದು:

1. ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಲಂಬವಾಗಿ a ಮತ್ತು b, ಅಂದರೆ c ^ a ಮತ್ತು c ^ ಬಿ ;

2. ಎ ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳ ಮೇಲೆ ನಿರ್ಮಿಸಲಾದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶಕ್ಕೆ ಸಂಖ್ಯಾತ್ಮಕವಾಗಿ ಸಮಾನವಾದ ಉದ್ದವನ್ನು ಹೊಂದಿದೆಬಿಬದಿಗಳಲ್ಲಿರುವಂತೆ (ಚಿತ್ರ 17 ನೋಡಿ), ಅಂದರೆ.

3. ವಾಹಕಗಳು a, b ಮತ್ತು c ಬಲಗೈ ಟ್ರಿಪಲ್ ಅನ್ನು ರೂಪಿಸುತ್ತವೆ.

ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು x b ಅಥವಾ [a,b] ಎಂದು ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಘಟಕ ವೆಕ್ಟರ್‌ಗಳ ನಡುವಿನ ಕೆಳಗಿನ ಸಂಬಂಧಗಳನ್ನು ನಾನು ನೇರವಾಗಿ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ವ್ಯಾಖ್ಯಾನದಿಂದ ಅನುಸರಿಸುತ್ತೇನೆ, ಜಮತ್ತು ಕೆ(ಚಿತ್ರ 18 ನೋಡಿ):

i x j = k, j x k = i, k x i = j.
ಉದಾಹರಣೆಗೆ, ಅದನ್ನು ಸಾಬೀತುಪಡಿಸೋಣ i xj =k.

1) ಕೆ ^ ಐ, ಕೆ ^ ಜೆ ;

2) |ಕೆ |=1, ಆದರೆ | ನಾನು x ಜೆ| = |i | |ಜೆ | ಪಾಪ(90°)=1;

3) ವೆಕ್ಟರ್‌ಗಳು i, j ಮತ್ತು ಕೆಬಲ ಟ್ರಿಪಲ್ ಅನ್ನು ರೂಪಿಸಿ (ಚಿತ್ರ 16 ನೋಡಿ).

7.2 ಅಡ್ಡ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳು

1. ಅಂಶಗಳನ್ನು ಮರುಹೊಂದಿಸುವಾಗ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಚಿಹ್ನೆಯನ್ನು ಬದಲಾಯಿಸುತ್ತದೆ, ಅಂದರೆ. ಮತ್ತು xb =(b xa) (Fig. 19 ನೋಡಿ).

ವೆಕ್ಟರ್‌ಗಳು a xb ಮತ್ತು b xa ಕಾಲಿನಿಯರ್ ಆಗಿರುತ್ತವೆ, ಒಂದೇ ಮಾಡ್ಯೂಲ್‌ಗಳನ್ನು ಹೊಂದಿರುತ್ತವೆ (ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವು ಬದಲಾಗದೆ ಉಳಿಯುತ್ತದೆ), ಆದರೆ ವಿರುದ್ಧವಾಗಿ ನಿರ್ದೇಶಿಸಲಾಗುತ್ತದೆ (ಟ್ರಿಪಲ್ಸ್ a, b, a xb ಮತ್ತು a, b, b x a ವಿರುದ್ಧ ದೃಷ್ಟಿಕೋನ). ಅದು axb = -(ಬಿ xa).

2. ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಸ್ಕೇಲಾರ್ ಅಂಶಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಸಂಯೋಜಿತ ಗುಣವನ್ನು ಹೊಂದಿದೆ, ಅಂದರೆ l (a xb) = (l a) x b = a x (l b).

l >0 ಅನ್ನು ಅನುಮತಿಸಿ. ವೆಕ್ಟರ್ ಎಲ್ (ಎ xb) ಎ ಮತ್ತು ಬಿ ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ. ವೆಕ್ಟರ್ ( ಎಲ್ a)x ಬಿ a ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ ಬಿ(ವೆಕ್ಟರ್‌ಗಳು a, ಎಲ್ಆದರೆ ಅದೇ ವಿಮಾನದಲ್ಲಿ ಸುಳ್ಳು). ಇದರರ್ಥ ವಾಹಕಗಳು ಎಲ್(ಎ xb) ಮತ್ತು ( ಎಲ್ a)x ಬಿಕೊಲಿನಿಯರ್. ಅವರ ನಿರ್ದೇಶನಗಳು ಹೊಂದಿಕೆಯಾಗುತ್ತವೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಅವು ಒಂದೇ ಉದ್ದವನ್ನು ಹೊಂದಿವೆ:

ಅದಕ್ಕೇ ಎಲ್(ಎ xb)= ಎಲ್ಒಂದು xb. ಇದು ಇದೇ ರೀತಿಯಲ್ಲಿ ಸಾಬೀತಾಗಿದೆ ಎಲ್<0.

3. ಎರಡು ಶೂನ್ಯವಲ್ಲದ ವಾಹಕಗಳು a ಮತ್ತು ಬಿಅವುಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಶೂನ್ಯ ವೆಕ್ಟರ್‌ಗೆ ಸಮನಾಗಿದ್ದರೆ ಮತ್ತು ಮಾತ್ರ ಕೋಲಿನಿಯರ್ ಆಗಿರುತ್ತವೆ, ಅಂದರೆ a ||b<=>ಮತ್ತು xb =0.

ನಿರ್ದಿಷ್ಟವಾಗಿ, i *i =j *j =k *k =0 .

4. ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ವಿತರಣಾ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿದೆ:

(a+b) xc = a xc + ಬಿ xs.

ಪುರಾವೆ ಇಲ್ಲದೇ ಒಪ್ಪಿಕೊಳ್ಳುತ್ತೇವೆ.

7.3 ನಿರ್ದೇಶಾಂಕಗಳ ವಿಷಯದಲ್ಲಿ ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ವ್ಯಕ್ತಪಡಿಸುವುದು

ನಾವು ವೆಕ್ಟರ್‌ಗಳ ಅಡ್ಡ ಉತ್ಪನ್ನ ಕೋಷ್ಟಕವನ್ನು ಬಳಸುತ್ತೇವೆ i, ಜಮತ್ತು ಕೆ:

ಮೊದಲ ವೆಕ್ಟರ್‌ನಿಂದ ಎರಡನೆಯದಕ್ಕೆ ಕಡಿಮೆ ಮಾರ್ಗದ ದಿಕ್ಕು ಬಾಣದ ದಿಕ್ಕಿನೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾದರೆ, ಉತ್ಪನ್ನವು ಮೂರನೇ ವೆಕ್ಟರ್‌ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ; ಅದು ಹೊಂದಿಕೆಯಾಗದಿದ್ದರೆ, ಮೂರನೇ ವೆಕ್ಟರ್ ಅನ್ನು ಮೈನಸ್ ಚಿಹ್ನೆಯೊಂದಿಗೆ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ.

ಎರಡು ವೆಕ್ಟರ್‌ಗಳನ್ನು a =a x i +a y ನೀಡಲಿ ಜ+a z ಕೆಮತ್ತು b =b x i+ಬಿ ವೈ ಜ+b z ಕೆ. ಈ ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಬಹುಪದೋಕ್ತಿಗಳಾಗಿ ಗುಣಿಸುವ ಮೂಲಕ ಕಂಡುಹಿಡಿಯೋಣ (ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳ ಪ್ರಕಾರ):

ಪರಿಣಾಮವಾಗಿ ಸೂತ್ರವನ್ನು ಇನ್ನಷ್ಟು ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಬರೆಯಬಹುದು:

ಸಮಾನತೆಯ ಬಲಭಾಗವು (7.1) ಮೊದಲ ಸಾಲಿನ ಅಂಶಗಳ ವಿಷಯದಲ್ಲಿ ಮೂರನೇ ಕ್ರಮಾಂಕದ ಡಿಟರ್ಮಿನಂಟ್‌ನ ವಿಸ್ತರಣೆಗೆ ಅನುಗುಣವಾಗಿರುವುದರಿಂದ ಸಮಾನತೆ (7.2) ನೆನಪಿಟ್ಟುಕೊಳ್ಳುವುದು ಸುಲಭ.

7.4 ಅಡ್ಡ ಉತ್ಪನ್ನದ ಕೆಲವು ಅಪ್ಲಿಕೇಶನ್‌ಗಳು

ವಾಹಕಗಳ ಕೋಲಿನಿಯರಿಟಿಯನ್ನು ಸ್ಥಾಪಿಸುವುದು

ಸಮಾನಾಂತರ ಚತುರ್ಭುಜ ಮತ್ತು ತ್ರಿಕೋನದ ಪ್ರದೇಶವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು

ವೆಕ್ಟರ್ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ ಎಮತ್ತು ಬಿ |ಎ xb | =|ಎ | * |b |sin g, ಅಂದರೆ S ಜೋಡಿಗಳು = |a x b |. ಮತ್ತು, ಆದ್ದರಿಂದ, D S =1/2|a x b |.

ಒಂದು ಹಂತದ ಬಗ್ಗೆ ಬಲದ ಕ್ಷಣದ ನಿರ್ಣಯ

A ಬಿಂದುವಿನಲ್ಲಿ ಬಲವನ್ನು ಅನ್ವಯಿಸೋಣ ಎಫ್ =ಎಬಿಹೋಗಲಿ ಬಿಡು ಬಗ್ಗೆ- ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಕೆಲವು ಪಾಯಿಂಟ್ (ಚಿತ್ರ 20 ನೋಡಿ).

ಎಂದು ಭೌತಶಾಸ್ತ್ರದಿಂದ ತಿಳಿದುಬರುತ್ತದೆ ಬಲದ ಕ್ಷಣ ಎಫ್ ಬಿಂದುವಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಬಗ್ಗೆವೆಕ್ಟರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಎಂ,ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದುಹೋಗುತ್ತದೆ ಬಗ್ಗೆಮತ್ತು:

1) ಬಿಂದುಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿ O, A, B;

2) ಸಂಖ್ಯಾತ್ಮಕವಾಗಿ ಪ್ರತಿ ತೋಳಿನ ಬಲದ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ

3) OA ಮತ್ತು A B ವಾಹಕಗಳೊಂದಿಗೆ ಬಲ ಟ್ರಿಪಲ್ ಅನ್ನು ರೂಪಿಸುತ್ತದೆ.

ಆದ್ದರಿಂದ, M = OA x F.

ರೇಖೀಯ ತಿರುಗುವಿಕೆಯ ವೇಗವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು

ವೇಗ vಕೋನೀಯ ವೇಗದೊಂದಿಗೆ ತಿರುಗುವ ಕಟ್ಟುನಿಟ್ಟಿನ ದೇಹದ ಬಿಂದು M ಡಬ್ಲ್ಯೂಸ್ಥಿರ ಅಕ್ಷದ ಸುತ್ತ, ಯೂಲರ್ನ ಸೂತ್ರದ ಮೂಲಕ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ v =w xr, ಅಲ್ಲಿ r =OM, ಅಲ್ಲಿ O ಅಕ್ಷದ ಕೆಲವು ಸ್ಥಿರ ಬಿಂದುವಾಗಿದೆ (ಚಿತ್ರ 21 ನೋಡಿ).

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಪರಿಕಲ್ಪನೆಯನ್ನು ನೀಡುವ ಮೊದಲು, ಮೂರು ಆಯಾಮದ ಜಾಗದಲ್ಲಿ ಒಂದು →, b →, c → ವೆಕ್ಟರ್‌ಗಳ ಆದೇಶದ ಟ್ರಿಪಲ್‌ನ ದೃಷ್ಟಿಕೋನದ ಪ್ರಶ್ನೆಗೆ ನಾವು ತಿರುಗೋಣ.

ಪ್ರಾರಂಭಿಸಲು, ಒಂದು ಬಿಂದುವಿನಿಂದ a → , b → , c → ವೆಕ್ಟರ್‌ಗಳನ್ನು ಪಕ್ಕಕ್ಕೆ ಇಡೋಣ. ಟ್ರಿಪಲ್ a → , b → , c → ನ ದೃಷ್ಟಿಕೋನವು ವೆಕ್ಟರ್ c → ನ ದಿಕ್ಕನ್ನು ಅವಲಂಬಿಸಿ ಬಲ ಅಥವಾ ಎಡವಾಗಿರಬಹುದು. ಟ್ರಿಪಲ್ a → , b → , c → ಪ್ರಕಾರವನ್ನು ವೆಕ್ಟರ್ c → ನ ಅಂತ್ಯದಿಂದ ವೆಕ್ಟರ್ a → ನಿಂದ b → ವರೆಗೆ ಕಡಿಮೆ ತಿರುವು ಮಾಡುವ ದಿಕ್ಕಿನಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.

ಚಿಕ್ಕದಾದ ತಿರುವು ಅಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿ ನಡೆಸಿದರೆ, ನಂತರ ವೆಕ್ಟರ್ಗಳ ಟ್ರಿಪಲ್ a → , b → , c → ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಬಲ, ಪ್ರದಕ್ಷಿಣಾಕಾರವಾಗಿದ್ದರೆ - ಬಿಟ್ಟರು.

ಮುಂದೆ, ಎರಡು ನಾನ್-ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳನ್ನು a → ಮತ್ತು b → ತೆಗೆದುಕೊಳ್ಳಿ. ನಾವು ನಂತರ A B → = a → ಮತ್ತು A C → = b → ಬಿಂದುವಿನಿಂದ ವೆಕ್ಟರ್‌ಗಳನ್ನು ರೂಪಿಸೋಣ. A B → ಮತ್ತು A C → ಎರಡಕ್ಕೂ ಏಕಕಾಲದಲ್ಲಿ ಲಂಬವಾಗಿರುವ ವೆಕ್ಟರ್ A D → = c → ಅನ್ನು ನಿರ್ಮಿಸೋಣ. ಹೀಗಾಗಿ, ವೆಕ್ಟರ್ ಅನ್ನು ನಿರ್ಮಿಸುವಾಗ A D → = c →, ನಾವು ಎರಡು ಕೆಲಸಗಳನ್ನು ಮಾಡಬಹುದು, ಅದಕ್ಕೆ ಒಂದು ದಿಕ್ಕನ್ನು ಅಥವಾ ವಿರುದ್ಧವಾಗಿ ನೀಡಬಹುದು (ಚಿತ್ರಣವನ್ನು ನೋಡಿ).

ನಾವು ಕಂಡುಕೊಂಡಂತೆ ವೆಕ್ಟರ್‌ನ ದಿಕ್ಕನ್ನು ಅವಲಂಬಿಸಿ a → , b → , c → ಆಫ್ ವೆಕ್ಟರ್‌ಗಳ ಆದೇಶದ ಟ್ರಿಪಲ್ ಬಲ ಅಥವಾ ಎಡವಾಗಿರಬಹುದು.

ಮೇಲಿನಿಂದ ನಾವು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಪರಿಚಯಿಸಬಹುದು. ಮೂರು ಆಯಾಮದ ಜಾಗದ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಎರಡು ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಈ ವ್ಯಾಖ್ಯಾನವನ್ನು ನೀಡಲಾಗಿದೆ.

ವ್ಯಾಖ್ಯಾನ 1

a → ಮತ್ತು b → ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ ಮೂರು ಆಯಾಮದ ಜಾಗದ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಅಂತಹ ವೆಕ್ಟರ್ ಅನ್ನು ನಾವು ಕರೆಯುತ್ತೇವೆ:

• a → ಮತ್ತು b → ವಾಹಕಗಳು ಕಾಲಿನಿಯರ್ ಆಗಿದ್ದರೆ, ಅದು ಶೂನ್ಯವಾಗಿರುತ್ತದೆ;
• ಇದು ವೆಕ್ಟರ್ ಎ → ಮತ್ತು ವೆಕ್ಟರ್ ಬಿ → ಎರಡಕ್ಕೂ ಲಂಬವಾಗಿರುತ್ತದೆ, ಅಂದರೆ. ∠ a → c → = ∠ b → c → = π 2 ;
• ಅದರ ಉದ್ದವನ್ನು ಸೂತ್ರದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ: c → = a → · b → · sin ∠ a → , b → ;
• ವೆಕ್ಟರ್‌ಗಳ ಟ್ರಿಪಲ್ a → , b → , c → ನೀಡಿದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಂತೆಯೇ ಅದೇ ದೃಷ್ಟಿಕೋನವನ್ನು ಹೊಂದಿದೆ.

ವಾಹಕಗಳ a → ಮತ್ತು b → ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಈ ಕೆಳಗಿನ ಸಂಕೇತಗಳನ್ನು ಹೊಂದಿದೆ: a → × b →.

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ನಿರ್ದೇಶಾಂಕಗಳು

ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಯಾವುದೇ ವೆಕ್ಟರ್ ಕೆಲವು ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿರುವುದರಿಂದ, ನಾವು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಎರಡನೇ ವ್ಯಾಖ್ಯಾನವನ್ನು ಪರಿಚಯಿಸಬಹುದು, ಇದು ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದಿಷ್ಟ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಅದರ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಮಗೆ ಅನುಮತಿಸುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ 2

ಮೂರು ಆಯಾಮದ ಜಾಗದ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ a → = (a x ; a y ; a z) ಮತ್ತು b → = (b x ; b y ; b z) ವೆಕ್ಟರ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , ಅಲ್ಲಿ i → ಸಹಭಾಗಗಳು, j → , j → ಗಳು

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಮೂರನೇ ಕ್ರಮಾಂಕದ ಚೌಕದ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವಾಗಿ ಪ್ರತಿನಿಧಿಸಬಹುದು, ಅಲ್ಲಿ ಮೊದಲ ಸಾಲಿನಲ್ಲಿ ವೆಕ್ಟರ್ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ i → , j → , k → , ಎರಡನೇ ಸಾಲು ವೆಕ್ಟರ್ a → , ಮತ್ತು ಮೂರನೇ ಸಾಲುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ ನಿರ್ದಿಷ್ಟ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ವೆಕ್ಟರ್ b → ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಒಳಗೊಂಡಿದೆ, ಇದು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ: c → = a → × b → = i → j → k → a x a y a z b z b x b y b

ಈ ನಿರ್ಣಾಯಕವನ್ನು ಮೊದಲ ಸಾಲಿನ ಅಂಶಗಳಾಗಿ ವಿಸ್ತರಿಸುವುದರಿಂದ, ನಾವು ಸಮಾನತೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · ix → a z · a z - b b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

ಅಡ್ಡ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳು

ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿನ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಮ್ಯಾಟ್ರಿಕ್ಸ್ c → = a → × b → = i → j → k → a x a y a z b x b y b z , ನಂತರ ಆಧಾರದ ಮೇಲೆ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ ಎಂದು ತಿಳಿದಿದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಡಿಟರ್ಮಿನಂಟ್ನ ಗುಣಲಕ್ಷಣಗಳುಕೆಳಗಿನವುಗಳನ್ನು ಪ್ರದರ್ಶಿಸಲಾಗುತ್ತದೆ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳು:

1. ಆಂಟಿಕಾಮ್ಯುಟಾಟಿವಿಟಿ a → × b → = - b → × a → ;
2. ವಿತರಣೆ a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → ಅಥವಾ a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. ಸಹಭಾಗಿತ್ವ λ a → × b → = λ a → × b → ಅಥವಾ a → × (λ b →) = λ a → × b →, ಇಲ್ಲಿ λ ಅನಿಯಂತ್ರಿತ ನೈಜ ಸಂಖ್ಯೆ.

ಈ ಗುಣಲಕ್ಷಣಗಳು ಸರಳ ಪುರಾವೆಗಳನ್ನು ಹೊಂದಿವೆ.

ಉದಾಹರಣೆಯಾಗಿ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಆಂಟಿಕಮ್ಯುಟೇಟಿವ್ ಆಸ್ತಿಯನ್ನು ನಾವು ಸಾಬೀತುಪಡಿಸಬಹುದು.

ಆಂಟಿಕಮ್ಯುಟಾಟಿವಿಟಿಯ ಪುರಾವೆ

ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ, a → × b → = i → j → k → a x a y a z b x b y b z ಮತ್ತು b → × a → = i → j → k → b x b y b z a x a y a z. ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ಎರಡು ಸಾಲುಗಳನ್ನು ಬದಲಾಯಿಸಿದರೆ, ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ನ ನಿರ್ಣಾಯಕ ಮೌಲ್ಯವು ವಿರುದ್ಧವಾಗಿ ಬದಲಾಗಬೇಕು, ಆದ್ದರಿಂದ, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k z - b → × a → , ಇದು ಮತ್ತು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಆಂಟಿಕಾಮ್ಯುಟೇಟಿವ್ ಎಂದು ಸಾಬೀತುಪಡಿಸುತ್ತದೆ.

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ - ಉದಾಹರಣೆಗಳು ಮತ್ತು ಪರಿಹಾರಗಳು

ಹೆಚ್ಚಿನ ಸಂದರ್ಭಗಳಲ್ಲಿ, ಮೂರು ರೀತಿಯ ಸಮಸ್ಯೆಗಳಿವೆ.

ಮೊದಲ ವಿಧದ ಸಮಸ್ಯೆಗಳಲ್ಲಿ, ಎರಡು ವೆಕ್ಟರ್ಗಳ ಉದ್ದಗಳು ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ನೀಡಲಾಗುತ್ತದೆ, ಮತ್ತು ನೀವು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಬಳಸಿ c → = a → · b → · sin ∠ a → , b → .

ಉದಾಹರಣೆ 1

ನಿಮಗೆ a → = 3, b → = 5, ∠ a →, b → = π 4 ತಿಳಿದಿದ್ದರೆ ವಾಹಕಗಳ a → ಮತ್ತು b → ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.

ಪರಿಹಾರ

ವಾಹಕಗಳ a → ಮತ್ತು b → ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ನಿರ್ಧರಿಸುವ ಮೂಲಕ, ನಾವು ಈ ಸಮಸ್ಯೆಯನ್ನು ಪರಿಹರಿಸುತ್ತೇವೆ: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2

ಉತ್ತರ: 15 2 2 .

ಎರಡನೇ ವಿಧದ ಸಮಸ್ಯೆಗಳು ವೆಕ್ಟರ್ಗಳ ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ಸಂಪರ್ಕವನ್ನು ಹೊಂದಿವೆ, ಅವುಗಳಲ್ಲಿ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ, ಅದರ ಉದ್ದ, ಇತ್ಯಾದಿ. ನೀಡಿರುವ ವೆಕ್ಟರ್‌ಗಳ ತಿಳಿದಿರುವ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ ಹುಡುಕಲಾಗುತ್ತದೆ a → = (a x; a y; a z) ಮತ್ತು b → = (b x ; b y ; b z) .

ಈ ರೀತಿಯ ಸಮಸ್ಯೆಗೆ, ನೀವು ಬಹಳಷ್ಟು ಕಾರ್ಯ ಆಯ್ಕೆಗಳನ್ನು ಪರಿಹರಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, a → ಮತ್ತು b → ವಾಹಕಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಸೂಚಿಸಲಾಗುವುದಿಲ್ಲ, ಆದರೆ ರೂಪದ ನಿರ್ದೇಶಾಂಕ ವಾಹಕಗಳಾಗಿ ಅವುಗಳ ವಿಸ್ತರಣೆಗಳು b → = b x · i → + b y · j → + b z · k → ಮತ್ತು c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, ಅಥವಾ ವೆಕ್ಟರ್‌ಗಳು a → ಮತ್ತು ಬಿ → ಗಳ ಸಹಭಾಗಿತ್ವದಿಂದ ಪ್ರಾರಂಭಿಸಬಹುದು ಮತ್ತು ಅಂತಿಮ ಬಿಂದುಗಳು.

ಕೆಳಗಿನ ಉದಾಹರಣೆಗಳನ್ನು ಪರಿಗಣಿಸಿ.

ಉದಾಹರಣೆ 2

ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಎರಡು ವಾಹಕಗಳನ್ನು ನೀಡಲಾಗುತ್ತದೆ: a → = (2; 1; - 3), b → = (0; - 1; 1). ಅವರ ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ಹುಡುಕಿ.

ಪರಿಹಾರ

ಎರಡನೇ ವ್ಯಾಖ್ಯಾನದ ಮೂಲಕ, ನೀಡಿರುವ ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + (- 3) · 0 - 2 · 1) · j → + (2 · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .

ನಾವು ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ನಿರ್ಣಾಯಕ ಮೂಲಕ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಬರೆದರೆ, ಈ ಉದಾಹರಣೆಯ ಪರಿಹಾರವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 -1 -1 1 = - 2 i → - 2 j → - 2 k → .

ಉತ್ತರ: a → × b → = - 2 i → - 2 j → - 2 k → .

ಉದಾಹರಣೆ 3

ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ i → - j → ಮತ್ತು i → + j → + k →, ಇಲ್ಲಿ i →, j →, k → ಇವುಗಳು ಆಯತಾಕಾರದ ಕಾರ್ಟೀಸಿಯನ್ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯ ಘಟಕ ವಾಹಕಗಳಾಗಿವೆ.

ಪರಿಹಾರ

ಮೊದಲಿಗೆ, ನೀಡಿರುವ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ನೀಡಲಾದ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯೋಣ i → - j → × i → + j → + k →.

i → - j → ಮತ್ತು i → + j → + k → ವಾಹಕಗಳು ಕ್ರಮವಾಗಿ (1; - 1; 0) ಮತ್ತು (1; 1; 1) ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿವೆ ಎಂದು ತಿಳಿದಿದೆ. ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ನಿರ್ಣಾಯಕವನ್ನು ಬಳಸಿಕೊಂಡು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ, ನಂತರ ನಾವು i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

ಆದ್ದರಿಂದ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ i → - j → × i → + j → + k → ನೀಡಿರುವ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು (- 1 ; - 1 ; 2) ಹೊಂದಿದೆ.

ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ (ವೆಕ್ಟರ್‌ನ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯುವ ವಿಭಾಗವನ್ನು ನೋಡಿ): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.

ಉತ್ತರ: i → - j → × i → + j → + k → = 6 . .

ಉದಾಹರಣೆ 4

ಆಯತಾಕಾರದ ಕಾರ್ಟೇಶಿಯನ್ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಮೂರು ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) ನೀಡಲಾಗುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ A B → ಮತ್ತು A C → ಗೆ ಲಂಬವಾಗಿರುವ ಕೆಲವು ವೆಕ್ಟರ್ ಅನ್ನು ಹುಡುಕಿ.

ಪರಿಹಾರ

ವೆಕ್ಟರ್‌ಗಳು A B → ಮತ್ತು A C → ಅನುಕ್ರಮವಾಗಿ ಕೆಳಗಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು (- 1 ; 2 ; 2) ಮತ್ತು (0 ; 4 ; 1) ಹೊಂದಿವೆ. A B → ಮತ್ತು A C → ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಕಂಡುಹಿಡಿದ ನಂತರ, ಇದು A B → ಮತ್ತು A C → ಎರಡಕ್ಕೂ ವ್ಯಾಖ್ಯಾನದ ಮೂಲಕ ಲಂಬವಾದ ವೆಕ್ಟರ್ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ, ಅಂದರೆ, ಇದು ನಮ್ಮ ಸಮಸ್ಯೆಗೆ ಪರಿಹಾರವಾಗಿದೆ. ಅದನ್ನು ಕಂಡುಹಿಡಿಯೋಣ A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

ಉತ್ತರ: - 6 i → + j → - 4 k → . - ಲಂಬ ವಾಹಕಗಳಲ್ಲಿ ಒಂದು.

ಮೂರನೇ ವಿಧದ ತೊಂದರೆಗಳು ವೆಕ್ಟರ್ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಬಳಸುವುದರ ಮೇಲೆ ಕೇಂದ್ರೀಕೃತವಾಗಿವೆ. ಅದನ್ನು ಅನ್ವಯಿಸಿದ ನಂತರ, ನಾವು ನೀಡಿದ ಸಮಸ್ಯೆಗೆ ಪರಿಹಾರವನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ಉದಾಹರಣೆ 5

ವಾಹಕಗಳು a → ಮತ್ತು b → ಲಂಬವಾಗಿರುತ್ತವೆ ಮತ್ತು ಅವುಗಳ ಉದ್ದಗಳು ಕ್ರಮವಾಗಿ 3 ಮತ್ತು 4 ಆಗಿರುತ್ತವೆ. ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವನ್ನು ಹುಡುಕಿ 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .

ಪರಿಹಾರ

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ವಿತರಣಾ ಗುಣಲಕ್ಷಣದ ಮೂಲಕ, ನಾವು 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

ಅಸೋಸಿಯೇಟಿವಿಟಿಯ ಆಸ್ತಿಯ ಮೂಲಕ, ನಾವು ಕೊನೆಯ ಅಭಿವ್ಯಕ್ತಿಯಲ್ಲಿ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನಗಳ ಚಿಹ್ನೆಯಿಂದ ಸಂಖ್ಯಾತ್ಮಕ ಗುಣಾಂಕಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತೇವೆ: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನಗಳು a → × a → ಮತ್ತು b → × b → 0 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಏಕೆಂದರೆ a → × a → = a → · a → · sin 0 = 0 ಮತ್ತು b → × b → = b → · b → · sin 0 = 0, ನಂತರ 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → .

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಆಂಟಿಕಾಮ್ಯುಟಾಟಿವಿಟಿಯಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × ಬಿ → . .

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಬಳಸಿಕೊಂಡು, ನಾವು ಸಮಾನತೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

ಷರತ್ತಿನ ಪ್ರಕಾರ, a → ಮತ್ತು b → ವಾಹಕಗಳು ಲಂಬವಾಗಿರುತ್ತವೆ, ಅಂದರೆ, ಅವುಗಳ ನಡುವಿನ ಕೋನವು π 2 ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಈಗ ಉಳಿದಿರುವುದು ಕಂಡುಬರುವ ಮೌಲ್ಯಗಳನ್ನು ಸೂಕ್ತವಾದ ಸೂತ್ರಗಳಾಗಿ ಬದಲಿಸುವುದು: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · ಪಾಪ (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .

ಉತ್ತರ: 3 a → - b → × a → - 2 b → = 60.

ವ್ಯಾಖ್ಯಾನದ ಪ್ರಕಾರ ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವು a → × b → = a → · b → · sin ∠ a → , b → . ತ್ರಿಕೋನದ ವಿಸ್ತೀರ್ಣವು ಅದರ ಎರಡು ಬದಿಗಳ ಉದ್ದದ ಅರ್ಧದಷ್ಟು ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಎಂದು ಈಗಾಗಲೇ ತಿಳಿದಿರುವುದರಿಂದ (ಶಾಲಾ ಕೋರ್ಸ್‌ನಿಂದ) ಈ ಬದಿಗಳ ನಡುವಿನ ಕೋನದ ಸೈನ್‌ನಿಂದ ಗುಣಿಸಲಾಗುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಉದ್ದವು ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ವಿಸ್ತೀರ್ಣಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ - ದ್ವಿಗುಣಗೊಂಡ ತ್ರಿಕೋನ, ಅವುಗಳೆಂದರೆ ವಾಹಕಗಳ ರೂಪದಲ್ಲಿ ಬದಿಗಳ ಉತ್ಪನ್ನ a → ಮತ್ತು b →, ಒಂದು ಬಿಂದುವಿನಿಂದ, ಸೈನ್ ಮೂಲಕ ಇಡಲಾಗಿದೆ ಅವುಗಳ ನಡುವಿನ ಕೋನವು ಪಾಪ ∠ a →, b →.

ಇದು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಜ್ಯಾಮಿತೀಯ ಅರ್ಥವಾಗಿದೆ.

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಭೌತಿಕ ಅರ್ಥ

ಮೆಕ್ಯಾನಿಕ್ಸ್ನಲ್ಲಿ, ಭೌತಶಾಸ್ತ್ರದ ಶಾಖೆಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನಕ್ಕೆ ಧನ್ಯವಾದಗಳು, ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ಒಂದು ಬಿಂದುವಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಬಲದ ಕ್ಷಣವನ್ನು ನೀವು ನಿರ್ಧರಿಸಬಹುದು.

ವ್ಯಾಖ್ಯಾನ 3

A ಬಿಂದುವಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ, B ಬಿಂದುವಿಗೆ F → ಅನ್ನು ಅನ್ವಯಿಸುವ ಬಲದ ಕ್ಷಣದಿಂದ, ನಾವು ಈ ಕೆಳಗಿನ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ A B → × F → ಅನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುತ್ತೇವೆ.

ನೀವು ಪಠ್ಯದಲ್ಲಿ ದೋಷವನ್ನು ಗಮನಿಸಿದರೆ, ದಯವಿಟ್ಟು ಅದನ್ನು ಹೈಲೈಟ್ ಮಾಡಿ ಮತ್ತು Ctrl+Enter ಒತ್ತಿರಿ

ವಾಹಕಗಳ ನಡುವಿನ ಕೋನ

ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಪರಿಕಲ್ಪನೆಯನ್ನು ನಾವು ಪರಿಚಯಿಸಲು, ಈ ವಾಹಕಗಳ ನಡುವಿನ ಕೋನದಂತಹ ಪರಿಕಲ್ಪನೆಯನ್ನು ನಾವು ಮೊದಲು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬೇಕು.

ನಮಗೆ ಎರಡು ವೆಕ್ಟರ್‌ಗಳನ್ನು ನೀಡೋಣ $\overline(α)$ ಮತ್ತು $\overline(β)$. ನಾವು ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ $O$ ಬಿಂದುವನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳನ್ನು $\overline(α)=\overline(OA)$ ಮತ್ತು $\overline(β)=\overline(OB)$, ನಂತರ ಕೋನ $AOB$ ಈ ವಾಹಕಗಳ ನಡುವಿನ ಕೋನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ (ಚಿತ್ರ 1).

ಸಂಕೇತ: $∠(\overline(α),\overline(β))$

ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಪರಿಕಲ್ಪನೆ ಮತ್ತು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ

ವ್ಯಾಖ್ಯಾನ 1

ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ನೀಡಲಾದ ಎರಡೂ ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ವೆಕ್ಟರ್ ಆಗಿದೆ, ಮತ್ತು ಅದರ ಉದ್ದವು ಈ ವೆಕ್ಟರ್‌ಗಳ ನಡುವಿನ ಕೋನದ ಸೈನ್‌ನೊಂದಿಗೆ ಈ ವೆಕ್ಟರ್‌ಗಳ ಉದ್ದದ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ಎರಡು ಆರಂಭಿಕ ಪದಗಳೊಂದಿಗೆ ಈ ವೆಕ್ಟರ್ ಹೊಂದಿದೆ ಕಾರ್ಟೀಸಿಯನ್ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಂತೆಯೇ ಅದೇ ದೃಷ್ಟಿಕೋನ.

ಸೂಚನೆ: $\overline(α)х\overline(β)$.

ಗಣಿತಶಾಸ್ತ್ರದಲ್ಲಿ ಇದು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

1. $|\overline(α)х\overline(β)|=|\overline(α)||\overline(β)|sin⁡∠(\overline(α),\overline(β))$
2. $\overline(α)х\overline(β)⊥\overline(α)$, $\overline(α)х\overline(β)⊥\overline(β)$
3. $(\ಓವರ್‌ಲೈನ್(α)x\ಓವರ್‌ಲೈನ್(β),\ಓವರ್‌ಲೈನ್(α),\ಓವರ್‌ಲೈನ್(β))$ ಮತ್ತು $(\ಓವರ್‌ಲೈನ್(i),\ಓವರ್‌ಲೈನ್(ಜೆ),\ಓವರ್‌ಲೈನ್(ಕೆ))$ ಅದೇ ಆಧಾರಿತ (ಚಿತ್ರ 2)

ನಿಸ್ಸಂಶಯವಾಗಿ, ವೆಕ್ಟರ್‌ಗಳ ಹೊರ ಉತ್ಪನ್ನವು ಎರಡು ಸಂದರ್ಭಗಳಲ್ಲಿ ಶೂನ್ಯ ವೆಕ್ಟರ್‌ಗೆ ಸಮನಾಗಿರುತ್ತದೆ:

1. ಒಂದು ಅಥವಾ ಎರಡೂ ವೆಕ್ಟರ್‌ಗಳ ಉದ್ದವು ಶೂನ್ಯವಾಗಿದ್ದರೆ.
2. ಈ ವಾಹಕಗಳ ನಡುವಿನ ಕೋನವು $180^\circ$ ಅಥವಾ $0^\circ$ ಗೆ ಸಮನಾಗಿದ್ದರೆ (ಈ ಸಂದರ್ಭದಲ್ಲಿ ಸೈನ್ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ).

ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಹೇಗೆ ಕಂಡುಬರುತ್ತದೆ ಎಂಬುದನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ನೋಡಲು, ಪರಿಹಾರಗಳ ಕೆಳಗಿನ ಉದಾಹರಣೆಗಳನ್ನು ಪರಿಗಣಿಸಿ.

ಉದಾಹರಣೆ 1

$\overline(δ)$ನ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ, ಇದು ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಫಲಿತಾಂಶವಾಗಿದೆ, ನಿರ್ದೇಶಾಂಕಗಳು $\overline(α)=(0,4,0)$ ಮತ್ತು $\overline(β) =(3,0,0)$.

ಪರಿಹಾರ.

ಕಾರ್ಟೀಸಿಯನ್ ನಿರ್ದೇಶಾಂಕ ಜಾಗದಲ್ಲಿ ಈ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಚಿತ್ರಿಸೋಣ (ಚಿತ್ರ 3):

ಚಿತ್ರ 3. ಕಾರ್ಟೀಸಿಯನ್ ನಿರ್ದೇಶಾಂಕ ಜಾಗದಲ್ಲಿ ವೆಕ್ಟರ್‌ಗಳು. ಲೇಖಕ24 - ವಿದ್ಯಾರ್ಥಿ ಕೃತಿಗಳ ಆನ್‌ಲೈನ್ ವಿನಿಮಯ

ಈ ವೆಕ್ಟರ್‌ಗಳು ಕ್ರಮವಾಗಿ $Ox$ ಮತ್ತು $Oy$ ಅಕ್ಷಗಳ ಮೇಲೆ ಇರುವುದನ್ನು ನಾವು ನೋಡುತ್ತೇವೆ. ಆದ್ದರಿಂದ, ಅವುಗಳ ನಡುವಿನ ಕೋನವು $90^\circ$ ಆಗಿರುತ್ತದೆ. ಈ ವೆಕ್ಟರ್‌ಗಳ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

$|\overline(α)|=\sqrt(0+16+0)=4$

$|\overline(β)|=\sqrt(9+0+0)=3$

ನಂತರ, ವ್ಯಾಖ್ಯಾನ 1 ರ ಮೂಲಕ, ನಾವು ಮಾಡ್ಯೂಲ್ $|\overline(δ)|$ ಅನ್ನು ಪಡೆಯುತ್ತೇವೆ

$|\overline(δ)|=|\overline(α)||\overline(β)|sin90^\circ=4\cdot 3\cdot 1=12$

ಉತ್ತರ: $12$.

ವೆಕ್ಟರ್ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು

ವ್ಯಾಖ್ಯಾನ 1 ತಕ್ಷಣವೇ ಎರಡು ವೆಕ್ಟರ್‌ಗಳಿಗೆ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಕಂಡುಹಿಡಿಯುವ ವಿಧಾನವನ್ನು ಸೂಚಿಸುತ್ತದೆ. ವೆಕ್ಟರ್, ಅದರ ಮೌಲ್ಯದ ಜೊತೆಗೆ, ದಿಕ್ಕನ್ನು ಸಹ ಹೊಂದಿರುವುದರಿಂದ, ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣವನ್ನು ಬಳಸಿ ಮಾತ್ರ ಅದನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅಸಾಧ್ಯ. ಆದರೆ ಇದರ ಜೊತೆಗೆ, ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬಳಸಿಕೊಂಡು ನಮಗೆ ನೀಡಿದ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವ ಮಾರ್ಗವೂ ಇದೆ.

ನಮಗೆ $\ಓವರ್‌ಲೈನ್(α)$ ಮತ್ತು $\ಓವರ್‌ಲೈನ್(β)$ ವಾಹಕಗಳನ್ನು ನೀಡೋಣ, ಇದು ಕ್ರಮವಾಗಿ $(α_1,α_2,α_3)$ ಮತ್ತು $(β_1,β_2,β_3)$ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ನಂತರ ಅಡ್ಡ ಉತ್ಪನ್ನದ ವೆಕ್ಟರ್ (ಅವುಗಳೆಂದರೆ ಅದರ ನಿರ್ದೇಶಾಂಕಗಳು) ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಕಂಡುಹಿಡಿಯಬಹುದು:

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\α_1&α_2&α_3\\β_1&β_2&β_3\end(vmatrix)$

ಇಲ್ಲದಿದ್ದರೆ, ನಿರ್ಣಾಯಕವನ್ನು ವಿಸ್ತರಿಸುವುದರಿಂದ, ನಾವು ಈ ಕೆಳಗಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ

$\overline(α)х\overline(β)=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

ಉದಾಹರಣೆ 2

$(0,3,3)$ ಮತ್ತು $(-1,2,6)$ ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ $\overline(α)$ ಮತ್ತು $\overline(β)$ ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ವೆಕ್ಟರ್ ಅನ್ನು ಹುಡುಕಿ.

ಪರಿಹಾರ.

ಮೇಲೆ ನೀಡಲಾದ ಸೂತ್ರವನ್ನು ಬಳಸೋಣ. ನಾವು ಪಡೆಯುತ್ತೇವೆ

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\0&3&3\\-1&2&6\end(vmatrix)=(18 -6)\ಓವರ್‌ಲೈನ್ (ಐ)-(0+3)\ಓವರ್‌ಲೈನ್(ಜೆ)+(0+3)\ಓವರ್‌ಲೈನ್(ಕೆ)=12\ಓವರ್‌ಲೈನ್(ಐ)-3\ಓವರ್‌ಲೈನ್(ಜೆ)+3\ಓವರ್‌ಲೈನ್(ಕೆ )=(12,-3,3)$

ಉತ್ತರ: $(12,-3,3)$.

ವಾಹಕಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಗುಣಲಕ್ಷಣಗಳು

ಅನಿಯಂತ್ರಿತ ಮಿಶ್ರಿತ ಮೂರು ವೆಕ್ಟರ್‌ಗಳಿಗೆ $\ಓವರ್‌ಲೈನ್(α)$, $\ಓವರ್‌ಲೈನ್(β)$ ಮತ್ತು $\ಓವರ್‌ಲೈನ್(γ)$, ಹಾಗೆಯೇ $r∈R$, ಈ ಕೆಳಗಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹಿಡಿದಿಟ್ಟುಕೊಳ್ಳುತ್ತದೆ:

ಉದಾಹರಣೆ 3

$(3,0,0)$, $(0,0,0)$, $(0,8,0)$ ಮತ್ತು $(3,8,0) ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಹೊಂದಿರುವ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವನ್ನು ಹುಡುಕಿ $.

ಪರಿಹಾರ.

ಮೊದಲಿಗೆ, ಈ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜವನ್ನು ನಿರ್ದೇಶಾಂಕ ಜಾಗದಲ್ಲಿ ಚಿತ್ರಿಸೋಣ (ಚಿತ್ರ 5):

ಚಿತ್ರ 5. ನಿರ್ದೇಶಾಂಕ ಜಾಗದಲ್ಲಿ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜ. ಲೇಖಕ24 - ವಿದ್ಯಾರ್ಥಿ ಕೃತಿಗಳ ಆನ್‌ಲೈನ್ ವಿನಿಮಯ

ಈ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಎರಡು ಬದಿಗಳನ್ನು $\overline(α)=(3,0,0)$ ಮತ್ತು $\overline(β)=(0,8,0)$ ನಿರ್ದೇಶಾಂಕಗಳೊಂದಿಗೆ ಕಾಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಬಳಸಿ ನಿರ್ಮಿಸಲಾಗಿದೆ ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ. ನಾಲ್ಕನೇ ಆಸ್ತಿಯನ್ನು ಬಳಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:

$S=|\overline(α)х\overline(β)|$

ವೆಕ್ಟರ್ $\overline(α)х\overline(β)$ ಅನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

$\overline(α)х\overline(β)=\begin(vmatrix)\overline(i)&\overline(j)&\overline(k)\\3&0&0\\0&8&0\end(vmatrix)=0\overline (i)-0\overline(j)+24\overline(k)=(0,0,24)$

ಆದ್ದರಿಂದ

$S=|\overline(α)х\overline(β)|=\sqrt(0+0+24^2)=24$

ನಿಸ್ಸಂಶಯವಾಗಿ, ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಸಂದರ್ಭದಲ್ಲಿ, ವೆಕ್ಟರ್‌ಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುವ ಕ್ರಮವು ಮುಖ್ಯವಾಗಿದೆ, ಮೇಲಾಗಿ,

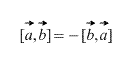
ಅಲ್ಲದೆ, ಯಾವುದೇ ಸ್ಕೇಲಾರ್ ಫ್ಯಾಕ್ಟರ್ ಕೆ (ಸಂಖ್ಯೆ) ಗೆ ಈ ಕೆಳಗಿನವು ನಿಜವೆಂದು ವ್ಯಾಖ್ಯಾನದಿಂದ ನೇರವಾಗಿ ಅನುಸರಿಸುತ್ತದೆ:

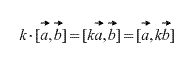
ಕೊಲಿನಿಯರ್ ವೆಕ್ಟರ್‌ಗಳ ಅಡ್ಡ ಉತ್ಪನ್ನವು ಶೂನ್ಯ ವೆಕ್ಟರ್‌ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಇದಲ್ಲದೆ, ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಅಡ್ಡ ಉತ್ಪನ್ನವು ಕಾಲಿನಿಯರ್ ಆಗಿದ್ದರೆ ಮತ್ತು ಮಾತ್ರ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ. (ಅವುಗಳಲ್ಲಿ ಒಂದು ಶೂನ್ಯ ವೆಕ್ಟರ್ ಆಗಿದ್ದರೆ, ಶೂನ್ಯ ವೆಕ್ಟರ್ ವ್ಯಾಖ್ಯಾನದಿಂದ ಯಾವುದೇ ವೆಕ್ಟರ್‌ಗೆ ಕೊಲಿನಿಯರ್ ಆಗಿದೆ ಎಂಬುದನ್ನು ನೆನಪಿಟ್ಟುಕೊಳ್ಳುವುದು ಅವಶ್ಯಕ).

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಹೊಂದಿದೆ ವಿತರಣಾ ಆಸ್ತಿ, ಅದು

ವೆಕ್ಟರ್‌ಗಳ ನಿರ್ದೇಶಾಂಕಗಳ ಮೂಲಕ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ವ್ಯಕ್ತಪಡಿಸುವುದು.

ಎರಡು ವಾಹಕಗಳನ್ನು ನೀಡೋಣ

(ವೆಕ್ಟರ್‌ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಅದರ ಪ್ರಾರಂಭ ಮತ್ತು ಅಂತ್ಯದ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಹೇಗೆ ಕಂಡುಹಿಡಿಯುವುದು - ವೆಕ್ಟರ್‌ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನ, ಐಟಂ ಡಾಟ್ ಉತ್ಪನ್ನದ ಪರ್ಯಾಯ ವ್ಯಾಖ್ಯಾನ ಅಥವಾ ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ನಿರ್ದಿಷ್ಟಪಡಿಸಿದ ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಲೇಖನವನ್ನು ನೋಡಿ.)

ನಿಮಗೆ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ ಏಕೆ ಬೇಕು?

ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ಬಳಸಲು ಹಲವು ಮಾರ್ಗಗಳಿವೆ, ಉದಾಹರಣೆಗೆ, ಮೇಲೆ ಬರೆದಂತೆ, ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಮೂಲಕ ಅವು ಕಾಲಿನಿಯರ್ ಎಂದು ನೀವು ಕಂಡುಹಿಡಿಯಬಹುದು.

ಅಥವಾ ಈ ವೆಕ್ಟರ್‌ಗಳಿಂದ ನಿರ್ಮಿಸಲಾದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಇದನ್ನು ಒಂದು ಮಾರ್ಗವಾಗಿ ಬಳಸಬಹುದು. ವ್ಯಾಖ್ಯಾನದ ಆಧಾರದ ಮೇಲೆ, ಪರಿಣಾಮವಾಗಿ ವೆಕ್ಟರ್ನ ಉದ್ದವು ನೀಡಿದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವಾಗಿದೆ.

ವಿದ್ಯುಚ್ಛಕ್ತಿ ಮತ್ತು ಕಾಂತೀಯತೆಯಲ್ಲಿಯೂ ಸಹ ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಅನ್ವಯಗಳಿವೆ.

ಆನ್‌ಲೈನ್ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನ ಕ್ಯಾಲ್ಕುಲೇಟರ್.

ಈ ಕ್ಯಾಲ್ಕುಲೇಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವನ್ನು ಕಂಡುಹಿಡಿಯಲು, ನೀವು ಮೊದಲ ಸಾಲಿನಲ್ಲಿ ಮೊದಲ ವೆಕ್ಟರ್‌ನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕ್ರಮವಾಗಿ ಮತ್ತು ಎರಡನೇ ಸಾಲಿನಲ್ಲಿ ಎರಡನೆಯದನ್ನು ನಮೂದಿಸಬೇಕಾಗುತ್ತದೆ. ವಾಹಕಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಅವುಗಳ ಆರಂಭ ಮತ್ತು ಅಂತ್ಯದ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಲೆಕ್ಕ ಹಾಕಬಹುದು (ಲೇಖನವನ್ನು ನೋಡಿ ವೆಕ್ಟರ್‌ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನ, ಐಟಂ ಡಾಟ್ ಉತ್ಪನ್ನದ ಪರ್ಯಾಯ ವ್ಯಾಖ್ಯಾನ, ಅಥವಾ ಅವುಗಳ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ನೀಡಲಾದ ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಡಾಟ್ ಉತ್ಪನ್ನವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು.)

ವೆಕ್ಟರ್ ಕಲಾಕೃತಿಎರಡು ಅಂಶಗಳಿಂದ ನಿರ್ಮಿಸಲಾದ ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿರುವ ಒಂದು ಸೂಡೊವೆಕ್ಟರ್ ಆಗಿದೆ, ಇದು ಮೂರು ಆಯಾಮದ ಯೂಕ್ಲಿಡಿಯನ್ ಜಾಗದಲ್ಲಿ ವೆಕ್ಟರ್‌ಗಳ ಮೇಲೆ ಬೈನರಿ ಕಾರ್ಯಾಚರಣೆ "ವೆಕ್ಟರ್ ಗುಣಾಕಾರ" ದ ಫಲಿತಾಂಶವಾಗಿದೆ. ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಕಮ್ಯುಟಾಟಿವಿಟಿ ಮತ್ತು ಅಸೋಸಿಯೇಟಿವಿಟಿ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿಲ್ಲ (ಇದು ಆಂಟಿಕಮ್ಯುಟೇಟಿವ್) ಮತ್ತು ವೆಕ್ಟರ್ಗಳ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನದಂತೆ, ವೆಕ್ಟರ್ ಆಗಿದೆ. ಅನೇಕ ಎಂಜಿನಿಯರಿಂಗ್ ಮತ್ತು ಭೌತಶಾಸ್ತ್ರದ ಅನ್ವಯಗಳಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಕೋನೀಯ ಆವೇಗ ಮತ್ತು ಲೊರೆಂಟ್ಜ್ ಬಲವನ್ನು ಗಣಿತೀಯವಾಗಿ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವಾಗಿ ಬರೆಯಲಾಗುತ್ತದೆ. ವಾಹಕಗಳ ಲಂಬತೆಯನ್ನು "ಅಳೆಯಲು" ಅಡ್ಡ ಉತ್ಪನ್ನವು ಉಪಯುಕ್ತವಾಗಿದೆ - ಎರಡು ವೆಕ್ಟರ್‌ಗಳ ಅಡ್ಡ ಉತ್ಪನ್ನದ ಮಾಡ್ಯುಲಸ್ ಲಂಬವಾಗಿದ್ದರೆ ಅವುಗಳ ಮಾಡ್ಯುಲಿಯ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳು ಸಮಾನಾಂತರ ಅಥವಾ ಆಂಟಿಪ್ಯಾರಲಲ್ ಆಗಿದ್ದರೆ ಶೂನ್ಯಕ್ಕೆ ಕಡಿಮೆಯಾಗುತ್ತದೆ.

ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ವಿಭಿನ್ನ ರೀತಿಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಬಹುದು, ಮತ್ತು ಸೈದ್ಧಾಂತಿಕವಾಗಿ, ಯಾವುದೇ ಆಯಾಮದ n ನ ಜಾಗದಲ್ಲಿ, n-1 ವೆಕ್ಟರ್‌ಗಳ ಉತ್ಪನ್ನವನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು, ಇದರಿಂದಾಗಿ ಅವುಗಳಿಗೆ ಲಂಬವಾಗಿರುವ ಏಕೈಕ ವೆಕ್ಟರ್ ಅನ್ನು ಪಡೆಯಬಹುದು. ಆದರೆ ಉತ್ಪನ್ನವು ವೆಕ್ಟರ್ ಫಲಿತಾಂಶಗಳೊಂದಿಗೆ ಕ್ಷುಲ್ಲಕವಲ್ಲದ ಬೈನರಿ ಉತ್ಪನ್ನಗಳಿಗೆ ಸೀಮಿತವಾಗಿದ್ದರೆ, ಸಾಂಪ್ರದಾಯಿಕ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವನ್ನು ಮೂರು ಆಯಾಮದ ಮತ್ತು ಏಳು ಆಯಾಮದ ಸ್ಥಳಗಳಲ್ಲಿ ಮಾತ್ರ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ. ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನದಂತೆ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಫಲಿತಾಂಶವು ಯೂಕ್ಲಿಡಿಯನ್ ಜಾಗದ ಮೆಟ್ರಿಕ್ ಅನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ಮೂರು ಆಯಾಮದ ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನ ವೆಕ್ಟರ್‌ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಸೂತ್ರಕ್ಕಿಂತ ಭಿನ್ನವಾಗಿ, ಅಡ್ಡ ಉತ್ಪನ್ನದ ಸೂತ್ರವು ಆಯತಾಕಾರದ ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯ ದೃಷ್ಟಿಕೋನವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ ಅಥವಾ ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಅದರ "ಚಿರಾಲಿಟಿ".

ವ್ಯಾಖ್ಯಾನ:
ಬಾಹ್ಯಾಕಾಶ R3 ನಲ್ಲಿ ವೆಕ್ಟರ್ a ಮತ್ತು ವೆಕ್ಟರ್ b ನ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಕೆಳಗಿನ ಅವಶ್ಯಕತೆಗಳನ್ನು ಪೂರೈಸುವ ವೆಕ್ಟರ್ c ಆಗಿದೆ:
ವೆಕ್ಟರ್ c ಯ ಉದ್ದವು ವೆಕ್ಟರ್‌ಗಳ ಉದ್ದಗಳ ಉತ್ಪನ್ನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ a ಮತ್ತು b ಮತ್ತು ಅವುಗಳ ನಡುವೆ φ ಕೋನದ ಸೈನ್:
|ಸಿ|=|ಎ||ಬಿ|ಸಿನ್ φ;
ವೆಕ್ಟರ್ ಸಿ ಪ್ರತಿಯೊಂದು ವೆಕ್ಟರ್ ಎ ಮತ್ತು ಬಿಗೆ ಆರ್ಥೋಗೋನಲ್ ಆಗಿದೆ;
ವೆಕ್ಟರ್ ಸಿ ಅನ್ನು ನಿರ್ದೇಶಿಸಲಾಗಿದೆ ಆದ್ದರಿಂದ ವೆಕ್ಟರ್‌ಗಳ ಟ್ರಿಪಲ್ ಎಬಿಸಿ ಬಲಗೈಯಾಗಿರುತ್ತದೆ;
ಸ್ಥಳ R7 ನ ಸಂದರ್ಭದಲ್ಲಿ, a, b, c ವೆಕ್ಟರ್‌ಗಳ ಟ್ರಿಪಲ್‌ನ ಸಹಭಾಗಿತ್ವದ ಅಗತ್ಯವಿದೆ.
ಹುದ್ದೆ:
c===a × b

ಅಕ್ಕಿ. 1. ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವು ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಮಾಡ್ಯುಲಸ್‌ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ

ಅಡ್ಡ ಉತ್ಪನ್ನದ ಜ್ಯಾಮಿತೀಯ ಗುಣಲಕ್ಷಣಗಳು:
ಎರಡು ಶೂನ್ಯವಲ್ಲದ ವೆಕ್ಟರ್‌ಗಳ ಕೋಲಿನಿಯರಿಟಿಗೆ ಅಗತ್ಯವಾದ ಮತ್ತು ಸಾಕಷ್ಟು ಸ್ಥಿತಿಯೆಂದರೆ ಅವುಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ಶೂನ್ಯಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಕ್ರಾಸ್ ಉತ್ಪನ್ನ ಮಾಡ್ಯೂಲ್ ಪ್ರದೇಶಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಎಸ್ವಾಹಕಗಳ ಮೇಲೆ ನಿರ್ಮಿಸಲಾದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜವನ್ನು ಸಾಮಾನ್ಯ ಮೂಲಕ್ಕೆ ಇಳಿಸಲಾಗಿದೆ ಎಮತ್ತು ಬಿ(ಚಿತ್ರ 1 ನೋಡಿ).

ಒಂದು ವೇಳೆ ಇ- ವೆಕ್ಟರ್‌ಗಳಿಗೆ ಆರ್ಥೋಗೋನಲ್ ಘಟಕ ವೆಕ್ಟರ್ ಎಮತ್ತು ಬಿಮತ್ತು ಮೂರು ಆದ್ದರಿಂದ ಆಯ್ಕೆ a,b,e- ಸರಿ, ಮತ್ತು ಎಸ್ಅವುಗಳ ಮೇಲೆ ನಿರ್ಮಿಸಲಾದ ಸಮಾನಾಂತರ ಚತುರ್ಭುಜದ ಪ್ರದೇಶವಾಗಿದೆ (ಸಾಮಾನ್ಯ ಮೂಲಕ್ಕೆ ಕಡಿಮೆಯಾಗಿದೆ), ನಂತರ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನದ ಸೂತ್ರವು ಮಾನ್ಯವಾಗಿರುತ್ತದೆ:
=ಎಸ್ ಇ

ಚಿತ್ರ.2. ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಮತ್ತು ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವನ್ನು ಬಳಸುವ ಸಮಾನಾಂತರ ಪೈಪ್‌ನ ಪರಿಮಾಣ; ಚುಕ್ಕೆಗಳ ರೇಖೆಗಳು ವೆಕ್ಟರ್ c ಯ ಪ್ರಕ್ಷೇಪಗಳನ್ನು a × b ಮತ್ತು ವೆಕ್ಟರ್ a b × c ಗೆ ತೋರಿಸುತ್ತವೆ, ಮೊದಲ ಹಂತವು ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು

ಒಂದು ವೇಳೆ ಸಿ- ಕೆಲವು ವೆಕ್ಟರ್, π - ಈ ವೆಕ್ಟರ್ ಹೊಂದಿರುವ ಯಾವುದೇ ವಿಮಾನ, ಇ- ಸಮತಲದಲ್ಲಿ ಮಲಗಿರುವ ಘಟಕ ವೆಕ್ಟರ್ π ಮತ್ತು ಆರ್ಥೋಗೋನಲ್ ಗೆ c,g- ಸಮತಲಕ್ಕೆ ಆರ್ಥೋಗೋನಲ್ ಘಟಕ ವೆಕ್ಟರ್ π ಮತ್ತು ವಾಹಕಗಳ ಟ್ರಿಪಲ್ ಅನ್ನು ನಿರ್ದೇಶಿಸಲಾಗಿದೆ ಇಸಿಜಿಸರಿ, ನಂತರ ವಿಮಾನದಲ್ಲಿ ಯಾವುದೇ ಸುಳ್ಳು π ವೆಕ್ಟರ್ ಎಸೂತ್ರವು ಸರಿಯಾಗಿದೆ:
=Pr e a |c|g
ಇಲ್ಲಿ Pr e a ಎಂಬುದು ವೆಕ್ಟರ್ e ನ ಪ್ರಕ್ಷೇಪಣವಾಗಿದೆ
|c|-ಮಾಡ್ಯುಲಸ್ ಆಫ್ ವೆಕ್ಟರ್ c

ವೆಕ್ಟರ್ ಮತ್ತು ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನಗಳನ್ನು ಬಳಸುವಾಗ, ಸಾಮಾನ್ಯ ಮೂಲಕ್ಕೆ ಕಡಿಮೆಯಾದ ವೆಕ್ಟರ್‌ಗಳ ಮೇಲೆ ನಿರ್ಮಿಸಲಾದ ಸಮಾನಾಂತರ ಪೈಪ್‌ನ ಪರಿಮಾಣವನ್ನು ನೀವು ಲೆಕ್ಕ ಹಾಕಬಹುದು a, bಮತ್ತು ಸಿ. ಮೂರು ವಾಹಕಗಳ ಅಂತಹ ಉತ್ಪನ್ನವನ್ನು ಮಿಶ್ರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
V=|a (b×c)|
ಈ ಪರಿಮಾಣವನ್ನು ಎರಡು ವಿಧಗಳಲ್ಲಿ ಕಾಣಬಹುದು ಎಂದು ಅಂಕಿ ತೋರಿಸುತ್ತದೆ: "ಸ್ಕೇಲಾರ್" ಮತ್ತು "ವೆಕ್ಟರ್" ಉತ್ಪನ್ನಗಳನ್ನು ಬದಲಾಯಿಸಿದಾಗಲೂ ಜ್ಯಾಮಿತೀಯ ಫಲಿತಾಂಶವನ್ನು ಸಂರಕ್ಷಿಸಲಾಗಿದೆ:
V=a×b c=a b×c

ಅಡ್ಡ ಉತ್ಪನ್ನದ ಪ್ರಮಾಣವು ಮೂಲ ವಾಹಕಗಳ ನಡುವಿನ ಕೋನದ ಸೈನ್ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಸ್ಕೇಲಾರ್ ಉತ್ಪನ್ನವನ್ನು "ಸಮಾನಾಂತರತೆಯ" ಪದವಿಯಂತೆ ನೋಡಬಹುದಾದಂತೆಯೇ, ಅಡ್ಡ ಉತ್ಪನ್ನವನ್ನು ವೆಕ್ಟರ್ಗಳ "ಲಂಬವಾದ" ಮಟ್ಟವೆಂದು ಗ್ರಹಿಸಬಹುದು. ”. ಮೂಲ ವೆಕ್ಟರ್‌ಗಳು ಲಂಬವಾಗಿದ್ದರೆ ಎರಡು ಯುನಿಟ್ ವೆಕ್ಟರ್‌ಗಳ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು 1 (ಯೂನಿಟ್ ವೆಕ್ಟರ್) ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ವೆಕ್ಟರ್‌ಗಳು ಸಮಾನಾಂತರ ಅಥವಾ ಆಂಟಿಪ್ಯಾರಲಲ್ ಆಗಿದ್ದರೆ 0 (ಶೂನ್ಯ ವೆಕ್ಟರ್) ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಕಾರ್ಟೀಸಿಯನ್ ನಿರ್ದೇಶಾಂಕಗಳಲ್ಲಿ ಅಡ್ಡ ಉತ್ಪನ್ನದ ಅಭಿವ್ಯಕ್ತಿ
ಎರಡು ವಾಹಕಗಳಾಗಿದ್ದರೆ ಎಮತ್ತು ಬಿಅವುಗಳ ಆಯತಾಕಾರದ ಕಾರ್ಟೇಶಿಯನ್ ನಿರ್ದೇಶಾಂಕಗಳಿಂದ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಅಥವಾ ಹೆಚ್ಚು ನಿಖರವಾಗಿ, ಆರ್ಥೋನಾರ್ಮಲ್ ಆಧಾರದ ಮೇಲೆ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ
a=(a x,a y,a z)
b=(b x ,b y ,b z)
ಮತ್ತು ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯು ಬಲಗೈಯಾಗಿರುತ್ತದೆ, ನಂತರ ಅವರ ವೆಕ್ಟರ್ ಉತ್ಪನ್ನವು ರೂಪವನ್ನು ಹೊಂದಿರುತ್ತದೆ
=(a y b z -a z b y ,a z b x -a x b z ,a x b y -a y b x)
ಈ ಸೂತ್ರವನ್ನು ನೆನಪಿಟ್ಟುಕೊಳ್ಳಲು:
i =∑ε ijk a jb k
ಎಲ್ಲಿ ε ijk- ಲೆವಿ-ಸಿವಿಟಾದ ಚಿಹ್ನೆ.